1. Introduction
In the past decades, the cooperative control problem of multiagent systems [
1,
2] has been extensively studied due to its wide applications in many engineering fields, e.g., multirobot cooperative control, formation control of unmanned aerial vehicles, traffic control, smart grid, and so on. As a fundamental problem of distributed cooperative control, consensus problem requires all agents to reach an agreement on the states of interest, and various consensus problems have been thoroughly studied, such as leader-following consensus [
3], group consensus [
4], finite-time consensus [
5], and so on.
Iterative learning control (ILC), a classic learning control strategy, is designed to improve tracking performance by applying information obtained from the past control experiment [
6,
7,
8]. The current input signal is usually generated by the previous input signal plus the tracking error (either the derivative of tracking error or the integral of the tracking error). ILC is used to accomplish control tasks that repeat on finite-time intervals, and it does not require an accurate system model. Due to this attractive feature of ILC, it has been widely used in practical systems and engineering practice, for example, industrial robots that perform repetitive tasks such as welding and handling [
9], servo systems whose command signals are periodic functions [
10], etc.
Many industry issues require repeated execution and coordination among several subsystems, for example, cooperative control of several robotic arms on an industrial production line. Recently, the consensus tracking problem of multiagent systems by ILC strategy has attracted the attention of researchers, since many industry issues can be solved under the ILC algorithm [
11,
12,
13,
14]. Unfortunately, existing results on consensus problems by ILC algorithm are mostly given for homogeneous multiagent systems, of which all the agents have the same dynamics. In some real engineering applications subjected to various restrictions or to reach the goals with lowest costs, the dynamics of cooperating agents are required to be distinct, e.g., coordination control of unmanned aerial vehicles and unmanned ground vehicles, so the study on heterogeneous multiagent systems is more practical and meaningful. Yang et al. [
15] proposed an ILC algorithm to solve the consensus tracking problems of homogeneous and heterogeneous multiagent systems, respectively, and the output consensus conditions have been obtained based on the concept of graph-dependent matrix norm. Li [
16] considered a heterogeneous multiagent system composed of first- and second-order dynamics, and the leader was assumed to have second-order dynamics. Different protocols have been designed for the heterogeneous following agents, so that all the following agents tracked the state of the leader asymptotically [
16].
As an important evaluation index of the ILC algorithm, the convergence rate refers to the speed at which the multiagent systems approach the reference trajectory, and has stimulated research interest for a long time. In order to accelerate the convergence rate of the ILC algorithm, taking the proportional differential (PD)-type learning law as an example, an acceleration correction algorithm with variable gain and adjustment of learning interval was designed for the linear time-invariant system [
17]. Tao et al. proposed an interpolating algorithm to regulate the reference trajectory in order to achieve faster convergence rate [
18]. The convergence rate of closed-loop ILC algorithm is obviously faster than that of open-loop ILC algorithm, due to real-time performance of closed-loop ILC algorithm [
19]. The convergence rate was greatly improved by introducing adaptive gains into the ILC algorithm [
20]. Sun et al. used the terminal converging strategy for ILC algorithm, and reached the finite-time convergence [
21]. For the consensus tracking problem of multiagent systems, Yang et al. proposed an ILC algorithm with input sharing, i.e., each agent exchanged its input information to the neighbors, and obtained a faster convergence rate [
22].
This paper focuses on the output consensus tracking problem of heterogeneous linear multiagent systems, in which the following agents are required to track the output trajectory of the leader. It is worth noting that the state dimensions of agents may be different, but the output must have the same dimension. In order to accelerate the consensus convergence rate of multiagent systems, a novel PD-type ILC consensus algorithm is proposed by using the fractional-power tracking error. Sufficient consensus condition, which depends on the control parameters, is obtained based on the operator theory.
2. Preliminaries
2.1. Digraph
In this paper, we study the consensus tracking problem via leader-following coordination control structure. The information flow among following agents forms a digraph
G [
23], and the leader is denoted by vertex 0.
The digraph composed of the following agents contains the vertex set , the edge set , and the adjacent matrix . A directed edge from i to j in G is denoted by , meaning that the node j can obtain information from the node i. Assume and for all . The set of neighbors of node i is denoted by . The Laplacian matrix of the digraph G is defined as , where is the degree matrix. In the digraph G, a directed path from node to node is a sequence of ordered edges of the form , where . A digraph is said to have a spanning tree if there exists a node that forms a directed path from this node to every other node.
Then, the interconnection among all agents is characterized by a compound digraph , and the coupling weight of the ith following agent to the leader is denoted by . if agent i can obtain information from the leader; otherwise . Besides, let .
Through this paper, we take into account the following topology.
Assumption 1. The interconnection topology of the following agents and the leader contains a spanning tree with the leader being its root.
Under Assumption 1, the eigenvalues of
all have positive real parts [
24].
2.2. Critical Definitions
Definition 1. For a given vector , is any vector norm. For any matrix , is the matrix norm induced by the vector norm. In particular, , , and , where is the spectral radius. For all matrices , , and , the following property is satisfied. Definition 2. [21] If a function s.t.where , then is Hölder continuous in region D. 2.3. Consensus Tracking Problem
The consensus tracking problem analyzed in this paper requires that spatially separative agents track a desired reference trajectory via cooperative control, and we take the ILC strategies for each agent. Additionally, we take into account a class of linear heterogeneous multiagent systems, and the dynamics of agent
i are in the following form at the
kth iteration.
where
,
, and
are the state and control input and output, respectively, of the agent
i,
,
, and
are matrices with proper dimension. The states of agents are different, because this paper studies the consensus problem of heterogeneous multiagent systems, which were mentioned in the article [
15]. Since this paper deal with the output tracking problem, the output dimensions of all agents must be consistent with the reference trajectory in order to facilitate comparison with the reference trajectory.
The reference trajectory
is defined on a time interval
, which is regarded as the leader’s output trajectory. In the distributed coordination control framework, the leader’s output trajectory
is only accessed by a subset of the following agents, and the left agents reach the leader’s trajectory indirectly. The control objective is to design a new ILC algorithm so that the output signals of all following agents converge to the reference trajectory
asymptotically, i.e.,
Remark 1. The leader in this paper is a virtual leader, i.e., the reference trajectory is generated by the virtual leader, but the leader does not actually exist, so there will be no collision between the leader and the following agents. Moreover, we assume that there will be no collision between all followers, and we avoid collision by placing all followers in a reasonable position. For example, system (2) formulates the dynamics of a robot in industrial production lines, the output denotes the angle of the robot’s joints, and the robots will not have collision problems due to their judicious distance.
3. Design And Analysis of ILC Consensus Algorithm
Firstly, we define the tracking error of each agent as
and
where
and
are the tracking errors with the leader and neighboring agents, respectively, of agent
i at the
kth iteration.
Let
denotes the information received or measured of the agent
i at the
kth iteration, and we get
where
is the adjacency elements associated with the edges of the digraph, and
is the coupling weight of the
ith following agent to the leader.
In terms of ILC algorithm, the tracking error continues to decrease with increasing iteration number, and the convergence rate will be slow when the tracking error is small. Hence, we are encouraged to appropriately amplifying the tracking error when the tracking error is small; the following agents can track the leader’s trajectory more quickly.
In this paper, we adopt the PD type ILC consensus algorithm and introduce a fractional-power proportional part as follows,
where
,
are the learning gains,
, and the sign function
is defined as
Moreover, the concrete steps of the algorithm (
6) are shown in Algorithm 1.
| Algorithm 1 Iterative learning control (ILC) consensus algorithm based on fractional-power error signals |
Parameters: agent i, iteration index k, , , ,,
Input: the reference trajectory
Output: the control input
1: initialize the iteration index k=1
2: while ()
3: initialize the initial state
4: calculate the output by the Equation (2),
5: calculate the tracking errors of each agent by the Equation (3),
6: calculate the tracking errors with the neighboring agents by the Equation (4),
7: calculate by the Equation (5)
8: if k=1
9: else
10: end if
11: set k=k+1
12: end while
13: print the control input |
Remark 2. Mishra et al. [
23]
used the sliding mode control to solve the finite-time consensus problem, where the sign function is used to force the state trajectories onto the sliding surface from any arbitrary initial location in the phase plane. However, the sign function in this paper is to extract the sign of the tracking errors, and then take fractional-power of the absolute value of the tracking errors. Fractional-power tracking errors can accelerate the convergence rate when the tracking errors are small. Then, it is obtained from (
3) and (
4) that
and then (
5) turns to be
Remark 3. It should be pointed out that, in order to ensure the convergence of the multiagent systems, α is in the range of 0 to 1 and cannot be too small.
Let
,
, and the systems (
2) are written in the compact-vector form as
where
,
and
. Defining
and
, and Equation (
8) can be written as
where
, and
L is the Laplacian matrix of
G.
Next, we define the following operators
and
,
and
Consequently, the compact-vector version of algorithm (
6) is
where
, and
.
Substituting (
10) into (
13), we have
To realize the consensus tracking, we need the following assumption on the initial states of agents.
Assumption A2. The initial tracking error resetting condition is satisfied for all agents, i.e., .
Now, we go to the main result, and some important lemmas are listed first.
Lemma 1. [25] Let , , and be a real valued continuous function on , and , ifthen, Lemma 2. [25] Let be a constant sequence that converges to zero. Define an operator: satisfyingwhere is a constant, and the norm of r dimensional vector takes the maximum value. Suppose that is a continuous function matrix of dimension, and let satisfyThen, holds uniformly with t, if . Theorem 1. Consider the heterogeneous multiagent systems (2) with the novel PD-type ILC consensus algorithm (6). With Assumptions 1 and 2, the following agents track the leader’s trajectory as , i.e., , if the following inequality holds, Proof. Available from Assumption 2, we have
. Take integral operation of dynamical system (
9) with (
14), and we get
Then, taking norms on two sides of (
16) yields
With Lemma 1 , Equation (
17) becomes
where
is a continuous vector function.
According to the Hölder continuity of the vector function, there is a constant
such that the following formulation holds,
Deduce from (
19) and (
18) that
where
Next, we analyze the tracking error, and it follows from (
3) that
Recursively, following (
16) yields
To recall Lemma 2, we define the following operators;
and
,
and
It is obvious that
P and
satisfy the definitions in Lemma 2.
Referring to Equations (
25) and (
26), Equation (
24) becomes
Take the norm of both sides of Equation (
26), and we substitute Equations (
19) and (
21) into it. Then, we get
where
. Consequently, operator
satisfies the condition of the operator defined in Lemma 2.
Based on Lemma 2, we can conclude from (
27) and (
29) that
if
. Hence, we complete the proof of Theorem 1. □
In the following, we consider two simple special cases for the heterogeneous multiagent systems (
2) and ILC consensus algorithm (
6).
Corollary 1. Consider the heterogeneous multiagent systems (2) with algorithm (6), and suppose that , where is a constant. With Assumptions 1 and 2, the following agents track the leader’s trajectory with as , if there exists a positive constant satisfying thatwhere are eigenvalues of . Proof. When
, the convergence condition in Theorem 1 becomes
Under Assumption 1,
a nonsingular matrix, and its eigenvalues have positive real parts [
24]. Therefore, the convergence condition of the spectral radius in Theorem 1 is simplified as the convergence condition of the eigenvalues. □
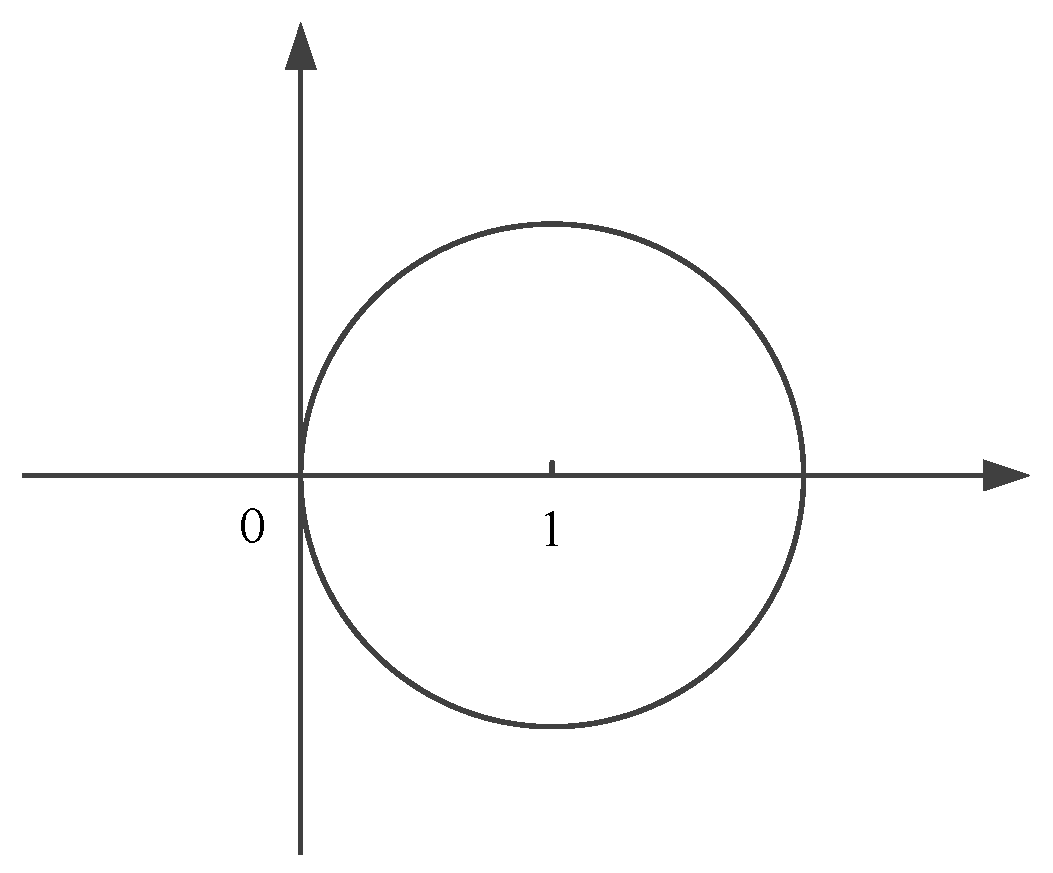
Condition (
30) requires that
lie in the circle shown in
Figure 1.
Additionally, we can get a more conservative distributed conditions when the topology is symmetric, i.e., .
Corollary 2. For heterogeneous multiagent system (2) with algorithm (6), we suppose that , where is a constant. Assume that the topology of agents (2) and leader is symmetric and has a spanning tree rooted at the leader. With Assumption 2, if there exists a positive constant satisfying thatthe following agents track the leader’s trajectory with as . Proof. With Assumptions in Corollary 2, the condition (
30) equals
Using the Gershgorin disk theorem for matrix
to estimate the eigenvalue, we get the condition (
32). □
4. Simulation And Discussion
In order to verify the efficiency of our proposed consensus algorithm, we consider a system consisting of the six heterogeneous following agents, given by
The leader’s trajectory is chosen as
.
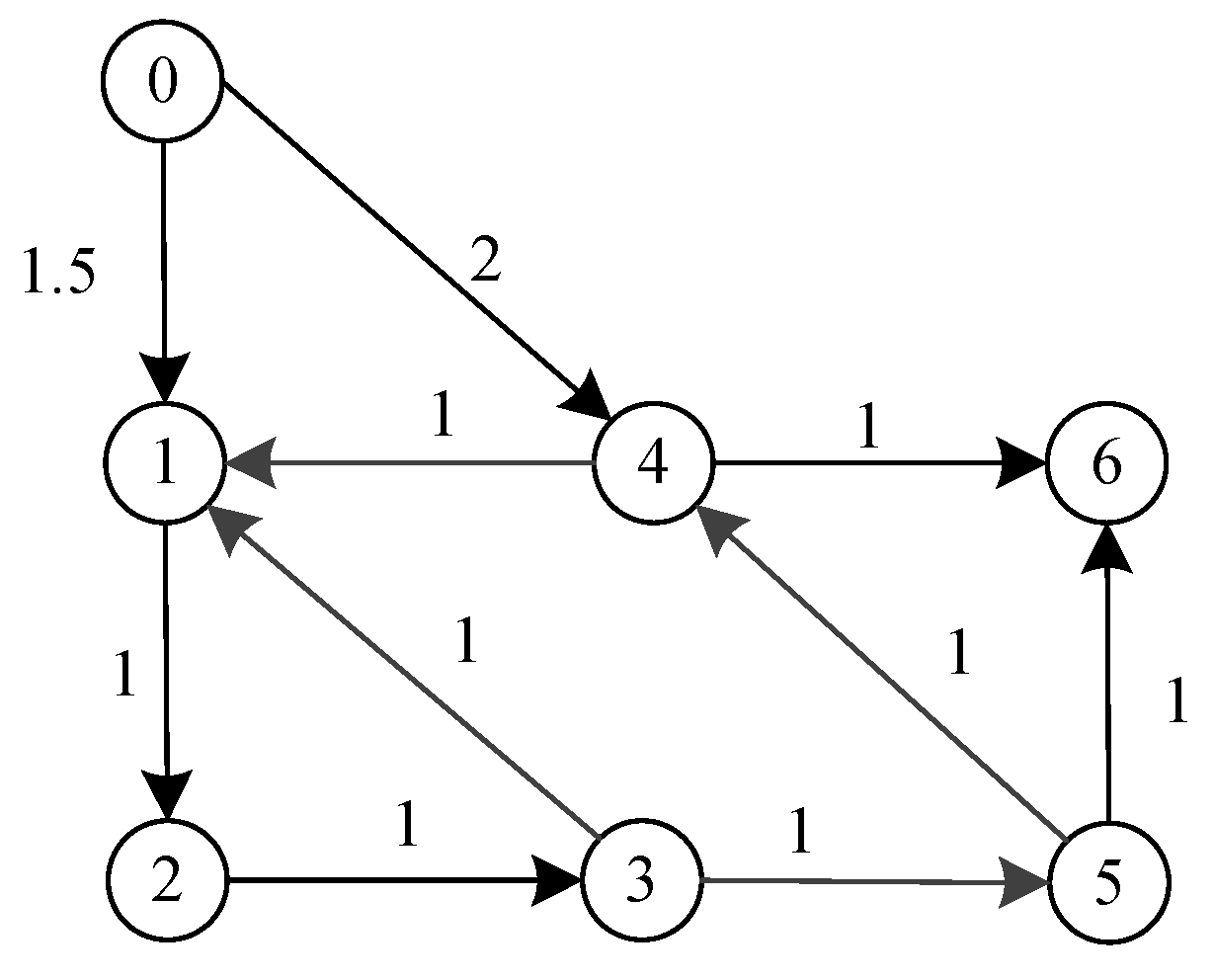
The digraph formed by the six following agents and the leader is shown in
Figure 2, where vertex 0 represents the leader and the vertices 1–6 represent the following agents.
The Laplacian for six following agents is
and
, so the eigenvalues of
are
.
The parameters of fractional-power ILC algorithm (
14) are chosen as
and
, and it is easy to verify that
, i.e., these parameters chosen above satisfy the condition (
15) of Theorem 1.
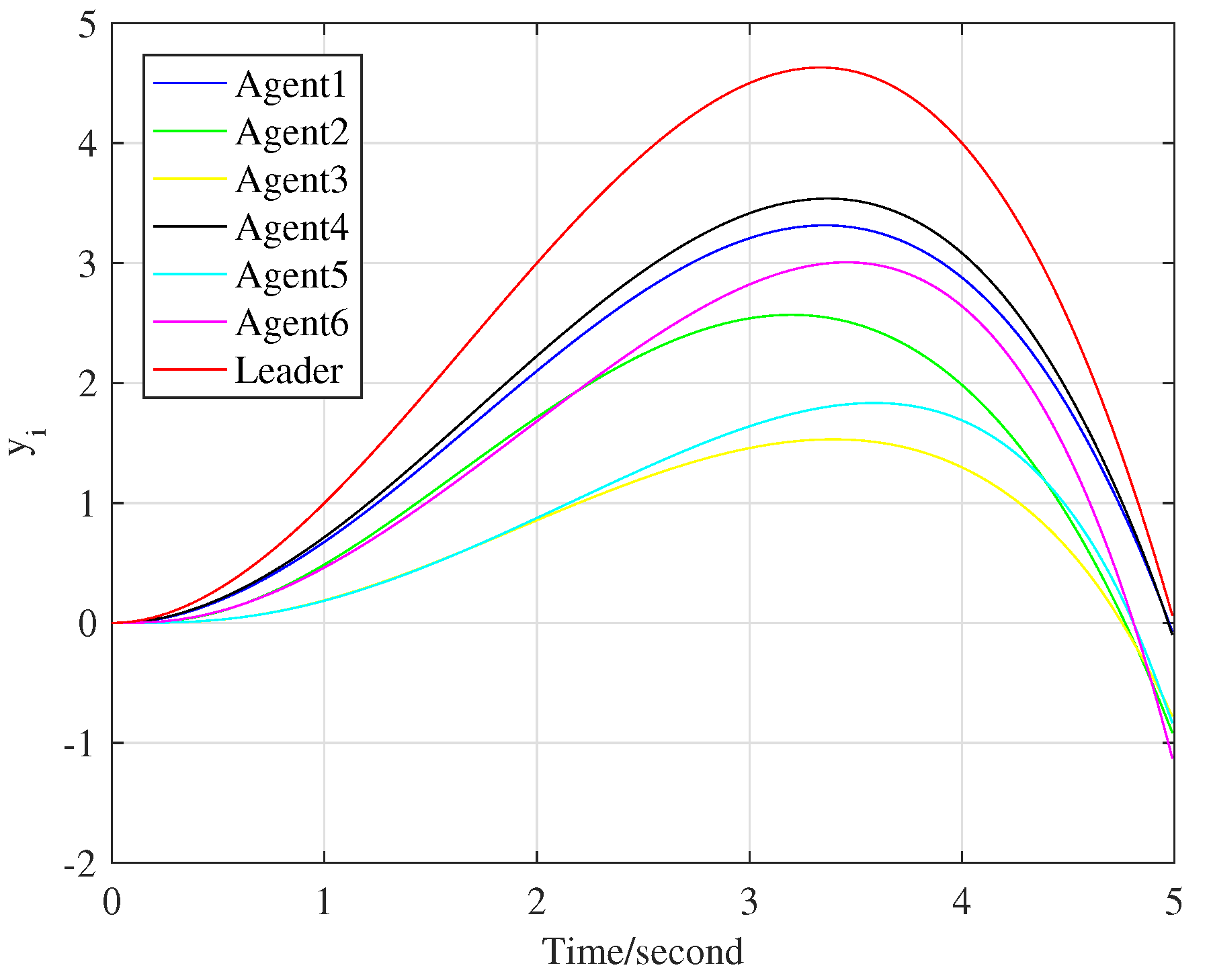
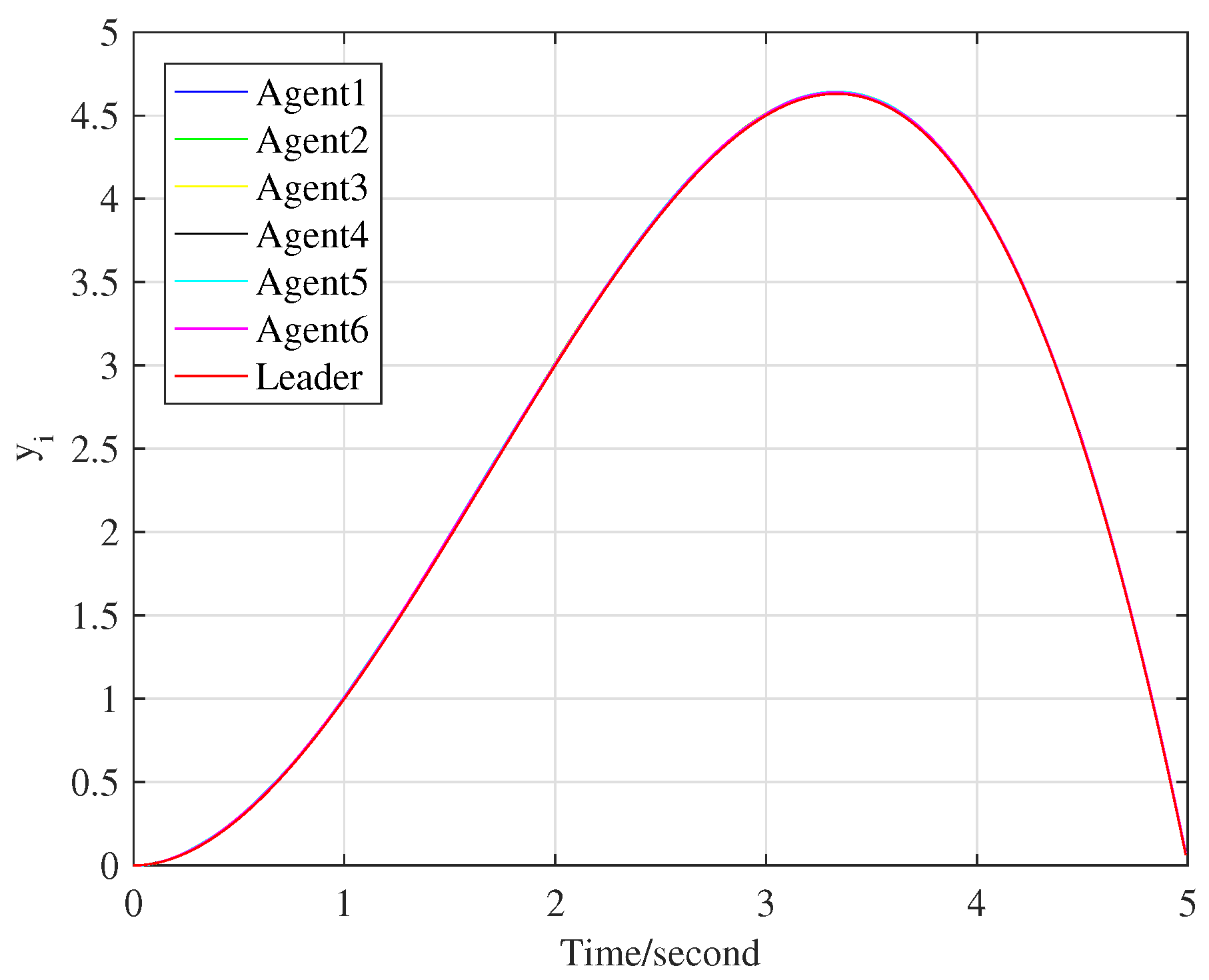
It is seen from Assumption 2 that the initial tracking errors are assumed to be zero, so all agents are reset to the same initial position after each iteration. The control input signals for the first iteration of all agents are set to 0.
We choose
as
, and the tracking processes at the 10th and 70th iteration are represented by
Figure 3 and
Figure 4, respectively.
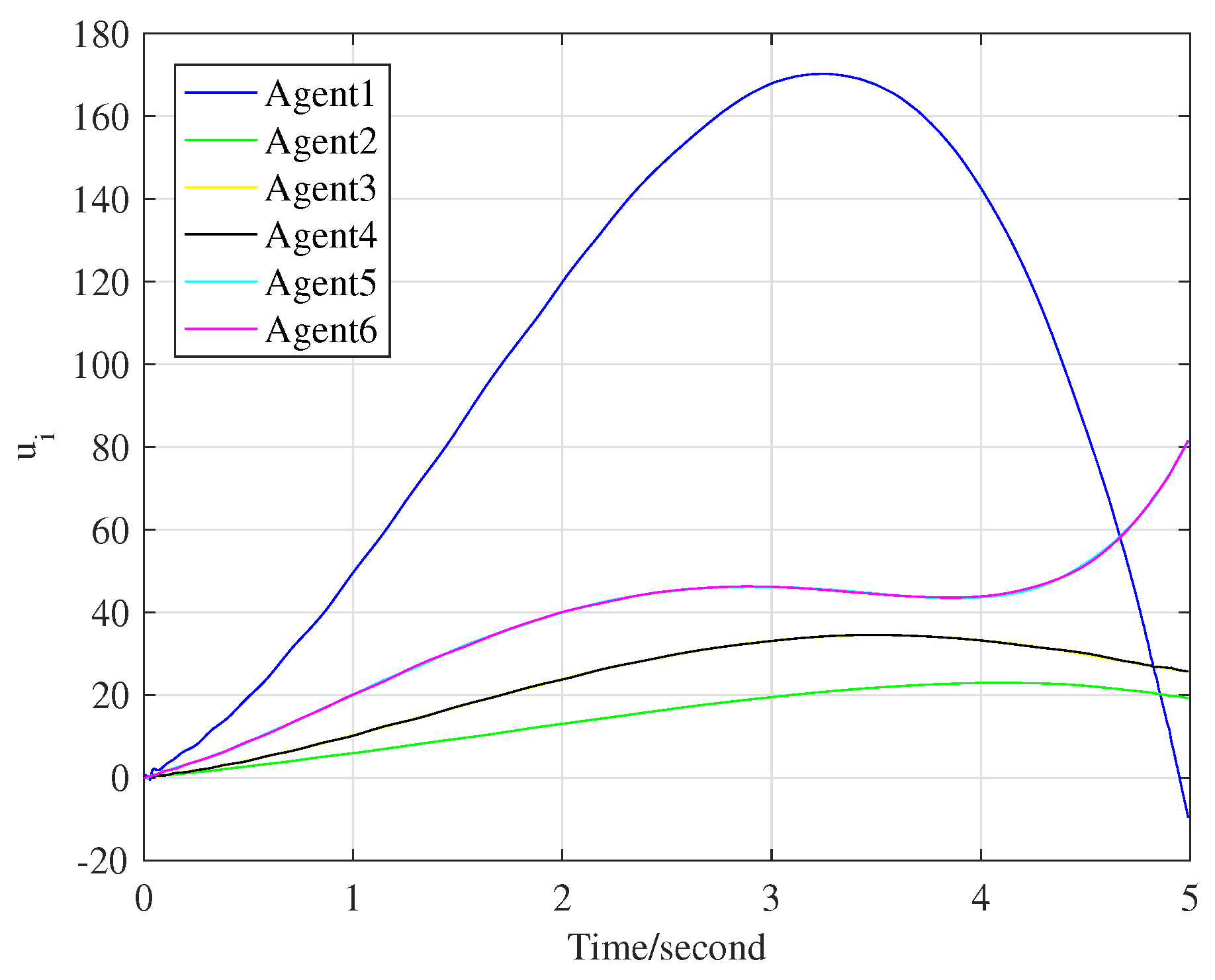
Figure 5 shows the control input signals when the six following agents fully track the leader’s trajectory. In addition,
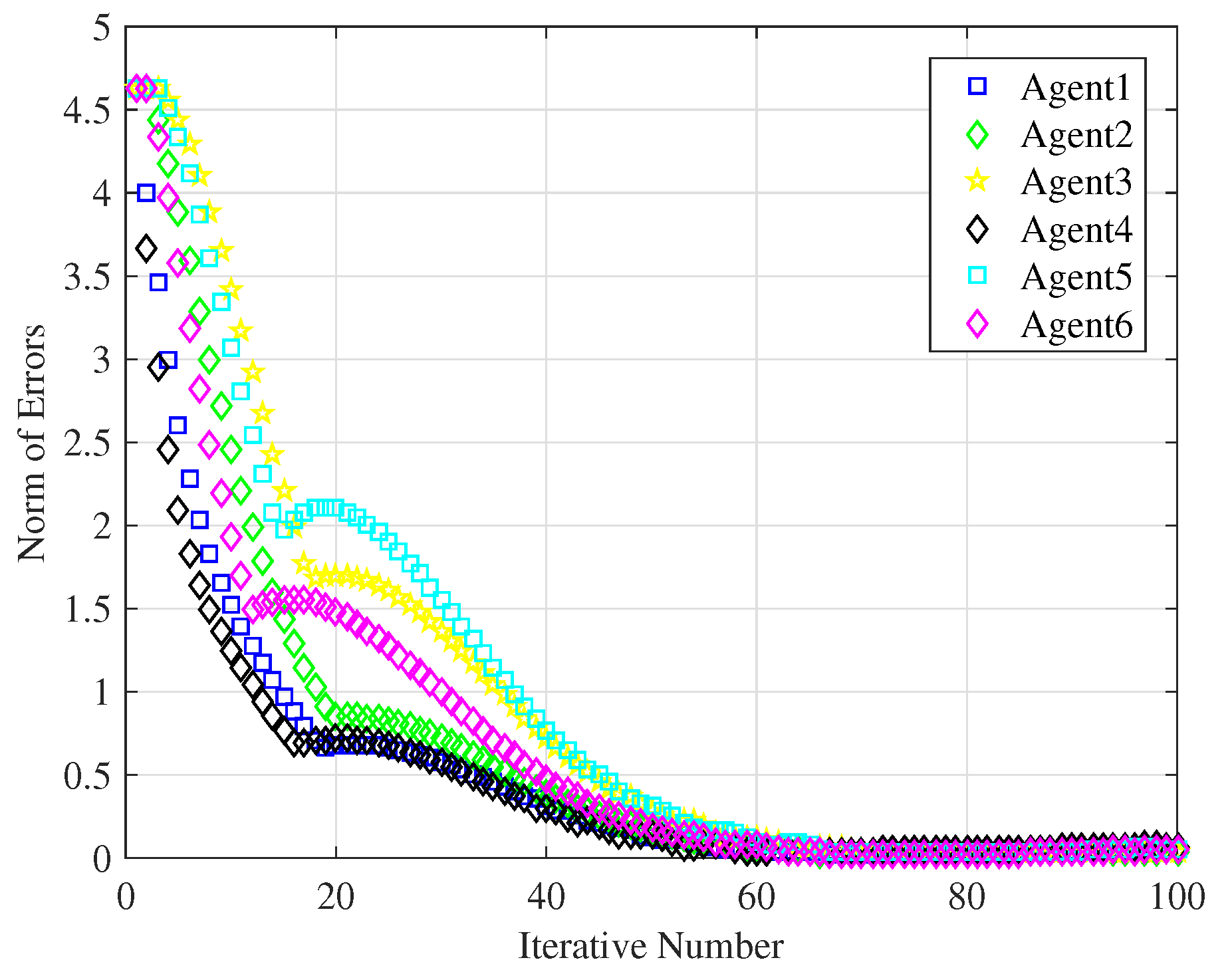
Figure 6 illustrates the evolution of each agent’s tracking error
. Set
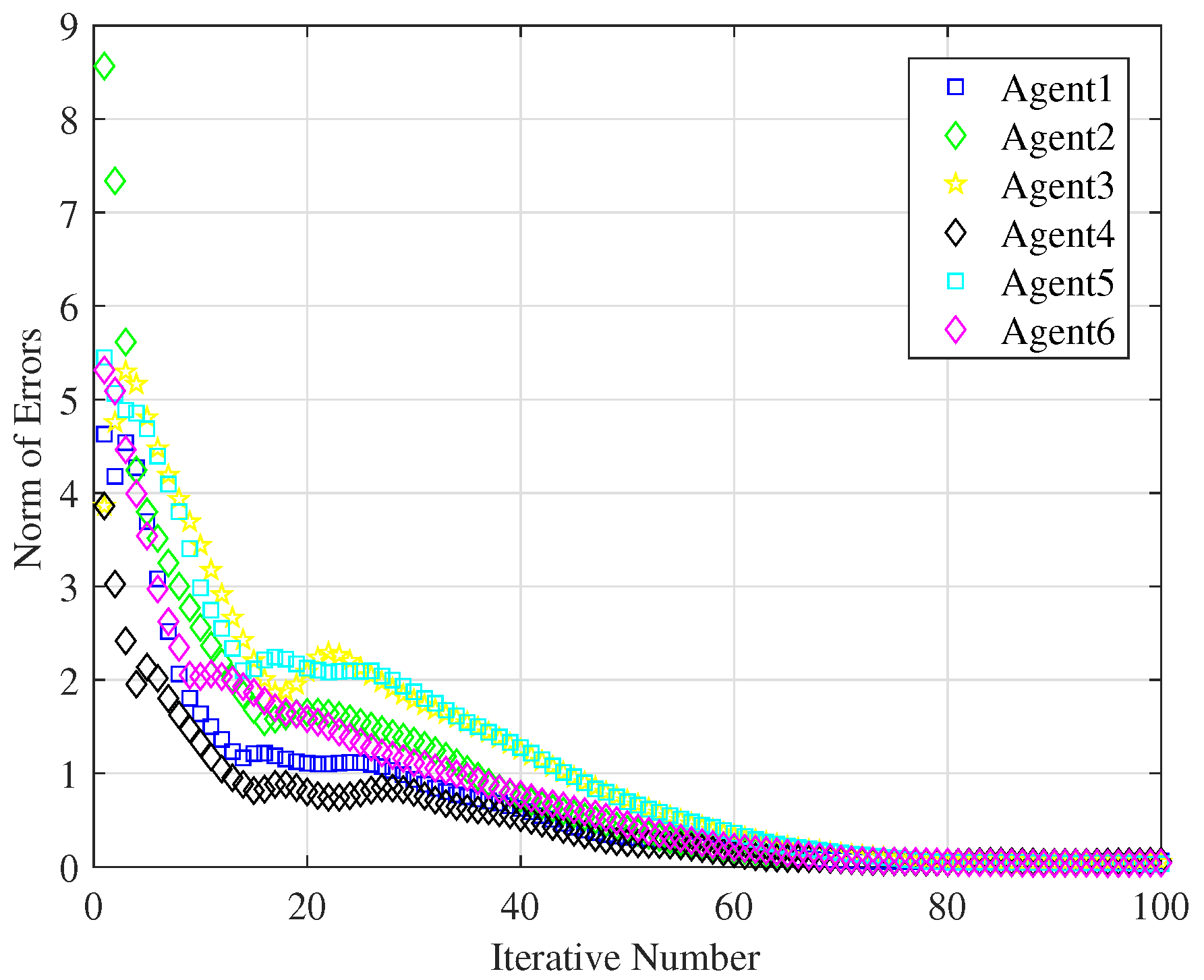
as the precision requirement,
Figure 6 clearly shows that all the following agents track the leader’s trajectory when the iteration reaches 70 times.
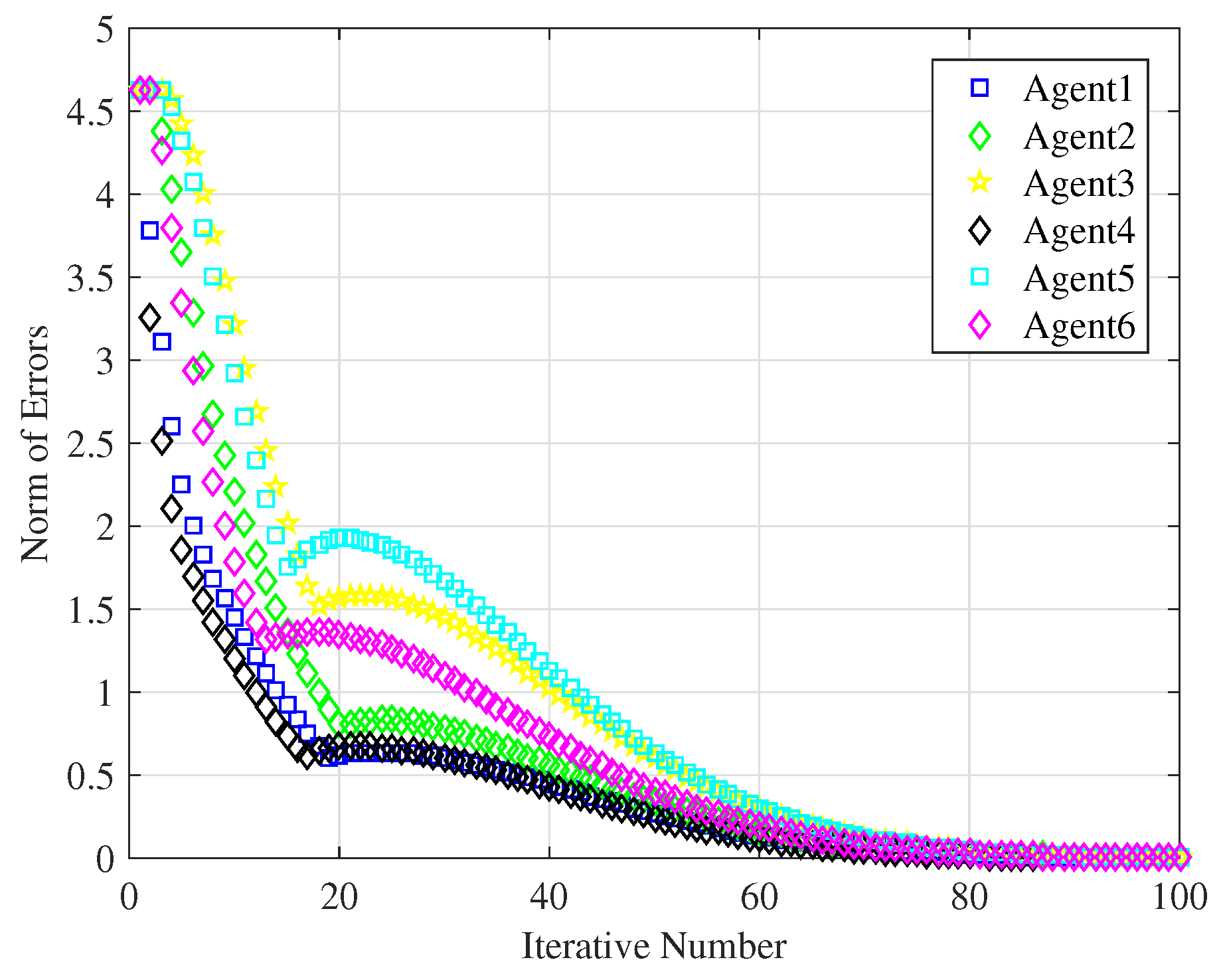
Then, we choose
; other parameters remain unchanged.
Figure 7 shows the tracking errors of the six following agents, and the novel ILC consensus algorithm needs to iterate 80 times so that all agents completely track the leader’s trajectory with
. Obviously, selecting different control parameters yields distinct consensus convergence rate, and how to get the best control parameters for the algorithm could refer to the main idea of the agent-based simulator for tourist urban routes in the work by the authors of [
26].
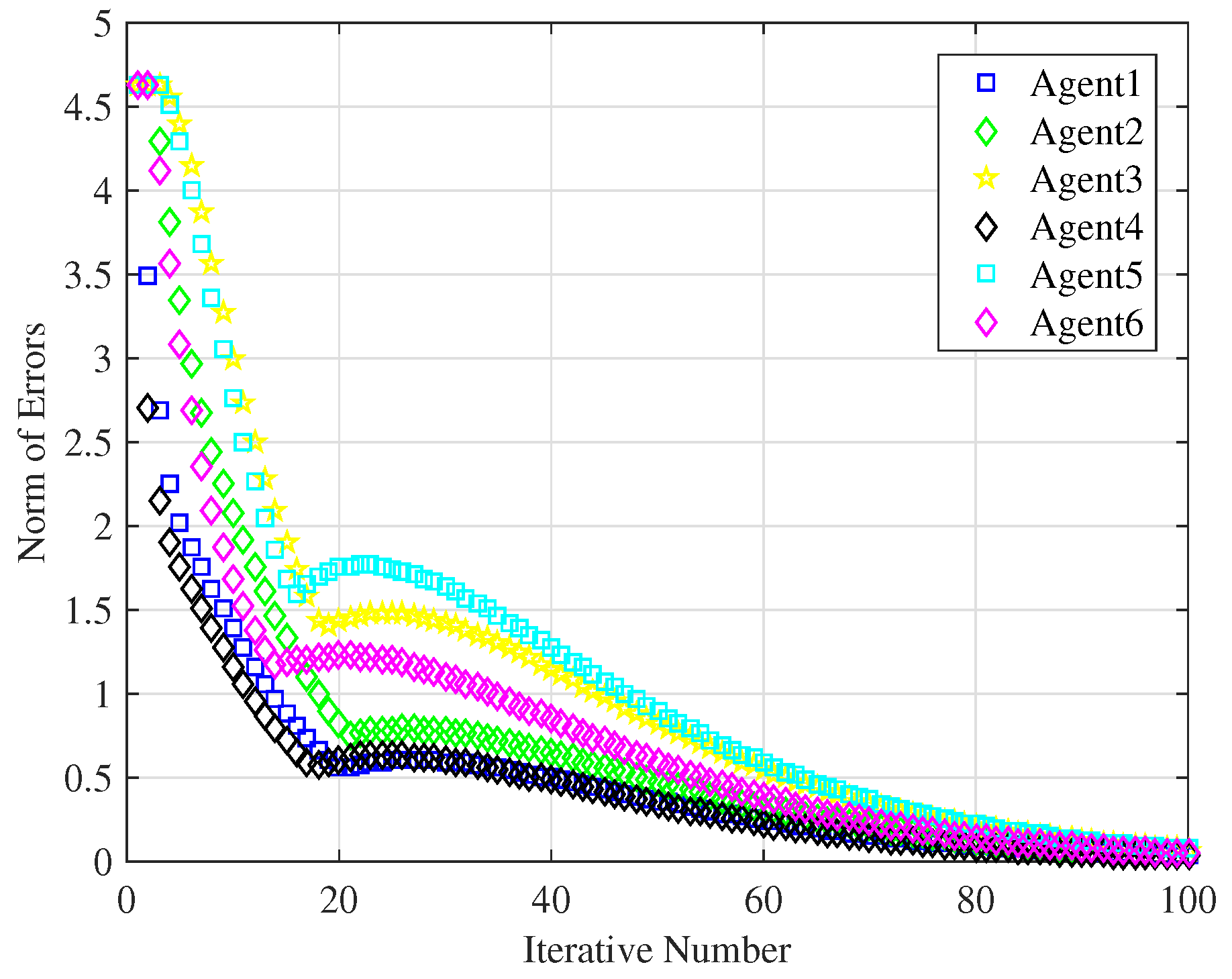
In order to compare the tracking performance of the novel ILC consensus algorithm based on fractional-power error signals with that of the traditional PD-type ILC algorithm, we choose
, so the algorithm (
14) is converted into the traditional PD-type ILC algorithm. In
Figure 8, all agents with the traditional ILC algorithm completely track the leader’s trajectory after the 100th iteration, but the convergence rate is slower than that of the ILC algorithm based on fractional-power error signals with
. As discussed above, it is discovered that fractional-power error signals show beneficial influences on the convergence rate.
In order to consider the external environmental effects, as well as model uncertainties of the multiagent systems, we use the following model to illustrate the robustness of the proposed ILC algorithm.
where
represents unmodeled dynamics and
denotes repetitive disturbance. Choose
,
,
,
,
,
,
,
,
; other parameters remain unchanged.
Figure 9 shows that the proposed ILC algorithm is sufficiently robust to model uncertainty and to repetitive disturbances.