Abstract
A rolling bearing is an important connecting part between rotating machines. It is susceptible to mechanical stress and wear, which affect the running state of bearings. In order to effectively identify the fault types and analyze the fault severity of rolling bearings, a rolling bearing fault diagnosis method based on multiscale amplitude-aware permutation entropy (MAAPE) and random forest is proposed in this paper. The vibration signals of rolling bearings to be analyzed are decomposed into different coarse-grained time series by using the coarse-graining procedure in multiscale entropy, highlighting the fault dynamic characteristics of vibration signals at different scales. The fault features contained in the coarse-grained time series at different time scales are extracted by using amplitude-aware permutation entropy’s sensitive characteristics to signal amplitude and frequency changes to form fault feature vectors. The fault feature vector set is used to establish the random forest multi-classifier, and the fault type identification and fault severity analysis of rolling bearings is realized through random forest. In order to demonstrate the feasibility and effectiveness of the proposed method, experiments were fully conducted in this paper. The experimental results show that multiscale amplitude-aware permutation entropy can effectively extract fault features of rolling bearings from vibration signals, and the extracted feature vectors have high separability. Compared with other rolling bearing fault diagnosis methods, the proposed method not only has higher fault type identification accuracy, but also can analyze the fault severity of rolling bearings to some extent. The identification accuracy of four fault types is up to 96.0% and the fault recognition accuracy under different fault severity reached 92.8%.
1. Introduction
A bearing is one of the core components of rotating mechanical system. It is a highly standardized precision mechanical device, which has the advantages of low friction, easy assembly and use, and high work efficiency [1]. However, as a connection between rotating parts, the bearing should also bear a certain load as a supporting part. Therefore, in the use of the bearing, it is inevitably subjected to a series of physical effects such as mechanical stress and mechanical wear, which will lead to deformation and corrosion of the bearing over time, leading to changes in the running state of the bearing. Moreover, due to the imperfect production technology and improper operation and installation, the bearing will also produce artificial damage, and the accumulation and deepening of this damage eventually leads to the failure of bearing [2]. Rolling bearings are mainly composed of inner race, outer race, ball elements and retainer, and the fault types of bearings are generally shown in the form of several parts defects described above, among which the most common types of rolling bearings are the failure of inner race, outer race and ball elements. A bearing is also the most easily worn out part of motor. According to statistics, more than 40% of motor faults are related to a bearing [3,4]. Therefore, fault diagnosis of rolling bearings is of great significance to ensure the reliability and safety of rotating mechanical system.
At present, fault diagnosis methods based on different theories have been successfully applied to fault diagnosis of rolling bearings [5], such as vibration, acoustic noise [6,7], stator current, thermal-imaging, and multiple sensor fusion, etc. The fault diagnosis method based on vibration signal is one of the most commonly used fault diagnosis methods for rolling bearings in rotating machinery. Firstly, it is convenient to acquire vibration signal of a rolling bearing, and the cost of monitoring equipment based on vibrating sensors is low. Secondly, the vibration signal is not easily affected by external environment noise. A rolling bearing inevitably generates vibration along with rotation during operation. Vibration, as an external manifestation of a bearing’s own dynamic characteristics, contains rich state information and can reflect bearing fault information. When there is a failure period of the rolling bearing, the vibration signal usually contains some periodic pulse signal. The signal is collected by the vibrating sensor on the bearing base for further analysis and processing, so that the rolling bearing state change information can be obtained and the bearing fault type can be identified. In recent years, scholars in the field of fault diagnosis of rolling bearings based on vibration signal continue to explore, and made a lot of research results. However, there is still the problem of low fault identification accuracy due to insufficient fault feature extraction. Especially, the research of fault severity analysis is one of the urgent problems in this field.
According to the characteristics of vibration signal of rolling bearings, the fault diagnosis methods based on data-driven method, mathematical model and pattern recognition method are widely used [8,9]. Although the data-driven method is flexible in use, it is often used for fault detection and has low fault identification accuracy. The mathematical model-based method needs to model the running state of rolling bearings and accurately model different fault types to obtain better fault diagnosis results. Therefore, pattern recognition is one of the important fault diagnosis methods to analyze the vibration signal of a rolling bearing. It is mainly divided into two parts: effective feature extraction contained in vibration signal and classification of the fault features.
For feature extraction of a rolling bearing vibration signal, the time-frequency analysis has become a principal method to extract the fault characteristics of rolling bearings because the vibration signal is often non-stationary. Wavelet transform (WT) is one of the common time-frequency analysis methods to extract the fault characteristics of rolling bearing vibration signals [10]. The wavelet basis function and kernel parameters need to be predefined, and the different selection of them will influence the effect of feature extraction of vibration signals. Therefore, WT cannot be used to adaptively decompose the signal according to its time-frequency characteristics, which to some extent limits the practical application of WT in rolling bearing fault diagnosis [11]. Wavelet packet transform (WPT) is also a typical time-frequency analysis method for vibration signal of rolling bearings [1]. However, it is necessary to determine the wavelet basis function and the number of decomposition layers of wavelet packet before applying WPT. Improper selection of these will directly affect the effectiveness of wavelet packet decomposition, so that the hidden essential features in the signal cannot be revealed. Empirical mode decomposition (EMD) is a self-adapting time-frequency decomposition technique that was presented by Huang N. E. in 1998 [12]. EMD can adaptively decompose a nonlinear and non-stationary signal into a series of intrinsic mode functions (IMFs) containing signal characteristics of different frequencies. EMD combined with different entropy methods provides an effective method for fault feature extraction of rolling bearings [13,14,15,16]. However, EMD is prone to boundary effect and mode mixing problems in the practical application process, which will lead to poor feature extraction effect. In order to avoid the above problems in EMD, ensemble empirical mode decomposition (EEMD), complete ensemble empirical mode decomposition (CEEMD) and local mean decomposition (LMD) have been proposed successively and successfully applied to rolling bearing fault diagnosis [17,18,19,20,21,22]. Although the above methods in principle solve the boundary effect and mode mixing problem, these problems cannot be completely avoided in real-world application.
The methods based on entropy theory can measure the complexity of complex time series effectively that are often used as the feature extraction methods of rolling bearing vibration signal. The decomposed signals of the above time-frequency analysis methods can be measured by different entropy theories and constitute the feature vector. Complexity of time series can be obtained through several measures such as approximate entropy, sample entropy, energy entropy, permutation entropy and so on. As the calculation result of approximate entropy (ApEn) is excessively dependent on the data length, Richman and Moorman proposed an improved time series complexity measurement method called sample entropy (SampEn) [23]. However, ApEn and SampEn can only measure the complexity of time series from single scale. For many time series, only describing their complexity on a single scale will lose a lot of important information. To more fully describe the complexity of time series, Costa et al. proposed the concept of multiscale entropy (MSE) in 2002 [24]. Firstly, spatial scale segmentation of time series is carried out, and then the SampEn at each scale is calculated, so as to obtain the complexity of time series at different scales. In recent years, combining with the characteristics of other entropy theories, multiscale permutation entropy [25] and multiscale fuzzy entropy [26] have been proposed and successfully applied in the fault feature extraction of rolling bearings. Therefore, it can be seen that the coarse-grained process of MSE to decompose the vibration signal of rolling bearings and using the entropy theory to describe the fault characteristics of the decomposed signals has become an effective way to realize the fault feature extraction of rolling bearings. However, the feature extraction method based on multiscale permutation entropy and multiscale fuzzy entropy ignore the influence of the amplitude of element on entropy in time series, which will make the extracted features have greater randomness and affect the fault identification accuracy. Azami and Escudero proposed the Amplitude-aware permutation entropy (AAPE) to improve the sensitivity of PE to the amplitude and frequency of time series [27]. Different from the permutation entropy algorithm, AAPE algorithm takes into account the mean of signal amplitude and the deviation between amplitudes. In this paper, in order to effectively extract the fault characteristics of rolling bearings, multiscale amplitude-aware permutation entropy (MAAPE) is used to extract the fault features of rolling bearings.
For fault type identification, high performance multi-classifier is used to identify the extracted fault features to determine the fault type or fault severity of rolling bearings. B. Li et al. presented an approach for motor rolling bearing fault diagnosis using neural networks and time-frequency domain bearing vibration analysis [28]. At present, the commonly used artificial neural network includes radical basis function (RBF) neural network and conventional back-propagation (BP) neural network. However, it is difficult to determine the structure of the neural network, since the number of hidden layers is usually selected according to experience. In order to ensure high identification accuracy, a large number of samples are required for training neural network. Support vector machine (SVM) is suitable for solving the classification problem under small sample conditions and has high classification accuracy and good generalization capabilities. Nonetheless, SVM is a kind of binary classifier that needs to use a suitable binary tree to realize multi-classification in the application of multi-classification [11]. Moreover, kernel function selection and kernel parameter setting of SVM have great influence on the identification results. Random forest classifier is an ensemble classifier with high performance that is composed of multiple decision trees [29]. It uses the classification results of all decision trees to determine categories through voting principle. Random forests require very little manual intervention. It does not need to do feature selection or data collation, that is to say, it can determine the features according to the data, so as to simplify the design process of random forest itself. In addition, it usually does not need to preprocess the data in observation data dimension, so it can resist and detect the gross errors that often exist in the form of outlier data. It can maintain a good accuracy when a large proportion of data is lost, and provide the estimation of lost data to simplify its engineering application. Random forests have very fast computing speeds. Since each node of the tree is mainly given by comparison operation, and the amount of calculation is proportional to the depth of a tree, it is very fast to do classification or regression on the well-grown trees.
A fault diagnosis method of rolling bearings based on multiscale amplitude-aware permutation entropy and random forest is proposed in this paper. The vibration of rolling bearings presents the characteristics of periodic instantaneous impact, and the location of bearing failure will lead to different impact characteristics. In order to more fully extract the rolling bearing fault information contained in the vibration signal, using AAPE’s sensitivity to the amplitude and frequency changes of vibration signals, the AAPE values at different time scales are calculated as the feature vector, which improves the effectiveness of fault feature extraction. A multiple classifier based on random forests is established by the feature vectors composed of multiscale amplitude-aware permutation entropy to identify the fault type and fault severity of rolling bearings. The contributions of this paper can be summarized as follows:
- (1)
- In this paper, a fault diagnosis method of rolling bearings is presented. On the basis of accurately identifying the fault types of rolling bearings, the fault severity of rolling bearings can be analyzed.
- (2)
- Multiscale amplitude-aware permutation entropy is proposed for the first time, and it is successfully applied to fault feature extraction of rolling bearings.
- (3)
- The random forest multi-classifier is used to identify the fault feature of rolling bearings and analyze the fault severity, and the fault identification accuracy is high.
The rest of this paper is organized as follows. Section 2 introduces the basic principle of the theoretical methods adopted in this paper. The fault diagnosis method of rolling bearings is described in detail in the Section 3. Section 4 introduces the experimental platform and samples, and the experimental results of the proposed fault diagnosis method. Finally, Section 5 summarizes the research content and results of this paper, and prospects the future research content.
2. Methods
2.1. Multiscale Entropy
The MSE is composed of two steps: coarse-graining procedure and computation of SampEn [30].
(1) For the original time series with length , coarse granulation is carried out for the given embedded dimension and similarity tolerance , so as to form a new coarse-grained time series ,
where is scale factor. The coarse-graining procedure diagram of MSE is shown in Figure 1.
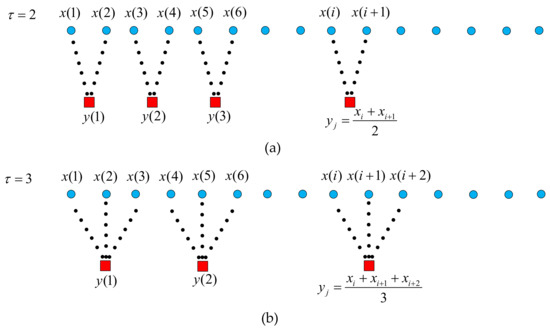
Figure 1.
Coarse-graining procedure diagram of multiscale entropy (MSE). (a) Scale factor ; (b) Scale factor .
(2) The sample entropy value of each coarse-grained time series is calculated, and the sample entropy of coarse-grained time series is expressed as scale factor function as shown below,
where similarity tolerance in which is the standard deviation of original time series . represents the sample entropy calculation function with scale factor , embedded dimension and similarity tolerance . The SampEn calculation process can be referred to Ref. [23].
2.2. Amplitude-Aware Permutation Entropy
Bandt proposed the concept of Permutation Entropy (PE) in 2002 [31]. Currently PE is widely used in the analysis of complex time series signals to measure the complexity of a nonlinear and non-stationary signal.
Suppose a given time series , and for each time point , embed signal into d-dimensional space to obtain reconstructed vector , where and represent embedded dimension and time delay, respectively. The magnitude of elements in each vector is arranged in ascending order, namely , where represents the order of elements in the reconstructed vector . Therefore, when the embedding dimension is , there are a total of permutations, and the th permutation order is demoted as .
The occurrence probability of is expressed as:
where is a function of counting the number of occurrences of the permutation order . Whenever the permutation order of the elements inside is , increases by 1. The definition of permutation entropy is as follows,
However, there are two main problems in describing complex time series by permutation entropy. First, traditional PE only considers the order of time series amplitude, but ignores the amplitude information of the corresponding elements in the time series. Second, the effect of elements with equal amplitude on PE value in time series is not clearly explained.
In view of this, literature [27] proposed AAPE to increase PE’s sensitivity to amplitude and frequency of time series. Different from the PE algorithm, AAPE algorithm considers the mean value of signal amplitudes and the deviation between amplitudes, and introduces the counting rule of replacing in PE with relatively normalized probability.
Assuming that the initial value of is 0, for the time series in the process of increasing from 1 to , whenever the permutation order is , has to be updated.
where, is the adjustment coefficient, and the weight of signal amplitude mean and amplitude deviation is adjusted, generally 0.5. So, is the probability of appearing in the whole time series.
The AAPE value of time series is expressed as
2.3. Random Forest
Random forest (RF) was proposed in 2001 by Breiman, an academician of the national academy of sciences. This algorithm is suitable for solving prediction and classification problems. RF integrates multiple weak classifiers and consists of many decision trees. Its output results are determined by voting principle according to the predicted results of each decision tree in the forest. The basic principle of RF is as follows:
Assuming that the RF classifier is composed of multiple decision trees , stands for random vectors that are independent and identically distributed. The training sample set of the random forest classifier is expressed as , where represents that the th training sample has eigenvalues, and represents the corresponding label of training sample . The training sample set is sampled for times with Bootstrap, and Bootstrap subsample . For each subsample , decision tree model (CART decision tree is generally used) is constructed, and finally a decision tree classifier composed of a group of decision trees is obtained. For a new test sample, the category that gets the most votes through decision trees is taken as the final category of the test sample. The classification decision is as follows:
where represents the th decision tree, is indicative function, that is, the value is 1 when this number is in the set, otherwise the value is 0, and represents the target variable formed by category label .
3. The Proposed Fault Diagnosis Method for Rolling Bearings
This paper presents a fault diagnosis method for rolling bearings based on multiscale amplitude-aware permutation entropy and random forest. Multiscale amplitude-aware permutation entropy is able to extract the fault features of rolling bearing vibration signal at different time scales. Random forest is established by the different fault features to identify the fault type of rolling bearings and analyze its fault severity. The proposed fault diagnosis method for rolling bearings consists of two main processes: training process and testing process. The principle diagram of proposed fault diagnosis method for rolling bearings is shown in Figure 2.
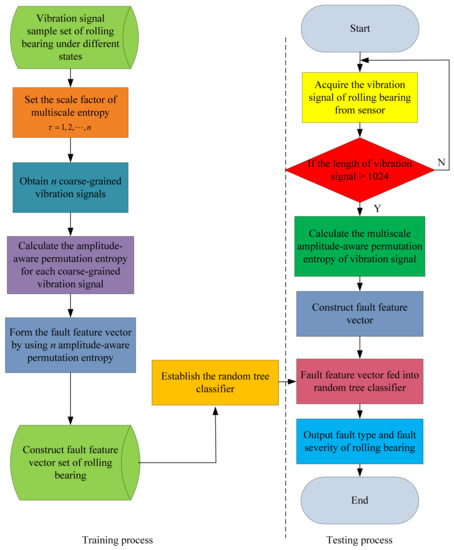
Figure 2.
The principle diagram of proposed fault diagnosis method for rolling bearings.
In the training process, the vibration signal sample set of rolling bearings under different states is used to extract the fault feature vectors that can establish the random forest classifier to identify the fault type of rolling bearings. In the testing process, the vibration signal of rolling bearings can be analyzed by the proposed fault diagnosis method, and the fault type and fault severity can be obtained. The main steps of proposed fault diagnosis method are as follows:
In order to ensure the effectiveness of fault diagnosis methods, sufficient samples of rolling bearing vibration signals under different fault states should be collected. These vibration signals construct the vibration signal set.
- (1)
- Set the scale factor of rolling bearings, and coarse-grained vibration signals are obtained for each vibration signal in the set.
- (2)
- For each coarse-grained vibration signal, calculate amplitude-aware permutation entropy values to construct the fault feature vector.
- (3)
- The fault feature vector set is constructed by the fault feature vectors extracted by Step (3).
- (4)
- The random tree classifier is established by the fault feature vector set.
- (5)
- The testing vibration signal can be analyzed by the proposed method and get the fault type and fault severity of rolling bearings.
4. Experiments and Results
4.1. Experimental Setup
In this paper, the rolling bearing fault data set provided by the Case Western Reserve University Bearing Data Center is used to verify the proposed fault diagnosis method [32,33,34]. In the experiment, Svenska Kullager-Fabriken (SKF) rolling bearing was taken as the research object. The data set collected the rolling bearing vibration signals in four states: normal (NM), inner race (IR) fault, outer race (OR) fault and ball elements (BE) fault through the acceleration sensor. The sampling frequency was 12 kHz for the three types of faults, with diameters of 7 mils, 14 mils and 21 mils that were selected for data acquisition.
The time-domain waveforms of rolling bearing vibration signals with different types and fault severity under 0 load are shown in Figure 3. It can be seen that changes in fault types and fault severity are correlated with changes in amplitude and frequency of vibration signals. Table 1 shows the composition of fault types and fault severity in the experimental sample set, which includes 10 different rolling bearing health states. Each rolling bearing vibration signal is divided into multiple data samples without overlapping, and each sample contains 1024 sampling points to form the experimental data set composed of 50 samples in each healthy state. Among them, 10 samples in each healthy state were used as training set and 40 samples as test set.
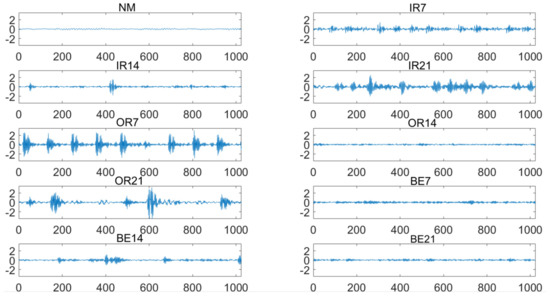
Figure 3.
The time-domain waveforms of rolling bearing vibration signals with different types and fault severity under 0 load.

Table 1.
The composition of fault types and fault severity in the experimental sample set.
4.2. Experimental Results
The MAAPE-based fault feature extraction method proposed in this paper can extract fault features contained in rolling bearing vibration signals at different scales. In order to highlight the fault characteristics in different time scales of vibration, the scale factor is set as 20 in the experiments of this paper since a too large τ will affect the computation efficiency, while a too small τ cannot extract enough information [26]. The MAAPE feature values of rolling bearing vibration signal under normal condition is shown in Figure 4. From Figure 4, there are obvious differences in the MAAPE feature values at the different scales. AAPE can describe the amplitude and frequency characteristics of vibration signals at different time scales. The characteristics of vibration signals in different time scales are different, which can highlight the fault characteristics more comprehensively.
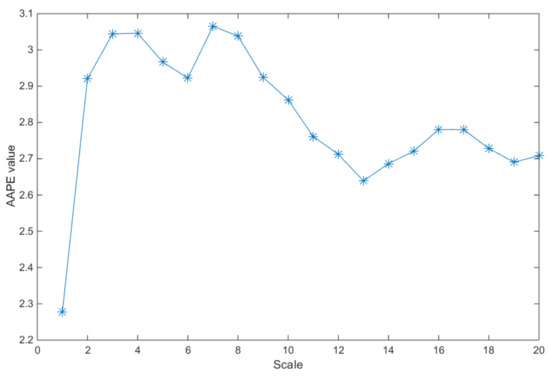
Figure 4.
MAAPE feature values of rolling bearing vibration signal under normal condition.
Figure 5 shows the MAAPE feature values of rolling bearing vibration signal under inner race fault condition with different loads. As shown in Figure 5, although the failure size of the inner race is the same and the trend of AAPE values under different scale factors is basically consistent, there are obvious differences in the MAAPE features of rolling bearing vibration signals under different loads. Under different loads, the MAAPE fault feature extraction method can describe the characteristics of vibration signals. In addition, as shown in Figure 4 and Figure 5, it can be seen that in the case of failure, the MAAPE feature extraction method can effectively describe the characteristics of vibration signals under inner race fault condition, and has obvious separability.
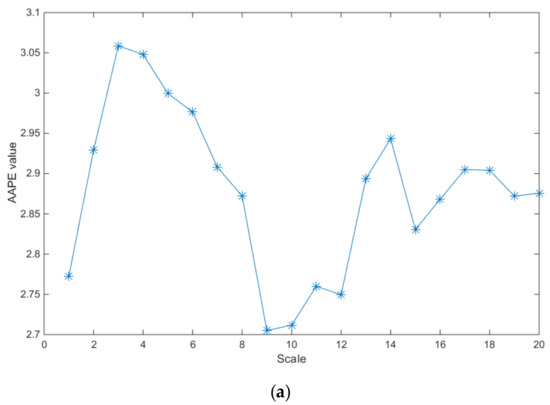
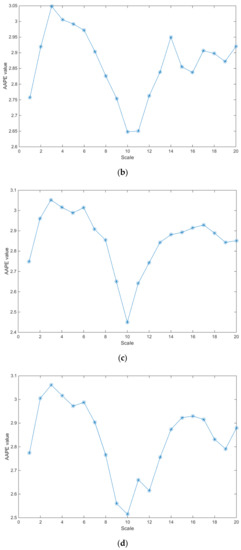
Figure 5.
MAAPE feature values of rolling bearing vibration signal under inner race fault condition with different loads. (a) Inner race fault, 7 mils, with load 0 hp. (b) Inner race fault, 7 mils, with load 1 hp. (c) Inner race fault, 7 mils, with load 2 hp. (d) Inner race fault, 7 mils, with load 3 hp.
MAAPE feature values of rolling bearing vibration signal under different fault conditions with the same loads are shown in Figure 6. It can be seen that under the same load conditions, although the size of faults is the same, the fault feature vectors extracted by MAAPE have obvious differences. Therefore, MAAPE can effectively extract the feature vector of vibration signals of rolling bearings with different fault types, and the difference of feature vectors is obvious. The fault feature extraction method based on MAAPE proposed in this paper has a good effect on fault feature description.
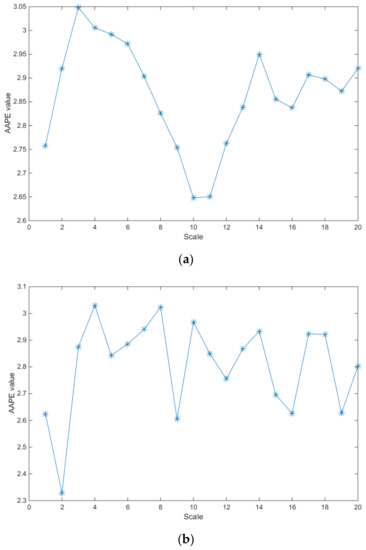
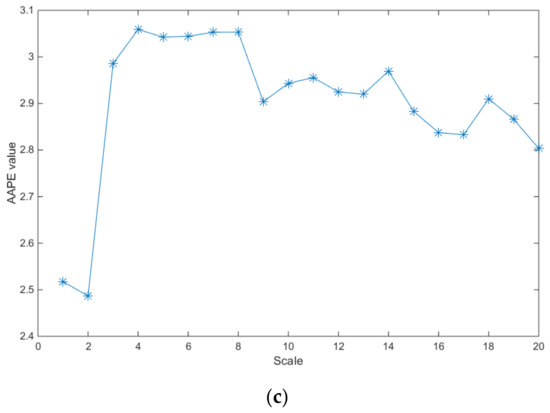
Figure 6.
MAAPE feature values of rolling bearing vibration signal under different fault conditions with the same loads. (a) Inner race fault, 7 mils, with load 1 hp. (b) Outer race fault, 7 mils, with load 1 hp. (c) Ball elements fault, 7 mils, with load 1 hp.
Figure 7 shows the feature clustering graph of MAAPE with different loads. In this figure, the 3-dimensional data in the 20-dimensional feature vector constitute the clustering graph. It can be seen that the characteristics of different fault types have certain separability in 3-dimensional space. Therefore, the fault feature extraction method based on MAAPE proposed in this paper can effectively describe the fault features of rolling bearings with different fault types.
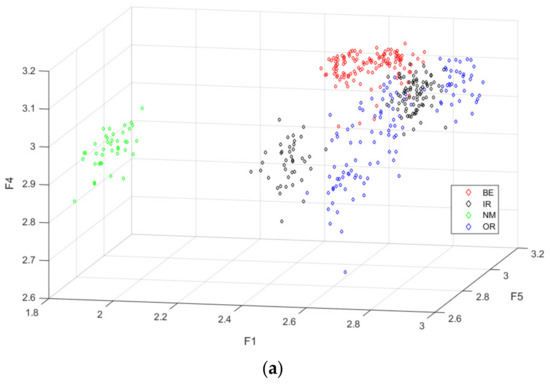
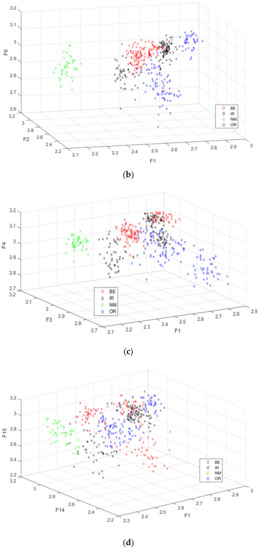
Figure 7.
Feature clustering graph of MAAPE with different loads. (a) Load 0 hp. (b) Load 1 hp. (c) Load 2 hp. (d) Load 3 hp.
Figure 8 shows that MAAPE feature clustering diagram of each fault severity under different loads. As shown in the figure, the 2-dimensional data in the 20-dimensional feature vector constitute the clustering graph. It can be seen that the fault feature extraction method of MAAPE rolling bearings proposed in this paper has certain feature description effect of fault severity. Fault features extracted under different fault severity have different characteristics which is helpful to identify the fault types and fault severity.
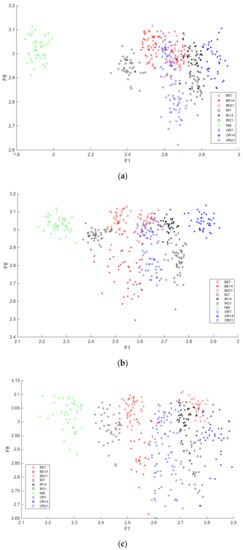
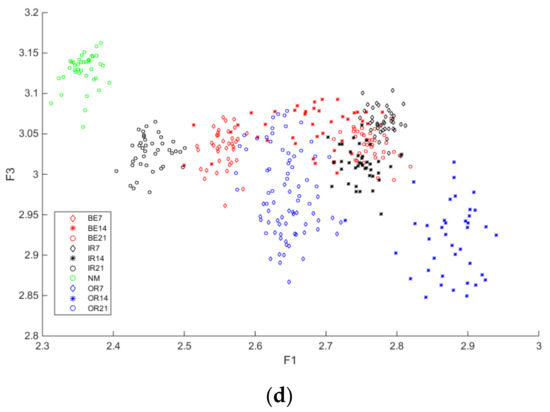
Figure 8.
MAAPE feature clustering diagram of each fault severity under different loads. (a) Load 0 hp. (b) Load 1 hp. (c) Load 2 hp. (d) Load 3 hp.
Table 2 and Table 3 respectively show the experimental results of performance comparison of rolling bearing fault feature extraction algorithms and fault identification accuracy by combining different fault feature extraction methods with random forest. In Table 2, the average between-class distance of MAAPE is less than improved multiscale entropy (IMSE), improved multiscale fuzzy entropy (IMFE) and refined composite multiscale entropy (RCMSE), but the average within-class distance of MAAPE is the smallest. In addition, the average time-consuming of MAAPE is relatively the lowest compared with other feature extraction methods. In Table 3, the fault identification accuracy of MAAPE coupled with random forest is 96.0% and the identification accuracy is slightly lower than RCMPE and IMFE. However, the computational efficiency is the highest as shown in Table 2. Through the above experiments, it can be seen that the rolling bearing fault diagnosis method proposed in this paper has high fault identification accuracy and good execution efficiency, which is more suitable for applications with high real-time requirements.

Table 2.
Performance comparison of rolling bearing fault feature extraction algorithms.

Table 3.
Fault identification accuracy by combining different fault feature extraction methods with random forest.
In order to illustrate the analytical ability of fault severity of the rolling bearing fault diagnosis method proposed in this paper, the identification accuracy experiments of different fault severity are carried out in this paper, and the experimental results are shown in Table 4. It can be seen from the experimental results that the fault accuracy of the proposed method is low when the ball elements fault severity is 14 mils and 21 mils, and the overall fault accuracy is 92.8%. As the vibration signal contains the natural vibration of rolling bearings, the influence of fault size and external interference, it will have a certain impact on the performance of AAPE fault feature extraction. In addition, the use of 20 different scales of AAPE feature vector to form the eigenvector will increase the uncertainty factor, thereby affecting the accuracy of fault identification. In spite of this, it can be seen from the experimental results that the fault diagnosis method proposed in this paper can analyze the severity of rolling bearing fault to a certain extent.

Table 4.
Identification rate of the proposed rolling bearing fault diagnosis method for different fault severity.
5. Conclusions
A rolling bearing fault diagnosis method based on multiscale amplitude-aware permutation entropy (MAAPE) and random forest is proposed in this paper. The MAAPE-based fault feature extraction method is proposed for the first time. In order to effectively extract fault features in vibration signals of rolling bearings, this paper uses a coarse-grained process in MSE to obtain a set of coarse-grained time series under different scale factors, and extracts fault features contained in different coarse-grained time series through AAPE to obtain feature vectors representing fault information of rolling bearings. Then, the random forest classifier is adopted to identify the fault feature vector extracted from vibration signal of rolling bearings. The proposed fault diagnosis method can effectively identify the fault type of rolling bearings and the identification accuracy of four fault types is up to 96.0%. The proposed method can further analyze the fault severity of rolling bearings, and the identification accuracy under different fault severity is 92.8%.
MAAPE can improve the stability of PE, become more sensitive to amplitude and frequency changes, and contribute to the description of fault characteristics. However, because it is too sensitive to the change of amplitude, it is easy for external interference to affect the extracted features, leading to a decline in identification accuracy. Therefore, how to avoid external interference and highlight bearing vibration signals before feature extraction will help improve the feature extraction effect of MAAPE. The following research direction is to further improve the fault feature description ability of MAAPE, and then improve the fault severity analysis ability of fault diagnosis method.
Author Contributions
Y.C. clarified the research content and ideas, and completed the writing of this paper. T.Z. and W.Z. studied the method and carried out experiments. Z.L. and K.S. analyzed the data and proofread the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under grant numbers 61803128, 61801148 and Heilongjiang Province Natural Science Foundation under grant numbers F2016021 and LH2019F026.
Acknowledgments
Thanks for the Bearing Data Center of Case Western Reserve University for supplying the rolling bearing data set.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| MAAPE | Multiscale amplitude-aware permutation entropy |
| WT | Wavelet transform |
| WPT | Wavelet packet transform |
| EMD | Empirical mode decomposition |
| EEMD | Ensemble empirical mode decomposition |
| CEEMD | Complete ensemble empirical mode decomposition |
| LMD | Local mean decomposition |
| ApEn | Approximate entropy |
| SampEn | Sample entropy |
| MSE | Multiscale entropy |
| PE | Permutation entropy |
| RBF | Radical basis function |
| BP | Back-propagation |
| SVM | Support vector machine |
| SKF | Svenska Kullager-Fabriken |
| RF | Random forest |
| IMPE | Improved multiscale permutation entropy |
| RCMPE | Refined composite multiscale permutation entropy |
| IMSE | Improved multiscale entropy |
| IMFE | Improved multiscale fuzzy entropy |
| RCMSE | Refined composite multiscale entropy |
References
- Chen, Y.; Zhang, T.; Luo, Z.; Sun, K. A novel rolling bearing fault diagnosis and severity analysis method. Appl. Sci. 2019, 9, 2356. [Google Scholar] [CrossRef]
- Shi, J.; Liang, M.; Guan, Y. Bearing fault diagnosis under variable rotational speed via the joint application of windowed fractal dimension transform and generalized demodulation: A method free from prefiltering and resampling. Mech. Syst. Signal Process. 2016, 68, 15–33. [Google Scholar] [CrossRef]
- Georgoulas, G.; Loutas, T.; Stylios, C.D.; Kostopoulos, V. Bearing fault detection based on hybrid ensemble detector and empirical mode decomposition. Mech. Syst. Signal Process. 2013, 41, 510–525. [Google Scholar] [CrossRef]
- Cerrada, M.; Sánchez, R.-V.; Li, C.; Pacheco, F.; Cabrera, D.; de Oliveira, J.V.; Vásquez, R.E. A review on data-driven fault severity assessment in rolling bearings. Mech. Syst. Signal Process. 2018, 99, 169–196. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, S.; Wang, B.; Habetler, T.G. Machine learning and deep learning algorithms for bearing fault diagnostics—A comprehensive review. arXiv 2019, arXiv:1901.08247. Available online: https://arxiv.org/abs/1901.08247 (accessed on 11 August 2019).
- Glowacz, A.; Glowacz, W.; Glowacz, Z.; Kozik, J. Early fault diagnosis of bearing and stator faults of the single-phase induction motor using acoustic signals. Measurement 2018, 113, 1–9. [Google Scholar] [CrossRef]
- Glowacz, A. Fault diagnosis of single-phase induction motor based on acoustic signals. Mech. Syst. Signal Process. 2019, 117, 65–80. [Google Scholar] [CrossRef]
- Martínez-García, C.; Astorga-Zaragoza, C.; Puig, V.; Reyes-Reyes, J.; López-Estrada, F. A simple nonlinear observer for state and unknown input estimation: DC motor applications. IEEE T. Circuits-II. 2019, 1. [Google Scholar]
- De Moura, E.P.; Souto, C.R.; Silva, A.A.; Irmão, M.A.S. Evaluation of principal component analysis and neural network performance for bearing fault diagnosis from vibration signal processed by RS and DF analyses. Mech. Syst. Signal Process. 2011, 25, 1765–1772. [Google Scholar] [CrossRef]
- Yan, R.; Gao, R.X.; Chen, X. Wavelets for fault diagnosis of rotary machines: A review with applications. Signal Process. 2014, 96, 1–15. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Wei, Y.; Huang, W. A new rolling bearing fault diagnosis method based on multiscale permutation entropy and improved support vector machine based binary tree. Measurement 2016, 77, 80–94. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Ali, J.B.; Fnaiech, N.; Saidi, L.; Chebel-Morello, B. Application of empirical mode decomposition and artificial neural network for automatic bearing fault diagnosis based on vibration signals. Appl. Acoust. 2015, 89, 16–27. [Google Scholar]
- Li, Y.X.; Li, Y.A.; Chen, Z.; Chen, X. Feature extraction of Ship-Radiated noise based on permutation entropy of the intrinsic mode function with the highest energy. Entropy 2016, 18, 393. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, K.; Zhou, Q.; Fang, J.; Zhou, Z. Feature extraction for gas metal arc welding based on EMD and time–frequency entropy. Int. J. Adv. Manuf. Tech. 2017, 92, 1439–1448. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, J.; He, Z.; Zuo, M.J. A review on empirical mode decomposition in fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2013, 35, 108–126. [Google Scholar] [CrossRef]
- Zhang, X.; Liang, Y.; Zhou, J.; Zang, Y. A novel bearing fault diagnosis model integrated permutation entropy, ensemble empirical mode decomposition and optimized SVM. Measurement 2015, 69, 164–179. [Google Scholar] [CrossRef]
- Fu, Q.; Jing, B.; He, P.; Si, S.; Wang, Y. Fault feature selection and diagnosis of rolling bearings based on EEMD and optimized Elman_AdaBoost algorithm. IEEE Sens. J. 2018, 18, 5024–5034. [Google Scholar] [CrossRef]
- Zhou, S.; Qian, S.; Chang, W.; Xiao, Y.; Cheng, Y. A novel bearing multi-fault diagnosis approach based on weighted permutation entropy and an improved SVM ensemble classifier. Sensors 2018, 18, 1934. [Google Scholar] [CrossRef]
- Abdelkader, R.; Kaddour, A.; Bendiabdellah, A.; Derouiche, Z. Rolling bearing fault diagnosis based on an improved denoising method using the complete ensemble empirical mode decomposition and the optimized thresholding operation. IEEE Sens. J. 2018, 18, 7166–7172. [Google Scholar] [CrossRef]
- Han, M.; Pan, J. A fault diagnosis method combined with LMD, sample entropy and energy ratio for roller bearings. Measurement 2015, 76, 7–19. [Google Scholar] [CrossRef]
- Sun, J.; Xiao, Q.; Wen, J.; Wang, F. Natural gas pipeline small leakage feature extraction and recognition based on LMD envelope spectrum entropy and SVM. Measurement 2014, 55, 434–443. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef]
- Morabito, F.C.; Labate, D.; Foresta, F.L.; Bramanti, A.; Morabito, G.; Palamara, I. Multivariate multi-scale permutation entropy for complexity analysis of Alzheimer’s disease EEG. Entropy 2012, 14, 1186–1202. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Wang, R.; Huang, W. A fault diagnosis scheme for rolling bearing based on local mean decomposition and improved multiscale fuzzy entropy. J. Sound Vib. 2016, 360, 277–299. [Google Scholar] [CrossRef]
- Azami, H.; Escudero, J. Amplitude-aware permutation entropy: Illustration in spike detection and signal segmentation. Comput. Meth. Programs Biomed. 2016, 128, 40–51. [Google Scholar] [CrossRef]
- Li, B.; Chow, M.Y.; Tipsuwan, Y.; Hung, J.C. Neural-network-based motor rolling bearing fault diagnosis. IEEE Trans. Ind. Electron. 2002, 47, 1060–1069. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Machine Learning; Springer: Berlin, Germany, 2001; pp. 5–32. [Google Scholar]
- Humeau-Heurtier, A. The multiscale entropy algorithm and its variants: A review. Entropy 2015, 17, 3110–3123. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Bearing Data Center, Case Western Reserve University. Available online: http://csegroups.case.edu/bearingdatacenter/pages/download-data-file (accessed on 31 January 2010).
- Li, Y.; Wang, X.; Si, S.; Huang, S. Entropy based fault classification using the Case Western Reserve University data: A benchmark study. IEEE Trans. Reliab. 2019, 1–14. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Liu, Z.; Liang, X.; Si, S. The entropy algorithm and its variants in the fault diagnosis of rotating machinery: A review. IEEE Access 2018, 6, 66723–66741. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).