Distributed Centrality Analysis of Social Network Data Using MapReduce
Abstract
1. Introduction
2. Methods
2.1. Definitions
2.2. Distributed Computation for Centrality Analysis
2.3. Distributed Approach for Degree and Closeness Centrality
| Algorithm 1 Distributed Calculation for Degree and Closeness Centrality |
| Input: Twitter datasets in edge list format. Output: Centrality score of each user 1: For every , 1.1. Calculate the denoting set of nodes at one-hop distance. 2: For each node (calculated in step 1) 2.1. Identify set of neighboring nodes at hop distance using Equation (2). 3: Calculate the number of elements in traveling from node i to node j by using Equation (3): |
2.4. Distributed Approach for Eigenvector Centrality
| Algorithm 2 Distributed approach for eigenvector centrality |
| Input: Twitter dataset in edge-list format. Output: Eigenvector Centrality for each user in the network. 1: Initialize a vector list for each node . 2: Initialize a weight list for each node . 3: For each node and for each of its neighbors , 3.1. Calculate relative importance by . 4: Update the vector list by setting . 5: Calculate sum of all numbers in vector list. 6: Divide each entry in vector list by the sum for eigenvector centrality. |
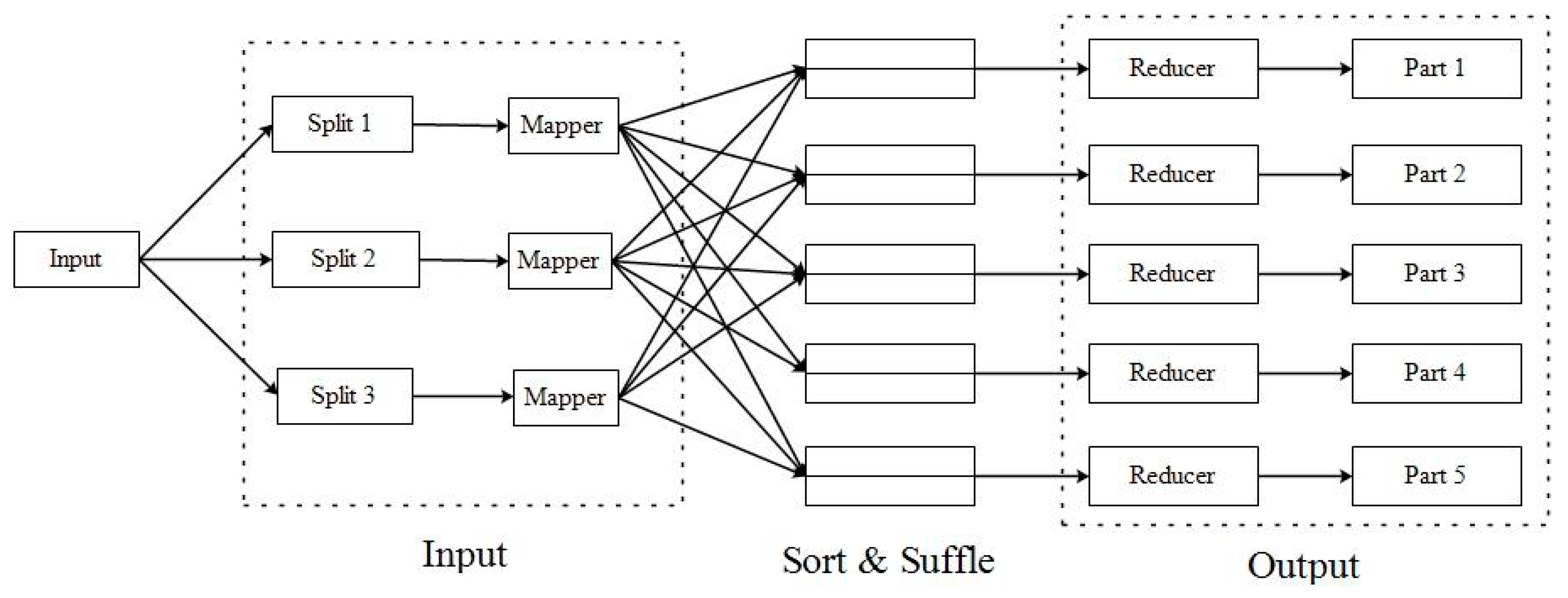
2.5. Distributed Computing Using MapReduce
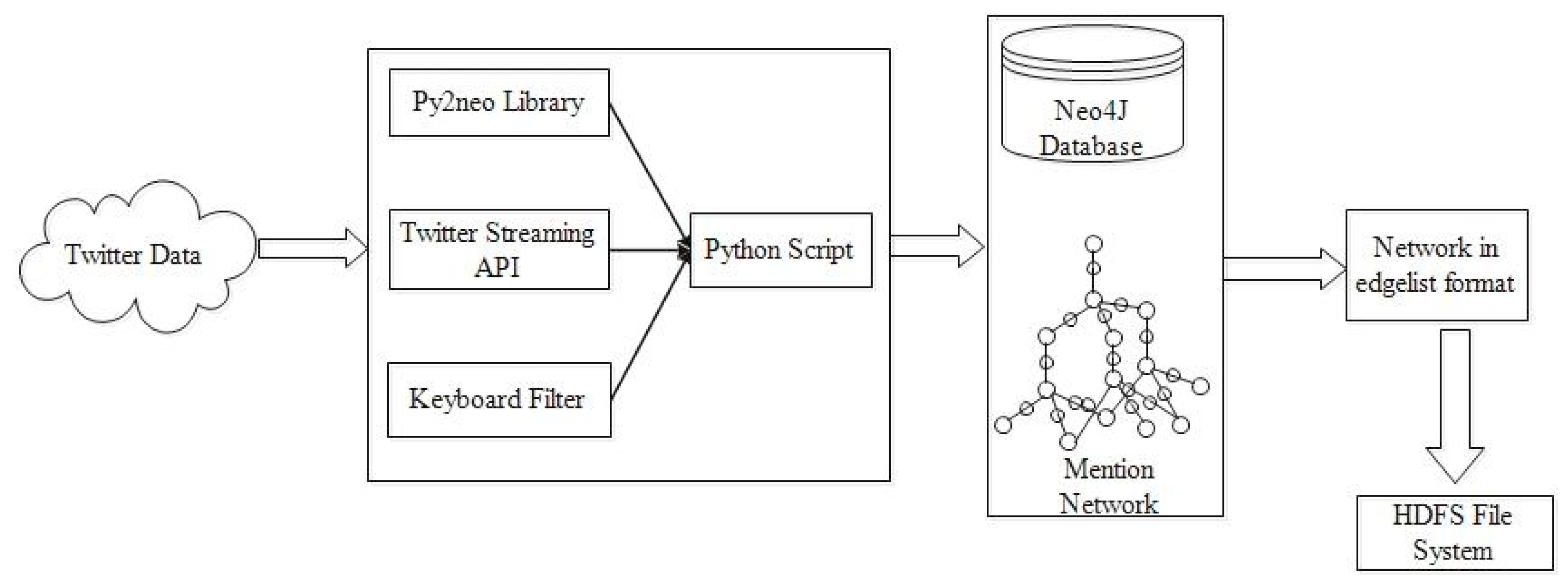
2.6. Data Collection
| Algorithm 3 Twitter data collection |
| Input: Twitter Source Output: Edge-list 1: Create a Tweet developer app and generate the user key, user key (secret), access token and access token (secret) were generated. 2: Establish a persistent connection with the Twitter Streaming API. 3: Read tweets incrementally and store in Neo4j Database (Nodes and Relationships). 4: Parse tweet text incrementally and write to a new text file, if any user mentions are present. 5: Create an edge-list text file with data in the form: UserName1 UserName2, which indicates a mention relationship from UserName1 to UserName2. UserName1 has mentioned UserName2 in his/her tweet text. 6: Store this file in HDFS as input for processing. |
3. Experiments and Results
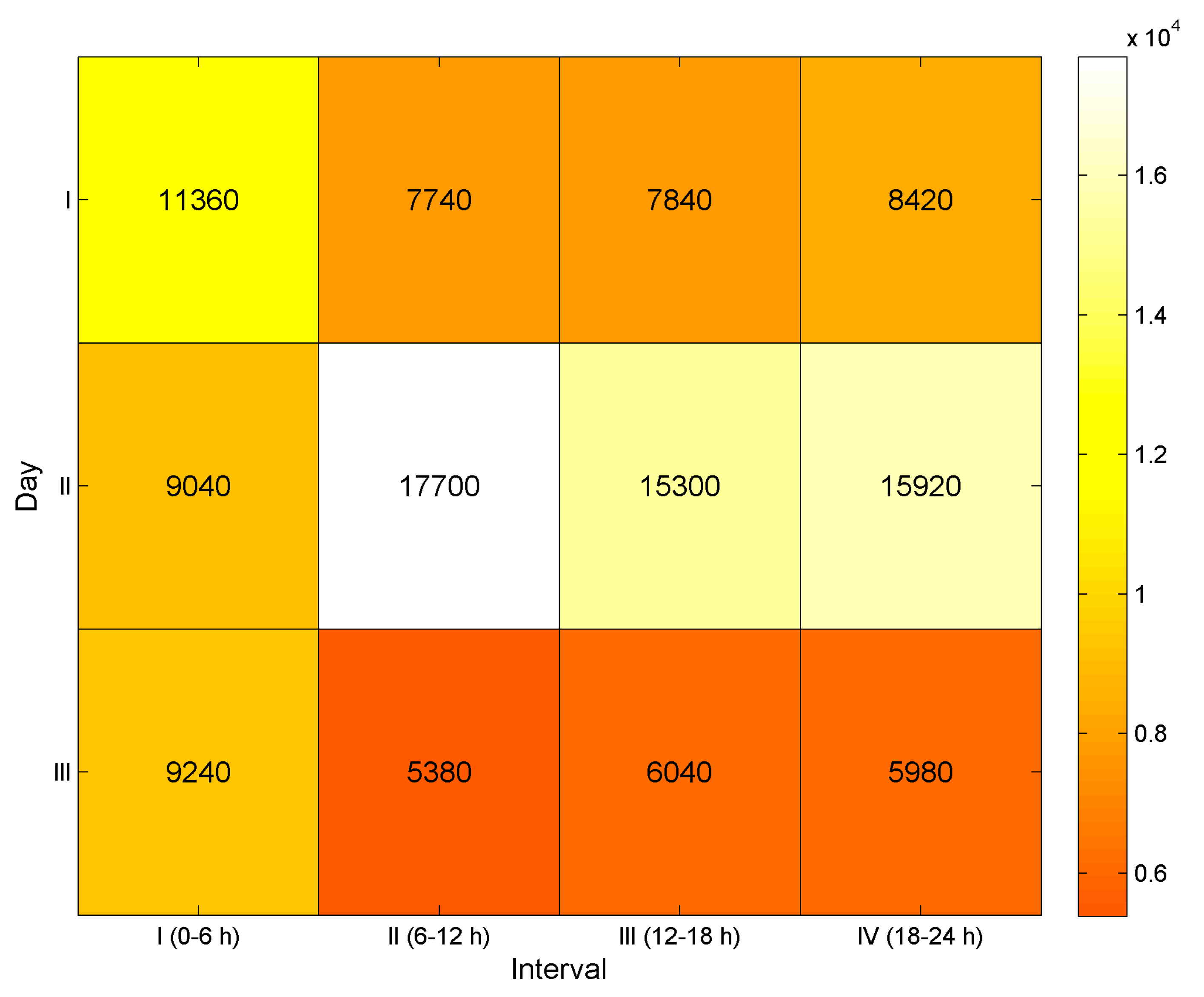
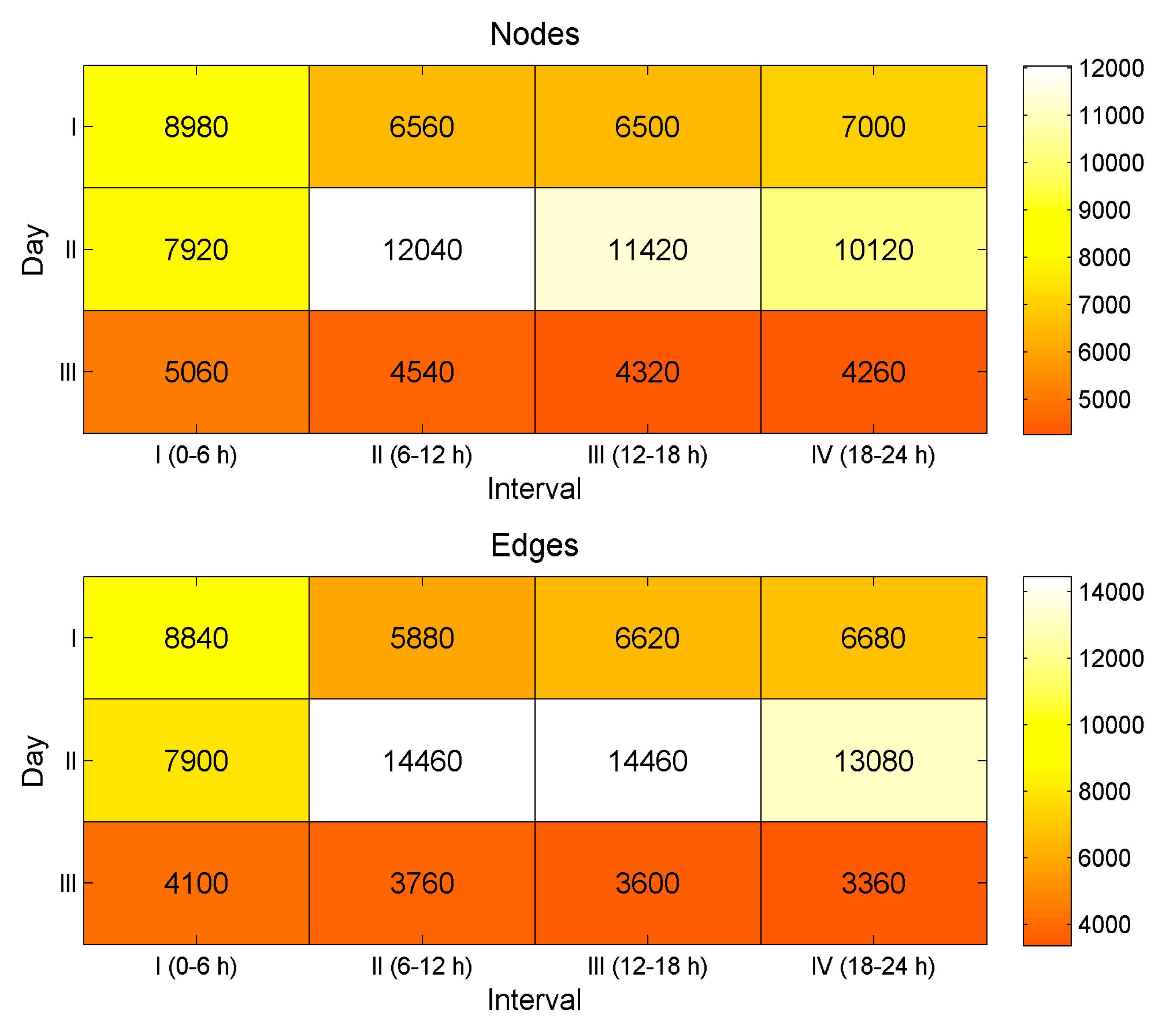
3.1. Dataset
3.2. Hardware
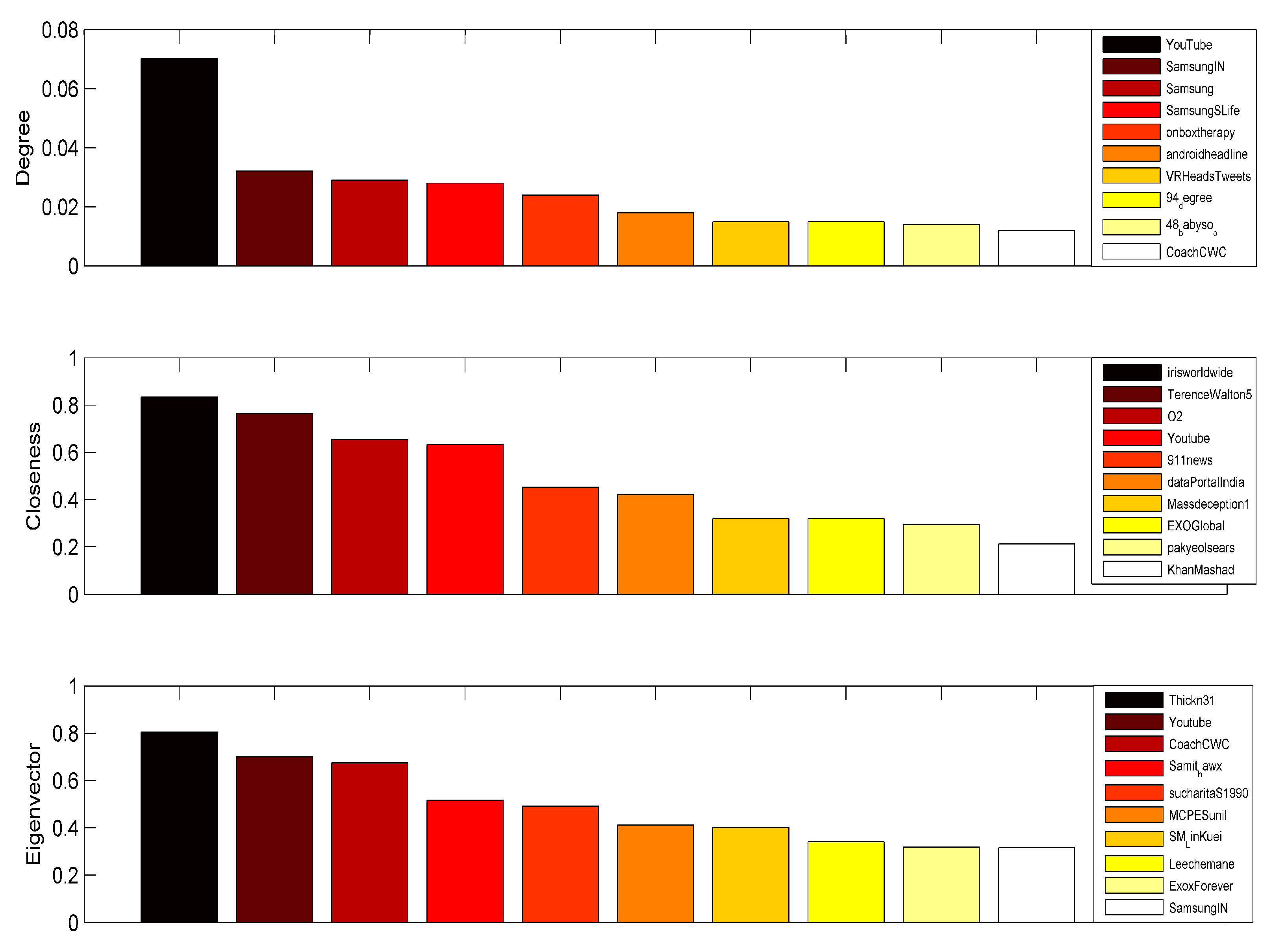
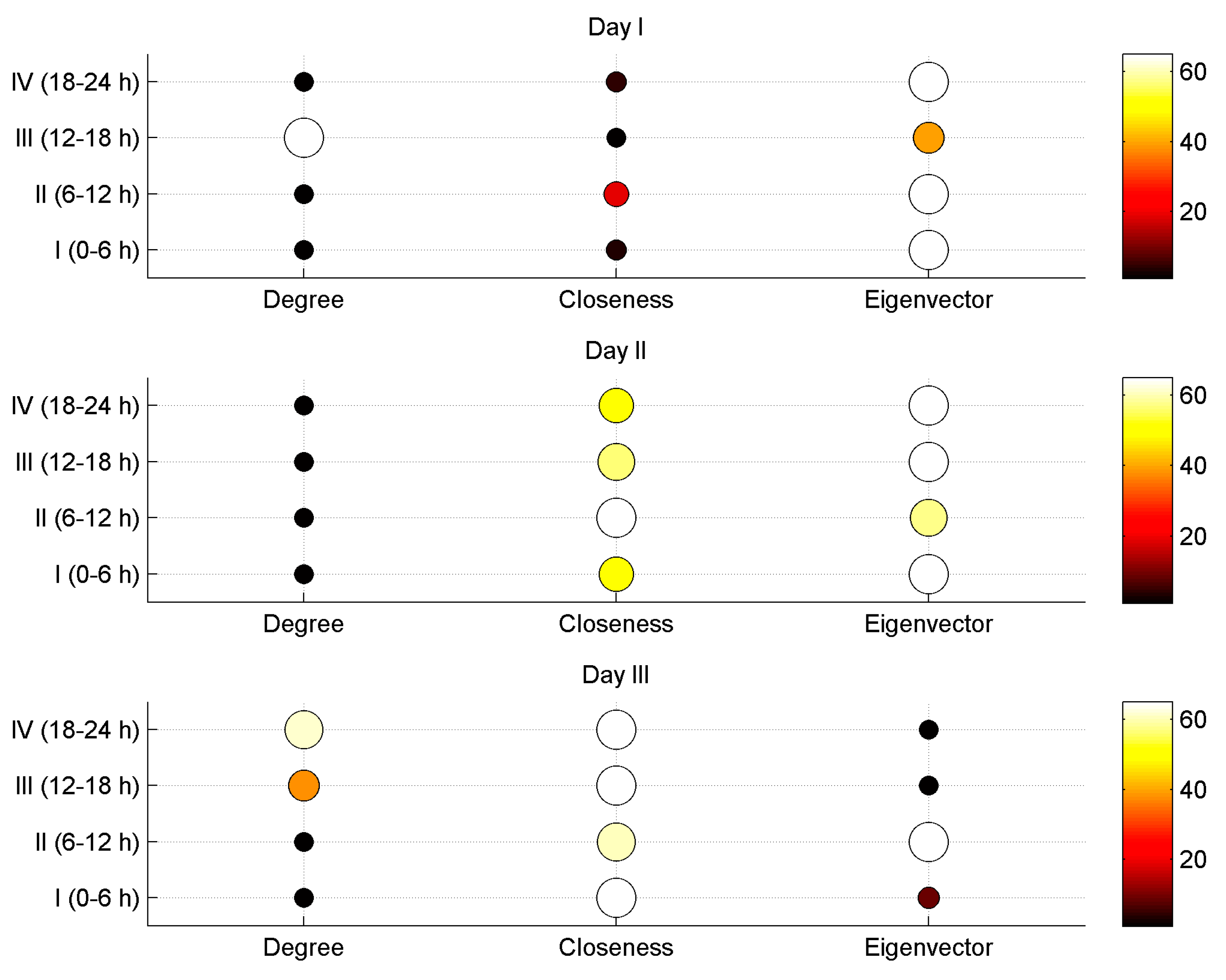
3.3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Landher, A.; Friedl, B.; Heidemann, J. A critical review of centrality measures in social networks. Wirtschaftsinformatik 2010, 52, 367–382. [Google Scholar] [CrossRef]
- El Gamal, A.; Kim, Y.H. Network Information Theory; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Tang, J. Computational Models for Social Network Analysis: A Brief Survey. In Proceedings of the 26th International Conference on World Wide Web Companion (WWW ‘17 Companion), Perth, Australia, 3–7 April 2017; pp. 921–925. [Google Scholar]
- Martinčić-Ipšić, S.; Močibob, E.; Perc, M. Link prediction on Twitter. PLoS ONE 2017, 12, e0181079. [Google Scholar] [CrossRef] [PubMed]
- Hansson, L.; Wrangmo, A.; Søilen, K. Optimal ways for companies to use Facebook as a marketing channel. J. Inf. Commun. Ethics Soc. 2013, 11, 112–126. [Google Scholar] [CrossRef]
- Das, K.; Samanta, S.; Pal, M. Study on centrality measures in social networks: A survey. Soc. Netw. Anal. Min. 2018, 8. [Google Scholar] [CrossRef]
- Basaras, P.; Iosifidis, G.; Katsaros, D.; Tassiulas, L. Identifying influential spreaders in complex multilayer networks: A centrality perspective. IEEE Trans. Netw. Sci. Eng. 2019, 6, 31–45. [Google Scholar] [CrossRef]
- Zhang, Y.; Pennacchiotti, M. Predicting purchase behaviors from social media. In Proceedings of the 22nd International Conference on World Wide Web (WWW ‘13), Rio de Janeiro, Brazil, 13–17 May 2013; pp. 1521–1532. [Google Scholar]
- De Meo, P.; Musial-Gabrys, K.; Rosaci, D.; Sarne, G.M.L.; Aroyo, L. Using centrality measures to predict helpfulness-based reputation in trust networks. ACM Trans. Internet Technol. 2017, 17, 8. [Google Scholar]
- Behera, R.K.; Rath, S.K.; Misra, S.; Damaševičius, R.; Maskeliūnas, R. Large Scale Community Detection Using a Small World Model. Appl. Sci. 2017, 7, 1173. [Google Scholar] [CrossRef]
- Hao, F.; Park, D.S.; Pei, Z. Exploiting the formation of maximal cliques in social networks. Symmetry 2017, 9, 100. [Google Scholar] [CrossRef]
- Peng, S.; Yang, A.; Cao, L.; Yu, S.; Xie, D. Social influence modeling using information theory in mobile social networks. Inf. Sci. 2017, 379, 146–159. [Google Scholar] [CrossRef]
- Liu, Y.; Pi, D.; Cui, L. Mining Community—Level Influence in Microblogging Network: A Case Study on Sina Weibo. Complexity 2017. [Google Scholar] [CrossRef]
- Chamberlain, B.P.; Levy-Kramer, J.; Humby, C.; Deisenroth, M.P. Real-time community detection in full social networks on a laptop. PLoS ONE 2018, 13, e0188702. [Google Scholar] [CrossRef] [PubMed]
- Saxena, R.; Kaur, S.; Bhatnagar, V. Social centrality using network hierarchy and community structure. Data Min. Knowl. Discov. 2018, 32, 1421–1443. [Google Scholar] [CrossRef]
- Bröhl, T.; Lehnertz, K. Centrality-based identification of important edges in complex networks. Chaos 2019, 29. [Google Scholar] [CrossRef]
- Ji, Z.; Pi, H.; Wei, W.; Xiong, B.; Wozniak, M.; Damasevicius, R. Recommendation Based on Review Texts and Social Communities: A Hybrid Model. IEEE Access 2019, 7, 40416–40427. [Google Scholar] [CrossRef]
- Louni, A.; Subbalakshmi, K.P. Diffusion of Information in Social Networks. In Intelligent Systems Reference Library; Panda, M., Dehuri, S., Wang, G.N., Eds.; Springer: Cham, Switzerland, 2014; Volume 65, pp. 1–22. [Google Scholar]
- Matas, N.; Martinčić-Ipšić, S.; Meštrović, A. Comparing Network Centrality Measures as Tools for Identifying Key Concepts in Complex Networks: A Case of Wikipedia. J. Digit. Inf. Manag. (JDIM) 2017, 15, 203–213. [Google Scholar]
- Wei, W.; Joseph, K.; Liu, H.; Carley, K.M. The Fragility of Twitter Social Networks Against Suspended Users. In Proceedings of the IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM ‘15), Paris, France, 25–28 August 2015; pp. 9–16. [Google Scholar]
- Qiao, T.; Shan, W.; Zhou, C. How to Identify the Most Powerful Node in Complex Networks? A Novel Entropy Centrality Approach. Entropy 2017, 19, 614. [Google Scholar] [CrossRef]
- Hall, A.; Towers, N. Understanding how millennial shoppers decide what to buy: Digitally connected unseen journeys. Int. J. Retail Distrib. Manag. 2017, 45, 498–517. [Google Scholar] [CrossRef]
- Sohn, J.-S.; Bae, U.-B.; Chung, I.-J. Contents Recommendation Method Using Social Network Analysis. Wirel. Pers. Commun. 2013, 73, 1529–1546. [Google Scholar] [CrossRef]
- Dewi, F.K.; Yudhoatmojo, S.B.; Budi, I. Identification of opinion leader on rumor spreading in online social network twitter using edge weighting and centrality measure weighting. In Proceedings of the 12th International Conference on Digital Information Management, Fukuoka, Japan, 12–14 September 2017; pp. 313–318. [Google Scholar] [CrossRef]
- Roy, S.; Dey, P.; Kundu, D. Social Network Analysis of Cricket Community Using a Composite Distributed Framework: From Implementation Viewpoint. IEEE Trans. Comput. Soc. Syst. 2018, 5, 64–81. [Google Scholar] [CrossRef]
- Guo, K.; Guo, W.; Chen, Y.; Qiu, Q.; Zhang, Q. Community discovery by propagating local and global information based on the MapReduce model. Inf. Sci. 2015, 323, 73–93. [Google Scholar] [CrossRef]
- Balkir, A.S.; Oktay, H.; Foster, I. Estimating graph distance and centrality on shared nothing architectures. Concurr. Comput. 2015, 27, 3587–3613. [Google Scholar] [CrossRef]
- Adoni, W.Y.H.; Nahhal, T.; Aghezzaf, B.; Elbyed, A. The MapReduce-based approach to improve the shortest path computation in large-scale road networks: The case of A algorithm. J. Big Data 2018, 5. [Google Scholar] [CrossRef]
- Al Aghbari, Z.; Bahutair, M.; Kamel, I. GeoSimMR: A MapReduce Algorithm for Detecting Communities based on Distance and Interest in Social Networks. Data Sci. J. 2019, 18. [Google Scholar] [CrossRef]
- Bakratsas, M.; Basaras, P.; Katsaros, D.; Tassiulas, L. Hadoop MapReduce Performance on SSDs for Analyzing Social Networks. Big Data Res. 2018, 11, 1–10. [Google Scholar] [CrossRef]
- Li, S.; Wang, B. Hybrid Parrallel Bayesian Network Structure Learning from Massive Data Using MapReduce. J. Signal Process. Syst. 2017, 90, 1115–1121. [Google Scholar] [CrossRef]
- Kang, U.; Papadimitriou, S.; Sun, J.; Tong, H. Centralities in large networks: Algorithms and observations. In Proceedings of the SIAM International Conference on Data Mining, Mesa, AZ, USA, 28–30 April 2011; pp. 119–130. [Google Scholar]
- Segarra, S.; Ribeiro, A. Stability and continuity of centrality measures in weighted graphs. IEEE Trans. Signal Process. 2016, 64, 543–555. [Google Scholar] [CrossRef]
- Howlader, P.; Sudeep, K.S. Degree centrality, eigenvector centrality and the relation between them in Twitter. In Proceedings of the IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT), Bangalore, India, 20–21 May 2016; pp. 678–682. [Google Scholar]
- Borgatti, S.P.; Everett, M.G. A graph-theoretic perspective on centrality. Soc. Netw. 2006, 28, 466–484. [Google Scholar] [CrossRef]
- Bonacich, P.; Lloyd, P. Eigenvector centrality and structural zeroes and ones: When is a neighbor not a neighbor? Soc. Netw. 2015, 43, 86–90. [Google Scholar] [CrossRef]
- Dean, J.; Ghemawat, S. MapReduce: Simplified data processing on large clusters. Commun. ACM 2008, 51, 107–113. [Google Scholar] [CrossRef]
- Marszałek, Z. Parallelization of Modified Merge Sort Algorithm. Symmetry 2017, 9, 176. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar Behera, R.; Kumar Rath, S.; Misra, S.; Damaševičius, R.; Maskeliūnas, R. Distributed Centrality Analysis of Social Network Data Using MapReduce. Algorithms 2019, 12, 161. https://doi.org/10.3390/a12080161
Kumar Behera R, Kumar Rath S, Misra S, Damaševičius R, Maskeliūnas R. Distributed Centrality Analysis of Social Network Data Using MapReduce. Algorithms. 2019; 12(8):161. https://doi.org/10.3390/a12080161
Chicago/Turabian StyleKumar Behera, Ranjan, Santanu Kumar Rath, Sanjay Misra, Robertas Damaševičius, and Rytis Maskeliūnas. 2019. "Distributed Centrality Analysis of Social Network Data Using MapReduce" Algorithms 12, no. 8: 161. https://doi.org/10.3390/a12080161
APA StyleKumar Behera, R., Kumar Rath, S., Misra, S., Damaševičius, R., & Maskeliūnas, R. (2019). Distributed Centrality Analysis of Social Network Data Using MapReduce. Algorithms, 12(8), 161. https://doi.org/10.3390/a12080161




