Soft Iterative Decoding Algorithms for Rateless Codes in Satellite Systems
Abstract
1. Introduction
2. HARQ Transmissions with Rateless Codes
2.1. Rateless Codes
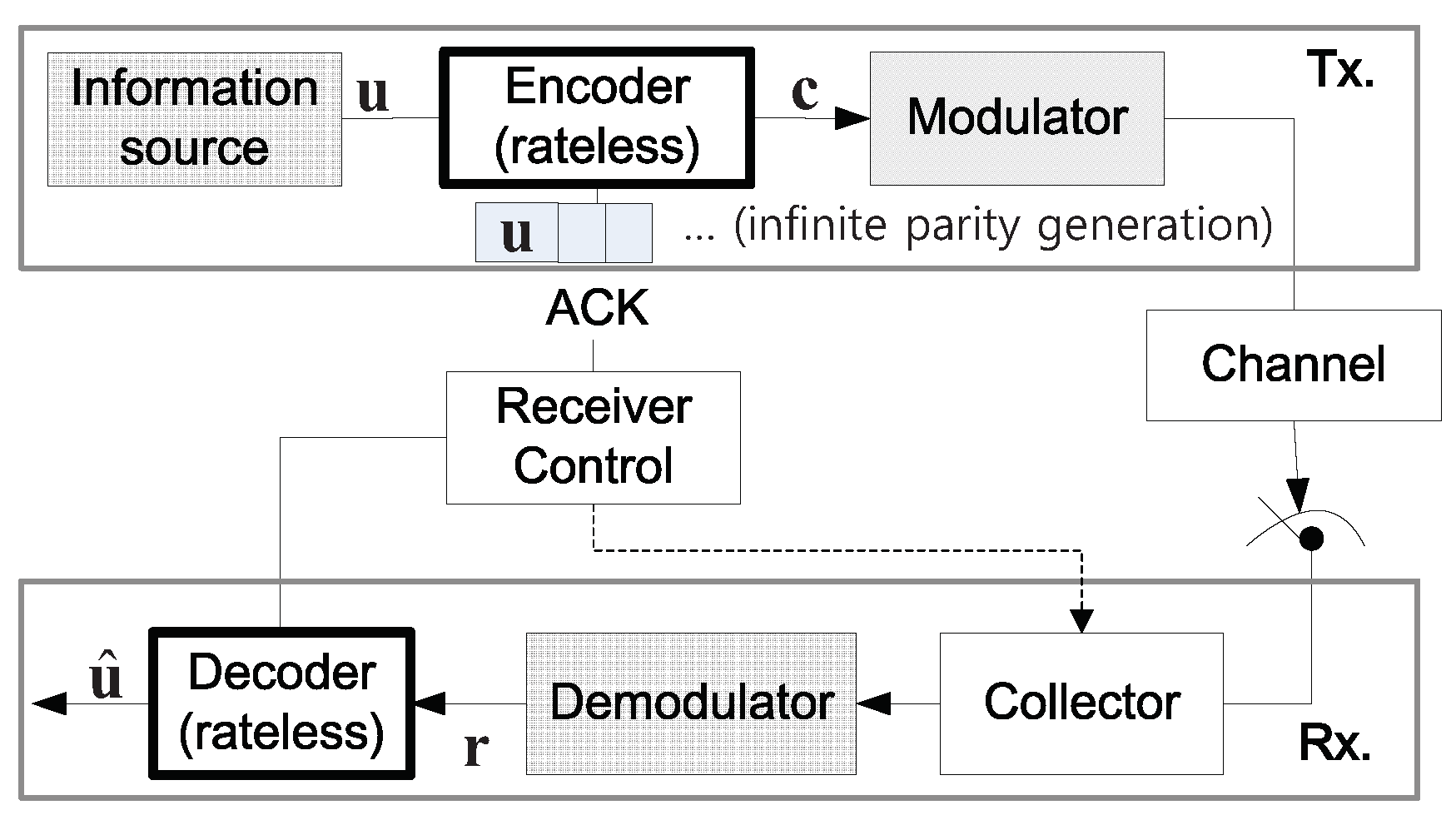
2.2. HARQ with Rateless Codes
3. Efficient Soft Iterative Decoding Algorithms for HARQ with Rateless Codes in Satellite Systems
3.1. HARQ for Satellite Systems
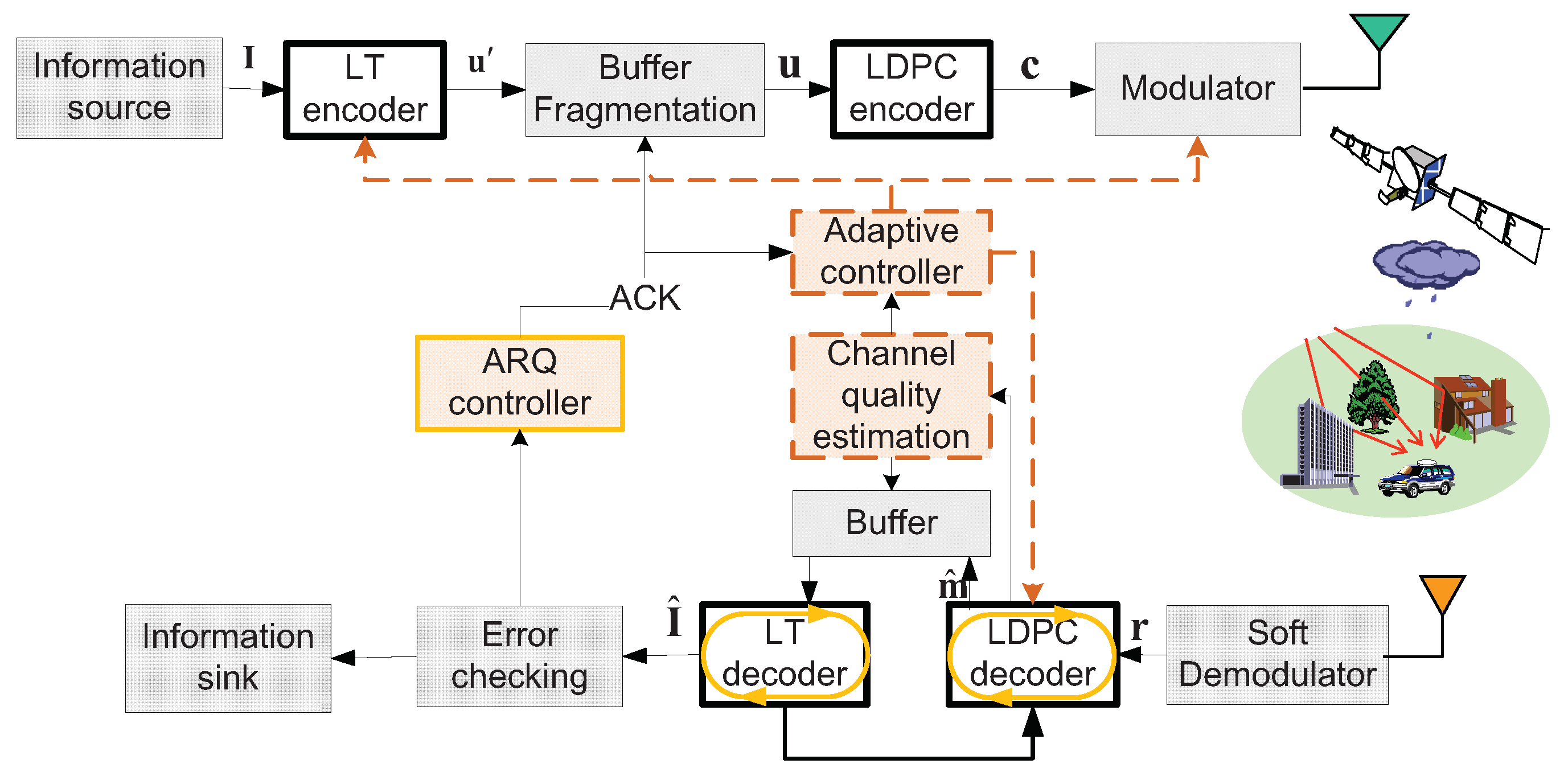
3.2. HARQ with Rateless LDPC Codes
3.2.1. Operational Principle
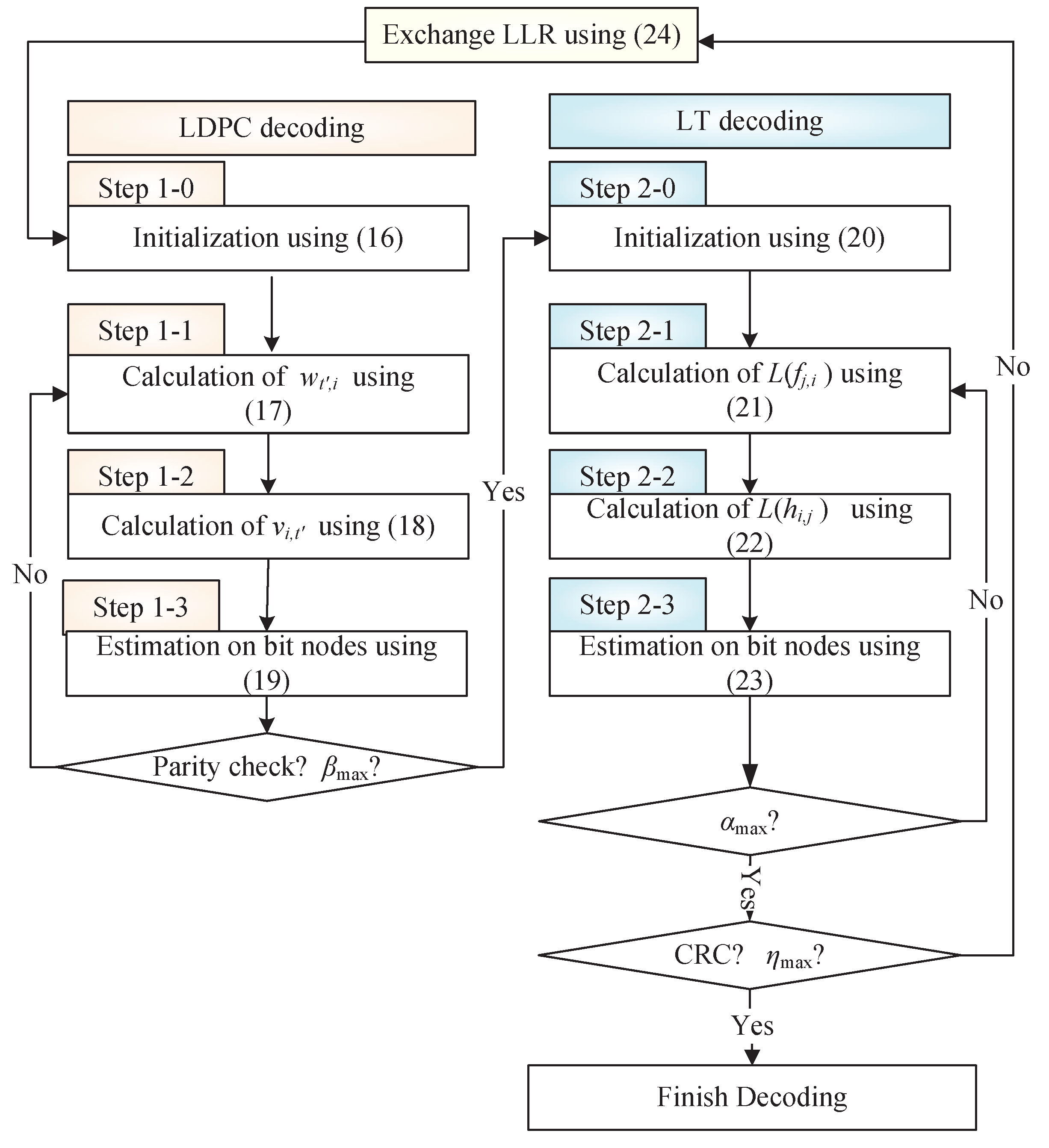
3.2.2. Soft Iterative Decoding Algorithms
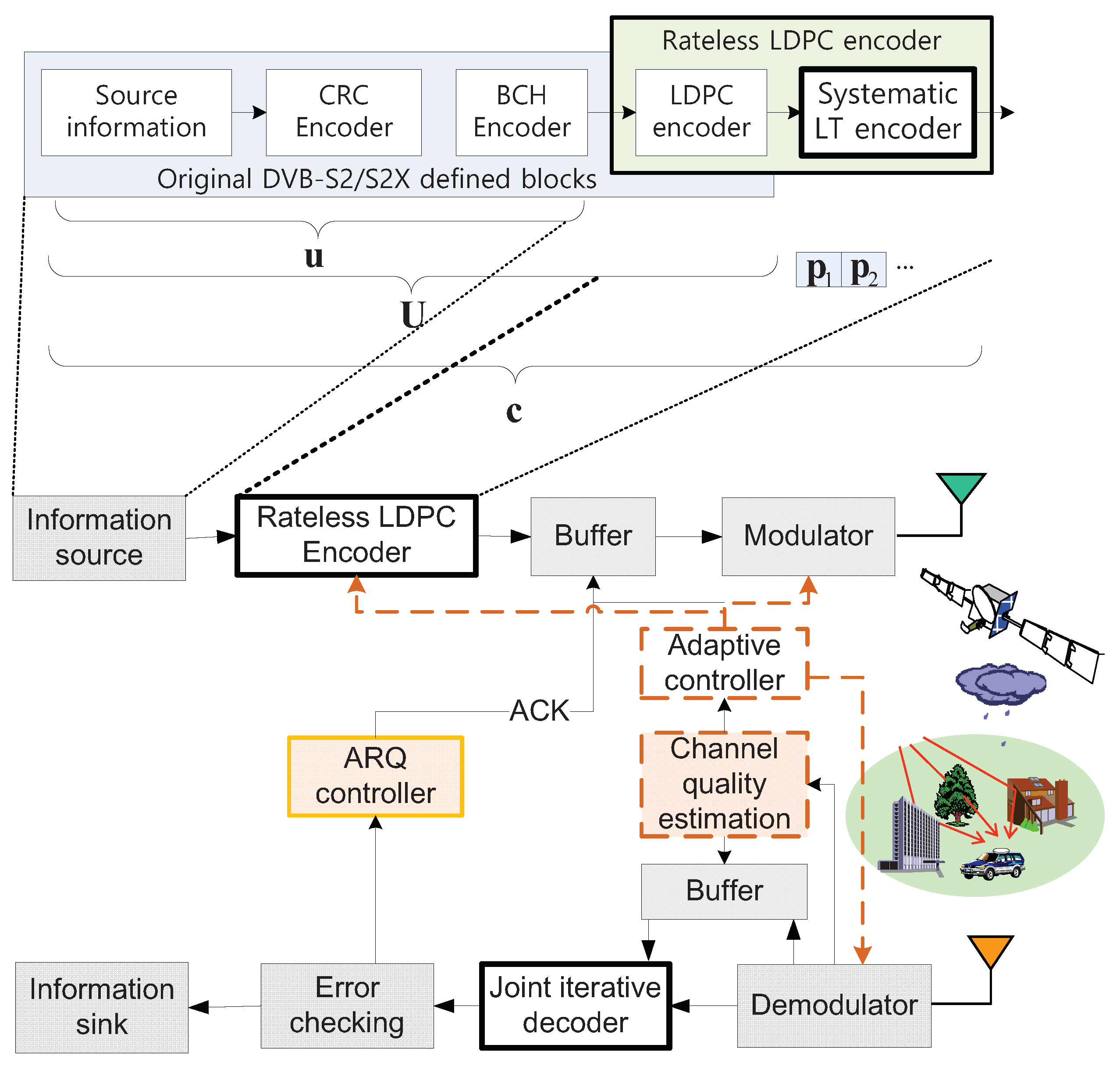
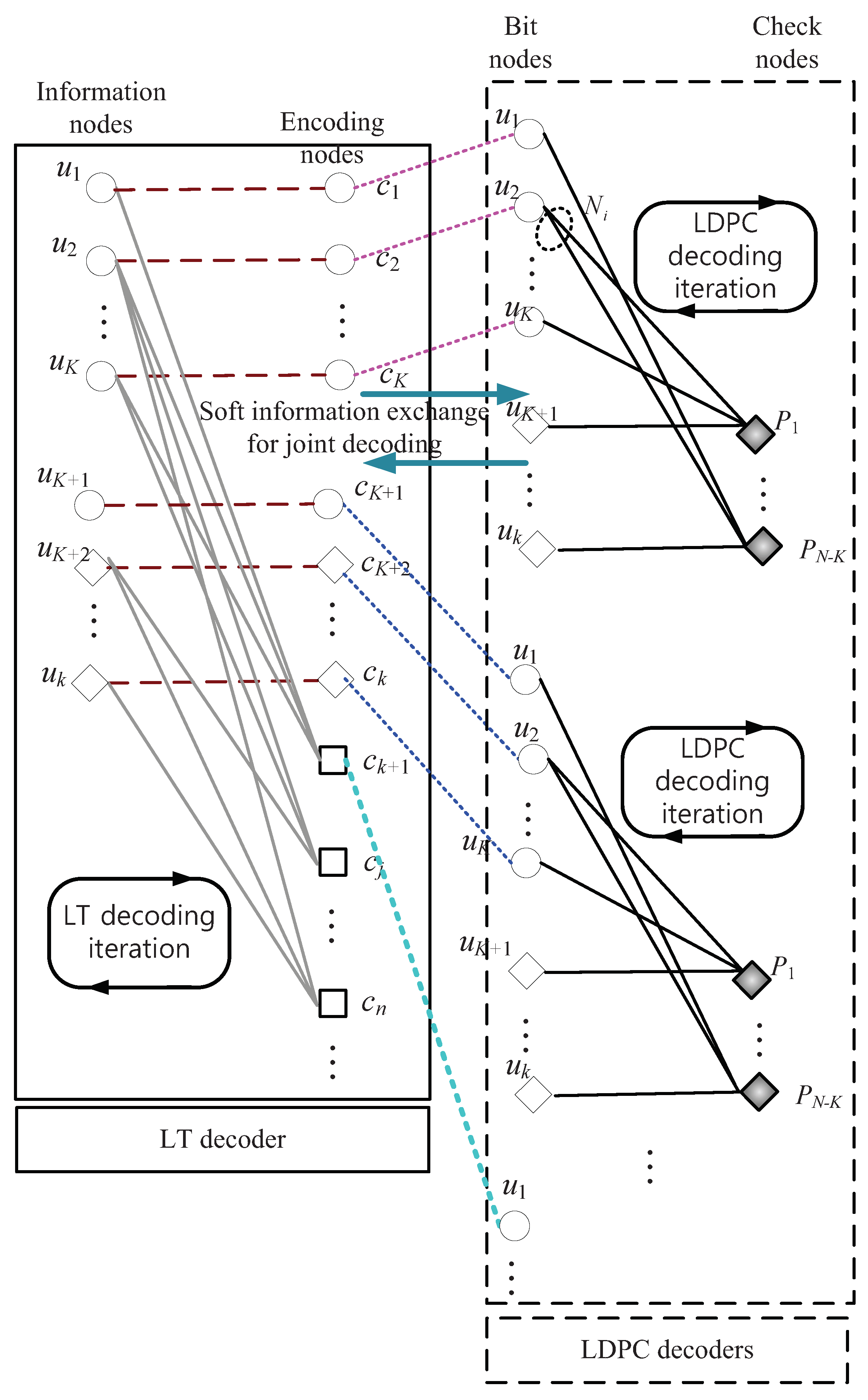
3.3. HARQ with Cross-Layer Rateless Codes
3.3.1. Operational Principle
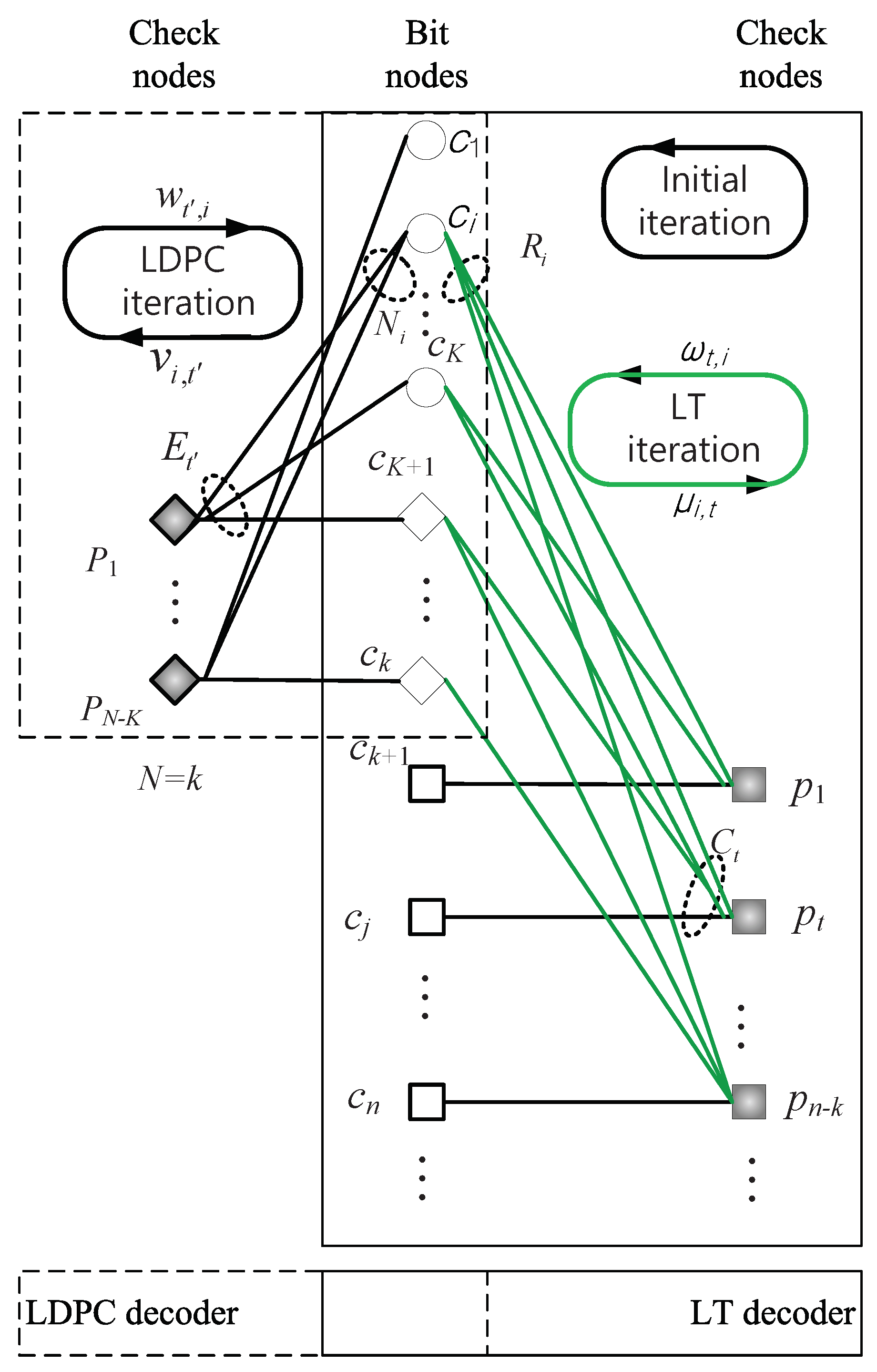
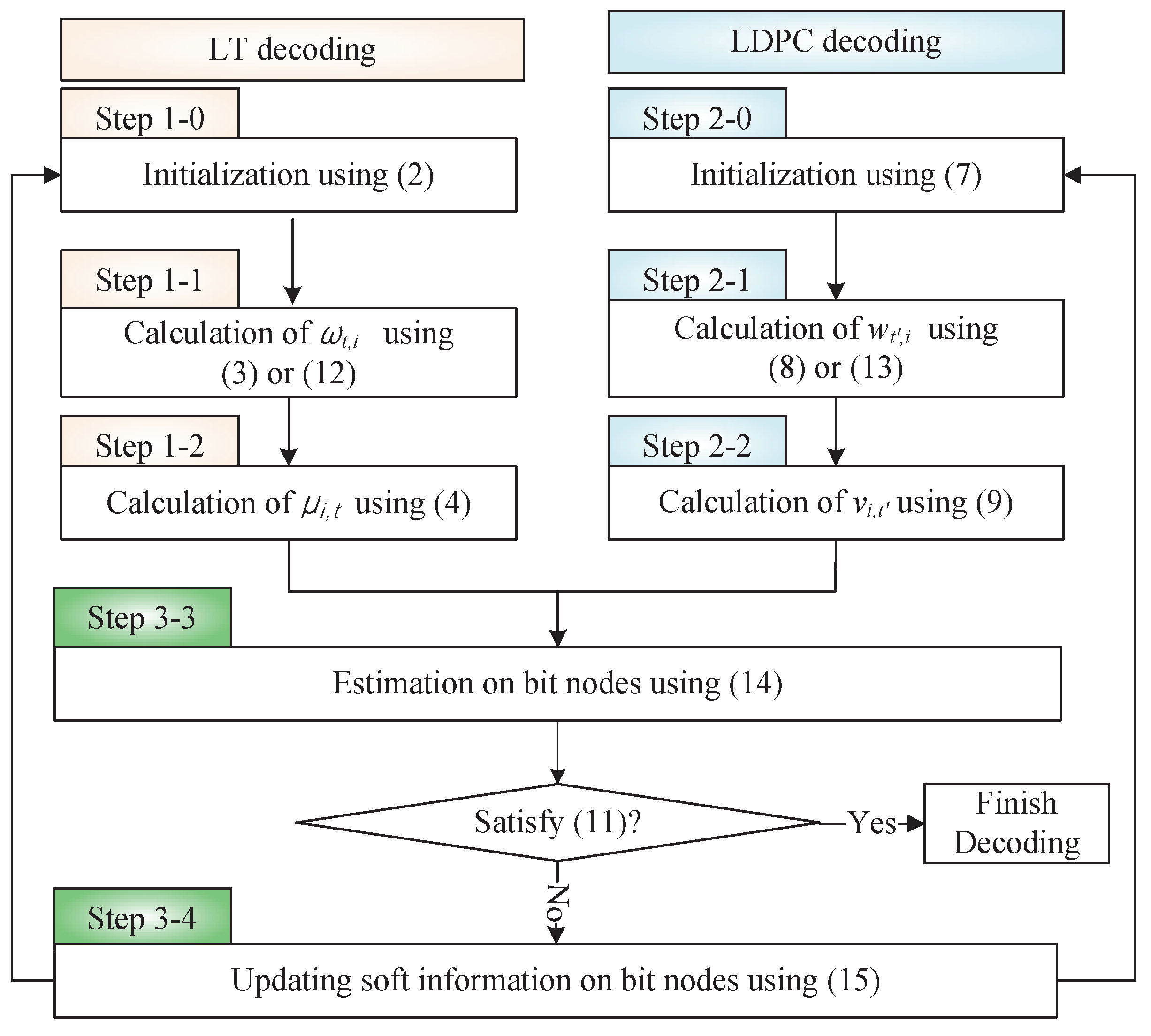
3.3.2. Soft Iterative Decoding Algorithms
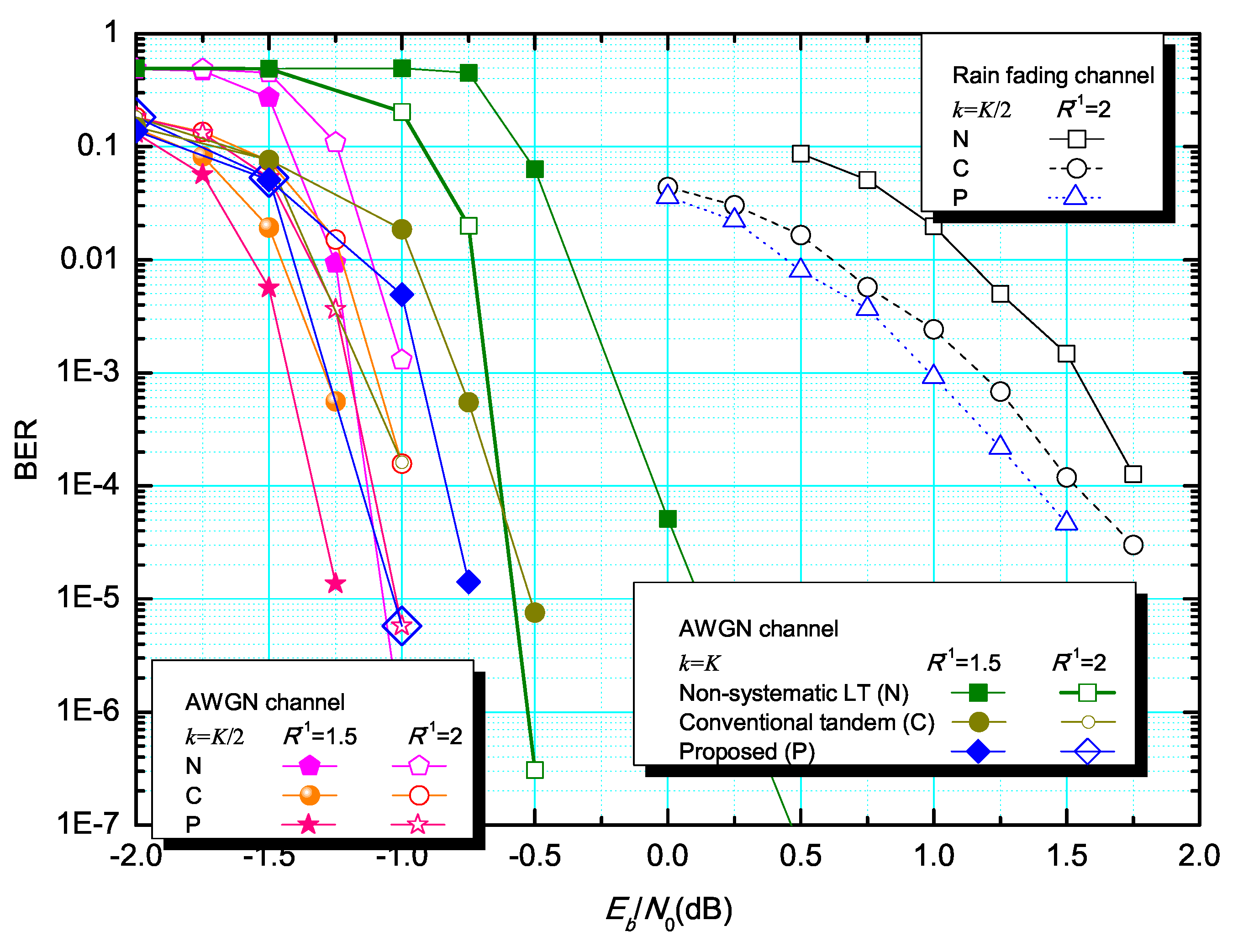
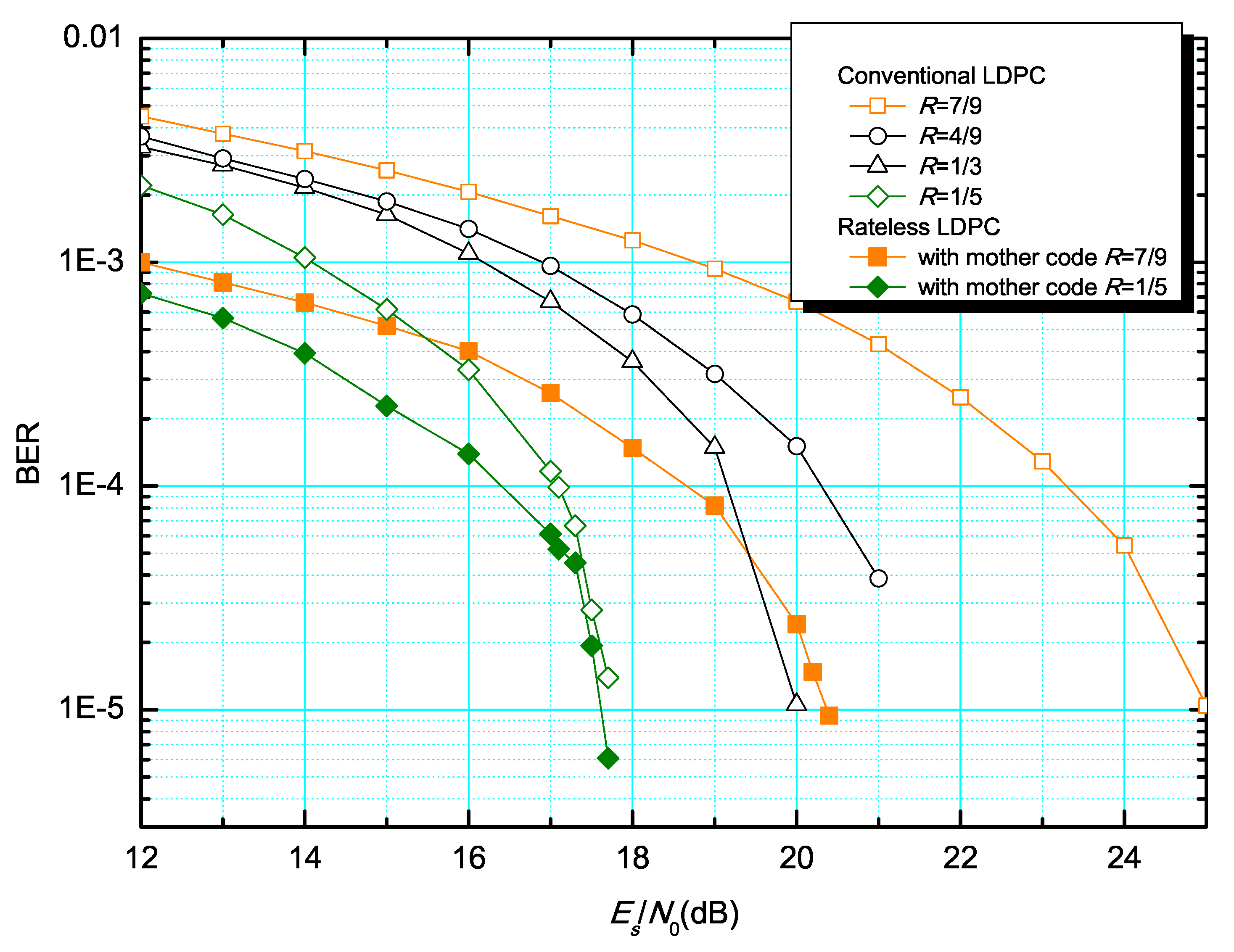
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Luby, M. LT Codes. In Proceedings of the 43rd Annual IEEE Symposium on Foundations of Computer Science, Vancouver, BC, Canada, 19 November 2002; pp. 271–280. [Google Scholar]
- Shokrollahi, A. Raptor Codes. IEEE Trans. Inf. Theory 2006, 52, 2551–2567. [Google Scholar] [CrossRef]
- Thota, J.; Bulut, B.; Doufexi, A.; Armour, S. Performance Evaluation of Multicast Video Distribution with User Cooperation in LTE-A Vehicular Environments. In Proceedings of the 2017 IEEE 86th Vehicular Technology Conference (VTC-Fall), Toronto, ON, Canada, 24–27 September 2017. [Google Scholar]
- Zhu, H.; Li, G.; Xie, Z. Advanced LT codes in Satellite Data Broadcasting System. In Proceedings of the 11th IEEE Singapore International Conference on Communication Systems, Guangzhou, China, 19–21 November 2008; pp. 1430–1435. [Google Scholar]
- Hagh, M.J.; Soleymani, M.R. Constellation Rotation for DVB Multiple Access Channels with Raptor coding. IEEE Trans. Broadcast. 2013, 59, 290–297. [Google Scholar] [CrossRef]
- Zhang, M.; Li, C.; Kim, S. Efficient Utilization of Rateless LDPC Codes for Satellite Broadcasting Services. In Proceedings of the 2016 International Conference on Wireless Communications & Signal Processing (WCSP 2016), Yangzhou, China, 13–15 October 2016. [Google Scholar]
- Wang, Z.; Wang, Z.; Gu, X.; Guo, Q. Cross-layer design of LT codes and LDPC codes for satellite multimedia broadcast/multicast services. Chin. J. Aeronaut. 2013, 26, 1269–1275. [Google Scholar] [CrossRef]
- Eroz, M.; Sun, F.; Lee, L. DVB-S2 Low Density Parity Check Codes with Near Shannon Limit Performance. Int. J. Satell. Commun. Netw. 2004, 22, 269–279. [Google Scholar] [CrossRef]
- Yao, W.; Yi, B.; Huang, T. Poisson robust soliton distribution for LT codes. IEEE Commun. Lett. 2016, 20, 1499–1502. [Google Scholar] [CrossRef]
- Zhang, M.; Kim, S. An Efficient Encoding Scheme for LT codes with Soft Iterative Decoding. IET Commun. 2018, 12, 1624–1629. [Google Scholar] [CrossRef]
- Hong, T.C.; Kang, K.-S.; Ku, B.-J.; Chang, D.-I. Receiver memory management method for HARQ in LTE-based satellite communication system. Int. J. Satell. Commun. Netw. 2017. [Google Scholar] [CrossRef]
- Zhang, M.; Kim, S.; Chang, J.Y.; Kim, W.-Y. A New Soft Decoding Method for Systematic Raptor Codes. IET Commun. 2015, 9, 1933–1940. [Google Scholar] [CrossRef]
- Wen, L.; Razavi, R.; Imran, M.A.; Xiao, P. Design of joint sparse graph for OFDM system. IEEE Trans. Wirel. Commun. 2014, 14, 1823–1836. [Google Scholar] [CrossRef]
- Zhang, M.; Kim, S.; Kim, Y. Universal Soft Decision Demodulator for M-ary Adaptive Modulation Systems. In Proceedings of the 2012 18th Asia-Pacific Conference on Communications (APCC), Jeju Island, South Korea, 15–17 October 2012; pp. 574–578. [Google Scholar]
- Zhang, M.; Kim, Y. Universal Soft Demodulation Schemes for M-ary Phase Shift Keying and Quadrature Amplitude Modulation. IET Commun. 2016, 10, 316–326. [Google Scholar] [CrossRef]
- Zhang, M.; Kim, S. A New Soft Decoding Method for Systematic LT Codes. In Proceedings of the 20th European Wireless Conference, Barcelona, Spain, 14–16 May 2014; pp. 1–6. [Google Scholar]
- Hu, K.; Castura, J.; Mao, Y. Performance-Complexity Tradeoffs of Raptor Codes over Gaussian Channels. IEEE Commun. Lett. 2007, 11, 343–345. [Google Scholar] [CrossRef]
- Jenka, H.; Mayer, T.; Stockhammer, T.; Xu, W. Soft Decoding of LT-codes for Wireless Broadcast. Available online: https://www.eurasip.org/Proceedings/Ext/IST05/papers/390.pdf (accessed on 28 July 2019).
- Ma, Y.; Yuan, D.; Zhang, H. Fountain Codes and Applications to Reliable Wireless Broadcast System. In Proceedings of the Information Theory Workshop, Chengdu, China, 22–26 October 2006; pp. 66–70. [Google Scholar]
- Zhang, M.; Kim, S. A Statistical Approach for Dynamic Rain Attenuation Model. In Proceedings of the 29th AIAA International Communications Satellite Systems Conference, Nara, Japan, 28 November–1 December 2011. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Chan, S.; Kim, S. Soft Iterative Decoding Algorithms for Rateless Codes in Satellite Systems. Algorithms 2019, 12, 151. https://doi.org/10.3390/a12080151
Zhang M, Chan S, Kim S. Soft Iterative Decoding Algorithms for Rateless Codes in Satellite Systems. Algorithms. 2019; 12(8):151. https://doi.org/10.3390/a12080151
Chicago/Turabian StyleZhang, Meixiang, Satya Chan, and Sooyoung Kim. 2019. "Soft Iterative Decoding Algorithms for Rateless Codes in Satellite Systems" Algorithms 12, no. 8: 151. https://doi.org/10.3390/a12080151
APA StyleZhang, M., Chan, S., & Kim, S. (2019). Soft Iterative Decoding Algorithms for Rateless Codes in Satellite Systems. Algorithms, 12(8), 151. https://doi.org/10.3390/a12080151





