OPTIMUS: Self-Adaptive Differential Evolution with Ensemble of Mutation Strategies for Grasshopper Algorithmic Modeling

Abstract

Most of the architectural design problems are basically real-parameter optimization problems. So, any type of evolutionary and swarm algorithms can be used in this field. However, there is a little attention on using optimization methods within the computer aided design (CAD) programs. In this paper, we present Optimus, which is a new optimization tool for grasshopper algorithmic modeling in Rhinoceros CAD software. Optimus implements self-adaptive differential evolution algorithm with ensemble of mutation strategies (jEDE). We made an experiment using standard test problems in the literature and some of the test problems proposed in IEEE CEC 2005. We reported minimum, maximum, average, standard deviations and number of function evaluations of five replications for each function. Experimental results on the benchmark suite showed that Optimus (jEDE) outperforms other optimization tools, namely Galapagos (genetic algorithm), SilverEye (particle swarm optimization), and Opossum (RbfOpt) by finding better results for 19 out of 20 problems. For only one function, Galapagos presented slightly better result than Optimus. Ultimately, we presented an architectural design problem and compared the tools for testing Optimus in the design domain. We reported minimum, maximum, average and number of function evaluations of one replication for each tool. Galapagos and Silvereye presented infeasible results, whereas Optimus and Opossum found feasible solutions. However, Optimus discovered a much better fitness result than Opossum. As a conclusion, we discuss advantages and limitations of Optimus in comparison to other tools. The target audience of this paper is frequent users of parametric design modelling e.g., architects, engineers, designers. The main contribution of this paper is summarized as follows. Optimus showed that near-optimal solutions of architectural design problems can be improved by testing different types of algorithms with respect to no-free lunch theorem. Moreover, Optimus facilitates implementing different type of algorithms due to its modular system.

1. Introduction

1.1. The Necessity of Optimization in Architecture

Architectural design problems have an excessive number of design parameters. All possible combinations of design parameters correspond to thousands of different design alternatives. It is difficult to choose the desirable design within such a big search space. In addition, architectural design requires different performance aspects to be satisfied as design objectives focus on various topics (e.g., social, economic, physiological, health, safety, structural, cultural, sustainability, etc.) [1]. Some of these performance aspects (e.g., energy, and daylight) require non-linear equations, which increase the level of the complexity. All these refer that decision-making is highly important in the early stages of the design process. Because, the decisions that are taken in the early design phases have a great impact on the following design stages. As a result, they influence the overall performance and the appearance of the constructed building. At this point, computational optimization techniques became a necessity in architectural design.

Regarding the computational optimization techniques, metaheuristic algorithms can play a vital role for not only presenting promising design alternatives but also for dealing with complexity [2]. On the other hand, these algorithms do not guarantee to finding the global optimal solutions [3]. However, they can present near-optimal results within a reasonable time. For a decision maker, providing a near-optimal solution in a reasonable time can be more advantageous than presenting the optimal solution within extremely long time. To discover desirable solutions, metaheuristics are usually inspired by the natural processes (such as interactions within swarms and evolution over the generations). Some of these metaheuristic algorithms are harmony search (HS) [4], particle swarm optimization (PSO) [5], differential evolution (DE) [6,7], genetic algorithm (GA) [8], ant colony optimization (ACO) [9], simulated annealing (SA) [10], and evolutionary algorithm (EA) [11]. According to current state of the art, evolutionary computation and swarm optimization algorithms are the most popular metaheuristics in architectural domain [2].

1.2. Performative Computational Architecture Framework

In order to investigate how the desirable solution can be found in the early phase of the design process, a general framework called performative computational architecture (PCA) [1,2] is considered in this paper. PCA proposes an iterative method based on form finding, performance evaluation, and optimization as illustrated in Figure 1. The form-finding stage includes the geometric generation using parameters in algorithmic modeling environments. The performance evaluation stage comprises of the numeric assessments of performance aspects to evaluate how well the form meets with the objectives. Optimization stage corresponds the metaheuristic algorithms for discovering desirable design solutions within a systematic search process.

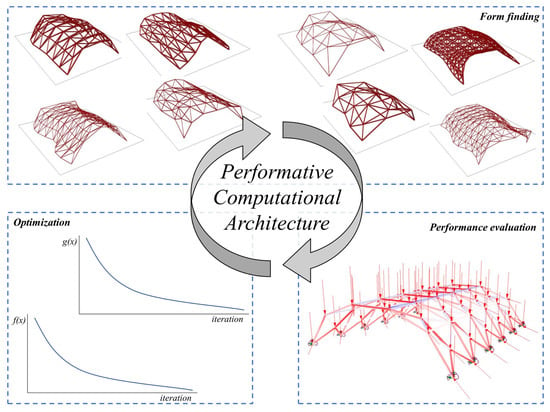
Figure 1. Performative computational architecture (PCA) framework.

1.3. Current Optimization Tools in Grasshopper

In this section, existing single objective optimization tools for grasshopper (GH) (available in www.food4rhino.com) are reviewed. Algorithm applications for specific optimization problems (such as topology optimization for structure) are not considered. In this context, Galapagos, Goat, Silvereye, Opossum, Dodo, and Nelder–Mead optimization plug-ins, shown in Figure 2, are explained. Some of these plug-ins have been compared in building optimization problems in the literature, that can be found in [12,13,14,15].

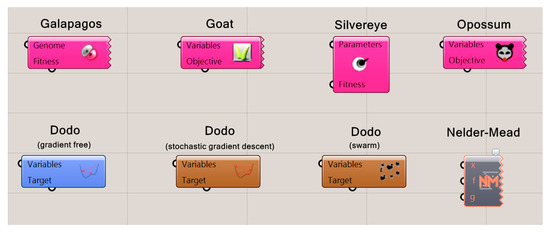
Figure 2. Existing single-objective optimization plug-ins in grasshopper (GH).

1.3.1. Galapagos

Galapagos [16] is one of the first released optimization plug-in for GH. The tool provides two heuristic optimization algorithms, which are GA [8] and SA [10]. Author of the tool suggests SA for rough landscape navigation, whereas evolutionary solver for finding reliable intermediate solutions. Majority of the design optimization papers in the literature utilized Galapagos tool in dealing with energy [17,18,19], daylight [20,21], both energy and daylight [22,23] and structure [24,25,26].

1.3.2. Goat

Goat [27] uses the NLopt library [28] in the graphical user interface of Galapagos. The tool considers a mathematically-rigorous approach (gradient-free optimization algorithm) to reach fast and deterministic results. Goat provides several optimization algorithms as well. These are constrained optimization by linear approximation (COBYLA), bound optimization by quadratic approximation (BOBYQA), subplex algorithm (Sbplx), the dividing rectangles algorithm (DIRECT), and controlled random search 2 (CRS2). Very recently, Goat is used for building energy optimization [14] and structure optimization [29,30].

1.3.3. Silvereye

Despite the gradient-free optimization and evolutionary computation, Silvereye [15] is one of the swarm intelligence optimization plug-ins released for GH. The tool considers ParticleSwarmOptimization.dll, which is a shared library containing an implementation of the core version of the PSO. In the literature, Silvereye is used in the design optimization problems that are focusing on energy [14], micro climate [31] and structural [29].

1.3.4. Opossum

Opossum [32] is the first model-based optimization tool for GH. The solver is based on an open-source library for black-box optimization with costly function evaluations (RBFOpt) [33] such as energy and daylight simulations. RBFOpt library uses the radial basis function with local search while discovering satisfactory solutions with a small number of function evaluations. Opossum is used in several design problems to deal with daylight [34], structure [29,30] and energy [14].

1.3.5. Dodo

Dodo [35] is a plug-in based on different implementation of optimization algorithms. These are non-linear gradient free optimization based on NLopt library [28], stochastic gradient descent algorithm, and swarm optimization. In addition, Dodo also provides several supervised and unsupervised neural network algorithms.

1.3.6. Nelder–Mead Optimization

Nelder–Mead Optimization [36] is the first tool based on the Nelder–Mead method [37], a local search-based optimization algorithm, in GH. Compared to heuristics, Nelder–Mead typically has fewer function evaluations for computationally expensive models. In addition, the implementation of Nelder–Mead Optimization also allows considering multiple constraints using Kreisselmeier-Steinhauser function [38].

1.4. This Study: Optimus

In the field of computer science, different types of metaheuristic algorithms have been suggested to solve real-parameter optimization problems by researchers and engineers in many years. As a common approach, the performance of each developed algorithm is tested by using a set of the standard benchmark problems such as Sphere, Schwefel’s, Rosenbrock’s, Rastrigin’s, etc. For real-world problems, this test is done by using benchmark instances. The main reason for comparing algorithms is based on the no free lunch theorem (NFLT) [39]. The performance of an optimization algorithm depends on the nature of the problem. In other words, one algorithm can outperform another algorithm in a specific problem. Thus, NFLT argues that there is no global optimization algorithm, which can present the best results for all real-world and benchmark problems.

In the field of architecture, testing different types of algorithms for the same architectural design problem is not a common approach. One of the most important reason of this fact is that computer aided design (CAD) tools of architects does not include optimization algorithms in a wide range. According to the current state of the art [40], only 3% of total users of optimization tools are architect in the domain of building performance optimization. This fact clearly shows that there is a little attention on using optimization methods within the CAD programs. Therefore, this paper introduces a new optimization solver, called Optimus, with significant features listed below:

• Compatible with parametric design models created in GH [16] algorithmic modeling for Rhinoceros [41] CAD software.
• Supports PCA framework outlined in previous section.
• Implements a self-adaptive [42] differential evolution algorithm with ensemble of mutation strategies [43] (jEDE), explained in Section 3.
• Presents the highest performance when compared to other optimization algorithms available in GH reviewed in Section 1.3.

  ○

  The performance of the Optimus is tested by benchmark suite, which consists of standard single objective unconstrained problems and some of the test problems proposed in IEEE Congress on Evolutionary Computation 2005 (CEC 2005) [44]. Problem formulations and optimization results of these benchmarks are given in Section 4.1.

  ○

  Finally, Optimus is tested with a design optimization problem. The problem formulation and optimization results are given in Section 4.2.

The development process of the Optimus is illustrated in Figure 3.

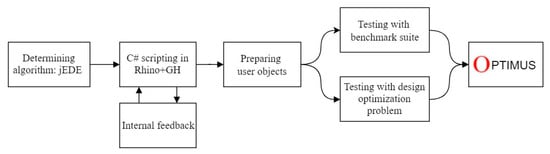
Figure 3. Optimus development process.

2. Self-Adaptive Differential Evolution Algorithm with Ensemble of Mutation Strategies

Metaheuristics are one of the most used optimization methods in the domain of architectural design [2]. These algorithms can avoid local minima and maxima while coping with real-parameters in large search spaces. In addition, metaheuristics can present near-optimal results when compared to other direct search methods in a reasonable time [3].

Swarm intelligence (SI) and evolutionary algorithms (EAs) are the most common sub-categories of metaheuristics. These algorithms are inspired by nature using different search strategies. SI is based on interactions of swarms such as flocks of birds, schools of fish, ants and bees. Some examples of SI can be shown as Ant Colony Optimization (ACO) [9] and Particle Swarm Optimization (PSO) [45,46]. EAs are in the class of population-based metaheuristic optimization algorithms. EAs are inspired by the mechanisms of biological evolution that mimics the selection and reproduction processes of living organisms. EAs are very effective to deal with NP-hard problems. Some examples of EAs are Genetic Algorithms (GAs) [8,47]. Genetic Programming (GP) [48], Evolution Strategy (ES) [49], and DE [7].

DE, which is introduced by Storn and Price [7], is potentially one of the most powerful stochastic real-parameter optimization algorithms in the literature. The algorithm can converge very fast in solving real-world problems such as in scheduling [50], optics [51], communication [6], power systems [52], pattern recognition [53] and recently in architectural design [54,55]. A recent survey by Das and Suganthan [56,57] clearly explained the history of DE and its success. DE algorithm has many advantages. The simple code structure of the algorithm facilitates its implementation. Other advantage is that the number of control parameters in DE is few, which are crossover rate ($CR$), mutation rate ($MR$), and population size ($NP$). In classical DE, these control parameters are constant during the whole optimization process. However, a simple change in $MR$ or $CR$ generation strategies can significantly improve the performance of the algorithm. Therefore, some variants of DE in the literature focus on parameter settings as presented in [42,58]. Moreover, DE can tackle the large scale and computationally expensive optimization problems. Because, the space complexity of DE is low as mentioned in [59].

2.1. The Basic Differential Evolution

The classical DE has four main stages. There is a recursive process among second, third and fourth steps as follows:

• Initialization for generating the initial target population once at the beginning.
• Reproduction with mutation for generating the mutant population by using the target population.
• Reproduction with crossover for generating the trial population by using the mutant population.
• Selection to choose the next generation among trial and target populations using one-to-one comparison. In each generation, individuals of the current population become the target population.

2.1.1. Initialization

In the basic $DE$ algorithm, the initial target population has $NP$ individuals with a $D$-dimensional real-parameter vectors. Each vector is obtained randomly and uniformly within the search space restricted by the given minimum and maximum bounds: $\left[x_{ij}^{min},x_{ij}^{max}\right]$. Thus, the initialization of j-th component of i-th vector can be defined as:

$$x_{ij}^0=x_{ij}^{min}+\left(x_{ij}^{max}-x_{ij}^{min}\right)\times r,$$

(1)

where $x_{ij}^0$ is the i-th target population at generation $g=0$; and $r$ is a uniform random number in the range $\left[0,1\right]$.

2.1.2. Mutation

The difference vector in mutation operator is one of the main strengths of DEs [7]. Hence, DE differs from other EAs since it relies on a difference vector with a scale factor $MR$. The mutation process is the first step to generate new solutions. In order to obtain mutant population, two individuals are randomly chosen from the target population. The weighted difference of these individuals is added to a third individual from the target population as in Equation (2).

$$v_{ij}^g=x_{kj}^{g-1}+MR\times \left(x_{lj}^{g-1}-x_{mj}^{g-1}\right)$$

(2)

where $k,l,m$ are three randomly chosen individuals from the target population such that $\left(k\ne l\ne m\ne i\in \left(1,..,NP\right)\right)$ and $j=1,..,D$. $MR>0$ is a mutation scale factor influencing the differential variation between two individuals. $v_{ij}^g$ is the mutant population in generation $g$.

2.1.3. Crossover

To obtain the trial population, a binomial crossover is applied to each variable. If a randomly and uniformly generated number $r\left[0,1\right]$ is less than or equal to the crossover rate ($CR$), the individuals from mutant population is chosen, otherwise target individuals are chosen. Simply, trial population is generated by recombining mutant individuals with their corresponding target individuals as follows:

$$u_{ij}^g=\{\begin{array}{cc}{v}_{ij}^g& if{r}_{ij}^g\le CRorj=D_j\\ x_{ij}^{g-1}& otherwise\end{array},$$

(3)

where the index $D_j$ is a randomly chosen dimension from $\left(j=1,..,D\right)$. It makes sure that at least one parameter of the trial population $u_{ij}^g$ will be different from the target population $x_{ij}^{g-1}$. $CR$ is a user-defined crossover constant in the range $\left[0,1\right]$, and $r_{ij}^g$ is a uniform random number in the interval $\left[0,1\right]$ whereas $u_{ij}^g$ is the trial population at generation $g$.

When trial population is obtained, parameter values might violate search boundaries. Therefore, the solution can be restricted. For this reason, parameter values that are violating the search range are randomly and uniformly re-generated as in Equation (4).

$$x_{ij}^g=x_{ij}^{min}+\left(x_{ij}^{max}-x_{ij}^{min}\right)\times r.$$

(4)

2.1.4. Selection

For the next generation, selection process is realized, which is based on the survival of the fittest among the trial and target populations. The population that has the lower fitness value is chosen according to one-to-one comparison, as in Equation (5).

$$x_i^g=\{\begin{array}{cc}{u}_i^g& iff\left(u_i^g\right)\le f\left(x_i^{g-1}\right)\\ x_i^{g-1}& otherwise\end{array}.$$

(5)

2.2. Self-Adaptive Approach

In this paper, self-adaptive DE [42], so called $jEDE$, is employed. The $jDE$ is very simple, effective and converges much faster than the basic DE, especially when the dimensionality of the problem is high or the problem is complex. In the $jDE$, each individual has its own $M{R}_i$ and $C{R}_i$ values. In this paper, they are initially taken as $C{R}_i=0.5$ and $M{R}_i=0.9$ and they are updated as follows:

$$M{R}_i^g=\{\begin{array}{cc}M{R}_l+r_1.M{R}_u& if{r}_2<t_1\\ M{R}_i^{g-1}& otherwise\end{array}$$

(6)

$$C{R}_i^g=\{\begin{array}{cc}{r}_3& if{r}_4<t_2\\ C{R}_i^{g-1}& otherwise\end{array},$$

(7)

where $r_j\in \left\{1,2,3,4\right\}$ are uniform random numbers in the range $\left[0,1\right]$. $t_1$ and $t_2$ represent the probabilities to adjust the $MR$ and $CR$. They are taken as $t_1=t_2=0.1$ and $M{R}_{\mathrm{l}}=0.1$ and $M{R}_{\mathrm{u}}=0.9$.

2.3. Ensemble Approach

In addition to the self-adaptive approach, an ensemble approach [43] is employed in the jDE, so called jEDE. This means that instead of using one type of mutation strategy with fixed parameter setting as in the basic DE, each mutant individual is generated according to different mutation strategies with different parameter settings. In this approach, each dimension has values pool for competition of producing better future offspring according to their success in the past generations. In this paper, following mutation strategies ($M_i$) are considered as in Equations (8)–(10). In $M_1$, the individuals that formed the mutant population are randomly selected. In $M_2$ and $M_3$, strategies are benefitted from the information of the best solution (xbest) so far.

$$ifST{R}_i=0M_1:v_i^{j,t+1}=x_k^{j,t}+M{R}_i\times \left(x_l^{j,t}-x_m^{j,t}\right)$$

(8)

$$ifST{R}_i=1M_2:v_{ij}^{j,t+1}=x_{best}^{j,t}+M{R}_i\times \left(x_l^{j,t}-x_m^{j,t}\right)$$

(9)

$$ifST{R}_i=2M_3:v_i^{j,t+1}=x_i^{j,t}+M{R}_i\times \left(x_{best}^{j,t}-x_i^{j,t}\right)+F\times \left(x_k^{j,t}-x_l^{j,t}\right),$$

(10)

where $k,l,m$ are three randomly selected individuals from the target population such that $\left(k\ne l\ne m\ne i\in \left(1,..,NP\right)\right)$ and $j=1,..,D$. $M{R}_i>0$ is a mutation scale factor, in our jEDE, it is generated by using self-adaptive procedure. $ST{R}_i$ is the strategy used in each population to choose different mutation strategies. The pseudo code of the jEDE is given in Algorithm 1.

Algorithm 1. The self-adaptive differential evolution algorithm with ensemble of mutation strategies.

1: Set parameters g = 0, NP = 100, $M_{max}$ = 4 2: Establish initial population randomly 3: $P^g=\left\{x_1^g,..,x_{NP}^g\right\}with{x}_i^g=\left\{x_{i1}^g,..,x_{iD}^g\right\}$ 4: Assign a mutation strategy to each individual randomly 5: $M_i=rand()\%M_{max}$ $fori=1,..,NP$ 6: Evaluate population and find $x_{best}^g$ 7: $f\left(P^g\right)=\left\{f\left(x_1^g\right),..,f\left(x_{NP}^g\right)\right\}$ 8: Assign CR[i] = 0.5 and F[i] = 0.9 to each individual 9: Repeat the following for each individual $x_i^g$ 10: Obtain $v_i^g=M_i\left(x_i^g\right)$ 11: Obtain $u_i^g=C{R}_i\left(x_i^g,v_i^g\right)$ 12: Obtain $x_i^g=\{\begin{array}{cc}{u}_i^g& iff\left(u_i^g\right)\le f\left(x_i^{g-1}\right)\\ x_i^{g-1}& otherwise\end{array}$ 13: If $f\left(u_i^g\right)>f\left(x_i^{g-1}\right)$, $M_i=rand()\%M_{max}$ 14: If $f\left(x_i^g\right)\le f\left(x_{best}^g\right)$, $x_{best}^g=x_i^g$ 15: Update $F_i^g$ and $C{R}_i^g$ 16: If the stopping criterion is not met, go to Lines 9–15 17: Else stop and return ${\pi }_{best}$

3. Optimus

Optimus is a new optimization plug-in (https://www.food4rhino.com/app/optimus) developed for GH. The beta version (1.0.0) of the plug-in implements the self-adaptive [42] differential evolution algorithm with ensemble of mutation strategies [43] (jEDE). The algorithm is coded in C#, which is one of the available programming languages for custom scripting component in the GH. Optimus is based on a modular approach with many C# items. Every step of the optimization process can be observed within these items. Figure 4 shows the eight components of Optimus, which are categorized under three main titles, as follows:

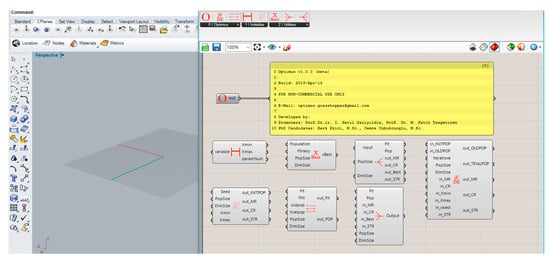
Figure 4. Components of Optimus v1.0.0 (beta).

• Optimus consists of
  • ReadMe (giving details about Optimus),
  • jEDE (using jEDE algorithm, generating mutant and trial populations)
  • One-to-one (enabling selection process for next generation)
• Initialize consists of
  • GetBound (taking the boundaries of design variables in $D$ dimensions)
  • InitPop (generating initial population for $NP$ population size in $D$ dimensions)
• Utilities consists of
  • xBest (finding chromosomes that has the lowest fitness value in the population)
  • Merge (collecting the fitness, population, xBest and optimization parameters)
  • Unmerge (separating the fitness, population, xBest and optimization parameters)

To manage the main loop of the Optimus, the HoopSnake component [60] is used for enabling feedback loops (recursive executions) within the GH.

In the Optimus, each of the eight components is transferred to GH clusters by defining collections of inputs and outputs as shown in Figure 5. This gives a flexibility to the user for improving the C# code according to his/her own implementation purposes. As next step, each cluster is converted to GH user object files, which are provided in the supplementary materials. By this way, Optimus can be used as a plug-in of the GH.

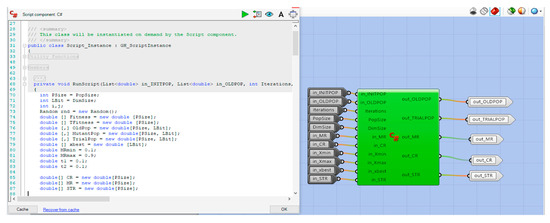
Figure 5. Example cluster implementation for self-adaptive differential evolution algorithm with ensemble of mutation strategies (jEDE) component.

The user needs to follow several steps for using Optimus:

• Place GetBound on the GH canvas and connect with number sliders.
• Define the population size.
• Get InitPop for initialization using population size and output of GetBound.
• Evaluate initial fitness using the output of InitPop.
• Internalize the initial fitness.
• Place xBest on the GH canvas.
• Get Merge and connect with internalized initial fitness and outputs of InitPop and xBest.
• Connect Merge with starting input (S) of HoopSnake.
• Place UnMerge on the GH canvas and connect with feedback output (F) of HoopSnake.
• Get jEDE and connect outputs of UnMerge, InitPop, GetBound.
• Evaluate trial fitness using the output of jEDE.
• Get One-to-One and connect with initial fitness, trial fitness and outputs of jEDE.
• Place xBest and connect outputs of One-to-one for updating the new best chromosome.
• Get Merge and connect outputs of jEDE, One-to-one, and xBest.
• Complete the loop by connecting the output of Merge to the data input (D) of the HoopSnake.

These steps are visualized in Figure 6 and an example file is shared in supplementary materials.

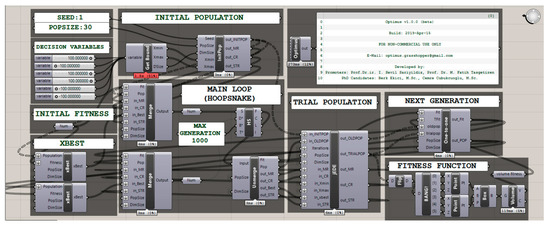
Figure 6. Visualization of the Optimus loop.

To save some computation time, Optimus does not update number sliders in the GH. During the optimization process of the design problem, the geometry is generated with initial and trial populations. For this reason, $NP$ size of geometries is observed in each iteration. During the initial stage, various types of design alternatives are generated. However, when the Optimus is converged, similar geometries are observed, as shown in Figure 7.

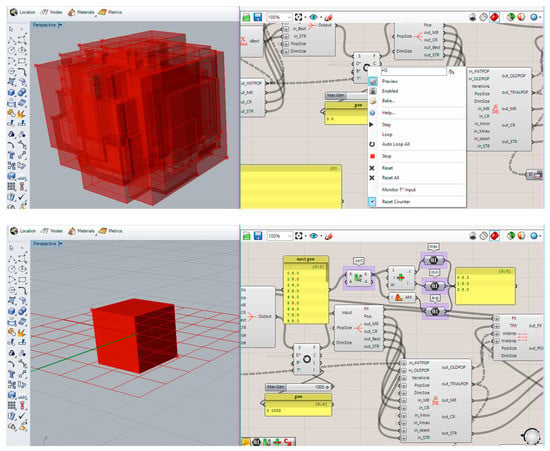
Figure 7. Examples of initial and optimized populations.

4. Experiments

In this section, we explain how the experiments were performed to test the performance of the Optimus in comparison to the other chosen plug-ins. As mentioned before, the evaluations are done by using standard benchmark problems in the literature and one architectural design problem proposed by the authors.

4.1. Benchmark Suite

The performance of the Optimus (jEDE algorithm) was firstly tested by using the following benchmark suite, which consists of 20 test functions. The first ten functions in the benchmark suite were classical test problems that have been commonly used in the literature. The remaining ten functions are taken from the benchmark suit presented in the CEC 2005 Special Session on Real-Parameter Optimization. These functions have been modified from the classical test problems in order to locate their global optimum under some circumstances such as shifted and/or rotated landscape, optimum placed on bounds, Gaussian noise and/or bias added etc. [44]. This fact makes these functions more difficult to solve than the classical test functions. In our test suit, $F_1$ to $F_5$ are unimodal, $F_6$ to $F_{10}$ are multimodal functions. All the benchmark functions are minimization problems. Our benchmark suite is presented in Table 1. These functions are summarized in Appendix A.

Table 1. Benchmark Suite.

Notation	Function
$F_{sph}$	Sphere Function
$F_{ros}$	Rosenbrock’s Function
$F_{ack}$	Ackley’s Function
$F_{grw}$	Griewank’s Function
$F_{ras}$	Rastrigin’s Function
$F_{sch}$	Generalized Schwefel’s Problem 2.26
$F_{sal}$	Salomon’s Function
$F_{wht}$	Whitely’s Function
$F_{pn1}$	Generalized Penalized Function 1
$F_{pn2}$	Generalized Penalized Function 2
$F_1$	Shifted Sphere Function
$F_2$	Shifted Schwefel’s Problem 1.2
$F_3$	Shifted Rotated High Conditioned Elliptic Function
$F_4$	Shifted Schwefel’s Problem 1.2 With Noise in Fitness
$F_5$	Schwefel’s Problem 2.6 With Global Optimum on Bounds
$F_6$	Shifted Rosenbrock’s Function
$F_7$	Shifted Rotated Griewank’s Function without Bounds
$F_8$	Shifted Rotated Ackley’s Function with Global Optimum on Bounds
$F_9$	Shifted Rastrigin’s Function
$F_{10}$	Shifted Rotated Rastrigin’s Function

4.1.1. Experimental Setup and Evaluation Criteria

All the benchmark functions were coded in C# as individual components in the GH environment. These components are also available in supplementary materials as GH files to contribute evaluations of further developed architectural design optimization tools. Furthermore, all the benchmark functions ran on a computer that has Intel Core I7-6500U CPU @ 2.50 GHz with 16 GB RAM. Both the number of dimension $D$ and the population size $NP$ are taken as 30 to limit the search space. To make a fair comparison, termination criteria defined as 30 min for each component. For each problem instance, five replications carried out for each function and for each tool (thus, the total run time is 12,000 min). For evaluating the performance of the algorithms (of the components), we simply reported $fx\_min$, $fx\_max$ and $fx\_avg$ where $fx\_min$ is the minimum fitness value of function $x$, $fx\_max$ is the maximum fitness value of function $x$ and $fx\_avg$ is the average fitness value of function $x$, after all replications for each tool. The maximum number of fitness evaluations ($FES$) within 30 min for each tool are also recorded, which means how many times the fitness is tested during each 30-min optimization process.

4.1.2. Experimental Results

As mentioned before, Galapagos employs GA, SilverEye (v1.1.0) uses PSO and Opossum (v1.5.0) considers RBFOpt for enabling architectural design optimization in the GH environment. We compared results of Optimus, which uses jEDE, with those three optimization tools to present its performance. In addition, all the runs for each component and for each function were taken by the authors. Table 1 shows the fitness results of Optimus, Opossum, SilverEye, and Galapagos together with optimal fitness values of each function. Table 2 clearly indicates the superiority of the Optimus over other optimization tools such that it yielded the lowest minimum function values ($fx\_min$) in nineteen (19) functions out of twenty (20) functions, significantly. On the other hand, Galapagos favors Optimus in only one function ($F_8$) with a very small difference. Maximum ($fx\_max$) and average ($fx\_avg$) function values in Table 1 further justify the better performance of the Optimus in such a way that the maximum and average function values of Optimus are closer to optimal fitness values in nineteen (19) functions than those yielded by other tools. Furthermore, the average number of function evaluations ($FES$) within thirty minutes in each problem were the highest in Optimus. This clearly shows high margins between Optimus and other components where Optimus was tremendously faster in each iteration. For example, when solving $F_{sph}$, the Optimus (jEDE) approximately realized 5844 FES/minute, whereas GA made 1643 FES/minute, PSO made 1205 FES/minute, RBFOpt made 85 FES/minute. These facts explicitly imply the superiority of Optimus over other components in solving benchmark suite.

Table 2. Comparison of Optimus, Opossum, Silvereye, Galapagos (D = 30, NP = 30, termination: 30 min).

		Optimus_jEDE	Opossum_RBFOpt	SilverEye_PSO	Galapagos_GA	Optimal
$F_{sph}$	$f\left(x\right)\_min$	0.0000000$\times {10}^0$	1.4000000$\times {10}^{-5}$	5.9000000$\times {10}^{-5}$	1.1709730$\times {10}^0$	0
	$f\left(x\right)\_max$	0.0000000$\times {10}^0$	5.8000000$\times {10}^{-5}$	2.7057298$\times {10}^1$	4.4052130$\times {10}^0$
	$f\left(x\right)\_avg$	0.0000000$\times {10}^0$	3.6400000$\times {10}^{-5}$	5.4171618$\times {10}^0$	2.7928586$\times {10}^0$
	Std.Dev.	0.0000000$\times {10}^0$	1.8039956$\times {10}^{-5}$	1.0820072$\times {10}^1$	1.1492298$\times {10}^0$
	FES	194,520	3225	31,560	34,260
$F_{ros}$	$f\left(x\right)\_min$	0.0000000$\times {10}^0$	2.7485056$\times {10}^1$	1.6689612$\times {10}^1$	6.0863438$\times {10}^3$	0
	$f\left(x\right)\_max$	3.9866240$\times {10}^0$	2.1030328$\times {10}^2$	5.8965910$\times {10}^4$	2.2859534$\times {10}^4$
	$f\left(x\right)\_avg$	2.3919744$\times {10}^0$	9.0892522$\times {10}^1$	1.3859753$\times {10}^4$	1.3060872$\times {10}^4$
	Std.Dev.	1.9530389$\times {10}^0$	7.1919037$\times {10}^1$	2.2886020$\times {10}^4$	6.7095472$\times {10}^3$
	FES	149,460	882	26,700	35,070
$F_{ack}$	$f\left(x\right)\_min$	0.0000000$\times {10}^0$	3.3550000$\times {10}^{-3}$	1.3404210$\times {10}^0$	5.7470000$\times {10}^{-2}$	0
	$f\left(x\right)\_max$	1.3404210$\times {10}^0$	2.4098540$\times {10}^0$	3.7340120$\times {10}^0$	1.0270860$\times {10}^0$
	$f\left(x\right)\_avg$	2.6808420$\times {10}^{-1}$	1.3795174$\times {10}^0$	2.2482728$\times {10}^0$	4.8037520$\times {10}^{-1}$
	Std.Dev.	5.3616840$\times {10}^{-1}$	8.5713298$\times {10}^{-1}$	9.1850828$\times {10}^{-1}$	4.0392221$\times {10}^{-1}$
	FES	206,370	1447	38,490	28,710
$F_{grw}$	$f\left(x\right)\_min$	0.0000000v	1.5840000$\times {10}^{-3}$	3.2081000$\times {10}^{-2}$	3.4407200$\times {10}^{-1}$	0
	$f\left(x\right)\_max$	0.0000000$\times {10}^0$	1.7086000$\times {10}^{-2}$	2.6292800$\times {10}^{-1}$	1.0657060$\times {10}^0$
	$f\left(x\right)\_avg$	0.0000000$\times {10}^0$	7.6638000$\times {10}^{-3}$	1.2049020$\times {10}^{-1}$	8.2474220$\times {10}^{-1}$
	Std.Dev.	0.0000000$\times {10}^0$	5.6121253$\times {10}^{-3}$	8.1064770$\times {10}^{-2}$	2.6131521$\times {10}^{-1}$
	FES	151,110	1089	26,610	37,410
$F_{ras}$	$f\left(x\right)\_min$	4.9747950$\times {10}^0$	2.5870757$\times {10}^1$	3.3829188$\times {10}^1$	7.0535550$\times {10}^0$	0
	$f\left(x\right)\_max$	2.3879007$\times {10}^1$	4.1789542$\times {10}^1$	6.1687356$\times {10}^1$	2.9072445$\times {10}^1$
	$f\left(x\right)\_avg$	1.3332448$\times {10}^1$	3.6218407$\times {10}^1$	4.8355074$\times {10}^1$	1.5404780$\times {10}^1$
	Std.Dev.	6.7363920$\times {10}^0$	5.4349940$\times {10}^0$	1.1424086$\times {10}^1$	9.1077975$\times {10}^0$
	FES	206,520	4149	37,650	51,480
$F_{sch}$	$f\left(x\right)\_min$	2.3687705$\times {10}^2$	1.2877414$\times {10}^3$	4.1089621$\times {10}^3$	1.9550066$\times {10}^3$	0
	$f\left(x\right)\_max$	4.7375372$\times {10}^2$	4.0111803$\times {10}^3$	6.1589437$\times {10}^3$	2.7977670$\times {10}^3$
	$f\left(x\right)\_avg$	4.0269072$\times {10}^2$	2.7169368$\times {10}^3$	5.2658793$\times {10}^3$	2.3201102$\times {10}^3$
	Std.Dev.	9.4750668$\times {10}^1$	8.8809862$\times {10}^2$	6.6677783$\times {10}^2$	2.8681876$\times {10}^2$
	FES	148,140	1487	27,210	35,940
$F_{sal}$	$f\left(x\right)\_min$	1.9987300$\times {10}^{-1}$	2.8070190$\times {10}^0$	2.9987300$\times {10}^{-1}$	1.4998750$\times {10}^0$	0
	$f\left(x\right)\_max$	4.9987300$\times {10}^{-1}$	4.3000810$\times {10}^0$	4.9987300$\times {10}^{-1}$	2.8375760$\times {10}^0$
	$f\left(x\right)\_avg$	3.1987300$\times {10}^{-1}$	3.4413810$\times {10}^0$	3.7987300$\times {10}^{-1}$	2.0682340$\times {10}^0$
	Std.Dev.	1.1661904$\times {10}^{-1}$	5.6623101$\times {10}^{-1}$	7.4833148$\times {10}^{-2}$	6.1557512$\times {10}^{-1}$
	FES	201,720	4769	38,640	51,360
$F_{wht}$	$f\left(x\right)\_min$	2.3704633$\times {10}^1$	9.6592754$\times {10}^2$	1.8455490$\times {10}^2$	2.3632742$\times {10}^5$	0
	$f\left(x\right)\_max$	2.4040716$\times {10}^2$	1.6904059$\times {10}^3$	6.2776811$\times {10}^2$	5.5055000$\times {10}^8$
	$f\left(x\right)\_avg$	1.0789137$\times {10}^2$	1.2610498$\times {10}^3$	4.0698894$\times {10}^2$	2.7440867$\times {10}^8$
	Std.Dev.	7.4951993$\times {10}^1$	2.6984398$\times {10}^2$	1.6923390$\times {10}^2$	2.2575944$\times {10}^8$
	FES	146,640	728	23,250	29,730
$F_{pn1}$	$f\left(x\right)\_min$	0.0000000$\times {10}^0$	2.9057000$\times {10}^{-2}$	3.1283800$\times {10}^{-1}$	1.4510000$\times {10}^{-3}$	0
	$f\left(x\right)\_max$	0.0000000$\times {10}^0$	9.0392970$\times {10}^0$	1.3487570$\times {10}^0$	1.7632000$\times {10}^{-2}$
	$f\left(x\right)\_avg$	0.0000000$\times {10}^0$	2.8243854$\times {10}^0$	6.7680180$\times {10}^{-1}$	6.0638000$\times {10}^{-3}$
	Std.Dev.	0.0000000$\times {10}^0$	3.1774566$\times {10}^0$	4.2868737$\times {10}^{-1}$	6.0403379$\times {10}^{-3}$
	FES	203,880	1394	39,420	57,720
$F_{pn2}$	$f\left(x\right)\_min$	0.0000000$\times {10}^0$	2.0400434$\times {10}^1$	1.0000000$\times {10}^{-11}$	1.8037300$\times {10}^{-1}$	0
	$f\left(x\right)\_max$	1.0987000$\times {10}^{-2}$	2.8693232$\times {10}^1$	9.3079800$\times {10}^{-1}$	2.7208440$\times {10}^0$
	$f\left(x\right)\_avg$	2.1974000$\times {10}^{-3}$	2.5384324$\times {10}^1$	2.2552480$\times {10}^{-1}$	1.0041520$\times {10}^0$
	Std.Dev.	4.3948000$\times {10}^{-3}$	3.4851206$\times {10}^0$	3.5679494$\times {10}^{-1}$	9.4298611$\times {10}^{-1}$
	FES	148,380	639	29,040	41,520
$F_1$	$f\left(x\right)\_min$	−4.5000000$\times {10}^2$	−4.4999898$\times {10}^2$	2.6232595$\times {10}^2$	−4.4995998$\times {10}^2$	−450
	$f\left(x\right)\_max$	−4.5000000$\times {10}^2$	−4.4999478$\times {10}^2$	8.0377273$\times {10}^3$	−4.4988406$\times {10}^2$
	$f\left(x\right)\_avg$	−4.5000000$\times {10}^2$	−4.4999680$\times {10}^2$	4.0824562$\times {10}^3$	−4.4992015$\times {10}^2$
	Std.Dev.	0.0000000$\times {10}^0$	1.4829922$\times {10}^{-3}$	2.9460423$\times {10}^3$	3.0428108$\times {10}^{-2}$
	FES	198,060	6156	45,580	66,180
$F_2$	$f\left(x\right)\_min$	−4.5000000$\times {10}^2$	3.4590652$\times {10}^4$	−3.8035693$\times {10}^2$	6.8476195$\times {10}^3$	−450
	$f\left(x\right)\_max$	−4.5000000$\times {10}^2$	4.7978174$\times {10}^4$	5.2590674$\times {10}^2$	1.2302281$\times {10}^4$
	$f\left(x\right)\_avg$	−4.5000000$\times {10}^2$	4.3226072$\times {10}^4$	−1.2838464$\times {10}^2$	1.0174618$\times {10}^4$
	Std.Dev.	0.0000000$\times {10}^0$	4.9030645$\times {10}^3$	3.3183646$\times {10}^2$	1.8557926$\times {10}^3$
	FES	146,010	1061	33,840	50,160
$F_3$	$f\left(x\right)\_min$	6.0045376$\times {10}^4$	1.5561000$\times {10}^7$	1.9264000$\times {10}^6$	1.1250000$\times {10}^7$	−450
	$f\left(x\right)\_max$	2.4850013$\times {10}^5$	7.5084000$\times {10}^7$	8.0820000$\times {10}^6$	2.7772000$\times {10}^7$
	$f\left(x\right)\_avg$	1.2857393$\times {10}^5$	3.7380600$\times {10}^7$	4.5525000$\times {10}^6$	1.7212200$\times {10}^7$
	Std.Dev.	6.4175884$\times {10}^4$	2.0647812$\times {10}^7$	2.0206526$\times {10}^6$	5.6281541$\times {10}^6$
	FES	205,260	1293	48,030	66,000
$F_4$	$f\left(x\right)\_min$	−4.5000000$\times {10}^2$	2.8373782$\times {10}^4$	−4.2715712$\times {10}^2$	7.8877685$\times {10}^3$	−450
	$f\left(x\right)\_max$	−4.5000000$\times {10}^2$	3.9404224$\times {10}^4$	4.0484178$\times {10}^3$	1.1191542$\times {10}^4$
	$f\left(x\right)\_avg$	−4.5000000$\times {10}^2$	3.2359668$\times {10}^4$	5.1724092$\times {10}^2$	9.4535270$\times {10}^3$
	Std.Dev.	0.0000000$\times {10}^0$	4.0412734$\times {10}^3$	1.7663033$\times {10}^3$	1.2966977$\times {10}^3$
	FES	147,240	1055	35,610	53,520
$F_5$	$f\left(x\right)\_min$	9.3362001$\times {10}^2$	4.7527012$\times {10}^3$	7.5856684$\times {10}^3$	1.8506721$\times {10}^4$	-310
	$f\left(x\right)\_max$	2.5603668$\times {10}^3$	5.8813877$\times {10}^3$	1.2910221$\times {10}^4$	2.4057172$\times {10}^4$
	$f\left(x\right)\_avg$	2.0333032$\times {10}^3$	5.3824799$\times {10}^3$	9.4390617$\times {10}^3$	2.0151105$\times {10}^4$
	Std.Dev.	570.1512256	438.2070353	2031.289127	2004.100331
	FES	195,720	1891	47,550	67,560
$F_6$	$f\left(x\right)\_min$	3.9000000$\times {10}^2$	1.4168473$\times {10}^3$	5.0073093$\times {10}^2$	9.7856127$\times {10}^2$	390
	$f\left(x\right)\_max$	3.9398662$\times {10}^2$	1.3904779$\times {10}^4$	4.1540000$\times {10}^9$	9.6995775$\times {10}^3$
	$f\left(x\right)\_avg$	3.9159465$\times {10}^2$	8.7212119$\times {10}^3$	9.8402870$\times {10}^8$	5.6395846$\times {10}^3$
	Std.Dev.	1.9530389$\times {10}^0$	4.6035484$\times {10}^3$	1.5972516$\times {10}^8$	3.5378379$\times {10}^3$
	FES	148,260	687	33,540	48,810
$F_7$	$f\left(x\right)\_min$	4.5162886$\times {10}^3$	4.5162896$\times {10}^3$	5.8669417$\times {10}^3$	4.5172240$\times {10}^3$	-180
	$f\left(x\right)\_max$	4.5162886$\times {10}^3$	4.5162985$\times {10}^3$	7.2432580$\times {10}^3$	4.5290168$\times {10}^3$
	$f\left(x\right)\_avg$	4.5162886$\times {10}^3$	4.5162936$\times {10}^3$	6.5251090$\times {10}^3$	4.5222540$\times {10}^3$
	Std.Dev.	0.0000000$\times {10}^0$	3.1911420$\times {10}^{-3}$	5.4380701$\times {10}^2$	4.7496031$\times {10}^0$
	FES	200,820	10,108	42,060	58,290
$F_8$	$f\left(x\right)\_min$	−1.1905178$\times {10}^2$	−1.1910166$\times {10}^2$	−1.1901775$\times {10}^2$	−1.1940297$\times {10}^2$	-140
	$f\left(x\right)\_max$	−1.1902135$\times {10}^2$	−1.1876717$\times {10}^2$	−1.1892500$\times {10}^2$	−1.1906700$\times {10}^2$
	$f\left(x\right)\_avg$	−1.1903319$\times {10}^2$	−1.1889866$\times {10}^2$	−1.1899553$\times {10}^2$	−1.1919711$\times {10}^2$
	Std.Dev.	1.0538581$\times {10}^{-2}$	1.1070562$\times {10}^{-1}$	3.5483336$\times {10}^{-2}$	1.4127484$\times {10}^{-2}$
	FES	149,670	2018	35,580	52,020
$F_9$	$f\left(x\right)\_min$	−3.1706554$\times {10}^2$	−2.5827181$\times {10}^2$	−2.3690804$\times {10}^2$	−3.1677970$\times {10}^2$	-330
	$f\left(x\right)\_max$	−3.1209075$\times {10}^2$	−2.3567358$\times {10}^2$	−1.6682751$\times {10}^2$	−3.1164785$\times {10}^2$
	$f\left(x\right)\_avg$	−3.1527462$\times {10}^2$	−2.4625749$\times {10}^2$	−1.8917798$\times {10}^2$	−3.1499413$\times {10}^2$
	Std.Dev.	1.7117897$\times {10}^0$	8.0334497$\times {10}^0$	2.5285354$\times {10}^1$	1.8617799$\times {10}^0$
	FES	212,160	5577	47,610	67,560
$F_{10}$	$f\left(x\right)\_min$	−2.7030257$\times {10}^2$	−2.3528777$\times {10}^2$	−1.3299956$\times {10}^2$	4.0215414$\times {10}^1$	-330
	$f\left(x\right)\_max$	−2.2751946$\times {10}^2$	−1.3298172$\times {10}^2$	−8.1262211$\times {10}^1$	1.8543670$\times {10}^2$
	$f\left(x\right)\_avg$	−2.5139841$\times {10}^2$	−1.8578676$\times {10}^2$	−1.0572303$\times {10}^2$	1.1181316$\times {10}^2$
	Std.Dev.	1.4307998$\times {10}^1$	3.9394042$\times {10}^1$	1.8528544$\times {10}^1$	5.7458318$\times {10}^1$
	FES	146,820	1192	35,220	53,070

Results presented in Table 1 are provided in supplementary materials containing minimum fitness values of each replication, as well as their corresponding chromosomes. Considering $fx\_min$, convergence of standard benchmarks is presented in Figure 8, whereas convergence of CEC 2005 benchmarks is given in Figure 9.

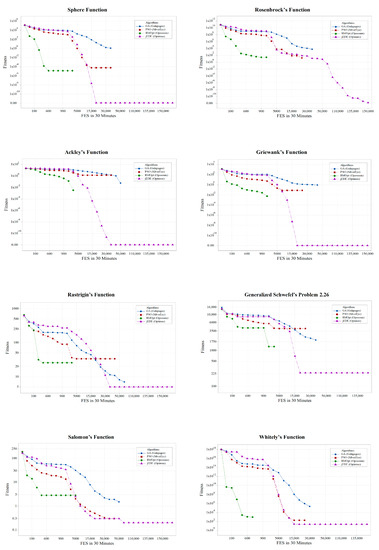
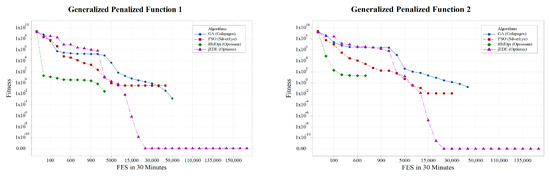
Figure 8. Convergence graphs of standard benchmark functions.

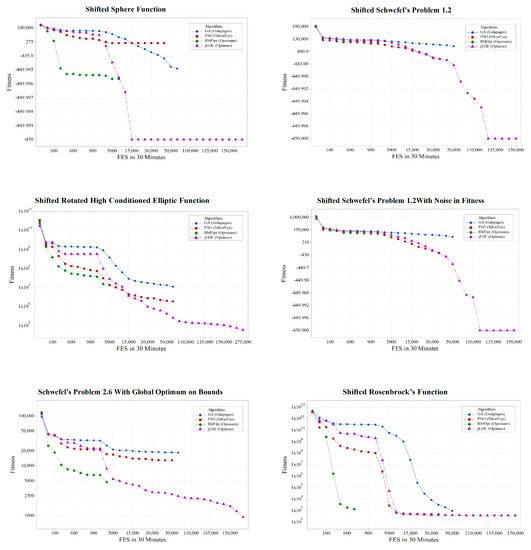
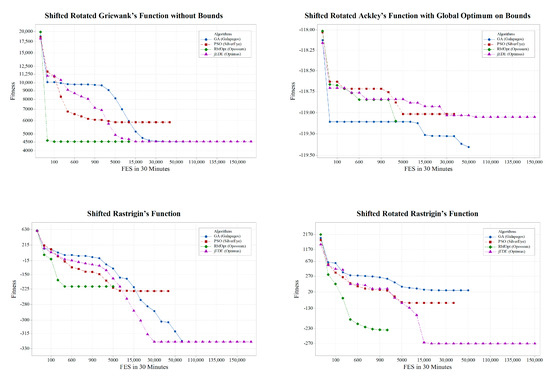
Figure 9. Convergence graphs of CEC2005 benchmark functions.

4.2. Design Optimization Problem

In this part, we present a design problem for a frame structure, which has a span for 30 m by 25 m. Before generating the frame structure, we executed a base surface, which controls the shape of the design. Therefore, a curved surface having 7.5 m height, five axes, and 25 controlling points is generated. Afterwards, 65 parameters are defined for 5 axes to change the shape of the base surface, so the shape of the frame structure. Points on ground level have two parameters for x and y directions, whereas other points have three parameters for changing the positions in all directions. In the next step, using the base surface, we generated the frame structure using truss structure component provided by LunchBox [61] plugin, which consists of several components using different geometrical shapes. In this component, the structure on the base surface is controlled by three parameters. These are division amounts on u and v directions, and the depth of the truss system. Finally, generated frame structure is combined with Karamba 3D plug-in [62], which provides evaluation of parametric structural models in GH. Structural evaluation process is mentioned on the following lines. Development of the parametric model is illustrated in Figure 10.

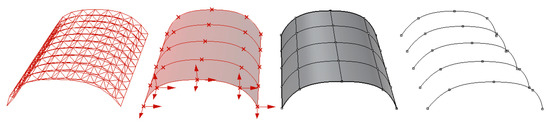
Figure 10. Process of parametric frame structure.

To evaluate each generated structure alternative, each line in the structure model is defined as beam, whereas each point located on the ground level is defined as support points. In addition, cross-section and its parameters are also defined by Karamba just before the evaluation process. For the problem on hand, rectangular cross-section is defined using three parameters. These are height, upper and lower widths of the cross-section. To finalize the necessary inputs, we defined gravity and lateral loads. As gravity load, we considered the distribution of the total mass for each intersecting point. For the lateral load, we applied 2 kN on each intersecting point, as well. The material type of the model is assigned as steel. An example of evaluated model is shown in Figure 11.

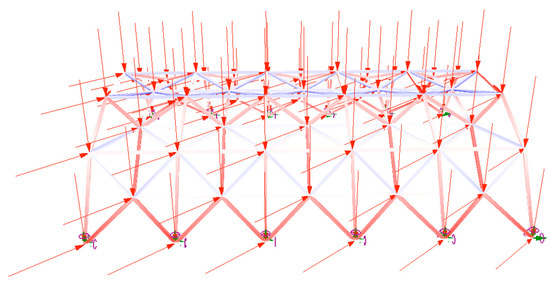
Figure 11. Evaluation of the structure model.

To sum up, 70 parameters are used to define the design optimization problem. This corresponds approximately 1.333 × ${10}^{177}$ alternatives in the search space. The reason of giving such a freedom is to investigate the impact of the design on the performance. Moreover, design problems are different than mathematical benchmark problems. A design problem can have more parameters due to an optimization task (e.g., optimizing the layout scheme and the façade design of a building to find the most desirable plan scheme with the lowest energy consumption). Properties of design parameters are given in Table 3. To show the divergence of the design problem, some of the frame structure alternatives are illustrated in Figure 12.

Table 3. Properties of design parameters.

Notation	Design Parameter	Min	Max	Type
x1–x13	Coordinates of control points in axis 1	−2.00	2.00	Continues
x14–x26	Coordinates of control points in axis 2	−2.00	2.00	Continues
x27–x39	Coordinates of control points in axis 3	−2.00	2.00	Continues
x40–x52	Coordinates of control points in axis 4	−2.00	2.00	Continues
x53–x65	Coordinates of control points in axis 5	−2.00	2.00	Continues
x66	Division amount on u direction	3	10	Discrete
x67	Division amount on v direction	3	10	Discrete
x68	Depth of the truss	0.50	1.00	Continues
x69	Height of the cross-section	10.00	30.00	Continues
x70	Upper and lower width of the cross-section	10.00	30.00	Continues

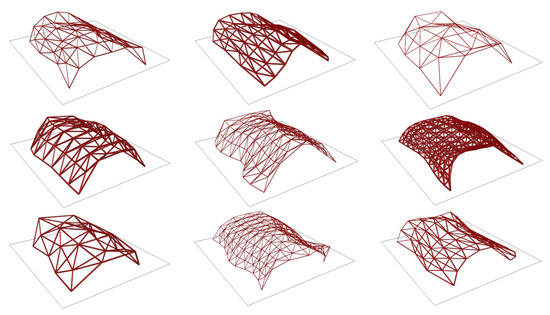
Figure 12. Some alternatives of the design problem.

Objective function, which is minimizing the mass ($m$) subject to displacement ($v$), is formulated as follows:

$Min\left(m\right)$ where $m$ is given by

$$m={\displaystyle \sum }_{i=1}^j{W}_i,$$

(11)

where $W_i$ is the weight of $i$th element of the frame structure and $j$ is the total number of the frame structure elements.

Subject to:

$$v\le 0.1\mathrm{m}$$

(12)

$$v=\frac{F}{K},$$

(13)

where $F$ is the loading force, and $K$ is the bending stiffness of the frame structure. To compare the optimization results of Optimus with others, we defined a penalty function by combining $m$ and $v$ as follows:

$$m=\{\begin{array}{c}mifv\le 0.1\\ 100\ast mo.w.\end{array}.$$

(14)

To sum up, for safety reasons, the final design should have minimum 0.1 m displacement. For this reason, displacement result that has smaller than 0.1 m is a feasible solution. In addition, for minimizing construction cost, the objective is defined as the minimization of the mass. Therefore, the final design should have the smallest amount of steel usage. The higher the mass is the lower the displacement, and the other way around.

4.2.1. Experimental Setup and Evaluation Criteria

The design optimization problem ran on a computer that had Intel Core I7-6500U CPU @ 2.50 GHz with 16 GB RAM. The number of dimensions $D$ was taken as 70, whereas the population size $NP$ was taken as 50. As such the CEC 2005 benchmark problems, the termination criteria was determined as 30 min for each run. For the instance on hand, only one replication carried out for each optimization tool. To evaluate the performance of different optimization tools, we report $fx\_min$, which is the minimum fitness value of the design problem, and $g\left(x\right)$, which is the constraint value of the minimum fitness. The maximum number of fitness evaluations ($FES$) within 30 min for each tool are also recorded, which means how many times the fitness is evaluated during the optimization process. This problem definition is also available in supplementary materials as GH file to contribute evaluations of further developed architectural design optimization tools.

4.2.2. Design Results

After 30 min run for each tool in GH, overview of optimization results is given Table 4. Convergence graph for Optimus, Opossum, SilverEye and Galapagos is also given in Figure 13. In addition, final designs proposed by each algorithm are also illustrated in Figure 14. Based on these results, Optimus and Opossum found feasible solutions, whereas SilverEye and Galapagos discovered infeasible alternatives. Looking at feasible solutions, there is a significant difference between jEDE and RbfOpt. Optimus found smaller mass amount than Opossum. During the optimization process, we also observed that Optimus evaluated fitness function more than other tools. From the point of proposed design alternatives, Galapagos and SilverEye found bigger frame structures with smaller profile dimensions. This causes an increment on both displacement and mass. On the other hand, Opossum presented similar size with Galapagos and Silvereye, but bigger dimension sizes for profile. This suggests smaller amount of displacement. However, the final solution has more than 22 tons of steel. From the point of Optimus, the final design alternative presents the smallest frame structure having small profile sizes. This gives not only an advantage on displacement, but also provides a design alternative having smaller amount of steel comparing with other algorithms. A parametric model with 70 decision variables is a challenging optimization problem in the domain of architecture. From this perspective, the impact of self-adaptive parameter update, and ensemble of mutation strategies can be seen for the architectural design problem.

Table 4. Comparison of Optimus, Opossum, Silvereye, Galapagos (D = 70, NP = 50, termination: 30 min).

		Optimus jEDE	Opossum RBFOpt	Silve Eye_PSO	Galapagos GA
Design problem	$f\left(x\right)\_min$	6.21637$\times {10}^3$	2.25410$\times {10}^4$	6.89062$\times {10}^5$	6.74560$\times {10}^5$
	$g\left(x\right)$	0.0994	0.0996	0.6674	0.9273
	FES	31,800	5102	17,100	19,000

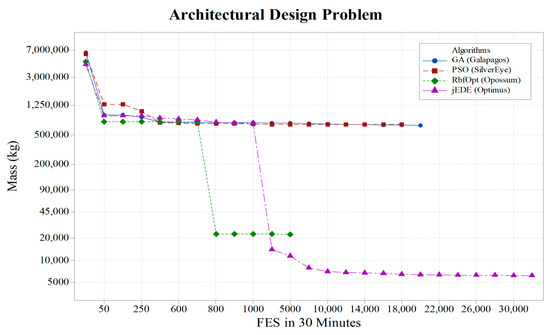
Figure 13. Convergence graph of architectural design problem.

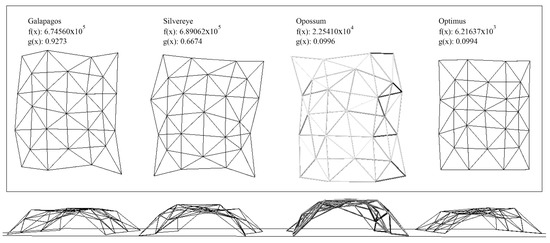
Figure 14. Optimized results of design problem.

Results presented in Table 3 are provided in supplementary materials containing minimum fitness values, and their corresponding chromosomes. The best result discovered by Optimus is illustrated in Figure 15.

Figure 15. Illustration of the best alternative (Optimus) result for design optimization problem.

5. Discussion

In this paper, we presented a new optimization tool called Optimus, which implements jEDE algorithm, for GH. We tested the performance of Optimus using 20 benchmark problems and a design optimization problem against GA, PSO, RBFOpt. Experimental results show that jEDE outperforms these algorithms by finding better fitness values. There are several reasons to explain this fact. First, Optimus uses self-adaptive approach for producing control parameters. This gives an advantage to adapt the algorithm itself according to the nature of the problem. Secondly, Optimus presented significantly smaller fitness values than the other tools. This is related to the ensemble of mutation strategies. While the other algorithms are based on only one mutation operator, Optimus uses three mutation operators. During searching for a better solution, using more than one mutation strategy enlarges the search space. This increases the ability of searching near-optimal results. Thirdly, Optimus does not update number sliders, which corresponds to parameters, for each iteration. Instead, generated populations are directly connected to the geometry. Therefore, required computation time for one generation is less than the other algorithms. Finally, optimal values of some problems are outside of the initialization range (e.g., $F_7$). One may argue that this situation can be faced in architectural design problems, as well. Generating chromosome values outside of the initialization range is possible in the Optimus, whereas it is not possible in the other tools.

RBFOpt algorithm is recently compared with metaheuristics using several building optimization problems in [12,13,14,32]. According to the results, RBFOpt found better solutions than metaheuristics. In these studies, termination criterion is defined as number of iterations during the evaluation of different algorithms. This gives an advantage for RBFOpt, due to ability to discover desirable solutions with small number of function evaluations. However, metaheuristics require more function evaluations to find the optimal solutions. In this study, we defined the termination criterion as run time for 30 min to make a fair comparison. Results show that RBFOpt requires more computation time to execute one function than metaheuristics. For this reason, while comparing these algorithms, rather than iterations and/or function evaluations, run time should be considered as termination criterion.

Fitness functions based on simulations (e.g., energy and daylight) may require a huge amount of time for the convergence during the optimization. From the point of metaheuristics, usage of surrogate models [63] can be a solution to overcome this drawback. Because, surrogate models require less amount of function evaluation while approximating the fitness. By this way, researchers can consider many replications in a short run time.

Furthermore, handling constraints is another important topic for architectural design optimization. Most of the real-world problems require design constraints that may restrict the design alternatives during the optimization process. There are many constraint handling methods that can be practically integrated to the optimization algorithms [64]. In the reviewed literature, only Nelder–Mead optimization tool provides a constraint handling method for the design optimization problems in the GH. To make a fair comparison with Galapagos, SilverEye, and Opossum, we considered penalty function as constraint to find the feasible solution in the design optimization problem. However, there are extremely hard constraints that can be tackled in the real-world problems e.g., equality constraints. Currently, this is not available in GH.

In addition to the advantages of Optimus mentioned above, there are some limitations, as well. Firstly, even though modular approach provides a flexibility when we want to use different algorithms, it requires more plug-in items to generate each step of the optimization. This effects the practical usage of Optimus. Another limitation is evaluation strategy of fitness function. In other words, Optimus creating NP size of list, where each element in the list has D size of dimensions. All these parameters (with NPxD size) are sending to the objective function for fitness evaluation. Then, we obtain NP size of fitness results simultaneously. In the other tools, each parameter is sending to the fitness function in sequence. Then, the fitness function is evaluated. This fact gives an advantage for Optimus in terms of computation time but it may not be suitable for some of the architectural design problems.

6. Conclusions

As the conclusion, this paper presented a new optimization plug-in, called Optimus for grasshopper algorithmic modelling (GH) in the Rhinoceros CAD program. A self-adaptive differential evolution algorithm with ensemble of mutation strategies was implemented in Optimus for architectural design optimization problems. To test the algorithm performance, experimental design was made by using standard test problems in the literature, some of the test problems proposed in IEEE CEC 2005 and an architectural design problem. In general, Optimus outperformed other optimization tools in GH. This paper showed that an algorithm that presents a good performance in solving real-parameter benchmark functions can also find more desirable solutions in solving architectural design problems.

As future work, Optimus will be further improved by implementing different types of metaheuristic algorithms due to NFLT. These algorithms can be variants of PSO, GA, HS, and DE. Moreover, Optimus can be updated for constrained optimization problems using near-feasibility threshold [65,66], Superior of Feasibility [67], and Epsilon constraint [68]. Moreover, ensemble of constraint handling techniques [69] can be used in Optimus that may play a crucial role in architectural design problems. Finally, Optimus can be simply extended for multi-objective optimization problems due to its modular system.