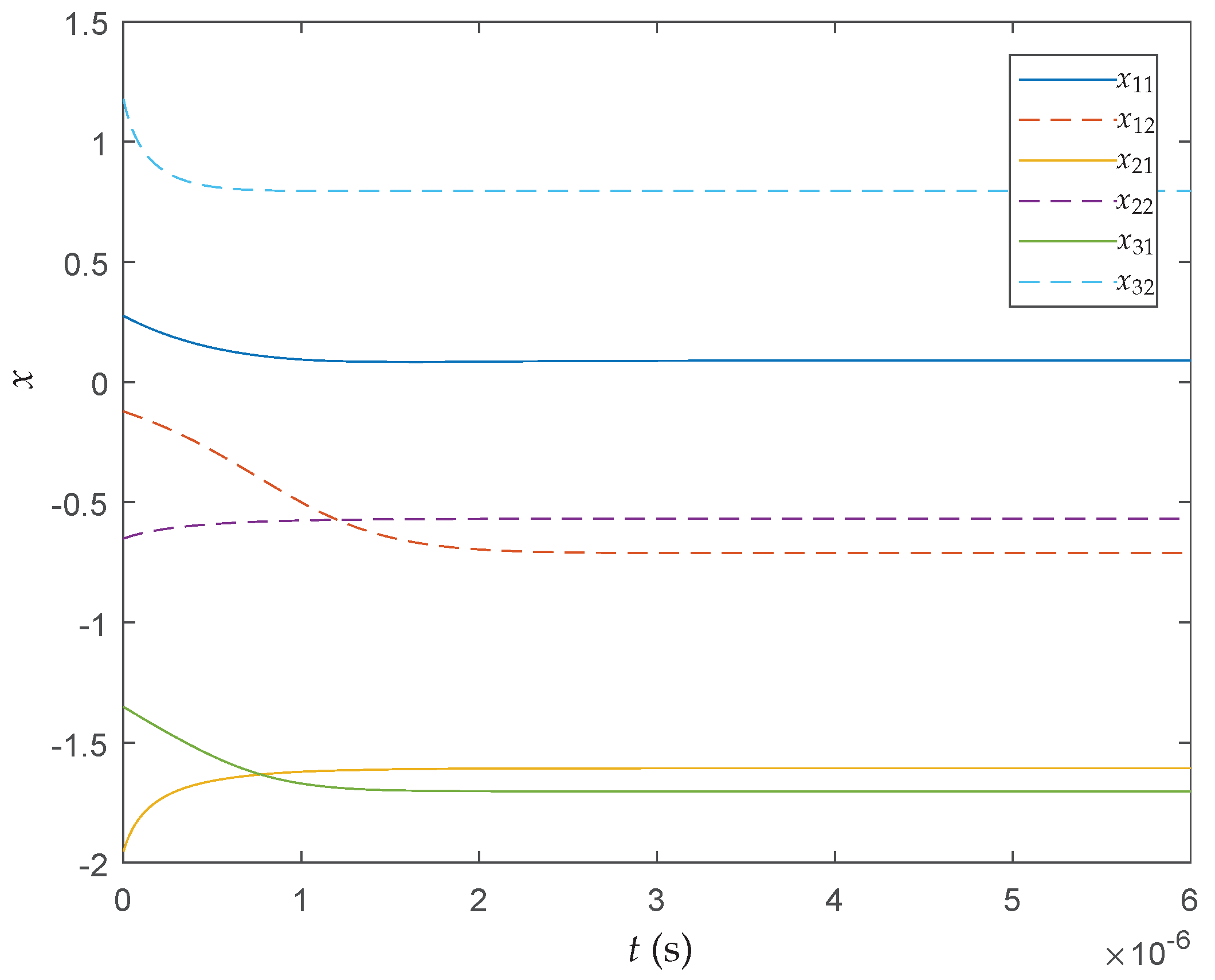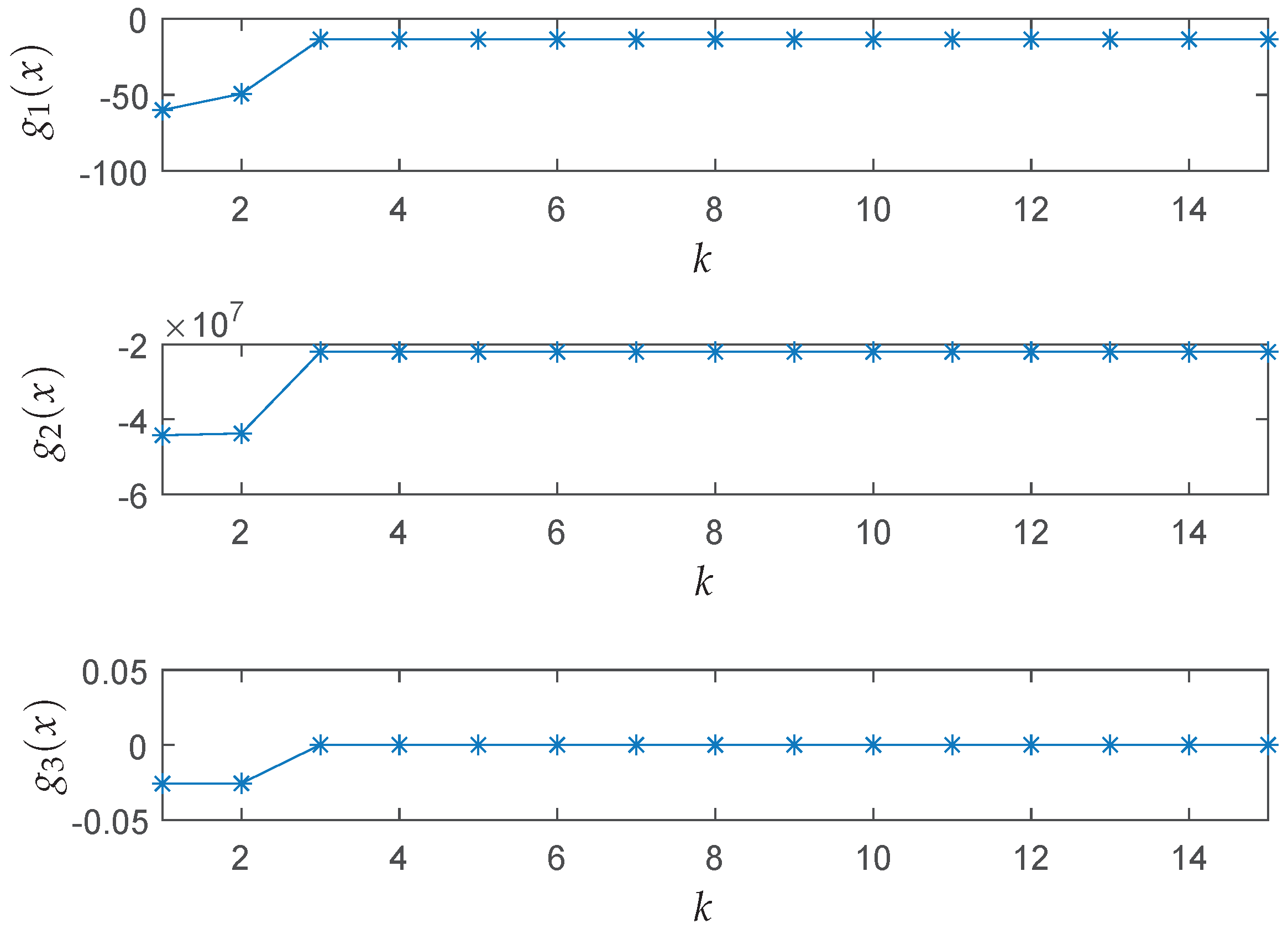1. Introduction
Constrained optimization problems arise in many scientific and engineering applications including robot control [
1], regression analysis [
2], economic forecasting [
3], filter design [
4] and so on. In many real-time applications, the optimization problems are often subject to complex and time-varying nature, which makes it difficult to compute global optimal solutions in real time using traditional numerical optimization techniques [
4,
5], such as Lagrange methods, descent methods and penalty function methods. A promising approach for handling these optimization problems is to employ neurodynamic optimization which is available for hardware implementation and possesses parallel and distributed computing ability. However, as pointed out in [
6], the dynamic behaviors of a neural network could change drastically and become unpredictable, when applying neurodynamic optimization to deal with general nonconvex optimization problems. To compute global optimal solutions in such optimization problems, one solution is resorting to strategies in the meta-heuristics research field.
Recently, neurodynamic optimization based on recurrent neural networks has attracted much focus in solving various linear and nonlinear optimization problems. The essence of such neurodynamic optimization approaches is fundamentally different from those of iterative numerical algorithms such as the sequential programming method and interior point algorithms. The gradient method has been widely used in optimization problems [
7,
8]. Recurrent neural networks are also based on the gradient method and many other methods have been used to improve recurrent neural networks such as dual neural network [
9,
10], projection neural network [
11], delayed neural network [
12], weight-constrained neural networks [
3,
13] and so on. Some researchers focused on improving the performance of neural networks. Leung et al. [
14] addressed a high-performance feedback neural network for solving convex nonlinear programming problems. Nazemi [
15] explored a high performance neural network model to solve chance constrained optimization problem. Some researchers give different forms of neural networks for specific problems. Mansoori et al. presented a kind of recurrent neural network to solve quadratic programming problems and nonlinear programming problems with fuzzy parameters in [
16,
17]. Xia and Kamel presented a cooperative projection neural network to solve the least absolute deviation problems with general linear constraints [
18]. Che and Wang presented a two-timescale duplex neurodynamic system for constrained biconvex optimization in [
19]. For some special nonconvex and nonsmooth problems, some achievements have been made in neurodynamic optimization. Based on projection method and differential inclusions, Yang et al. [
20] proposed a generalized neural network. In [
21], a one-layer recurrent projection neural network was utilized for solving pseudoconvex optimization problems with general convex constraints. Li et al. [
22] provided a one-layer recurrent neural network based on an exact penalty function method for solving nonconvex optimization problems subject to general inequality constraints. Bian et al. [
23] proposed a one-layer recurrent neural network for solving a class of nonsmooth, pseudoconvex optimization problems with general convex constraints.
Despite great progresses of neurodynamic optimization approaches in solving optimization problems with convex or some pseudoconvex functions with constraints, it is difficult to find global optimal solutions for the optimization problems with more nonconvex functions. In addition, many neural networks seems inadequate when dealing with constrained optimization problems containing multiple local minima. As one of population-based evolutionary computation approaches, the well-known particle swarm optimization (PSO) introduced by by Kennedy and Eberhart [
24] is a popular meta-heuristic method for global optimization with multimodal objective functions. In the PSO algorithm, a simple velocity and displacement model to adjust the position according to the group optimal value and its own optimal value. It has strong global search ability and robustness. However, the PSO algorithm has at least three shortcomings. Firstly, it has been proved by Frans in [
25] that, when the number of iterations tends to infinity, the traditional PSO algorithm can not converge to the global optimal solution with probability
. Secondly, in the PSO algorithm, the velocity of particles has an upper limit to ensure that particles can aggregate and avoid divergence, which limits the search space of particles and thus makes the algorithm ineffective to jump out of local optimal solutions. Thirdly, as the evolution equation of the PSO algorithm is based on a set of simple state equations of velocity and position, which makes the randomness and swarm intelligence relatively low. Due to its simple calculation, easy implementation, and few control parameters, many improved PSO algorithms have been to overcome the drawbacks (e.g., see [
26,
27,
28]). Yan et al. [
6] presented a collective neurodynamic optimization approach by combining the traditional PSO algorithm and a projection neural network to solve nonconvex optimization problems with box constraints. Later, Yan et al. [
29] apply an adaptive PSO algorithm together with a one-layer recurrent neural network to solve nonconvex general constrained optimization problems.
Among the improved PSO algorithms, the quantum-behaved particle swarm optimization (QPSO) algorithm introduced in [
30] is also one promising alternate, which describes particle behavior with probability. Compared with the traditional PSO algorithm, the QPSO algorithm has certain advantages in global optimization and speed of convergence. The convergence proof of QPSO is also given in [
27]. Applying the QPSO algorithm for global search intermittently by incorporating a novel feedback neural network for local search in a hybrid mode can be a good choice.
In this paper, we propose a quantum-behaved neurodynamic swarm optimization (QNSO) approach combined with an efficient neural network and the QPSO algorithm to solve the nonconvex optimization problems with constraints. We improve an efficient feedback neural network proposed in [
14] and prove the global convergence of the neural network for a class of nonconvex optimization problems. Inspired by [
6,
14,
29], we employ the feedback neural network and present a quantum-behaved neurodynamic swarm approach for solving the nonconvex optimization problems with inequality constraints efficiently. The proposed QNSO approach combining the QPSO algorithm [
30] and the feedback neural network is applied to deal with constrained optimization problems with multiple global minima. Compared with the methods in [
6,
29], it shows a better convergence performance. Both numerical examples and practical applications are provided to demonstrate the effectiveness of the QNSO approach.
This paper is organized as follows. In
Section 2, a constrained optimization problem is described and some theoretical analysis of an improved neural network is given. In
Section 3, combined with the QPSO algorithm and the proposed neural network, the QNSO approach is developed for solving the constrained optimization problems. In
Section 4, we perform experiments on two multimodal functions to demonstrate the performance of the QNSO algorithm. In
Section 5, we apply the QNSO method to the optimization problems of the hollow transmission shaft, heat exchangers and crank–rocker mechanism. Finally,
Section 6 concludes the paper.
2. Problem Statement and Model Description
Consider the following constrained optimization problem given by
where
is the decision vector,
is a continuously differentiable function,
(
) are continuously differentiable functions, denoting the inequality constraints.
and
are not necessarily convex. The feasible region
is assumed to be a nonempty set.
Denote
. Then, the problem (
1) can be written as
Let
be a lower bound of the optimal value of
in the problem (
1), i.e.,
, where
is an optimal solution of (
1). Denote
and
. Consider an energy function
where
is a penalty parameter, and
is the sign function.
Then, inspired by [
14,
22], we construct the following feedback neural network for minimizing
Remark 1. In [14], Leung et al. proposed the energy function for the convex nonlinear programming problem In fact, for some equality constraint , one can transform the equality constraint into inequality constraints and . The energy function in (3) contains a penalty parameter γ. Such a penalty γ can strengthen the constraints and make the results converge into the constraints more efficiently in optimization problems with inequality constraints. In addition, as we will show later, the penalty parameter γ makes the neural network feasible to fit in the network model for solving some nonconvex problems in [22]. To derive the convergence results of the feedback neural network (
4), we first introduce the following definitions.
Definition 1. [22] Suppose that f is a differentiable function and defined on an open convex set . Then, f is quasiconvex if . Definition 2. [22] Suppose that f is a differentiable function and defined on an open convex set . Then, f is pseudoconvex if . Theorem 1. If in (2) is a pseudoconvex function, then in (3) is also a pseudoconvex function. Proof of Theorem 1. Let us rewrite
as
By definition of
, i.e.,
, we have
and
Note that
holds when
Using the definition of
again, it follows that
implies that both
and
holds. Therefore, using the fact that
is a pseudoconvex function,
also implies
. In addition, since
implies
, it follows from (
5) that
if
. The proof is completed. □
Remark 2. From the proof of Theorem 1, it should be noted that the function F is constructed as a semi-positive definition function and the term can be seen as an adaptive adjustment function when computing the gradient of . That is, when approaches , becomes smaller and plays a minor role in computing the gradient of ; when is far away from , becomes larger and plays an important role in computing the gradient of .
To establish a relationship between the feedback neural network (
4) and the neural network in [
22], we consider the following notion and lemmas.
Definition 3. [29] (Clarke’s generalized gradient) The generalized gradient of f at x, denoted by , is the convex hull of the set of limits of the form , where as . Lemma 1. [22] [Proposition 6] Let be continuously differentiable. Then, is a regular function, its Clarke’s generalized gradient iswhere . Lemma 2. [22] [Theorem 4] For the problem (1), if one of the following two conditions holds, - (a)
and , are convex functions;
- (b)
is a pseudoconvex function and , are quasiconvex functions,
then, for a sufficiently small penalty factor , any state of the following recurrent neural networkconverges to an optimal solution of problem (1). Definition 4. (KKT Point) For the problem (1), suppose that : is differentiable and : are differentiable functions. If satisfies the following conditions:then is said to be a KKT point of problem (1). The KKT conditions provide first-order necessary conditions for nonlinear programming problem and can be considered as local optimization points for programming problem. Under some acceptable assumptions (see [
22] for details), the following properties hold.
Proposition 1. [22] [Theorem 1] When the penalty parameter σ is sufficiently small, then any state of (6) is guaranteed to be convergent to the feasible region in finite time and stay there thereafter. Proposition 2. [22] [Corollary 1] When the penalty parameter σ is sufficiently small, any state of the neural network (6) will converge to an equilibrium point and any equilibrium point of the neural network (6) corresponds to a KKT twofold of the problem (1). Next, we claim that for the problem (
1), the neural network (
4) is a special form of neural network (
6). Firstly, note that, to solve the the problem
with the constraint
, it is equivalent to solving the problem
with the constraint
Secondly, take
in Lemma 1, the neural network (
4) can be written as
Define
in (
7). It follows that
which is a special case of the neural network (
6) in Lemma 2 if
has the same property of the function
f in Lemma 2.
The following result shows the convergence property of the proposed neural network.
Theorem 2. The neural network (4) converges to an optimal solution of problem (1) if there exists a large enough penalty parameter and one of the following two conditions holds - (a)
and , are convex functions;
- (b)
is a pseudoconvex function and , are quasiconvex functions.
Proof of Theorem 2. Firstly, if condition (a) holds, it follows from [
14] [Theorem 1] that
in (
3) is also a convex function. Then, condition (a) in Lemma 2 holds. Secondly, if condition (b) holds, it follows from Theorem 1 that
in (
3) is also a pseudoconvex function. Then, condition (b) in Lemma 2 holds. In addition, it follows from the above discussion that the neural network (
4) fits in the form of neural network (
6). Therefore, by Lemma 2, the proof is completed. □
Remark 3. Theorem 2 shows that the proposed neural network (4) will converge to an optimal solution for some nonconvex optimization problems and (4) satisfies the properties in Propositions 1 and 2, that is, the neural network (4) can converge to the feasible region of the optimization problem in finite time and find a KKT point which is a local optimal point of the problem (1). 3. Quantum-Behaved Neurodynamic Swarm Approach
To solve the nonconvex programming problems with box constraints, a collective neurodynamic approach is proposed in [
6], which can be seen as a combination of neurodynamic optimization and particle swarm optimization. In order to improve the convergence speed of the optimization algorithm, we explore a quantum-behaved neurodynamic approach combining the QPSO algorithm with the feedback neural network model (
7) for nonconvex programming problems with general constraints. In the QPSO algorithm, each particle represents a position, which represents a potential optimal solution of optimization problem. Imitating the swarm intelligence behavior of animals, the renewal of particles is related to their optimal position and global optimal position. Unlike the basic PSO algorithm, the updating equation of particle position follows the quantum-behaved model. The QPSO algorithm has the aggregation of particles with the iteration, increases the intelligence of particle behavior, and makes the possible search range of particles wider. Therefore, the ability of global optimization increases.
Given
q particles, define the position of the
ith particle as
, the individual best position of the
ith particle as
and the best position of the swarm as
. The particle renewal equation of the QPSO algorithm is given by
where
and
are random numbers between
,
,
,
is an adjustable parameter,
is the center of attraction potential field of
.
is the average optimal position of particle. The iteration stops when the maximum number of iterations is reached or the given conditions is achieved.
Note that, despite of its excellent global optimization ability, the QPSO algorithm lacks the ability for constraint processing and deep local searching. Inspired by neurodynamic optimization, during the local search process, we apply the feedback neural network to optimize each particle and improve the search efficiency. Next, we explore the QNSO approach to deal with constrained optimization problems, where the QPSO algorithm is applied to adjust the initial conditions of the feedback neural network at each local search phrase.
The steps of the QNSO algorithm are summarized as follows:
- Step 1:
Initialize the position of particles.
- Step 2:
Initialize the individual best position of the ith particle, and the global best position of the particle swarm.
- Step 3:
Each particle reaches a local optimal solution based on the feedback neural network (
7).
- Step 4:
Update the individual best position of the ith particle, and the global best position of the particle swarm.
- Step 5:
Update the position of each particles based on (
8).
- Step 6:
Repeat Step 3 to Step 5 before reaching the given conditions.
Following the description in
Section 2, we simply consider the energy function in (
3) as the fitness value of the QPSO algorithm. Then, the individual best position
of the
ith particle is updated according to
where
and
k represent the
th iteration and
kth iteration, respectively. The global best position
of the particle swarm is updated by
Remark 4. The fitness value of the QNSO algorithm could be different from the energy function of the neural network. A large γ may bring a better performance as it effectively restricts particles to diverge beyond the feasible region.
QNSO can always find the accurate local minimum of each particle within one iteration. Compared with general global optimization algorithms (such as PSO), when the number of local minimum is small, QNSO is extremely insensitive to heuristic parameters; when the number of local minimum is large, the QNSO algorithm needs sufficient divergence ability of heuristic parameters to jump out of local minimum. In other words, appropriately larger in QPSO can be more suitable for the QNSO algorithm.
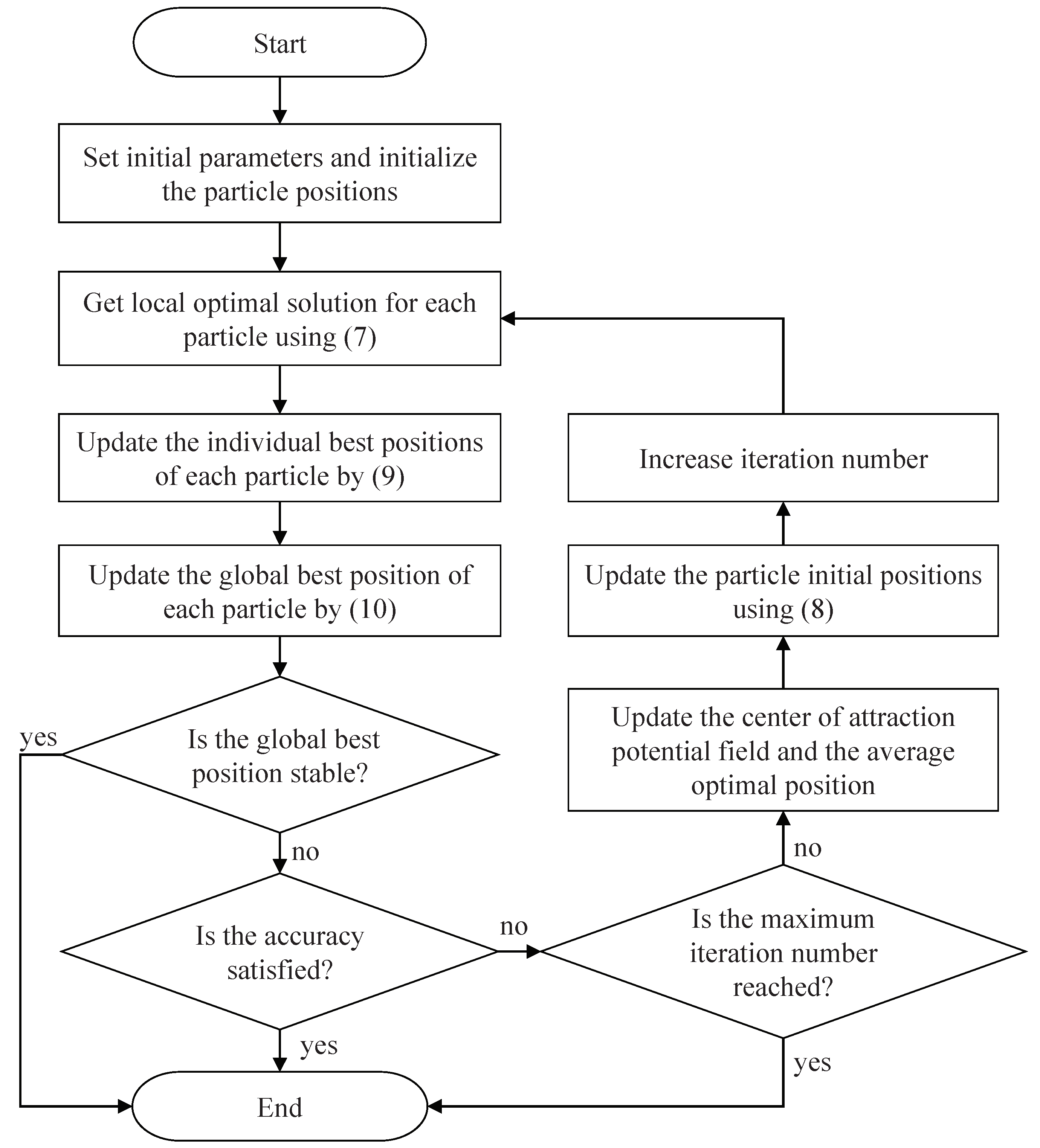
Detailed steps of the QNSO algorithm are given in Algorithm 1. During local search process, the feedback neural network in the algorithm is applied to solve the local optimization problem with constraints. The QPSO algorithm is applied to perform global search process. Therefore, the advantages of the QPSO algorithm and the feedback neural network can complement each other. The flow chart of QNSO is shown in
Figure 1.
| Algorithm 1 QNSO Algorithm. |
- 1:
Set the swarm size q, parameter , tolerance error precision , the maximum number of iterations, the expected cost function value , the lower bound of cost function and the initial step . - 2:
Initialize the position of particles, using uniform random distribution, and get the initial individual best positions and global best position. - 3:
Carry out the following feedback neural network to obtain a local optimal solution for each particle:
where is a scaling parameter which is introduced to accelerate the convergence rate of the neural network. - 4:
Update the individual best position of the ith particle, and the global best position of the particle swarm using
and
- 5:
Update the position of each particle, that is, the initial conditions of the feedback neural network, using the following the renewal equations:
where and . - 6:
The iteration stops if one of the following conditions is satisfied:
- (a)
The algorithm reaches the maximum iteration value . - (b)
. - (c)
stops updating for five consecutive iterations.
Otherwise, set and go to step 3.
|
4. Function Tests
In this section, we consider two multimodal benchmark problems, i.e., the constrained six-hump camel back function [
6] and the constrained Rastrigrin function, to illustrate the proposed optimization approach. The first example is provided to verify the convergence performance of the proposed QNSO algorithm, while the second example is provided to demonstrate the constraint processing ability of the algorithm.
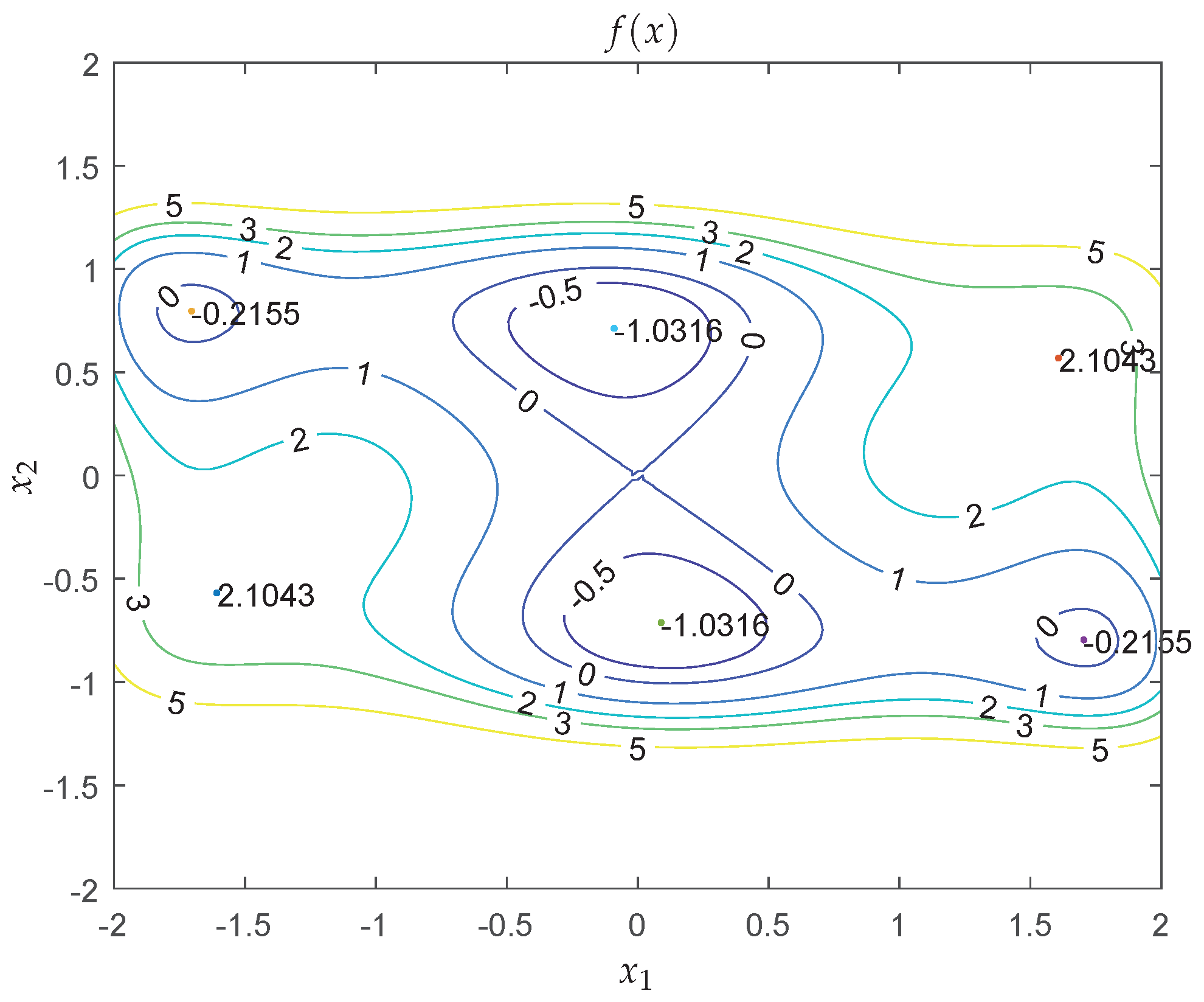
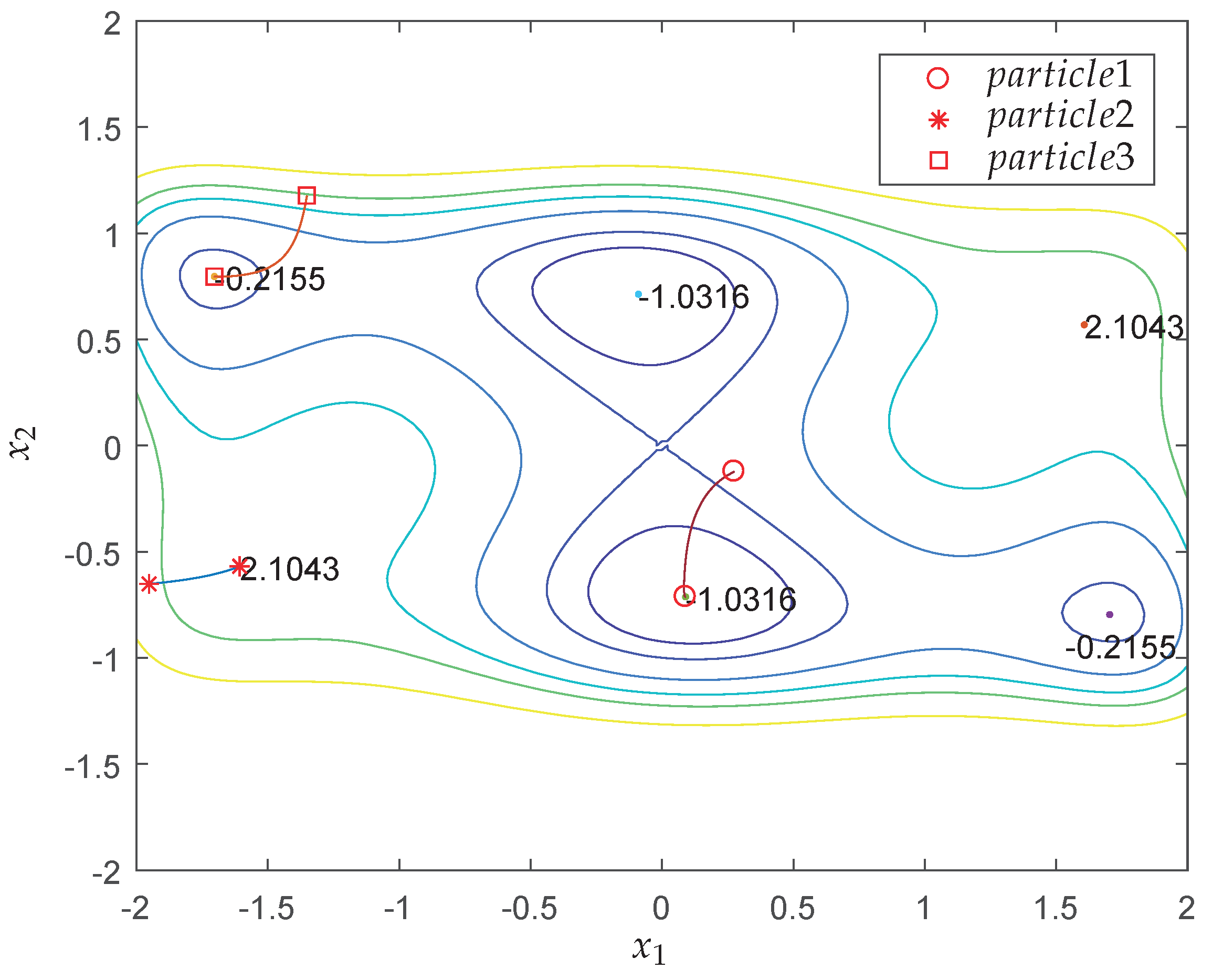
Example 1. Consider the six-hump camel back function [6] Figure 2 shows the contour map of the six-hump camel back function with box constraints. It is seen that there are multiple local minima in the area. In fact, the optimization problem has six minima
Two of them are the global minima, located at and , respectively. To carry out the QNSO algorithm, set swarm size , parameter , tolerance error precision , the maximum iteration number , and . Before performing the simulation, initialize the position of particles, , using uniform random distribution. After 50 experiments, we obtain the two global minima at every experiment. Except two experiments, the global minima are found at the first step iteration for most cases, which shows that the QNSO algorithm has a high efficiency and good accuracy to find the optimal solution for the problem in this example.
In order to verify the convergence efficiency of the proposed method, we compare the optimization results of the QNSO algorithm with the results derived by the approaches in [
6,
29]. For the neural networks in all the three methods, we take the scaling parameter
.
Figure 3,
Figure 4 and
Figure 5 show the convergence of the trajectory of the proposed neural network (
7), the projection neural network in [
6], and the recurrent neural network in [
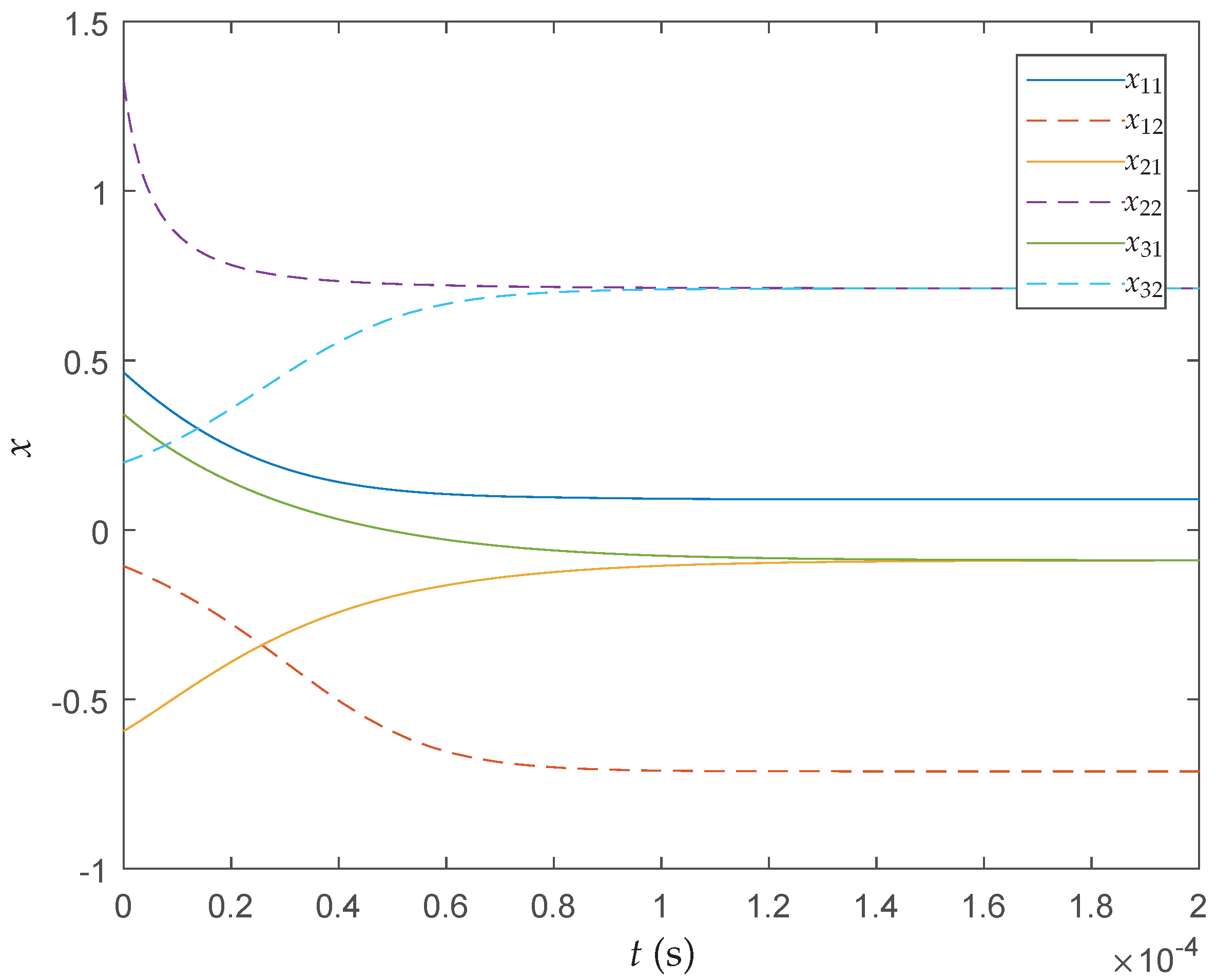
29] at the first iteration, respectively. As shown in the figures, each particle converges to its local optimum shortly. It can be seen that, among the three methods, the proposed neural network has the fastest convergence speed.
Figure 6 shows the behavior of particles in the search process by the proposed QNSO algorithm. The initial positions of particles are randomly selected. After one iteration, two particles reach the global minima along the direction perpendicular to the contour.
Example 2. Consider the optimization problem of the constrained Rastrigrin function described bywhich has hundreds of local minima and many global minima for . Note that the origin, which is the global minimum point for unconstrained Rastrigrin function, is not within the feasible range. The complexity of this problem depends on the size of n and the number of minima increases exponentially with the increase of n. To carry out the QNSO algorithm, set the initial parameters of QNSO algorithm:
,
decreased from
to
on the course of the search, swarm size
, tolerance error precision
, the maximum iteration number
. To establish a reference for comparison with the QNSO algorithm in this paper, we performed experiments with Rastrigrin function in
4 and 10 dimensions, respectively. Some other optimization methods were also examined for performance comparisons, including the latest standard particle swarm optimization (SPSO) [
31], the adaptive particle swarm optimization (APSO) [
32], the random drift particle swarm optimization (RDPSO) [
33], the firefly algorithm (FA) [
34], the repair genetic algorithm (RGA) [
35], the QPSO [
30], and the method in [
29]. We set swarm size
, tolerance error precision
, the maximum iteration number
for all the tested methods. Standard normal distribution was used in RGA as mutation operator. The parameters for QPSO were the same as those in this paper. Other parameters for SPSO, APSO, FA, RDPSO and RGA were the same as those recommended in [
31,
32,
33,
34,
35] and these methods used the same fitness value (
3) with a large
to keep optimizations within the feasible range.
Table 1,
Table 2 and
Table 3 show the computational results, where the best result, the average result, the worst result, the standard deviation (Std.) result of
, and the average number of iterations (No. of Iterations) over 50 experiments are provided. The optimum results are coarsened with boldface in these tables. Obviously, when the particles and the iterations are limited, the general optimization algorithm has obvious deficiencies with the increase of the complexity of the problem, but the method in [
29] and QNSO can obtain accurate optimal solutions with good robustness. QNSO requires the least iterations with a stable optimization efficiency as shown in
Table 1 and
Table 2.
5. Applications
In this section, three optimization problems in applications, including hollow transmission shaft [
36], heat exchangers [
37] and crank–rocker mechanism [
36], are solved using the proposed QNSO algorithm.
Application 1. (Hollow transmission shaft) Consider the hollow transmission shaft optimization problem in [
36], where
D and
d are the outer diameter and inner diameter,
mm, shaft length
m. The power transmitted by the shaft is
kW and the speed
. Shaft material density p = 7800
, shear modulus
GPa, and allowable shear stress
MPa, allowable torsion angle per unit length
m. The aim is to minimize the mass of the shaft under the limitations of torsional strength and torsional stiffness:
- (1)
Decision variables and cost function
In this problem, there is only one decision variable . According to the design requirements, the optimization goal is to minimize the mass of the shaft that is, .
- (2)
Restrictions
- (a)
Torsional strength condition is where T is the torque received by the round shaft, , is the torsional section modulus, .
- (b)
Torsional stiffness condition is where is unit length twist angle, G is shear modulus, is polar moment of inertia, .
- (c)
Outer diameter minimum limit condition is
Following the above analysis, we summarize the optimization problem as follows:
For the above problem (
12), one can use the
function in Matlab to obtain a solution
mm with
kg [
36]. To carry out the QNSO algorithm, we set swarm size
, parameter
, tolerance error precision
, the maximum iteration number
,
and
. The initial values of the position
of particles,
are randomly chosen. We perform 50 realizations and obtain an optimal solution
mm with
kg, which is slightly better than that obtained in [
36].
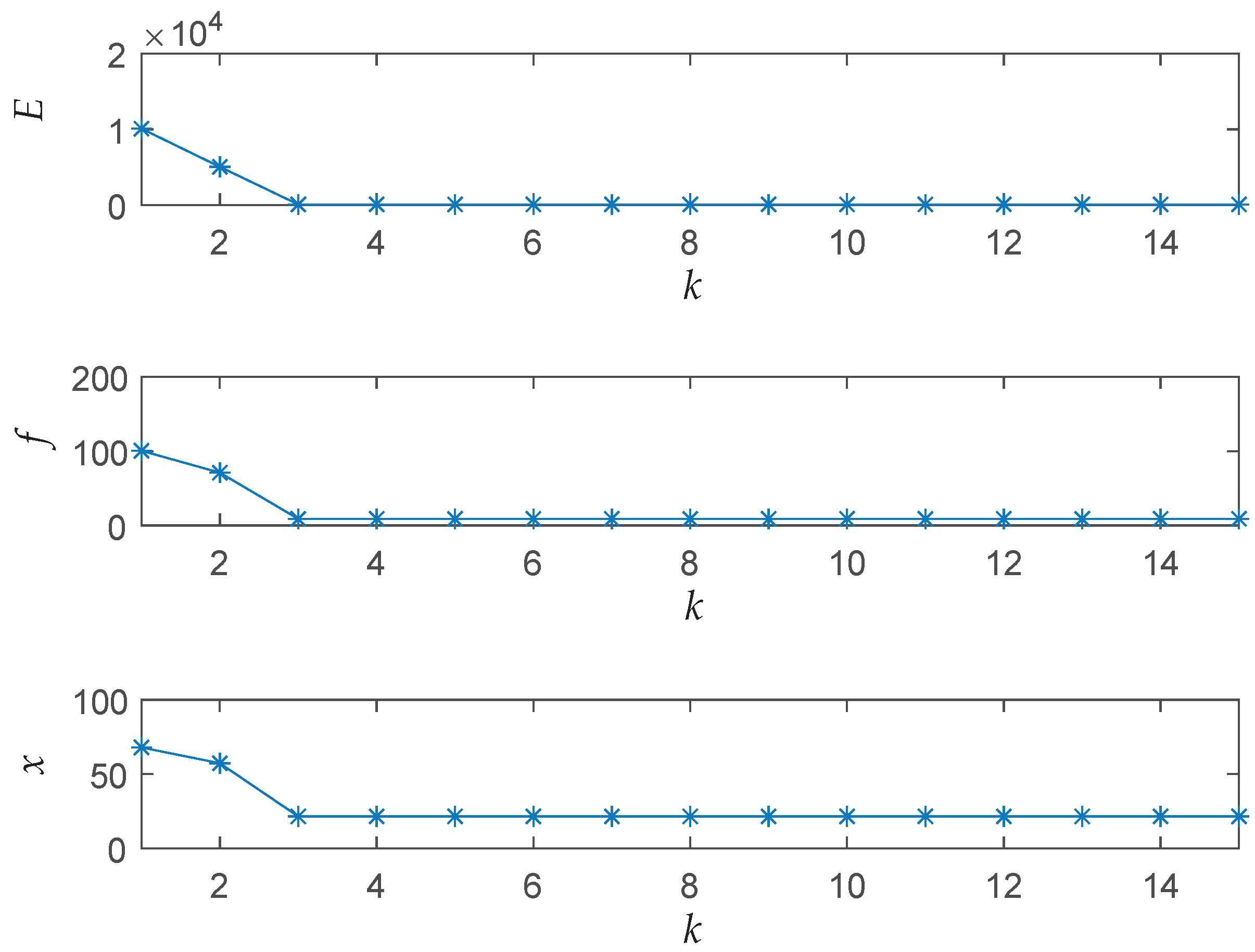
Figure 7 shows the iteration results of the energy function
E, the cost function
f and the solution
x of the best particle among five particles. As seen from the results, the proposed algorithm successfully solves the optimization problem with a fast convergence speed and finds a relative ideal solution within five iterations.
Figure 8 depicts the iteration results of the inequality constraint functions and illustrates the ability of the algorithm to deal with constraints.
Table 4 shows the best result, the average result, the worst result, and the standard deviation result of
over 50 realizations.
Application 2. (Heat exchangers [
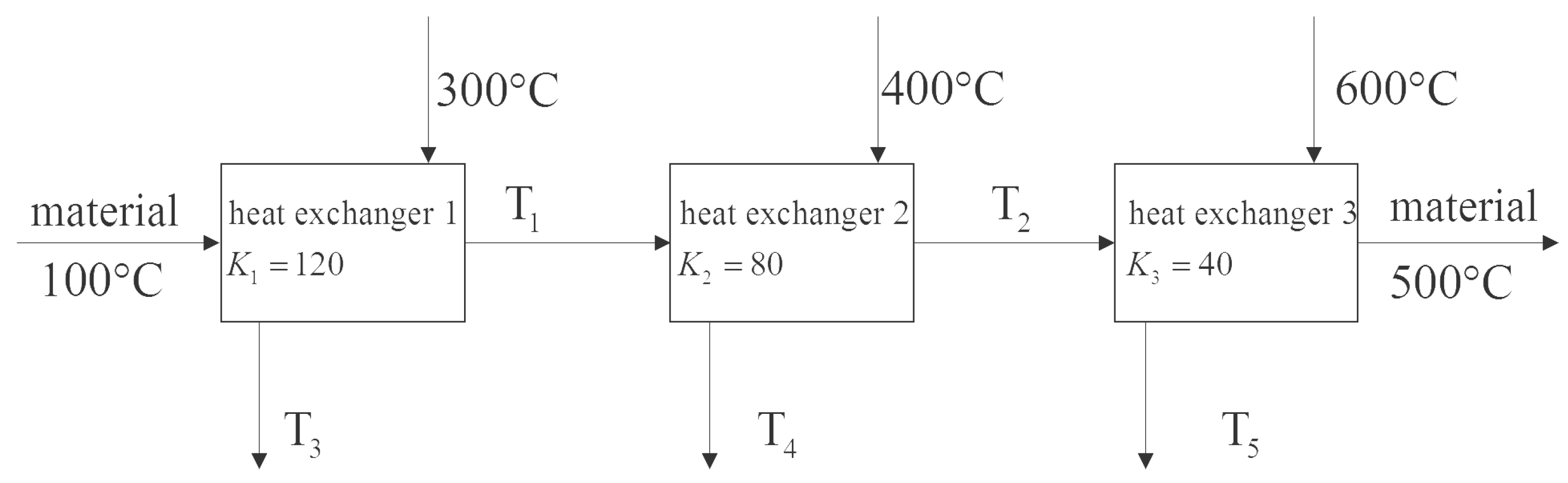
37]) Consider three connected heat exchangers as shown
Figure 9, which are used to heat a material temperature from
to
. Let
, where
m is the mass flow rate of the fluid and
is the specific heat capacity of the fluid. The heat transfer coefficients of the three heat exchangers are
,
and
, respectively. For simplicity, the temperature difference
uses arithmetic mean value and the above values are obtained through dimensionless processing. The aim is to minimize the total heat transfer area by selecting the appropriate temperature.
The decision variables are
. The restrictions are given by
and
It follows from the law of conservation of heat that
The arithmetic mean values of temperature difference of heat exchangers are
Therefore, according to the design requirements, the cost function is obtained
To sum up, the optimization problem can be written as
In [
37], the obtained minimum cost function value is
by using sequence quadratic programming. To carry out the QNSO algorithm, we set swarm size
, parameter
, tolerance error precision
, the maximum iteration number
,
and
. The initial values of the position
of particles,
are randomly chosen. Since the problem is relatively simple, after performing the simulation, we can obtain the optimal solution at the first iteration almost every time. We perform 50 realizations and obtain the same results which are shown in
Table 5.
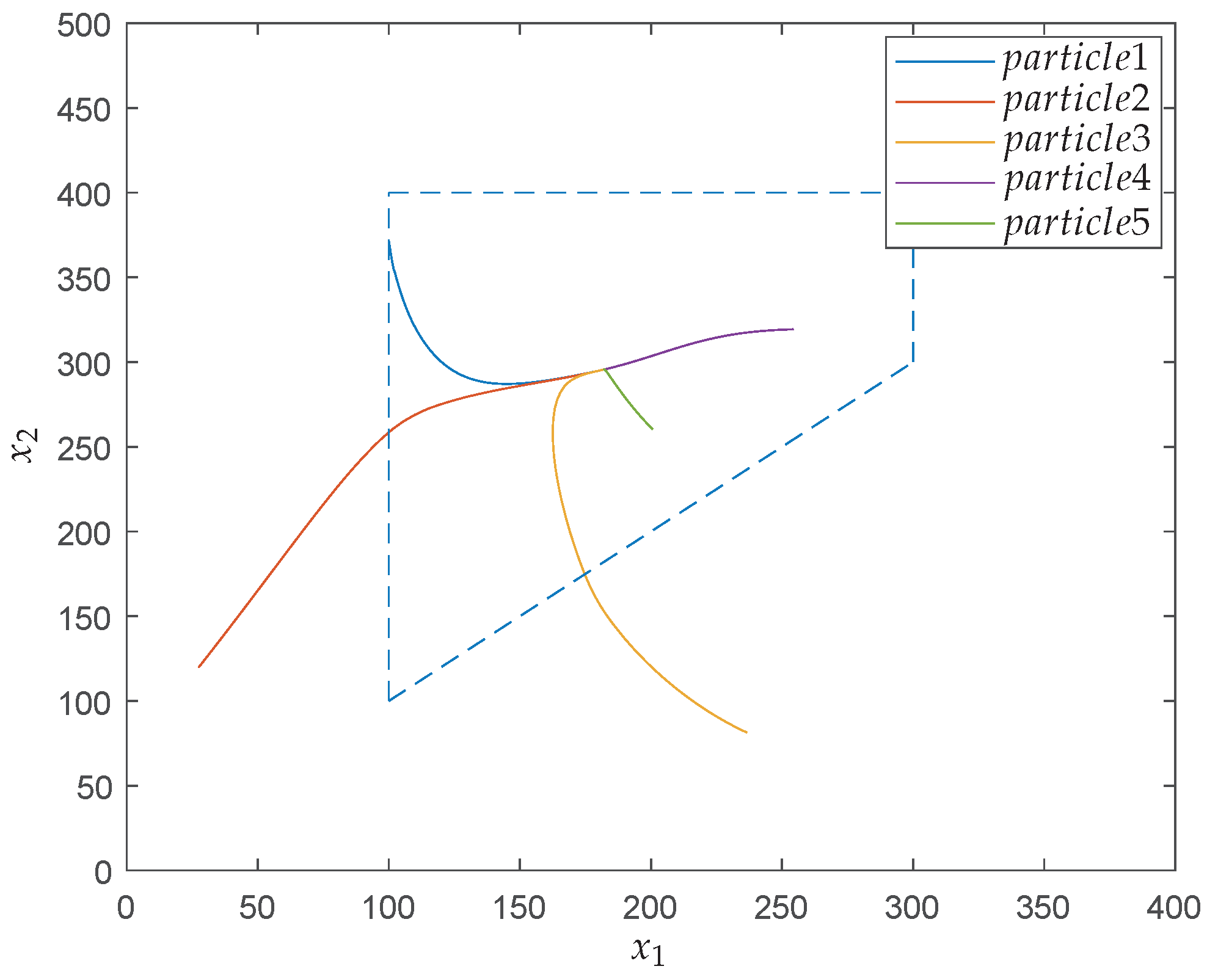
Figure 10 shows the behavior of particles in the search process in the phase plot by the proposed QNSO algorithm. It can be found that all particles move into the feasible region and reach some local optimal solutions.
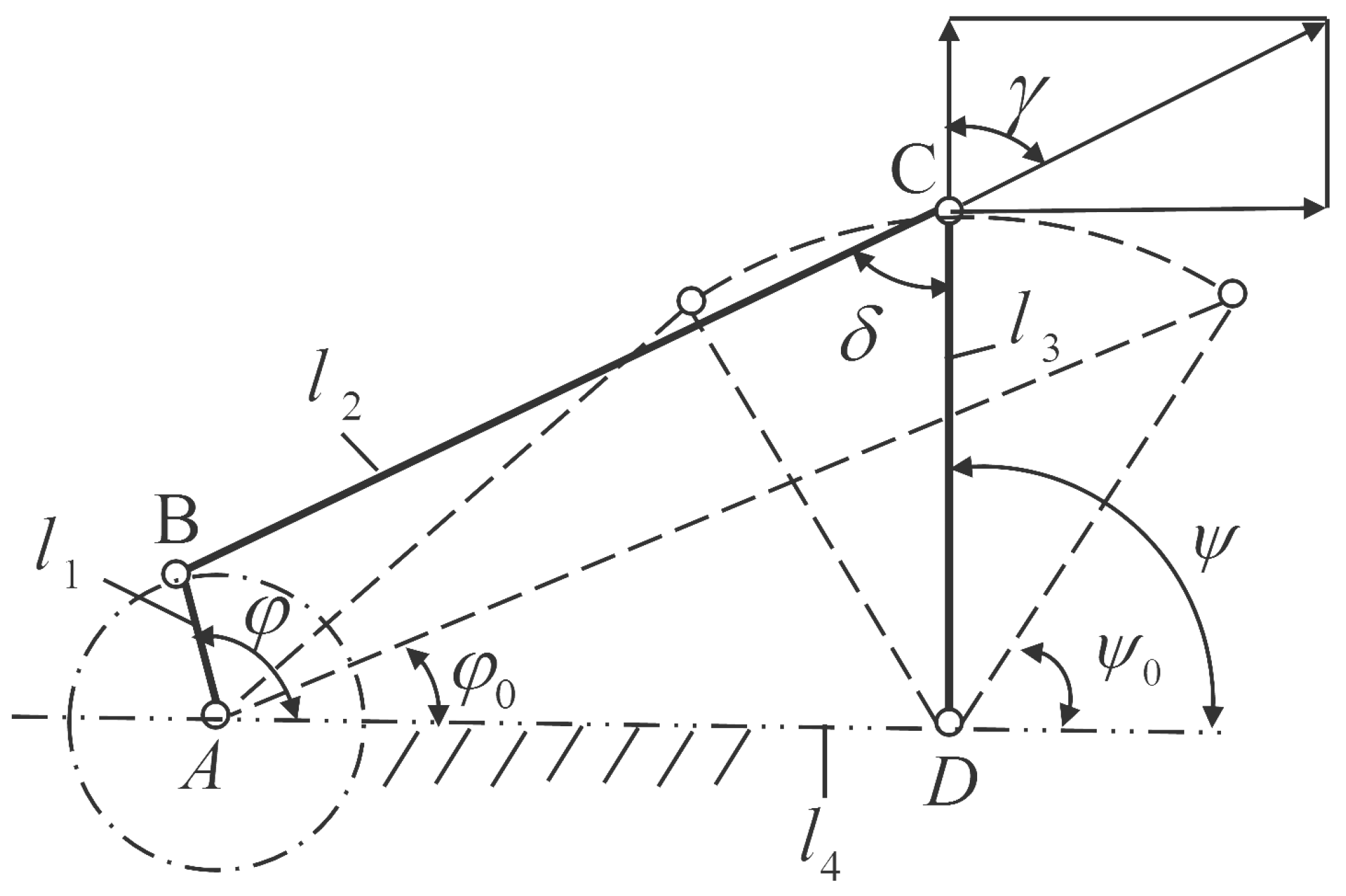
Application 3. (Crank–rocker mechanism [
36]) Consider a crank–rocker mechanism as shown in
Figure 11. The anti-clockwise angle is calculated with the frame
as the baseline.
and
correspond to the position angles of the rocker and the crank respectively when the rocker is in the right limit position. The minimum transmission angle
is greater than
. The crank–rocker mechanism is required to be designed when the crank is transferred from
to
and the output angle
of the rocker meets the following predetermined motion rules
:
It is shown in
Figure 11 that the lengths of the four shafts are marked as
and
, respectively.
is the length of short shaft. Set
be the unit length that is,
. Set the decision variable
. It follows from the cosine theorem that
According to the design requirements, the optimization goal is to minimize
To numerically minimize
, discretizing the cost function by dividing the interval
into 50 parts yields
The actual output angle of the crank–rocker mechanism is
which can be calculated by
where
The minimum transmission angle constraints are given by
which are equivalent to
The length constraints are given by
Following the above analysis, we summarize the optimization problem as follows:
where
In this problem, the cost function and constraints are more complicated than those problems in Applications 1 and 2. In [
36], the obtained cost function value is
at the optimal solution
when the upper bound of
x is limited to
. For comparison, we also impose the upper bound of
x as
. To carry out the QNSO algorithm, we set swarm size
, the parameter
decreased from 1 to
, tolerance error precision
, the maximum iteration number
,
and
. The initial values of the position
of particles,
are randomly chosen.
We perform 20 realizations and obtain
, the minimum cost function value is
, which is better than the result obtained in [
36].
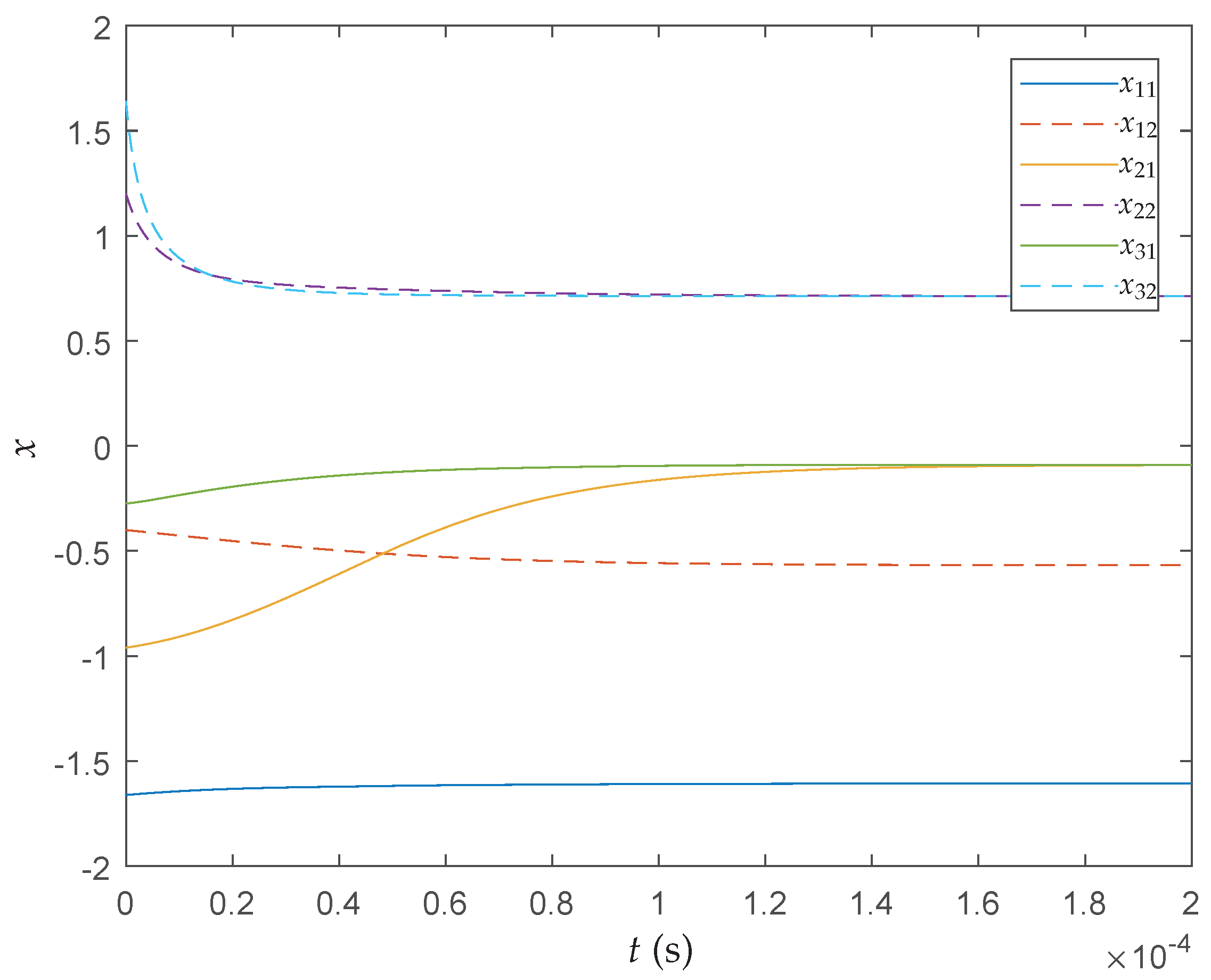
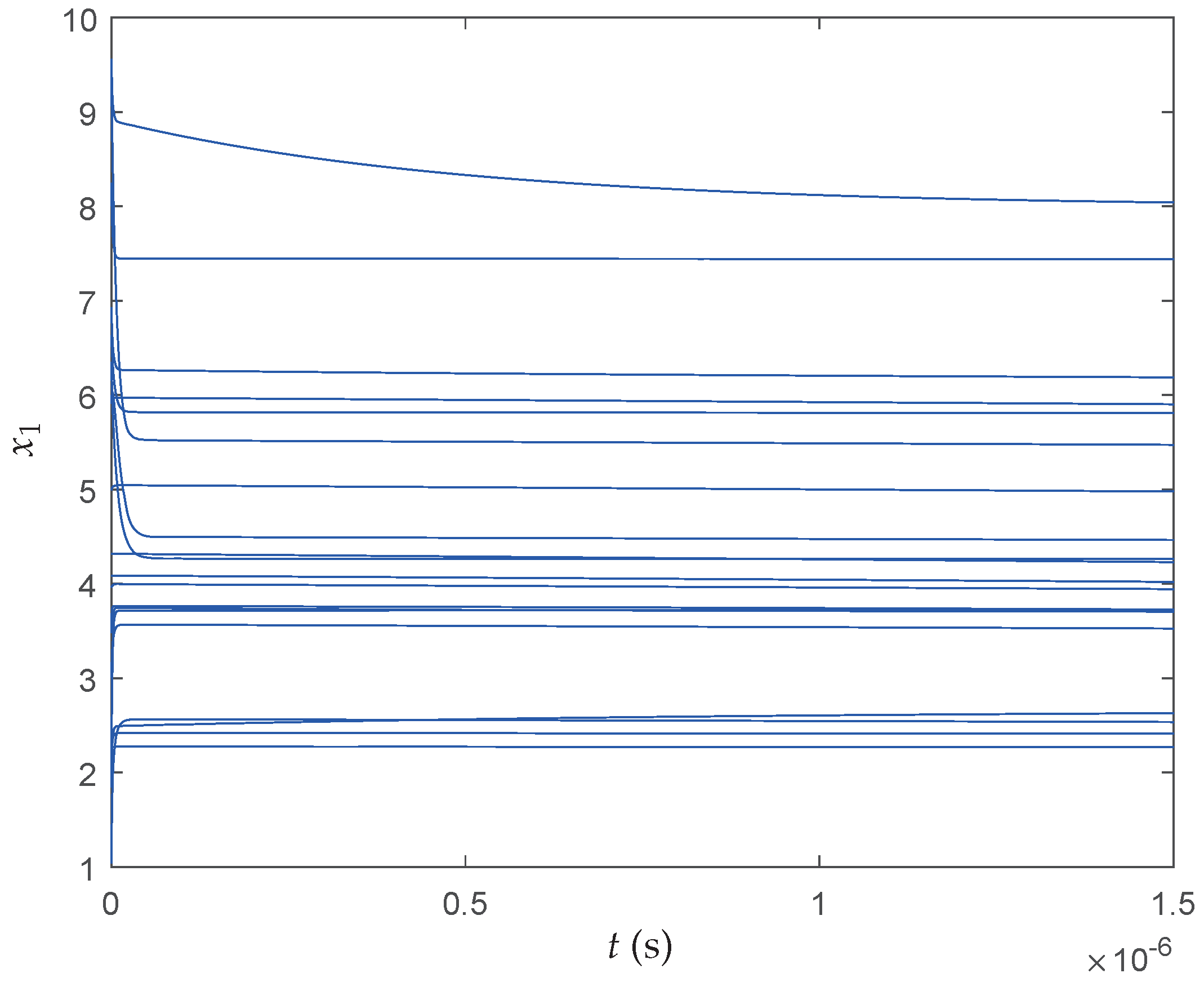
Figure 12,
Figure 13 and
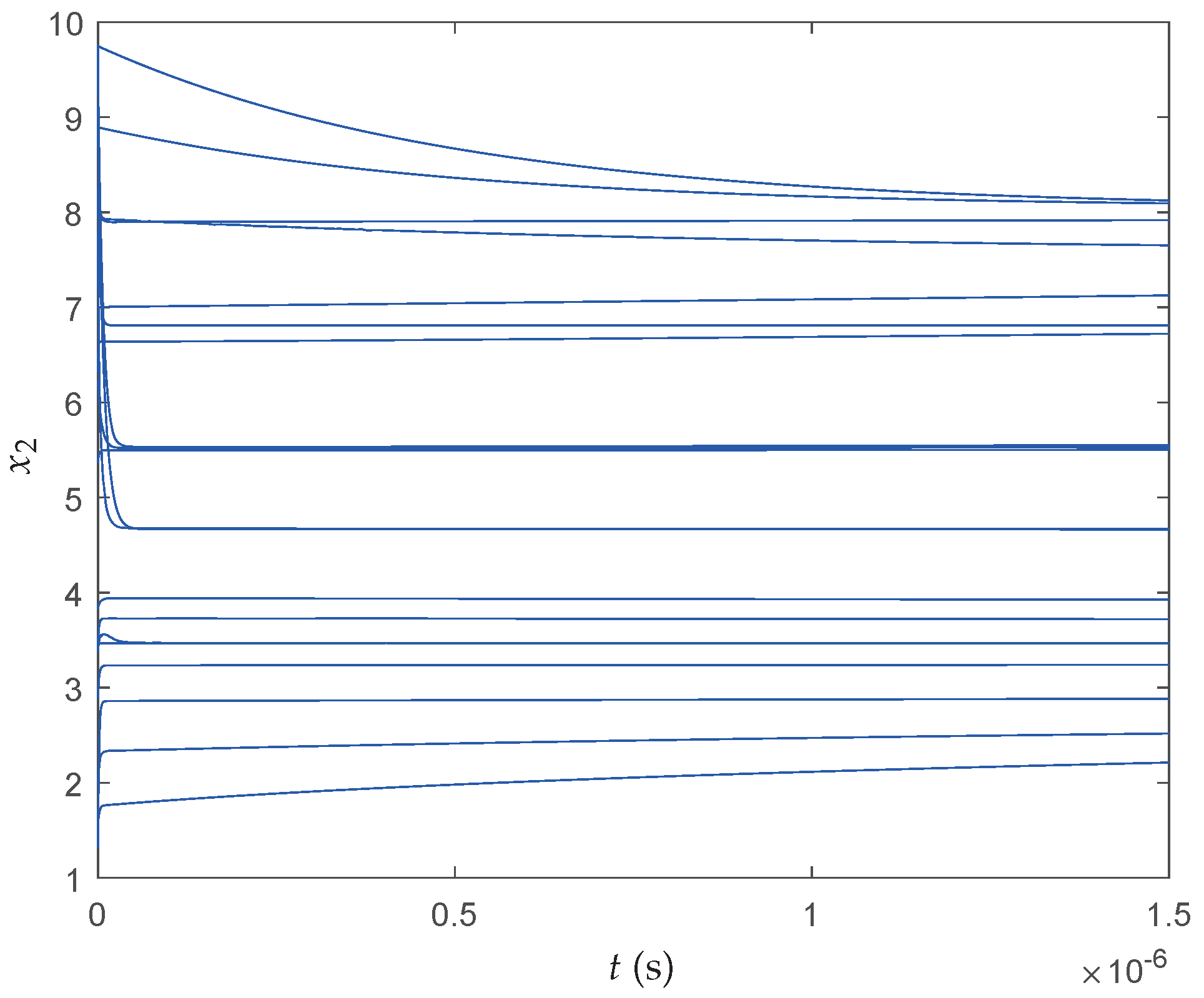
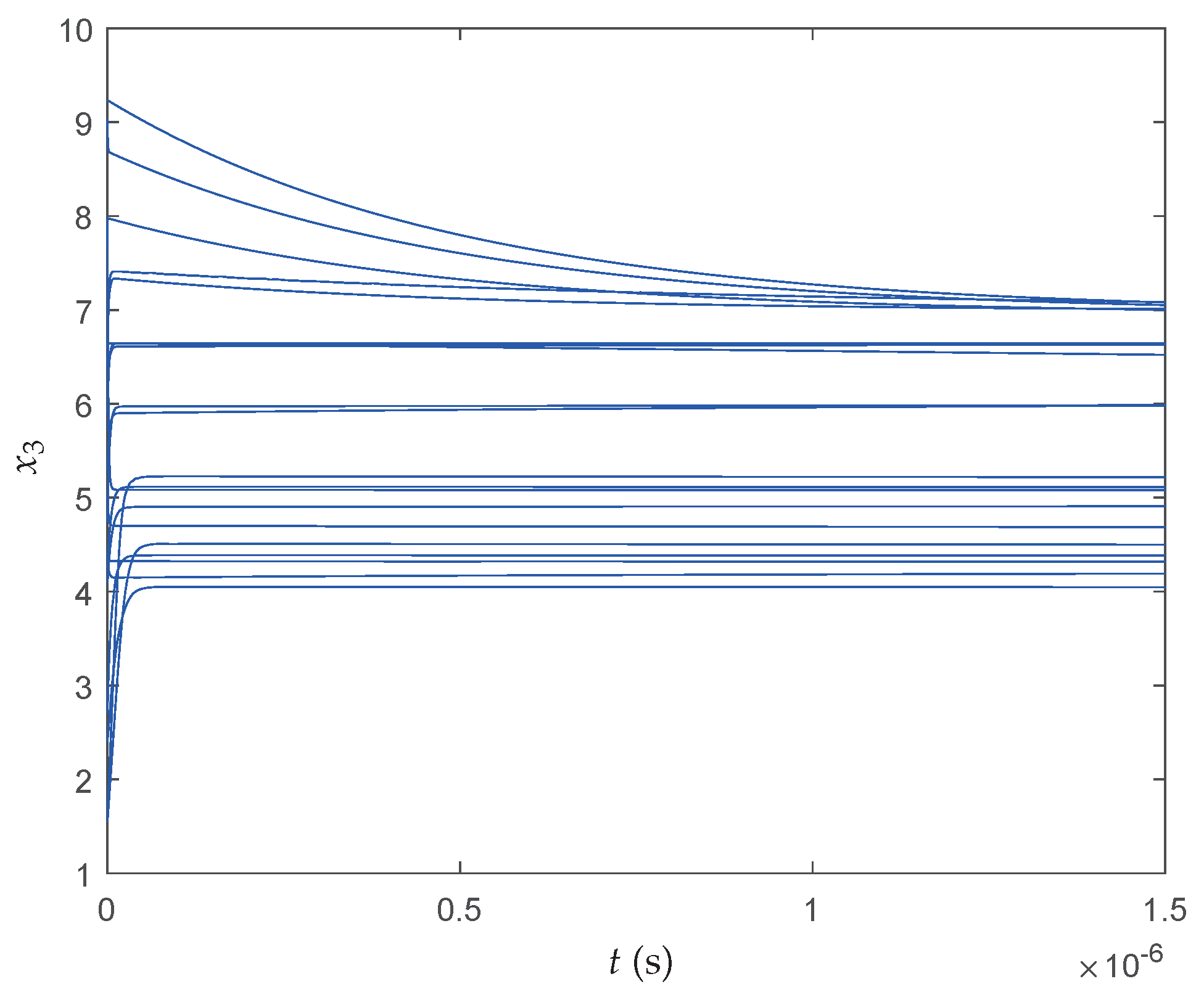
Figure 14 show the transient behaviors of
,
and
of the proposed neural network initialized from 20 random particles for each state, respectively. It can be found that all states converge instantaneously local optimal solutions since the cost function itself has many local optima and the searching space is divided into many nonconvex areas by the constraints. Therefore, more iterations have been required to make full use of interconnections of particles so that the QNSO algorithm is able to fully exploit the parallel nature of the computation and produce results that are more globally optimal.
Table 6 shows the best result, the average result, the worst result, and the standard deviation result of
over 20 experiments.