Pulmonary Fissure Detection in 3D CT Images Using a Multiple Section Model

Abstract

As a typical landmark in human lungs, the detection of pulmonary fissures is of significance to computer aided diagnosis and surgery. However, the automatic detection of pulmonary fissures in CT images is a difficult task due to complex factors like their 3D membrane shape, intensity variation and adjacent interferences. Based on the observation that the fissure object often appears as thin curvilinear structures across 2D section images, we present an efficient scheme to solve this problem by merging the fissure line detection from multiple cross-sections in different directions. First, an existing oriented derivative of stick (ODoS) filter was modified for pulmonary fissure line enhancement. Then, an orientation partition scheme was applied to suppress the adhering clutters. Finally, a multiple section model was proposed for pulmonary fissure integration and segmentation. The proposed method is expected to improve fissure detection by extracting more weak objects while suppressing unrelated interferences. The performance of our scheme was validated in experiments using the publicly available open Lobe and Lung Analysis 2011 (LOLA11) dataset. Compared with manual references, the proposed scheme achieved a high segmentation accuracy, with a median F₁-score of 0.8916, which was much better than conventional methods.

1. Introduction

Human lungs consist of five parts, separated by pulmonary fissures. In CT images, pulmonary fissures often appear as bright thin curvilinear shapes in 2D space or plate-like structures in 3D space [1]. For clinical diagnosis, some postoperative cardiopulmonary complications can be predicted by the degree of fissure completeness [2]. However, pulmonary fissure detection in CT images is not an easy task due to complex factors like the thin membrane shape, low contrast, intensity variety, pathological deformation and partial volume effect [3].

In recent years, many valuable studies have been presented on pulmonary fissure detection, most of which were designed by identifying the points of interest, the curved lines or the plate-like structures in CT images to achieve detection. To identify the points of interest in CT images, Wiemker et al. [4] proposed an automatic and robust algorithm for pulmonary fissure segmentation in CT images. To better suppress tubular structures, Lassen et al. [5], Shamonin et al. [6] and Doel et al. [7] added one or more tubular structure inhibitors. Using a different strategy, Chen et al. [8] introduced a modified ant colony optimization framework to identify lobe fissures. Because the prior linear and planar shape features are not taken into account, these approaches may partly account for missed fissures.

Motivated by a fact that pulmonary fissures appear like curved lines in the 2D cross-section of CT scans, Kube et al. [9] presented a template matching method to segment pulmonary fissures. Similarly, Zhang et al. [10] used a ridgeness measure model to enhance pulmonary fissures, then a fuzzy reasoning system was applied to highlight pulmonary fissure representation. Wang et al. [11] used a ridge map method to enhance the major fissures and applied a Bayesian network model to segment pulmonary fissures. However, these methods [10,11] generally need some manual interaction. To automatically extract pulmonary fissures and overcome the above disadvantages [10,11], a line enhancing filter [12] was designed for pulmonary fissure segmentation. Recently, Xiao et al. [13] proposed a derivative of stick filter (DoS) to enhance pulmonary fissures and designed a post-processing pipeline for pulmonary fissure segmentation. However, this approach utilized only the magnitude information in CT images, ignoring orientation information. Its improved version [14] presented a novel approach by integrating magnitude information and orientation information to segment pulmonary fissures. Assuming the pulmonary fissure to be a plate-like surface in 3D space, Pu et al. [15] presented a computational geometry model to extract pulmonary fissures. Their later improvement [16] included a piecewise plane model to locally fit the fissure surface, but the model could deviate from the abnormality of fissures in real images, thus resulting in missed detection.

In this paper, a novel scheme is proposed for fissure detection in CT images. Following the idea of previous work [13,14], we utilized the 2D curvilinear shape feature to detect the fissure lines across a series of 2D images. In contrast to the existing work, a multiple section model with multiple planes cutting through the 3D volume image was introduced for fissure profile detection. This was expected to avoid the missed detection of fissure patches located along specific section planes. Moreover, an improved orientation partition scheme was developed to separate the plate-like fissure surface from adhering clutters, and finally refine the fissure segmentation result.

2. Related Works

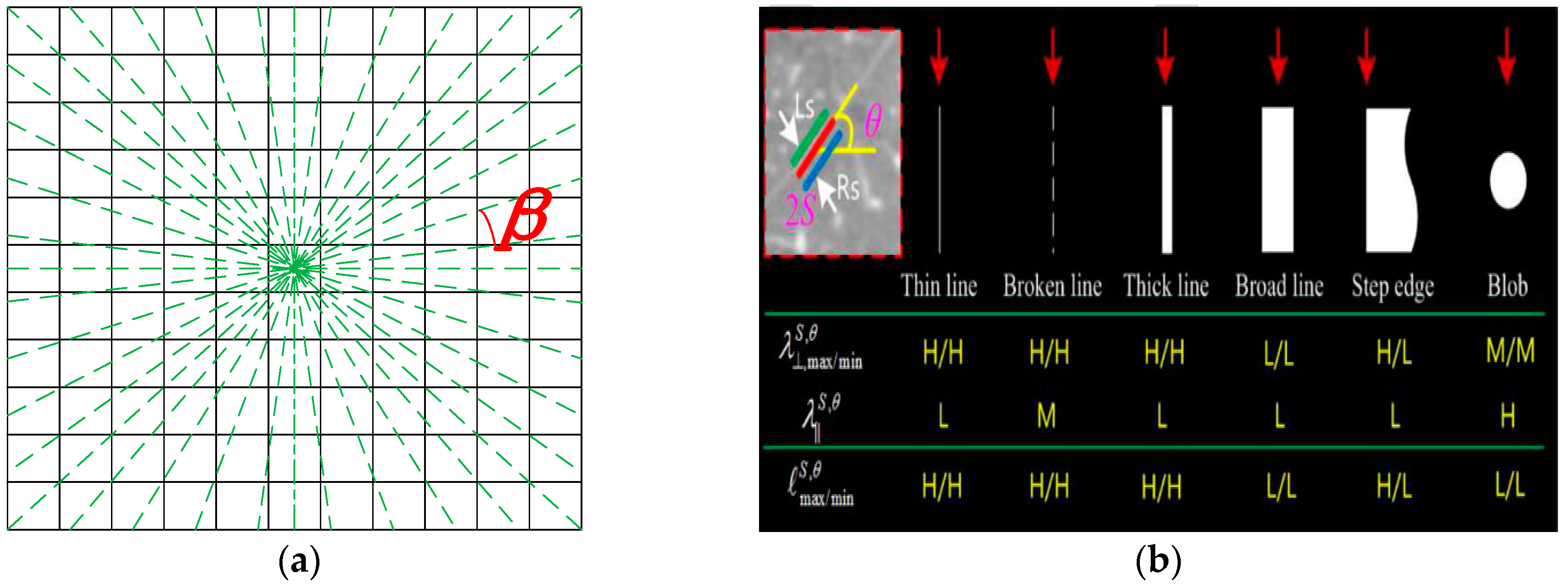
2.1. A Derivative of Stick Filter (DoS) for Fissure Enhancement

Considering the typical thin curvilinear shape of fissure profiles inside 2D cross-sections, Xiao et al. [13,14] proposed a DoS filter for pulmonary fissure enhancement in CT images. Their main idea was to simulate the fissure-line appearance by defining a nonlinear derivative with three parallel stick kernels in varying directions from 0 to π. The benchmark angle β of the stick kernels is approximately π/20 with the sticks length L = 11 pixel as shown in Figure 1a. The method is useful and effective for fissure enhancement, but it only utilizes the intensity information and discards the orientation information of the operators, which might lead to a problem in the case of low contrast and adhering clutter interference.

Figure 1. The principle of the derivative of stick (DoS) filter. Here, (a) denotes the orientation of the DoS filter, (b) depicts the responses of the DoS filter on typical pulmonary structures with the characters H, M and L indicate the high, moderate and low values, respectively. Note this figure is copied from [13] with permission.

To better express the DoS filter, we used $u_M$, $u_L$ and $u_R$ to indicate the mean intensity respectively along the middle (red), left (green) and right (blue) sticks of the kernel in Figure 1b. The mean intensity was calculated with

$$u=\frac{1}{L}{\displaystyle \sum _{j=1}^L{I}_j}$$

(1)

The nonlinear derivatives perpendicular to the sticks can be described as

$${\lambda }_{\perp ,\max /\min }^{S,\theta }\left(x\right)=\max /\min \left(u_M-u_L,u_M-u_R\right)0\le \theta \le 20\beta$$

(2)

where S denotes the spacing between adjacent sticks, θ is the stick orientation and x the spatial location within the lung. To further suppress the blob shape, a measurement criteria was described:

$${\lambda }_{\left|\right|}^{S,\theta }\left(x\right)=\sqrt{E\left(I_j^2\right)-{\left(E\left(I_j\right)\right)}^2}$$

(3)

with E being an expected value operator. Accordingly, two 2D line strength measures $l_{\max }$ and $l_{\min }$ can be formulated as

$$l_{\max /\min }^{S,\theta }\left(x\right)={\lambda }_{\perp ,\max /\min }^{S,\theta }\left(x\right)-k\ast {\lambda }_{\left|\right|}^{S,\theta }(x)$$

(4)

Here, k = 0.7 is a coefficient [13]. Thus, the multiple directional information can be integrated with

$$F_{\max /\min }\left(x\right)=\max \left(\underset{1\le i\le 20}{\max }\left(l_{\max /\min }^{S,{\theta }_i}\right),0\right)$$

(5)

Then, a max–min cascaded filter was designed to over-emphasize the step-edge suppression. Therefore, the fissure response can be described as:

$$F_o\left(x\right)=F_{\max }\left(x\right)o{F}_{\min }\left(x\right)$$

(6)

Finally, the 3D shape-tuned fissure response was defined as

$$F^{3D}=(F_o^A+F_o^S+F_o^C)\ast \frac{median(F_o^A,F_o^S,F_o^C)}{\max (F_o^A,F_o^S,F_o^C)}$$

(7)

with $F_o^A$, $F_o^S$ and $F_o^C$ respectively corresponding to the response across the orthogonal, sagittal and coronal sections.

2.2. An Oriented Derivative of Stick (ODoS) Filter for Fissure Enhancement

Although plausible results were reported in the study in [13], the clutters still remain a serious problem for the accurate segmentation of lobar fissures. As a remedy, Peng et al. [14] attempted to improve the original DoS filter by merging its orientation response. The orientation response was defined as

$${\theta }_{\max }=\{\begin{array}{ccc}\hfill \arg \max (l_{\max }^{S,\theta }),& if\hfill & l_{\max }^{S,\theta }>0\hfill \\ \hfill NaN,& else\hfill & \end{array}$$

(8)

Therefore, the vector field can be calculated with

$${\overrightarrow{V}}_1=F^{3D}\cdot (\cos {\theta }_{\max },\sin {\theta }_{\max })$$

(9)

To demonstrate the ODoS orientation response, a sagittal slice was selected in Figure 2a and the corresponding vector field is shown in Figure 2b. Figure 2c shows the zoomed rectangle region of Figure 2b. It can be seen that the vector field was regularized after applying the ODoS filtering. However, the original ODoS filter [14] used only the 2D orientation information in thesagittal plane, which might lead to an ambiguous definition of orientation if there exists local deformation or discontinuity along a specific plane. To further remedy this shortcoming, we extended the original ODoS vector field to a three-dimensional space, i.e., the 2D vectors in the axial plane, sagittal plane and coronal plane were independently analyzed and their coplanar property were investigated.

Figure 2. The orientation response of an oriented derivative of stick (ODoS) filter: (a) original image, (b) vector filed, (c) zoomed image of the red rectangle region in (b).

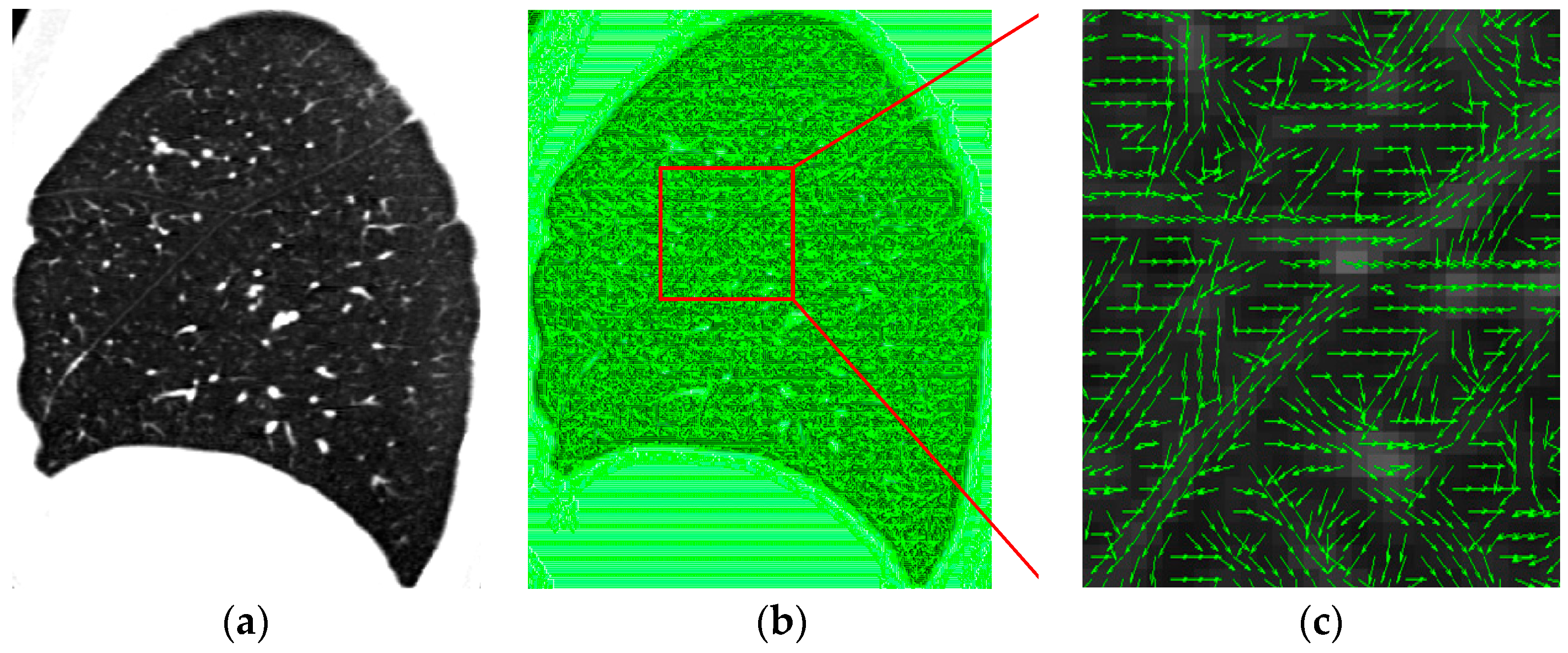
3. Pulmonary Fissure Detection

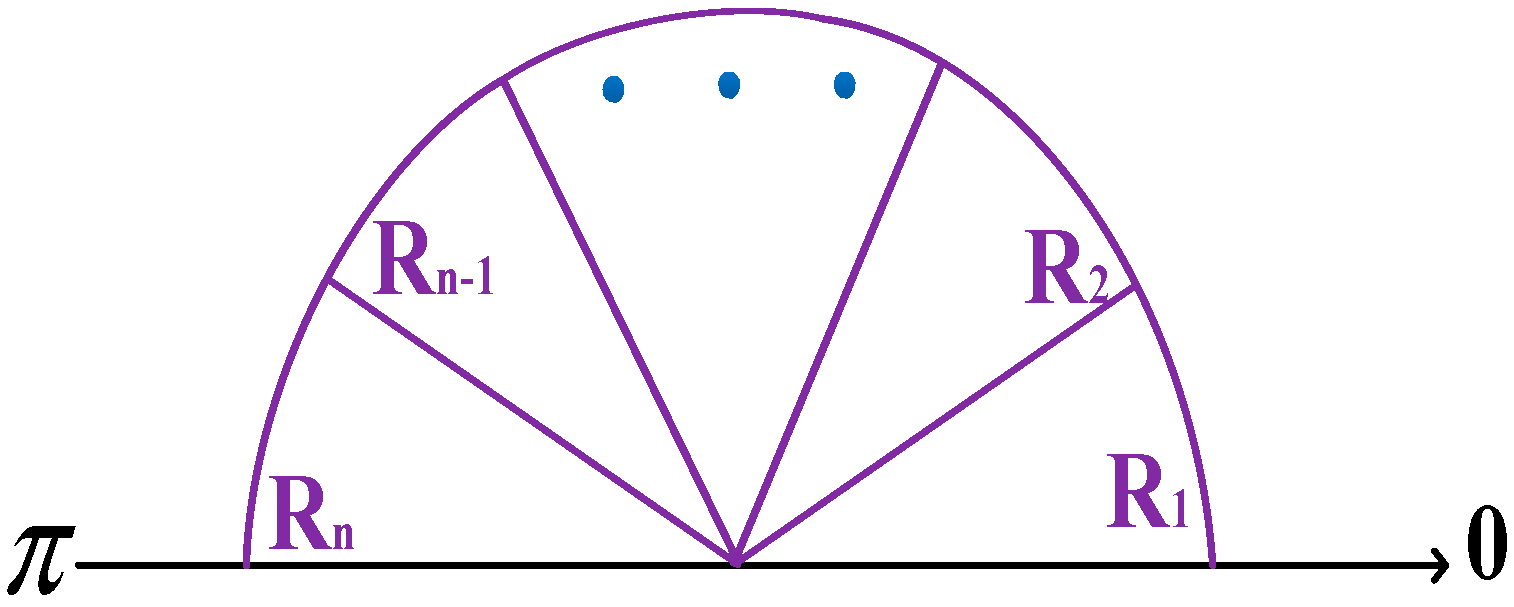
3.1. Improved Orientation Partition Scheme

Peng et al. [14] presented an orientation partition scheme for pulmonary fissure segmentation, but the approach may cause part of the fissures to remain undetected. To solve the problem and suppress clutters, we first used a threshold T to modulate the vector field:

$${\overrightarrow{V}}_2=\{\begin{array}{cc}\hfill \frac{{\overrightarrow{V}}_1}{F^{3D}},& if{F}^{3D}>T\\ \hfill 0,& else\end{array}$$

(10)

Then, we divided the stick kernel orientation θ range from 0 to $\pi$ into n non-overlapped partition. The n sub-regions were marked with R₁, R₂, …, R_n and are shown in Figure 3. The mathematical expression is as follows:

$$F_i=\{\begin{array}{cc}1,& if\theta \in R_{i}and{\overrightarrow{V}}_2\ne 01\le i\le n\\ 0,& else\end{array}$$

(11)

Figure 3. Improved orientation partition scheme.

In each partition F_i, we considered objects with a volume smaller than a threshold Vth to be clutters and marked them with N_i. The reason is that clutters appear as smaller objects in the partition F_i and usually have a lower volume. The purified results can then be represented as

$$F={\displaystyle \sum _{i=1}^n{F}_i}-{\displaystyle \sum _{i=1}^n{N}_i}$$

(12)

The purified results in the axial plane, sagittal plane and coronal plane are described with $F^A$, $F^S$ and $F^C$.

To illustrate the effect of the proposed method, we marked the clutters N_i with different colors, as shown in Figure 4a. The purified results F^A, F^S and F^C are shown in Figure 4b–d, respectively. It can be seen that a number of clutters have been largely removed.

Figure 4. Clutters suppression. (a) N_i. (b) F^A. (c) F^S. (d) F^C.

3.2. Multiple Section Model

As observed in Figure 5, the clutter-like airways or vessels labeled with yellow may appear as curvilinear structures in a single cross-section (e.g., the sagittal slice in Figure 5b, but appear as ellipse-like structures in the coronal, axial or diagonal planes. In contrast, pulmonary fissures labeled with green appear as curve-lines in the cross-sections. Therefore, we can use the shape features to suppress clutters and highlight the fissure representation.

Figure 5. Investigate the shape feature of various pulmonary structures: (a) 3D visualization of a human lung, and its (b) sagittal slice, (c) coronal slice, (d) coronal slice.

To achieve this purpose, a morphology and connected component-based region operator like the Matlab function ‘regionprops’ was used to calculate the selected object property [17,18] such as the major axis length H and minor axis length W. We used $S$ to represent each object in the axial, coronal, sagittal or diagonal planes. To suppress the ellipse-like structures, a line measure criterion was defined:

$$W(S)/H(S)\le T_L$$

(13)

Based on the fact that the oblique fissure is oriented at approximately 45 degrees relative to the Z (vertical) axis and the angle that the horizontal fissure makes with the X-Y plane is small in most cases [19,20], we only used the line measure criterion to suppress clutters in seven specific planes. In other words, the planes marked with yellow and green color in Figure 6 must not be taken into account. This is because pulmonary fissures may appear as ellipse-like structures in the planes.

Figure 6. A multiple section model.

After using the line measure criterion to suppress the ellipse-like structures in multi-sections, we subsequently used the volume sorting scheme to pick out the surface patches as candidate pulmonary fissures [13]. The results corresponding to F^A, F^S and F^C are respectively shown in Figure 7a–c. It can be seen that parts of fissures are undetected. To overcome the problem, a morphological OR operation was used to integrate all of the results. Finally, we followed the work of Xiao et al. [13] and used the volume sorting scheme to isolate the fissure patches for pulmonary fissure segmentation, and the integration results are shown in Figure 7d.

Figure 7. Fissure segmentations, respectively, corresponding to (a) F^A, (b) F^S, (c) F^C and their integration (d).

4. Experimental Results

4.1. Data and References

The computer is configured with 20GB RAM, Windows 10 operating system. The parameters related to our scheme are empirically configured, T = 1, Vth = 1000 and T_L = 0.5. Our scheme is validated in the Lobe and Lung Analysis 2011 (LOLA11) dataset [21], which includes 55 CT scans acquired from a variety of scanners and protocols. The fissure references were taken from Xiao et al. [13] with permission and were verified by two specialists [13].

4.2. Evaluation Criteria

The fissure segmentation result and its adjacent 3 mm regions were marked with S₁. In the same way, the manual reference and its adjacent 3 mm regions were marked with R. The overlapped regions between the fissure segmentation result and R were regarded as TP₁, and the rest as FP. Similarly, the overlapped regions between the manual reference and S₁ were regarded as TP₂, and the rest as FN. Therefore, the false discovery rate (FDR), false negative rate (FNR) and F₁-score (F₁) were defined as:

FDR = FP/(TP₁ + FP)

(14)

FNR = FN/(TP₂ + FN)

(15)

F₁ = 2 × (1 − FDR)(1 − FNR)/(2 – FDR − FNR)

(16)

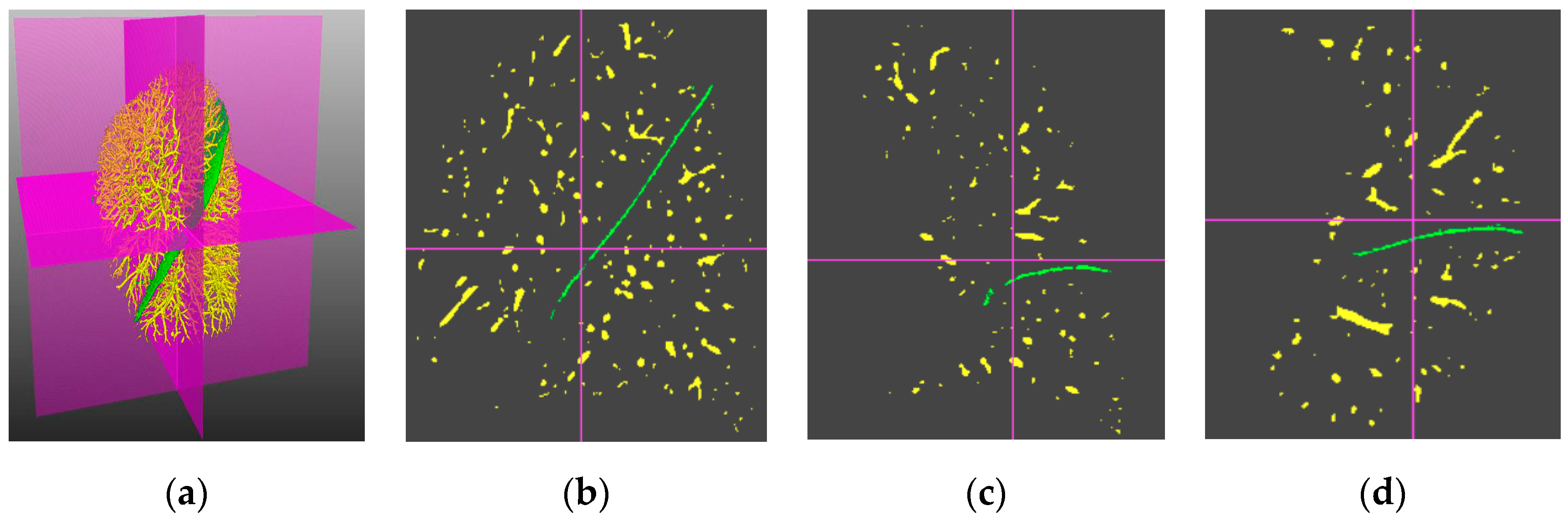
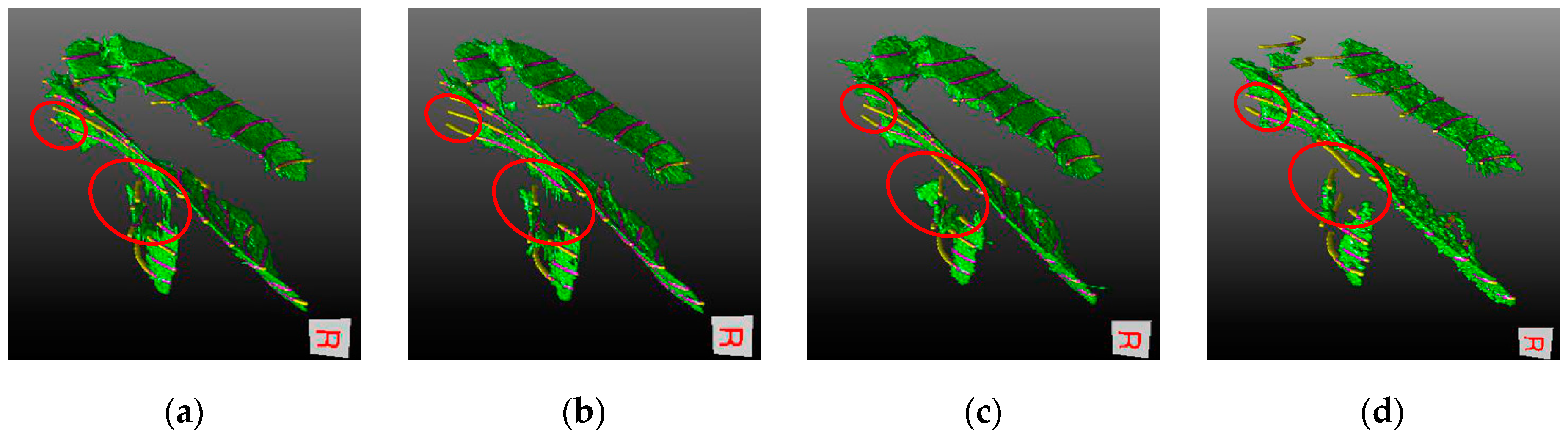
4.3. Visual Inspection

The fissure segmentation results of the proposed method, the ODoS filter [14], the DoS filter [13] and the fissureness filter [7] are respectively shown in Figure 8a–d. Note that the visualization was implemented with the Mevislab software, and the standard anatomical direction terms (i.e., right, left, anterior, posterior, inferior and superior) are used to indicate the view directions. The fissure references, the segmentation results and their overlapping regions are respectively rendered in yellow, green and purple. The advantage of the proposed method can be found in the areas labeled with red ellipses, as parts of weak objects can be detected by the proposed method and reduce the FNR value, while the compared methods [7,13,14] may cause parts of fissures to remain undetected. It can be seen that the proposed method showed good performance in terms of pulmonary fissure segmentation.

Figure 8. 3D fissure segmentation results from: (a) the proposed method, (b) the ODoS filter, (c) the DoS filter, and (d) the fissureness filter. Here, the cubes at the lower right corner indicate the view direction of the visualization in a standard anatomical coordinate system.

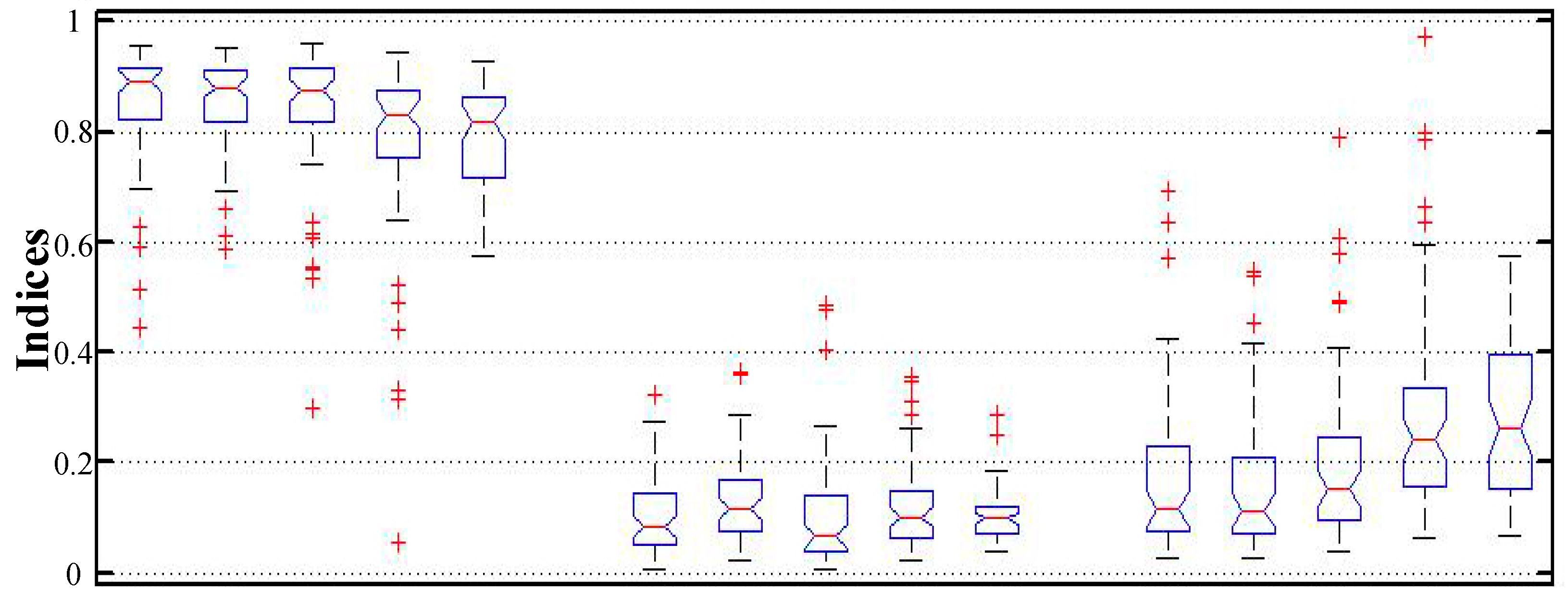
4.4. Quantitative Evaluation

Our scheme was validated in the LOLA11 dataset including 55 CT scans. The box-plots of the indices (FDR, FNR and F₁) corresponding to the proposed method (n = 5), the proposed method (n = 4), ODoS filter (od) [14], DoS filter (d) [13] and fissureness filter (f) [7] are displayed in Figure 9. The median values of the box-plots were 0.8916, 0.8812, 0.8768, 0.8331, 0.8181, 0.0846, 0.1157, 0.0654, 0.1020, 0.0981, 0.1172, 0.1139, 0.1524, 0.2418 and 0.2635. It can be seen that the proposed method gained a higher median F₁-score than the compared methods [7,13,14]. In other words, our scheme outperformed the compared methods [7,13,14] in pulmonary fissure segmentation. The good performance of our scheme is demonstrated in Figure 8 and Figure 9 due to the lower FNR value, which means that the completeness of the pulmonary fissure detection improved with our scheme.

Figure 9. Quantitative validation of pulmonary fissure segmentation on the LOLA11 dataset using different methods. Here, the F1, FDR, FNR indices of five different methods are plotted from left to right, and the subscripts m5 and m4 represent the proposed method with the parameter n = 5 and 4. The subscripts od, d and f indicate the ODoS filter [14], DoS filter and fissureness filter [7], respectively.

Furthermore, to compare the computation efficiency of different methods, we tested them on a typical 400 × 512 × 512 size CT image. As shown in Table 1, the original fissureness filter took the least amount of time due to its simple implementation. The proposed method required the second shortest time, but had much better performance than the similar DoS and ODoS methods.

Table 1. The runtime of the proposed method, ODoS method, DoS method and fissureness method for a typical 400 × 512 × 512 size image.

400 × 512 × 512	Proposed method	ODoS	DoS	Fissureness
Runtime	1410s	1390s	1470s	600s

5. Discussion

In this study, a novel method was presented for pulmonary fissure segmentation in CT images. It has a variety of characteristics and merits. First, multi-section vector information was used for pulmonary fissure enhancement, whereas many existing methods [12,13,22] use only the magnitude information to enhance pulmonary fissures, which cannot efficiently distinguish between fissures and clutters. Second, an improved orientation partition scheme was presented to suppress clutters. This approach had the capability to highlight fissure representation and simultaneously reduce the loss of fissures. Third, a specific multiple section model was introduced to separate pulmonary fissures. Generally, the proposed method resulted in a salient improvement in both fissure segmentation and interference suppression. Compared with many conventional methods [7,13,14], the presented method appeared to be more efficient at pulmonary fissure segmentation, obtaining the highest F1-score and the lowest FDR and FNR indices in the validating experiments. The reason for this is that our method is able to identify weaker fissure objects and perform better on noise suppression due to the adoption of a new multiple section model. This model is responsible for the low missing detection ratio of FDR and low false detection of FNR thus resulting in a higher accuracy.

However, as the presented method originated from the DoS and ODoS filters, it inevitably inherited the drawbacks of these line detection methods. While the fissure lines take a point-cloud like distribution, the large intensity variance along the objects might mean that some remain undetected. In the future, we will attempt to merge stronger or more global prior constraints into the model to improve its noise immunity and ability to resist interference. Additionally, the machine learning, group component analysis and other feature extraction algorithms could be potential research directions. Furthermore, we will seek collaboration with medical experts and researchers to apply our method in clinical diagnosis and surgical navigation, for example in COPD quantitative assessment and assisting lung nodule detection.

6. Conclusions

A multiple section model and related detection scheme for pulmonary fissure detection in CT images was proposed in this paper. Considering the fact that clutters often take on an orientation that is saliently different from desirable pulmonary fissure objects, an orientation field was adopted to describe the fissure profiles. Another contribution is to the fissure segmentation, with a specifically designed multiple section model to suppress clutters and separate pulmonary fissures in a noisy environment. The proposed method was validated in experiments using a publicly available LOLA11 dataset. It was verified that our scheme can outperform the conventional methods in terms of clutter suppression and weak object detection.