Parameterized Algorithms in Bioinformatics: An Overview

Abstract

Bioinformatics regularly poses new challenges to algorithm engineers and theoretical computer scientists. This work surveys recent developments of parameterized algorithms and complexity for important NP-hard problems in bioinformatics. We cover sequence assembly and analysis, genome comparison and completion, and haplotyping and phylogenetics. Aside from reporting the state of the art, we give challenges and open problems for each topic.

1. Introduction

With the dawn of molecular biology came the need for biologists to process and analyze data way over human capacity, implying the need for computer programs to assemble sequences, measure genomic distances, spot (exceptions to) patterns, and build and compare phylogenetic relationships, to name only few examples. While many of these problems have efficient solutions, others are inherently hard. In this work, we survey selected NP-hard problems in genome comparison and completion (Section 2), sequence assembly and analysis (Section 3), haplotyping (Section 4), and phylogenetics (Section 5), along with important results regarding parameterized algorithms and hardness. While trying to be accessible to a large audience, we assume that the reader is somewhat familiar with common notions of algorithms and fixed-parameter tractability, such as the $O^{*}(.)$-notation, giving only exponential parts of a running time, ignoring polynomial factors (for details about parameterized complexity, we refer to the recent monographs [1,2]). In a nutshell, parameterized complexity exploits the fact that the really hard instances are pathological and real-world processes generate data which, although enormous in size, are very structured and governed by simple processes. It seems straightforward that biological datasets abide by this “law of low real-world complexity”.

While excellent surveys of fixed-parameter tractable (FPT) problems in bioinformatics exist [3,4,5,6], this work tries to present an update, summarizing the state of the FPT-art as well as reporting on some additional “hot topics”. We further aim at: 1. iterating that parameterized algorithms are a viable and widespread tool to attack NP-hard problems in the context of biological data; and 2. supplying engineers and problem-solvers with computational problems that are actually being solved in practice, inspiring research on concrete open questions. Herein, we focus on problems that are particular for bioinformatics, avoiding more universal and general problems such as the various versions of Clustering which, while important for bioinformatics, have applications in many areas.

Generally, each topic has a problem description, a results section, some open problems and, possibly, an assortment of notes, giving additional information about less popular variants, often only mentioning results or problems related to the main topic without going into details. Finally, we want to apologize for the limited coverage of relevant work but, as our colleague Jesper Jansson wrote,

“Writing a survey about bioinformatics-related FPT results sounds like a monumental task!”

2. Genome Comparison and Completion

This section considers genetic data at its largest scale, i.e., as a sequence of genes, independent of their underlying DNA sequences. At this scale, long-range evolutionary events occur, cutting and pasting whole segments of chromosomes (“chromosomal rearrangement”) [7]. The number of such rearrangements between the genomes of two species can be used to estimate their “genetic distance” which, in turn, allows for phylogenetic reconstruction. Further, we consider the problems of identifying genes with a common ancestor after duplications, and filling the gaps in an incomplete genome.

In the most general setting, a genome G may be represented as a collection of strings and circular strings, where each string represents a chromosome and each character represents a gene or gene family. However, for ease of representation, most models use a single-sequence representation of the genome (which generalizes easily to multi chromosomal inputs in most cases). There is however an important distinction between the string model, allowing gene repetitions (also called duplicates, or paralogs), and the permutation model enforcing that each gene appears exactly once. Many problems in the following sections can be formulated in both models. The string model is obviously the most general in practice, but often comes with a prohibitive algorithmic cost. Parameterized algorithms can offer a good solution, using the fact that most genes only have a small number of occurrences. Thus, the maximum number of occurrences of any character in an input string, denoted occ in this paper, is a ubiquitous parameter. In both models, a genome is signed if each gene is given a sign (+ or −) representing its orientation along the DNA strand.

In the following, a string $s^{\prime }$ is called substring of a string s if $s^{\prime }=s$ or $s^{\prime }$ is the result of removing the first or last character of some substring of s. Further, $s^{\prime }$ is called subsequence of s if $s^{\prime }=s$ or $s^{\prime }$ is the result of removing any character from a subsequence of s. We say that two strings are balanced if each character appears with the same number of occurrences in both.

2.1. Genomic Distances

The problems in this section aim at computing a distance between genomes, reflecting the “amount of evolution” that occurred since the last common ancestor. Among the most basic distances for the permutation model is the breakpoint distance, counting the number of pairs of genes that occur consecutively in one genome but not in the other (a pair $\mathtt{ab}$ is considered to be identical to $\mathtt{ba}$ in the unsigned model, however $+\mathtt{a}+\mathtt{b}$ is identical only to $+\mathtt{a}+\mathtt{b}$ and $-\mathtt{b}-\mathtt{a}$ in the signed model). Its complement is a measure of similarity, the number of common adjacencies (the number of pairs of consecutive genes that occur in both genomes). Common adjacencies can easily be generalized in the string model: adjacencies of each genome are seen as a multi-set, and the number of common adjacencies is the size of the intersection of these multi-sets.

More advanced genomic distances are rearrangement distances. A rearrangement acts on the genome by reordering some genes in a certain way, mimicking a large-scale evolutionary event. The core question in rearrangement distances is to compute the minimum number of rearrangements transforming a genome into another. These distances are more precise—in the sense that they directly describe parsimonious evolutionary scenarios—but in most cases significantly more difficult to compute than the breakpoint distance. Note that balanced genomes are usually considered, i.e., any character appears with the same number of occurrences in every genome. See the work of Fertin et al. [8] for an extensive survey on rearrangement distances.

2.1.1. Double-Cut and Join Distance

Problem Description. The double-cut and join distance needs the most general genome model as intermediary steps, that is, a multi-set of strings and circular strings. A double-cut and join operation splits the genome in two positions and joins the four created endpoints in any way (see Figure 1). For signed genomes, this operation is required to maintain consistent orientation of each gene. We focus on the case where the source and target genomes have a single chromosome (i.e., strings or permutations).

Results. The DCJ distance can be computed in linear time in the signed permutations model [9,10]. However, it is NP-hard in the unsigned permutation or string models [11]. On the positive side, it admits an $O\left(2^{2k}n\right)$-time algorithm for unsigned permutations [12].

An issue with the DCJ distance is that the solution space might be very large, as many different scenarios may yield the same distance. Thus, more precise models have been designed to “focus” the solution towards the most realistic scenarios. Fertin et al. [13] introduced the wDCJ distance, where intergene distances are added to the genome model and must be accounted for in the DCJ scenario (when breaking between consecutive genes, the number of intergenomic bases must be shared among both sides). This variant makes the problem NP-hard for signed permutations, but fixed-parameter tractable for the parameter k. Another constraint focuses on common intervals, which are segments of the genomes that have exactly the same gene content, but in different orders. A DCJ scenario is perfect if it never breaks a common interval. Bérard et al. [14] showed that finding a perfect scenario with a minimum number of operations is FPT for a parameter given by the common interval structure.

2.1.2. Reversal Distance

Problem Description. A reversal [15] is a rearrangement reversing the order of the characters in any substring of the genome. When considering signed genomes, a reversal additionally switches all the signs in the reversed substring (see Figure 2).

Results. Sorting by Reversals is polynomial-time solvable in the signed-permutations model [16]. However, it is NP-hard for unsigned permutations [17] and for strings, even when occ = 2 [18] and for binary signed strings [19]. For unsigned permutations, Sorting by Reversals is easily FPT for k, using the fact that reversals never need to cut at positions that are not breakpoints [20]. For balanced strings, a possible parameter, $b_{max}$, is the number of blocks of the input strings, where a block is a maximal factor of the form ${\mathtt{a}}^n$ for some character $\mathtt{a}$. Sorting by Reversals can be solved in $O^{*}\left(b_{max}^{O\left(b_{max}\right)}\right)$ time in both the signed and unsigned variants [21]. As for DCJ, the variant restricting scenarios to reversals preserving common intervals is also NP-hard, and FPT for a parameter given by the common interval structure [22].

Notes. Other rearrangements can be considered, such as transpositions (two consecutive factors are swapped), and the prefix and/or suffix variants of reversals and transpositions (that is, reversals and transpositions affecting the first or last character of the sequence, respectively) (see, e.g., [23]).

No polynomial-time algorithm is known for computing these rearrangement distances, although NP-completeness is still open, notably on permutations for signed prefix reversals and prefix transpositions. Fixed-parameter tractability results may be achieved in the permutation model using the relationship between these rearrangements and breakpoints [24], and in the string model using the number of blocks $b_{max}$ as a parameter [21,25].

2.2. Common Partitions

Two strings $S_1$ and $S_2$ have a common string partition S if S is a (multi-)set of strings called blocks such that both $S_1$ and $S_2$ can be seen as the concatenation of the blocks of S. Furthermore, S is a common strip partition if each of its blocks has length at least two. Note that any two balanced strings have a common string partition, but may not have a common strip partition. Common strings or common strips may be used to identify syntenic regions between two genomes. Intuitively, most genes from the genomes of two close species should have a simple common string partition.

2.2.1. Minimum Common String Partition

Problem Description. The most natural partition problem is Minimum Common String Partition [18] (see Figure 3), which admits slightly different formulations [26,27]. It can be seen as a generalization of the breakpoint distance on balanced strings. Indeed, a common string partition may be seen as a mapping between the characters of both strings, i.e., a permutation, whose breakpoints correspond to the limits between consecutive blocks. Rather than a genomic distance, it can also be seen as a method for assigning orthologs across two genomes, assuming that all duplication events happened before their last common ancestor. For example, depending on how orthologs are matched, genomes abacd and acdab may be seen as permutations 12345 and 34512 (i.e., matching two blocks ab and acd), or 12345 and 14532 (matching four blocks a, b, a, and cd). Gene sequences alone may not be sufficient to distinguish both cases: in such a situation, the first option presumably reflects better the evolutionary history of these species, since it involves fewer large-scale events in the genome.

Results. MCSP is FPT for several combinations of parameters, depending on the relative size of the blocks, the size k of the partition and/or the maximum number occ of occurrences of a character  [28,29]. It can also be solved in $k^{O\left(k^2\right)}$ time [30], although this is too slow to be of practical interest. Finally, MCSP admits a more practical algorithm for the parameter $k+$ occ, running in O(occ^2kkn) time [31]. This last algorithm also applies to unbalanced strings where the problem is extended as follows: excessive characters may be removed from their respective input strings, but only between consecutive blocks.

Another possible parameter is the number of preserved duos, $k^{\prime }=\left|G_1\right|-k$. Note that MCSP is denoted Maximum-Duo Preserving String Mapping in the context of approximations and parameterized algorithms maximizing $k^{\prime }$. This version is FPT as well, and admits a kernel of size $O\left(k^{\prime 8}\right)$ [32].

2.2.2. Maximal Strip Recovery

Problem Description. In the Maximal Strip Recovery problem [33] (see Figure 4), the goal is again to identify common blocks between two genomes. But here, we may remove characters (genes) from the input strings so that the resulting subsequences can be partitioned into common strips. Only the number of deleted genes is counted in the objective function, rather than the number of strips.

Results. In the permutation model, this problem admits a linear kernel [34] and an $O^{*}\left({2.36}^k\right)$ FPT algorithm [35]. The picture is less simple for parameter $|G_1^{\prime }|$ (i.e., the Maximal Strip Recovery problem) in the permutation model. The generalization to four strings instead of two is W[1]-hard [36]. On the other hand, it is FPT for parameter $|G_1^{\prime }|+\delta$, where $\delta$ is the maximum number of consecutive characters deleted within any strip [35]. The main case (MSR with two strings and parameter $|G_1^{\prime }|$ only) is still open.

Open Problems. Very little is known about MSR and CMSR in the string model. Both are NP-hard, and MSR is polynomially solvable for constant parameter values (by enumerating all possible subsequences of a given size and their strip partitions), but no other parameterized result is known. In particular, is CMSR NP-hard on strings for $k=0$? In other words, is there a polynomial-time algorithm finding any common strip partition of two balanced strings?

2.3. Genome Completion

In both problems in this section, the goal is no longer to compare two genomes (either by building a rearrangement scenario or identifying conserved regions), but to generate a complete genome, based on incomplete data and/or genomic sequences of close species.

2.3.1. Scaffold Filling

Problem Description. A scaffold is a partial representation of the genome, obtained after creating and ordering contigs from reads. Errors during DNA sequencing, low coverage, or sequence repetitions yield unavoidable gaps in the genome assembly (see Section 3). One solution to obtain an approximation of the original genome is to use a better-known genome to infer the missing genes. A completion of genome $G_1$ with respect to $G_2$ is a supersequence $G_1^{\prime }$ of $G_1$ such that $G_1^{\prime }$ and $G_2$ are balanced. The quality of the completion is evaluated by a genomic distance (DCJ, breakpoints, etc.) denoted by d in the following.

Results. In the signed permutations model, d-SF can be solved in polynomial time when the considered distance d is the DCJ distance [37]. On the other hand, for the string model, only weaker distances have been considered: the problem turns out to be NP-hard even for the common adjacencies measure, but is FPT for this measure as parameter [38]. The string algorithms can be generalized to the variant where one seeks extensions of both input genomes at the same time (the “two-sided” case).

Open Problems. What is the parameterized complexity of MCSP-SF on strings? As MCSP is NP-hard, this problem must be too, but it may admit efficient algorithms parameterized by the MCSP distance and/or the parameter occ. Another open question is the DCJ algorithm can be fully generalized to the two-sided case.

2.3.2. Breakpoint Median

Problem Description. In the Breakpoint Median problem, the goal is to build a most-likely common ancestor from three genomes, which can in turn be used to recreate all ancestral genomes in a phylogenetic tree [39].

Results. The problem can be seen as a special case of Traveling Salesman [39] and can be solved in $O\left({2.15}^{d}n\right)$ time.

3. Genome Assembly and Sequence Analysis

Producing the genetic code (sequence of bases A, C, G, and T) present in a sample lies at the core of almost all research in molecular biology. This, however, requires solving an intricate puzzle with millions of pieces (“reads”), involving many computational problems on sequences, such as the Scaffolding problem [40].

Moreover, to draw conclusions from sequences, they have to be analyzed and compared. Such comparisons are made difficult, at the most basic level, by the amount of genetic variation and errors that can appear all along the sequences. A central task is to detect character insertions, deletions, and substitutions within a set of strings representing “similar” DNA or peptide sequences, thereby identifying a common structure [41].

3.1. Multiple Sequence Alignment

Problem Description. Multiple Sequence Alignment is the central alignment problem in bioinformatics, used to align DNA sequences along one another, taking insertions, deletions, and substitutions into account (see Figure 5). An extension of a string s is a string obtained from s by inserting any number of gap characters, denoted -. An alignment of strings $s_1,\dots ,s_k$ is obtained by creating an extension $s_1^{\prime },\dots ,s_k^{\prime }$ of each input string, all of the same size. Column i of an alignment is the tuple $(s_1^{\prime }\left[i\right],\dots ,s_k^{\prime }\left[i\right])$. A cost function is any function assigning a positive cost to a column. The unit cost function counts the total number of mismatches in a column, i.e., the number of pairs $(j,j^{\prime })$ such that $s_j\left[i\right]\ne s_{j^{\prime }}\left[i\right]$.

Results. Multiple Sequence Alignment can be solved by a straightforward dynamic programming in time ${\ell }^{O\left(k\right)}$ for any cost function (where ℓ is an upper-bound on the input string length). It is NP-hard for a wide range of cost functions, including all metric cost functions (even on binary strings), and in particular the unit cost function [42,43,44]. Due to its central position in DNA analysis, this problem has been the subject of over 100 heuristics over the last decades (this was already said in 2009 [45]), but there does not seem to be any success so far in terms of exact parameterized algorithms.

Open Problems. Does Multiple Sequence Alignment admit an FPT algorithm for parameter k? If not, can ${\ell }^{o\left(k\right)}$ be achieved?

3.2. Identifying Common Patterns

3.2.1. Closest String (and Variants)

Problem Description. In Closest String, the goal is to find, given a set of strings, a center string that is close enough to all others (counting the number of mismatches, i.e., the Hamming distance, denoted by Ham). This problem and many variants have been widely studied under the point of view of parameterized algorithms: we only highlight some prominent results, and refer the reader to the work of Bulteau et al. [46] for a more exhaustive review.

Results. Closest String is NP-hard, even for binary alphabets [47]. On the other hand, it is FPT for any of the following parameters: $d_r$, k, and ℓ [48]. However, the algorithm for k makes use of an integer linear program with at most $2^k$ variables, implying a mostly impractical combinatorial explosion. An easier (actually trivial) variant, denoted Consensus String, aims at minimizing the sum (or average) of the hamming distances to the center, rather than the worst-case distance.

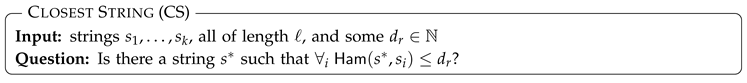
Closest Substring. 

A common generalization of CS called Closest SubString asks for a common pattern in all input strings, i.e., it allows trimming input strings until they reach a desired given length m. In this case, the consensus variant, optimizing the sum of distances, is no longer trivial and is denoted Consensus Pattern. Although these problems become much harder than Closest String and are W[1]-hard for any single parameter among ℓ, k, d, and m, they still admit FPT algorithms for several combinations of these parameters [49,50,51,52].

Closest String with Outliers. 

Another noteworthy variant allows ignoring a small number t of outliers from the input set of strings [53]. Interestingly, all parameterized algorithms for Closest String extend to this variant when t is considered as an additional parameter.

Radius or sum. 

A generalization for Closest String (that also applies to the variants above) considers both a constraint on the maximum hamming distance (the radius, $d_r$) and on the sum of hamming distances (denoted $d_s$). Indeed, the radius constraint only focuses on worst-case strings, and the sum constraint tends to overfit large sets of clustered strings, so taking both constraints can help reduce those problems. All algorithms mentioned for the radius-only version can be extended, in one way or another, to take both constraints into account without additional parameters [54].

Another point of view consists in seeing the radius and sum measures as the $L_1$ and $L_{\infty }$ norms, respectively, of the vector $(d(s^{*},s_1),\dots ,d(s^{*},s_k))$. Thus, a possible compromise consists in optimizing the $L_p$ norm of this vector for any rational p, $1<p<\infty$. Chen et al. [55] studied Closest String under these norms on binary alphabets, proved its NP-hardness, and gave an FPT algorithm for parameter k.

3.2.2. Longest Common Subsequence

Problem Description. The Longest Common Subsesquence problem in its simplest version asks for a string of maximal length that is a subsequence of two input strings (see Figure 6(left)). It admits a classical dynamic programming algorithm, with complexity $O\left(n^2\right)$. However, the problem becomes NP-hard when we increase the number of strings, as follows.

Results. The foremost parameters for Longest Common Subsesquence are k, ℓ, m, and the alphabet size denoted $|\Sigma |$. However, it is W[1]-hard (or worse) for all combinations of these parameters that do not yield a simple brute-force enumeration algorithm, i.e., $k+m$ with any $|\Sigma |$, and k with $|\Sigma |=2$ [56,57].

Omitted letters. 

Another possible parameter is the number of omitted letters, $\ell -m$: Longest Common Subsesquence is FPT for parameters $\ell -m$ and k [58], and the complexity is open for parameter $\ell -m$ only.

Sub-quadratic time? ($\mathit{k}\mathbf{=}\mathit{2}$) 

For two strings, there is no sub-quadratic algorithm unless the strong exponential time hypothesis fails [59]. However, parameterized algorithms can help subdue this lower bound to some extent: Bringmann and Künnemann [60] proposed an extensive study of the possible combinations of parameters yielding “FPT in P” algorithms (also sometimes referred to as “fully polynomial FPT”, see [61,62,63]), with matching lower-bounds in each case.

Constrained LCS. ($\mathit{k}\mathbf{=}\mathit{2}$) 

In this variant, the solution must contain each of a given set of f restriction strings as subsequences. The problem is in P for $f=1$ [64], NP-hard in general, and W[1]-hard for parameter f [65]. Finally, it is FPT for the total size of the restriction strings [66].

Restricted LCS. 

Here, the restriction strings are forbidden subsequences (rather than mandatory). The problem is FPT for the parameter $\ell +k+f$ [67], as well as for the total size of restriction strings (with $k=2$) [66].

Open Problems. What is the complexity of Longest Common Subsesquence parameterized by $\ell -m$, i.e., the maximal number of letters deleted in any string?

3.2.3. Shortest Common Supersequence

Problem Description. In Shortest Common Supersequence, we now want to find a larger string of which every input string is a subsequence (see Figure 6(right)).

Results. As for LCS, Shortest Common Supersequence is W[1]-hard for parameter k even on binary alphabets [56], and does not admit an ${\ell }^{o\left(k\right)}$ algorithm [68]. It does admit an FPT algorithm for the number of repetitions, $m-|\Sigma |$ when occ = 1 (each character appears at most once in any string) [69].

Open Problems. Can the FPT algorithm for occ = 1 be extended to more general strings?

3.2.4. Center and Median Strings

Problem Description. In the problems described so far in this section, the goal is to find a string minimizing the distance to all input strings, where the distance counts the number of substitutions (Closest String and Consensus String), deletions (Longest Common Subsesquence) or insertions (Shortest Common Supersequence). Each problem has its own applications, depending on the input data and allowed operations. A more generic variant allows for all three operations, i.e., uses the edit distance (also referred to as the Levenshtein distance, denoted $\mathsf{Lev}$) to measure the similarity to the solution string.

Results. Both problems are NP-hard and W[1]-hard for k, even on binary strings [70]. On the other hand, Center String is FPT for parameter $d+k$ [71].

Open Problems. Are these problems FPT when parameterized by d only, or by the string length?

3.3. Scaffolding

Problem Description. As mentioned previously, overlapping reads usually does not lead to a fully reconstructed (that is, one sequence per chromosome) genome. Instead, assembly algorithms usually produce fairly long and correct substrings called contigs that cannot be extended by overlapping reads. However, current sequencing techniques (“Next-Generation Sequencing” (NGS)) yield additional information about reads. Indeed, NGS-produced reads come in pairs (“mate pairs”) and a rough estimate about the number of base-pairs between the two reads of a pair is known. Thus, it is possible that a read r of a pair $(r,r^{\prime })$ aligns well with parts of some contig c while $r^{\prime }$ aligns well with parts of contig $c^{\prime }$. This presents evidence that, in the target genome, contig c is followed by contig $c^{\prime }$ and gives us an approximation of the distance between them (see Hunt et al. [72] for more details). To represent this information, we can construct a scaffold graph by representing contigs as pairs of vertices connected by a perfect matching, and connecting contig extremities u and v with an edge weighted by the number of mate-pairs indicating that u is followed by v in the chromosome. In this graph, we are looking for a cover of all matching edges using a small number of paths and cycles (corresponding to linear and circular chromosomes in the genome).

Huson et al. [73] considered G as multigraph in which each non-contig edge has an approximate length. This makes for more realistic modeling since two hypotheses involving different gap-sizes between contigs should be incompatible. The authors showed NP-completeness for this problem.

To better support repetitions, (Chateau et al. [74] unpublished) added multiplicities to the contig edges, which can be roughly estimated from coverage numbers. Then, a solution is a set of $\le {\sigma }_p$ open and $\le {\sigma }_c$ closed walks in G. They presented an ILP solving a slight generalization of this problem, but no parameterized algorithms are known in this case. However, the multiplicity-supporting version of Scaffolding gives rise to another problem: optimal solutions are much less likely to be unique and each individual optimal solution is thus likely to correspond to chimeric sequences (a genomic sequence is called chimeric if it contains material from different chromosomes or from unrelated parts of one chromosome). This gives rise to the problem of removing inter-contig edges such as to extract the sub-walks that are shared by all decompositions of a solution into walks [75].

Results. Gao et al. [76] presented an $O\left(\right|V\left(G\right){|}^w\left|E\left(G\right)\right|)$-time algorithm for SCA where w is the maximum number of contigs spanned by any inter-contig edge in the solution ordering. SCA is known to be W[1]-hard for k [75] but solvable in $O^{*}\left({(tw!)}^2\right)$ time [77], where $tw$ denotes the treewidth of G. A simple reduction from Hamiltonian Path proves SCA NP-hard even on bipartite planar graphs with constant edge weights and ${\sigma }_p+{\sigma }_c=1$ [75]. For a variation of this problem, they proved a kernel for a parameter involving the feedback edge set number of G. Finally, Scaffold Linearization has been shown to be NP-hard under multiple cost-measures for the solution X [78], but can be solved in $O^{*}\left(c^{tw}\right)$ time for different $c\le 5$, depending on the cost-measure [79].

Notes. Donmez and Brudno [80] approached scaffolding by first computing an orientation of the contigs, formulated as Odd Cycle Transversal (the problem of removing few vertices from a graph such that the result is bipartite), and then ordering them in the scaffold graph using a formulation as Feedback Arc Set. Note further that advances in engineering resulted in so-called “third-generation sequencing” techniques that allow researchers to read large chunks of DNA from a single chromosome [81]. Since these “long reads” have an elevated error rate, focus has recently shifted to detecting and correcting these errors with short reads instead of scaffolding paired reads.

Open Questions. Dallard et al. [82] observed that a simple, fast greedy heuristic often produces good scaffolds. It would be interesting to know if those scaffolds are generally similar to optimal scaffolds and, if so, consider parameters measuring this distance.

4. Haplotyping

Cells of diploid (or, more generally, polyploid) species have two (multiple) copies of each chromosome. These copies are imperfect in that they can differ in a tiny percentage of their positions (“sites”) and such positions are called Single-nucleotide polymorphisms (SNPs). When sequencing a diploid genome (see Section 3 for more on sequencing), each read comes from one of the copies of some chromosome but, a priori, there is no way of knowing whether two reads came from the same copy or not. Thus, an assembled diploid genome of an individual contains SNPs where both chromosomes agree (“homozygous sites”) and SNPs where they disagree (“heterozygous sites”). Since the vast majority of SNPs exist in only two states (“biallelic SNPs”) [83,84], the SNPs of a chromosome can be represented as a string over the alphabet $\{\mathtt{0},\mathtt{1}\}$ called a haplotype and the SNPs of a diploid individual can be represented as a string over the alphabet $\{\mathtt{0},\mathtt{1},\mathtt{2}\}$ called the genotype, where $\mathtt{0}$ and $\mathtt{1}$ mean that the two chromosomes agree on one of the biallelic states, whereas 2 means that the chromosomes disagree. Now, experimentally determining the genotype of an individual is (relatively) cheap and easy while experimentally determining the haplotypes of the chromosomes is expensive [85,86]. For many applications, however, knowledge of the haplotypes is required and, thus, computational methods have been developed to infer haplotype data (“haplotyping” or “phasing”). In Section 4.1, we consider the problem of inferring the haplotypes by overlapping reads from a diploid genome, similar to the reconstruction of DNA sequences (see Figure 7). In Section 4.2, we consider the problem of inferring the haplotypes of a population, given its genotypes (see Figure 8). This requires assuming that the distribution of haplotypes follows a parsimony criterion. Although most parsimonious solutions often do not reflect the truth [87], they can form the basis for more precise algorithms in the future.

For surveys on both variants of haplotyping, refer to the works in [88,89,90,91,92,93,94,95].

4.1. Haplotype Assembly

Problem Description. A matrix M with m length-n rows (“fragments”) over $\{\mathtt{0},\mathtt{1},-\}$ is called in conflict if there are rows r and $r^{\prime }$ and a position $i<n$ such that $r\left[i\right]$, $r^{\prime }\left[i\right]$ and − are pairwise distinct (that is, $-\ne r\left[i\right]\ne r^{\prime }\left[i\right]\ne -$) and conflict-free (or 1-conflict-free), otherwise. For all $p\ge 1$, M is called p-conflict-free if its rows can be partitioned into p conflict-free sets of rows. While we prefer stating the general (“polyploid”) version of this problem, the special case that $p=2$ (“diploid” genome) is by far the most commonly considered.

p-IH can be interpreted as a clustering problem that finds p consensus strings such as to minimize the sum of the radii needed to capture all input strings (rows), where the distance function depends on the nature of allowed “operations”. Most of the results are for diploid genomes, that is, for the 2-IH problem. In the following, a row r is called active in position j if there are i and ℓ such that $i\le j<\ell$ and $r\left[i\right]\ne -\ne r[\ell ]$, the set of positions in which r is active is called $\alpha \left(r\right)$ and a gap in a row r is any position $i\in \alpha \left(r\right)$ with $r\left[i\right]=-$. We let g denote the maximum number of gaps in any row of M, we let $\ell :={max}_r\left|\alpha \left(r\right)\right|$ denote the maximum number of active positions of any row, and we let $c:={max}_j{\alpha }^{-1}\left(j\right)$ denote the “coverage”, that is, the maximum over all positions j of the number of rows r that are active in j. Note that gapless rows can still contain chains of -at the beginning and end.

Results. The complexity of 2-IH depends on the type of operations allowed on the matrix. Mainly, three operations have been considered in the literature:

Deleting rows. 

The problem of turning M 2-conflict-free by row-deletions is known as Minimum Fragment Removal (MFR). It is equivalent to turning the “conflict graph” bipartite by removing vertices (this problem is called Odd Cycle Transversal or Vertex Bipartization in the literature). Herein, the vertices of the conflict graph are the rows of M and rows u and v have an edge if they cannot be assigned to the same chromosome, that is, $-\ne u\left[i\right]\ne v\left[i\right]\ne -$ for some position i. MFR is NP-hard even if each row has at most one gap [96], but becomes polynomial-time solvable for gapless M [96,97]. It can be solved in $O(2^{2g}{m}^{2}n+2^{3g}{m}^3)$ time [97] and in $O(nc{3}^c+mlogm+m\ell )$ time [98]. Of course, results for Odd Cycle Transversal apply to MFR: it admits $O^{*}\left(3^k\right)$-time [99,100] and $O\left({2.32}^k\right)$-time [101] algorithms as well as a randomized kernel of size $O\left(k^{4.5}\right)$ [102].

Deleting columns. 

The problem of turning M 2-conflict-free by column-deletions is known as Minimum SNP Removal (MSR). It has been shown to be NP-hard even if each row has at most two gaps [96], but polynomial-time solvable for gapless M [96,103]. Bafna et al. [97] showed an $O\left(2^{g}m{n}^2\right)$-time algorithm.

Flipping values. 

By far the most studied approach is turning M 2-conflict-free by flipping values, that is, turning a 1 into a 0 or vice versa. This problem is known as Minimum Error Correction (MEC) or Minimum Letter Flip in the literature and it is has been shown to be NP-hard, even on gapless inputs [104]. A simple reduction from Edge Bipartization [105] further shows that MEC is still NP-hard if each row contains at most three non-(-) characters and each column contains at most two non-(-) characters, thus excluding parameterized algorithms, even for the combined parameter. A parameterized algorithm with running time $O^{*}\left(2^m\right)$ is trivial (assign each row to one of the two partitions/chromosomes) and an $O^{*}\left(2^n\right)$-time algorithm was presented by Wang et al. [106]. Further research focused on the coverage c, which is very small in practice. $O^{*}\left(2^c\right)$-time algorithms with various polynomial factors were presented by Xie et al. [107], Deng et al. [108], Patterson et al. [109], Pirola et al. [110], and Garg et al. [111]. MEC can be linearly reduced to Odd Cycle Transversal [105], implying that results for Odd Cycle Transversal carry over to MEC as well ($O^{*}\left(3^k\right)$ time [99,100], $O^{*}\left({2.32}^k\right)$ time [101], and $O\left(k^{4.5}\right)$-size randomized kernel [102]).

On gapless inputs, MEC can be solved in $O\left(2^{\ell }mn\right)$ time [112] (assuming that all positions in the corrected matrix are “heterozygous”, that is, contain both 0 and 1) or in $O(3^{\ell }\ell m)$ time [105].

Notes. A variant of MFR in which rows are to be removed such as to make M 2-conflict-free and to maximize the number of SNPs covered by the solution, called Longest Haplotype Reconstruction, has been shown to be NP-hard but solvable in $O\left(n^2(n+m)\right)$ time [104] for gapless M. A more practical variant of MEC, incorporating the aspect of sequencing that each position in a read is given as four probabilities (probability for C, G, A, and T (or U)) instead of a single character was considered by Xie et al. [107], who included a “GenoSpectrum” in the input and give an algorithm running in $O(nc{2}^c+mlogm+m\ell )$ time. Another version of MEC, constraining output matrices by a “guide-genotype” was considered by Zhang et al. [113], showing that this version can be solved in $O\left(4^{\ell }m\right)$ time. A slight modification of the MEC problem, asking for two haplotypes $h_1$ and $h_2$ and a bipartition $(R_1,R_2)$ of the rows such that $h_i$ is at most k flips away from the reads in $R_i$ for $i\in \{1,2\}$, was considered by Hermelin and Rozenberg [114]. Their algorithm solves this problem in $O\left(2^g{k}^{k}mn\right)$ time.

Since diploid species usually inherit one chromosome from each of their parents, it seems plausible that knowledge of the pedigree of a group of species helps infer their haplotypes. In this context, Garg et al. [115] considered a set I of individuals and a set T of mother–father–child relations, given in addition to the fragment-matrices of each individual, and ask for a set of flips in each fragment-matrix such as to minimize the cost of the flips plus a cost function penalizing unlikely inheritance scenarios. They solved this modified problem in $O^{*}\left(2^{4\left|T\right|+\left|I\right|+c}\right)$ time.

Finally, regarding polyploidy (that is, $p>2$), Li et al. [116] showed that p-ploid MFR can be solved in $O(2^{2g}n{m}^2+2^t{\left(2m\right)}^{p+1})$ time and in $O(n{m}^2+m^{p+1})$ time if the input matrix M is gapless. Further, p-ploid MEC can be solved in $O^{*}\left(2^{p(\ell +1)}\right)$ time and in $O^{*}\left(p^c\right)$ time [105].

Open Questions. Parameterizations for the IH problem focus mainly around the number g of gaps per row and the coverage c. While the coverage c was reasonably estimated with 10–30 for past sequencing projects, future technology is expected to increase this number. Even today, whole-exome-sequencing uses coverages of at least 100 [117]. Quoting Garg [118],

“developing a parameterized algorithm for this integrative framework and deciding parameters that work well in practice is very important.”

Thus, a future challenge will be to find more relevant parameters and exploit them to design parameterized algorithms. We suspect that graph-measures of the conflict graph might come to the rescue here, using the known reductions to bipartization problems [105]. Indeed, a more thorough investigation into the multivariate complexity of Odd Cycle Transversal would certainly yield important consequences for the presented variants of (Single) Individual Haplotyping.

A second challenge for (Single) Individual Haplotyping is the development of efficient preprocessing strategies. While some effective reduction rules for variants of IH are known [119,120,121], many of them are formulated and tuned for ILP formulations—kernelization results, whether positive or negative, have been amiss.

Finally, an obvious open question is to extend the results for the polyploid case, where only little is known in terms of parameterized complexity. Indeed, algorithms deciding the vertex-deletion distance into p-colorable graphs would be a good starting point to attack this problem.

4.2. Haplotype Inference

Problem Description. A genotype g is a string over the alphabet $\{\mathtt{0},\mathtt{1},\mathtt{2}\}$ and a haplotype is a string over the alphabet $\{\mathtt{0},\mathtt{1}\}$. Two haplotypes h and $h^{\prime }$ resolve a genotype g if, for each position i, $g\left[i\right]=h\left[i\right]$ if $h\left[i\right]=h^{\prime }\left[i\right]$ and $g\left[i\right]=\mathtt{2}$, otherwise. Then, a list of haplotypes resolves a list of genotypes if, for each genotype on the list, there are two haplotypes on the list that resolve it.

Results. The literature considers two major variants of the HI problem.

Pure Parsimony. 

In the Pure Parsimony Haplotyping problem, the cost is the number k of different haplotypes needed to explain the given genotypes. This problem is NP-hard [122,123,124,125,126], even for three letters 2 per genotype and three letters 2 per position in the genotypes, but becomes polynomial-time solvable if each genotype has at most two letters 2 [104,127] or each position has at most one letter 2 [126,128]. Further special cases were considered by Sharan et al. [125] who also presented an $O\left(k^{k^2+k}m\right)$-time algorithm for the general case [125]. A variant where haplotypes can only be picked from a prescribed pool $H^{\prime }$ was considered by Fellows et al. [129] who showed a $O\left(k^{O\left(k^2\right)}{n}^{2}m\right)$-time algorithm. Fleischer et al. [130] later presented an $O\left(k^{4k+3}m\right)$-time algorithm for the unconstrained version that can also solve the constraint version in $O\left(k^{4k+3}m\right|H^{\prime }{|}^2)$ time (indeed, these running times can be decreased to $O\left(k^{4k+2}m\right)$ and $O\left(k^{4k+2}m\right|H^{\prime }\left|\right)$ on average using perfect hashing) as well as a size-$O\left(2^k{k}^2\right)$ kernel. Their algorithm can also output all optimal solutions.

Perfect Phylogeny. 

In the Haplotyping by Perfect Phylogeny problem, haplotypes are required to fit a “perfect phylogeny”, that is, a tree whose leaves are labeled by the haplotypes resolving the input genotypes such that, for each position i, the subtrees induced by the leaves with 0 and 1 at position i do not intersect. Gusfield [131] introduced this problem for $k=\infty$ and showed an almost-linear-time algorithm, which was later improved to linear time [132,133]. Otherwise, the problem is NP-hard [126] but admits some polynomial-time solvable special cases based on the number of 2s in the genotypes [126].

Notes. A variant of Pure Parsimony Haplotyping is XOR-Haplotyping, where genotypes do not contain the letter 2 and two haplotypes resolve a genotype if it is the result of the bitwise XOR of the haplotypes. While not known to be NP-hard, this variant can be solved in $O\left(m(2^{k^2}k+n)\right)$ time [120]. Note that the $O^{*}\left(k^{4k}\right)$-time algorithm of Fleischer et al. [130] can be adapted for this problem.

Another problem called Shared Center that aims at identifying SNPs that correlate with certain diseases was considered from the viewpoint of parameterized complexity by Chen et al. [134] who showed hardness and tractability for it.

Open Questions. A prominent open question is whether Pure Parsimony Haplotyping can be solved in polynomial time when the number of 2s per position is bounded by two [125,135,136]. For parameterized complexity, one of the most important questions is whether Pure Parsimony Haplotyping admits a single-exponential-time algorithm or a polynomial-size kernel when parameterized by k. Further, parameterizations for this problem have mostly focused on the “natural parameter” k but, in practice, other parameters may be more relevant and promising. Some measure of how convoluted the given genotypes are may be a promising avenue for future research. From a biological point of view, a parameter related to the number of 2s may be promising, but the known results suggest that such a parameter can only lead to FPT-results if combined with others. Finally, from a practical point of view, it may be interesting to combine the Haplotype Inference and (Single) Individual Haplotyping problems. For example, it would be interesting to find a set of few haplotypes that explain the given genotypes modulo few errors or to infer few haplotypes given a set of genotypes along with a pedigree indicating their inheritance.

5. Phylogenetics

To put sequences of different species in perspective and to understand historical evolution, as well as try to predict future directions of the development of life on Earth, a “phylogeny” [137] (evolutionary tree or network) needs to be constructed. Indeed, some see the reconstruction and interpretation of a species phylogeny as the pinnacle of biological research [138]. A likely evolutionary scenario can be constructed from a multiple alignment, a character-state matrix, or a collection of sub-phylogenies, and methods for this are plentiful [139,140]. In the scope of this survey, however, we focus on recent results for NP-hard problems surrounding phylogenetic trees and networks.

5.1. Preliminaries

An evolutionary (or phylogenetic) network N is a graph whose degree-one nodes $\mathcal{L}\left(T\right)$ (“leaves”) are labeled (by “taxa”). A rooted phylogenetic network N is a rooted acyclic directed graph whose non-root nodes either have in-degree one or out-degree one and whose out-degree-zero nodes $\mathcal{L}\left(T\right)$ (“leaves”) are labeled (by “taxa”). A (rooted) phylogenetic tree is a (rooted) phylogenetic network whose underlying undirected graph is acyclic. In the context of this section, we drop the prefix “phylogenetic” for brevity and sometimes refer to networks as “phylogenies”. Some works consider trees in which each leaf-label may occur more than once. These objects are called multi-labeled trees (or MUL trees). For a set $\mathcal{T}$ of networks, we abbreviate ${\bigcup }_{T\in \mathcal{T}}\mathcal{L}\left(T\right)=:\mathcal{L}\left(\mathcal{T}\right)$. An important parameter of networks is their level, referring to the largest number of reticulations in any biconnected component of the underlying undirected graph (see [141]).The restriction of T to L, denoted by $T{\mid }_L$, is the result of removing all leaves not in L from T and repeatedly removing unlabeled leaves and suppressing (that is, contracting any one of its incident edges/arcs) degree-two nodes. A network N displays a network T if T is a topological minor of N, respecting leaf-labels, that is, N contains a subdivision of T as a subgraph. Herein, a directed edge can only be subdivided in accordance to its direction, that is, the subdivision of an arc $uv$ creates a new node w and replaces $uv$ by the arcs $uw$ and $wv$. This notion can be generalized to the case that N is the disjoint union of some networks (see Section 5.2.3). For non-binary networks, there are two different notions of display: the “hard”-version is defined analogously to the binary case, while we say that a network N “soft”-displays a network T if any binary resolution of N displays any binary resolution of T, where a binary resolution of a network N is any binary network that can be turned into N by contracting edges/arcs. “Soft” and “hard” versions of display are derived from the concept of “soft” and “hard” polytomies, meaning high degree nodes that represent either a lack of knowledge of the correct evolutionary history leading to the children taxa (“soft”) or a large fan-out of species due to high evolutionary pressure (“hard”).

Note that many kernelization results in phylogenetics bound only on the number of labels in a reduced instance. If the input contains many trees or an intricate network, kernelization results should more fittingly be described as “partial kernel” (see [142]). We thus usually refer to such results as “kernel with … taxa”.

5.2. Combining and Comparing Phylogenies

Problem Description. An approach to reconstruct a phylogeny from the genomes of a set of species is to first reconstruct the phylogenies of the genes (using multiple alignments and after clustering them together into families) into so-called “gene trees” and then to combine these trees into a tree representing the evolutionary history of the set of species called the “species tree” (see also Section 5.3 for more on the divergence between gene trees and species trees). In general, given trees $T_i$ each on the taxon-set $X_i$, we want to “amalgamate” the trees into a single tree T, which, since it agrees with and contains all the $T_i$, is called an agreement supertree. This problem is known as Tree Consistency (and, sometimes Tree Compatibility).

For surveys about the combination of phylogenies (“consensus methods”) we refer to Bryant [143] and Degnan [144].

Results. For unrooted trees, TCY can be solved in polynomial time if all $T_i$ share a common taxon [145] but is NP-complete in general, even if all input trees contain four taxa [145] (such a “quartet” is the smallest meaningful unrooted tree since unrooted trees with at most three taxa do not carry any phylogenetic information). This restricted problem is also known as Quartet Inconsistency. TCY can be solved in polynomial-time for two unrooted (non-binary) trees [146]. More generally, using powerful meta-theorems [147,148] (problems formulatable in “Monadic Second Order Logic” (MSOL) are FPT for the treewidth of the input structure), TCY is fixed-parameter tractable for the treewidth of the display graph [149,150] (that is, the result of identifying all leaves of the same label in the disjoint union of the input trees), which is smaller than the number t of trees. Baste et al. [151] improved the impractical running time resulting from the application of the meta-theorems, showing an $O^{*}\left(2^{O\left(t^2\right)}\right)$-time algorithm.

For rooted trees, Tree Consistency can be solved in polynomial time [152,153] (even for non-binary trees) but, due to noisy data and more complicated evolutionary processes, practically relevant instances are not expected to have an agreement supertree [154,155]. Thus, derivations of the problem arose, asking for a smallest amount of modification to the input such that an agreement supertree exists. The most prominent modification types are removing trees (Rooted Triplet Inconsistency), removing taxa (Maximum Agreement Supertree), and removing edges (Maximum Agreement Forest), which we discuss in the following.

5.2.1. Consensus by Removing Trees

When reconstructing a species tree from gene trees, we may hope that the gene trees of most of the sampled gene families actually agree with the species phylogeny and only few such families describe outliers that developed nonconformingly. In this case, we can hope to recover the true phylogeny by removing a small number of gene trees.

Results. Rooted Triplet Inconsistency is NP-hard [156,157,158], even on “dense” triplet sets [159] (a triplet set $\mathcal{T}$ is called dense or complete if for each leaf-triple $\{a,b,c\}$, $\mathcal{T}$ contains exactly one of $ab\mid c$, $ac\mid b$ and $bc\mid a$). While the general problem is W[2]-hard for k [159], the dense version admits parameterized algorithms. Indeed, Guillemot and Mnich [160] showed parameterized algorithms running in $O\left(4^k{n}^3\right)$ and in $O^{*}\left(2^{O(k^{1/3}logk)}\right)$ time, as well as an $O\left(n^4\right)$-time computable, sunflower-based kernel containing $O\left(k^2\right)$ taxa (see [161] for details on the sunflower kernelization technique). Their result has recently been improved to linear size by Paul et al. [162].

Notes. Generalizing RTI to ask for a level-ℓ network displaying the input trees yields a somewhat harder problem, which can be solved for dense inputs in $O\left(\right|T{|}^{\ell +1}{n}^{4\ell /3+1})$ time [163] and in $O\left(\right|T{|}^{\ell +1})$ time for a particular class of networks [164].

The unrooted-tree version of dense RTI (where the input consists of quartets) is known to be solvable in $O(4^{k}n+n^4)$ time [165].

5.2.2. Consensus by Removing Taxa

In many sciences, the most interesting knowledge can be gained by looking more closely to the non-conforming data points. In this spirit, biologists are particularly interested in taxa causing non-compatibility, that is, whose removal allows for an agreement supertree. In the spirit of parsimony, we are thus tempted to ask for a smallest number of taxa to remove from the input trees such that an agreement supertree exists.

Results. While MASP can be solved in $O\left(n^{1.5}\right)$ time for two rooted trees [166,167,168] (n denoting the total number of labels in the input), it is NP-hard for $t>2$, even if all $T_i$ are triplets [166,169], and the NP-hardness persists for fixed t [166] (but large trees). Guillemot and Berry [170] showed that, on dense, binary, rooted inputs, MASP can be solved in $O\left(4^k{n}^3\right)$ and $O({3.12}^k+n^4)$ time by reduction to 4-Hitting Set. They further improved an $O\left(t{\left(2n^2\right)}^{3t^2}\right)$-time algorithm of Jansson et al. [166] for binary $T_i$ to $O\left({\left(8n\right)}^t\right)$ time [170], which was subsequently improved to $O\left({\left(6n\right)}^t\right)$ time by Hoang and Sung [171]. The latter also gave an $O\left({(t\Delta )}^{t\Delta +3}{\left(2n\right)}^t\right)$-time algorithm for general rooted inputs ($\Delta$ denoting the maximum out-degree among the input trees). MASP is W[2]-hard for k, even if the input consists of rooted triplets [169], and W[1]-complete in the rooted case for the dual parameter $n-k$, even if we add t to it [170]. On the positive side, the problem can be solved in $O\left({\left(2t\right)}^{k}t{n}^2\right)$ time for binary trees [170] which has been generalized to arbitrary trees by Fernández-Baca et al. [172]. For completeness, we want to point out that many of the results for MASP also hold for MASP’s sister problem Maximum Compatible Supertree  (MCSP), in which equality with the restricted agreement supertree $T^{*}$ is relaxed to being a contraction of $T^{*}$ (with the notable exception that MCSP can be solved in $O\left(2^{2t\Delta }{n}^t\right)$ time in both the rooted and unrooted case [171]).

Notes. The special case of MASP in which ${\mathcal{X}}_1={\mathcal{X}}_2=\dots$ is called Maximum Agreement Subtree  (MAST) and has been studied extensively. While still NP-hard for $t=3$ non-binary trees [173], MAST can be solved in $O(k{n}^3+n^{\Delta })$ [157,174], in which time we can also compute a “kernel agreement subtree”, denoting the intersection of all leaf-sets of all optimal maximum agreement subtrees [175]. MAST is fixed-parameter tractable for k with parameterized algorithms running in time $O(min\{3^{k}tn,{2.18}^k+t{n}^3\})$ [176,177,178] (by reduction to 3-Hitting Set).

More fine-grained versions of MAST that allow removal of different taxa from each $T_i$ were introduced by Chauve et al. [179]. In Agreement Subtree by Leaf-Removal  (AST-LR), the objective is to minimize the total number q of removed leaves and, in AST-LR-d, the objective is to minimize the maximum number d of leaves that have to be removed from any of the trees. Both versions are NP-hard [179] but can be solved in $O\left({(4q-2)}^q{t}^2{n}^2\right)$ (AST-LR) and $O\left(c^d{d}^{3d}(n^3+tnlogn)\right)$ time for some constant c (AST-LR-d) [179,180].

Lafond et al. [181] considered MAST for multi-labeled trees showing that it remains NP-hard and can be solved in $O^{*}\left({\left(2n\right)}^t{k}^{kt}\right)$ time.

Finally, Choy et al. [141] showed that a “maximum agreement subnetwork” for two binary networks of level ${\ell }_1$ and ${\ell }_2$, respectively, can be computed in $O^{*}\left(2^{{\ell }_1+{\ell }_2}\right)$ time.

5.2.3. Consensus by Removing Edges—Agreement Forests and Tree Distances

An important biological phenomenon that governs the discordance of gene trees are non-tree-like processes such as hybridization and horizontal gene transfer (HGT) (see also Section 5.3). If a branch in a gene tree corresponds to a horizontal transfer, then we expect that deleting this branch results in a forest, which is in agreement with the other gene trees. This gives rise to the idea of “agreement forests”, resulting from the deletion of branches in the input phylogenies.

Maximum agreement forests come in three major flavors: unrooted maximum agreement forests (uMAFs), rooted maximum agreement forests (rMAFs), and maximum acyclic agreement forests (MAAFs). Herein, “acyclic” makes reference to the constraint that the “inheritance graph is acyclic” (see Figure 9). Formally, the inheritance graph of an agreement forest F for two trees $T_1$ and $T_2$ has the trees of F as nodes and an arc $uv$ if and only if the root of u is an ancestor of the root of v in $T_1$ or in $T_2$. Demanding acyclicity of this graph forbids, for example, that a tree u of F is “above” another tree v in $T_1$ but “below” v in $T_2$. This definition generalizes straightforwardly to more than two trees $T_i$. In the following, the size of an agreement forest F is the number of trees in F and it is equal to the number of branches to remove in each input tree to form (a subdivision of) F and F is called maximum if it minimizes this number. For surveys about tree distances and agreement forests, we refer to Shi et al. [182] and Whidden [183].

Results. Evidently, results heavily depend on the type of agreement forest we are looking for. Interestingly, each of the three versions corresponds to a known and well-studied distance measure between trees and we thus also include results stated for the corresponding distance-measure.

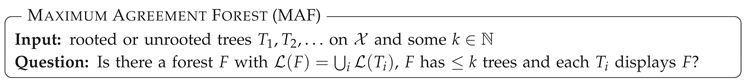
Unrooted Agreement Forest. 

The size of a uMAF of two binary trees $T_1$ and $T_2$ is exactly equal to the minimum number of “TBR moves” necessary to turn $T_1$ into $T_2$ [184,185] (and vice versa; indeed, this defines a metric and it is called the “TBR distance” between $T_1$ and $T_2$). Herein, a TBR (tree bisection and reconnection) move consists of removing an edge $uv$ from a tree (“bisecting” the tree) and inserting a new edge between any two edges of the resulting subtrees (“reconnecting” the trees), that is, subdividing an edge in each of the subtrees and adding a new edge between the two new nodes.

For two trees, deciding uMAF is NP-hard [184], but fixed-parameter tractable in k. More precisely, the problem can be solved in $O^{*}\left(k^O\left(k\right)\right)$ time [185], $O(4^k{k}^5+n^{O\left(1\right)})$ time [186], and $O(4^{k}k+n^{O\left(1\right)})$ time [187]. These results make use of the known kernelizations with $15k$ [185,188] and $11k$ taxa [189]. For $t>2$ binary trees, Shi et al. [190] presented an $O\left(4^{k}nt\right)$-time algorithm. Chen et al. [191] considered the uMAF problem on multifurcating trees, showing that it still corresponds to the TBR problem and can be solved in $O\left(3^{k}n\right)$ time.

Rooted Agreement Forest. 

The size of an rMAF of two rooted binary trees $T_1$ and $T_2$ is exactly one more than the minimum number of “rSPR moves” necessary to turn $T_1$ into $T_2$ [192,193] (and vice versa; indeed, this defines a metric and it is called the “rSPR distance” between $T_1$ and $T_2$). Herein, an rSPR (rooted subtree prune and regraft) move consists of removing (“pruning”) an arc $uv$ from a tree and “regrafting” it onto another arc $xy$, that is, subdividing $xy$ with a new node z and inserting the arc $zv$.

The problem is known to be NP-hard and algorithms parameterized by k have been extensively studied and improved. An initial $O\left(4^k{n}^4\right)$-time algorithm [187,194] was improved to $O\left(3^{k}n\right)$ time [187], $O\left({2.42}^{k}n\right)$ time [195], $O\left({2.344}^{k}n\right)$ time [196], and the current best $O\left(2^{k}n\right)$-time algorithm by Whidden [183]. In contrast, a kernel with $28k$ taxa [193] has stood since 2005. For $t>2$ trees, rMAF can be decided in $O^{*}\left(6^k\right)$ time [197] and $O\left(3^{k}nt\right)$ time [190].

Collins [198] showed that using “soft”-display, rMAFs still correspond to computing the rSPR distance between two multifurcating trees. This problem can be solved in $O^{*}\left(4^k\right)$ time [199] and in $O\left({2.42}^{k}n\right)$ time [183,200] and admits a kernel with $64k$ taxa [198,201]. For $t>2$ trees, the multifurcating rMAF problem is solvable in $O\left({2.74}^k{t}^3{n}^5\right)$ time [202]. Notably, Shi et al. [202] also considered the “hard” version of the problem and presented an $O\left({2.42}^k{t}^3{n}^4\right)$-time algorithm for it.

Acyclic Agreement Forest. 

The size of a MAAF of two rooted binary trees $T_1$ and $T_2$ is exactly one more than the minimum number of reticulations found in any phylogenetic network displaying both $T_1$ and $T_2$ [192] and this relation holds also if $T_1$ and $T_2$ are non-binary [203].

Deciding this number is known as the Hybridization Number (HN) problem and it has been shown to be NP-hard by Bordewich and Semple [204]. The problem can be solved in $O\left(3^{n}n\right)$ time by crawling a bounded search-tree [205]. In 2009, Whidden and Zeh claimed an $O(3^{k}nlogn)$-time algorithm, which they later retracted and replaced by an $O\left({3.18}^{k}n\right)$-time algorithm [183,195]. For $t=3$ binary trees, HN can be decided in $O^{*}\left(c^k\right)$ time, where c is an “astronomical constant” [206].

Concerning preprocessing, a kernel with at most $9k$ taxa is known [188,201] and this kernelization result has been generalized to the case of deciding HN for $t>2$ binary trees (in which case HN and MAAF no longer coincide) by van Iersel and Linz [207], showing a kernel with $20k^2$ taxa for this case, which has again been generalized to $t>2$ non-binary trees by van Iersel et al. [208], showing a kernel with at most $20k^2(\Delta -1)$ (and at most $4k{\left(5k\right)}^t$) taxa [208]. For MAAF with $t=2$ non-binary trees, Linz and Semple [203] showed a linear bikernel (that is, a kernelization into a different problem, see [209]) with $89k$ taxa, which implies a quadratic-size classical kernel. For this setting, algorithms running in $O^{*}(6^{k}k!)$ [210] and $O^{*}\left({4.83}^k\right)$ [211] time are also known.

Notes. Any algorithm for binary uMAF, rMAF, and MAAF with running time $f\left(k\right)n^{O\left(1\right)}$ can be turned into an algorithm running in $f(\ell )n^{O\left(1\right)}$, where ℓ is the level of any binary network displaying the two input trees [212]. Furthermore, all three agreement forest variants are fixed-parameter tractable for the treewidth of the display graph of the input trees [213] (see corresponding results for unrooted Tree Consistency [149,150]). The rSPR distance has been generalized to a distance measure for phylogenetic networks called SNPR and its computation is fixed-parameter tractable [214] parameterized by the distance. Variations of the discussed distance measures include: (1) the uSPR distance, which does not have an agreement-forest formulation, is NP-hard to decide [215], admits a kernel with $76k^2$ taxa [216] (in a preprint, Whidden and Matsen [217] claimed an improvement to $28k$ taxa), and can be calculated in $O^{*}(\left(28k\right)!!{16}^k)$ time [218] (using the mentioned preprint-kernel); (2) its close sibling, the replug distance, which admits a formulation as “maximum endpoint agreement forest”, is conjectured to be NP-hard to decide but admits an $O^{*}\left({16}^k\right)$-time algorithm [218]; (3) the “temporal hybridization number”, denoting the smallest amount of reticulation required to explain trees with a temporal network, which was shown to be NP-hard for two trees [219] but admits an $O^{*}\left({\left(9k\right)}^{9k}\right)$-time algorithm [220]; and (4) the parsimony distance, which is NP-hard [221,222] but can be solved in $O^{*}\left({1.618}^{38d_{\mathrm{TBR}}}\right)$ time [223], where $d_{\mathrm{TBR}}$ is the TBR distance between the input trees.

Open Questions. Consensus methods in phylogenetics can profit from a wide range of parameters, describing the particularities of likely set of inputs. While we would indeed expect that the consensus has a small distance to the input trees, a lot depends on how we choose to measure this distance. More general distance measures make for stronger parameters and, while the Hybridization Number problem can be solved in single-exponential time for the “standard parameter” k, it would be interesting to parameterize by a stronger parameter, such as the rSPR radius in which the input trees lie.

Inspired by the groundbreaking results of Bryant and Lagergren [149], research into the display graph and its treewidth has been conducted with some success [150,224]. However, we have yet to design concrete, practical algorithms for consensus problems parameterized by the treewidth of the display graph. As this would potentially yield very fast, practical algorithms, we suspect that this would be a fruitful topic in the coming years. Another interesting parameter is the “book thickness” of the display graph, that is, the minimum number of edge-colors needed to color the display graph such that each color class permits an outerplanar drawing. For obvious reasons, this parameter is smaller than the number t of input trees. Can the results for t be strengthened to work with the book thickness instead?

5.3. Reconciliation

Problem Description. In practice, trees depicting the evolutionary history of families of genes sampled from a set of species do not agree with the evolutionary history of the species themselves; hybridization, horizontal gene transfer, and incomplete lineage sorting being only few known causes for such discrepancies. In theory, even gene duplication and gene loss are enough to explain gene trees differing arbitrarily from the corresponding species tree. To better understand how a family of genes developed in the genome of a concurrently developing set of species, we can compute an “embedding” of the gene tree nodes to the edges of the species phylogeny called a reconciliation (see Figure 10). Reconciliations also allow drawing conclusions when comparing phylogenies of co-evolving species such as hosts/parasites or flowers/pollinators. More formally, a DL-reconciliation of a (gene-)phylogeny G with a (species-)phylogeny S is a pair $(G^{\prime },r)$ where $G^{\prime }$ is a subdivision of G and $r:V\left(G\right)\to V\left(S\right)$ is a mapping such that:

(a)

for all arcs $uv$ of G, either $r\left(u\right)=r\left(v\right)$ (in which case u is called “duplication”) or $r\left(v\right)$ is a child of $r\left(u\right)$ (in which case u is called “speciation”);

(b)

for arcs $uv$ and $uw$ in G, we have $r\left(u\right)=r\left(v\right)\iff r\left(u\right)=r\left(w\right)$ (that is, no node of G can be a speciation and a duplication at the same time); and

(c)

if u is a leaf in G, then $r\left(u\right)$ is a leaf labeled with the contemporary species that $r\left(u\right)$ was sampled in.

We can then define the number of losses in $(G^{\prime },r)$ as the sum over all speciations u of the outdegree of $r\left(u\right)$ in S minus the outdegree of u in $G^{\prime }$. If horizontal transfers are allowed, Condition (a) is replaced by

(a’)

for all arcs $uv$ of G, either $r\left(u\right)=r\left(v\right)$ (in which case u is called “duplication”) or $r\left(v\right)$ is a child of $r\left(u\right)$ (in which case u is called “speciation”), or $r\left(v\right)$ is incomparable to $r\left(u\right)$ (in which case u is called a “transfer” and $uv$ is called a “transfer arc”),

and Condition (b) is restricted to non-transfer arcs, and each transfer with out-degree one causes an additional loss. In this case, we call r a DTL-reconciliation. Since, in reality, transfers occur only between species existing at the same time, Condition (a’) introduces further restrictions. In particular, a reconciliation r is called time-consistent if G can be “dated”, that is, there is a mapping $t:V\left(G\right)\to \mathbb{N}$ such that, for all arcs $uv$ of G, we have 1. $t\left(u\right)\le t\left(v\right)$; and 2. $t\left(u\right)=t\left(v\right)$ if and only if $uv$ is a transfer arc of G under r.

A DTL-reconciliation may be time-inconsistent if, for example, there are transfer arcs $uv$ and $xy$ such that u and x are ancestors of y and v, respectively, in G.

Now, the parsimonious principle is used to define an optimization criterion. To this end, each evolutionary event is given a cost such as to reflect how unlikely it is to see a certain event. By the biological setup, it is usually assumed that speciations have cost zero.

We specify the allowed type of embedding by prepending “DL”, “DTL”, etc. to the problem name. The study of the formal reconciliation problem was initiated by Ma et al. [225] and Bonizzoni et al. [226] and is surveyed in [227,228,229,230].

Results. Optimal binary DL-reconciliations can be computed—independently of the costs—by the LCA-mapping, which maps each node of G to the LCA of the nodes that its children are mapped to [231]. Thus, this problem can be solved in linear time [232,233] using $O\left(1\right)$-time LCA queries [234,235]. The non-binary variant, while not quite as straightforward, can still be solved in polynomial time [236,237].

The complexity of computing DTL-reconciliations depends heavily on their time-consistency. If we allow producing time-inconsistent reconciliations or the given species tree already comes with a dating function, then optimal DTL-reconciliations can be computed in polynomial time [238,239,240]. In general, however, the problem is NP-hard [238,241], but can be solved in $O\left(3^k\right|G|+|S\left|\right)$ time [238]. Hallett and Lagergren [242] showed that DTL-reconciliations with at most $\alpha$ speciations mapped to any one node in the species tree is FPT in $\alpha +\tau$.

Duplication, transfer, and loss are not the only evolutionary events shaping a gene tree. Hasić and Tannier [243,244] recently introduced “replacing transfers” (T_R) and “gene conversion” (C) which model important evolutionary events and showed that DLC-reconciliations can be decided in polynomial time [243] while deciding T_R-reconciliations is NP-hard and FPT for k [244]. Finally, the concept of “incomplete lineage sorting” (ILS) is an important factor influencing discrepancies between gene and species phylogenies, especially when speciation occurs in rapid succession [245]. Roughly, ILS refers to the possibility that an earlier duplication or transfer does not pervade a population at the time a speciation occurs. Thus, one branch of a speciation may carry a gene lineage while the other does not (see Figure 11 for an illustration). In DL-reconciliation, this scenario requires a loss, but this would not reflect the true evolutionary history. Unfortunately, no particular mathematical model of ILS is widely accepted, so the following results might be incomparable. In 2017, Bork et al. [246] showed that incorporating ILS into DL-reconciliation makes the problem NP-hard, even for dated species trees. Furthermore, DTL-reconciliation for dated, non-binary species trees allows ILS to be computed in $O^{*}\left(4^{\Delta }\right)$ time [247,248].

To and Scornavacca [249] started looking into the problem of reconciling rooted gene trees with a rooted species network, showing that, for the DL model, this problem is NP-hard, but solvable in $O^{*}\left(2^k\right)$ time.

Open Questions. There are three major challenges for bioinformatics concerning reconciliation. The first and more obvious task is to include all known genomic players in the reconciliation game, meaning to establish a standard model incorporating duplication, transfer, loss, replacing transfers, conversion, and incomplete lineage sorting. While Hasić and Tannier [243,244] made good progress towards this goal, their model seems too clunky and lacks ILS support. The second challenge is to remove the need to provide $\delta$, $\tau$, etc. in the input for the Reconciliation problem. In practice, some biologists using implementations of algorithms for reconciliations just “play around” with these numbers until the results roughly fit their expectations, which is understandable since nobody knows the correct values. Indeed, in all likelihood, there are no “correct values” because the underlying assumption that the rates of genetic modification is constant throughout a phylogeny is invalid [250]. A more realistic approach might define expected frequencies of events for each branch and combine them with the length of this branch in order to dynamically price duplication, transfer, loss, etc. in this branch.

5.4. Miscellaneous

Given a phylogeny T, the parsimony score of T with respect to a labeling c of its nodes is the number of arcs in T whose extremities have a different label under c. In the Small Parsimony problem, we are given a phylogeny T and a leaf-labeling $c_L$ and have to extend $c_L$ to a labeling of all nodes of T such as to minimize the parsimony score. If T is a network, aside from the above definition (“hardwired”), the “softwired” version exists, asking for the minimum parsimony score of any tree $T^{*}$ (on the same leaf-set as T) displayed by T. While Small Parsimony is polynomial for trees [251], the problem is NP-hard in the softwired case, even for binary T and $c_L$, as well as in the hardwired case, unless $c_L$ is binary [252,253]. Fischer et al. [253] also showed that hardwired Small Parsimony is FPT for the solution parsimony score and softwired Small Parsimony is FPT for the level of the input network.

The problem of deciding whether a phylogeny T is displayed by another phylogeny N is called Tree Containment and it is NP-hard, even if T is a tree [254]. Tree Containment has polynomial-time algorithms for many special cases of N [254,255,256,257,258,259,260,261] and can be solved in $O^{*}\left({1.62}^{\ell }\right)$ time [262] (where ℓ denotes the level of N; the authors also showed an algorithm for the related Cluster Containment problem) and in $O^{*}\left(3^t\right)$ time [261], where t is the number of “invisible tree components” (that is, the number of tree-nodes u whose parent v is a reticulation that is not ”visible“ in N (that is, for each leaf a, there is a root-a-path avoiding v)). Tree Containment stays NP-hard even if the arcs of both T and N are annotated with “branch lengths”, but admits an $O^{*}\left(2^{\ell }\right)$-time algorithm in this case [263].

Recent research into the problem of rooting an unrooted network was conducted by Huber et al. [264], showing that orienting an undirected binary network as a directed network of a certain class is FPT for the level ℓ for some classes of N.