Parameterized Algorithms in Bioinformatics: An Overview
Abstract
1. Introduction
“Writing a survey about bioinformatics-related FPT results sounds like a monumental task!”
2. Genome Comparison and Completion
2.1. Genomic Distances
2.1.1. Double-Cut and Join Distance

2.1.2. Reversal Distance

2.2. Common Partitions
2.2.1. Minimum Common String Partition

2.2.2. Maximal Strip Recovery

2.3. Genome Completion
2.3.1. Scaffold Filling

2.3.2. Breakpoint Median

3. Genome Assembly and Sequence Analysis
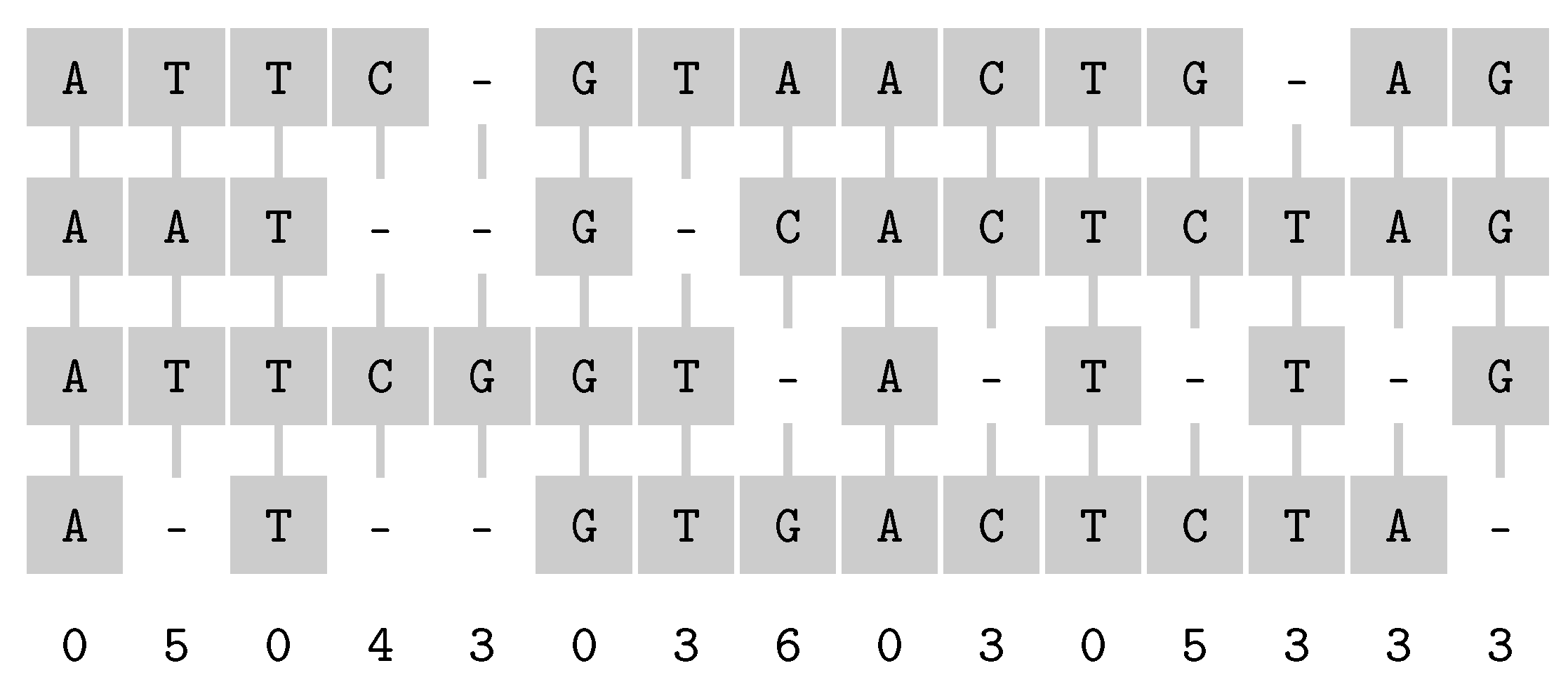
3.1. Multiple Sequence Alignment

3.2. Identifying Common Patterns
3.2.1. Closest String (and Variants)
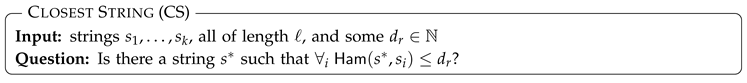
- Closest Substring.
- A common generalization of CS called Closest SubString asks for a common pattern in all input strings, i.e., it allows trimming input strings until they reach a desired given length m. In this case, the consensus variant, optimizing the sum of distances, is no longer trivial and is denoted Consensus Pattern. Although these problems become much harder than Closest String and are W[1]-hard for any single parameter among ℓ, k, d, and m, they still admit FPT algorithms for several combinations of these parameters [49,50,51,52].
- Closest String with Outliers.
- Another noteworthy variant allows ignoring a small number t of outliers from the input set of strings [53]. Interestingly, all parameterized algorithms for Closest String extend to this variant when t is considered as an additional parameter.
- Radius or sum.
- A generalization for Closest String (that also applies to the variants above) considers both a constraint on the maximum hamming distance (the radius, ) and on the sum of hamming distances (denoted ). Indeed, the radius constraint only focuses on worst-case strings, and the sum constraint tends to overfit large sets of clustered strings, so taking both constraints can help reduce those problems. All algorithms mentioned for the radius-only version can be extended, in one way or another, to take both constraints into account without additional parameters [54].Another point of view consists in seeing the radius and sum measures as the and norms, respectively, of the vector . Thus, a possible compromise consists in optimizing the norm of this vector for any rational p, . Chen et al. [55] studied Closest String under these norms on binary alphabets, proved its NP-hardness, and gave an FPT algorithm for parameter k.
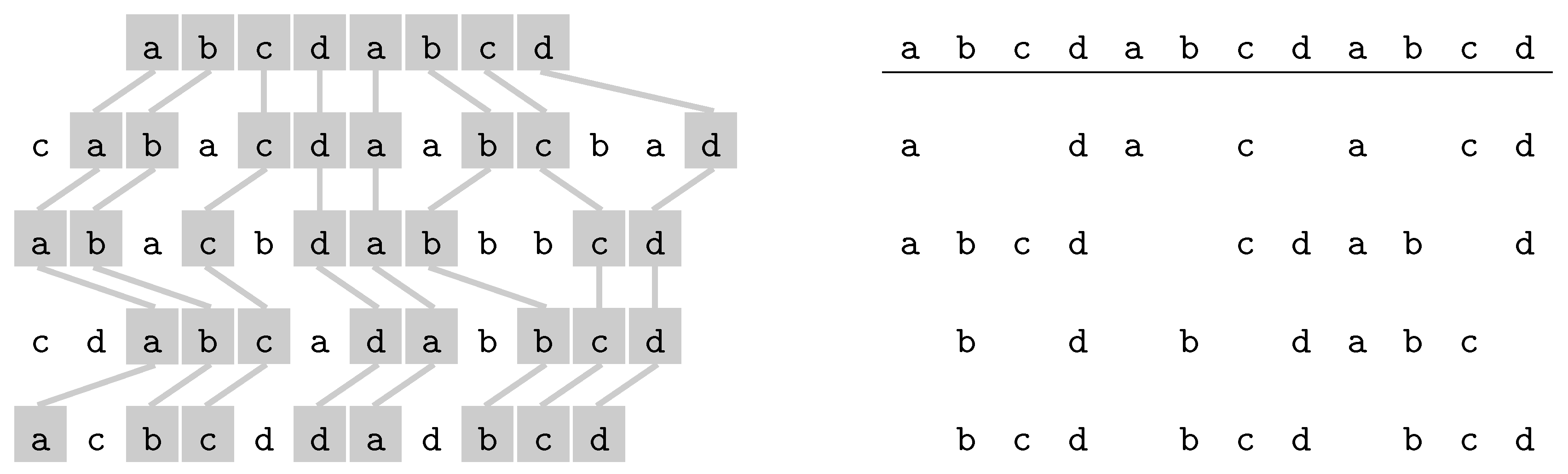
3.2.2. Longest Common Subsequence

- Omitted letters.
- Another possible parameter is the number of omitted letters, : Longest Common Subsesquence is FPT for parameters and k [58], and the complexity is open for parameter only.
- Sub-quadratic time? ()
- For two strings, there is no sub-quadratic algorithm unless the strong exponential time hypothesis fails [59]. However, parameterized algorithms can help subdue this lower bound to some extent: Bringmann and Künnemann [60] proposed an extensive study of the possible combinations of parameters yielding “FPT in P” algorithms (also sometimes referred to as “fully polynomial FPT”, see [61,62,63]), with matching lower-bounds in each case.
- Constrained LCS. ()
- Restricted LCS.
3.2.3. Shortest Common Supersequence

3.2.4. Center and Median Strings

3.3. Scaffolding


4. Haplotyping
4.1. Haplotype Assembly

- Deleting rows.
- The problem of turning M 2-conflict-free by row-deletions is known as Minimum Fragment Removal (MFR). It is equivalent to turning the “conflict graph” bipartite by removing vertices (this problem is called Odd Cycle Transversal or Vertex Bipartization in the literature). Herein, the vertices of the conflict graph are the rows of M and rows u and v have an edge if they cannot be assigned to the same chromosome, that is, for some position i. MFR is NP-hard even if each row has at most one gap [96], but becomes polynomial-time solvable for gapless M [96,97]. It can be solved in time [97] and in time [98]. Of course, results for Odd Cycle Transversal apply to MFR: it admits -time [99,100] and -time [101] algorithms as well as a randomized kernel of size [102].
- Deleting columns.
- Flipping values.
- By far the most studied approach is turning M 2-conflict-free by flipping values, that is, turning a 1 into a 0 or vice versa. This problem is known as Minimum Error Correction (MEC) or Minimum Letter Flip in the literature and it is has been shown to be NP-hard, even on gapless inputs [104]. A simple reduction from Edge Bipartization [105] further shows that MEC is still NP-hard if each row contains at most three non-(-) characters and each column contains at most two non-(-) characters, thus excluding parameterized algorithms, even for the combined parameter. A parameterized algorithm with running time is trivial (assign each row to one of the two partitions/chromosomes) and an -time algorithm was presented by Wang et al. [106]. Further research focused on the coverage c, which is very small in practice. -time algorithms with various polynomial factors were presented by Xie et al. [107], Deng et al. [108], Patterson et al. [109], Pirola et al. [110], and Garg et al. [111]. MEC can be linearly reduced to Odd Cycle Transversal [105], implying that results for Odd Cycle Transversal carry over to MEC as well ( time [99,100], time [101], and -size randomized kernel [102]).
“developing a parameterized algorithm for this integrative framework and deciding parameters that work well in practice is very important.”
4.2. Haplotype Inference

- Pure Parsimony.
- In the Pure Parsimony Haplotyping problem, the cost is the number k of different haplotypes needed to explain the given genotypes. This problem is NP-hard [122,123,124,125,126], even for three letters 2 per genotype and three letters 2 per position in the genotypes, but becomes polynomial-time solvable if each genotype has at most two letters 2 [104,127] or each position has at most one letter 2 [126,128]. Further special cases were considered by Sharan et al. [125] who also presented an -time algorithm for the general case [125]. A variant where haplotypes can only be picked from a prescribed pool was considered by Fellows et al. [129] who showed a -time algorithm. Fleischer et al. [130] later presented an -time algorithm for the unconstrained version that can also solve the constraint version in time (indeed, these running times can be decreased to and on average using perfect hashing) as well as a size- kernel. Their algorithm can also output all optimal solutions.
- Perfect Phylogeny.
- In the Haplotyping by Perfect Phylogeny problem, haplotypes are required to fit a “perfect phylogeny”, that is, a tree whose leaves are labeled by the haplotypes resolving the input genotypes such that, for each position i, the subtrees induced by the leaves with 0 and 1 at position i do not intersect. Gusfield [131] introduced this problem for and showed an almost-linear-time algorithm, which was later improved to linear time [132,133]. Otherwise, the problem is NP-hard [126] but admits some polynomial-time solvable special cases based on the number of 2s in the genotypes [126].
5. Phylogenetics
5.1. Preliminaries
5.2. Combining and Comparing Phylogenies

5.2.1. Consensus by Removing Trees

5.2.2. Consensus by Removing Taxa

5.2.3. Consensus by Removing Edges—Agreement Forests and Tree Distances
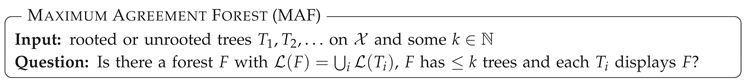
- Unrooted Agreement Forest.
- The size of a uMAF of two binary trees and is exactly equal to the minimum number of “TBR moves” necessary to turn into [184,185] (and vice versa; indeed, this defines a metric and it is called the “TBR distance” between and ). Herein, a TBR (tree bisection and reconnection) move consists of removing an edge from a tree (“bisecting” the tree) and inserting a new edge between any two edges of the resulting subtrees (“reconnecting” the trees), that is, subdividing an edge in each of the subtrees and adding a new edge between the two new nodes.For two trees, deciding uMAF is NP-hard [184], but fixed-parameter tractable in k. More precisely, the problem can be solved in time [185], time [186], and time [187]. These results make use of the known kernelizations with [185,188] and taxa [189]. For binary trees, Shi et al. [190] presented an -time algorithm. Chen et al. [191] considered the uMAF problem on multifurcating trees, showing that it still corresponds to the TBR problem and can be solved in time.
- Rooted Agreement Forest.
- The size of an rMAF of two rooted binary trees and is exactly one more than the minimum number of “rSPR moves” necessary to turn into [192,193] (and vice versa; indeed, this defines a metric and it is called the “rSPR distance” between and ). Herein, an rSPR (rooted subtree prune and regraft) move consists of removing (“pruning”) an arc from a tree and “regrafting” it onto another arc , that is, subdividing with a new node z and inserting the arc .The problem is known to be NP-hard and algorithms parameterized by k have been extensively studied and improved. An initial -time algorithm [187,194] was improved to time [187], time [195], time [196], and the current best -time algorithm by Whidden [183]. In contrast, a kernel with taxa [193] has stood since 2005. For trees, rMAF can be decided in time [197] and time [190].Collins [198] showed that using “soft”-display, rMAFs still correspond to computing the rSPR distance between two multifurcating trees. This problem can be solved in time [199] and in time [183,200] and admits a kernel with taxa [198,201]. For trees, the multifurcating rMAF problem is solvable in time [202]. Notably, Shi et al. [202] also considered the “hard” version of the problem and presented an -time algorithm for it.
- Acyclic Agreement Forest.
- The size of a MAAF of two rooted binary trees and is exactly one more than the minimum number of reticulations found in any phylogenetic network displaying both and [192] and this relation holds also if and are non-binary [203].Deciding this number is known as the Hybridization Number (HN) problem and it has been shown to be NP-hard by Bordewich and Semple [204]. The problem can be solved in time by crawling a bounded search-tree [205]. In 2009, Whidden and Zeh claimed an -time algorithm, which they later retracted and replaced by an -time algorithm [183,195]. For binary trees, HN can be decided in time, where c is an “astronomical constant” [206].Concerning preprocessing, a kernel with at most taxa is known [188,201] and this kernelization result has been generalized to the case of deciding HN for binary trees (in which case HN and MAAF no longer coincide) by van Iersel and Linz [207], showing a kernel with taxa for this case, which has again been generalized to non-binary trees by van Iersel et al. [208], showing a kernel with at most (and at most ) taxa [208]. For MAAF with non-binary trees, Linz and Semple [203] showed a linear bikernel (that is, a kernelization into a different problem, see [209]) with taxa, which implies a quadratic-size classical kernel. For this setting, algorithms running in [210] and [211] time are also known.
5.3. Reconciliation
- (a)
- for all arcs of G, either (in which case u is called “duplication”) or is a child of (in which case u is called “speciation”);
- (b)
- for arcs and in G, we have (that is, no node of G can be a speciation and a duplication at the same time); and
- (c)
- if u is a leaf in G, then is a leaf labeled with the contemporary species that was sampled in.
- (a’)
- for all arcs of G, either (in which case u is called “duplication”) or is a child of (in which case u is called “speciation”), or is incomparable to (in which case u is called a “transfer” and is called a “transfer arc”),

5.4. Miscellaneous
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Downey, R.G.; Fellows, M.R. Fundamentals of Parameterized Complexity; Texts in Computer Science; Springer: Berlin, Germany, 2013. [Google Scholar] [CrossRef]
- Cygan, M.; Fomin, F.V.; Kowalik, L.; Lokshtanov, D.; Marx, D.; Pilipczuk, M.; Pilipczuk, M.; Saurabh, S. Parameterized Algorithms; Springer: Berlin, Germany, 2015. [Google Scholar] [CrossRef]
- Ávila, L.F.; García, A.; Serna, M.J.; Thilikos, D.M. Parameterized Problems in Bioinformatics. unpublished manuscript.
- Cai, L.; Huang, X.; Liu, C.; Rosamond, F.; Song, Y. Parameterized Complexity and Biopolymer Sequence Comparison. Comput. J. 2008, 51, 270–291. [Google Scholar] [CrossRef]
- Hüffner, F.; Komusiewicz, C.; Niedermeier, R.; Wernicke, S. Parameterized Algorithmics for Finding Exact Solutions of NP-Hard Biological Problems. In Bioinformatics: Volume II: Structure, Function, and Applications; Springer: New York, NY, USA, 2017; pp. 363–402. [Google Scholar] [CrossRef]
- Gramm, J.; Nickelsen, A.; Tantau, T. Fixed-Parameter Algorithms in Phylogenetics. Comput. J. 2007, 51, 79–101. [Google Scholar] [CrossRef]
- Griffiths, A.J.; Gelbart, W.M.; Miller, J.H.; Lewontin, R.C. Chromosomal Rearrangements. In Modern Genetic Analysis; W.H.Freeman: New York, NY, USA, 1999; Chapter 8. [Google Scholar]
- Fertin, G.; Labarre, A.; Rusu, I.; Tannier, E.; Vialette, S. Combinatorics of Genome Rearrangements; Computational Molecular Biology; MIT Press: Cambridge, MA, USA, 2009; p. 312. [Google Scholar]
- Yancopoulos, S.; Attie, O.; Friedberg, R. Efficient sorting of genomic permutations by translocation, inversion and block interchange. Bioinformatics 2005, 21, 3340–3346. [Google Scholar] [CrossRef]
- Bergeron, A.; Mixtacki, J.; Stoye, J. A unifying view of genome rearrangements. In International Workshop on Algorithms in Bioinformatics; Springer: Berlin, Germany, 2006; pp. 163–173. [Google Scholar]
- Chauve, C.; Fertin, G.; Rizzi, R.; Vialette, S. Genomes containing duplicates are hard to compare. In International Conference on Computational Science; Springer: Berlin, Germany, 2006; pp. 783–790. [Google Scholar]
- Jiang, H.; Zhu, B.; Zhu, D. Algorithms for sorting unsigned linear genomes by the DCJ operations. Bioinformatics 2010, 27, 311–316. [Google Scholar] [CrossRef][Green Version]
- Fertin, G.; Jean, G.; Tannier, E. Algorithms for computing the double cut and join distance on both gene order and intergenic sizes. Algorithms Mol. Biol. 2017, 12, 16. [Google Scholar] [CrossRef]
- Bérard, S.; Chateau, A.; Chauve, C.; Paul, C.; Tannier, E. Perfect DCJ rearrangement. In RECOMB International Workshop on Comparative Genomics; Springer: Berlin, Germany, 2008; pp. 158–169. [Google Scholar]
- Watterson, G.; Ewens, W.; Hall, T.; Morgan, A. The chromosome inversion problem. J. Theor. Biol. 1982, 99, 1–7. [Google Scholar] [CrossRef]
- Hannenhalli, S.; Pevzner, P.A. Transforming Cabbage into Turnip: Polynomial Algorithm for Sorting Signed Permutations by Reversals. J. ACM 1999, 46, 1–27. [Google Scholar] [CrossRef]
- Christie, D.A. Genome Rearrangement Problems. Ph.D. Thesis, University of Glasgow, Glasgow, UK, 1998. [Google Scholar]
- Chen, X.; Zheng, J.; Fu, Z.; Nan, P.; Zhong, Y.; Lonardi, S.; Jiang, T. Assignment of Orthologous Genes via Genome Rearrangement. IEEE/ACM Trans. Comput. Biol. Bioinform. 2005, 2, 302–315. [Google Scholar] [CrossRef]
- Radcliffe, A.; Scott, A.; Wilmer, E. Reversals and transpositions over finite alphabets. SIAM J. Discret. Math. 2006, 19, 224. [Google Scholar] [CrossRef]
- Kececioglu, J.; Sankoff, D. Exact and approximation algorithms for sorting by reversals, with application to genome rearrangement. Algorithmica 1995, 13, 180. [Google Scholar] [CrossRef]
- Bulteau, L.; Fertin, G.; Komusiewicz, C. Reversal distances for strings with few blocks or small alphabets. In Symposium on Combinatorial Pattern Matching; Springer: Berlin, Germany, 2014; pp. 50–59. [Google Scholar]
- Bérard, S.; Chauve, C.; Paul, C. A more efficient algorithm for perfect sorting by reversals. Inf. Process. Lett. 2008, 106, 90–95. [Google Scholar] [CrossRef]
- Dias, Z.; Meidanis, J. Sorting by prefix transpositions. In International Symposium on String Processing and Information Retrieval; Springer: Berlin, Germany, 2002; pp. 65–76. [Google Scholar]
- Whidden, C. Sorting by Transpositions: Fixed-Parameter Algorithms and Structural Properties. Bachelor’s Thesis, Dalhousie University, Halifax, NS, Canada, 2007. [Google Scholar]
- Fertin, G.; Jankowiak, L.; Jean, G. Prefix and suffix reversals on strings. Discret. Appl. Math. 2018, 246, 140–153. [Google Scholar] [CrossRef]
- Lopresti, D.; Tomkins, A. Block edit models for approximate string matching. Theor. Comput. Sci. 1997, 181, 159–179. [Google Scholar] [CrossRef]
- Swenson, K.M.; Marron, M.; Earnest-DeYoung, J.V.; Moret, B.M. Approximating the true evolutionary distance between two genomes. J. Exp. Algorithmics (JEA) 2008, 12, 3–5. [Google Scholar] [CrossRef]
- Damaschke, P. Minimum common string partition parameterized. In International Workshop on Algorithms in Bioinformatics; Springer: Berlin, Germany, 2008; pp. 87–98. [Google Scholar]
- Jiang, H.; Zhu, B.; Zhu, D.; Zhu, H. Minimum common string partition revisited. J. Comb. Optim. 2012, 23, 519–527. [Google Scholar] [CrossRef]
- Bulteau, L.; Komusiewicz, C. Minimum common string partition parameterized by partition size is fixed-parameter tractable. In Proceedings of the Twenty-Fifth Annual ACM-SIAM Symposium on Discrete Algorithms, SIAM, Portland, OR, USA, 5–7 January 2014; pp. 102–121. [Google Scholar]
- Bulteau, L.; Fertin, G.; Komusiewicz, C.; Rusu, I. A fixed-parameter algorithm for minimum common string partition with few duplications. In International Workshop on Algorithms in Bioinformatics; Springer: Berlin, Germany, 2013; pp. 244–258. [Google Scholar]
- Beretta, S.; Castelli, M.; Dondi, R. Parameterized tractability of the maximum-duo preservation string mapping problem. Theor. Comput. Sci. 2016, 646, 16–25. [Google Scholar] [CrossRef][Green Version]
- Zheng, C.; Zhu, Q.; Sankoff, D. Removing noise and ambiguities from comparative maps in rearrangement analysis. IEEE/ACM Trans. Comput. Biol. Bioinform. 2007, 4, 515–522. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Liu, H.; Wang, J.; Xiang, L.; Yang, Y. An improved linear kernel for complementary maximal strip recovery: Simpler and smaller. Theor. Comput. Sci. 2019, 786, 55–66. [Google Scholar] [CrossRef]
- Bulteau, L.; Fertin, G.; Jiang, M.; Rusu, I. Tractability and approximability of maximal strip recovery. Theor. Comput. Sci. 2012, 440, 14–28. [Google Scholar] [CrossRef]
- Jiang, M. On the parameterized complexity of some optimization problems related to multiple-interval graphs. Theor. Comput. Sci. 2010, 411, 4253–4262. [Google Scholar] [CrossRef]
- Muñoz, A.; Zheng, C.; Zhu, Q.; Albert, V.A.; Rounsley, S.; Sankoff, D. Scaffold filling, contig fusion and comparative gene order inference. BMC Bioinform. 2010, 11, 304. [Google Scholar] [CrossRef] [PubMed]
- Bulteau, L.; Carrieri, A.P.; Dondi, R. Fixed-parameter algorithms for scaffold filling. Theor. Comput. Sci. 2015, 568, 72–83. [Google Scholar] [CrossRef]
- Sankoff, D.; Blanchette, M. Multiple genome rearrangement and breakpoint phylogeny. J. Comput. Biol. 1998, 5, 555–570. [Google Scholar] [CrossRef] [PubMed]
- Waterston, R.H.; Lander, E.S.; Sulston, J.E. On the sequencing of the human genome. Proc. Natl. Acad. Sci. USA 2002, 99, 3712–3716. [Google Scholar] [CrossRef]
- Notredame, C. Recent Evolutions of Multiple Sequence Alignment Algorithms. PLOS Comput. Biol. 2007, 3, 1–4. [Google Scholar] [CrossRef]
- Bonizzoni, P.; Della Vedova, G. The complexity of multiple sequence alignment with SP-score that is a metric. Theor. Comput. Sci. 2001, 259, 63–79. [Google Scholar] [CrossRef]
- Just, W. Computational complexity of multiple sequence alignment with SP-score. J. Comput. Biol. 2001, 8, 615–623. [Google Scholar] [CrossRef]
- Elias, I. Settling the intractability of multiple alignment. In International Symposium on Algorithms and Computation; Springer: Berlin, Germany, 2003; pp. 352–363. [Google Scholar]
- Kemena, C.; Notredame, C. Upcoming challenges for multiple sequence alignment methods in the high-throughput era. Bioinformatics 2009, 25, 2455–2465. [Google Scholar] [CrossRef]
- Bulteau, L.; Hüffner, F.; Komusiewicz, C.; Niedermeier, R. Multivariate Algorithmics for NP-Hard String Problems. Bull. EATCS 2014, 114, 1–43. [Google Scholar]
- Frances, M.; Litman, A. On covering problems of codes. Theory Comput. Syst. 1997, 30, 113–119. [Google Scholar] [CrossRef]
- Gramm, J.; Niedermeier, R.; Rossmanith, P. Fixed-parameter algorithms for closest string and related problems. Algorithmica 2003, 37, 25–42. [Google Scholar] [CrossRef]
- Evans, P.A.; Smith, A.D.; Wareham, H.T. On the complexity of finding common approximate substrings. Theor. Comput. Sci. 2003, 306, 407–430. [Google Scholar] [CrossRef]
- Fellows, M.R.; Gramm, J.; Niedermeier, R. On the parameterized intractability of motif search problems. Combinatorica 2006, 26, 141–167. [Google Scholar] [CrossRef]
- Marx, D. Closest substring problems with small distances. SIAM J. Comput. 2008, 38, 1382–1410. [Google Scholar] [CrossRef][Green Version]
- Schmid, M.L. Finding consensus strings with small length difference between input and solution strings. ACM Trans. Comput. Theory (TOCT) 2017, 9, 13. [Google Scholar] [CrossRef]
- Boucher, C.; Ma, B. Closest string with outliers. BMC Bioinform. 2011, 12, S55. [Google Scholar] [CrossRef]
- Bulteau, L.; Schmid, M. Consensus Strings with Small Maximum Distance and Small Distance Sum. In Proceedings of the 43rd International Symposium on Mathematical Foundations of Computer Science (MFCS 2018), Liverpool, UK, 27–31 August 2018. [Google Scholar]
- Chen, J.; Hermelin, D.; Sorge, M. On Computing Centroids According to the p-Norms of Hamming Distance Vectors. In Proceedings of the 27th Annual European Symposium on Algorithms, ESA 2019, Schloss Dagstuhl—Leibniz-Zentrum für Informatik, Munich/Garching, Germany, 9–11 September 2019; Volume 144, pp. 28:1–28:16. [Google Scholar] [CrossRef]
- Pietrzak, K. On the parameterized complexity of the fixed alphabet shortest common supersequence and longest common subsequence problems. J. Comput. Syst. Sci. 2003, 67, 757–771. [Google Scholar] [CrossRef]
- Bodlaender, H.L.; Downey, R.G.; Fellows, M.R.; Wareham, H.T. The parameterized complexity of sequence alignment and consensus. Theor. Comput. Sci. 1995, 147, 31–54. [Google Scholar] [CrossRef]
- Irving, R.W.; Fraser, C.B. Two algorithms for the longest common subsequence of three (or more) strings. In Annual Symposium on Combinatorial Pattern Matching; Springer: Berlin, Germany, 1992; pp. 214–229. [Google Scholar]
- Abboud, A.; Backurs, A.; Williams, V.V. Tight hardness results for LCS and other sequence similarity measures. In Proceedings of the 2015 IEEE 56th Annual Symposium on Foundations of Computer Science, Berkeley, CA, USA, 17–20 October 2015; pp. 59–78. [Google Scholar]
- Bringmann, K.; Künnemann, M. Multivariate fine-grained complexity of longest common subsequence. In Proceedings of the Twenty-Ninth Annual ACM-SIAM Symposium on Discrete Algorithms, Society for Industrial and Applied Mathematics, New Orleans, LA, USA, 7–10 January 2018; pp. 1216–1235. [Google Scholar]
- Giannopoulou, A.C.; Mertzios, G.B.; Niedermeier, R. Polynomial fixed-parameter algorithms: A case study for longest path on interval graphs. Theor. Comput. Sci. 2017, 689, 67–95. [Google Scholar] [CrossRef]
- Mertzios, G.B.; Nichterlein, A.; Niedermeier, R. The Power of Linear-Time Data Reduction for Maximum Matching. In Proceedings of the 42nd International Symposium on Mathematical Foundations of Computer Science (MFCS 2017), Aalborg, Denmark, 21–25 August 2017; Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik: Dagstuhl, Germany, 2017; Volume 83, pp. 46:1–46:14. [Google Scholar] [CrossRef]
- Coudert, D.; Ducoffe, G.; Popa, A. Fully Polynomial FPT Algorithms for Some Classes of Bounded Clique-width Graphs. ACM Trans. Algorithms 2019, 15, 33:1–33:57. [Google Scholar] [CrossRef]
- Tsai, Y.T. The constrained longest common subsequence problem. Inf. Process. Lett. 2003, 88, 173–176. [Google Scholar] [CrossRef]
- Bonizzoni, P.; Della Vedova, G.; Dondi, R.; Pirola, Y. Variants of constrained longest common subsequence. Inf. Process. Lett. 2010, 110, 877–881. [Google Scholar] [CrossRef]
- Chen, Y.C.; Chao, K.M. On the generalized constrained longest common subsequence problems. J. Comb. Optim. 2011, 21, 383–392. [Google Scholar] [CrossRef]
- Gotthilf, Z.; Hermelin, D.; Landau, G.M.; Lewenstein, M. Restricted lcs. In International Symposium on String Processing and Information Retrieval; Springer: Berlin, Germany, 2010; pp. 250–257. [Google Scholar]
- Chen, J.; Huang, X.; Kanj, I.A.; Xia, G. On the computational hardness based on linear FPT-reductions. J. Comb. Optim. 2006, 11, 231–247. [Google Scholar] [CrossRef]
- Fellows, M.; Hallett, M.; Korostensky, C.; Stege, U. Analogs and Duals of the MAST Problem for Sequences and Trees. In European Symposium on Algorithms; Springer: Berlin, Germany, 1998; pp. 103–114. [Google Scholar]
- Nicolas, F.; Rivals, E. Complexities of the centre and median string problems. In Annual Symposium on Combinatorial Pattern Matching; Springer: Berlin, Germany, 2003; pp. 315–327. [Google Scholar]
- Maji, H.; Izumi, T. Listing center strings under the edit distance metric. In Combinatorial Optimization and Applications; Springer: Berlin, Germany, 2015; pp. 771–782. [Google Scholar]
- Hunt, M.; Newbold, C.; Berriman, M.; Otto, T.D. A comprehensive evaluation of assembly scaffolding tools. Genome Biol. 2014, 15, R42. [Google Scholar] [CrossRef] [PubMed]
- Huson, D.H.; Reinert, K.; Myers, E.W. The Greedy Path-merging Algorithm for Contig Scaffolding. J. ACM 2002, 49, 603–615. [Google Scholar] [CrossRef]
- Chateau, A.; Giroudeau, R.; Poss, M.; Weller, M. Scaffolding with repeated contigs using flow formulations. unpublished manuscript.
- Weller, M.; Chateau, A.; Dallard, C.; Giroudeau, R. Scaffolding Problems Revisited: Complexity, Approximation and Fixed Parameter Tractable Algorithms, and Some Special Cases. Algorithmica 2018, 80, 1771–1803. [Google Scholar] [CrossRef]
- Gao, S.; Sung, W.K.; Nagarajan, N. Opera: Reconstructing Optimal Genomic Scaffolds with High-Throughput Paired-End Sequences. J. Comput. Biol. 2011, 18, 1681–1691. [Google Scholar] [CrossRef]
- Weller, M.; Chateau, A.; Giroudeau, R. Exact approaches for scaffolding. BMC Bioinform. 2015, 16, S2. [Google Scholar] [CrossRef][Green Version]
- Weller, M.; Chateau, A.; Giroudeau, R. On the Linearization of Scaffolds Sharing Repeated Contigs. In Proceedings of the 11th International Conference on Combinatorial Optimization and Applications (COCOA’17) Part II, Shanghai, China, 16–18 December 2017; pp. 509–517. [Google Scholar] [CrossRef]
- Davot, T.; Chateau, A.; Giroudeau, R.; Weller, M. Linearizing Genomes: Exact Methods and Local Search. In Proceedings of the SOFSEM’20, Nový Smokovec, Slovakia, 27–30 January 2019. [Google Scholar]
- Donmez, N.; Brudno, M. SCARPA: scaffolding reads with practical algorithms. Bioinformatics 2012, 29, 428–434. [Google Scholar] [CrossRef]
- Cao, M.D.; Nguyen, S.H.; Ganesamoorthy, D.; Elliott, A.G.; Cooper, M.A.; Coin, L.J.M. Scaffolding and completing genome assemblies in real-time with nanopore sequencing. Nat. Commun. 2017, 8, 14515. [Google Scholar] [CrossRef]
- Dallard, C.; Weller, M.; Chateau, A.; Giroudeau, R. Instance Guaranteed Ratio on Greedy Heuristic for Genome Scaffolding. In Combinatorial Optimization and Applications; Springer International Publishing: Cham, Switzerland, 2016; pp. 294–308. [Google Scholar]
- Hodgkinson, A.; Eyre-Walker, A. Human triallelic sites: Evidence for a new mutational mechanism? Genetics 2010, 184, 233–241. [Google Scholar] [CrossRef][Green Version]
- International SNP Map Working Group. A map of human genome sequence variation containing 1.42 million single nucleotide polymorphisms. Nature 2001, 409, 928. [Google Scholar] [CrossRef]
- Andrés, A.M.; Clark, A.G.; Shimmin, L.; Boerwinkle, E.; Sing, C.F.; Hixson, J.E. Understanding the accuracy of statistical haplotype inference with sequence data of known phase. Genet. Epidemiol. 2007, 31, 659–671. [Google Scholar] [CrossRef] [PubMed]
- Orzack, S.H.; Gusfield, D.; Olson, J.; Nesbitt, S.; Subrahmanyan, L.; Stanton, V.P. Analysis and Exploration of the Use of Rule-Based Algorithms and Consensus Methods for the Inferral of Haplotypes. Genetics 2003, 165, 915–928. [Google Scholar]
- Climer, S.; Jäger, G.; Templeton, A.R.; Zhang, W. How frugal is mother nature with haplotypes? Bioinformatics 2008, 25, 68–74. [Google Scholar] [CrossRef]
- Zhang, X.S.; Wang, R.S.; Wu, L.Y.; Chen, L. Models and Algorithms for Haplotyping Problem. Curr. Bioinform. 2006, 1, 105–114. [Google Scholar] [CrossRef]
- Halldórsson, B.V.; Bafna, V.; Edwards, N.; Lippert, R.; Yooseph, S.; Istrail, S. A Survey of Computational Methods for Determining Haplotypes. In Computational Methods for SNPs and Haplotype Inference; Springer: Berlin/Heidelberg, Germany, 2004; pp. 26–47. [Google Scholar]
- Lancia, G. Algorithmic approaches for the single individual haplotyping problem. RAIRO Recherche Opérationnelle 2016, 50. [Google Scholar] [CrossRef][Green Version]
- Zhao, Y.; Xu, Y.; Zhang, Q.; Chen, G. An overview of the haplotype problems and algorithms. Front. Comput. Sci. China 2007, 1, 272–282. [Google Scholar] [CrossRef]
- Schwartz, R. Theory and Algorithms for the Haplotype Assembly Problem. Commun. Inf. Syst. 2010, 10, 23–38. [Google Scholar] [CrossRef]
- Geraci, F. A comparison of several algorithms for the single individual SNP haplotyping reconstruction problem. Bioinformatics 2010, 26, 2217–2225. [Google Scholar] [CrossRef]
- Xie, M.; Wang, J.; Chen, J.; Wu, J.; Liu, X. Computational Models and Algorithms for the Single Individual Haplotyping Problem. Curr. Bioinform. 2010, 5, 18–28. [Google Scholar] [CrossRef]
- Rhee, J.K.; Li, H.; Joung, J.G.; Hwang, K.B.; Zhang, B.T.; Shin, S.Y. Survey of computational haplotype determination methods for single individual. Genes Genom. 2016, 38, 1–12. [Google Scholar] [CrossRef]
- Lancia, G.; Bafna, V.; Istrail, S.; Lippert, R.; Schwartz, R. SNPs Problems, Complexity, and Algorithms. In Algorithms—ESA 2001; Springer: Berlin/Heidelberg, Germany, 2001; pp. 182–193. [Google Scholar]
- Bafna, V.; Istrail, S.; Lancia, G.; Rizzi, R. Polynomial and APX-hard cases of the individual haplotyping problem. Theor. Comput. Sci. 2005, 335, 109–125. [Google Scholar] [CrossRef]
- Xie, M.; Wang, J. An Improved (and Practical) Parameterized Algorithm for the Individual Haplotyping Problem MFR with Mate-Pairs. Algorithmica 2008, 52, 250–266. [Google Scholar] [CrossRef]
- Reed, B.; Smith, K.; Vetta, A. Finding odd cycle transversals. Oper. Res. Lett. 2004, 32, 299–301. [Google Scholar] [CrossRef]
- Hüffner, F. Algorithm Engineering for Optimal Graph Bipartization. J. Graph Algorithms Appl. 2009, 13, 77–98. [Google Scholar] [CrossRef]
- Lokshtanov, D.; Narayanaswamy, N.S.; Raman, V.; Ramanujan, M.S.; Saurabh, S. Faster Parameterized Algorithms Using Linear Programming. ACM Trans. Algorithms 2014, 11, 15:1–15:31. [Google Scholar] [CrossRef]
- Kratsch, S.; Wahlström, M. Compression via Matroids: A Randomized Polynomial Kernel for Odd Cycle Transversal. ACM Trans. Algorithms 2014, 10, 20:1–20:15. [Google Scholar] [CrossRef]
- Xie, M.; Chen, J.; Wang, J. Research on parameterized algorithms of the individual haplotyping problem. J. Bioinform. Comput. Biol. 2007, 5, 795–816. [Google Scholar] [CrossRef]
- Cilibrasi, R.; van Iersel, L.; Kelk, S.; Tromp, J. The Complexity of the Single Individual SNP Haplotyping Problem. Algorithmica 2007, 49, 13–36. [Google Scholar] [CrossRef]
- Bonizzoni, P.; Dondi, R.; Klau, G.W.; Pirola, Y.; Pisanti, N.; Zaccaria, S. On the Minimum Error Correction Problem for Haplotype Assembly in Diploid and Polyploid Genomes. J. Comput. Biol. 2016, 23, 718–736. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.S.; Wu, L.Y.; Li, Z.P.; Zhang, X.S. Haplotype reconstruction from SNP fragments by minimum error correction. Bioinformatics 2005, 21, 2456–2462. [Google Scholar] [CrossRef] [PubMed]
- Xie, M.; Wang, J.; Chen, J. A model of higher accuracy for the individual haplotyping problem based on weighted SNP fragments and genotype with errors. Bioinformatics 2008, 24, i105–i113. [Google Scholar] [CrossRef][Green Version]
- Deng, F.; Cui, W.; Wang, L. A highly accurate heuristic algorithm for the haplotype assembly problem. BMC Genom. 2013, 14, S2. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Patterson, M.; Marschall, T.; Pisanti, N.; van Iersel, L.; Stougie, L.; Klau, G.W.; Schönhuth, A. WhatsHap: Weighted Haplotype Assembly for Future-Generation Sequencing Reads. J. Comput. Biol. 2015, 22, 498–509. [Google Scholar] [CrossRef]
- Pirola, Y.; Zaccaria, S.; Dondi, R.; Klau, G.W.; Pisanti, N.; Bonizzoni, P. HapCol: accurate and memory-efficient haplotype assembly from long reads. Bioinformatics 2015, 32, 1610–1617. [Google Scholar] [CrossRef][Green Version]
- Garg, S.; Rautiainen, M.; Novak, A.M.; Garrison, E.; Durbin, R.; Marschall, T. A graph-based approach to diploid genome assembly. Bioinformatics 2018, 34, i105–i114. [Google Scholar] [CrossRef]
- He, D.; Choi, A.; Pipatsrisawat, K.; Darwiche, A.; Eskin, E. Optimal algorithms for haplotype assembly from whole-genome sequence data. Bioinformatics 2010, 26, i183–i190. [Google Scholar] [CrossRef]
- Zhang, X.S.; Wang, R.S.; Wu, L.Y.; Zhang, W. Minimum Conflict Individual Haplotyping from SNP Fragments and Related Genotype. Evolut. Bioinform. 2006, 2. [Google Scholar] [CrossRef]
- Hermelin, D.; Rozenberg, L. Parameterized complexity analysis for the Closest String with Wildcards problem. Theor. Comput. Sci. 2015, 600, 11–18. [Google Scholar] [CrossRef]
- Garg, S.; Martin, M.; Marschall, T. Read-based phasing of related individuals. Bioinformatics 2016, 32, i234–i242. [Google Scholar] [CrossRef]
- Li, Z.p.; Wu, L.y.; Zhao, Y.y.; Zhang, X.s. A Dynamic Programming Algorithm for the k-Haplotyping Problem. Acta Mathematicae Applicatae Sinica 2006, 22, 405–412. [Google Scholar] [CrossRef]
- Bao, R.; Huang, L.; Andrade, J.; Tan, W.; Kibbe, W.A.; Jiang, H.; Feng, G. Review of Current Methods, Applications, and Data Management for the Bioinformatics Analysis of Whole Exome Sequencing. Cancer Inform. 2014, 13s2, CIN.S13779. [Google Scholar] [CrossRef]
- Garg, S. Computational Haplotyping: Theory and Practice. Ph.D. Thesis, Universität des Saarlandes, Saarbrücken, Germany, 2018. [Google Scholar] [CrossRef]
- Gusfield, D. Haplotype Inference by Pure Parsimony. In Combinatorial Pattern Matching; Springer: Berlin/Heidelberg, Germany, 2003; pp. 144–155. [Google Scholar]
- Bonizzoni, P.; Della Vedova, G.; Dondi, R.; Pirola, Y.; Rizzi, R. Pure Parsimony Xor Haplotyping. IEEE/ACM Trans. Comput. Biol. Bioinform. 2010, 7, 598–610. [Google Scholar] [CrossRef] [PubMed]
- Graça, A.; Lynce, I.; Marques-Silva, J.; Oliveira, A.L. Haplotype Inference by Pure Parsimony: A Survey. J. Comput. Biol. 2010, 17, 969–992. [Google Scholar] [CrossRef]
- Hubbell, E.; (GRAIL, Inc. LinkedIn, Menlo Park, CA, USA). Finding a Parsimony Solution to Haplotype Phase is NP-Hard. Personal communication, 2002. [Google Scholar]
- Lancia, G.; Pinotti, M.C.; Rizzi, R. Haplotyping Populations by Pure Parsimony: Complexity of Exact and Approximation Algorithms. INFORMS J. Comput. 2004, 16, 348–359. [Google Scholar] [CrossRef]
- Huang, Y.T.; Chao, K.M.; Chen, T. An Approximation Algorithm for Haplotype Inference by Maximum Parsimony. J. Comput. Biol. 2005, 12, 1261–1274. [Google Scholar] [CrossRef]
- Sharan, R.; Halldorsson, B.V.; Istrail, S. Islands of Tractability for Parsimony Haplotyping. IEEE/ACM Trans. Comput. Biol. Bioinform. 2006, 3, 303–311. [Google Scholar] [CrossRef]
- van Iersel, L.; Keijsper, J.; Kelk, S.; Stougie, L. Shorelines of Islands of Tractability: Algorithms for Parsimony and Minimum Perfect Phylogeny Haplotyping Problems. IEEE/ACM Trans. Comput. Biol. Bioinform. 2008, 5, 301–312. [Google Scholar] [CrossRef]
- Lancia, G.; Rizzi, R. A polynomial case of the parsimony haplotyping problem. Oper. Res. Lett. 2006, 34, 289–295. [Google Scholar] [CrossRef]
- van Iersel, L.J.J. Algorithms, Haplotypes and Phylogenetic Networks. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2009. [Google Scholar]
- Fellows, M.R.; Hartman, T.; Hermelin, D.; Landau, G.M.; Rosamond, F.A.; Rozenberg, L. Haplotype Inference Constrained by Plausible Haplotype Data. IEEE/ACM Trans. Comput. Biol. Bioinform. 2011, 8, 1692–1699. [Google Scholar] [CrossRef] [PubMed]
- Fleischer, R.; Guo, J.; Niedermeier, R.; Uhlmann, J.; Wang, Y.; Weller, M.; Wu, X. Extended Islands of Tractability for Parsimony Haplotyping. In Combinatorial Pattern Matching; Springer: Berlin/Heidelberg, Germany, 2010; pp. 214–226. [Google Scholar]
- Gusfield, D. Haplotyping As Perfect Phylogeny: Conceptual Framework and Efficient Solutions. In Proceedings of the Sixth Annual International Conference on Computational Biology, RECOMB ’02, Washington, DC, USA, 18–21 April 2002; ACM: New York, NY, USA, 2002; pp. 166–175. [Google Scholar] [CrossRef]
- Ding, Z.; Filkov, V.; Gusfield, D. A Linear-Time Algorithm for the Perfect Phylogeny Haplotyping (PPH) Problem. J. Comput. Biol. 2006, 13, 522–553. [Google Scholar] [CrossRef] [PubMed]
- Bonizzoni, P. A Linear-Time Algorithm for the Perfect Phylogeny Haplotype Problem. Algorithmica 2007, 48, 267–285. [Google Scholar] [CrossRef]
- Chen, Z.Z.; Ma, W.; Wang, L. The Parameterized Complexity of the Shared Center Problem. Algorithmica 2014, 69, 269–293. [Google Scholar] [CrossRef][Green Version]
- Keijsper, J.; Oosterwijk, T. Tractable Cases of (*, 2)-Bounded Parsimony Haplotyping. IEEE/ACM Trans. Comput. Biol. Bioinform. 2015, 12, 234–247. [Google Scholar] [CrossRef]
- Cicalese, F.; Milanivc, M. On Parsimony Haplotyping; Technical Report; Universitẗ Bielefeld: Bielefeld, Germany, 2008. [Google Scholar]
- Haeckel, E. Generelle Morphologie der Organismen. Allgemeine Grundzüge der organischen Formen-Wissenschaft, mechanisch begründet durch die von C. Darwin reformirte Descendenz-Theorie, etc.; Verlag von Georg Reimer: Berlin, Germany, 1866; Volume 2. [Google Scholar]
- Dobzhansky, T. Nothing in Biology Makes Sense except in the Light of Evolution. Am. Biol. Teach. 1973, 35, 125–129. [Google Scholar] [CrossRef]
- De Bruyn, A.; Martin, D.P.; Lefeuvre, P. Phylogenetic Reconstruction Methods: An Overview. In Molecular Plant Taxonomy: Methods and Protocols; Humana Press: Totowa, NJ, USA, 2014; pp. 257–277. [Google Scholar] [CrossRef]
- Huson, D.H.; Rupp, R.; Scornavacca, C. Phylogenetic Networks—Concepts, Algorithms and Applications; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Choy, C.; Jansson, J.; Sadakane, K.; Sung, W.K. Computing the maximum agreement of phylogenetic networks. Theor. Comput. Sci. 2005, 335, 93–107. [Google Scholar] [CrossRef]
- Betzler, N.; Guo, J.; Komusiewicz, C.; Niedermeier, R. Average parameterization and partial kernelization for computing medians. J. Comput. Syst. Sci. 2011, 77, 774–789. [Google Scholar] [CrossRef]
- Bryant, D. A classification of consensus methods for phylogenetics. DIMACS Ser. Discrete Math. Theor. Comput. Sci. 2003, 61, 163–184. [Google Scholar]
- Degnan, J.H. Consensus Methods, Phylogenetic. In Encyclopedia of Evolutionary Biology; Elsevier: Amsterdam, The Netherlands, 2016; Volume 1, pp. 341–346. [Google Scholar]
- Steel, M. The complexity of reconstructing trees from qualitative characters and subtrees. J. Classif. 1992, 9, 91–116. [Google Scholar] [CrossRef]
- Böcker, S.; Bryant, D.; Dress, A.W.; Steel, M.A. Algorithmic Aspects of Tree Amalgamation. J. Algorithms 2000, 37, 522–537. [Google Scholar] [CrossRef]
- Arnborg, S.; Lagergren, J.; Seese, D. Easy problems for tree-decomposable graphs. J. Algorithms 1991, 12, 308–340. [Google Scholar] [CrossRef]
- Courcelle, B. The monadic second-order logic of graphs. I. Recognizable sets of finite graphs. Inf. Comput. 1990, 85, 12–75. [Google Scholar] [CrossRef]
- Bryant, D.; Lagergren, J. Compatibility of unrooted phylogenetic trees is FPT. Theor. Comput. Sci. 2006, 351, 296–302. [Google Scholar] [CrossRef]
- Scornavacca, C.; van Iersel, L.; Kelk, S.; Bryant, D. The agreement problem for unrooted phylogenetic trees is FPT. J. Graph Algorithms Appl. 2014, 18, 385–392. [Google Scholar] [CrossRef][Green Version]
- Baste, J.; Paul, C.; Sau, I.; Scornavacca, C. Efficient FPT Algorithms for (Strict) Compatibility of Unrooted Phylogenetic Trees. In Algorithmic Aspects in Information and Management; Springer International Publishing: Cham, Switzerland, 2016; pp. 53–64. [Google Scholar]
- Aho, A.; Sagiv, Y.; Szymanski, T.; Ullman, J. Inferring a Tree from Lowest Common Ancestors with an Application to the Optimization of Relational Expressions. SIAM J. Comput. 1981, 10, 405–421. [Google Scholar] [CrossRef]
- Ng, M.P.; Wormald, N.C. Reconstruction of rooted trees from subtrees. Discret. Appl. Math. 1996, 69, 19–31. [Google Scholar] [CrossRef]
- Maddison, W.P. Gene Trees in Species Trees. Syst. Biol. 1997, 46, 523–536. [Google Scholar] [CrossRef]
- Linder, C.R.; Rieseberg, L.H. Reconstructing patterns of reticulate evolution in plants. Am. J. Bot. 2004, 91, 1700–1708. [Google Scholar] [CrossRef]
- Jansson, J. On the complexity of inferring rooted evolutionary trees. Electron. Notes Discret. Math. 2001, 7, 50–53. [Google Scholar] [CrossRef]
- Bryant, D. Building Trees, Hunting for Trees, and Comparing Trees: Theory and Methods in Phylogenetic Analysis. Ph.D. Thesis, University of Canterbury, Canterbury, UK, 1997. [Google Scholar]
- Wu, B.Y. Constructing the Maximum Consensus Tree from Rooted Triples. J. Comb. Optim. 2004, 8, 29–39. [Google Scholar] [CrossRef]
- Byrka, J.; Guillemot, S.; Jansson, J. New results on optimizing rooted triplets consistency. Discret. Appl. Math. 2010, 158, 1136–1147. [Google Scholar] [CrossRef]
- Guillemot, S.; Mnich, M. Kernel and Fast Algorithm for Dense Triplet Inconsistency. In Theory and Applications of Models of Computation; Springer: Berlin/Heidelberg, Germany, 2010; pp. 247–257. [Google Scholar]
- Fomin, F.V.; Lokshtanov, D.; Saurabh, S.; Zehavi, M. Kernelization: Theory of Parameterized Preprocessing; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar] [CrossRef]
- Paul, C.; Perez, A.; Thomassé, S. Linear kernel for Rooted Triplet Inconsistency and other problems based on conflict packing technique. J. Comput. Syst. Sci. 2016, 82, 366–379. [Google Scholar] [CrossRef]
- Habib, M.; To, T.H. Constructing a minimum phylogenetic network from a dense triplet set. J. Bioinform. Comput. Biol. 2012, 10, 1250013. [Google Scholar] [CrossRef] [PubMed]
- van Iersel, L.; Kelk, S. Constructing the Simplest Possible Phylogenetic Network from Triplets. Algorithmica 2011, 60, 207–235. [Google Scholar] [CrossRef]
- Gramm, J.; Niedermeier, R. A fixed-parameter algorithm for minimum quartet inconsistency. J. Comput. Syst. Sci. 2003, 67, 723–741. [Google Scholar] [CrossRef]
- Jansson, J.; Ng, J.H.K.; Sadakane, K.; Sung, W.K. Rooted Maximum Agreement Supertrees. Algorithmica 2005, 43, 293–307. [Google Scholar] [CrossRef]
- Steel, M.A.; Penny, D. Distributions of Tree Comparison Metrics—Some New Results. Syst. Biol. 1993, 42, 126–141. [Google Scholar] [CrossRef]
- Goddard, W.; Kubicka, E.; Kubicki, G.; McMorris, F. The agreement metric for labeled binary trees. Math. Biosci. 1994, 123, 215–226. [Google Scholar] [CrossRef]
- Berry, V.; Nicolas, F. Maximum agreement and compatible supertrees. J. Discret. Algorithms 2007, 5, 564–591. [Google Scholar] [CrossRef]
- Guillemot, S.; Berry, V. Fixed-Parameter Tractability of the Maximum Agreement Supertree Problem. IEEE/ACM Trans. Comput. Biol. Bioinform. 2010, 7, 342–353. [Google Scholar] [CrossRef]
- Hoang, V.T.; Sung, W.K. Improved Algorithms for Maximum Agreement and Compatible Supertrees. Algorithmica 2011, 59, 195–214. [Google Scholar] [CrossRef]
- Fernández-Baca, D.; Guillemot, S.; Shutters, B.; Vakati, S. Fixed-Parameter Algorithms for Finding Agreement Supertrees. SIAM J. Comput. 2015, 44, 384–410. [Google Scholar] [CrossRef]
- Amir, A.; Keselman, D. Maximum Agreement Subtree in a Set of Evolutionary Trees: Metrics and Efficient Algorithms. SIAM J. Comput. 1997, 26, 1656–1669. [Google Scholar] [CrossRef]
- Farach, M.; Przytycka, T.M.; Thorup, M. On the agreement of many trees. Inf. Process. Lett. 1995, 55, 297–301. [Google Scholar] [CrossRef]
- Wang, B.; Swenson, K.M. A Faster Algorithm for Computing the Kernel of Maximum Agreement Subtrees. IEEE/ACM Trans. Comput. Biol. Bioinform. 2019. [Google Scholar] [CrossRef]
- Downey, R.G.; Fellows, M.R.; Stege, U. Computational Tractability: The View From Mars. Bull. EATCS 1999, 69, 73–97. [Google Scholar]
- Alber, J.; Gramm, J.; Niedermeier, R. Faster exact algorithms for hard problems: A parameterized point of view. Discret. Math. 2001, 229, 3–27. [Google Scholar] [CrossRef]
- Berry, V.; Nicolas, F. Improved Parameterized Complexity of the Maximum Agreement Subtree and Maximum Compatible Tree Problems. IEEE/ACM Trans. Comput. Biol. Bioinform. 2006, 3, 289–302. [Google Scholar] [CrossRef]
- Chauve, C.; Jones, M.; Lafond, M.; Scornavacca, C.; Weller, M. Constructing a Consensus Phylogeny from a Leaf-Removal Distance. CoRR 2017, arXiv:abs/1705.05295. [Google Scholar]
- Chen, Z.Z.; Ueta, S.; Li, J.; Wang, L.; Skums, P.; Li, M. Computing a Consensus Phylogeny via Leaf Removal. In Bioinformatics Research and Applications; Springer International Publishing: Cham, Switzerland, 2019; pp. 3–15. [Google Scholar]
- Lafond, M.; El-Mabrouk, N.; Huber, K.; Moulton, V. The complexity of comparing multiply-labelled trees by extending phylogenetic-tree metrics. Theor. Comput. Sci. 2019, 760, 15–34. [Google Scholar] [CrossRef]
- Shi, F.; Feng, Q.; Chen, J.; Wang, L.; Wang, J. Distances between phylogenetic trees: A survey. Tsinghua Sci.Technol. 2013, 18, 490–499. [Google Scholar] [CrossRef]
- Whidden, C. Efficient Computation and Application of Maximum Agreement Forests. Ph.D. Thesis, Dalhousie University, Halifax, NS, Canada, 2013. [Google Scholar]
- Hein, J.; Jiang, T.; Wang, L.; Zhang, K. On the complexity of comparing evolutionary trees. Discret. Appl. Math. 1996, 71, 153–169. [Google Scholar] [CrossRef]
- Allen, B.L.; Steel, M. Subtree Transfer Operations and Their Induced Metrics on Evolutionary Trees. Ann. Comb. 2001, 5, 1–15. [Google Scholar] [CrossRef]
- Hallett, M.; McCartin, C. A Faster FPT Algorithm for the Maximum Agreement Forest Problem. Theory Comput. Syst. 2007, 41, 539–550. [Google Scholar] [CrossRef]
- Whidden, C.; Zeh, N. A Unifying View on Approximation and FPT of Agreement Forests. In Algorithms in Bioinformatics; Springer: Berlin/Heidelberg, Germany, 2009; pp. 390–402. [Google Scholar]
- Kelk, S.; Linz, S. A tight kernel for computing the tree bisection and reconnection distance between two phylogenetic trees. CoRR 2018, arXiv:abs/1811.06892. [Google Scholar] [CrossRef]
- Kelk, S.; Linz, S. New reduction rules for the tree bisection and reconnection distance. arXiv 2019, arXiv:1905.01468. [Google Scholar]
- Shi, F.; Wang, J.; Chen, J.; Feng, Q.; Guo, J. Algorithms for parameterized maximum agreement forest problem on multiple trees. Theor. Comput. Sci. 2014, 554, 207–216. [Google Scholar] [CrossRef]
- Chen, J.; Fan, J.H.; Sze, S.H. Parameterized and approximation algorithms for maximum agreement forest in multifurcating trees. Theor. Comput. Sci. 2015, 562, 496–512. [Google Scholar] [CrossRef]
- Baroni, M.; Grünewald, S.; Moulton, V.; Semple, C. Bounding the Number of Hybridisation Events for a Consistent Evolutionary History. J. Math. Biol. 2005, 51, 171–182. [Google Scholar] [CrossRef]
- Bordewich, M.; Semple, C. On the Computational Complexity of the Rooted Subtree Prune and Regraft Distance. Ann. Comb. 2005, 8, 409–423. [Google Scholar] [CrossRef]
- Bordewich, M.; McCartin, C.; Semple, C. A 3-approximation algorithm for the subtree distance between phylogenies. J. Discret. Algorithms 2008, 6, 458–471. [Google Scholar] [CrossRef]
- Whidden, C.; Beiko, R.; Zeh, N. Fixed-Parameter Algorithms for Maximum Agreement Forests. SIAM J. Comput. 2013, 42, 1431–1466. [Google Scholar] [CrossRef]
- Chen, Z.Z.; Wang, L. Faster Exact Computation of rSPR Distance. In Frontiers in Algorithmics and Algorithmic Aspects in Information and Management; Springer: Berlin/Heidelberg, Germany, 2013; pp. 36–47. [Google Scholar]
- Chen, Z.Z.; Wang, L. Algorithms for Reticulate Networks of Multiple Phylogenetic Trees. IEEE/ACM Trans. Comput. Biol. Bioinform. 2012, 9, 372–384. [Google Scholar] [CrossRef]
- Collins, J.S. Rekernelisation Algorithms in Hybrid Phylogenies. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 2009. [Google Scholar]
- van Iersel, L.; Kelk, S.; Lekić, N.; Stougie, L. Approximation Algorithms for Nonbinary Agreement Forests. SIAM J. Discret. Math. 2014, 28, 49–66. [Google Scholar] [CrossRef][Green Version]
- Whidden, C.; Beiko, R.G.; Zeh, N. Fixed-Parameter and Approximation Algorithms for Maximum Agreement Forests of Multifurcating Trees. Algorithmica 2016, 74, 1019–1054. [Google Scholar] [CrossRef][Green Version]
- Bordewich, M.; Semple, C. Computing the Hybridization Number of Two Phylogenetic Trees Is Fixed-Parameter Tractable. IEEE/ACM Trans. Comput. Biol. Bioinform. 2007, 4, 458–466. [Google Scholar] [CrossRef]
- Shi, F.; Chen, J.; Feng, Q.; Wang, J. A parameterized algorithm for the Maximum Agreement Forest problem on multiple rooted multifurcating trees. J. Comput. Syst. Sci. 2018, 97, 28–44. [Google Scholar] [CrossRef]
- Linz, S.; Semple, C. Hybridization in Nonbinary Trees. IEEE/ACM Trans. Comput. Biol. Bioinform. 2009, 6, 30–45. [Google Scholar] [CrossRef]
- Bordewich, M.; Semple, C. Computing the minimum number of hybridization events for a consistent evolutionary history. Discret. Appl. Math. 2007, 155, 914–928. [Google Scholar] [CrossRef]
- Albrecht, B.; Scornavacca, C.; Cenci, A.; Huson, D.H. Fast computation of minimum hybridization networks. Bioinformatics 2011, 28, 191–197. [Google Scholar] [CrossRef]
- van Iersel, L.; Kelk, S.; Lekić, N.; Whidden, C.; Zeh, N. Hybridization Number on Three Rooted Binary Trees is EPT. SIAM J. Discret. Math. 2016, 30, 1607–1631. [Google Scholar] [CrossRef]
- van Iersel, L.; Linz, S. A quadratic kernel for computing the hybridization number of multiple trees. Inf. Process. Lett. 2013, 113, 318–323. [Google Scholar] [CrossRef]
- van Iersel, L.; Kelk, S.; Scornavacca, C. Kernelizations for the hybridization number problem on multiple nonbinary trees. J. Comput. Syst. Sci. 2016, 82, 1075–1089. [Google Scholar] [CrossRef]
- Alon, N.; Gutin, G.; Kim, E.J.; Szeider, S.; Yeo, A. Solving MAX-r-SAT Above a Tight Lower Bound. Algorithmica 2011, 61, 638–655. [Google Scholar] [CrossRef][Green Version]
- Piovesan, T.; Kelk, S.M. A Simple Fixed Parameter Tractable Algorithm for Computing the Hybridization Number of Two (Not Necessarily Binary) Trees. IEEE/ACM Trans. Comput. Biol. Bioinform. 2013, 10, 18–25. [Google Scholar] [CrossRef][Green Version]
- Li, Z. Fixed-Parameter Algorithm for Hybridization Number of Two Multifurcating Trees. Master’s Thesis, Dalhousie University, Halifax, NS, Canada, 2014. [Google Scholar]
- Bordewich, M.; Scornavacca, C.; Tokac, N.; Weller, M. On the fixed parameter tractability of agreement-based phylogenetic distances. J. Math. Biol. 2017, 74, 239–257. [Google Scholar] [CrossRef][Green Version]
- Kelk, S.; van Iersel, L.; Scornavacca, C.; Weller, M. Phylogenetic incongruence through the lens of Monadic Second Order logic. J. Graph Algorithms Appl. 2016, 20, 189–215. [Google Scholar] [CrossRef]
- Klawitter, J.; Linz, S. On the Subnet Prune and Regraft Distance. arXiv 2018, arXiv:1805.07839. [Google Scholar]
- Hickey, G.; Dehne, F.; Rau-Chaplin, A.; Blouin, C. SPR Distance Computation for Unrooted Trees. Evolut. Bioinform. 2008, 4, EBO.S419. [Google Scholar] [CrossRef]
- Bonet, M.L.; St. John, K. On the Complexity of uSPR Distance. IEEE/ACM Trans. Comput. Biol. Bioinform. 2010, 7, 572–576. [Google Scholar] [CrossRef]
- Whidden, C.; Matsen, F. Chain Reduction Preserves the Unrooted Subtree Prune-and-Regraft Distance. arXiv 2016, arXiv:1611.02351. [Google Scholar]
- Whidden, C.; Matsen, F. Calculating the Unrooted Subtree Prune-and-Regraft Distance. IEEE/ACM Trans. Comput. Biol. Bioinform. 2019, 16, 898–911. [Google Scholar] [CrossRef]
- Döcker, J.; van Iersel, L.; Kelk, S.; Linz, S. Deciding the existence of a cherry-picking sequence is hard on two trees. Discret. Appl. Math. 2019, 260, 131–143. [Google Scholar] [CrossRef]
- Humphries, P.J.; Linz, S.; Semple, C. Cherry Picking: A Characterization of the Temporal Hybridization Number for a Set of Phylogenies. Bull. Math. Biol. 2013, 75, 1879–1890. [Google Scholar] [CrossRef]
- Fischer, M.; Kelk, S. On the Maximum Parsimony Distance Between Phylogenetic Trees. Ann. Comb. 2016, 20, 87–113. [Google Scholar] [CrossRef]
- Kelk, S.; Fischer, M. On the Complexity of Computing MP Distance Between Binary Phylogenetic Trees. Ann. Comb. 2017, 21, 573–604. [Google Scholar] [CrossRef][Green Version]
- Kelk, S.; Fischer, M.; Moulton, V.; Wu, T. Reduction rules for the maximum parsimony distance on phylogenetic trees. Theor. Comput. Sci. 2016, 646, 1–15. [Google Scholar] [CrossRef]
- Janssen, R.; Jones, M.; Kelk, S.; Stamoulis, G.; Wu, T. Treewidth of display graphs: bounds, brambles and applications. J. Graph Algorithms Appl. 2019, 23, 715–743. [Google Scholar] [CrossRef]
- Ma, B.; Li, M.; Zhang, L. From Gene Trees to Species Trees. SIAM J. Comput. 2000, 30, 729–752. [Google Scholar] [CrossRef]
- Bonizzoni, P.; Vedova, G.D.; Dondi, R. Reconciling a gene tree to a species tree under the duplication cost model. Theor. Comput. Sci. 2005, 347, 36–53. [Google Scholar] [CrossRef]
- Doyon, J.P.; Ranwez, V.; Daubin, V.; Berry, V. Models, algorithms and programs for phylogeny reconciliation. Brief. Bioinform. 2011, 12, 392–400. [Google Scholar] [CrossRef] [PubMed]
- Szöllősi, G.J.; Tannier, E.; Daubin, V.; Boussau, B. The Inference of Gene Trees with Species Trees. Syst. Biol. 2014, 64, e42–e62. [Google Scholar] [CrossRef] [PubMed]
- Rusin, L.Y.; Lyubetskaya, E.; Gorbunov, K.Y.; Lyubetsky, V. Reconciliation of gene and species trees. BioMed Res. Int. 2014, 2014, 642089. [Google Scholar] [CrossRef] [PubMed]
- Scornavacca, C. Phylogenomics among Trees and Networks: A Challenging Accrobranche. 2019; in press. [Google Scholar]
- Górecki, P.; Tiuryn, J. DLS-trees: A model of evolutionary scenarios. Theor. Comput. Sci. 2006, 359, 378–399. [Google Scholar] [CrossRef]
- ZHANG, L. On a Mirkin-Muchnik-Smith Conjecture for Comparing Molecular Phylogenies. J. Comput. Biol. 1997, 4, 177–187. [Google Scholar] [CrossRef]
- Zmasek, C.M.; Eddy, S.R. A simple algorithm to infer gene duplication and speciation events on a gene tree. Bioinformatics 2001, 17, 821–828. [Google Scholar] [CrossRef]
- Harel, D.; Tarjan, R.E. Fast Algorithms for Finding Nearest Common Ancestors. SIAM J. Comput. 1984, 13, 338–355. [Google Scholar] [CrossRef]
- Bender, M.A.; Farach-Colton, M. The LCA Problem Revisited. In LATIN 2000: Theoretical Informatics; Springer: Berlin/Heidelberg, Germany, 2000; pp. 88–94. [Google Scholar]
- Chang, W.C.; Eulenstein, O. Reconciling Gene Trees with Apparent Polytomies. In Computing and Combinatorics; Springer: Berlin/Heidelberg, Germany, 2006; pp. 235–244. [Google Scholar]
- Lafond, M.; Swenson, K.M.; El-Mabrouk, N. An Optimal Reconciliation Algorithm for Gene Trees with Polytomies. In Algorithms in Bioinformatics; Springer: Berlin/Heidelberg, Germany, 2012; pp. 106–122. [Google Scholar]
- Tofigh, A.; Hallett, M.; Lagergren, J. Simultaneous Identification of Duplications and Lateral Gene Transfers. IEEE/ACM Trans. Comput. Biol. Bioinform. 2011, 8, 517–535. [Google Scholar] [CrossRef]
- Doyon, J.P.; Scornavacca, C.; Gorbunov, K.Y.; Szöllősi, G.J.; Ranwez, V.; Berry, V. An Efficient Algorithm for Gene/Species Trees Parsimonious Reconciliation with Losses, Duplications and Transfers. In Comparative Genomics; Springer: Berlin/Heidelberg, Germany, 2010; pp. 93–108. [Google Scholar]
- Bansal, M.S.; Alm, E.J.; Kellis, M. Efficient algorithms for the reconciliation problem with gene duplication, horizontal transfer and loss. Bioinformatics 2012, 28, i283–i291. [Google Scholar] [CrossRef] [PubMed]
- Ovadia, Y.; Fielder, D.; Conow, C.; Libeskind-Hadas, R. The Cophylogeny Reconstruction Problem Is NP-Complete. J. Comput. Biol. 2011, 18, 59–65. [Google Scholar] [CrossRef] [PubMed]
- Hallett, M.T.; Lagergren, J. Efficient Algorithms for Lateral Gene Transfer Problems. In Proceedings of the Fifth Annual International Conference on Computational Biology (RECOMB ’01), Montreal, QC, Canada, 22–25 April 2001; ACM: New York, NY, USA, 2001; pp. 149–156. [Google Scholar] [CrossRef]
- Hasić, D.; Tannier, E. Gene tree species tree reconciliation with gene conversion. J. Math. Biol. 2019, 78, 1981–2014. [Google Scholar] [CrossRef] [PubMed]
- Hasić, D.; Tannier, E. Gene tree reconciliation including transfers with replacement is NP-hard and FPT. J. Comb. Optim. 2019, 38, 502–544. [Google Scholar] [CrossRef]
- Maddison, W.P.; Knowles, L.L. Inferring Phylogeny Despite Incomplete Lineage Sorting. Syst. Biol. 2006, 55, 21–30. [Google Scholar] [CrossRef] [PubMed]
- Bork, D.; Cheng, R.; Wang, J.; Sung, J.; Libeskind-Hadas, R. On the computational complexity of the maximum parsimony reconciliation problem in the duplication-loss-coalescence model. Algorithms Mol. Biol. 2017, 12, 6:1–6:12. [Google Scholar] [CrossRef]
- Stolzer, M.; Lai, H.; Xu, M.; Sathaye, D.; Vernot, B.; Durand, D. Inferring duplications, losses, transfers and incomplete lineage sorting with nonbinary species trees. Bioinformatics 2012, 28, i409–i415. [Google Scholar] [CrossRef]
- ban Chan, Y.; Ranwez, V.; Scornavacca, C. Inferring incomplete lineage sorting, duplications, transfers and losses with reconciliations. J. Theor. Biol. 2017, 432, 1–13. [Google Scholar] [CrossRef]
- To, T.H.; Scornavacca, C. Efficient algorithms for reconciling gene trees and species networks via duplication and loss events. BMC Genom. 2015, 16, S6. [Google Scholar] [CrossRef]
- Bromham, L. The genome as a life-history character: why rate of molecular evolution varies between mammal species. Philos. Trans. R. Soc. B Biol. Sci. 2011, 366, 2503–2513. [Google Scholar] [CrossRef]
- Fitch, W.M. Toward Defining the Course of Evolution: Minimum Change for a Specific Tree Topology. Syst. Biol. 1971, 20, 406–416. [Google Scholar] [CrossRef]
- Jin, G.; Nakhleh, L.; Snir, S.; Tuller, T. Parsimony Score of Phylogenetic Networks: Hardness Results and a Linear-Time Heuristic. IEEE/ACM Trans. Comput. Biol. Bioinform. 2009, 6, 495–505. [Google Scholar] [CrossRef] [PubMed]
- Fischer, M.; van Iersel, L.; Kelk, S.; Scornavacca, C. On Computing the Maximum Parsimony Score of a Phylogenetic Network. SIAM J. Discret. Math. 2015, 29, 559–585. [Google Scholar] [CrossRef][Green Version]
- Kanj, I.A.; Nakhleh, L.; Than, C.; Xia, G. Seeing the trees and their branches in the network is hard. Theor. Comput. Sci. 2008, 401, 153–164. [Google Scholar] [CrossRef]
- Gambette, P.; Gunawan, A.D.; Labarre, A.; Vialette, S.; Zhang, L. Solving the tree containment problem in linear time for nearly stable phylogenetic networks. Discret. Appl. Math. 2018, 246, 62–79. [Google Scholar] [CrossRef]
- Fakcharoenphol, J.; Kumpijit, T.; Putwattana, A. A faster algorithm for the tree containment problem for binary nearly stable phylogenetic networks. In Proceedings of the 2015 12th International Joint Conference on Computer Science and Software Engineering (JCSSE), Songkhla, Thailand, 22–24 July 2015; pp. 337–342. [Google Scholar]
- Bordewich, M.; Semple, C. Reticulation-visible networks. Adv. Appl. Math. 2016, 78, 114–141. [Google Scholar] [CrossRef]
- Gunawan, A.D.; DasGupta, B.; Zhang, L. A decomposition theorem and two algorithms for reticulation-visible networks. Inf. Comput. 2017, 252, 161–175. [Google Scholar] [CrossRef]
- Van Iersel, L.; Semple, C.; Steel, M. Locating a tree in a phylogenetic network. Inf. Process. Lett. 2010, 110, 1037–1043. [Google Scholar] [CrossRef][Green Version]
- Gunawan, A.D.M. Solving the Tree Containment Problem for Reticulation-Visible Networks in Linear Time. In Algorithms for Computational Biology; Springer International Publishing: Cham, Switzerland, 2018; pp. 24–36. [Google Scholar]
- Weller, M. Linear-Time Tree Containment in Phylogenetic Networks. In Proceedings of the 16th International Conference on Comparative Genomics (RECOMB-CG 2018), Magog-Orford, QC, Canada, 9–12 October 2018; pp. 309–323. [Google Scholar] [CrossRef]
- Gunawan, A.D.; Lu, B.; Zhang, L. A program for verification of phylogenetic network models. Bioinformatics 2016, 32, i503–i510. [Google Scholar] [CrossRef][Green Version]
- Gambette, P.; van Iersel, L.; Kelk, S.; Pardi, F.; Scornavacca, C. Do Branch Lengths Help to Locate a Tree in a Phylogenetic Network? Bull. Math. Biol. 2016, 78, 1773–1795. [Google Scholar] [CrossRef]
- Huber, K.T.; van Iersel, L.; Janssen, R.; Jones, M.; Moulton, V.; Murakami, Y.; Semple, C. Rooting for phylogenetic networks. arXiv 2019, arXiv:1906.07430. [Google Scholar]



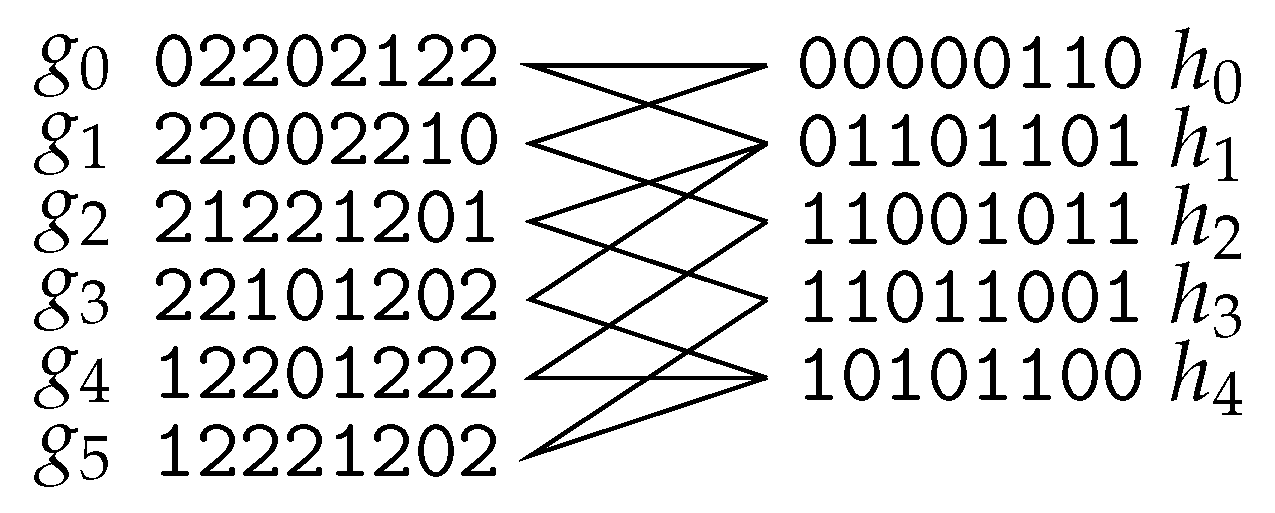



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bulteau, L.; Weller, M. Parameterized Algorithms in Bioinformatics: An Overview. Algorithms 2019, 12, 256. https://doi.org/10.3390/a12120256
Bulteau L, Weller M. Parameterized Algorithms in Bioinformatics: An Overview. Algorithms. 2019; 12(12):256. https://doi.org/10.3390/a12120256
Chicago/Turabian StyleBulteau, Laurent, and Mathias Weller. 2019. "Parameterized Algorithms in Bioinformatics: An Overview" Algorithms 12, no. 12: 256. https://doi.org/10.3390/a12120256
APA StyleBulteau, L., & Weller, M. (2019). Parameterized Algorithms in Bioinformatics: An Overview. Algorithms, 12(12), 256. https://doi.org/10.3390/a12120256




