A General Integrated Method for Design Analysis and Optimization of Missile Structure
Abstract
:1. Introduction
2. Theory
2.1. CST Parameterization Method
2.2. Augmented Fourier Series-Based Polynomial Surrogate Model
3. Design of Module
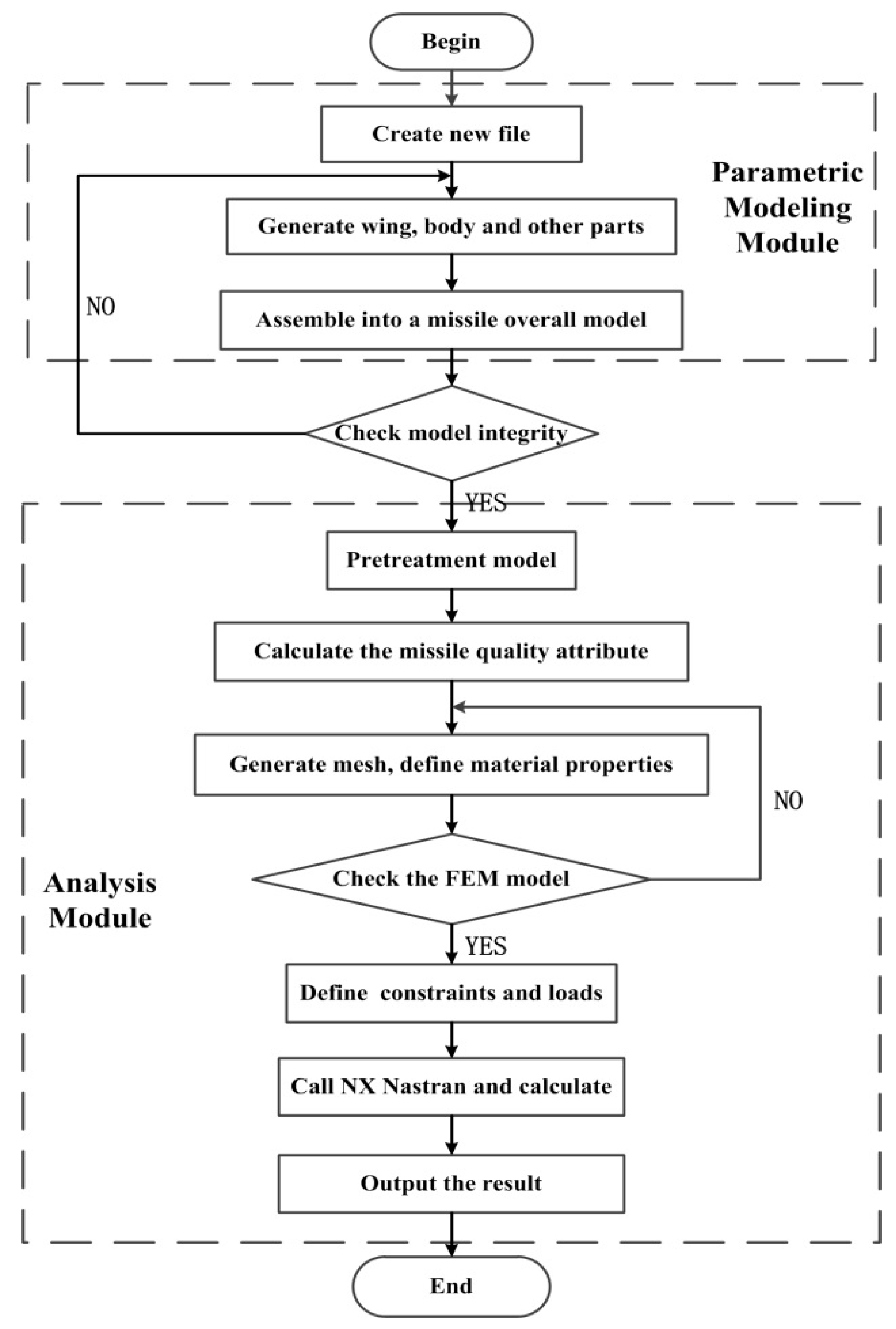
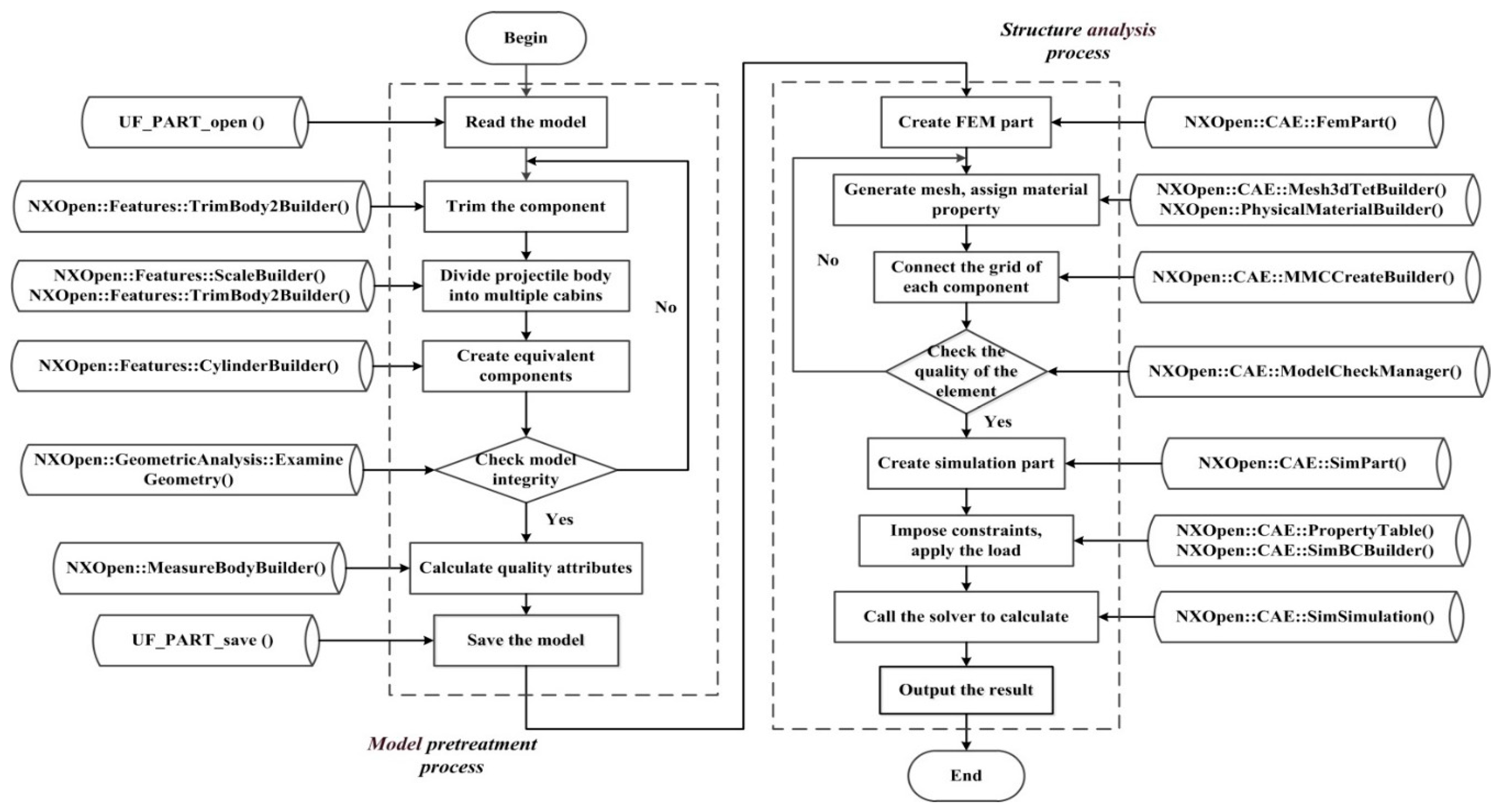
3.1. Design of Parametric Modeling Module
3.2. Design of Analysis Module
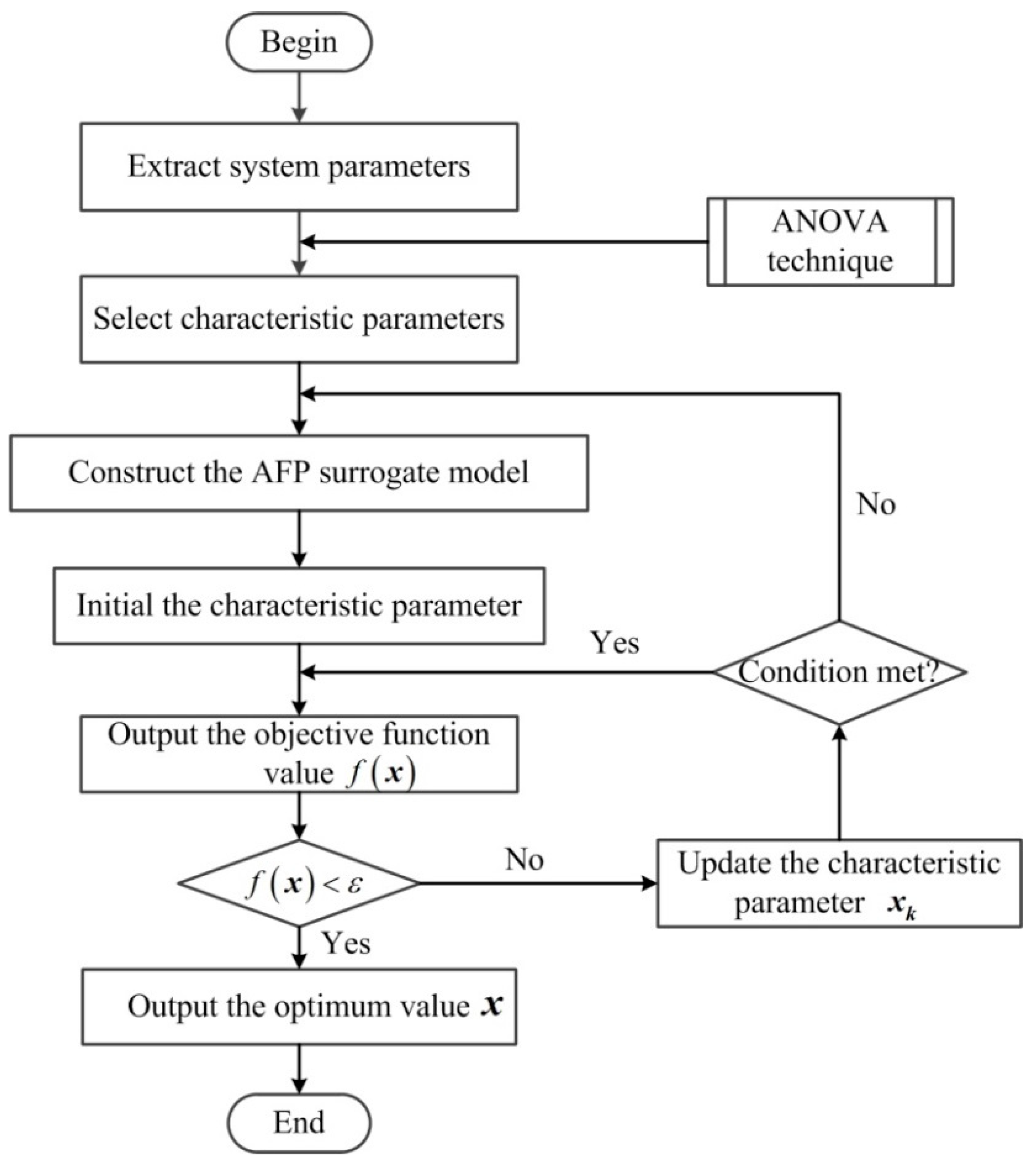
4. Optimation Strategy
5. Validation Examples
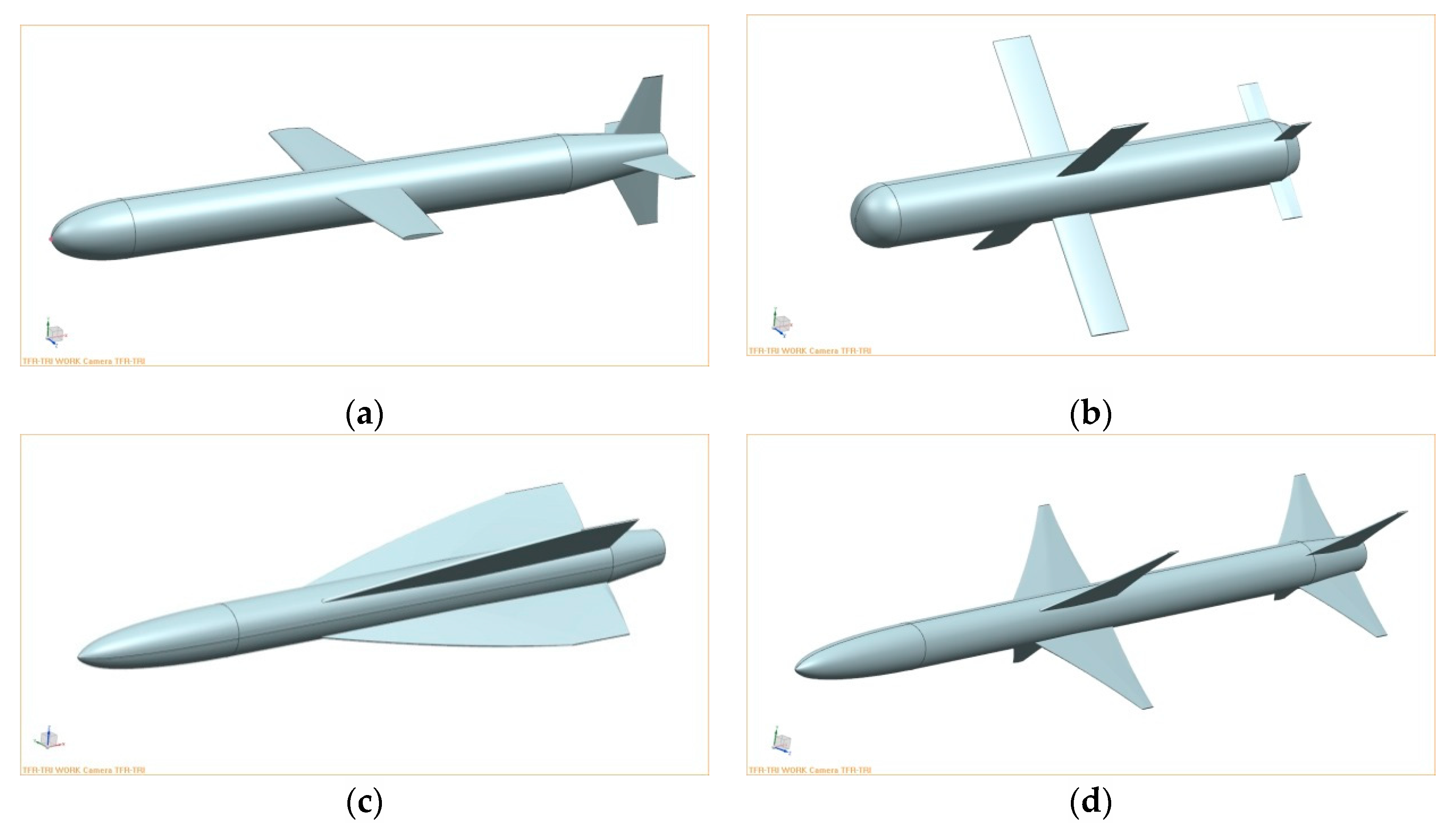
5.1. Parametric Modeling
5.2. Parametric Structure Analysis
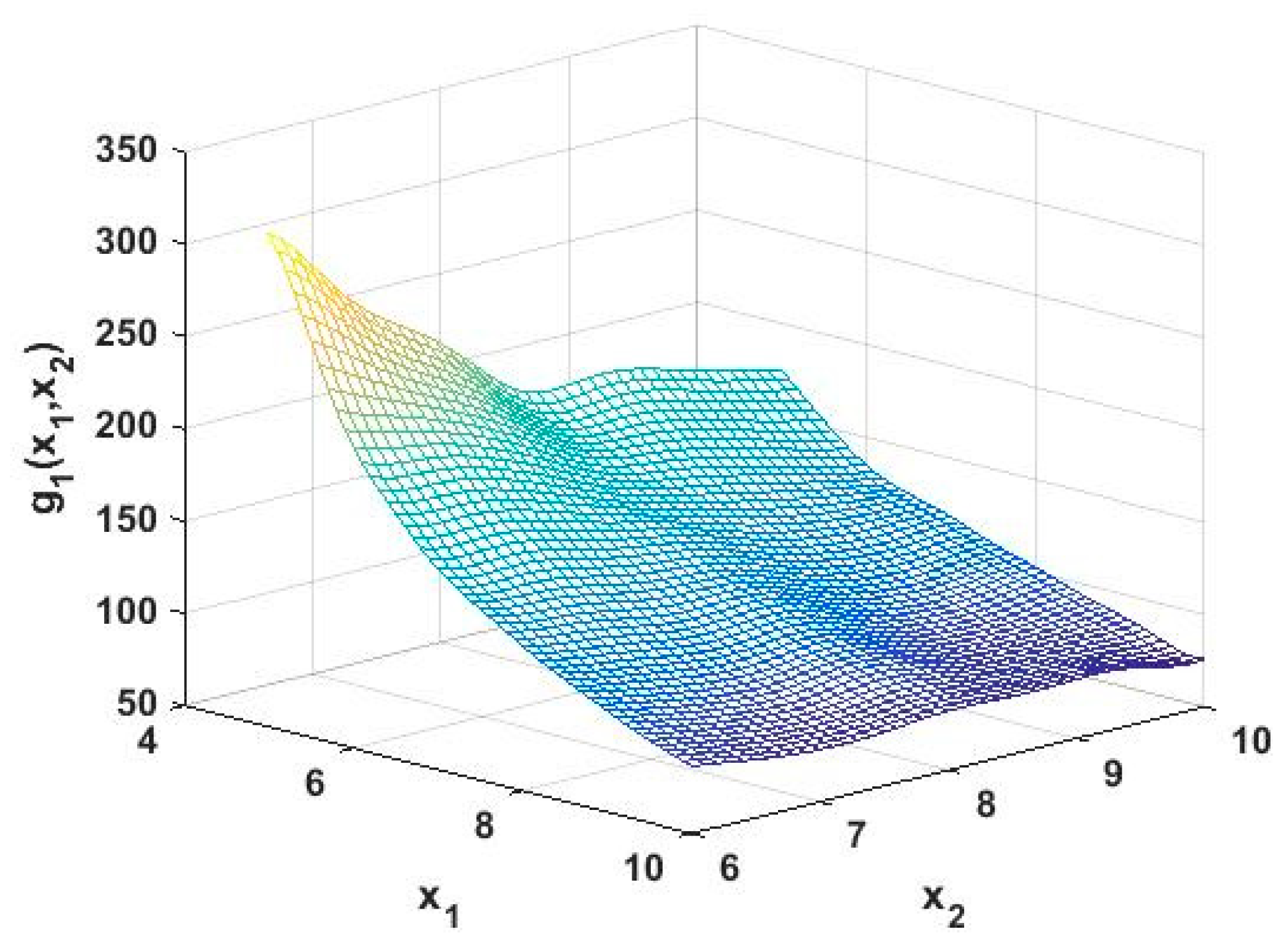
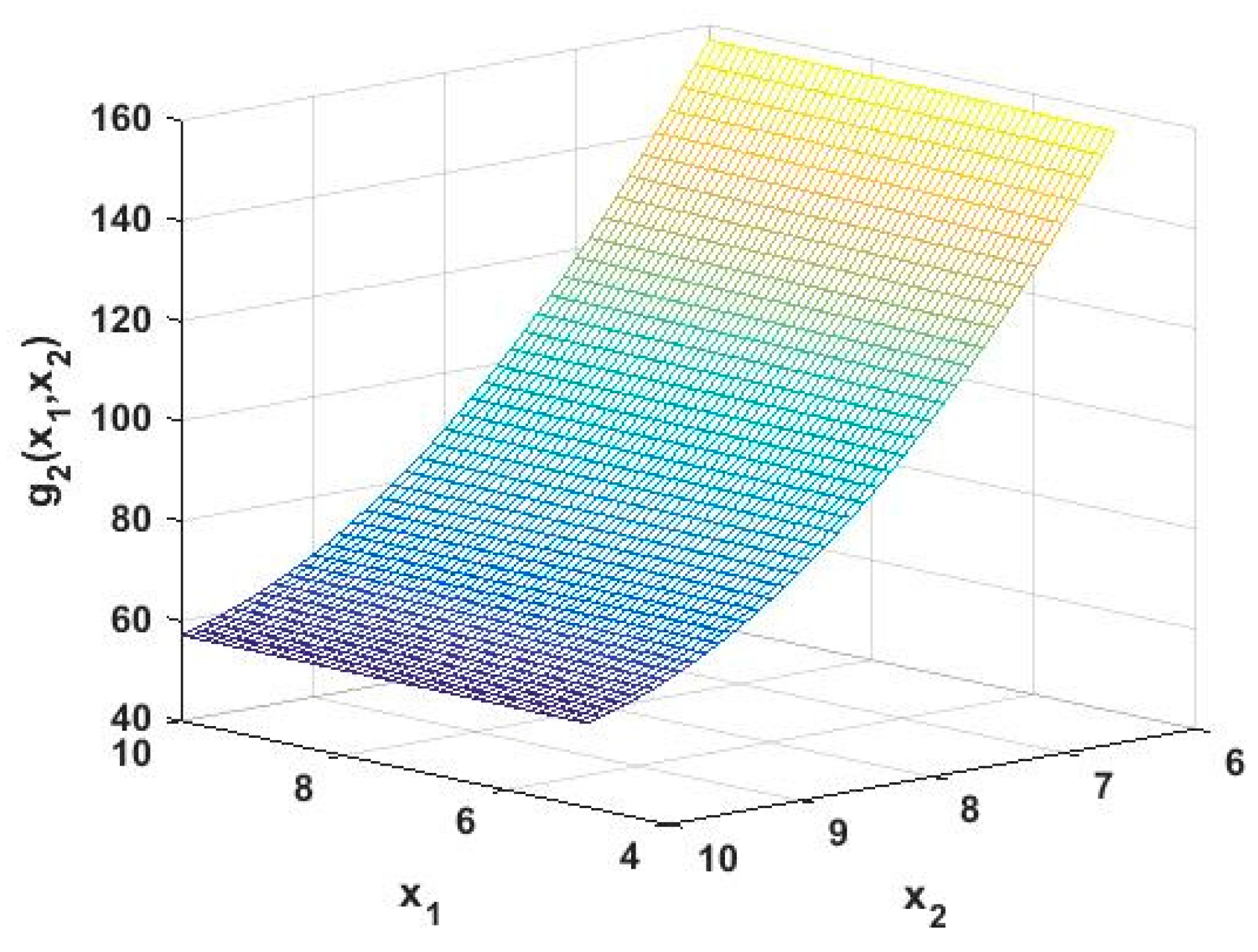
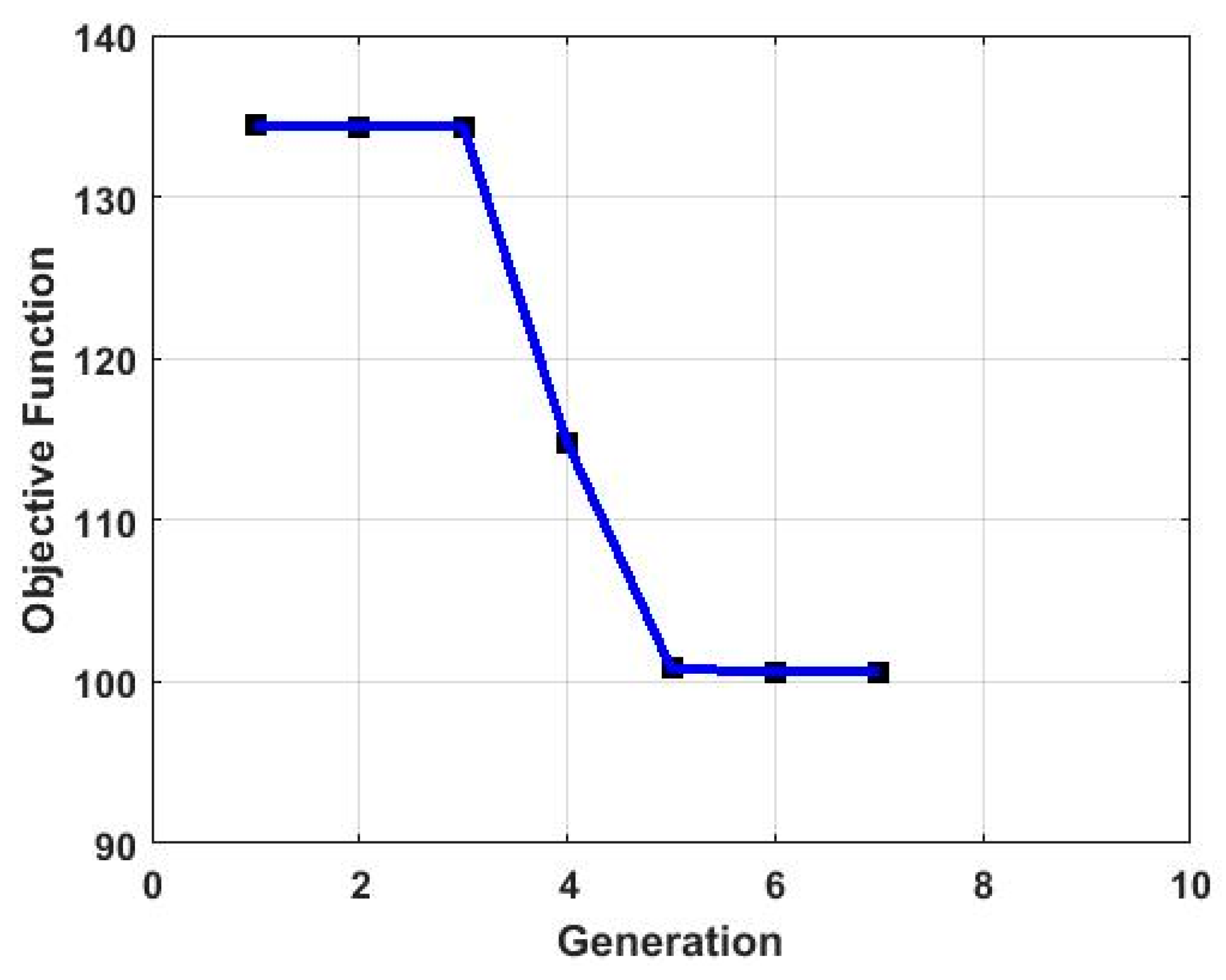
5.3. Structure Optimation
6. Conclusions
- (1)
- The CST parameterization methodology is derived, which can accurately model any airfoil in the entire design space with fewer variables;
- (2)
- The parametric modeling and analysis module of the missile is developed in C/C++ language on the basis of the CST parametric method and UG secondary development technology. Moreover, several various examples are presented to verify the validity and the versatility of this module;
- (3)
- By introducing a linear polynomial, a novel Augmented Fourier series-based polynomial surrogate model can be obtained. It can more accurately reflect the mathematical relationship between input and output data, which has the advantages of efficiency, transparency, and conceptual simplicity, especially for strong non-linear problems;
- (4)
- A novel surrogate model-based optimation strategy is designed to obtain a relatively light mass missile structure under the existing shape size, and satisfactory results are obtained when applied the structure optimation procedure to a missile example;
- (5)
- Compared with the traditional manual method, the parametric modeling and analysis method proposed in this paper can significantly improve the design efficiency of the missile, and shorten the design cycle, which provides a method with great value in engineering;
- (6)
- Subsequently, a comprehensive analysis platform of the missile can be established by using the parametric modeling module and the parametric analysis module developed in this paper, and other analysis modules, such as aerodynamic analysis module and stealth performance analysis module, which would provide a comprehensive method to realize the multidisciplinary optimization design of missiles.
Author Contributions
Funding
Conflicts of Interest
References
- Gu, L.X.; Wen, B.H. Missile General Design Principle; Xi’an Northwestern Polytechnical University Press: Xi’an, China, 2004. (In Chinese) [Google Scholar]
- Pegemanyfar, N.; Pfitzner, M.; Eggels, R.; Von Der Bank, R.; Zedda, M. Development of an Automated Preliminary Combustion Chamber Design Tool. In ASME Turbo Expo 2006: Power for Land, Sea, and Air; ASME GT2006-90430: 1-10; ASME: New York, NY, USA, 2006. [Google Scholar]
- Liu, X.K.; Zhu, X.C.; Du, Z.H. The blade design and automatic modeling of horizontal axis wind turbine. Energy Technol. 2010, 31, 155–158. (In Chinese) [Google Scholar]
- Wang, L.Y.; Huang, H.H.; Rae, W.W. Impeller modeling and analysis based on UG NX/KF and Fluent. J. Cent. South Univ. 2012, 19, 3430–3434. [Google Scholar] [CrossRef]
- He, Y.; Song, B.; Cao, Y. Structural optimization of an underwater glider with blended wing body. Adv. Mech. Eng. 2017, 9, 1–11. [Google Scholar] [CrossRef]
- Kulfan, B.M.; Bussoletti, J.E. Fundamental Parametric Geometry Representations for Aircraft Component Shapes. In Proceedings of the 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Portsmouth, VA, USA, 6–8 September 2006; p. 6948. [Google Scholar]
- Mousavi, A.; Castonguay, P.; Nadarajah, S.K. Survey of Shape Parameterization Techniques and its Effect on Three-Dimensional Aerodynamic Shape Optimization. In Proceedings of the AIAA 37th Fluid Dynamics Conference and Exhibit, Miami, FL, USA, 25–28 June 2007; p. 3837. [Google Scholar]
- Ceze, M.; Hayashi, M.; Volpe, E. A study of the CST parameterization characteristics. In Proceedings of the AIAA-2009-3767, San Antonio, TX, USA, 22–25 June 2009; p. 3767. [Google Scholar]
- Straathof, M.H.; Van Tooren, M.J.L. Extension to the class-Shape-Transformation method based on B-Splines. AIAA J. 2011, 49, 780–790. [Google Scholar] [CrossRef]
- Straathof, M.H.; Van Tooren, M.J.L. Development and Implementation of a Novel Parametrization Technique for Multidisciplinary Design Initialization. In Proceedings of the 51st AIAA Structures, Structural Dynamics, and Material Conference, Orlando, FL, USA, 12–15 April 2010; p. 3004. [Google Scholar]
- Vu, N.A.; Lee, J.W. Aerodynamic design optimization of helicopter rotor blades including airfoil shape for forward flight. Aerosp. Sci. Technol. 2015, 42, 106–117. [Google Scholar] [CrossRef]
- Iuliano, E. Global optimization of benchmark aerodynamic cases using physics-Based surrogate models. Aerosp. Sci. Technol. 2017, 67, 273–286. [Google Scholar] [CrossRef]
- Liu, X.Q.; He, W.L. Airfoil Optimization Design based on the Pivot Element Weighting Iterative Method. Algorithms 2018, 11, 163. [Google Scholar] [CrossRef]
- Wu, J.L.; Luo, Z.; Zhang, Y.Q.; Zhang, N. An interval uncertain optimization method for vehicle suspensions using Chebyshev metamodels. Appl. Math. Model. 2015, 38, 3706–3723. [Google Scholar] [CrossRef]
- Li, K.; Yu, Y.Y.; He, J.Y.; Lin, Y. An integrated beam-Plate structure multi-Level optimal design framework based on bi-Directional evolutionary structural optimization and surrogate model. Adv. Eng. Softw. 2018, 115, 230–247. [Google Scholar] [CrossRef]
- Zeng, W.; Ren, T.; Yu, L.J.; Huang, J.J. Design optimization of a VX gasket structure for a subsea connector based on the kriging surrogate model-NSGA-II algorithm considering the load randomness. Algorithms 2019, 12, 42. [Google Scholar] [CrossRef]
- Li, T.Z.; Yang, X.L. An efficient uniform design for Kriging-Based response surface method and its application. Comput. Geotech. 2019, 109, 12–22. [Google Scholar] [CrossRef]
- Wang, X.; Cai, J.S.; Qu, K.; Liu, C.Z. Airfoil optimization based on improved CST parametric method and transition mode. Acta Aeronaut. Astronaut. Sin. 2015, 36, 449–461. (In Chinese) [Google Scholar]
- Wang, X.G.; He, W.L.; Zhao, L.G. Novel Interval Parameter Identification Method Using Augmented Fourier Series-Based Polynomial Surrogate Model. IEEE Access 2019, 7, 70862–70875. [Google Scholar]
- Wang, R.H. Numerical Approximation; Higher Education Press: Beijing, China, 2012. [Google Scholar]
- Liu, Z.Z.; Wang, T.S.; Liu, J.F. A trigonometric interval method for dynamic response analysis of uncertain nonlinear systems. Sci. China Phys. Mech. Astron. 2015, 58, 1–13. [Google Scholar] [CrossRef]
- Fang, H.B.; Horstemeyer, M.F. Global response approximation with radial basis functions. Eng. Optim. 2006, 38, 407–424. [Google Scholar] [CrossRef]
- Fleeman, E.L. Tactical Missile Design; American Institute of Aeronautics and Astronautics Press: Heathrow, FL, USA, 2001. [Google Scholar]
- Dong, Z.W.; Tian, L.Z.; Fu, Y.L. UG/Open API Programming Basis; Tsinghua University Press: Beijing, China, 2002; pp. 191–245. (In Chinese) [Google Scholar]
- Zheng, L.; Dong, Y.; He, J.Z. C++ Programming Language; Tsinghua University Press: Beijing, China, 2010. (In Chinese) [Google Scholar]
- Deng, Z.M.; Guo, Z.P.; Zhang, X.J. Interval model updating using perturbation method and radius basis function neural networks. Mech. Syst. Signal. Process. 2017, 84, 699–716. [Google Scholar] [CrossRef]
- Lei, X.S.; Shuang, J.J.; Yang, P.; Liu, Y.W. Parametric study and optimization of dimpled tubes based on Response Surface Methodology and desirability approach. Int. J. Heat Mass Transf. 2019, 142, 118453. [Google Scholar] [CrossRef]
- Jiang, M.L.; Liu, L. Lightweight Parametric Geometry Modeling for Missile Based on Open CASCADE. J. Proj. Rocket. Missiles Guid. 2015, 35, 1–9. (In Chinese) [Google Scholar]
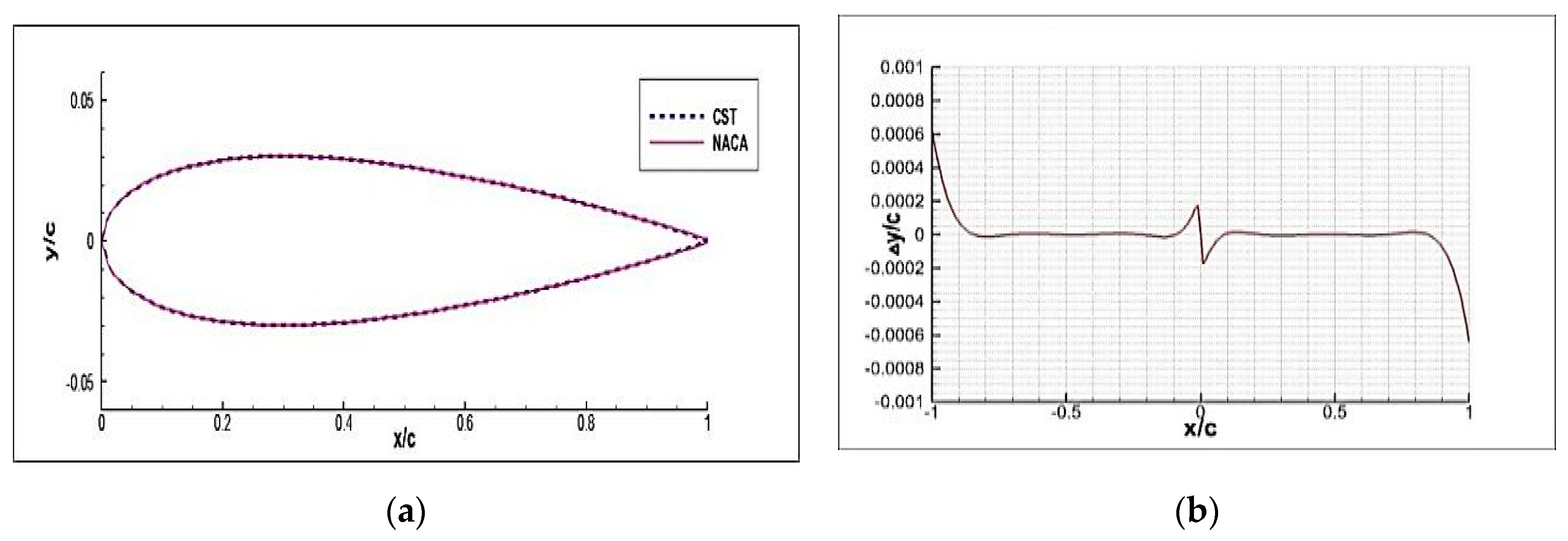
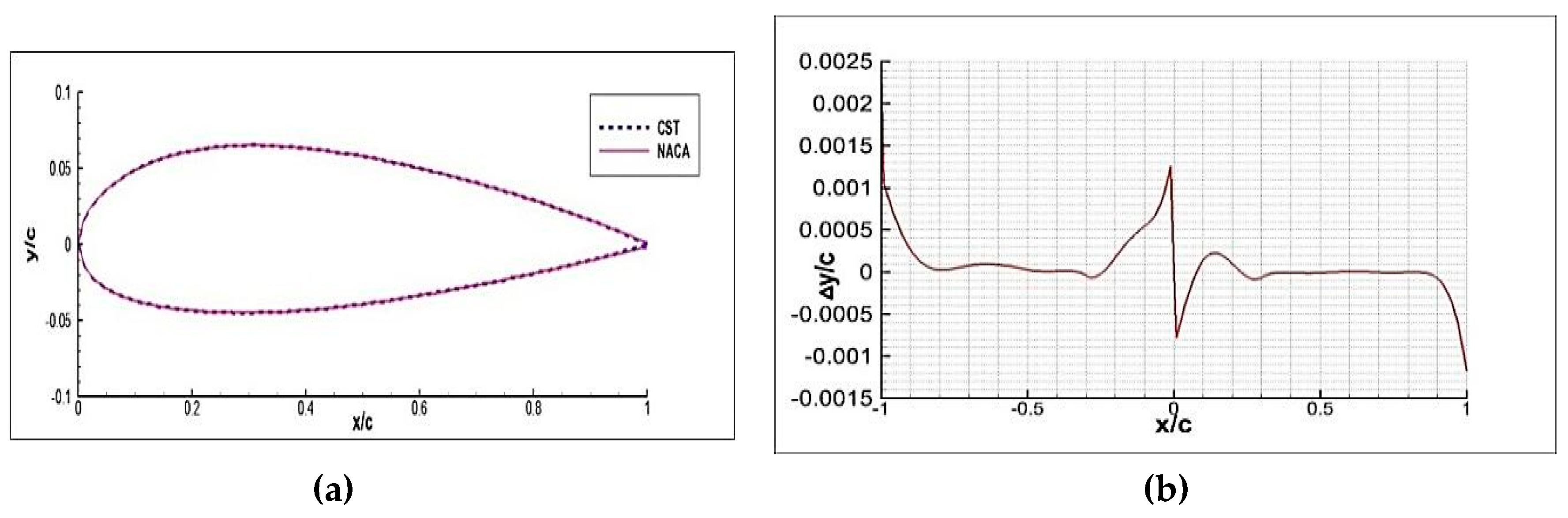





| Part | Parameter Names | Variables | Part | Parameter Names | Variables |
|---|---|---|---|---|---|
| Body | Total Length | Len | Wing | Wingroot Shape | Swroot[ ] |
| Nose Fineness Ratio | Rnd | Wingtip Shape | Swtip[ ] | ||
| Nose Length | Lnose | Sweep Angle | Awsweep | ||
| Boattail Length | Ltail | Wingspan | Lwspan | ||
| Nose Shape | Snose[ ] | Wing Position | Pwing[ ] | ||
| Projectile Body Shape | Spb_1[ ] | Installation Angle | Ains | ||
| Boattail Shape | Stail[ ] | Number of Wings | Nass |
| Part | Parameter | Variables | Part | Parameter | Variables |
|---|---|---|---|---|---|
| Cabin | Number | Num_C | Wing | Type | Type |
| position | Pos_C[ ] | Size | Siz_W | ||
| thickness | Thick | Material property | Mat_W[ ] | ||
| length | Len | Number | Num_W | ||
| Material | Mat_E[ ] | Loads | Position | Pos_L[ ] | |
| Components | Position | Pos_E[ ] | Magnitude | Mag | |
| Size | Size_E[ ] | Direction | Dir[ ] |
| Objects | Modeling Process | Analysis Process |
|---|---|---|
| Traditional manual | 1 h | 2 h |
| Parametric method | 20 s | 100 s |
| Saving time | 99.44% | 98.61% |
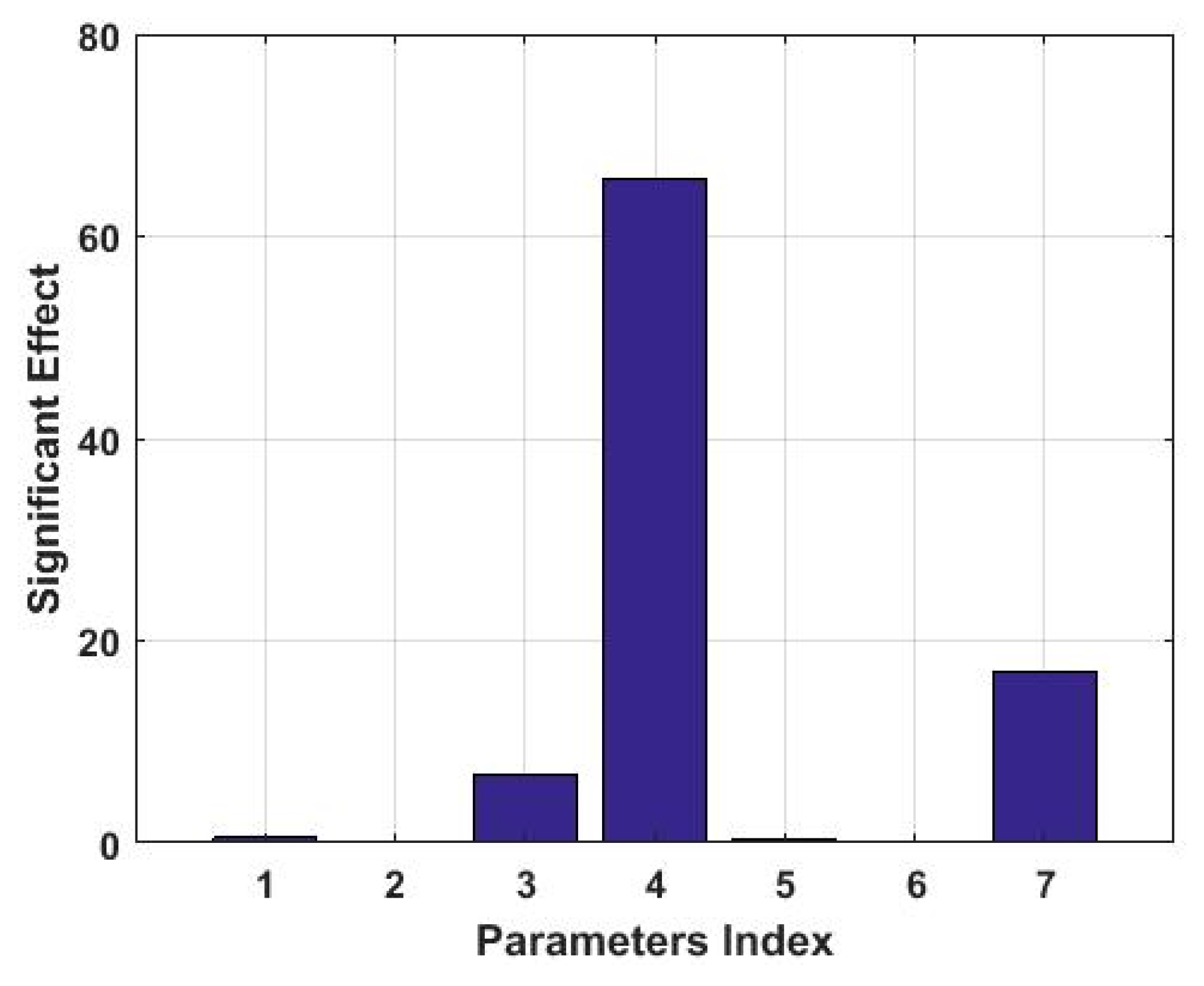
| Index | Parameter | Description |
|---|---|---|
| 1 | t1 | Thickness of cabin 1 |
| 2 | t2 | Thickness of cabin 2 |
| 3 | t3 | Thickness of cabin 3 |
| 4 | t4 | Thickness of cabin 4 |
| 5 | t5 | Thickness of cabin 5 |
| 6 | t6 | Thickness of cabin 6 |
| 7 | t7 | Thickness of wing |
| Objects | Optimum Value |
|---|---|
| Thickness of cabin 4 (mm) | 7.96 |
| Thickness of wing (mm) | 6.94 |
| Weight (kg) | 100.58 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Yang, J.; Guo, J.; Guo, J. A General Integrated Method for Design Analysis and Optimization of Missile Structure. Algorithms 2019, 12, 257. https://doi.org/10.3390/a12120257
Wang X, Yang J, Guo J, Guo J. A General Integrated Method for Design Analysis and Optimization of Missile Structure. Algorithms. 2019; 12(12):257. https://doi.org/10.3390/a12120257
Chicago/Turabian StyleWang, Xiaoguang, Jun Yang, Jian Guo, and Jun Guo. 2019. "A General Integrated Method for Design Analysis and Optimization of Missile Structure" Algorithms 12, no. 12: 257. https://doi.org/10.3390/a12120257
APA StyleWang, X., Yang, J., Guo, J., & Guo, J. (2019). A General Integrated Method for Design Analysis and Optimization of Missile Structure. Algorithms, 12(12), 257. https://doi.org/10.3390/a12120257





