An Improved Genetic Algorithm with Adaptive Variable Neighborhood Search for FJSP

Abstract

For solving the complex flexible job-shop scheduling problem, an improved genetic algorithm with adaptive variable neighborhood search (IGA-AVNS) is proposed. The improved genetic algorithm first uses a hybrid method combining operation sequence (OS) random selection with machine assignment (MA) hybrid method selection to generate the initial population, and it then groups the population. Each group uses an improved genetic operation for global search, then the better solutions from each group are stored in the elite library, and finally, the adaptive local neighborhood search is used in the elite library for detailed local searches. The simulation experiments are carried out by three sets of international standard examples. The experimental results show that the IGA-AVNS algorithm is an effective algorithm for solving flexible job-shop scheduling problems.

1. Introduction

Along with the rapid development of modern manufacturing, science, and technology, consumers’ demands are becoming more and more personalized and customized. The production mode of the manufacturing companies is gradually shifting from continuous, large quantity production to multi-variety and small quantity production. The flexible job-shop scheduling problem (FJSP) embodies the flexibility of production, that is, the different operations of each job in FJSP can be processed on different machines with different processing times. The job can select the machine according to the actual situation, such as workload and the idle state of the machine. It is more suitable for actual production practice activities and has certain theoretical and practical value for its research.

The FJSP problem was first proposed by Bruker and Schile in 1990. In recent years, many scholars have achieved certain results in solving the FJSP problem. Huang et al. [1] proposed the method of combining multi-objective particle swarm optimization and variable neighborhood search to solve the FJSP problem effectively. Ning et al. [2] proposed an improved quantum genetic algorithm based on the earliness/tardiness penalty coefficient. The double penalty coefficient is designed in the algorithm, and a double-chain coding method was proposed. At last, the standard example demonstrates the effectiveness of the algorithm. Vilcot et al. [3] used a combination of tabu search (TS) and genetic algorithm (GA) to optimize the two goals of maximum completion time and cost reduction. A hybrid non-dominated sorting simulated annealing algorithm for FJSP was proposed by Shivasankaran et al. [4], in which critical or incapable machines were eliminated by non-dominated sorting for all operations and simulated annealing was used to search for an optimal solution. Nouri et al. [5] solve the flexible job-shop problem with a multi-agent model based on mixed-element heuristics. Zhao et al. [6] proposed a bilevel neighborhood search hybrid algorithm to solve FJSP, which achieved remarkable results. Driss et al. [7] proposed a new genetic algorithm (NGA) for FJSP, which used a new chromosome representation and different crossover and mutation strategies and obtained better experimental results.

Chang et al. [8] proposed a hybrid genetic algorithm (HGA), which used the Taguchi method to optimize the parameters of the genetic algorithm, and in the paper, a novel coding mechanism was proposed to solve the problem of invalid work assignment. Yi et al. [9] proposed an effective memetic algorithm (MA), which combines the local search ability of TS with the global search capability of GA to provide an effective way to "explore" and "exploit." Wang et al. [10] developed a hybrid evolutionary algorithm (HEA), which proposed a new operator based on the average Hamming distance to maintain population diversity, adopted different crossover and mutation strategies, and introduced the critical path theory and local search process of the preferred strategy to improve the convergence speed. Li et al. [11] proposed an efficient hybrid algorithm (HA), which combines the genetic algorithm (GA) and tabu search (TS), and this algorithm uses TS with a good local search ability to mine, which balances the intensity and diversity of the scheduling.

In view of these, this paper proposes an improved genetic algorithm with an adaptive variable neighborhood search (IGA-AVNS) for solving FJSP. Genetic algorithm (GA) is characterized by parallelism, adaptiveness, and self-learning, whose principle is simple, robust, versatile, has good global search performance, and can quickly find most solutions in the solution space. However, a single GA has a poor local search capability, so the entire search process is time-consuming and the efficiency of the algorithm is not high. However, variable neighborhood search (VNS) [12,13,14] can make up for the above defects and has a strong local search ability. Variable neighborhood search (VNS) escapes from local optimization by searching for systematic changes in the neighborhood structure.

First, divide the entire initial population into a series of subpopulations and optimize each subpopulation with improved GA. Then the optimization results of each subpopulation form elite populations and the adaptive local neighborhood search algorithm is used in the elite population for accurate local search. In this paper, three neighborhood structures are designed to generate the neighborhood solution and the three neighborhood structures are selected adaptively, that is, the neighborhood with the best search effect is adaptively selected for searching, which greatly reduces the search time and improves search efficiency. This makes full use of the characteristics of GA and VNS search, which not only increases the diversity of the population and prevents the loss of the optimal solution, but also accelerates the convergence speed and improves the efficiency of the algorithm.

The paper provides the following contributions:

(1) The initial population is generated by the hybrid method, namely 60% global selection by operation (GSO), 20% tournament selection, and 20% random selection. When the GSO is selected, the machine with the lowest global load is selected in the optional machine set to process, the workload of the machine is reduced as much as possible, the optimization time is shortened, and the quality of the initial solution is guaranteed. The tournament selection and the random selection increase the diversity of the population and prevent the loss of the optimal solution. The combination of the three methods to generate the initial population greatly improves the quality of the solution and the speed of obtaining the optimal solution.

(2) In the crossover process of the improved genetic algorithm, the operation sequence (OS) adopts the precedence operation crossover (POX) and the improved uniform crossover, and the MA adopts the single-point crossover. This operation not only ensures the rapid improvement of the search ability, but also ensures that the generated solution is always feasible; the late mutation of the genetic algorithm increases the diversity of the population, enhances the local search ability of the algorithm, and prevents the algorithm from falling into immature convergence.

(3) Adaptive neighborhood search is used for the optimal solution in the elite library. The three neighborhood structures proposed in this paper are selected adaptively according to the search effect of different neighborhood structures, so that VNS can adaptively select better neighborhood types according to the search performance of each neighborhood, instead of using the fixed neighborhood search, which effectively promotes the competition between neighborhoods, makes the neighborhood method with better search performance have a higher probability for further search, thereby improving the search efficiency and search quality of the algorithm.

(4) Introduce an elite library to store the best individuals. It prevents the loss of the optimal solution during evolution.

The rest of this article is organized as follows: Section 2 introduces the FJSP data model, and Section 3 describes the overall flow of the IGA-AVNS algorithm. Section 4 introduces the detailed implementation of the IGA-AVNS algorithm including encoding and decoding, the generation of initial solutions, improved genetic operations, and adaptive variable neighborhood search. Section 5 shows the results of computational studies using the IGA-AVNS algorithm and its comparisons with other algorithms. Section 6 is the conclusion and direction of future research.

2. Mathematical Model of FJSP

A FJSP problem can be described as follows:

There are n jobs J = ($J_1$, $J_2$, …, $J_n$), which are processed on m different machines M = ($M_1$, $M_2$, …, $M_m$). Each job $J_i$ contains $n_i$ non-preemptable ordered operations, expressed as the operation set $O_i$= {$O_{i,1}, O_{i,2}, \dots , O_{i,n_i}$}. L is the total number of operations of all jobs. Each operation $O_{i,j}$ selects the machine to be processed from a set of available machines (this paper studies the partial FJSP (P-FJSP), machine set $M_{i,j}\in M$. If it is a total FJSP (T-FJSP), the machine set $M_{i,j}$ = $M$). The processing time of the operation on different machines $t_{i,j,k}$ (1 ≤ i ≤ n, 1 ≤ j ≤ n_i, 1 ≤ k ≤ m) is predefined. The optimization goal of FJSP is to select the machine M_k from the machine set M_i,j for each operation O_i,j, and determine the start time st_i,j and completion time ft_i,j of each operation, and minimize the completion time of all machines, see the Equation (1).

$$f=\min ({\displaystyle \sum }_{i=1}^n\max (f{t}_{i,n_i}))$$

(1)

FJSP processing also satisfies the following constraints and assumptions (5 and 6 are assumptions):

• All machines are available at time 0, and each operation can be processed at time 0;
• At a certain time, one operation can only be processed by one machine at a time. Once the operation is completed, the machine can be used in other operations;
• Once the processing begins, it cannot be interrupted;
• There are no successive constraints on the operations of different jobs, and there are successive constraints between the operations of the same job;
• The setting time of the machine and the transportation time of the operation are negligible;
• There are no emergencies (such as machine failures, new orders, etc.).

3. Flow of the IGA-AVNS

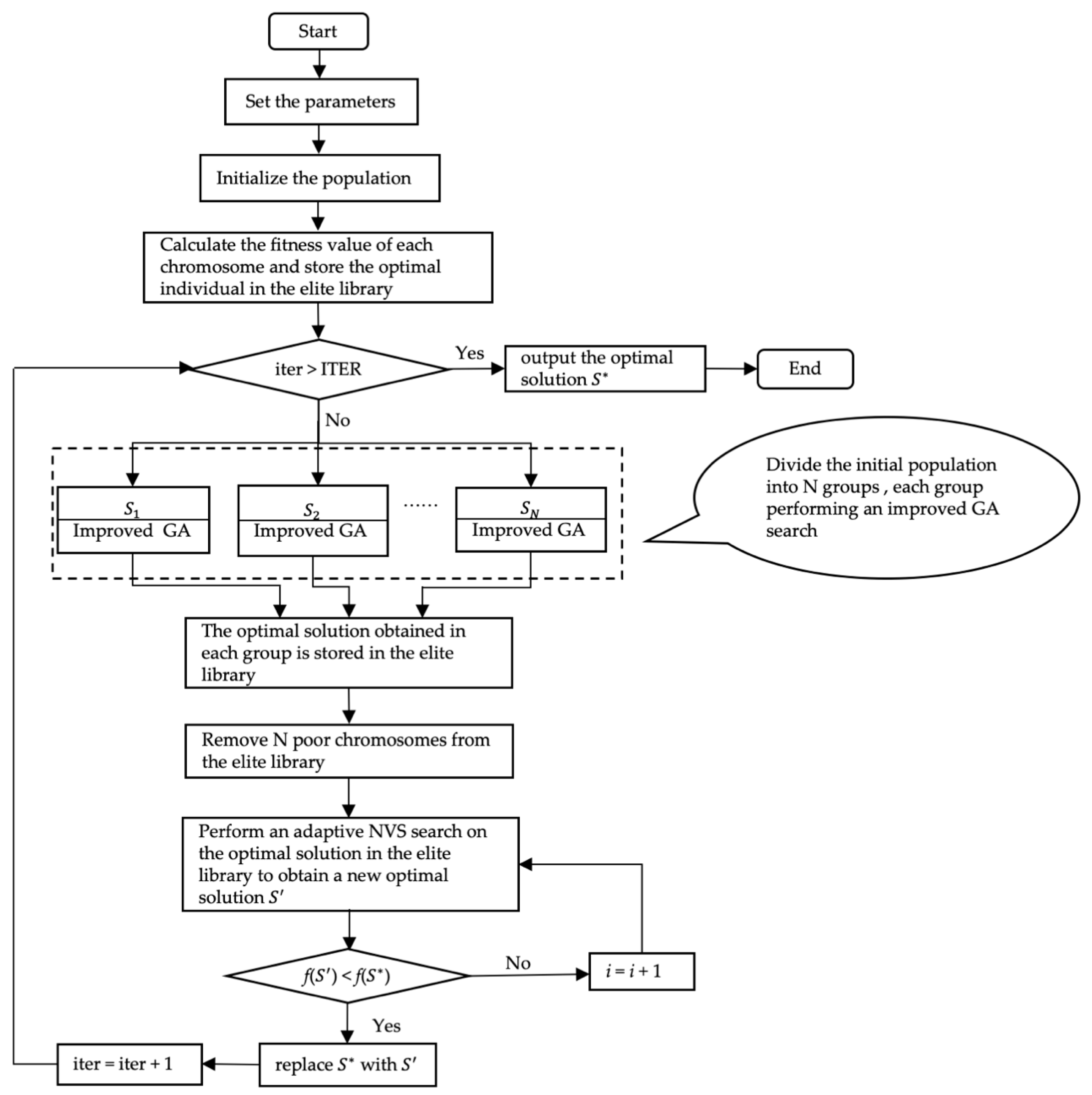
Based on the strong global search ability of the genetic algorithm, the strong local search ability of the variable neighborhood search, and the characteristics of the FJSP problem, an improved genetic algorithm (IGA-AVNS) with an adaptive variable neighborhood search is proposed. The operation steps are as follows. The flow chart is shown in Figure 1.

Step 1: Set the parameters—total iteration number ITER, population size POPSIZE, crossover probability $P_c$, mutation probability $P_m$, etc.;

Step 2: Initialize the population using the method in Section 4.2, generate POPSIZE chromosomes, evaluate the fitness values of all the individuals, and store the optimal individuals in the elite library, set the number of cycles—iter = 0;

Step 3: Determine whether the termination criterion (iter > ITER) is satisfied, and if so, output the optimal solution, $S^{*}$, otherwise go to Step 4;

Step 4: Divide the initial population into N subordinate groups, $S_i$ (i = 1, 2, ..., N), and N is generally taken as $\frac{POPSIZE}{10}$. In each $S_i$, genetic operations (selection, crossover, and mutation) are performed according to Section 4.3. Evaluate the fitness value of each individual in $S_i$, save the best individual in each $S_i$ into the elite library, and replace the original N poor solutions of the elite library;

Step 5: Select the optimal chromosome in the elite library, and do the neighborhood search according to Section 4.4 to get the new optimal solution $S^{\prime }$; if f($S^{\prime }$) < f($S^{*}$), replace $S^{*}$ with $S^{\prime }$, iter = iter + 1, otherwise, $S^{*}$ remains unchanged, and go to Step 3.

4. IGA-AVNS

4.1. Encoding and Decoding

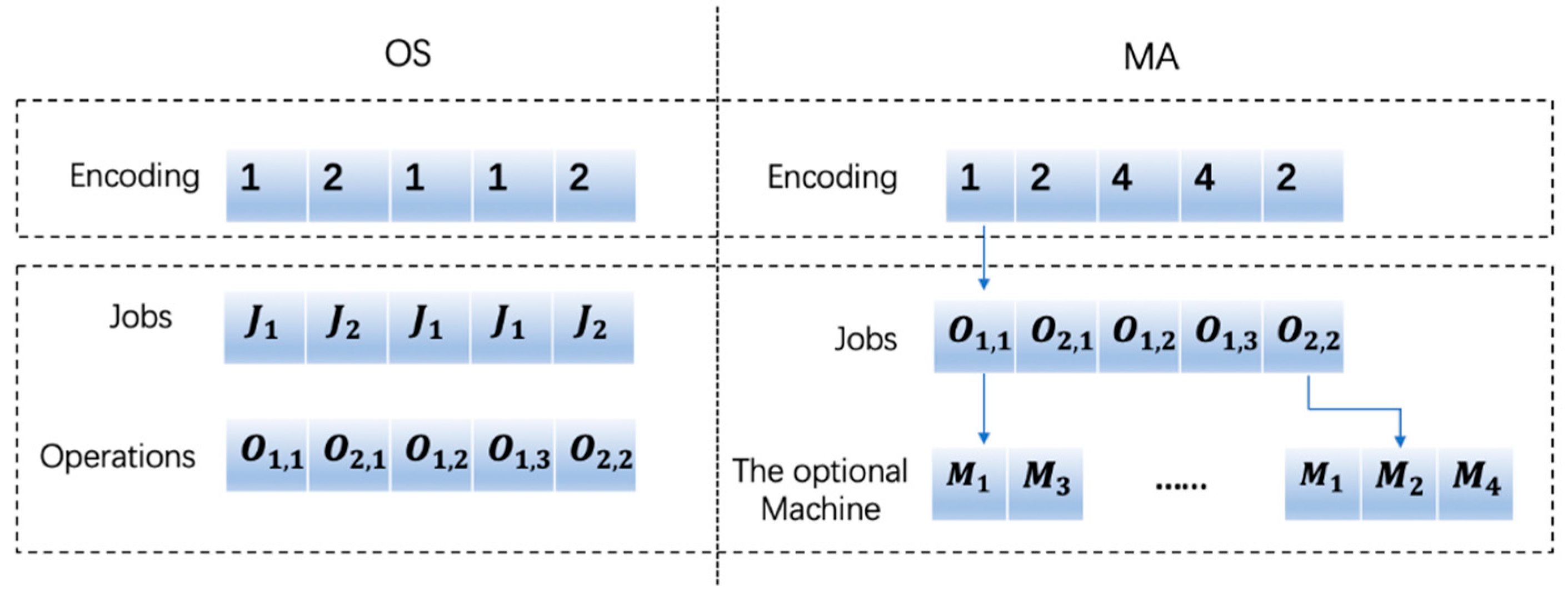
Each solution of FJSP consists of two parts [15]: one is to sort the operations assigned on the machine, that is, the operation sequence (OS); the other is to assign each operation to a machine set, that is, machine assignment (MA), which means that the algorithm assigns each operation to the corresponding machine and calculates its start time and end time. The number in the sequence OS is the operation index. The order in which each job j appears in the OS represents the processing order of each operation of the job. See the OS of the chromosome in Figure 2: 1 2 1 1 2. The first 1 represents the operation ${\mathrm{O}}_{1,1}$ the job $J_1$, the first 2 represents the first operation $O_{2,1}$ of the job $J_2$, the second 1 represents the second operation $O_{1,2}$ of the job $J_1$, and so on. The processing order of each operation of this chromosome is:

$${\mathrm{O}}_{1,1}\to O_{2,1}\to O_{1,2}\to O_{1,3}\to O_{2,2}$$

The number in the MA is the machine number. Each number indicates the machine number of the corresponding operation selected in the optional machine set. See Figure 2, where the first 1 in the figure indicates the processing machine number of the corresponding operation $O_{1,1}$ in the optional machine M = {$M_1$, $M_3$}, that is, $M_1$. MA and OS have the same length, which is equal to the sum of the operations of all the jobs, that is, L, and the length of the chromosome is 2L.

Table 1. Processing time on the 2 × 4 problem.

Jobs	Operation	${\mathit{M}}_1$	${\mathit{M}}_2$	${\mathit{M}}_3$	${\mathit{M}}_4$
$J_1$	$O_{1,1}$	2	999	3	999
	$O_{1,2}$	5	999	999	2
	$O_{1,3}$	999	3	4	1
$J_2$	$O_{2,1}$	7	3	9	999
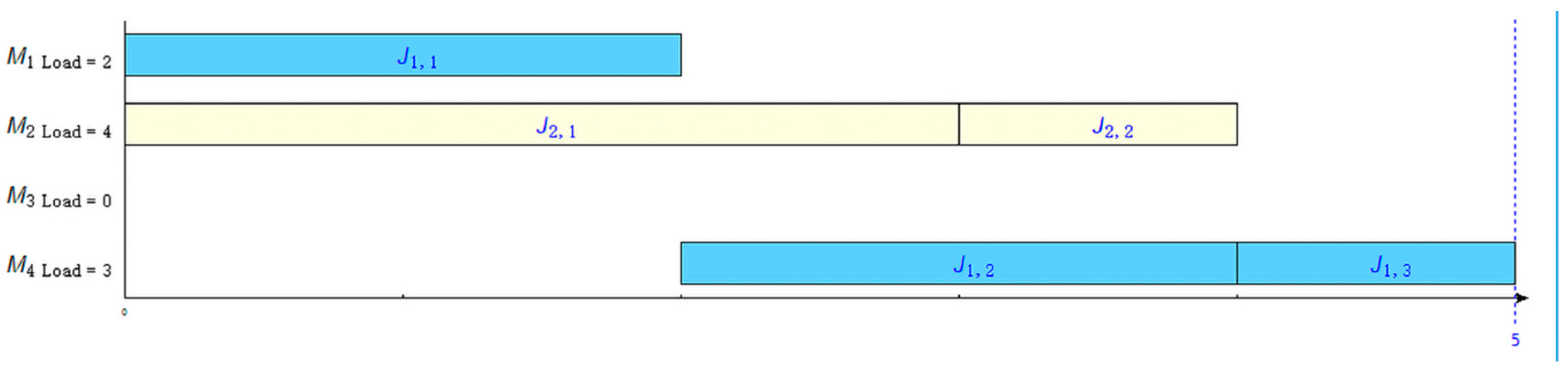
	$O_{2,2}$	3	1	999	6

is the processing schedule for the 2 × 4 problem, and Figure 3 is the Gantt chart for solving the problem.

Decoding is the process of converting a chromosome code into feasible scheduling. The steps are as follows:

Step 1: Read each gene of the OS and convert it to the corresponding operation $O_{i,j}$;

Step 2: Read each gene on the MA, obtain the processing machine number $M_k$ corresponding to each operation, and obtain the processing time $t_{i,j,k}$ of each operation from the processing time matrix;

Step 2.1: If the operation $O_{i,j}$ is the first operation of the job i, process directly from the zero time on the machine $M_k$; if the process $O_{i,j}$ is the first operation of the machine $M_k$, process from the end time of the previous operation $O_{i-1,j}$ on the machine, $M_k$. Otherwise, find the idle interval period [$S_t$,$E_t$] of the machine $M_k$, in which $S_t$ represents the start time of the time interval, and $E_t$ represents the end time of the time interval. Equation (2) obtains the earliest processing time $ES{T}_1$ of the operation $O_{i,j}$;

Step 2.2: Determine whether the appropriate idle interval to process the current operation $O_{i,j}$ is found according to (3), and if yes, insert $O_{i,j}$ into the current time period, otherwise process the machine $M_k$ at the earliest processing time of $ES{T}_2$ obtained according to Equation (4);

Step 3: Update the processing information of each machine;

Step 4: Determine whether all the genes of the chromosome are decoded, and if yes, end, otherwise, go to Step 2.

$$ES{T}_1=\max \left\{f{t}_{i\left(j-1\right)},S_t\right\}$$

(2)

$$ES{T}_1+t_{i,j,k}\le E_t$$

(3)

$$ES{T}_2=\max \left\{f{t}_{i\left(j-1\right)},E_k\right\}$$

(4)

$f{t}_{i\left(j-1\right)}$ is the processing completion time of the operation $O_{i,j-1}$; $S_{ijk}$ is the starting time of the operation $O_{ij}$ on the machine $M_k$, and $E_{ijk}$ is the ending time of the operation $O_{ij}$ on the machine $M_k$, $E_k$ is the completion time of the last operation on the machine $M_k$.

4.2. Population Initialization

The quality of the initial population often affects the convergence speed of the algorithm. It is both a hope for obtaining the global optimal solution and a wide diversity for the population. To some extent, the initial population usually affects the performance of the algorithm. Generating high-quality initial populations is often the key to an algorithm’s success. The initialization process of FJSP includes operation sequence and the machine assignment. Kacem et al. [16] first proposed the method of initializing the population (approach by localization, AL) and Pezzella et al. [17] used three scheduling rules to initialize the operation sequence. A method for GLR (global search, local search and random search) machine selection was proposed in [18,19], which combines three methods of global selection (GS), local selection (LS), and random selection (RS). This paper tries to select the machine with the shortest processing time in the selection stage. It not only considers the workload balance of the machine but also increases the diversity of the population by adding random selection. The experiment proves that it has achieved good results. But the method is to start from the first job, which increases the search time. Based on the above literature research, this paper proposes a method combining OS random selection with MA hybrid method selection. The MA selection refers to the method by which an operation selects machines in its optional machine set. The scheduling generated in this way is feasible. The special steps are as follows:

(1) Random selection: random generation;

(2) Tournament selection: First a certain number of individuals are taken out of the population and then the best one is selected to enter as the offspring population. The specific steps are as follows:

Step 1: Determine the number of individuals selected each time, generally two individuals.

Step 2: Select an individual randomly from the population (each subject has the same probability of inclusion) to form a group, and select the individual with the best fitness value to enter the progeny population according to the fitness value of each individual.

Step 3: Repeat Step 2, and the resulting individuals constitute a new generation population.

(3) Global selection by operation (GSO): Since the OS is randomly coded, each gene in the MA is a processing machine selected for the process in the OS. So our goal is to select the machine with the lowest global load for processing in the optional machine set. The specific steps are as follows:

Step 1: Define a one-dimensional array ML (machine load) to represent the workload of all the machines. The length of the ML is the number of machines, the initial values are 0, and the array value corresponds to the total load on the machine [$M_1$, $M_2$, …, $M_m$];

Step 2: For each operation of the OS (record $O_k$), repeat Step 3–Step 6 until all the operations in the OS are completed;

Step 3: Find the processing time array OT (order time) of the $O_k$ in the $O_k$ optional processing machine set;

Step 4: Define a temporary array TT (temporary time), the structure is the same as ML, the initial values are 0, the value of the corresponding machine in the array OT is added to the corresponding position of the ML, and the result is stored in the TT;

Step 5: Select the minimum number of machines $M_i$ in TT and store it in the MA;

Step 6: Update ML: the position of $M_i$ in ML equals to the original value plus the value of OT’s $M_i$ position.

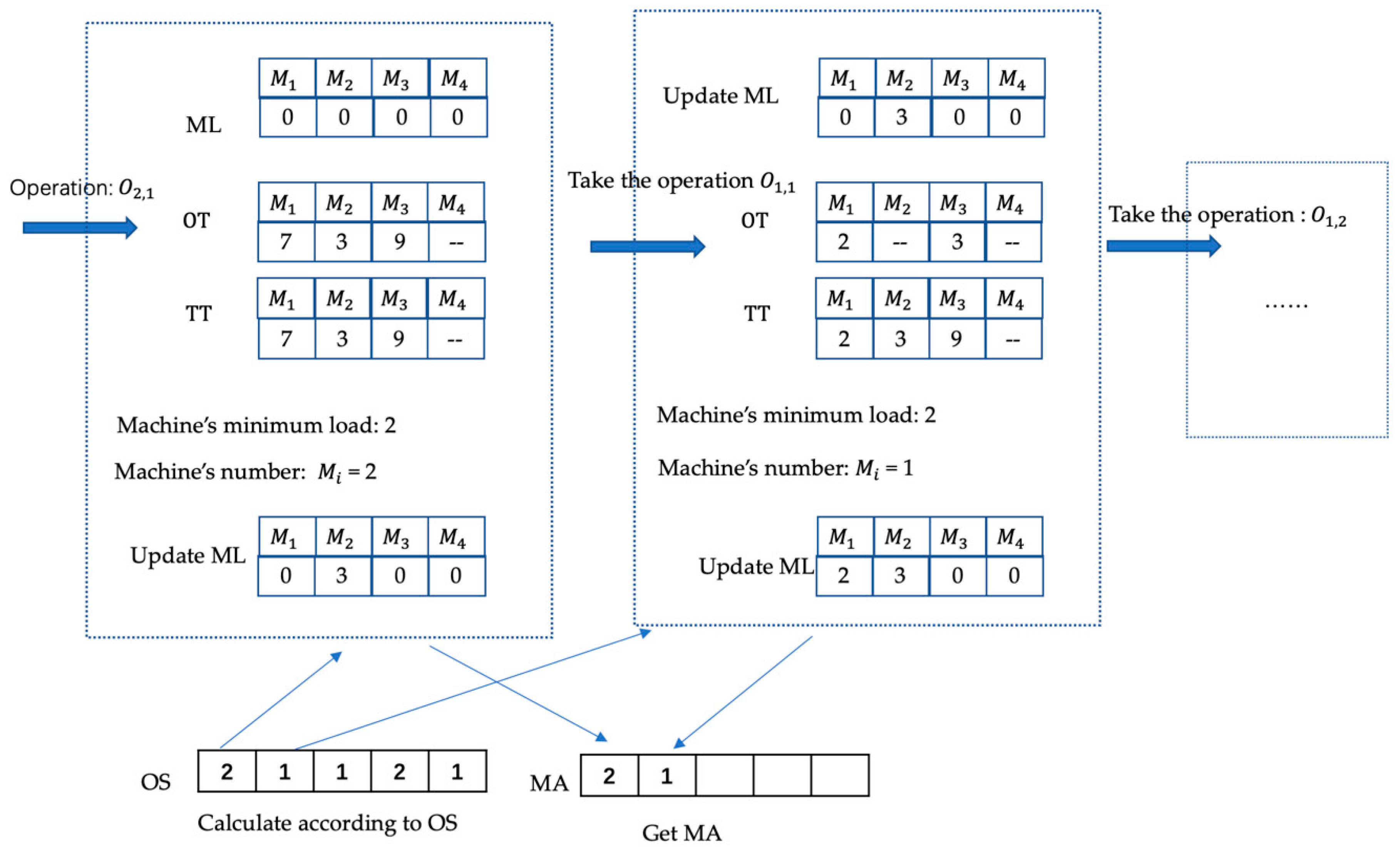
For 2 × 4 P-FJSP in Table 1, the OS is randomly generated: 2 1 1 2 1. First take 2, indicating the operation $O_{21}$, and the second time take 1, indicating the operation $O_{11}$, which is executed sequentially, and the GSO search process is shown in Figure 4.

4.3. Improved Genetic Operation

4.3.1. Selection

The MA parts of the chromosome in the initial population are generated by the 60% GSO, 20% tournament selection, and 20% random selection, and the OS parts are all randomly generated.

Tournament selection: Randomly select two individuals from the population. If the generated random values are less than 0.8, select the better one, otherwise select another one.

After generating the initial population, firstly, evaluate the fitness value, and store the optimal individuals into the elite library, then divide the entire population into groups, and finally, for each subpopulation after grouping, perform the crossover according to Section 4.3.2 and perform the mutation according to Section 4.3.3.

4.3.2. Crossover

Crossover is the main operation in the genetic algorithm, which determines the global search ability of the algorithm to a large extent. The crossover of MA and OS is separately conducted in this paper. The OS sequence selects the POX crossover in (1) and the improved uniform crossover in (2). The MA sequence selects the improved single-point crossover in selection (3).

(1) POX Crossover: The parent chromosomes after the coding are recorded as $P_1$, $P_2$, …, $P_n$, and the offspring chromosomes obtained after the crossover are recorded as $C_1$, $C_2$, …, $C_n$ (n is the population). The crossover is as follows:

Step 1: $P_1$ and $P_2$ are sequentially taken out from the parent chromosomes. Copy all the operations included in job $J_1$ in $P_1$ to $C_1$ in the original order, and copy all the operations contained in job $J_2$ in $P_2$ to $C_1$ in the original order;

Step 2: Copy all the operations included in job $J_2$ in $P_1$ to $C_2$ in the original order, and copy all the operations of the job $J_1$ in $P_2$ to $C_2$ in the original order;

Step 3: Repeat Step 1–Step 2 in the parent chromosomes until n offspring chromosomes $C_1$, $C_2$, …, $C_n$ are obtained;

(2) Improved uniform crossover: Randomly generate a binary code R, and the length is L. Assign all genes with a value of 1 corresponding to R in the parent chromosome $P_1$ to the offspring $C_1$, and after removing the gene copied to $C_1$ in $P_2$, the remaining genes are sequentially assigned to $C_1$. Similarly, all the genes with a value of 1 corresponding to R in the parent chromosome $P_2$ are assigned to the offspring $C_2$, and the genes copied to $C_2$ are removed in $P_1$, and the remaining genes are sequentially assigned to $C_2$.

Since R is randomly generated, the diversity of the population is enhanced, and the search in the solution space is promoted, making the search more robust.

(3) Improved single-point crossover: Divide all the chromosomes involved in the crossover into $\frac{n}{2}$ groups, and perform single-point crossover for the two parent chromosomes in each group: randomly select one crossover point, and exchange the machines assigned by the operations included in the two parents before the crossover point, which ensures that the chromosomes obtained after the crossover are all feasible scheduling.

4.3.3. Mutation

(1) Mutation based on OS: Randomly select a chromosome according to the mutation probability $P_m$, and select one of the operations. Since the job has a sequence order constraint, firstly, determine the position of the precursor operation $O_f^{\prime }$ and the subsequent operation $O_s^{\prime }$ of the operation $O^{\prime }$, and then randomly select a position to insert the operation between these two positions, which ensures that the resulting schedule is a feasible solution.

(2) Mutation based on MA: Select a parent chromosome for the mutation according to the mutation probability $P_m$, and select one of the processing operations $O^{″}$. Since each operation can be processed on multiple machines, each operation has a collection of optional processing machines. Randomly select a machine in the processing machine of $O^{″}$ to complete the mutation.

4.4. Adaptive Variable Neighborhood Search

In order to effectively search in the solution space and obtain high-quality solutions in FJSP, this paper combines the method of variable neighborhood search proposed in [20,21,22] and improves it to obtain the following three different neighborhood structures.

4.4.1. Neighborhood Structure

(1) The $VN{S}_1$ (for MA sequence) neighborhood generation method is as follows:

• Randomly generate s random numbers, s ∈ [1, M], and M is the total number of operations;
• Randomly select s positions from the chromosome MA;
• For each corresponding process of s, select the machine with the shortest processing time from its optional machine set to replace it, and evaluate the new solution. If the machine with the minimum time has been selected, select the machine with the second shortest machining time.

(2) The VNS2 (for OS) neighborhood generation method is as follows:

• Randomly generate two operations $J_1$ and $J_2$, let the number of $J_1$ < the number of $J_2$, and record the positions of $J_1$ and $J_2$ in the OS, respectively;
• Place each operation of $J_1$ at the positions corresponding to $J_2$ from left to right, and place each operation of $J_2$ in the remaining positions.

(3) The $VN{S}_3$ (for OS) neighborhood generation method is as follows:

• Select t random positions, t ≤ total number of operations;
• Reverse the genes at the t positions in the original OS and reinsert them into the same positions of the new solution.

4.4.2. Flow of Adaptive Variable Neighborhood Search Algorithm

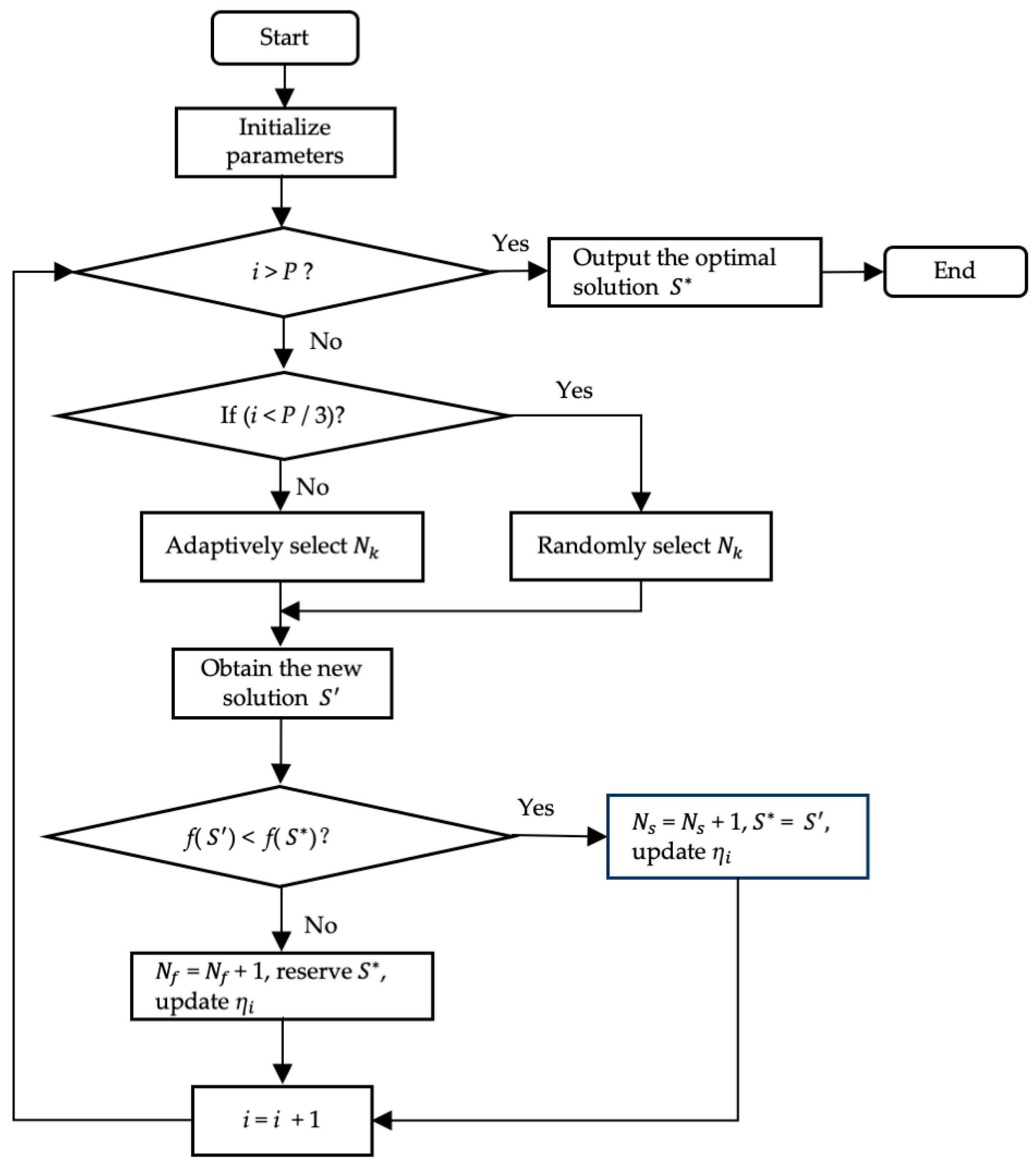
Different from the previous VNS using a fixed search order, this paper proposes an adaptive neighborhood selection strategy based on neighborhood search performance. The adaptive strategy is to learn the validity of each neighborhood search in the current optimization algorithm as the iteration proceeds. In order to promote effective competition between neighborhoods, the neighborhood method with a better search strategy has a higher probability to be used for the optimization of the algorithm. The steps of the adaptive neighborhood search algorithm are as follows and the flow chart is shown in Figure 5.

Step 1: Initialize parameters—initial solution S (from elite population), number of iterations P, the neighborhood structure $N_k$ (k = 1, 2, 3), loop variable i = 1, the success and failure times of neighborhood search that are expressed as $N_s$ = 0, $N_f$ = 0;

Step 2: Judge whether the termination criterion (i > P) is satisfied, and if so, output the optimal solution $S^{*}$, otherwise go to Step 3;

Step 3: If i < P/3, randomly select the neighborhood $N_k$ for the search to get a new solution $S^{\prime }$. Otherwise, calculate the probability ${\eta }_i$ according to Equations (5) and (6) (select the larger ${\eta }_i$ value), and select the neighborhood $N_k$ for neighborhood search to obtain a new solution $S^{\prime }$;

Step 4: If f($S^{\prime }$) < f($S^{*}$), $S^{*}$ = $S^{\prime }$, $N_s$ = $N_s$ + 1; otherwise, $N_f$ = $N_f$ + 1;

Step 5: Update the ${\eta }_i$ values of each neighborhood, i = i + 1. Go to Step 2.

$$\mathsf{\zeta } = \mathsf{\alpha }·\frac{N_s}{N_s + N_f}$$

(5)

$${\eta }_i= \frac{{\zeta }_i}{{{\displaystyle \sum }}_{k = 1}^3{\zeta }_k}$$

(6)

$$\mathsf{\alpha }=\frac{f\left(s^{*}\right)}{f\left(c\right)}$$

(7)

The parameter ζ is used to the measure the improvement degree of the chromosome. α denotes the relative fitness value, f($S^{*}$) is the global optimal solution obtained in the current elite library, f(c) is the fitness value of the chromosome in the current neighborhood search, and the probability ${\eta }_i$ of each neighborhood is calculated according to ζ in the search process.

5. Simulation and Analysis

The algorithm was written in Python programming language version 3.7.3 and was run on a MacBook Pro with a 2.7 GHz processor and 8 GB RAM of APPLE inc. in 2015. Tested by three international standard examples, each example runs the IGA-AVNS algorithm 10 times to find the minimum value of the completion time. As the difficulty of the FJSP problem is closely related to the scale of the problem, the parameters are selected according to the following rules: n is the number of jobs, m is the number of machines; number of iterations equal 10 × n × m; population size equals to n × m; the crossover probability $p_c$ is 0.8; the mutation probability $p_m$ is 0.1; the number of neighborhood cycles p is 10. Initial population generation method: MA—60% GSO, 20% tournament, and 20% random; OS—random generation.

The first set of data are selected from a set of three questions proposed by Kacem et al. [16]. Problem 8 × 8 is a P-FJSP that is composed of 8 jobs with 27 operations which can be processed on 8 machines; problem 10 × 10 is a T-FJSP that consists of 10 jobs with 30 operations that can be processed on 10 machines; problem 15 × 10 is a T-FJSP that is comprised of 15 jobs with 56 operations which can be performed on 10 machines. The details about Kacem data can be found in [23]. The test results are compared with the results obtained by the Kacem method [16], the Xia method [23], the hybrid genetic tabu search (HGTS) proposed by Palacios et al. [24], the proposed varibale neighbourhood search (PVNS) proposed by Amiri et al. [25], and the Heuristic proposed by Ziae et al. [26]. The simulation results are shown in

Table 2. Comparison with other algorithms on flexible job-shop scheduling problems (FJSPs) from the Kacem data.

n × m	Kacem	Xia	HGTS	PVNS	Heuristic	IGA-AVNS
8 × 8	15	15	14	14	15	14
10 × 10	7	7	7	7	7	7
15 × 15	24	12	11	12	12	11

HGTS: hybrid genetic tabu search; PVNS: proposed varibale neighbourhood search.

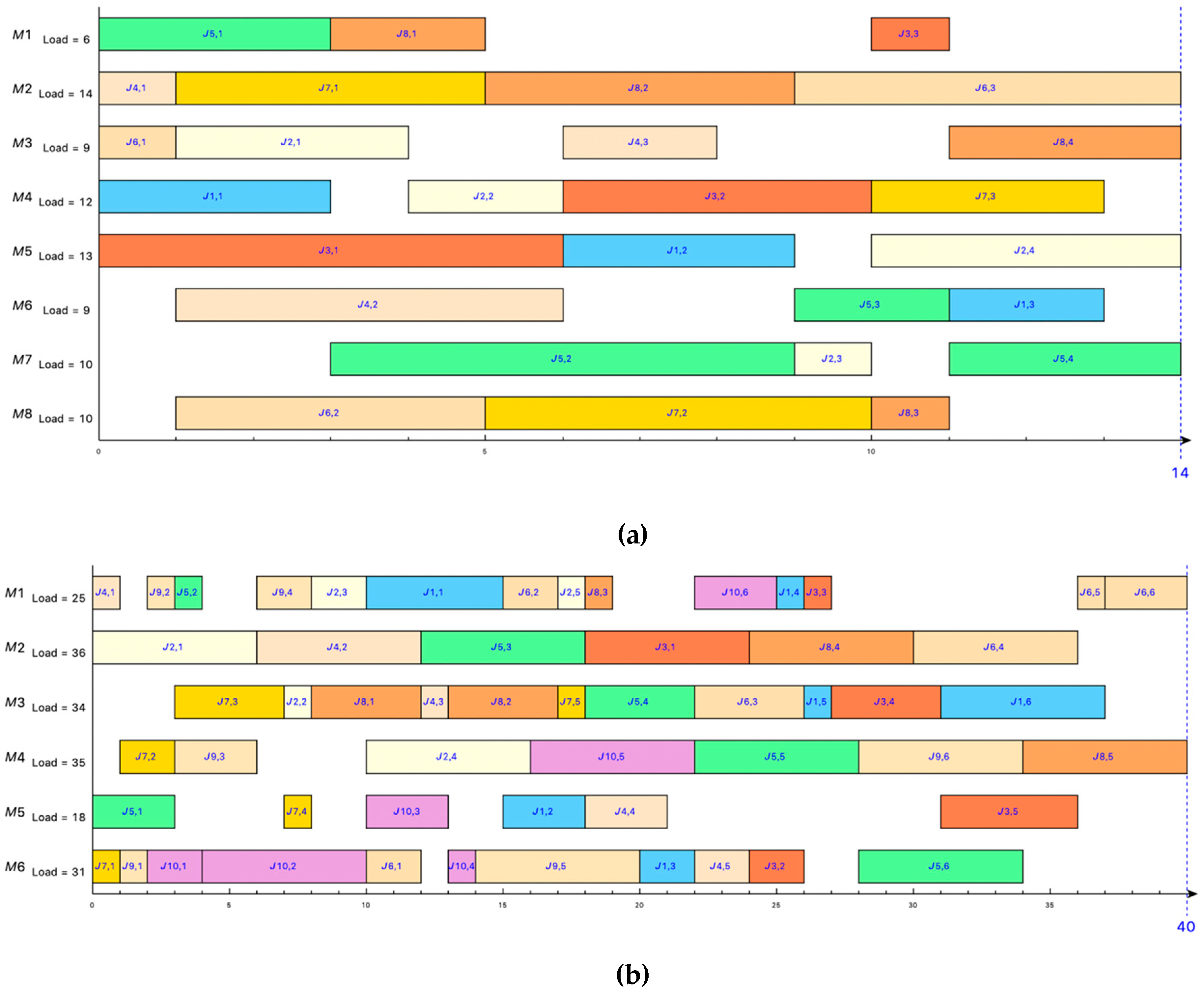
. Figure 6a is a Gantt chart of the optimal solution for the Kacem 8 × 8 problem obtained by the IGA-AVNS.

The second set of data comes from the BRdata (Brandimarte 1993 [27]), which includes 10 problems. The number of jobs is from 10 to 20, the number of machines is from 4 to 15, and the number of operations of each problem ranges from 5 to 15.

Table 3. Simulation results on FJSPs from BRdata.

Problem	n × m	L	LB	IGA-AVNS
				Populations	Iterations	x*	Av(x*)	$\mathit{d}\mathit{e}{\mathit{v}}_1(\%)$
MK01	10 × 6	55	36	60	600	40	40.1	11
MK02	10 × 6	58	24	60	600	26	27.2	8.3
MK03	15 × 8	150	204	120	1200	204	204	0
MK04	15 × 8	90	48	120	1200	60	61.8	25
MK05	15 × 4	106	168	60	600	173	175.2	2.9
MK06	10 × 15	150	33	150	1500	60	60.08	81.8
MK07	20 × 5	100	133	100	1000	144	144.5	8.3
MK08	20 × 10	225	523	200	2000	523	523	0
MK09	20 × 10	240	299	200	2000	307	307	2.7
MK10	20 × 15	240	165	300	3000	208	209.9	26

lists the results of the algorithm in this paper:

Best heuristic solution $x^{*}$: The minimum value of the completion time obtained after 10 times of operations;

Average value Av($x^{*}$): The average of the completion time obtained after 10 times of operations;

The relative deviation $de{v}_1$: The equation of the relative deviation between the best heuristic solution $x^{*}$ and the best-known lower bound (LB). The calculation method is shown in Equation (8). Figure 6b shows the Gantt chart of the best heuristic solution of the BRdata MK01 problem obtained by the IGA-AVNS algorithm.

The relative deviation $de{v}_2$: The equation of relative deviation for the best heuristic solution obtained by IGA-AVNS and the compared algorithms. The calculation method is shown in Equation (9). $C{M}_{our}$ represents the optimal result obtained by IGA-AVNS. $C{M}_{other}$ represents the best heuristic solution of the compared algorithms. If the value of $de{v}_2$ is positive, the solution obtained by the compared algorithm is better. If the value of $de{v}_2$ is negative, the solution obtained by the IGA-AVNS is better.

$$de{v}_1=\frac{x^{*}-LB}{LB}\times 100\%$$

(8)

$$de{v}_2=(\frac{C{M}_{our}-C{M}_{other}}{C{M}_{our}})\times 100\%$$

(9)

Table 4. Comparison with other algorithms on FJSPs from BRdata.

Problem	n × m	LB	GA		GATS + HM			HEA		NGA		IGA-AVNS
			${\mathit{C}}_{\mathit{m}}$	$\mathit{d}\mathit{e}{\mathit{v}}_2(\%)$	${\mathit{C}}_{\mathit{m}}$	$\mathbf{Av}\left({\mathit{C}}_{\mathit{m}}\right)$	$\mathit{d}\mathit{e}{\mathit{v}}_2(\%)$	${\mathit{C}}_{\mathit{m}}$	$\mathit{d}\mathit{e}{\mathit{v}}_2(\%)$	${\mathit{C}}_{\mathit{m}}$	$\mathit{d}\mathit{e}{\mathit{v}}_2(\%)$	x*	Av(x*)
MK01	10 × 6	36	40	0	40	40.8	0	40	0	37	7.5	40	40.1
MK02	10 × 6	24	26	0	27	27.8	–3.8	27	–3.8	26	0	26	27.2
MK03	15 × 8	204	204	0	204	204.0	0	204	0	204	0	204	204
MK04	15 × 8	48	60	0	64	65.6	–6.7	60	0	60	0	60	61.8
MK05	15 × 4	168	173	0	173	174.8	0	173	0	173	0	173	175.2
MK06	10 × 15	33	63	–5	65	67.0	–8.3	59	1.7	67	–11.7	60	60.08
MK07	20 × 5	133	139	3.47	144	144.0	0	144	0	148	–2.8	144	144.5
MK08	20 × 10	523	523	0	523	523.0	0	523	0	523	0	523	523
MK09	20 × 10	299	311	0	311	311.8	–1.3	307	0	307	0	307	307
MK10	20 × 15	165	212	–1.3	222	224.8	–6.7	209	–0.48	212	–1.9	208	209.9

shows the comparison results between IGA-AVNS and the following algorithms: the Genetic Algorithm (GA) proposed by Pezzella et al. [17], the Genetic Algorithm Combined with Tabu Search in a Holonic Multiagent model (GATS + HM) proposed by Nouri et al. [5], the hybrid evlolutionary agorithm (HEA) proposed by Wang et al. [10], and the neighborhood-based genetic algorithm (NGA) proposed by Driss et al. [7]. The data in the table are from the corresponding literature. The parameters used by $x^{*}$ and Av($x^{*}$) of IGA-AVNS algorithm are the same as the Kacem instances. L is the total number of the operations, LB is the best-known lower bound.

Among the 10 problems in the BRdata, for MK01, the NGA obtained the best solution, which is better than other algorithms; while for the MK03, MK05, and MK08 problems, all the compared methods obtained the same better solution.

Referring to the value of $de{v}_2$,compared with GA: IGA-AVNS algorithm is better than GA algorithm for MK06 and MK10 problems. GA gets a better solution for the MK07 problem; compared with GATS + HM algorithm for MK02, MK04, MK06, MK09, and MK10 problems, the solution obtained by the IGA-AVNS algorithm is better than that obtained by GATS + HM algorithm; compared with the HEA algorithm for the MK06 problem, HEA gets better solution, and for the MK02 and MK10 problems, the IGA-AVNS algorithm gets a better solution. For the MK01 problem, the NGA algorithm gets a better solution than the other algorithms, and for the MK06, MK07, and MK10 problems, the IGA-AVNS algorithm gets a better solution. In summary, it can be concluded that the IGA-AVNS algorithm is an effective method for solving FJSP.

The third set of data is the BCdata (Barnes and Chambers 1996) [25]. We select 14 instances of the dataset considering a number of jobs ranging from 10 to 15 with a number of operations for each job ranging from 10 to 15, which will be processed on a number of machines ranging from 11 to 18.

Table 5. Results of the Barnes and Chambers data instances.

Problem	n × m	LB	GATS + HM		IGA-AVNS
			x*	$\mathit{d}\mathit{e}{\mathit{v}}_1(\%)$	x*	$\mathit{d}\mathit{e}{\mathit{v}}_1(\%)$	$\mathit{d}\mathit{e}{\mathit{v}}_2(\%)$
mt10c1	10 × 11	655	927	41.5	927	41.5	0
mt10cc	10 × 12	655	917	40.0	908	38.6	−0.99
mt10x	10 × 11	655	923	40.9	918	40.2	−0.5
mt10xx	10 × 12	655	918	40.2	918	40.2	0
mt10xxx	10 × 13	655	918	40.2	918	40.2	0
mt10xy	10 × 12	655	908	38.6	905	38.2	−0.3
mt10xyz	10 × 13	655	868	32.5	868	32.5	0
setb4c9	15 × 11	857	927	8.2	914	6.7	−1.42
setb4cc	15 × 12	857	938	9.5	944	10.2	0.6
setb4x	15 × 11	846	944	11.6	926	9.5	−1.9
setb4xx	15 × 12	846	942	11.3	926	9.5	−1.7
setb4xxx	15 × 13	846	949	12.2	926	9.5	−2.42
setb4xy	15 × 12	845	931	10.2	938	11.0	0.75
setb4xyz	15 × 13	838	926	10.5	926	10.5	0

shows the comparison results between the IGA-AVNS and GATS + HM [5] proposed by Nouri et al.

In Table 5, for the value of $de{v}_1$, the smaller the value, the closer to LB. For the value of $de{v}_2$, 0 indicates that the two algorithms get the same solution, a positive value indicates that the solution obtained by GATS + HM is better, and if the value is negative, the solution obtained by IGA-AVNS is better. It can be seen from these two sets of values that the two algorithms get the same solutions in 5 out of 12 instances, our IGA-AVNS outperforms the GATS + HM in 7 out of 12 instances, and the GATS + HM only obtains 2 out of 14 better solutions than our IGA-AVNS algorithm. Figure 7 shows the comparison of $de{v}_1$ obtained by the two algorithms when solving the BCdata. We can conclude that IGA-AVNS is better than the GATS + HM algorithm in most cases when solving the BCdata. Therefore, the feasibility and effectiveness of the IGA-AVNS algorithm for solving the FJSP are further proved.

6. Conclusions

In this paper, the improved genetic algorithm and the variable neighborhood search algorithm are combined to solve the FJSP. The algorithm makes full use of GA’s global search ability and VNS’s local search ability to balance exploration and development. The optimization model is established for the proposed algorithm, and the famous Kacem example and BRdata example are applied to simulate the experiment. The experimental results show that the proposed IGA-AVNS is a promising and very effective method for solving the FJSP problem. The simulation results are compared with the existing algorithms at home and abroad. The results prove that IGA-AVNS is more reasonable and effective for solving FJSP problems.

At present, although some achievements have been made in solving the FJSP problem, more research is needed to solve this problem in view of the complexity and multi-objectiveness of the FJSP problem. The main directions for future research are issues such as reducing enterprise costs, improving competitiveness, and establishing a green and low-carbon FJSP.