Exploring an Ensemble of Methods that Combines Fuzzy Cognitive Maps and Neural Networks in Solving the Time Series Prediction Problem of Gas Consumption in Greece
Abstract
1. Introduction
1.1. Related Literature
1.2. Research Aim and Approach
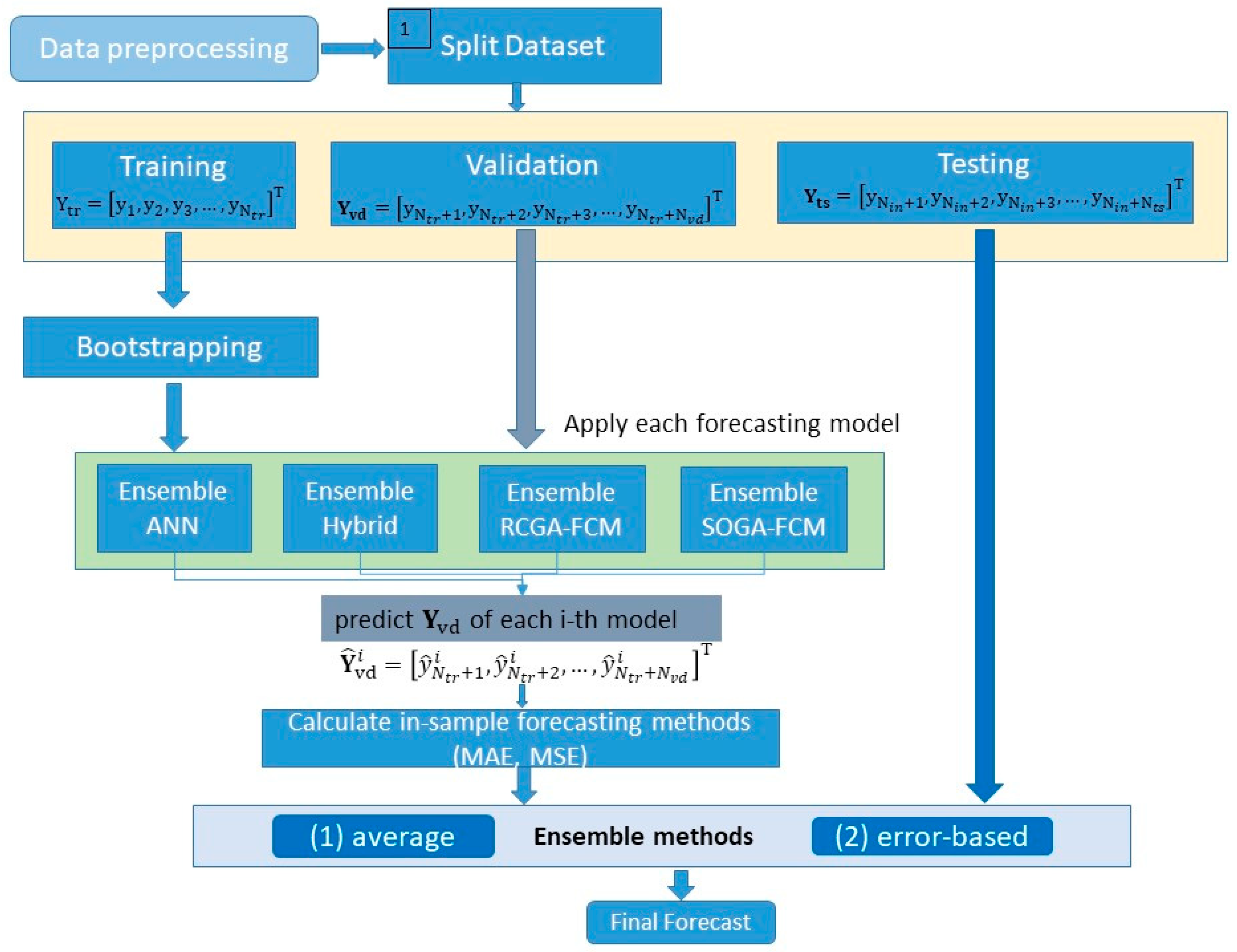
2. Materials and Methods
2.1. Material-Dataset
2.2. Methods
2.2.1. Fuzzy Cognitive Maps Overview
2.2.2. Fuzzy Cognitive Maps Evolutionary Learning
Real-Coded Genetic Algorithm (RCGA)
Structure Optimization Genetic Algorithm (SOGA)
2.2.3. Artificial Neural Networks
2.2.4. Hybrid Approach Based on FCMs, SOGA, and ANNs
- Construction of the FCM model based on the SOGA algorithm to reduce the concepts that have no significant influence on data error.
- Considering the selected concepts (data attributes) as the inputs for the ANN and ANN learning with the use of backpropagation method with momentum.
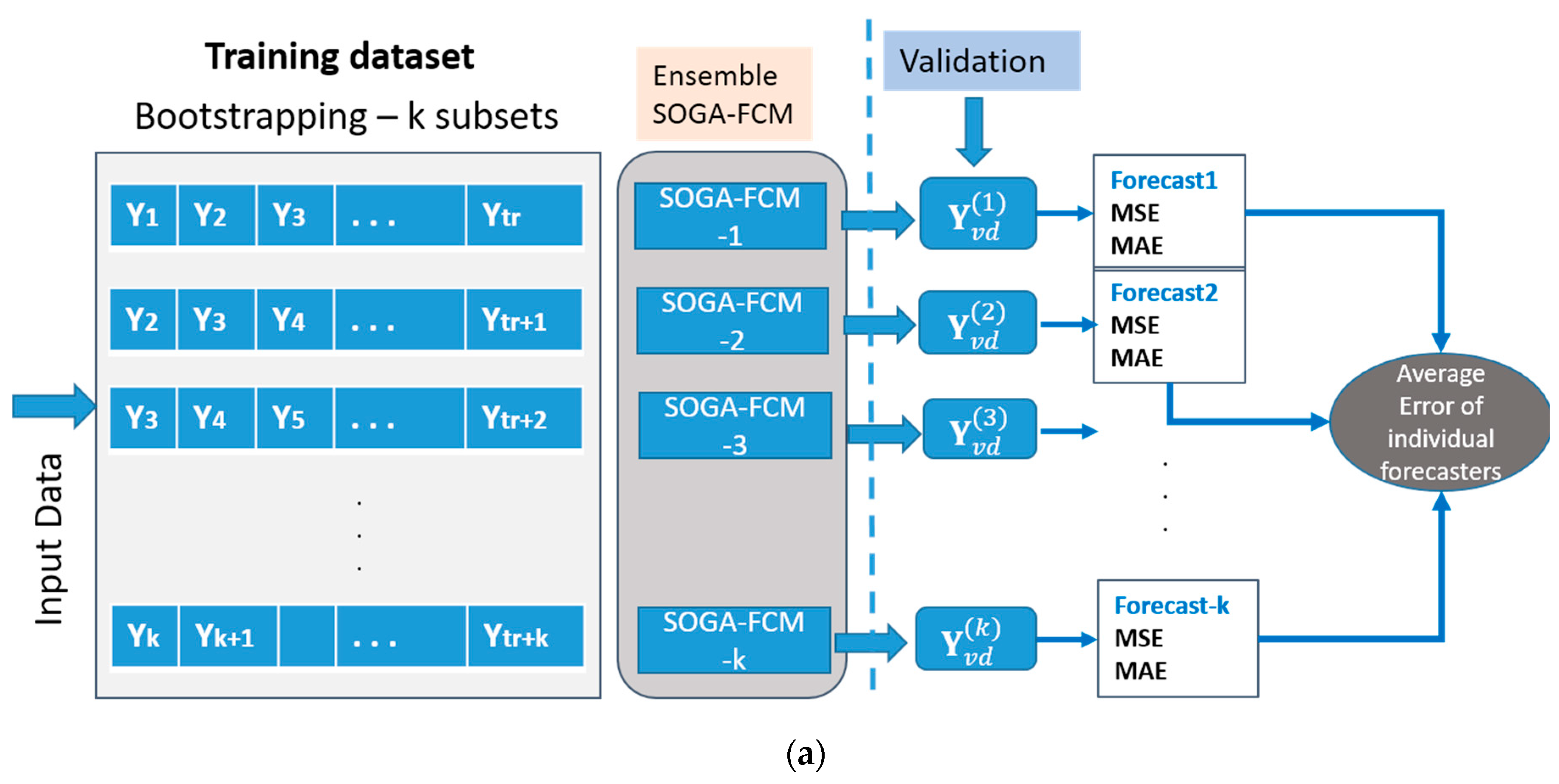
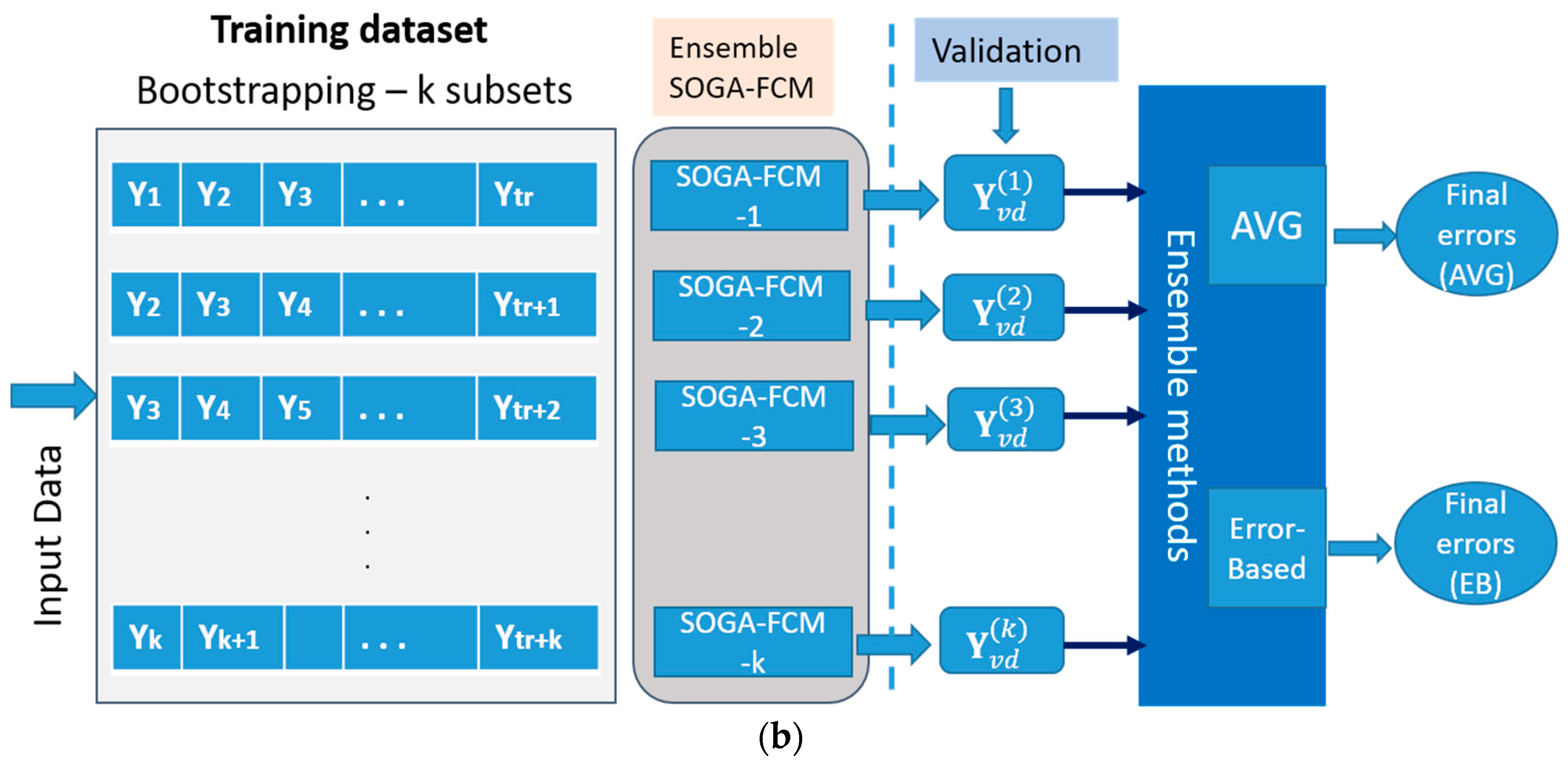
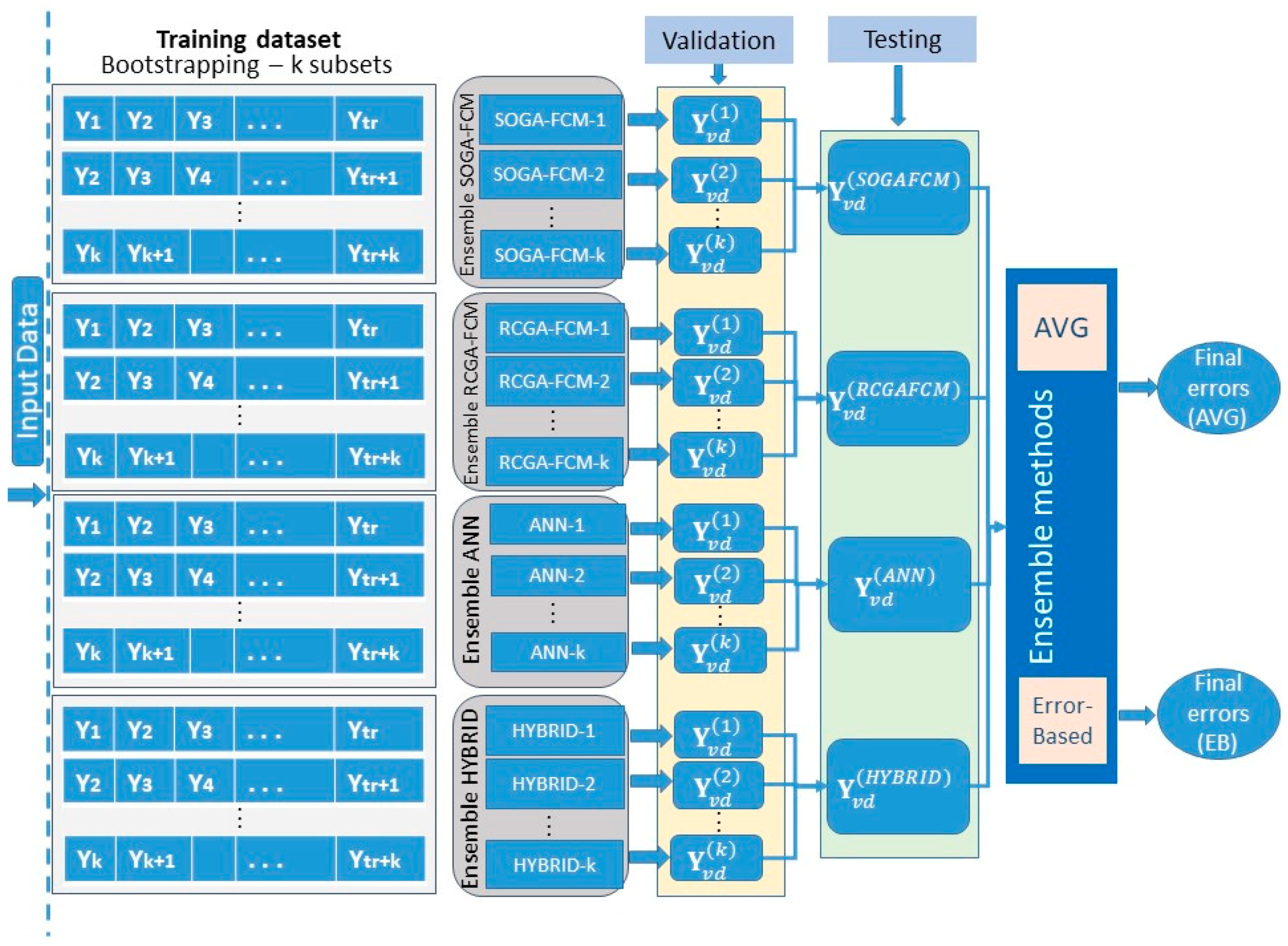
2.2.5. The Ensemble Forecasting Method
- The simple average (AVG) method [82] is an unambiguous technique, which assigns the same weight to every single forecast. Based on empirical studies in the literature, it has been observed that the AVG method is robust and able to generate reliable predictions, while it can be characterized as remarkably accurate and impartial. Being applied in several models, with respect to effectiveness, the AVG improved the average accuracy when increasing the number of combined single methods [82]. Comparing the referent method with the weighted combination techniques, in terms of forecasting performance, the researchers in [84] concluded that a simple average combination might be more robust than weighted average combinations. In the simple average combination, the weights can be specified as follows:
- The error-based (EB) method [16] consists of component forecasts, which are given weights that are inversely proportional to their in-sample forecasting errors. For instance, researchers may give a higher weight to a model with lower error, while they may assign a less weight value to a model that presents more error, respectively. In most of the cases, the forecasting error is calculated using total absolute error statistic, such as the sum of squared error (SSE) [80,83]. The combining weight for individual prediction is mathematically given by:
3. The Proposed Forecast Combination Methodology
4. Results and Discussion
4.1. Case Study and Datasets
4.2. Case Study Results
4.3. Discussion of Results
- After a thorough analysis of the Table 3, Table 4, Table 5, Table 6, Table 7 and Table 8, on the basis of examining the MAE and MSE errors, it could be clearly stated that the EB method presented lower errors concerning the individual forecasters (ANN, hybrid, RCGA-FCM, and SOGA-FCM) for all three cities (Athens, Thessaloniki, and Larisa). EB seemed to outperform the AVG method in terms of achieving overall better forecasting results when applied to individual forecasters (see Figure 6).
- Considering the ensemble forecasters, it could be seen from the obtained results that none of the two forecast combination methods had attained consistently better accuracies compared to each other, as far as the cities of Athens and Thessaloniki were concerned. Specifically, from Table 3, Table 4, Table 5 and Table 6, it was observed that the MAE and MSE values across the two combination methods were similar for the two cities; however, their errors were lower than those produced by each separate ensemble forecaster.
- Although the AVG and the EB methods performed similarly for Athens and Thessaloniki datasets, the EB forecast combination technique presented lower MAE and MSE errors than the AVG for the examined dataset of Larissa (see Figure 5).
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Descriptive Statistics | Athens | Thessaloniki | Larissa | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Z(t) | X(t)AVG | X(t) EB | Z(t) | X(t)AVG | X(t) EB | Z(t) | X(t)AVG | X(t) EB | |
| Mean | 0.2540 | 0.2464 | 0.2464 | 0.2611 | 0.2510 | 0.2510 | 0.2689 | 0.2565 | 0.2575 |
| Median | 0.1154 | 0.1366 | 0.1366 | 0.1335 | 0.1393 | 0.1394 | 0.1037 | 0.1194 | 0.1211 |
| St. Deviation | 0.2391 | 0.2203 | 0.2203 | 0.2373 | 0.2228 | 0.2228 | 0.2604 | 0.2429 | 0.2429 |
| Kurtosis | 0.3610 | −0.2748 | −0.2741 | −0.1839 | −0.5807 | −0.5774 | −0.6564 | −0.8881 | −0.8847 |
| Skewness | 1.1605 | 0.9801 | 0.9803 | 0.9328 | 0.8288 | 0.8298 | 0.8112 | 0.7520 | 0.7516 |
| Minimum | 0.0277 | 0.0367 | 0.0367 | 0.0043 | 0.0305 | 0.0304 | 0.0000 | 0.0235 | 0.0239 |
| Maximum | 1.0000 | 0.8429 | 0.8431 | 1.0000 | 0.8442 | 0.8448 | 1.0000 | 0.8361 | 0.8383 |
| Descriptive Statistics | Athens | Thessaloniki | Larissa | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Z(t) | X(t)AVG | X(t) EB | Z(t) | X(t)AVG | X(t) EB | Z(t) | X(t)AVG | X(t) EB | |
| Mean | 0.2479 | 0.2433 | 0.2433 | 0.2588 | 0.2478 | 0.2478 | 0.2456 | 0.2279 | 0.2291 |
| Median | 0.1225 | 0.1488 | 0.1488 | 0.1179 | 0.1304 | 0.1304 | 0.0695 | 0.0961 | 0.0972 |
| St. Deviation | 0.2159 | 0.2020 | 0.2021 | 0.2483 | 0.2236 | 0.2237 | 0.2742 | 0.2399 | 0.2404 |
| Kurtosis | 0.6658 | 0.2785 | 0.2792 | 0.1755 | −0.1254 | −0.1219 | −0.0113 | −0.1588 | –0.1502 |
| Skewness | 1.2242 | 1.1138 | 1.1140 | 1.1348 | 1.0469 | 1.0479 | 1.1205 | 1.0900 | 1.0921 |
| Minimum | 0.0000 | 0.0359 | 0.0359 | 0.0079 | 0.0358 | 0.0357 | 0.0000 | 0.0233 | 0.0237 |
| Maximum | 0.9438 | 0.8144 | 0.8144 | 0.9950 | 0.8556 | 0.8562 | 1.0000 | 0.8291 | 0.8310 |
| Validation | Testing | Testing | |||||||
|---|---|---|---|---|---|---|---|---|---|
| MAE | MSE | MAE | MSE | Weights | MAE | MSE | Weights | ||
| RCGA1 | 0.0386 | 0.0036 | 0.0425 | 0.0038 | 0.2531 | SOGA1 | 0.0435 | 0.0037 | 0.2520 |
| RCGA2 | 0.0391 | 0.0038 | 0.0430 | 0.0039 | 0 | SOGA2 | 0.0423 | 0.0038 | 0.2509 |
| RCGA3 | 0.0399 | 0.0039 | 0.0428 | 0.0039 | 0 | SOGA3 | 0.0425 | 0.0038 | 0 |
| RCGA4 | 0.0384 | 0.0036 | 0.0419 | 0.0038 | 0.2522 | SOGA4 | 0.0449 | 0.0042 | 0 |
| RCGA5 | 0.0389 | 0.0037 | 0.0423 | 0.0039 | 0 | SOGA5 | 0.0429 | 0.0040 | 0 |
| RCGA6 | 0.0392 | 0.0036 | 0.0424 | 0.0039 | 0.2472 | SOGA6 | 0.0432 | 0.0038 | 0.2494 |
| RCGA7 | 0.0398 | 0.0038 | 0.0434 | 0.0041 | 0 | SOGA7 | 0.0421 | 0.0039 | 0 |
| RCGA8 | 0.0386 | 0.0037 | 0.0416 | 0.0039 | 0 | SOGA8 | 0.0422 | 0.0039 | 0 |
| RCGA9 | 0.0398 | 0.0036 | 0.0436 | 0.0041 | 0.2472 | SOGA9 | 0.0434 | 0.0042 | 0 |
| RCGA10 | 0.0388 | 0.0037 | 0.0417 | 0.0039 | 0 | SOGA10 | 0.0422 | 0.0040 | 0 |
| RCGA11 | 0.0393 | 0.0038 | 0.0419 | 0.0039 | 0 | SOGA11 | 0.0420 | 0.0038 | 0.2475 |
| RCGA12 | 0.0396 | 0.0037 | 0.0434 | 0.0041 | 0 | SOGA12 | 0.0425 | 0.0040 | 0 |
| AVG | 0.0385 | 0.0036 | 0.0418 | 0.0038 | AVG | 0.0422 | 0.0039 | ||
| EB | 0.0388 | 0.0036 | 0.0422 | 0.0038 | EB | 0.0422 | 0.0037 | ||
| Validation | Testing | Testing | |||||||
|---|---|---|---|---|---|---|---|---|---|
| MAE | MSE | MAE | MSE | Weights | MAE | MSE | Weights | ||
| Hybrid1 | 0.0356 | 0.0030 | 0.0390 | 0.0036 | 0.2565 | SOGA1 | 0.0414 | 0.0040 | 0 |
| Hybrid2 | 0.0381 | 0.0036 | 0.0409 | 0.0042 | 0 | SOGA2 | 0.0417 | 0.0040 | 0 |
| Hybrid3 | 0.0371 | 0.0032 | 0.0398 | 0.0039 | 0.2422 | SOGA 3 | 0.0394 | 0.0034 | 0 |
| Hybrid4 | 0.0376 | 0.0032 | 0.0403 | 0.0039 | 0 | SOGA 4 | 0.0406 | 0.0038 | 0 |
| Hybrid5 | 0.0373 | 0.0032 | 0.0401 | 0.0040 | 0 | SOGA 5 | 0.0388 | 0.0033 | 0.2541 |
| Hybrid6 | 0.0375 | 0.0033 | 0.0403 | 0.0040 | 0 | SOGA 6 | 0.0413 | 0.0038 | 0 |
| Hybrid7 | 0.0378 | 0.0033 | 0.0405 | 0.0040 | 0 | SOGA 7 | 0.0415 | 0.0039 | 0 |
| Hybrid8 | 0.0373 | 0.0032 | 0.0402 | 0.0040 | 0 | SOGA 8 | 0.0399 | 0.0036 | 0 |
| Hybrid9 | 0.0378 | 0.0034 | 0.0407 | 0.0041 | 0 | SOGA 9 | 0.0392 | 0.0035 | 0.2448 |
| Hybrid10 | 0.0371 | 0.0032 | 0.0397 | 0.0039 | 0.2410 | SOGA10 | 0.0400 | 0.0037 | 0 |
| Hybrid11 | 0.0370 | 0.0033 | 0.0402 | 0.0040 | 0 | SOGA11 | 0.0403 | 0.0036 | 0.2439 |
| Hybrid12 | 0.0364 | 0.0030 | 0.0406 | 0.0036 | 0.2601 | SOGA12 | 0.0397 | 0.0034 | 0.2569 |
| AVG | 0.0369 | 0.0032 | 0.0398 | 0.0039 | AVG | 0.0398 | 0.0036 | ||
| EB | 0.0361 | 0.0031 | 0.0394 | 0.0037 | EB | 0.0391 | 0.0034 | ||
| Validation | Testing | Testing | |||||||
|---|---|---|---|---|---|---|---|---|---|
| MAE | MSE | MAE | MSE | Weights | MAE | MSE | Weights | ||
| ANN1 | 0.0339 | 0.0032 | 0.0425 | 0.0047 | 0.2511 | Hybrid1 | 0.0411 | 0.0043 | 0.2531 |
| ANN2 | 0.0353 | 0.0036 | 0.0438 | 0.0052 | 0 | Hybrid2 | 0.0435 | 0.0051 | 0 |
| ANN3 | 0.0343 | 0.0033 | 0.0433 | 0.0050 | 0 | Hybrid3 | 0.0418 | 0.0045 | 0.2472 |
| ANN4 | 0.0347 | 0.0033 | 0.0429 | 0.0049 | 0 | Hybrid4 | 0.0424 | 0.0048 | 0 |
| ANN5 | 0.0353 | 0.0035 | 0.0436 | 0.0051 | 0 | Hybrid5 | 0.0436 | 0.0051 | 0 |
| ANN6 | 0.0352 | 0.0035 | 0.0432 | 0.0049 | 0 | Hybrid6 | 0.0436 | 0.0051 | 0 |
| ANN7 | 0.0354 | 0.0035 | 0.0441 | 0.0053 | 0 | Hybrid7 | 0.0434 | 0.0050 | 0 |
| ANN8 | 0.0348 | 0.0033 | 0.0427 | 0.0049 | 0 | Hybrid8 | 0.0425 | 0.0047 | 0.2398 |
| ANN9 | 0.0351 | 0.0035 | 0.0439 | 0.0052 | 0 | Hybrid9 | 0.0423 | 0.0047 | 0 |
| ANN10 | 0.0343 | 0.0033 | 0.0431 | 0.0049 | 0.2406 | Hybrid10 | 0.0432 | 0.0050 | 0 |
| ANN11 | 0.0342 | 0.0032 | 0.0436 | 0.0049 | 0.2472 | Hybrid11 | 0.0444 | 0.0053 | 0 |
| ANN12 | 0.0331 | 0.0031 | 0.0428 | 0.0047 | 0.2610 | Hybrid12 | 0.0426 | 0.0043 | 0.2597 |
| AVG | 0.0345 | 0.0033 | 0.0431 | 0.0049 | AVG | 0.0427 | 0.0048 | ||
| EB | 0.0337 | 0.0032 | 0.0428 | 0.0048 | EB | 0.0417 | 0.0044 | ||
| X(t) AVG Athens | X(t) EB Athens | |
|---|---|---|
| Mean | 0.243342155 | 0.243346733 |
| Variance | 0.040822427 | 0.040826581 |
| Observations | 196 | 196 |
| Pearson Correlation | 0.99999997 | |
| Hypothesized Mean Difference | 0 | |
| df | 195 | |
| t Stat | –1.278099814 | |
| P(T<=t) one-tail | 0.101366761 | |
| t Critical one-tail | 1.65270531 | |
| P(T<=t) two-tail | 0.202733521 | |
| t Critical two-tail | 1.972204051 |
| X(t) AVG | X(t) EB | |
|---|---|---|
| Mean | 0.247811356 | 0.247811056 |
| Variance | 0.050004776 | 0.050032786 |
| Observations | 365 | 365 |
| Pearson Correlation | 0.999999788 | |
| Hypothesized Mean Difference | 0 | |
| df | 364 | |
| t Stat | 0.036242052 | |
| P(T<=t) one-tail | 0.485554611 | |
| t Critical one-tail | 1.649050545 | |
| P(T<=t) two-tail | 0.971109222 | |
| t Critical two-tail | 1.966502569 |
| X(t) AVG Larisa | X(t) EB Larisa | |
|---|---|---|
| Mean | 0.227903242 | 0.229120614 |
| Variance | 0.057542802 | 0.05781177 |
| Observations | 365 | 365 |
| Pearson Correlation | 0.999972455 | |
| Hypothesized Mean Difference | 0 | |
| df | 364 | |
| t Stat | –12.44788062 | |
| P(T<=t) one-tail | 3.52722E-30 | |
| t Critical one-tail | 1.649050545 | |
| P(T<=t) two-tail | 7.05444E-30 | |
| t Critical two-tail | 1.966502569 |
References
- Li, H.Z.; Guo, S.; Li, C.J.; Sun, J.Q. A hybrid annual power load forecasting model based on generalized regression neural network with fruit fly optimization algorithm. Knowl.-Based Syst. 2013, 37, 378–387. [Google Scholar] [CrossRef]
- Bodyanskiy, Y.; Popov, S. Neural network approach to forecasting of quasiperiodic financial time series. Eur. J. Oper. Res. 2006, 175, 1357–1366. [Google Scholar] [CrossRef]
- Livieris, I.E.; Kotsilieris, T.; Stavroyiannis, S.; Pintelas, P. Forecasting stock price index movement using a constrained deep neural network training algorithm. Intell. Decis. Technol. 2019, 1–14. Available online: https://www.researchgate.net/publication/334132665_Forecasting_stock_price_index_movement_using_a_constrained_deep_neural_network_training_algorithm (accessed on 10 September 2019).
- Livieris, I.E.; Pintelas, H.; Kotsilieris, T.; Stavroyiannis, S.; Pintelas, P. Weight-constrained neural networks in forecasting tourist volumes: A case study. Electronics 2019, 8, 1005. [Google Scholar] [CrossRef]
- Chen, C.F.; Lai, M.C.; Yeh, C.C. Forecasting tourism demand based on empirical mode decomposition and neural network. Knowl.-Based Syst. 2012, 26, 281–287. [Google Scholar] [CrossRef]
- Lu, X.; Wang, J.; Cai, Y.; Zhao, J. Distributed HS-ARTMAP and its forecasting model for electricity load. Appl. Soft Comput. 2015, 32, 13–22. [Google Scholar] [CrossRef]
- Zeng, Y.R.; Zeng, Y.; Choi, B.; Wang, L. Multifactor-influenced energy consumption forecasting using enhanced back-propagation neural network. Energy 2017, 127, 381–396. [Google Scholar] [CrossRef]
- Lin, W.Y.; Hu, Y.H.; Tsai, C.F. Machine learning in financial crisis prediction: A survey. IEEE Trans. Syst. Man Cybern. 2012, 42, 421–436. [Google Scholar]
- Raza, M.Q.; Khosravi, A. A review on artificial intelligence-based load demand techniques for smart grid and buildings. Renew. Sustain. Energy Rev. 2015, 50, 1352–1372. [Google Scholar] [CrossRef]
- Weron, R. Electricity price forecasting: A review of the state-of-the-art with a look into the future. Int. J. Forecast. 2014, 30, 1030–1081. [Google Scholar] [CrossRef]
- Meade, N.; Islam, T. Forecasting in telecommunications and ICT-A review. Int. J. Forecast. 2015, 31, 1105–1126. [Google Scholar] [CrossRef]
- Donkor, E.; Mazzuchi, T.; Soyer, R.; Alan Roberson, J. Urban water demand forecasting: Review of methods and models. J. Water Resour. Plann. Managem. 2014, 140, 146–159. [Google Scholar] [CrossRef]
- Fagiani, M.; Squartini, S.; Gabrielli, L.; Spinsante, S.; Piazza, F. A review of datasets and load forecasting techniques for smart natural gas and water grids: Analysis and experiments. Neurocomputing 2015, 170, 448–465. [Google Scholar] [CrossRef]
- Chandra, D.R.; Kumari, M.S.; Sydulu, M. A detailed literature review on wind forecasting. In Proceedings of the IEEE International Conference on Power, Energy and Control (ICPEC), Sri Rangalatchum Dindigul, India, 6–8 February 2013; pp. 630–634. [Google Scholar]
- Zhang, G. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Adhikari, R.; Verma, G.; Khandelwal, I. A model ranking based selective ensemble approach for time series forecasting. Procedia Comput. Sci. 2015, 48, 14–21. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C. Time Series Analysis: Forecasting and Control, 3rd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1994. [Google Scholar]
- Kumar, K.; Jain, V.K. Autoregressive integrated moving averages (ARIMA) modeling of a traffic noise time series. Appl. Acoust. 1999, 58, 283–294. [Google Scholar] [CrossRef]
- Ediger, V.S.; Akar, S. ARIMA forecasting of primary energy demand by fuel in Turkey. Energy Policy 2007, 35, 1701–1708. [Google Scholar] [CrossRef]
- Poczeta, K.; Kubus, L.; Yastrebov, A.; Papageorgiou, E.I. Temperature forecasting for energy saving in smart buildings based on fuzzy cognitive map. In Proceedings of the 2018 Conference on Automation (Automation 2018), Warsaw, Poland, 21–23 March 2018; pp. 93–103. [Google Scholar]
- Poczęta, K.; Yastrebov, A.; Papageorgiou, E.I. Application of fuzzy cognitive maps to multi-step ahead prediction of electricity consumption. In Proceedings of the IEEE 2018 Conference on Electrotechnology: Processes, Models, Control and Computer Science (EPMCCS), Kielce, Poland, 12–14 November 2018; pp. 1–5. [Google Scholar]
- Khashei, M.; Rafiei, F.M.; Bijari, M. Hybrid fuzzy auto-regressive integrated moving average (FARIMAH) model for forecasting the foreign exchange markets. Int. J. Comput. Intell. Syst. 2013, 6, 954–968. [Google Scholar] [CrossRef]
- Chu, F.L. A fractionally integrated autoregressive moving average approach to forecasting tourism demand. Tour. Manag. 2008, 29, 79–88. [Google Scholar] [CrossRef]
- Yu, H.K.; Kim, N.Y.; Kim, S.S. Forecasting the number of human immunodeficiency virus infections in the Korean population using the autoregressive integrated moving average model. Osong Public Health Res. Perspect. 2013, 4, 358–362. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Doganis, P.; Alexandridis, A.; Patrinos, P.; Sarimveis, H. Time series sales forecasting for short shelf-life food products based on artificial neural networks and evolutionary computing. J. Food Eng. 2006, 75, 196–204. [Google Scholar] [CrossRef]
- Kim, M.; Jeong, J.; Bae, S. Demand forecasting based on machine learning for mass customization in smart manufacturing. In Proceedings of the ACM 2019 International Conference on Data Mining and Machine Learning (ICDMML 2019), Hong Kong, China, 28–30 April 2019; pp. 6–11. [Google Scholar]
- Wang, D.M.; Wang, L.; Zhang, G.M. Short-term wind speed forecast model for wind farms based on genetic BP neural network. J. Zhejiang Univ. (Eng. Sci.) 2012, 46, 837–842. [Google Scholar]
- Breiman, L. Stacked regressions. Mach. Learn. 1996, 24, 49–64. [Google Scholar] [CrossRef]
- Clemen, R. Combining forecasts: A review and annotated bibliography. J. Forecast. 1989, 5, 559–583. [Google Scholar] [CrossRef]
- Perrone, M. Improving Regression Estimation: Averaging Methods for Variance Reduction with Extension to General Convex Measure Optimization. Ph.D. Thesis, Brown University, Providence, RI, USA, 1993. [Google Scholar]
- Wolpert, D. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Geman, S.; Bienenstock, E.; Doursat, R. Neural networks and the bias/variance dilemma. Neural Comput. 1992, 4, 1–58. [Google Scholar] [CrossRef]
- Krogh, A.; Sollich, P. Statistical mechanics of ensemble learning. Phys. Rev. 1997, 55, 811–825. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R. Experiments with a new boosting algorithm. In Proceedings of the 13th International Conference on Machine Learning (ICML 96), Bari, Italy, 3–6 July 1996; pp. 148–156. [Google Scholar]
- Schapire, R. The strength of weak learnability. Mach. Learn. 1990, 5, 197–227. [Google Scholar] [CrossRef]
- Che, J. Optimal sub-models selection algorithm for combination forecasting model. Neurocomputing 2014, 151, 364–375. [Google Scholar] [CrossRef]
- Wei, N.; Li, C.J.; Li, C.; Xie, H.Y.; Du, Z.W.; Zhang, Q.S.; Zeng, F.H. Short-term forecasting of natural gas consumption using factor selection algorithm and optimized support vector regression. J. Energy Resour. Technol. 2018, 141, 032701. [Google Scholar] [CrossRef]
- Tamba, J.G.; Essiane, S.N.; Sapnken, E.F.; Koffi, F.D.; Nsouandélé, J.L.; Soldo, B.; Njomo, D. Forecasting natural gas: A literature survey. Int. J. Energy Econ. Policy 2018, 8, 216–249. [Google Scholar]
- Sebalj, D.; Mesaric, J.; Dujak, D. Predicting natural gas consumption a literature review. In Proceedings of the 28th Central European Conference on Information and Intelligent Systems (CECIIS ’17), Varazdin, Croatia, 27–29 September 2017; pp. 293–300. [Google Scholar]
- Azadeh, I.P.; Dagoumas, A.S. Day-ahead natural gas demand forecasting based on the combination of wavelet transform and ANFIS/genetic algorithm/neural network model. Energy 2017, 118, 231–245. [Google Scholar]
- Gorucu, F.B.; Geris, P.U.; Gumrah, F. Artificial neural network modeling for forecasting gas consumption. Energy Sources 2004, 26, 299–307. [Google Scholar] [CrossRef]
- Karimi, H.; Dastranj, J. Artificial neural network-based genetic algorithm to predict natural gas consumption. Energy Syst. 2014, 5, 571–581. [Google Scholar] [CrossRef]
- Khotanzad, A.; Erlagar, H. Natural gas load forecasting with combination of adaptive neural networks. In Proceedings of the International Joint Conference on Neural Networks (IJCNN 99), Washington, DC, USA, 10–16 July 1999; pp. 4069–4072. [Google Scholar]
- Khotanzad, A.; Elragal, H.; Lu, T.L. Combination of artificial neural-network forecasters for prediction of natural gas consumption. IEEE Trans. Neural Netw. 2000, 11, 464–473. [Google Scholar] [CrossRef]
- Kizilaslan, R.; Karlik, B. Combination of neural networks forecasters for monthly natural gas consumption prediction. Neural Netw. World 2009, 19, 191–199. [Google Scholar]
- Kizilaslan, R.; Karlik, B. Comparison neural networks models for short term forecasting of natural gas consumption in Istanbul. In Proceedings of the First International Conference on the Applications of Digital Information and Web Technologies (ICADIWT), Ostrava, Czech Republic, 4–6 August 2008; pp. 448–453. [Google Scholar]
- Musilek, P.; Pelikan, E.; Brabec, T.; Simunek, M. Recurrent neural network based gating for natural gas load prediction system. In Proceedings of the 2006 IEEE International Joint Conference on Neural Networks, Vancouver, BC, Canada, 16–21 July 2006; pp. 3736–3741. [Google Scholar]
- Soldo, B. Forecasting natural gas consumption. Appl. Energy 2012, 92, 26–37. [Google Scholar] [CrossRef]
- Szoplik, J. Forecasting of natural gas consumption with artificial neural networks. Energy 2015, 85, 208–220. [Google Scholar] [CrossRef]
- Potočnik, P.; Soldo, B.; Šimunović, G.; Šarić, T.; Jeromen, A.; Govekar, E. Comparison of static and adaptive models for short-term residential natural gas forecasting in Croatia. Appl. Energy 2014, 129, 94–103. [Google Scholar] [CrossRef]
- Akpinar, M.; Yumusak, N. Forecasting household natural gas consumption with ARIMA model: A case study of removing cycle. In Proceedings of the 7th IEEE International Conference on Application of Information and Communication Technologies (ICAICT 2013), Baku, Azerbaijan, 23–25 October 2013; pp. 1–6. [Google Scholar]
- Akpinar, M.M.; Adak, F.; Yumusak, N. Day-ahead natural gas demand forecasting using optimized ABC-based neural network with sliding window technique: The case study of regional basis in Turkey. Energies 2017, 10, 781. [Google Scholar] [CrossRef]
- Taşpınar, F.; Çelebi, N.; Tutkun, N. Forecasting of daily natural gas consumption on regional basis in Turkey using various computational methods. Energy Build. 2013, 56, 23–31. [Google Scholar] [CrossRef]
- Azadeh, A.; Asadzadeh, S.M.; Ghanbari, A. An adaptive network-based fuzzy inference system for short-term natural gas demand estimation: Uncertain and complex environments. Energy Policy 2010, 38, 1529–1536. [Google Scholar] [CrossRef]
- Behrouznia, A.; Saberi, M.; Azadeh, A.; Asadzadeh, S.M.; Pazhoheshfar, P. An adaptive network based fuzzy inference system-fuzzy data envelopment analysis for gas consumption forecasting and analysis: The case of South America. In Proceedings of the 2010 International Conference on Intelligent and Advanced Systems (ICIAS), Manila, Philippines, 15–17 June 2010; pp. 1–6. [Google Scholar]
- Viet, N.H.; Mandziuk, J. Neural and fuzzy neural networks for natural gas prediction consumption. In Proceedings of the 13th IEEE Workshop on Neural Networks for Signal Processing (NNSP 2003), Toulouse, France, 17–19 September 2003; pp. 759–768. [Google Scholar]
- Yu, F.; Xu, X. A short-term load forecasting model of natural gas based on optimized genetic algorithm and improved BP neural network. Appl. Energy 2014, 134, 102–113. [Google Scholar] [CrossRef]
- Papageorgiou, E.I. Fuzzy Cognitive Maps for Applied Sciences and Engineering from Fundamentals to Extensions and Learning Algorithms; Intelligent Systems Reference Library, Springer: Heidelberg, Germany, 2014. [Google Scholar]
- Poczeta, K.; Papageorgiou, E.I. Implementing fuzzy cognitive maps with neural networks for natural gas prediction. In Proceedings of the 30th IEEE International Conference on Tools with Artificial Intelligence (ICTAI 2018), Volos, Greece, 5–7 November 2018; pp. 1026–1032. [Google Scholar]
- Homenda, W.; Jastrzebska, A.; Pedrycz, W. Modeling time series with fuzzy cognitive maps. In Proceedings of the 2014 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Beijing, China, 6–11 July 2014; pp. 2055–2062. [Google Scholar]
- Homenda, W.; Jastrzębska, A.; Pedrycz, W. Nodes selection criteria for fuzzy cognitive maps designed to model time series. Adv. Intell. Syst. Comput. 2015, 323, 859–870. [Google Scholar]
- Salmeron, J.L.; Froelich, W. Dynamic optimization of fuzzy cognitive maps for time series forecasting. Knowl -Based Syst. 2016, 105, 29–37. [Google Scholar] [CrossRef]
- Froelich, W.; Salmeron, J.L. Evolutionary learning of fuzzy grey cognitive maps for the forecasting of multivariate, interval-valued time series. Int. J. Approx. Reason 2014, 55, 1319–1335. [Google Scholar] [CrossRef]
- Papageorgiou, E.I.; Poczęta, K.; Laspidou, C. Application of fuzzy cognitive maps to water demand prediction, fuzzy systems. In Proceedings of the 2015 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Istanbul, Turkey, 2–5 August 2015; pp. 1–8. [Google Scholar]
- Poczeta, K.; Yastrebov, A.; Papageorgiou, E.I. Learning fuzzy cognitive maps using structure optimization genetic algorithm. In Proceedings of the 2015 Federated Conference on Computer Science and Information Systems (FedCSIS), Lodz, Poland, 13–16 September 2015; pp. 547–554. [Google Scholar]
- Jastriebow, A.; Poczęta, K. Analysis of multi-step algorithms for cognitive maps learning. Bull. Pol. Acad. Sci. Technol. Sci. 2014, 62, 735–741. [Google Scholar] [CrossRef]
- Stach, W.; Kurgan, L.; Pedrycz, W.; Reformat, M. Genetic learning of fuzzy cognitive maps. Fuzzy Sets Syst. 2005, 153, 371–401. [Google Scholar] [CrossRef]
- Papageorgiou, E.I.; Poczeta, K. A two-stage model for time series prediction based on fuzzy cognitive maps and neural networks. Neurocomputing 2017, 232, 113–121. [Google Scholar] [CrossRef]
- Anagnostis, A.; Papageorgiou, E.; Dafopoulos, V.; Bochtis, D. Applying Long Short-Term Memory Networks for natural gas demand prediction. In Proceedings of the 10th International Conference on Information, Intelligence, Systems and Applications (IISA 2019), Patras, Greece, 15–17 July 2019. [Google Scholar]
- Kosko, B. Fuzzy cognitive maps. Int. J. Man Mach. Stud. 1986, 24, 65–75. [Google Scholar] [CrossRef]
- Kardaras, D.; Mentzas, G. Using fuzzy cognitive maps to model and analyze business performance assessment. In Advances in Industrial Engineering Applications and Practice II; Chen, J., Mital, A., Eds.; International Journal of Industrial Engineering: San Diego, CA, USA, 12–15 November 1997; pp. 63–68. [Google Scholar]
- Lee, K.Y.; Yang, F.F. Optimal reactive power planning using evolutionary algorithms: A comparative study for evolutionary programming, evolutionary strategy, genetic algorithm, and linear programming. IEEE Trans. Power Syst. 1998, 13, 101–108. [Google Scholar] [CrossRef]
- Dickerson, J.A.; Kosko, B. Virtual Worlds as Fuzzy Cognitive Maps. Presence 1994, 3, 173–189. [Google Scholar] [CrossRef]
- Hossain, S.; Brooks, L. Fuzzy cognitive map modelling educational software adoption. Comput. Educ. 2008, 51, 1569–1588. [Google Scholar] [CrossRef]
- Fogel, D.B. Evolutionary Computation. Toward a New Philosophy of Machine Intelligence, 3rd ed.; Wiley: Hoboken, NJ, USA; IEEE Press: Piscataway, NJ, USA, 2006. [Google Scholar]
- Herrera, F.; Lozano, M.; Verdegay, J.L. Tackling real-coded genetic algorithms: Operators and tools for behavioural analysis. Artif. Intell. Rev. 1998, 12, 265–319. [Google Scholar] [CrossRef]
- Livieris, I.E. Forecasting Economy-related data utilizing weight-constrained recurrent neural networks. Algorithms 2019, 12, 85. [Google Scholar] [CrossRef]
- Livieris, I.E.; Pintelas, P. A Survey on Algorithms for Training Artificial Neural Networks; Technical Report; Department of Mathematics, University of Patras: Patras, Greece, 2008. [Google Scholar]
- Adhikari, R.; Agrawal, R.K. Performance evaluation of weight selection schemes for linear combination of multiple forecasts. Artif. Intell. Rev. 2012, 42, 1–20. [Google Scholar] [CrossRef]
- Livieris, I.E.; Kanavos, A.; Tampakas, V.; Pintelas, P. A weighted voting ensemble self-labeled algorithm for the detection of lung abnormalities from X-rays. Algorithms 2019, 12, 64. [Google Scholar] [CrossRef]
- Makridakis, S.; Winkler, R.L. Averages of forecasts: Some empirical results. Manag. Sci. 1983, 29, 987–996. [Google Scholar] [CrossRef]
- Lemke, C.; Gabrys, B. Meta-learning for time series forecasting and forecast combination. Neurocomputing 2010, 73, 2006–2016. [Google Scholar] [CrossRef]
- Palm, F.C.; Zellner, A. To combine or not to combine? Issues of combining forecasts. J. Forecast. 1992, 11, 687–701. [Google Scholar] [CrossRef]
- Kreiss, J.; Lahiri, S. Bootstrap methods for time series. In Time Series Analysis: Methods and Applications; Rao, T., Rao, S., Rao, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Shalabi, L.A.; Shaaban, Z. Normalization as a preprocessing engine for data mining and the approach of preference matrix. In Proceedings of the International Conference on Dependability of Computer Systems (DepCos-RELCOMEX), Szklarska Poreba, Poland, 25–27 May 2006; pp. 207–214. [Google Scholar]
- Nayak, S.; Misra, B.B.; Behera, H. Evaluation of normalization methods on neuro-genetic models for stock index forecasting. In Proceedings of the 2012 World Congress on Information and Communication Technologies (WICT 2012), Trivandrum, India, 30 October–2 November 2012; pp. 602–607. [Google Scholar]
- Jayalakshmi, T.; Santhakumaran, A. Statistical normalization and back propagation for classification. Int. J. Comput. Theory Eng. 2011, 3, 89–93. [Google Scholar] [CrossRef]
- Brown, A. A new software for carrying out one-way ANOVA post hoc tests. Comput. Methods Programs Biomed. 2005, 79, 89–95. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Xu, M.; Tu, J.; Wang, H.; Niu, X. Relationship between omnibus and post-hoc tests: An investigation of performance of the F test in ANOVA. Shanghai Arch. Psychiatry 2018, 30, 60–64. [Google Scholar] [PubMed]
- Understanding the LSTM Networks. Available online: http://colah.github.io (accessed on 10 September 2019).
- Holzinger, A. From machine learning to explainable AI. In Proceedings of the 2018 World Symposium on Digital Intelligence for Systems and Machines (IEEE DISA), Kosice, Slovakia, 23–25 August 2018; pp. 55–66. [Google Scholar]

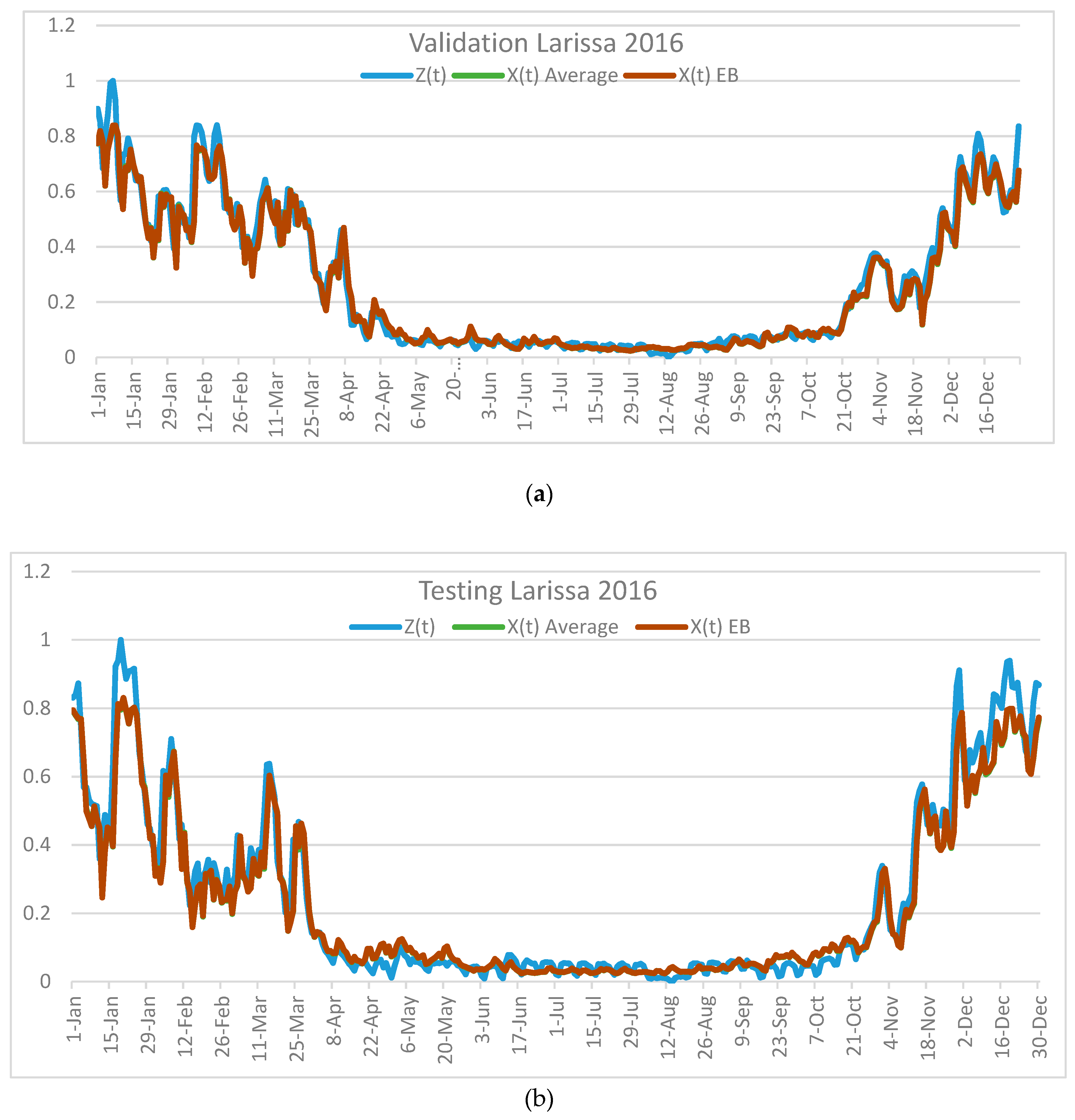
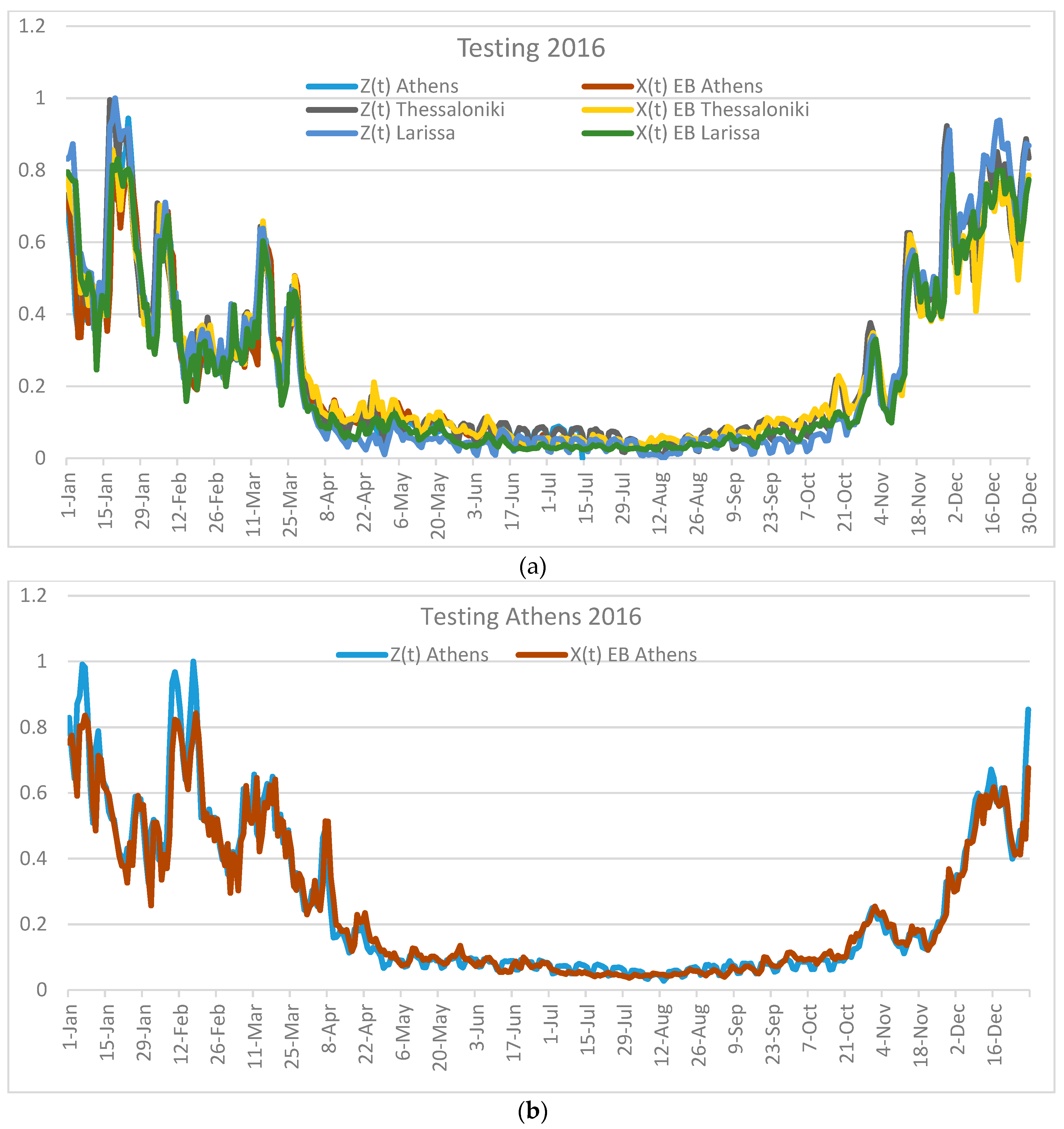

| Validation | Testing | Testing | |||||||
|---|---|---|---|---|---|---|---|---|---|
| MAE | MSE | MAE | MSE | Weights | MAE | MSE | Weights | ||
| ANN1 | 0.0334 | 0.0035 | 0.0350 | 0.0036 | 0.2552 | Hybrid1 | 0.0336 | 0.0034 | 0.2520 |
| ANN2 | 0.0354 | 0.0041 | 0.0387 | 0.0043 | 0 | Hybrid2 | 0.0387 | 0.0043 | 0 |
| ANN3 | 0.0350 | 0.0037 | 0.0375 | 0.0039 | 0.2442 | Hybrid3 | 0.0363 | 0.0037 | 0 |
| ANN4 | 0.0341 | 0.0038 | 0.0365 | 0.0039 | 0 | Hybrid4 | 0.0352 | 0.0035 | 0 |
| ANN5 | 0.0335 | 0.0036 | 0.0358 | 0.0037 | 0.2505 | Hybrid5 | 0.0339 | 0.0034 | 0 |
| ANN6 | 0.0337 | 0.0039 | 0.0355 | 0.0038 | 0 | Hybrid6 | 0.0348 | 0.0036 | 0.2468 |
| ANN7 | 0.0336 | 0.0037 | 0.0362 | 0.0038 | 0 | Hybrid7 | 0.0345 | 0.0035 | 0.2506 |
| ANN8 | 0.0340 | 0.0039 | 0.0360 | 0.0039 | 0 | Hybrid8 | 0.0354 | 0.0036 | 0 |
| ANN9 | 0.0341 | 0.0039 | 0.0367 | 0.0040 | 0 | Hybrid9 | 0.0349 | 0.0036 | 0 |
| ANN10 | 0.0332 | 0.0036 | 0.0355 | 0.0037 | 0.2501 | Hybrid10 | 0.0359 | 0.0038 | 0 |
| ANN11 | 0.0338 | 0.0038 | 0.0365 | 0.0039 | 0 | Hybrid11 | 0.0353 | 0.0038 | 0 |
| ANN12 | 0.0345 | 0.0038 | 0.0349 | 0.0037 | 0 | Hybrid12 | 0.0347 | 0.0033 | 0.2506 |
| AVG | 0.0336 | 0.0037 | 0.0359 | 0.0038 | AVG | 0.0350 | 0.0036 | ||
| EB | 0.0335 | 0.0036 | 0.0358 | 0.0037 | EB | 0.0340 | 0.0034 | ||
| Athens | Thessaloniki | Larissa | |
|---|---|---|---|
| Weights based on scores | |||
| ANN | 0.3320 | 0.34106 | 0.3369 |
| Hybrid | 0.3357 | 0.35162 | 0.3546 |
| RCGA-FCM | 0.3323 | 0 | 0 |
| SOGA-FCM | 0 | 0.30731 | 0.3083 |
| Validation | ANN | Hybrid | RCGA | SOGA | Ensemble AVG | Ensemble EB |
|---|---|---|---|---|---|---|
| MAE | 0.0328 | 0.0333 | 0.0384 | 0.0391 | 0.0336 | 0.0326 |
| MSE | 0.0036 | 0.0035 | 0.0036 | 0.0037 | 0.0032 | 0.0032 |
| Testing | ||||||
| MAE | 0.0321 | 0.0328 | 0.0418 | 0.0424 | 0.0345 | 0.0328 |
| MSE | 0.0033 | 0.0032 | 0.0038 | 0.0040 | 0.0032 | 0.0031 |
| Validation | ANN Ensemble | Hybrid Ensemble | RCGA Ensemble | SOGA Ensemble | Ensemble AVG | Ensemble EB |
|---|---|---|---|---|---|---|
| MAE | 0.0335 | 0.0330 | 0.0388 | 0.0380 | 0.0337 | 0.0337 |
| MSE | 0.0036 | 0.0035 | 0.0036 | 0.0035 | 0.0032 | 0.0032 |
| Testing | ||||||
| MAE | 0.0358 | 0.0340 | 0.0422 | 0.0422 | 0.0352 | 0.0352 |
| MSE | 0.0037 | 0.0034 | 0.0038 | 0.0037 | 0.0032 | 0.0032 |
| Validation | ANN | Hybrid | RCGA | SOGA | Ensemble AVG | Ensemble EB |
|---|---|---|---|---|---|---|
| MAE | 0.0343 | 0.0341 | 0.0381 | 0.0380 | 0.0347 | 0.0340 |
| MSE | 0.0029 | 0.0028 | 0.0032 | 0.0032 | 0.0028 | 0.0027 |
| Testing | ||||||
| MAE | 0.0366 | 0.0381 | 0.0395 | 0.0399 | 0.0371 | 0.0369 |
| MSE | 0.0032 | 0.0033 | 0.0035 | 0.0036 | 0.0032 | 0.0031 |
| Validation | ANN Ensemble | Hybrid Ensemble | RCGA Ensemble | SOGA Ensemble | Ensemble AVG | Ensemble EB |
|---|---|---|---|---|---|---|
| MAE | 0.0363 | 0.0361 | 0.0378 | 0.0374 | 0.0355 | 0.0355 |
| MSE | 0.0031 | 0.0031 | 0.0031 | 0.0030 | 0.0028 | 0.0028 |
| Testing | ||||||
| MAE | 0.0393 | 0.0394 | 0.0399 | 0.0391 | 0.0381 | 0.0381 |
| MSE | 0.0037 | 0.0037 | 0.0036 | 0.0034 | 0.0034 | 0.0034 |
| Validation | ANN | Hybrid | RCGA | SOGA | Ensemble AVG | Ensemble EB |
|---|---|---|---|---|---|---|
| MAE | 0.0322 | 0.0324 | 0.0372 | 0.0365 | 0.0326 | 0.0319 |
| MSE | 0.0030 | 0.0028 | 0.0033 | 0.0032 | 0.0027 | 0.0027 |
| Testing | ||||||
| MAE | 0.0412 | 0.0417 | 0.0466 | 0.0468 | 0.0427 | 0.0417 |
| MSE | 0.0043 | 0.0041 | 0.0047 | 0.0047 | 0.0040 | 0.0040 |
| Validation | ANN Ensemble | Hybrid Ensemble | RCGA Ensemble | SOGA Ensemble | Ensemble AVG | Ensemble EB |
|---|---|---|---|---|---|---|
| MAE | 0.0337 | 0.0332 | 0.0371 | 0.0362 | 0.0329 | 0.0326 |
| MSE | 0.0032 | 0.0030 | 0.0032 | 0.0031 | 0.0027 | 0.0026 |
| Testing | ||||||
| MAE | 0.0428 | 0.0417 | 0.0458 | 0.0460 | 0.0426 | 0.0423 |
| MSE | 0.0048 | 0.0044 | 0.0045 | 0.0045 | 0.0041 | 0.0040 |
| Best Ensemble | LSTM (Dropout = 0.2) | ||
|---|---|---|---|
| Case (A) (Individual) | Case (B) (Ensemble) | 1 layer | |
| Validation | ATHENS | ||
| MAE | 0.0326 | 0.0337 | 0.0406 |
| MSE | 0.0032 | 0.0032 | 0.0039 |
| Testing | |||
| MAE | 0.0328 | 0.0352 | 0.0426 |
| MSE | 0.0031 | 0.0032 | 0.0041 |
| Validation | THESSALONIKI | ||
| MAE | 0.0340 | 0.0355 | 0.0462 |
| MSE | 0.0027 | 0.0028 | 0.0043 |
| Testing | |||
| MAE | 0.0369 | 0.0381 | 0.0489 |
| MSE | 0.0031 | 0.0034 | 0.0045 |
| Validation | LARISSA | ||
| MAE | 0.0319 | 0.0326 | 0.0373 |
| MSE | 0.0027 | 0.0026 | 0.0029 |
| Testing | |||
| MAE | 0.0417 | 0.0423 | 0.0462 |
| MSE | 0.0040 | 0.0040 | 0.0042 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papageorgiou, K.I.; Poczeta, K.; Papageorgiou, E.; Gerogiannis, V.C.; Stamoulis, G. Exploring an Ensemble of Methods that Combines Fuzzy Cognitive Maps and Neural Networks in Solving the Time Series Prediction Problem of Gas Consumption in Greece. Algorithms 2019, 12, 235. https://doi.org/10.3390/a12110235
Papageorgiou KI, Poczeta K, Papageorgiou E, Gerogiannis VC, Stamoulis G. Exploring an Ensemble of Methods that Combines Fuzzy Cognitive Maps and Neural Networks in Solving the Time Series Prediction Problem of Gas Consumption in Greece. Algorithms. 2019; 12(11):235. https://doi.org/10.3390/a12110235
Chicago/Turabian StylePapageorgiou, Konstantinos I., Katarzyna Poczeta, Elpiniki Papageorgiou, Vassilis C. Gerogiannis, and George Stamoulis. 2019. "Exploring an Ensemble of Methods that Combines Fuzzy Cognitive Maps and Neural Networks in Solving the Time Series Prediction Problem of Gas Consumption in Greece" Algorithms 12, no. 11: 235. https://doi.org/10.3390/a12110235
APA StylePapageorgiou, K. I., Poczeta, K., Papageorgiou, E., Gerogiannis, V. C., & Stamoulis, G. (2019). Exploring an Ensemble of Methods that Combines Fuzzy Cognitive Maps and Neural Networks in Solving the Time Series Prediction Problem of Gas Consumption in Greece. Algorithms, 12(11), 235. https://doi.org/10.3390/a12110235








