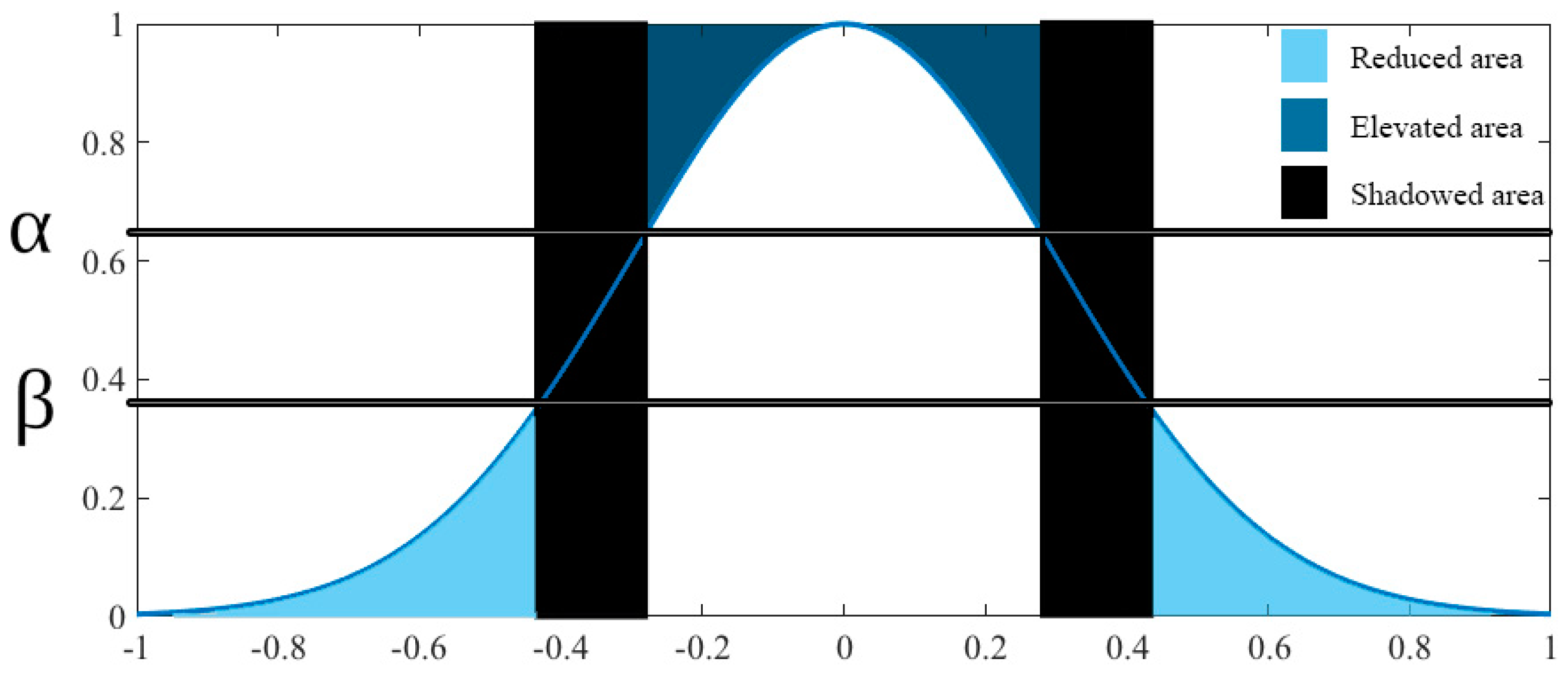
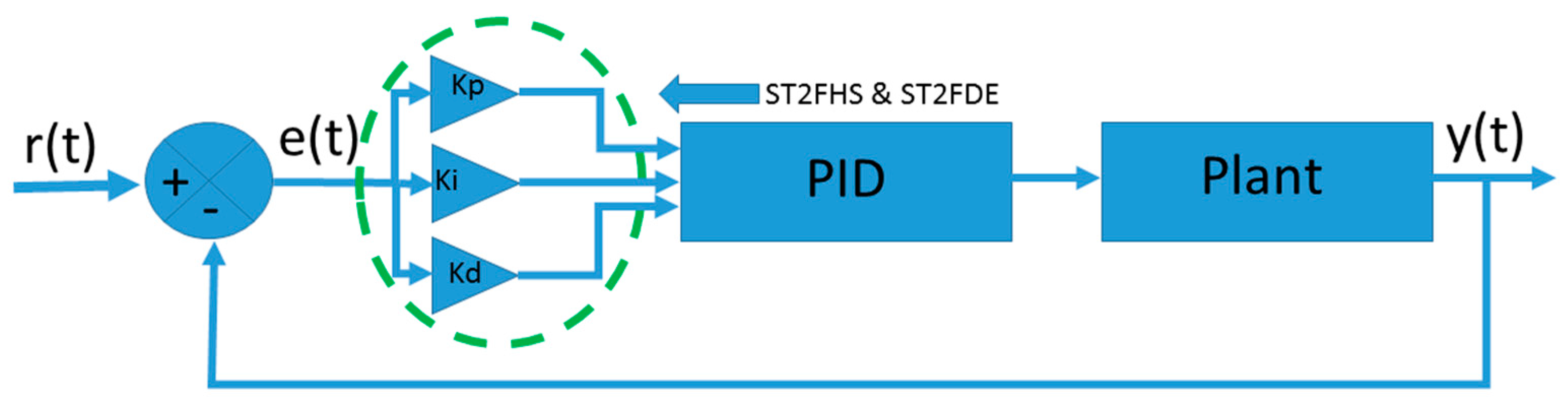
Figure 1.
Shadowed set representation.
Figure 1.
Shadowed set representation.
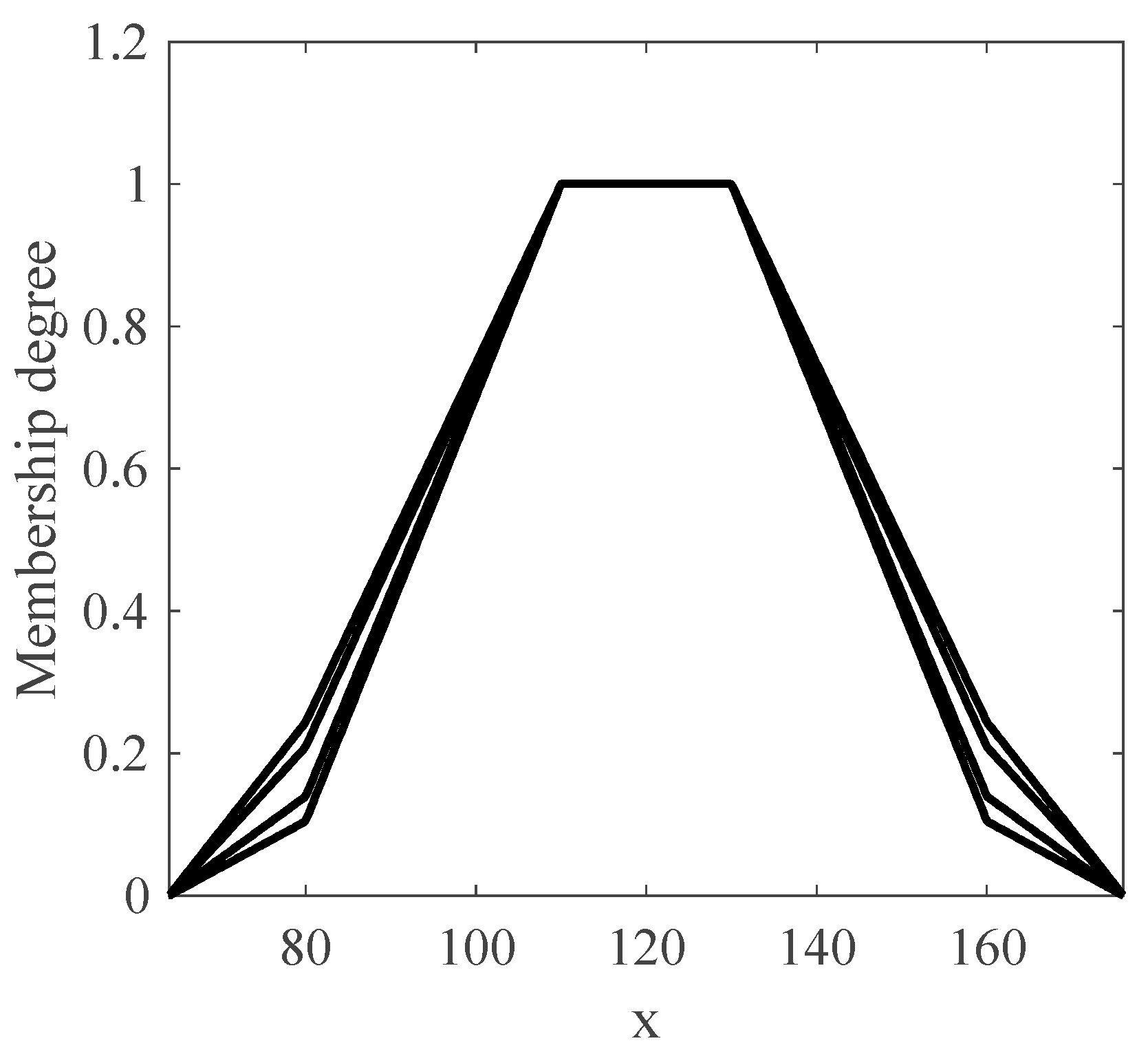
Figure 2.
Trapezoidal Shadowed Type-2 (ST2) MF.
Figure 2.
Trapezoidal Shadowed Type-2 (ST2) MF.
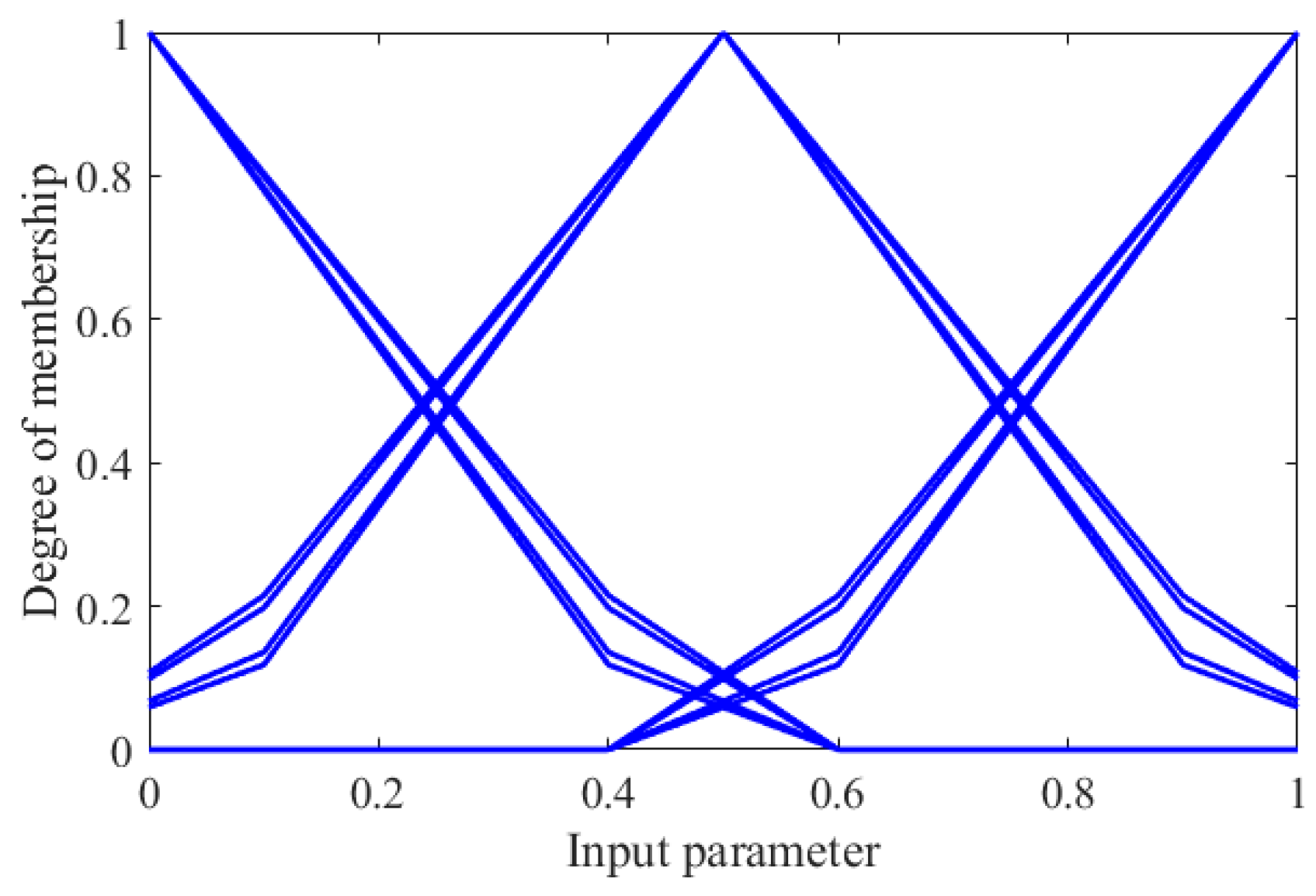
Figure 3.
Input parameter membership functions.
Figure 3.
Input parameter membership functions.
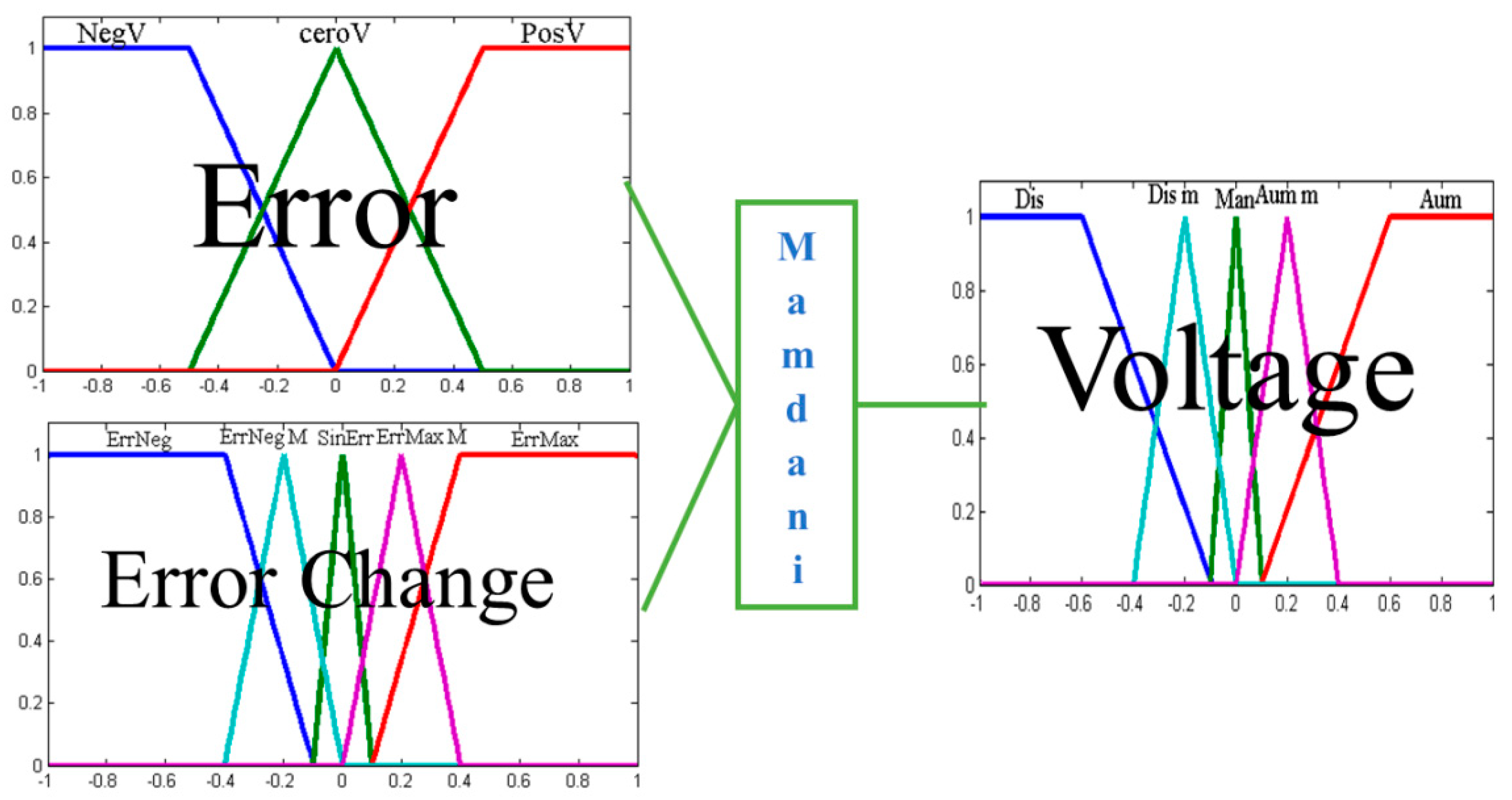
Figure 4.
Output parameter membership functions.
Figure 4.
Output parameter membership functions.
Figure 5.
Motor position plant.
Figure 5.
Motor position plant.
Figure 6.
Structure of the motor position.
Figure 6.
Structure of the motor position.
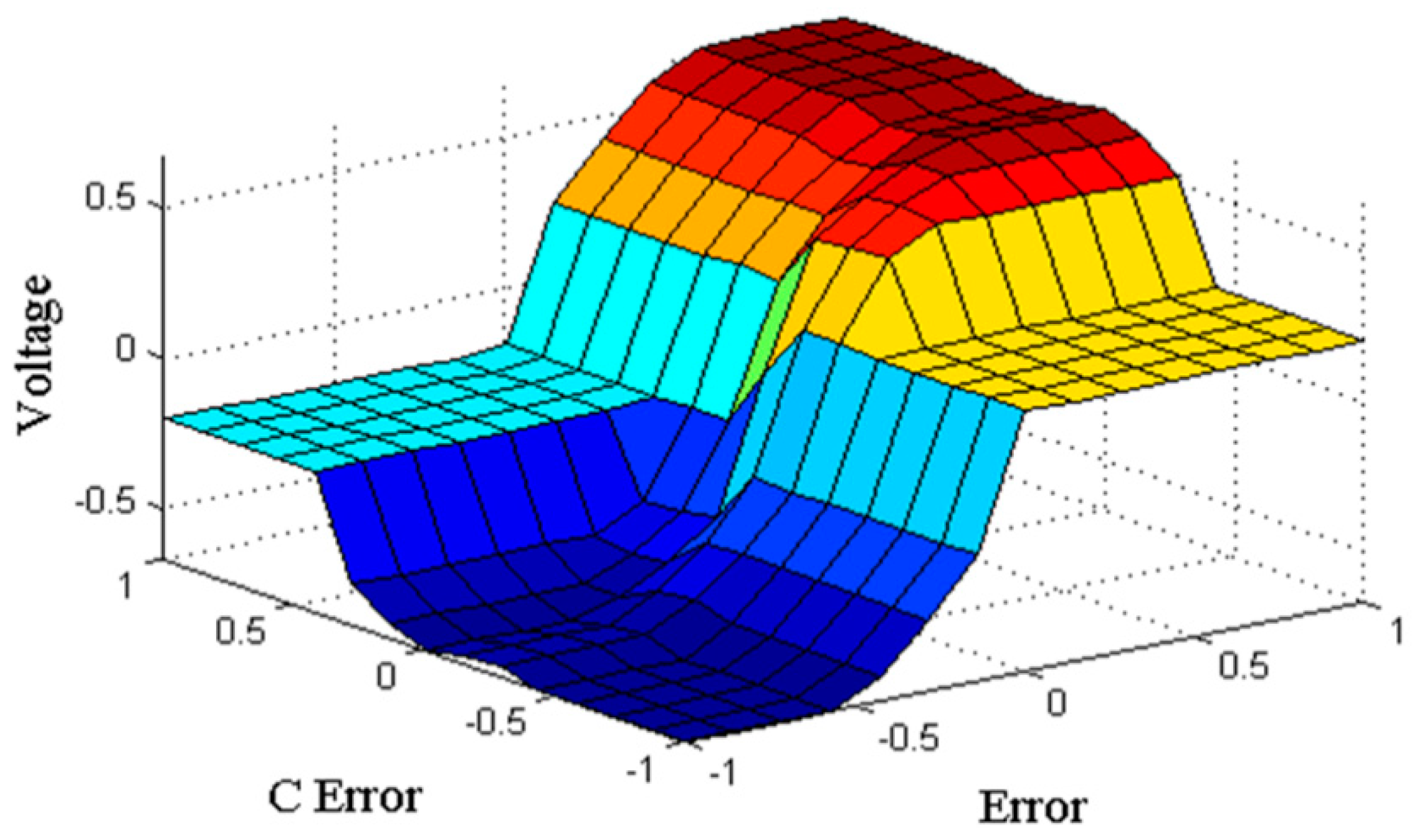
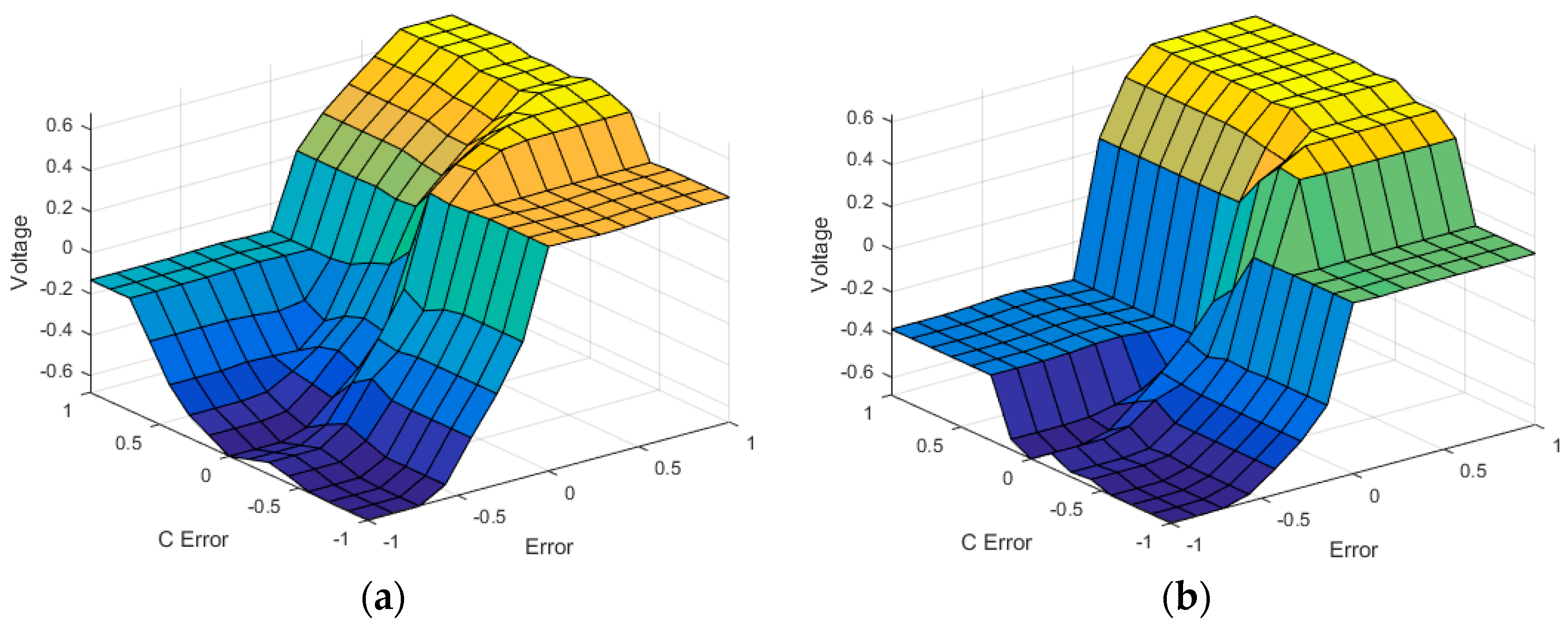
Figure 7.
Surface of the fuzzy system.
Figure 7.
Surface of the fuzzy system.
Figure 8.
Representation of the individuals for the T1 FIS.
Figure 8.
Representation of the individuals for the T1 FIS.
Figure 9.
HS and ST2FHS without noise.
Figure 9.
HS and ST2FHS without noise.
Figure 10.
HS and ST2FHS with noise.
Figure 10.
HS and ST2FHS with noise.
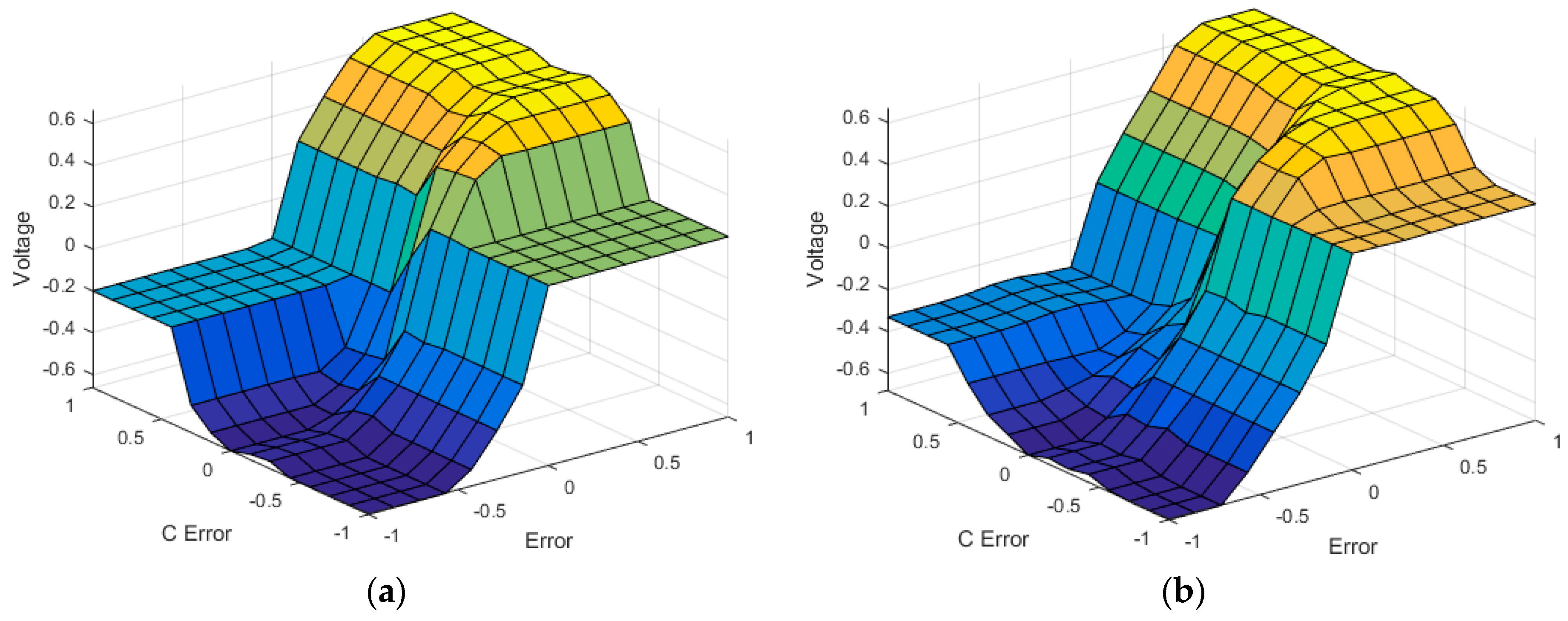
Figure 11.
Comparison of the surface for each method for the motor position controller: (a) HS without noise algorithm; (b) ST2FHS without noise algorithm.
Figure 11.
Comparison of the surface for each method for the motor position controller: (a) HS without noise algorithm; (b) ST2FHS without noise algorithm.
Figure 12.
Comparison of the surface for each method for the motor position controller: (a) HS with noise algorithm; (b) ST2FHS with noise algorithm.
Figure 12.
Comparison of the surface for each method for the motor position controller: (a) HS with noise algorithm; (b) ST2FHS with noise algorithm.
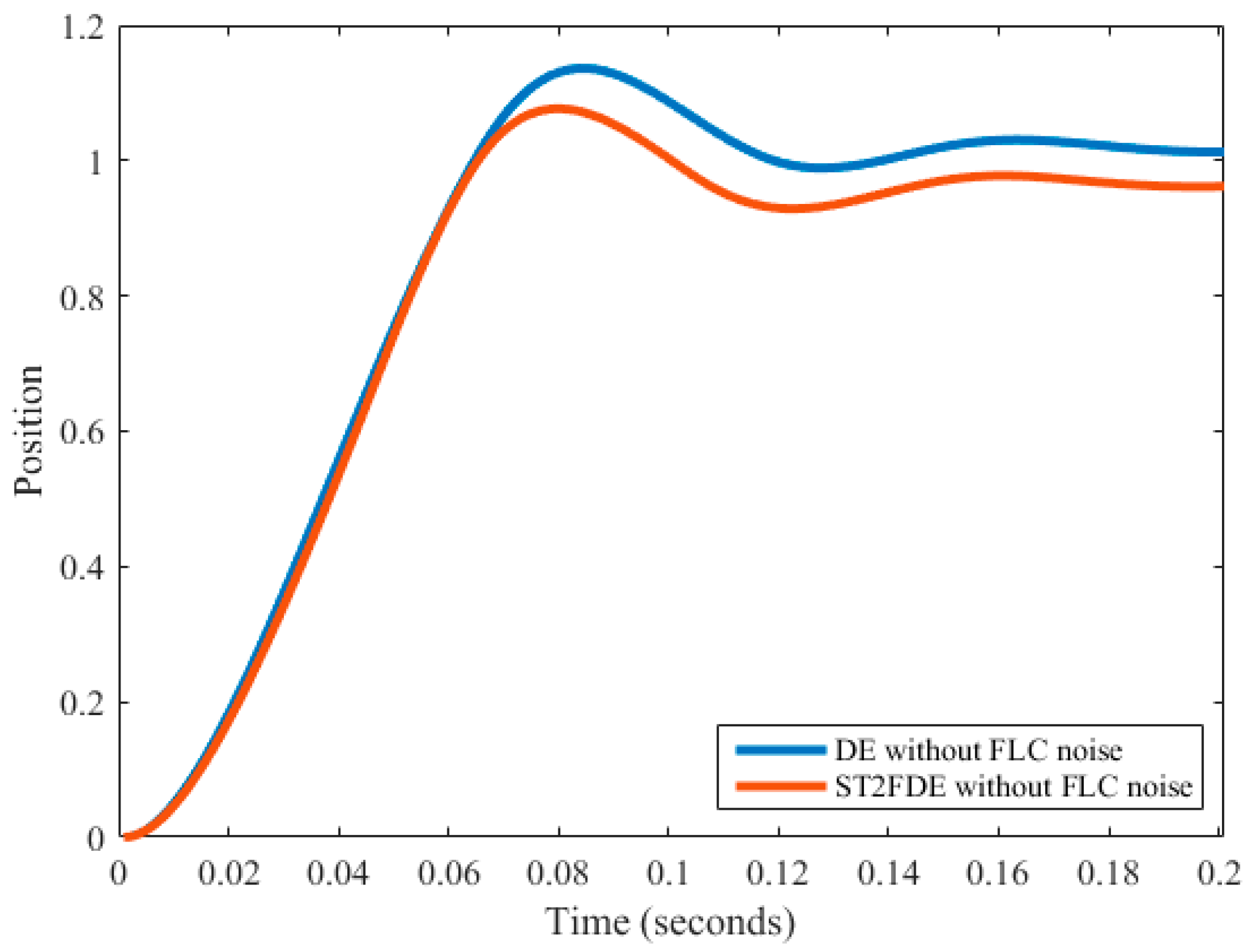
Figure 13.
DE and ST2FDE without noise.
Figure 13.
DE and ST2FDE without noise.
Figure 14.
DE and ST2FDE with noise.
Figure 14.
DE and ST2FDE with noise.
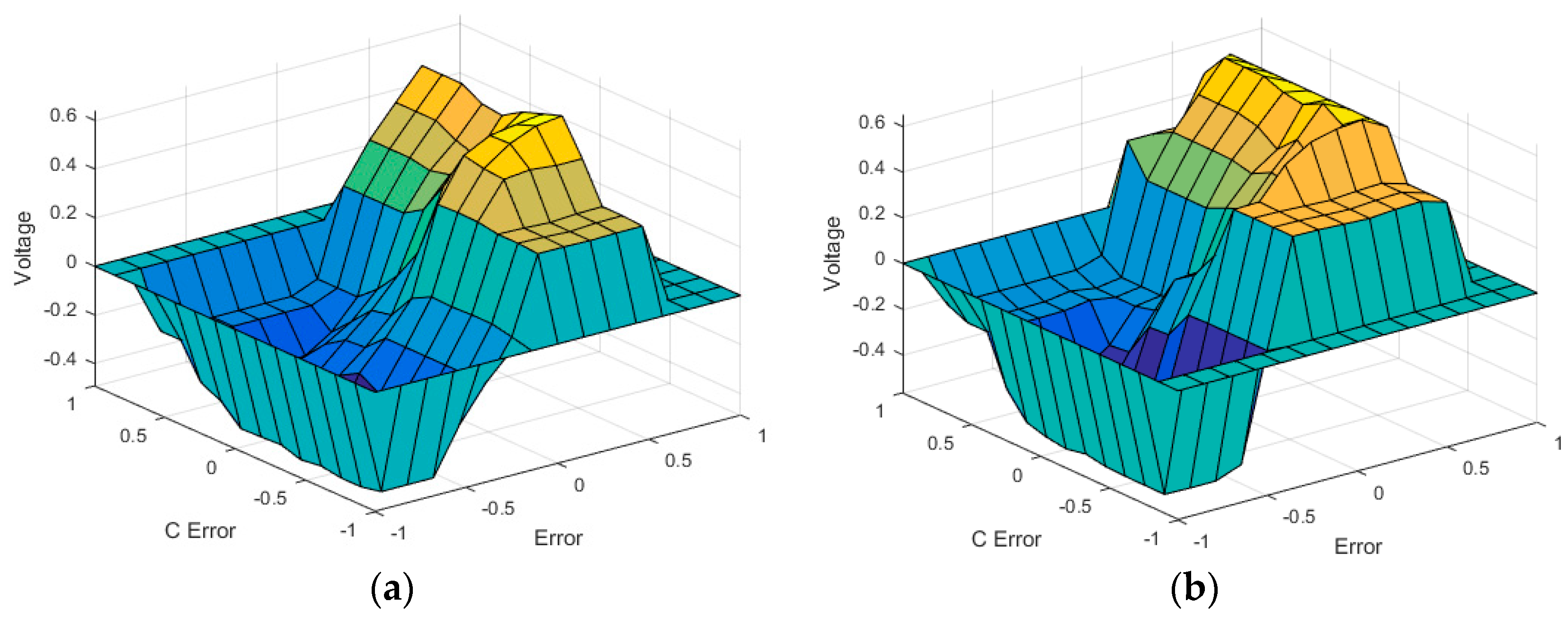
Figure 15.
Comparison of the surface for each method for the motor position controller: (a) DE without noise algorithm; (b) ST2FDE without noise algorithm.
Figure 15.
Comparison of the surface for each method for the motor position controller: (a) DE without noise algorithm; (b) ST2FDE without noise algorithm.
Figure 16.
Comparison of the surface for each method for the motor position controller: (a) DE with noise algorithm; (b) ST2FDE with noise algorithm.
Figure 16.
Comparison of the surface for each method for the motor position controller: (a) DE with noise algorithm; (b) ST2FDE with noise algorithm.
Figure 17.
Structure of the PID (Proportional-Integral-Derivative) DC motor.
Figure 17.
Structure of the PID (Proportional-Integral-Derivative) DC motor.
Figure 18.
Best result obtained from the HS and ST2FHS methods.
Figure 18.
Best result obtained from the HS and ST2FHS methods.
Figure 19.
Best results obtained from the DE and ST2FDE methods.
Figure 19.
Best results obtained from the DE and ST2FDE methods.
Table 1.
Rules of the ST2FHS fuzzy system.
Table 1.
Rules of the ST2FHS fuzzy system.
| | HMR | Low | Medium | High |
|---|
| Iteration | |
|---|
| Low | Low | − | − |
| Medium | − | Medium | − |
| High | − | − | High |
Table 2.
Rules of the ST2FDE fuzzy system.
Table 2.
Rules of the ST2FDE fuzzy system.
| | F | Low | Medium | High |
|---|
| Generation | |
|---|
| Low | − | − | Low |
| Medium | − | Medium | − |
| High | High | − | − |
Table 3.
Benchmark mathematical functions.
Table 3.
Benchmark mathematical functions.
| Function | Search Domain | f min | Equation |
|---|
| Sum Squares | [−10, 10]n | 0 | |
| Trid | [−100, 100]n | −200 | |
| Zakharov | [−5, 10]n | 0 | |
| Ackley | [−15, 30]n | 0 | |
| Dixon & Price | [−10, 10]n | 0 | |
| Levy | [−10, 10]n | 0 | |
| Griewank | [−600, 600]n | 0 | |
| Powell | [−4, 5]n | 0 | |
| Power Sum | [0, 10]n | 0 | |
Table 4.
Results for the Sum Squares function.
Table 4.
Results for the Sum Squares function.
| Dimension | 10 | Z-Value | 50 | Z-Value |
|---|
| Method | HS | ST2FHS | −16.78 | HS | ST2FHS | −52.09 |
| Best | 3.80 × 10−1 | 9.76 × 10−4 | 5.89 × 10−1 | 1.90 × 10−3 |
| Worst | 1.26 × 10 | 3.50 × 10−3 | 1.02 × 10 | 3.00 × 10−3 |
| Average | 7.07 × 10−1 | 2.02 × 10−3 | 8.10 × 10−1 | 2.28 × 10−3 |
| SD | 2.30 × 10−1 | 5.19 × 10−4 | 8.48 × 10−2 | 2.67 × 10−4 |
Table 5.
Results for the Zakharov function.
Table 5.
Results for the Zakharov function.
| Dimension | 10 | Z-Value | 50 | Z-Value |
|---|
| Method | HS | ST2FHS | −4.72 | HS | ST2FHS | −2.41 |
| Best | 7.34 × 10−11 | 4.00 × 10−13 | 2.04 × 10−4 | 3.12 × 10−4 |
| Worst | 1.35 × 10−8 | 2.0869 × 10−9 | 6.97 × 10−3 | 9.47 × 10−4 |
| Average | 3.27 × 10−9 | 3.63 × 10−10 | 1.42 × 10−3 | 6.37 × 10−4 |
| SD | 3.33 × 10−9 | 4.73 × 10−10 | 1.76 × 10−3 | 1.49 × 10−4 |
Table 6.
Results for the Dixon & Price function.
Table 6.
Results for the Dixon & Price function.
| Dimension | 10 | Z-Value | 50 | Z-Value |
|---|
| Method | HS | ST2FHS | −0.4 | HS | ST2FHS | −7.67 |
| Best | 7.30 × 10−3 | 1.39 × 10−3 | 2.56 × 10 | 1.53 × 10 |
| Worst | 8.64 × 10−1 | 8.53 × 10−1 | 1.50 × 10 | 4.99 × 10 |
| Average | 5.27 × 10−1 | 4.94 × 10−1 | 7.95 × 10 | 2.72 × 10 |
| SD | 3.19 × 10−1 | 3.07 × 10−1 | 3.66 × 10 | 7.73 × 10−1 |
Table 7.
Results for the Levy function.
Table 7.
Results for the Levy function.
| Dimension | 10 | Z-Value | 50 | Z-Value |
|---|
| Method | HS | ST2FHS | −0.23 | HS | ST2FHS | −8.4 |
| Best | 1.18 × 10−4 | 5.44 × 10−5 | 1.42 × 10−2 | 1.19 × 10−2 |
| Worst | 3.39 × 10−4 | 3.25 × 10−4 | 1.98 × 10−2 | 1.63 × 10−2 |
| Average | 2.25 × 10−4 | 1.90 × 10−4 | 1.66 × 10−2 | 1.41 × 10−2 |
| SD | 5.64 × 10−5 | 1.92 × 10−4 | 1.33 × 10−3 | 1.01 × 10−3 |
Table 8.
Results for the Griewank function.
Table 8.
Results for the Griewank function.
| Dimension | 10 | Z-Value | 50 | Z-Value |
|---|
| Method | HS | ST2FHS | −0.29 | HS | ST2FHS | 0.22 |
| Best | 4.57 × 10−2 | 1.55 × 10−1 | 3.65 × 10−2 | 9.75 × 10−1 |
| Worst | 8.49 × 10−1 | 2.94 × 10−1 | 2.15 × 10 | 1.02 × 10 |
| Average | 2.28 × 10−1 | 2.25 × 10−1 | 1.00 × 10 | 1.00 × 10 |
| SD | 4.57 × 10−2 | 3.65 × 10−2 | 1.59 × 10−2 | 1.02 × 10−2 |
Table 9.
Results for the Power Sum function.
Table 9.
Results for the Power Sum function.
| Dimension | 4 | Z-Value |
|---|
| Method | HS | ST2FHS | −0.59 |
| Best | 2.02 × 10−2 | 0.00 × 10 |
| Worst | 2.47 × 10 | 0.00 × 10 |
| Average | 2.23 × 10 | 1.71 × 10 |
| SD | 4.48 × 10 | 1.84 × 10 |
Table 10.
Results for the Trid function.
Table 10.
Results for the Trid function.
| Dimension | 10 | Z-Value | 50 | Z-Value |
|---|
| Method | HS | ST2FHS | −8.31 | HS | ST2FHS | 0.49 |
| Best | −1.23 × 10+2 | −1.90 × 10+2 | −3.49 × 10+3 | −2.98 × 10+3 |
| Worst | −1.19 × 10+2 | −1.80 × 10+2 | −1.33 × 10+3 | −1.39 × 10+3 |
| Average | −1.21 × 10+2 | −1.85 × 10+2 | −2.26 × 10+3 | −2.20 × 10+3 |
| SD | 9.64 × 10−1 | 1.99 × 10 | 5.19 × 10+2 | 4.07 × 10+2 |
Table 11.
Results for the Ackley function.
Table 11.
Results for the Ackley function.
| Dimension | 10 | Z-Value | 50 | Z-Value |
|---|
| Method | HS | ST2FHS | −0.05 | HS | ST2FHS | −0.6 |
| Best | 5.66 × 10−5 | 6.68 × 10−5 | 5.14 × 10−2 | 5.75 × 10−2 |
| Worst | 6.64 × 10−4 | 8.46 × 10−4 | 1.67 × 10 | 5.75 × 10−2 |
| Average | 2.76 × 10−4 | 2.74 × 10−4 | 1.66 × 10−1 | 1.21 × 10−1 |
| SD | 1.50 × 10−4 | 1.65 × 10−4 | 3.48 × 10−1 | 2.08 × 10−1 |
Table 12.
Results for the Powell function.
Table 12.
Results for the Powell function.
| Dimension | 10 | Z-Value | 50 | Z-Value |
|---|
| Method | HS | ST2FHS | −7.03 | HS | ST2FHS | −4.33 |
| Best | 8.20 × 10−3 | 3.64 × 10−4 | 1.23 × 10−2 | 4.30 × 10−3 |
| Worst | 1.70 × 10−1 | 2.40 × 10−3 | 4.32 × 10−1 | 1.76 × 10−2 |
| Average | 5.88 × 10−2 | 1.37 × 10−3 | 8.18 × 10−2 | 1.11 × 10−2 |
| SD | 4.47 × 10−2 | 5.17 × 10−4 | 8.90 × 10−2 | 3.43 × 10−3 |
Table 13.
Results for the Sum Squares function.
Table 13.
Results for the Sum Squares function.
| Dimension | 10 | Z-Value | 50 | Z-Value |
|---|
| Method | DE | ST2FDE | 4.5513 | DE | ST2FDE | −34.1921 |
| Best | 9.48146 × 10−33 | 2.2026 × 10−31 | 3.703507 | 2.7471 × 10−7 |
| Worst | 3.80055 × 10−31 | 1.0944 × 10−29 | 6.582105 | 8.4137 × 10−7 |
| Average | 1.14269 × 10−31 | 1.7395 × 10−30 | 4.851488 | 4.72 × 10−7 |
| SD | 9.32651 × 10−32 | 1.9536 × 10−30 | 0.777158 | 1.41 × 10−7 |
Table 14.
Results for the Zakharov function.
Table 14.
Results for the Zakharov function.
| Dimension | 10 | Z-Value | 50 | Z-Value |
|---|
| Method | DE | ST2FDE | −10.5785 | DE | ST2FDE | −37.0422 |
| Best | 1.04 × 10−4 | 1.84 × 10−8 | 7.70 × 10 | 2.57 × 10−2 |
| Worst | 7.64 × 10−4 | 1.87 × 10−7 | 1.43 × 10+2 | 1.06 × 10−1 |
| Average | 3.40 × 10−4 | 8.13 × 10−8 | 1.13 × 10+2 | 5.87 × 10−2 |
| SD | 1.76 × 10−4 | 4.82 × 10−8 | 1.67 × 10 | 2.41 × 10−2 |
Table 15.
Results for the Dixon & Price function.
Table 15.
Results for the Dixon & Price function.
| Dimension | 10 | Z-Value | 50 | Z-Value |
|---|
| Method | DE | ST2FDE | 0.4408 | DE | ST2FDE | −26.3743 |
| Best | 1.77 × 10−1 | 2.54 × 10−1 | 1.60 × 10+2 | 6.68 × 10−1 |
| Worst | 6.67 × 10−1 | 6.67 × 10−1 | 4.01 × 10+2 | 7.55 × 10−1 |
| Average | 5.98 × 10−1 | 6.13 × 10−1 | 2.66 × 10+2 | 6.79 × 10−1 |
| SD | 1.49 × 10−1 | 1.12 × 10−1 | 5.51 × 10 | 1.81 × 10−2 |
Table 16.
Results for the Levy function.
Table 16.
Results for the Levy function.
| Dimension | 10 | Z-Value | 50 | Z-Value |
|---|
| Method | DE | ST2FDE | 0 | DE | ST2FDE | −33.7726 |
| Best | 1.50 × 10−32 | 1.50 × 10−32 | 3.20 × 10 | 4.74 × 10−7 |
| Worst | 1.50 × 10−32 | 1.50 × 10−32 | 5.94 × 10 | 1.55 × 10−6 |
| Average | 1.50 × 10−32 | 1.50 × 10−32 | 4.68 × 10 | 9.43 × 10−7 |
| SD | 2.78 × 10−48 | 8.35 × 10−48 | 7.59 × 10−1 | 2.69 × 10−7 |
Table 17.
Results for the Power Sum function.
Table 17.
Results for the Power Sum function.
| Dimension | 4 | Z-Value |
|---|
| Method | DE | ST2FDE | −1.6605 |
| Best | 5.80 × 10−4 | 7.67 × 10−4 |
| Worst | 2.21 × 10−2 | 2.26 × 10−2 |
| Average | 9.15 × 10−3 | 6.65 × 10−3 |
| SD | 6.18 × 10−3 | 5.46 × 10−3 |
Table 18.
Results for the Trid function.
Table 18.
Results for the Trid function.
| Dimension | 10 | Z-Value | 50 | Z-Value |
|---|
| Method | DE | ST2FDE | 0 | DE | ST2FDE | −76.9252 |
| Best | −209 | −209 | −861.94 | −884.656 |
| Worst | −209 | −209 | −854.374 | −884.646 |
| Average | −209 | −209 | −858.184 | −884.651 |
| SD | 0 | 0 | 1.884478 | 0.002398 |
Table 19.
Results for the Ackley function.
Table 19.
Results for the Ackley function.
| Dimension | 10 | Z-Value | 50 | Z-Value |
|---|
| Method | DE | ST2FDE | −5.3864 | DE | ST2FDE | −65.4158 |
| Best | 4.44 × 10−15 | 8.88 × 10−16 | 1.82 × 10 | 1.60 × 10−4 |
| Worst | 4.44 × 10−15 | 4.44 × 10−15 | 2.55 × 10 | 2.74 × 10−4 |
| Average | 4.44 × 10−15 | 2.66 × 10−15 | 2.15 × 10 | 2.16 × 10−4 |
| SD | 1.60 × 10−30 | 1.81 × 10−15 | 1.80 × 10−1 | 2.75 × 10−5 |
Table 20.
Results for the Powell function.
Table 20.
Results for the Powell function.
| Dimension | 10 | Z-Value | 50 | Z-Value |
|---|
| Method | DE | ST2FDE | −9.5085 | DE | ST2FDE | −36.7394 |
| Best | 3.30 × 10−7 | 3.15 × 10−8 | 7.59 × 10+2 | 3.54 × 10−2 |
| Worst | 5.76 × 10−6 | 3.54 × 10−7 | 1.32 × 10+3 | 1.13 × 10−1 |
| Average | 1.99 × 10−6 | 9.44 × 10−8 | 1.08 × 10+3 | 6.62 × 10−2 |
| SD | 1.09 × 10−6 | 6.50 × 10−8 | 1.61 × 10+2 | 1.94 × 10−2 |
Table 21.
Parameters of the motor position.
Table 21.
Parameters of the motor position.
| Symbol | Definition | Value |
|---|
| J | Moment of inertia of the rotor | 3.2284 × 10−6 kg.m2 |
| b | Motor viscous friction constant | 3.5077 × 10−6 Nms |
| Ke | Electromotive force constant | 0.0274 V/rad/sec |
| Kt | Motor torque constant | 0.0274 Nm/Amp |
| R | Electric resistance | 4 ohm |
| L | Electric inductance | 2.75 × 10−6 H |
Table 22.
Type-1 membership functions.
Table 22.
Type-1 membership functions.
| Input Error |
| MF | A | b | c | d |
| NegV | −1 | −1 | −0.5 | 0 |
| CeroV | −0.5 | 0 | 0.5 | - |
| PosV | 0 | 0.5 | 1 | 1 |
| Input Error Change |
| ErrNeg | −1 | −1 | −0.4 | −0.1 |
| ErrNegM | −0.4 | −0.2 | 0 | - |
| SinErr | −0.09 | 0 | 0.10 | - |
| ErrMaxM | 0 | 0.2 | 0.4 | - |
| ErrMax | 0.1 | 0.4 | 1 | - |
| Output Voltage |
| MDis | −1 | −1 | −0.6 | −0.09 |
| MDism | −0.4 | −0.2 | 0 | - |
| Man | −0.1 | 0 | 0.1 | - |
| Aumm | 0 | 0.2 | 0.4 | - |
| Aum | 0.09 | 0.6 | 1 | 1 |
Table 23.
Fuzzy rules for the controller.
Table 23.
Fuzzy rules for the controller.
| Voltage | | Error Change |
|---|
| | | ErrNeg | ErrNeg_M | SinErr | ErrMax_M | ErrMax |
| Error | NegV | Dis | Dis | Dis | Dis | Dis_m |
| CeroV | Aum_m | Aum_m | Man | Dis_m | Dis_m |
| PosV | Aum_m | Aum | Aum | Aum | Aum |
Table 24.
Boundary T1 membership functions parameters of the vector.
Table 24.
Boundary T1 membership functions parameters of the vector.
| | Input 1 | Input 2 | Output |
|---|
| MF parameters | First MF
| First MF
| First MF
|
| | Second MF
| Second MF
|
Second MF
| Third MF
| Third MF
|
| | Fourth MF
| Fourth MF
|
| | Third MF
| Fifth MF
| Fifth MF
|
Table 25.
Results for the ST2FHS method.
Table 25.
Results for the ST2FHS method.
| Method | HS-FLC without Noise | ST2FHS-FLC without Noise | HS-FLC with Noise | ST2FHS-FLC FLC with Noise |
|---|
| Best | 7.86 × 10−3 | 7.32 × 10−3 | 4.22 × 10−2 | 1.95 × 10−2 |
| Worst | 5.16 × 10−1 | 5.66 × 10−2 | 1.09 × 10 | 9.07 × 10−1 |
| Average | 1.65 × 10−1 | 9.22 × 10−3 | 5.90 × 10−1 | 4.62 × 10−1 |
| SD | 1.37 × 10−1 | 3.45 × 10−3 | 3.07 × 10−1 | 2.83 × 10−1 |
Table 26.
Results for the ST2FDE method.
Table 26.
Results for the ST2FDE method.
| Method | DE-FLC without Noise | ST2FDE-FLC without Noise | DE-FLC with Noise | ST2FDE-FLC with Noise |
|---|
| Best | 7.34 × 10−3 | 4.35 × 10−3 | 2.24 × 10−2 | 5.89 × 10−4 |
| Worst | 2.1 × 10−2 | 7.43 × 10−3 | 4.85 × 10−1 | 7.47 × 10−2 |
| Average | 1.71 × 10−2 | 7.24 × 10−3 | 2.44 × 10−1 | 2.18 × 10−2 |
| SD | 2.81 × 10−3 | 5.35 × 10−4 | 1.36 × 10−1 | 1.90 × 10−2 |
Table 27.
Results for the statistical test of the DC motor.
Table 27.
Results for the statistical test of the DC motor.
| Method | | | Z-Value |
|---|
| ST2FHS | FLC without noise | HS | −6.23 |
| FLC with noise | HS with noise | −1.67 |
| ST2FDE | FLC without noise | DE | −18.8799 |
| FLC with noise | DE with noise | −8.8627 |
Table 28.
Results for the experiments with PID for the DC motor.
Table 28.
Results for the experiments with PID for the DC motor.
| Method | | | | Best Settling Time |
|---|
| PID | 21 | 500 | 0.15 | 0.0338 |
| HS | 600 | 12,000 | 6 | 0.00029 |
| DE | 900 | 18000 | 9 | 0.00020 |
| ST2FHS | 900 | 30,000 | 9 | 0.00020 |
| ST2FDE | 1500 | 30,000 | 15 | 0.00012 |
Table 29.
Results for the statistical test of the PID motor.
Table 29.
Results for the statistical test of the PID motor.
| Method | ST2FHS | HS | Z-Value |
|---|
| | Average | Std. | Average | SD | −3.21 |
| | 3.90 × 10−4 | 1.83 × 10−4 | 5.72 × 10−3 | 9.07 × 10−3 |
| Method | ST2FDE | DE | −2.53 |
| | Average | Std. | Average | SD |
| | 3.03 × 10−4 | 2.15 × 10−4 | 4.22 × 10−3 | 8.46 × 10−3 |