Estimating the Volume of the Solution Space of SMT(LIA) Constraints by a Flat Histogram Method
Abstract
1. Introduction
2. Backgrounds
2.1. SMT(LIA) Formulas and Their Solution Spaces
2.2. Hot/Cold Path Analysis
- The conditions along the first path: (x > 49) ((y < 36) (z > 11)), whose volume is 4,085,328.
- The condition of the second path is the logical complement of the first condition. Its volume is 255 × 255 × 255 − 4,085,328 = 12,496,047. As 12,496,047:4,085,328 ≈ 3.06:1, we predict that the second path (which executes i = 6) is a hot path and more test cases should be generated for it. Note that, we assume the ranges of variables x, y and z be [−128, 127].
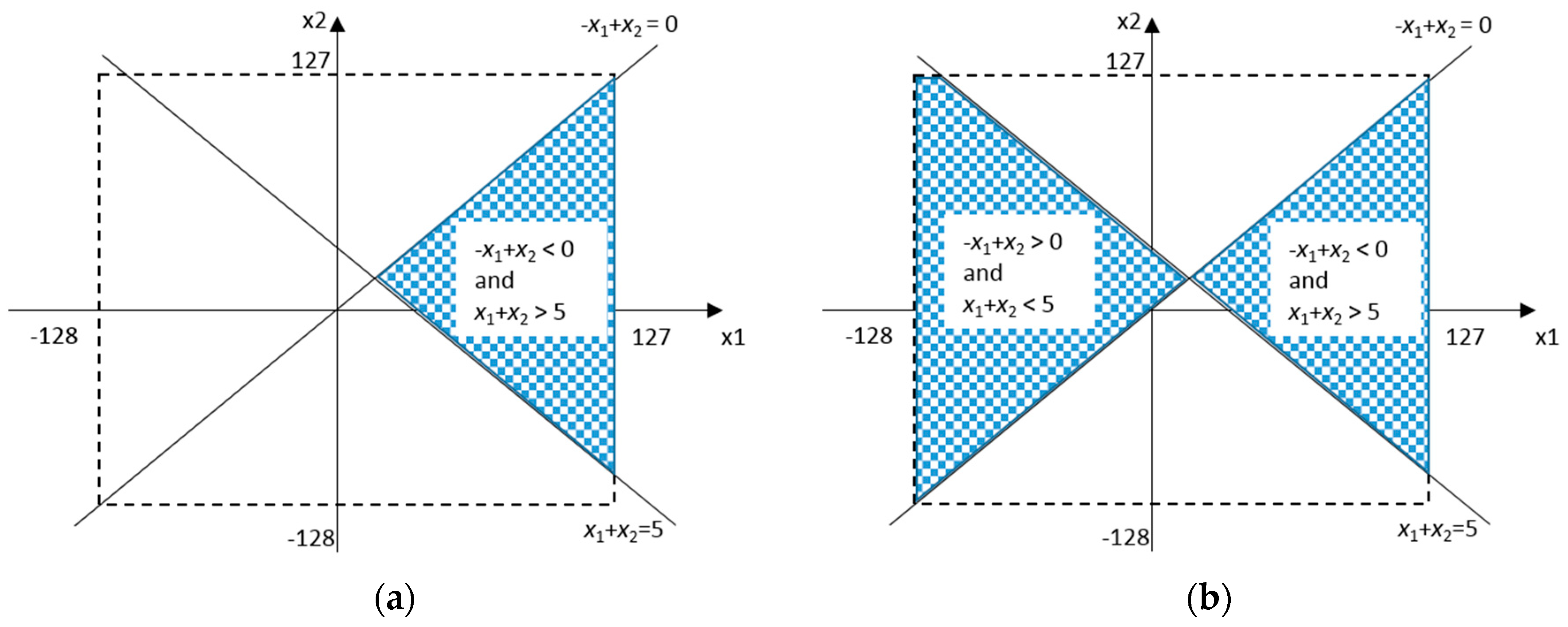
2.3. Volumes of Convex Bodies and SMT(LIA) Formulas
2.4. Markov Chain Monte Carlo and the Flat Histogram Method
3. Related Works
- Our techniques vs. VolCE+LattE [9]: Both techniques are suited for #SMT(LIA). VolCE+LattE is an exact method whereas our methods are approximate. In our experiments, VolCE+LattE fails to scale on many convex body instances (obtained from [24]) that are with more than six variables, whereas one of our techniques succeed in reporting solutions for the test set. Note that both techniques require low memories. In our test, their required memory on all instances is less than 1 GB. So, a failure of VolCE+LattE is due to time out.
- Our techniques vs. SMTApproxMC [19] and ApproxMC2 [21]: The three are approximate techniques. SMTApproxMC and ApproxMC2 provide a guarantee that if given a tolerance ε >0 and a confidence 1–δ (0, 1), its output lies in the interval [(1 + ε)−1 RF, (1 + ε) RF] with probability greater than δ, where RF is the real count of a formula. Our techniques do not provide such a guarantee. However, experiments will show that our techniques lead to a relative error smaller than 20% in most of the tests. In addition, our methods are capable of working on tested instances with 4,000,000 and more solutions, whereas SMTApproxMC cannot. ApproxMC2 has similar scalability issue as well (see Section 5: More Results on Convex Bodies).
- Our techniques vs. the direct Monte Carlo method [23]: Both techniques are not complicated applications of the Monte Carlo sampling method. The direct Monte Carlo method is reported to fail in sampling from the solution area of convex body instances with seven or more variables, whereas one of our techniques succeeds in obtaining a lot of samplings from the solution areas for many instances extracted from the same test set.
4. The Proposed Flat Histogram Method
- A specialized energy function g over the valuations of the SMT(LIA) formula, which satisfies that for any valuation γ, g(γ) = 0 if γ is a solution and g(γ) > 0 otherwise.
- A MCMC algorithm based on the flat histogram method to estimate the density of states with respect to g.
- Histogram reweighting strategies and flatness evaluating methods.
4.1. The Energy Function
4.2. The Sampling Algorithm
| Algorithm 1.MCMC-Flat for #SMT(LIA) |
| N′(E) ← 1 for every energy level E F ← F0 Randomly generate a valuation σ n′(σ) ← n′(σ) × F H(σ) ← H(σ) + 1 repeat repeat Generate a new valuation σ′ if n′(g(σ′)) < n′(g(σ)) then σ ← σ′ else Move to σ′ with probability defined in Equation (2) end if n′(σ) ← n′(σ) × F//reweighting the density H(σ) ← H(σ) + 1//increase the visit histogram until IsFlat(H) F ← Update(F) //prepare to a new sweep H(E) ← 0 for every E until F is close enough to Ffinal Normalize n′ return n′(0) using Equation (6) |
4.3. Updating Strategy for the Modification Factor
- MCMC-Flat1/2 (the 1/2-strategy): Initially, set F to 1.5, and update F to F1/2 when H is flat. Each time F is updated, reset H(∙) [14].
- MCMC-Flat1/t (the 1/t-strategy): Initially, set F to 1.0. After a constant MC time (e.g., 1000), check H(E), and if H(E) ≠ 0 for all E then refine F ← F/2 and reset H(∙). If F ≤ 1/t (t = j/N, j is the number of trails and N is the number of energy levels.) then F ← 1/t and keep the value in following trails. If F < Ffinal, we stop the sampling process [25].
4.4. Evaluating the Flatness of Visit Histogram
| Algorithm 2.Pseudo Visit (PV) of Histogram |
| Input:A visit histogram H Output:A Boolean value indicates if every energy is visited for each i in H if H[i] = 0 H[i] ← 1 return false end if end for return true |
5. Experimental Evaluation
More Results on Convex Bodies
- In terms of scalability, our MCMC-Flat1/2 method is superior to SMTApproxMC and ApproxMC2. In [9], the word-level hash-mapping-based method SMTApproxMC was shown to handle instances with less than 3.98 × 106 models (around 4,000,000) and failed on others. On our test platform, SMTApproxMC got a result of 1.04 × 107 on instance 6-5-5. However, SMTApproxMC can return a value 15 out of 22 instances, whereas MCMC-Flat1/2 returns values on all the 22 instances. Notably, MCMC-Flat1/2 reports a result of 1.74 × 108 on the problem 6-5-1 with a low relative error 6.21%. From the results, the scalability of SMTApproxMC is better than ApproxMC2, as the former solved 15 instances whereas the latter solved 11 instances. Therefore, MCMC-Flat1/2 is the best, with respect to scalability.
- In terms of accuracy, MCMC-Flat1/2 is better than SMTApproxMC and ApproxMC2. Among 13 instances for which the exact volume is known by Volce+LattE (see Table 5), MCMC-Flat1/2 returns best results on 8 instances, and ApproxMC2 does the best on the other 5 instances, in terms of relative error. The accuracy of SMTApproxMC is not competitive to either MCMC-Flat1/2 or ApproxMC2. The variance in relative errors of ApproxMC2 is better than that of MCMC-Flat1/2, as we can observe from Table 6 that on instances where ApproxMC2 returns none-zero results the relative error of ApproxMC2 is better than that of MCMC-Flat1/2. On the other hand, ApproxMC2 seems to have big difficulty in working on instances having volume greater than 1.0 × 106, as it takes relatively long time on instances 5-10-1, 6-10-1, and 7-10-1.
- In terms of efficiency, MCMC-Flat1/2 is significantly better than SMTApproxMC and ApproxMC2. As can be seen from the bottom row in Table 6, over the ten instances (5-10-1, 5-10-2, 5-10-4, 5-10-5, 5-20-1, 5-20-2, 5-20-3, 5-20-4, 5-20-5, 6-10-1) on which all the three methods return none-zero results, the averaged time costs of MCMC-Flat1/2, SMTApproxMC, and ApproxMC2 are 344.5, 955.80, and 463.33, respectively. Obviously, MCMC-Flat1/2 is the fastest.
- Regarding the ability of obtaining samples from the solution area for large size instances, MCMC-Flat1/2 is superior to the direct Mont Carlo method in [24]. Note that, all the test instances are took from [24], and the direct Mont Carlo method in [24] is reported to give results of RE of 100% on all instances with 7 variables (We failed to run that method due to that its call on Matlab 2010b leads to segment faults). That is, the direct Mont Carlo method failed to sample any solution when the problem size is large. In contrast, MCMC-Flat1/2 is able to reach the solution area on all the tested instances with 7 variables.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Barrett, C.; Sebastiani, R.; Seshia, S.A.; Tinelli, C. Satisfiability modulo theories. In Handbook of Satisfiability; Biere, A., Ed.; IOS Press: Amsterdam, The Netherlands, 2009; Volume 185, pp. 825–885. ISBN 978-1-58603-929-5. [Google Scholar]
- Dyer, M.E.; Frieze, A.M.; Kannan, R. A random polynomial time algorithm for approximating the volume of convex bodies. In Proceedings of the 21st Annual ACM Symposium on Theory of Computing, Seattle, WA, USA, 14–17 May 1989; pp. 375–381. [Google Scholar]
- Dyer, M.E.; Frieze, A.M. On the complexity of computing the volume of a polyhedron. SIAM J. Comput. 1988, 17, 967–974. [Google Scholar] [CrossRef]
- Hahn, E.M.; Hartmanns, A.; Hermanns, H.; Katoen, J. A compositional modelling and analysis framework for stochastic hybrid systems. Form. Methods Syst. Des. 2013, 43, 191–232. [Google Scholar] [CrossRef]
- Immler, F. Verified reachability analysis of continuous systems’. In Proceedings of the Tools and Algorithms for the Construction and Analysis of Systems—21st International Conference, TACAS 2015, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2015, London, UK, 11–18 April 2015; pp. 37–51. [Google Scholar]
- Hadarean, L.; Barrett, C.; Reynolds, A.; Tinelli, C.; Deters, M. Fine grained SMT proofs for the theory of fixed-width bit-vectors. In Proceedings of the 20th International Conference on Logic for Programming, Artificial Intelligence, and Reasoning, LPAR-20, Suva, Fiji, 24–28 November 2015; pp. 340–355. [Google Scholar]
- Anand, S.; Burke, E.K.; Chen, T.Y.; Clark, J.; Cohen, M.B.; Grieskamp, W.; Harman, M.; Harrold, M.J.; McMinn, P. An orchestrated survey of methodologies for automated software test case generation. J. Syst. Softw. 2013, 86, 1978–2001. [Google Scholar] [CrossRef]
- Zhang, J. Specification analysis and test data generation by solving Boolean combinations of numeric constraints. In Proceedings of the First Asia-Pacific Conference on Quality Software, Hongkong, China, 30–31 October 2000; pp. 267–274. [Google Scholar]
- Ge, C.; Ma, F.; Zhang, P.; Zhang, J. Computing and estimating the volume of the solution space of SMT (LA) constraints. Theor. Comput. Sci. 2018, 743, 110–129. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, J. An efficient method to generate feasible paths for basis path testing. Inform. Process. Lett. 2008, 107, 87–92. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, X. A constraint solver and its application to path feasibility analysis. Int. J. Softw. Eng. Knowl. Eng. 2001, 11, 139–156. [Google Scholar] [CrossRef]
- Li, Y.T.S.; Malik, S. Performance analysis of embedded software using implicit path enumeration. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 1997, 16, 1477–1487. [Google Scholar] [CrossRef]
- Ammons, G.; Larus, J.R. Improving data-flow analysis with path profiles. ACM Sigplan Not. 2004, 39, 568–582. [Google Scholar] [CrossRef]
- Wang, F.; Landau, D.P. Efficient, multiple-range random walk algorithm to calculate the density of states. Phys. Rev. Lett. 2001, 86. [Google Scholar] [CrossRef] [PubMed]
- Whitmer, J.K.; Chiu, C.C.; Joshi, A.A.; De Pablo, J.J. Basis function sampling: A new paradigm for material property computation. Phys. Rev. Lett. 2014, 113. [Google Scholar] [CrossRef] [PubMed]
- Whitmer, J.K.; Fluitt, A.M.; Antony, L.; Qin, J.; McGovern, M.; De Pablo, J.J. Sculpting bespoke mountains: Determining free energies with basis expansions. J. Chem. Phys. 2015, 143. [Google Scholar] [CrossRef] [PubMed]
- Zablotskiy, S.V.; Ivanov, V.A.; Paul, W. Multidimensional stochastic approximation Monte Carlo. Phys. Rev. E 2016, 93. [Google Scholar] [CrossRef] [PubMed]
- Ma, F.; Liu, S.; Zhang, J. Volume computation for boolean combination of linear arithmetic constraints. In Proceedings of the Automated Deduction—CADE-22, 22nd International Conference on Automated Deduction, Montreal, QC, Canada, 2–7 August 2009; pp. 453–468. [Google Scholar]
- Chakraborty, S.; Meel, K.S.; Mistry, R.; Vardi, M.Y. Approximate Probabilistic Inference via Word-Level Counting. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; pp. 3218–3224. [Google Scholar]
- Meel, K.S.; Vardi, M.Y.; Chakraborty, S.; Fremont, D.J.; Seshia, S.A.; Fried, D.; Ivrii, A.; Malik, S. Constrained Sampling and Counting: Universal Hashing Meets SAT Solving. In Proceedings of the AAAI’16 Workshop: Beyond NP, Phoenix, AZ, USA, 12–13 February 2016; pp. 344–351. [Google Scholar]
- Chakraborty, S.; Meel, K.S.; Vardi, M.Y. Algorithmic improvements in approximate counting for probabilistic inference: From linear to logarithmic SAT calls. In Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence, New York, NY, USA, 9–15 July 2016; pp. 3569–3576. [Google Scholar]
- Ermon, S.; Gomes, C.P.; Selman, B. Computing the density of states of Boolean formulas. In Proceedings of the Principles and Practice of Constraint Programming—CP 2010—16th International Conference, Scotland, UK, 6–10 September 2010; pp. 38–52. [Google Scholar]
- De Loera, J.A.; Hemmecke, R.; Tauzer, J.; Yoshida, R. Effective lattice point counting in rational convex polytopes. J. Symb. Comput. 2004, 38, 1273–1302. [Google Scholar] [CrossRef]
- Zhou, M.; He, F.; Song, X.; He, S.; Chen, G.; Gu, M. Estimating the Volume of Solution Space for Satisfiability Modulo Linear Real Arithmetic. Theor. Comput. Syst. 2015, 56, 347–371. [Google Scholar] [CrossRef]
- Belardinelli, R.E.; Pereyra, V.D. Fast algorithm to calculate density of states. Phys. Rev. E 2007, 75. [Google Scholar] [CrossRef] [PubMed]
- Jacob, P.E.; Ryder, R.J. The Wang-Landau algorithm reaches the flat histogram criterion in finite time. Ann. Appl. Probab. 2014, 24, 34–53. [Google Scholar] [CrossRef]
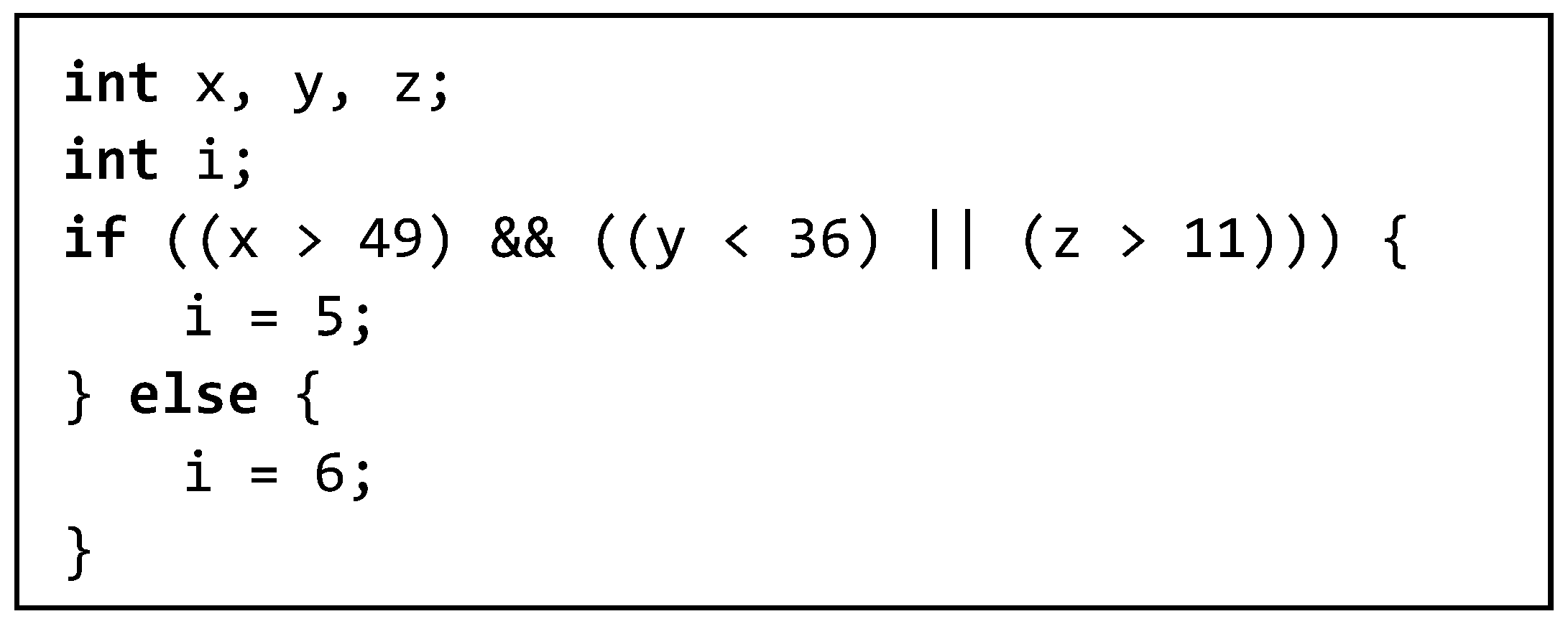
| Problem | Number of Variables | Number of LIA Constraints | Number of Clauses |
|---|---|---|---|
| ran1 | 5 | 10 | 20 |
| ran2 | 15 | 20 | 40 |
| ran3 | 8 | 10 | 20 |
| ran4 | 10 | 20 | 50 |
| ran5 | 5 | 20 | 40 |
| ran6 | 5 | 15 | 40 |
| ran7 | 8 | 20 | 50 |
| ran8 | 7 | 20 | 50 |
| ran9 | 7 | 20 | 80 |
| ran10 | 8 | 20 | 100 |
| ran11 | 9 | 20 | 50 |
| ran12 | 8 | 16 | 80 |
| Problems | Exact Method | MCMC-Flat1/2 | MCMC-Flat1/t−pv | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Vol. | Time | Vol. | Time | RE (%) | SR | Vol. | Time | RE (%) | SR | |
| s1 | 4 | 0 | 16.11 | 1.31 | 302.69 | 1.0 | 15.92 | 1.07 | 297.97 | 1.0 |
| s2 | 16 | 0 | 25.38 | 1.56 | 58.61 | 1.0 | 36.19 | 1.07 | 126.21 | 1.0 |
| s3 | 64 | 0 | 95.71 | 0.47 | 49.54 | 1.0 | 99.94 | 1.07 | 56.15 | 1.0 |
| s4 | 256 | 0 | 322.06 | 0.14 | 25.80 | 1.0 | 322.71 | 1.06 | 26.06 | 1.0 |
| s5 | 1024 | 0 | 1215.48 | 0.19 | 18.70 | 1.0 | 1137.09 | 1.05 | 11.04 | 1.0 |
| s6 | 4096 | 0 | 4478.05 | 0.17 | 9.33 | 1.0 | 4327.27 | 1.04 | 5.65 | 1.0 |
| s7 | 16129 | 0 | 17,020.84 | 0.06 | 5.53 | 1.0 | 16,396.42 | 0.98 | 1.66 | 1.0 |
| Problems | Exact Method | MCMC-Flat1/2 | MCMC-Flat1/t−pv | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Vol. | Time | Vol. | Time | RE (%) | SR | Vol. | Time | RE (%) | SR | |
| ran1 | 5.86 × 1011 | 0.15 | 5.84 × 1011 | 7.59 | −0.35 | 1.0 | 5.84 × 1011 | 12.65 | −0.51 | 1.0 |
| ran2 | MO | \ | 4.18 × 1035 | 2186.25 | \ | 1.0 | 4.22 × 1035 | 62.82 | \ | 1.0 |
| ran3 | 2.71 × 1018 | 8.36 | 2.72 × 1018 | 4.58 | 0.04 | 1.0 | 2.73 × 1018 | 14.23 | 0.44 | 1.0 |
| ran4 | MO | \ | 5.22 × 1023 | 65.51 | \ | 1.0 | 5.21 × 1023 | 74.92 | \ | 1.0 |
| ran5 | 4.02 × 1010 | 37.51 | 4.06 × 1010 | 2087.45 | 0.91 | 1.0 | 4.07 × 1010 | 47.05 | 1.04 | 1.0 |
| ran6 | 3.84 × 1010 | 0.73 | 3.81 × 1010 | 31.37 | −0.74 | 1.0 | 3.82 × 1010 | 45.65 | −0.59 | 1.0 |
| ran7 | MO | \ | 4.89 × 1016 | 474.35 | \ | 1.0 | 4.85 × 1016 | 76.38 | \ | 1.0 |
| ran8 | 1.24 × 1014 | 4.36 | 1.29 × 1014 | 188.96 | 4.25 | 1.0 | 1.27 × 1014 | 73.15 | 2.07 | 1.0 |
| ran9 | 3.14 × 1016 | 3625.2 | 3.13 × 1016 | 3266.07 | −0.33 | 0.1 | 3.15 × 1016 | 205.18 | 0.22 | 1.0 |
| ran10 | MO | \ | 3.20 × 1017 | 476.1 | \ | 0.5 | 3.25 × 1017 | 378.83 | \ | 1.0 |
| ran11 | MO | \ | 2.90 × 1019 | 655.12 | \ | 1.0 | 2.94 × 1019 | 76.85 | \ | 1.0 |
| ran12 | 5.23 × 1018 | 709.74 | 5.21 × 1018 | 45.94 | −0.35 | 1.0 | 5.21 × 1018 | 196.62 | −0.27 | 1.0 |
| Problems | #Variable | #Constraint | Space | Volume/Space (%) |
|---|---|---|---|---|
| 5-10-1 | 5 | 10 | 2.43 × 107 | 0.0171276 |
| 5-10-2 | 5 | 10 | 2.43 × 107 | 0.0198066 |
| 5-10-3 | 5 | 10 | 2.43 × 107 | 0.6724568 |
| 5-10-4 | 5 | 10 | 2.43 × 107 | 0.0487407 |
| 5-10-5 | 5 | 10 | 2.43 × 107 | 0.9811399 |
| 5-20-1 | 5 | 20 | 2.43 × 107 | 0.0014280 |
| 5-20-2 | 5 | 20 | 2.43 × 107 | 0.0010206 |
| 5-20-3 | 5 | 20 | 2.43 × 107 | 0.0044444 |
| 5-20-4 | 5 | 20 | 2.43 × 107 | 0.0000329 |
| 5-20-5 | 5 | 20 | 2.43 × 107 | 0.0000494 |
| 6-5-1 | 6 | 5 | 7.29 × 108 | 25.3803016 |
| 6-5-2 | 6 | 5 | 7.29 × 109 | 0.1043014 |
| 6-5-3 | 6 | 5 | 7.29 × 1010 | NA |
| 6-5-4 | 6 | 5 | 7.29 × 1011 | 0.0017279 |
| 6-5-5 | 6 | 5 | 7.29 × 1012 | NA |
| 6-10-1 | 6 | 10 | 7.29 × 1013 | NA |
| 7-5-1 | 7 | 5 | 2.187 × 1010 | NA |
| 7-5-2 | 7 | 5 | 2.187 × 1010 | NA |
| 7-5-3 | 7 | 5 | 2.187 × 1010 | NA |
| 7-5-4 | 7 | 5 | 2.187 × 1010 | NA |
| 7-5-5 | 7 | 5 | 2.187 × 1010 | NA |
| 7-10-1 | 7 | 10 | 2.187 × 1010 | NA |
| Prob | Volce+LattE | MCMC-Flat1/2 | |||
|---|---|---|---|---|---|
| Vol. | Time | Vol. | Time | RE (%) | |
| 5-10-1 | 4162 | 13.5 | 4394.4 | 625.51 | 5.6 |
| 5-10-2 | 4813 | 111.43 | 7319.1 | 60.11 | 52.1 |
| 5-10-3 | 1.63 × 105 | 218.25 | 1.94 × 105 | 9.73 | 19.0 |
| 5-10-4 | 11844 | 302.69 | 13169.6 | 16.34 | 11.2 |
| 5-10-5 | 2.38 × 105 | 95.22 | 2.43 × 105 | 56.09 | 2.1 |
| 5-20-1 | 347 | 383.69 | 347.5 | 75.47 | 0.1 |
| 5-20-2 | 248 | 366.6 | 260.4 | 1555.6 | 5.0 |
| 5-20-3 | 1080 | 194.86 | 898.3 | 91.32 | −16.8 |
| 5-20-4 | 8 | 257.82 | 7.9 | 162.1 | −1.3 |
| 5-20-5 | 12 | 643.42 | 17.8 | 719.27 | 48.3 |
| 6-5-1 | 1.85 × 108 | 2248.59 | 1.74 × 108 | 28.67 | −6.2 |
| 6-5-2 | 7.60 × 106 | 1059.29 | 6.52 × 106 | 5.7 | −14.2 |
| 6-5-3 | \ | \ | 5.37 × 106 | 796.73 | \ |
| 6-5-4 | 1.26 × 107 | 839.3 | 9.43 × 106 | 5.62 | −25.2 |
| 6-5-5 | \ | \ | 7.45 × 106 | 9.71 | \ |
| 6-10-1 | \ | \ | 1.48 × 105 | 83.67 | \ |
| 7-5-1 | \ | \ | 4.91 × 108 | 21.86 | \ |
| 7-5-2 | \ | \ | 1.41 × 108 | 9.31 | \ |
| 7-5-3 | \ | \ | 7.00 × 108 | 25.09 | \ |
| 7-5-4 | \ | \ | 6.58 × 108 | 8.23 | \ |
| 7-5-5 | \ | \ | 1.65 × 108 | 14.54 | \ |
| 7-10-1 | \ | \ | 6.58 × 104 | 634.31 | \ |
| Prob. | MCMC-Flat1/2 | SMTApproxMC | ApproxMC2 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Vol. | Time | RE (%) | Vol. | Time | RE (%) | Vol. | Time | RE (%) | |
| 5-10-1 | 4394.4 | 625.51 | 5.6 | 16 | 504.15 | −99.6 | 4416 | 28.37 | 6.1 |
| 5-10-2 | 7319.1 | 60.11 | 52.1 | 19.5 | 552.85 | −99.6 | 4608 | 34.99 | −4.3 |
| 5-10-3 | 1.94 × 105 | 9.73 | 19.0 | 1.97 × 105 | 2158.77 | 20.3 | 0 | 4.20 × 103 | −100 |
| 5-10-4 | 13169.6 | 16.34 | 11.2 | 45 | 1276.02 | −99.6 | 12,288 | 104.77 | 3.7 |
| 5-10-5 | 2.43 × 105 | 56.09 | 2.1 | 3 | 1570.6 | −100 | 2.21 × 105 | 2.43 × 103 | −7.2 |
| 5-20-1 | 347.5 | 75.47 | 0.1 | 21 | 562.4 | −93.9 | 352 | 24.6 | 1.4 |
| 5-20-2 | 260.4 | 1555.6 | 5.0 | 239 | 489.37 | −3.6 | 248 | 22.75 | 0.0 |
| 5-20-3 | 898.3 | 91.32 | −16.8 | 833 | 545.84 | −22.9 | 880 | 28.13 | −18.5 |
| 5-20-4 | 7.9 | 162.1 | -1.3 | 2.5 | 85.53 | −68.8 | 8 | 28.94 | 0.0 |
| 5-20-5 | 17.8 | 719.27 | 48.3 | 3.5 | 310.64 | −70.8 | 12 | 1.55 | 0.0 |
| 6-5-1 | 1.74 × 108 | 28.67 | −6.2 | \ | \ | \ | 0 | 5.74 × 103 | −100 |
| 6-5-2 | 6.52 × 106 | 5.7 | −14.2 | 2.56 × 106 | 56,611.85 | −66.4 | 0 | 6.00 × 103 | −100 |
| 6-5-3 | 5.37 × 106 | \ | 796.73 | 79.5 | 52,437.11 | \ | 0 | 6.00 × 103 | \ |
| 6-5-4 | 9.43 × 106 | 5.62 | −25.2 | 192.5 | 65,540.31 | −100 | 0 | 6.00 × 103 | −100 |
| 6-5-5 | 7.45 × 106 | 9.71 | \ | 1.04 × 107 | 68,279.69 | \ | 0 | 6.00 × 103 | \ |
| 6-10-1 | 1.48 × 105 | 83.67 | \ | 1.31 × 105 | 3660.63 | \ | 1.19 × 105 | 1.93 × 103 | \ |
| 7-5-1 | 4.91 × 108 | 21.86 | \ | \ | \ | \ | 0 | 5.29 × 103 | \ |
| 7-5-2 | 1.41 × 108 | 9.31 | \ | \ | \ | \ | 0 | 6.00 × 103 | \ |
| 7-5-3 | 7.00 × 108 | 25.09 | \ | \ | \ | \ | 0 | 6.00 × 103 | \ |
| 7-5-4 | 6.58 × 108 | 8.23 | \ | \ | \ | \ | 0 | 6.00 × 103 | \ |
| 7-5-5 | 1.65 × 108 | 14.54 | \ | \ | \ | \ | 0 | 6.00 × 103 | \ |
| 7-10-1 | 6.58 × 104 | 634.31 | \ | \ | \ | \ | 5.63 × 104 | 1.15 × 103 | \ |
| #Solved | 22 | 15 | 11 | ||||||
| #BestRE | 8 | 0 | 5 | ||||||
| AvgTime | 344.55 | 955.80 | 463.33 | ||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, W.; Lv, H.; Zhang, Q.; Cai, D. Estimating the Volume of the Solution Space of SMT(LIA) Constraints by a Flat Histogram Method. Algorithms 2018, 11, 142. https://doi.org/10.3390/a11090142
Gao W, Lv H, Zhang Q, Cai D. Estimating the Volume of the Solution Space of SMT(LIA) Constraints by a Flat Histogram Method. Algorithms. 2018; 11(9):142. https://doi.org/10.3390/a11090142
Chicago/Turabian StyleGao, Wei, Hengyi Lv, Qiang Zhang, and Dunbo Cai. 2018. "Estimating the Volume of the Solution Space of SMT(LIA) Constraints by a Flat Histogram Method" Algorithms 11, no. 9: 142. https://doi.org/10.3390/a11090142
APA StyleGao, W., Lv, H., Zhang, Q., & Cai, D. (2018). Estimating the Volume of the Solution Space of SMT(LIA) Constraints by a Flat Histogram Method. Algorithms, 11(9), 142. https://doi.org/10.3390/a11090142





