Online Adaptive Parameter Estimation for Quadrotors

Abstract

The stability and robustness of quadrotors are always influenced by unknown or immeasurable system parameters. This paper proposes a novel adaptive parameter estimation technology to obtain high-accuracy parameter estimation for quadrotors. A typical mathematical model of quadrotors is first obtained, which can be used for parameter estimation. Then, an expression of the parameter estimation error is derived by introducing a set of auxiliary filtered variables. Moreover, an augmented matrix is constructed based on the obtained auxiliary filtered variables, which is then used to design new adaptive laws to achieve exponential convergence under the standard persistent excitation (PE) condition. Finally, a simulation and an experimental verification for a typical quadrotor system are shown to illustrate the effectiveness of the proposed method.

1. Introduction

Adaptive control and parameter estimation have been hot topics in the control fields [1,2], since, in control engineering practice, many unknown or immeasurable parameters and dynamics exist in a wide range of control plants. In order to address this problem, adaptive control was proposed as an effective and powerful method [3,4,5]. In this methodology, the unknown or immeasurable parameters and dynamics can be updated online or estimated by using control errors to ensure a closed-loop system’s stability [5]. Nevertheless, in the past few years, standard adaptive control with a gradient-based algorithm has focused mainly on tracking a given reference trajectory rather than guaranteeing that the estimated parameters converge to their true values [6]. However, according to the equivalence theorem [7], accurate parameter estimation can be essential to enhancing the stability and robustness of adaptive systems for the purpose of tracking control. Hence, developing adaptive laws with guaranteed convergence is always a critical issue in adaptive control designs.

Recently, in order to solve the problems of parameter estimation, some scholars have made great efforts, and many well-recognized results have been reported; e.g., the gradient descent, least squares (LS) [3,4,5], neural network [8,9], and projection algorithms [10]. Moreover, a new adaptive parameter estimation framework has recently been proposed and applied in many applications [11,12,13,14], where the adaptive laws are driven by the parameter estimation error such that exponential or even finite-time convergence can be achieved. In [6], a new adaptive law was also studied to reconstruct unknown system parameters when an intermediate matrix is positive. However, most of the existing results are suitable for linearly parameterized systems only, and cannot be directly used for nonlinearly parameterized systems.

In parameter estimation, the parameter error convergence rate is also an important issue. To address this issue, a finite-time sliding neural network observer was studied in [8], where the observed state derivatives are used to estimate parameters, and some known nonlinear functions in the system are needed. Moreover, the inverse of these matrices should exist and be available. In a recent research work [6], under the condition that the persistent excitation (PE) is satisfied, a novel parameter estimation was given, which allows exact reconstruction of the unknown parameters. However, this method needs to verify online the inevitability for a matrix and compute its inverse when it is appropriate. Besides this, an observer is needed to be designed for this parameter estimation method, such that the corresponding computational cost is also increased.

Nowadays, quadrotors are playing a more and more important role in daily life, since they can perform versatile maneuvers and are able to complete various missions [15]. Therefore, a lot of attention has been paid to the modeling and control of quadrotors in the past few years [16,17,18,19]. However, some parameters in quadrotors are unknown for the controller’s design. In particular, the stability and robustness of control systems for quadrotors are always influenced by the unknown or immeasurable parameters. Hence, inspired by the above facts, in this paper, we will propose an adaptive parameter estimation technology for quadrotors with unknown parameters to enhance the stability and robustness of quadrotors. Firstly, a typical quadrotor mathematical model is given, and then an expression of the parameter estimation error is derived by introducing auxiliary filtered variables. Moreover, an augmented matrix is constructed based on the auxiliary filtered variables, which is further used to design the adaptive law to achieve convergence under the standard persistent excitation (PE) condition. Finally, simulation and experimental verification results for quadrotors are shown to illustrate the effectiveness of the proposed method.

The main contributions for this paper can be summarized as:

(1)

A parameter estimation is developed to obtain the parameter error information by using system dynamics and the estimated parameters with simple filter operations.

(2)

Novel parameter-error-based adaptive parameter estimation algorithms are suggested for quadrotors to guarantee fast convergence.

(3)

A constructive method is suggested to validate the standard persistent excitation (PE) condition online.

2. Adaptive Parameter Estimation

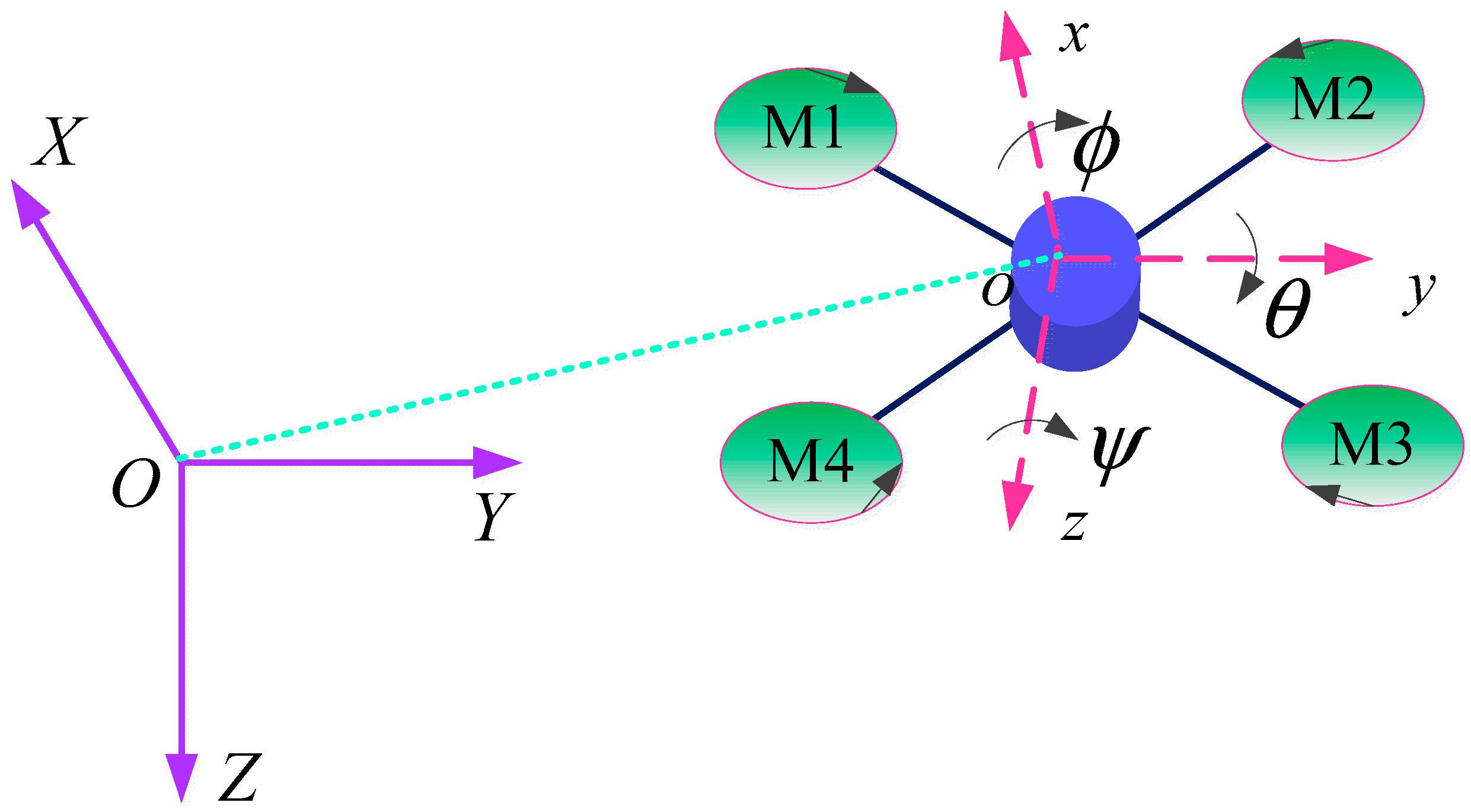
In this section, an adaptive parameter estimation technology is proposed for quadrotors. The schematic diagram of a ground coordinate system and a body axes coordinate system is given in Figure 1. Consider the following typical quadrotor mathematical model [20]

$$\begin{array}{l}\ddot{x}=(\cos \psi \sin \theta \cos \varphi +\sin \psi \sin \varphi )U_1/m\\ \ddot{y}=(\sin \psi \sin \theta \cos \varphi +\sin \varphi \sin \psi )U_1/m\\ \ddot{z}=(\cos \theta \cos \varphi )U_1/m-g\\ \ddot{\varphi }=[l{U}_2+\dot{\theta }\dot{\psi }(J_z-J_x)]/J_y\\ \ddot{\theta }=[l{U}_3+\dot{\varphi }\dot{\psi }(J_y-J_z)]/J_x\\ \ddot{\psi }=[U_4+\dot{\varphi }\dot{\theta }(J_x-J_y)]/J_z\end{array}$$

(1)

where $x$ is the displacement of the $x$-axis direction, $y$ is the displacement of the $y$-axis direction, $z$ is the displacement of the $z$-axis direction, $\psi$ denotes the yaw angle, $\varphi$ means the rolling angle, and $\theta$ defines the pitching angle. $U_1,U_2,U_3$ and $U_4$ denote the control actions of the vertical direction, roll direction, pitch direction, and the yaw direction, respectively, $m$ denotes the total mass of the quadrotor, $J$ is the moment inertia of the quadrotor, and $g$ denotes the gravitational acceleration.

In order to facilitate the parameter estimation, Equation (1) can be rewritten as

$$\begin{array}{l}\ddot{x}=a_1(\cos \psi \sin \theta \cos \varphi +\sin \psi \sin \varphi )U_1\\ \ddot{y}=a_1(\sin \psi \sin \theta \cos \varphi +\sin \varphi \sin \psi )U_1\\ \ddot{z}=a_1(\cos \theta \cos \varphi )U_1-g\\ \ddot{\varphi }=a_2{U}_2+a_3\dot{\theta }\dot{\psi }\\ \ddot{\theta }=a_4{U}_3+a_5\dot{\varphi }\dot{\psi }\\ \ddot{\psi }=a_6{U}_4+a_7\dot{\varphi }\dot{\theta }\end{array}$$

(2)

where $a_1=1/m$, $a_2=l/J_y$, $a_3=(J_z-J_x)/J_y$, $a_4=l/J_x$, $a_5=(J_y-J_z)/J_x$, $a_6=1/J_z$, and $a_7=(J_x-J_y)/J_z$. $a_1,a_2,a_3,a_4,a_5,a_6$ and $a_7$ are the unknown parameters to be estimated.

The aim of this paper is to suggest a novel parameter estimation methodology and a novel adaptive law for estimating $a_1,a_2,a_3,a_4,a_5,a_6$ and $a_7$ of system (2).

In this section, we will introduce a new adaptive parameter error framework, which is driven by the estimation error as [11,12,13]. In order to complete the parameter estimation, the filtered variables ${\dot{x}}_f,{\dot{\varphi }}_f,{\dot{\theta }}_f,{\dot{\psi }}_f$ of $\dot{x},\dot{\varphi },\dot{\theta }$ and $\dot{\psi }$ can be defined as

$$\{\begin{array}{l}k{\ddot{x}}_f+{\dot{x}}_f=\dot{x},{\dot{x}}_f(0)=0\\ k{\ddot{\varphi }}_f+{\dot{\varphi }}_f=\dot{\varphi },{\dot{\varphi }}_f(0)=0\\ k{\ddot{\theta }}_f+{\dot{\theta }}_f=\dot{\theta },{\dot{\theta }}_f(0)=0\\ k{\ddot{\psi }}_f+{\dot{\psi }}_f=\dot{\psi },{\dot{\psi }}_f(0)=0\end{array}$$

(3)

where $k>0$ is the filtered parameter.

Then, we can obtain the following equation from (2) and (3)

$$\{\begin{array}{l}{\ddot{x}}_f=\frac{\dot{x}-{\dot{x}}_f}{k}=a_1\cdot F_1{}_f\cdot U_1\\ {\ddot{\varphi }}_f=\frac{\dot{\varphi }-{\dot{\varphi }}_f}{k}=a_2\cdot U_2+a_3{F}_{2f}\\ {\ddot{\theta }}_f=\frac{\dot{\theta }-{\dot{\theta }}_f}{k}=a_4\cdot U_3+a_5\cdot F_{3f}\\ {\ddot{\psi }}_f=\frac{\dot{\psi }-{\dot{\psi }}_f}{k}=a_6\cdot U_4+a_7\cdot F_{4f}\end{array}$$

(4)

where $F_1=\cos \psi \sin \theta \cos \varphi +\sin \psi \sin \varphi$, $F_2=\dot{\theta }\dot{\psi }$, $F_3=\dot{\varphi }\dot{\psi }$, and $F_4=\dot{\varphi }\dot{\theta }$. $F_1$, $F_2$, $F_3$, and $F_4$ are the defined functions, and $F_{1f}$, $F_{2f}$, $F_{3f}$, and $F_{4f}$ are the filtered variables of $F_1$, $F_2$, $F_3$, and $F_4$, respectively. In order to complete the parameters estimation, Equation (4) can be rewritten in a more compact form as

$$X=YZ$$

(5)

where

$$X=\left[\begin{array}{c}\frac{\dot{x}-{\dot{x}}_f}{k}\\ \frac{\dot{\varphi }-{\dot{\varphi }}_f}{k}\\ \frac{\dot{\theta }-{\dot{\theta }}_f}{k}\\ \frac{\dot{\psi }-{\dot{\psi }}_f}{k}\end{array}\right],\begin{array}{c}\end{array}Y=\left[\begin{array}{ccccccc}{F}_{1f}{U}_1& 0& 0& 0& 0& 0& 0\\ 0& U_2& F_{2f}& 0& 0& 0& 0\\ 0& 0& 0& U_3& F_{3f}& 0& 0\\ 0& 0& 0& 0& 0& U_4& F_{4f}\end{array}\right],\begin{array}{c}\end{array}Z=\left[\begin{array}{c}{a}_1\\ a_2\\ a_3\\ a_4\\ a_5\\ a_6\\ a_7\end{array}\right].$$

(6)

We can define an auxiliary filtered and ‘integrated’ regressor matrix $P$ and a vector $Q$ as

$$\{\begin{array}{cc}\dot{P}=-\ell P+Y^{T}Y,& P(0)=0\\ \dot{Q}=-\ell Q+Y^{T}X,& Q(0)=0\end{array}$$

(7)

where $P\in {ℝ}^{b\times b}$ and $Q\in {ℝ}^{b\times n}$, $\ell >0$ is a design parameter, and the terms $\ell P$ and $\ell Q$ can be taken as the forgetting factors, which can make $P$ and $Q$ bounded in a compact set $\mathsf{\Omega }$ [21].

Considering that (7) is a differential equation, we can calculate the solution of (7) as

$$\{\begin{array}{c}P(t)={\displaystyle {\int }_0^t{e}^{-\ell (t-r)}}{Y}^T(r)Y(r)dr\\ Q(t)={\displaystyle {\int }_0^t{e}^{-\ell (t-r)}}{Y}^T(r)X(r)dr\end{array}.$$

(8)

Hence, it can be verified that $P$ and $Q$ are bounded for any given bounded $Y$ and $X$ due to the introduced forgetting factors $\ell P$ and $\ell Q$ in (7).

One defines an auxiliary vector $W\in {ℝ}^{b\times n}$ calculated based on $P(t)$, $Q(t)$ given in (8) as

$$W(t)=P(t)\widehat{Z}-Q(t)$$

(9)

where $\widehat{Z}$ is the estimation for the unknown parameter $Z$, which can be updated online via the following Equation (12).

According to Equations (4) and (8), Equation (9) can be rewritten as

$$Q=PZ.$$

(10)

Then, the auxiliary matrix $W$ can be represented as

$$W=P\widehat{Z}-PZ=-P\tilde{Z}$$

(11)

with the estimated error $\tilde{Z}=Z-\widehat{Z}$.

From Equation (11), one knows that the vector $W$ can be applied to estimate the unknown matrix $Z$ as analyzed in [21].

Then, the estimation algorithm of the unknown parameters can be designed as

$$\dot{\widehat{Z}}=-\mathsf{\Gamma }W$$

(12)

where $\mathsf{\Gamma }>0$ is a positive learning gain.

To solve the parameter estimation convergence, the positive definiteness property of $P(t)$ should be firstly studied. One defines ${\lambda }_{\max }(\cdot )\mathrm{and}{\lambda }_{\min }(\cdot )$ as the maximum and minimum eigenvalues of the corresponding matrices, respectively. Then, we can obtain the following Lemmas:

Lemma 1 ([13]).

The matrix $Y$ defined in (8) is persistently excited (PE), then the matrix $P$ defined in (8) is positive definite, i.e., ${\lambda }_{\min }(P)>\sigma >0$ for a positive constant $\sigma$.

Proof of Lemma 1.

Please refer to [13]. □

Theorem 1 ([22,23]).

Consider Equation (5) with adaptation law (12), one supposes that the regressor matrix $Y$ is PE, then the estimation error $\tilde{Z}=\widehat{Z}-Z$ exponentially converges to zero with the convergence rate $\mu =2\sigma /{\lambda }_{\max }({\mathsf{\Gamma }}^{-1})$.

Proof of Theorem 1.

Assume that $Y$ is PE, one knows ${\lambda }_{\max }(P)>\sigma >0$ based on Lemma 1. Choose the Lyapunov function as $V_{}=\frac{1}{2}{\tilde{Z}}^T{\mathsf{\Gamma }}^{-1}\tilde{Z}$, then one knows $Q=PZ$ and $W=-P\tilde{Z}$ according to Equations (9)–(12). Hence, we can obtain the derivative $\dot{V}$ as

$$\dot{V}={\tilde{Z}}^T{\mathsf{\Gamma }}^{-1}\dot{\tilde{Z}}={\tilde{Z}}^{T}W=-{\tilde{Z}}^{T}P(t)\tilde{Z}\le -\mu V$$

(13)

where $\mu =2\sigma /{\lambda }_{\max }({\mathsf{\Gamma }}^{-1})$ is positive for all $t>0.$ From Equation (13), one knows that the exponential convergence of the error $\tilde{Z}$ to zero with the rate $\mu$ is guaranteed, which depends on the excitation level $\sigma$ and learning rate $\mathsf{\Gamma }$. □

Remark 1.

The purpose of this paper is using the adaptive law for estimating parameters online. Therefore, the regressor $Y$ defined in (6) should be known. In fact, this condition has been well-recognized in the system identification field. For those systems without a fully known regress $Y$, the adaptive algorithm may not be suitable. In this case, other artificial intelligent algorithms (e.g., particle swarm optimization (PSO), genetic algorithm (GA)) may have to be used, which should be run offline.

Remark 2.

To implement the proposed parameter estimation scheme, we need to measure the attitude of the quadrotors, e.g., $x,\varphi ,\theta ,\psi$ and $\dot{x},\dot{\varphi },\dot{\theta },\dot{\psi }$, to construct the parameterized form (5). In practical quadrotors, they can be obtained by using the configured transducers.

3. Simulation

In this section, the proposed method is applied to a quadrotor model for simulations. In order to complete the simulation, some parameters should be chosen for the quadrotor model (1), which are displayed in

Table 1. Some physical parameters for the quadrotor.

Parameter	Value	Unit	Parameter	Value	Unit
m	0.25	Kg	Jz	0.061	Kg·m2
l	0.25	m	g	9.8	m/s2
Jx	0.033	Kg·m2	-------	-------	-------
Jy	0.033	Kg·m2	-------	-------	-------

.

The purpose of this paper is to estimate the parameters of quadrotors to enhance the stability and robustness of quadrotors. According to Equation (2), one knows that the parameters to be estimated are: $a_1,a_2,a_3,a_4,a_5,a_6$, and $a_7$. From Table 1, we have $a_1=4$, $a_2=7.57$, $a_3=0.85$, $a_4=7.57$, $a_5=-0.85$, $a_6=4.10$, and $a_7=0$. The other parameters used in the simulations can be set as $k=0.001$, $\ell =1$, and $\mathsf{\Gamma }=10$.

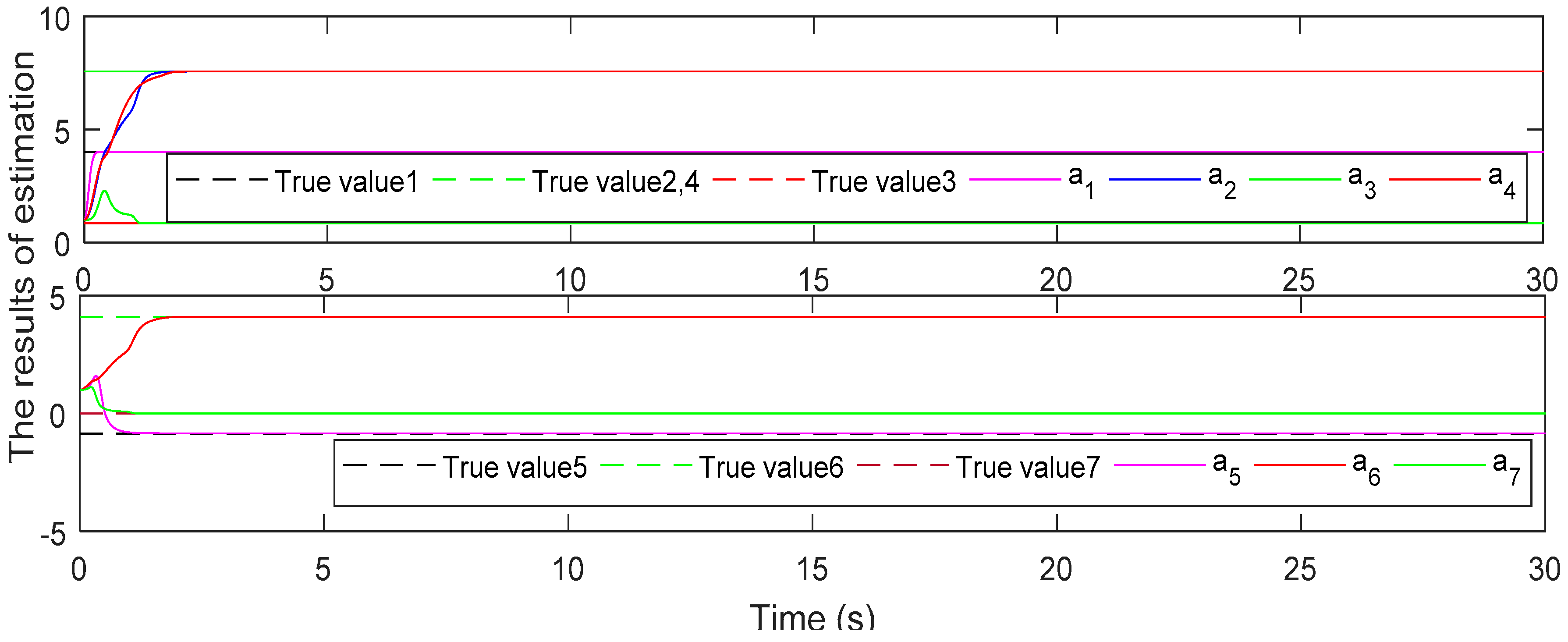
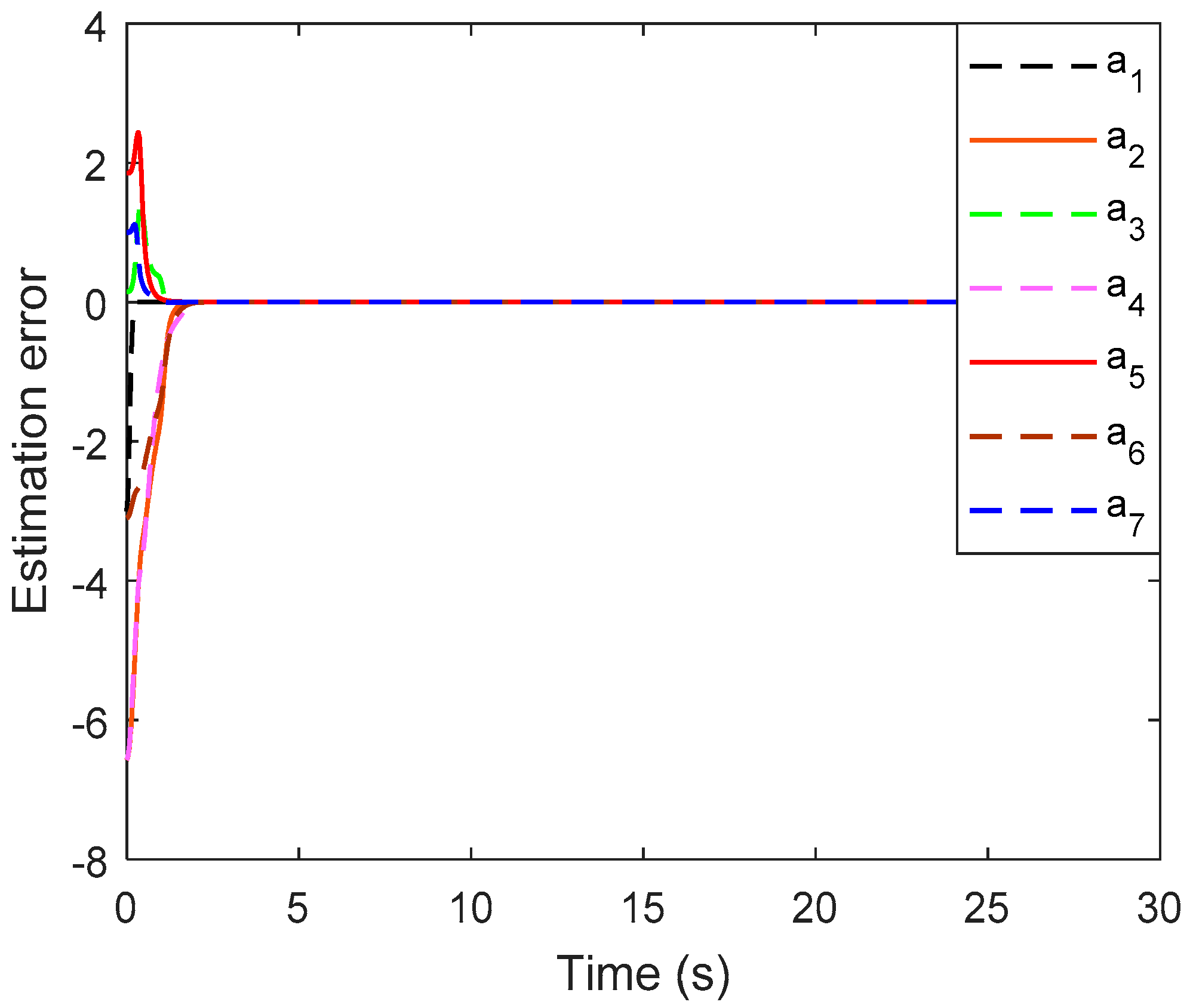
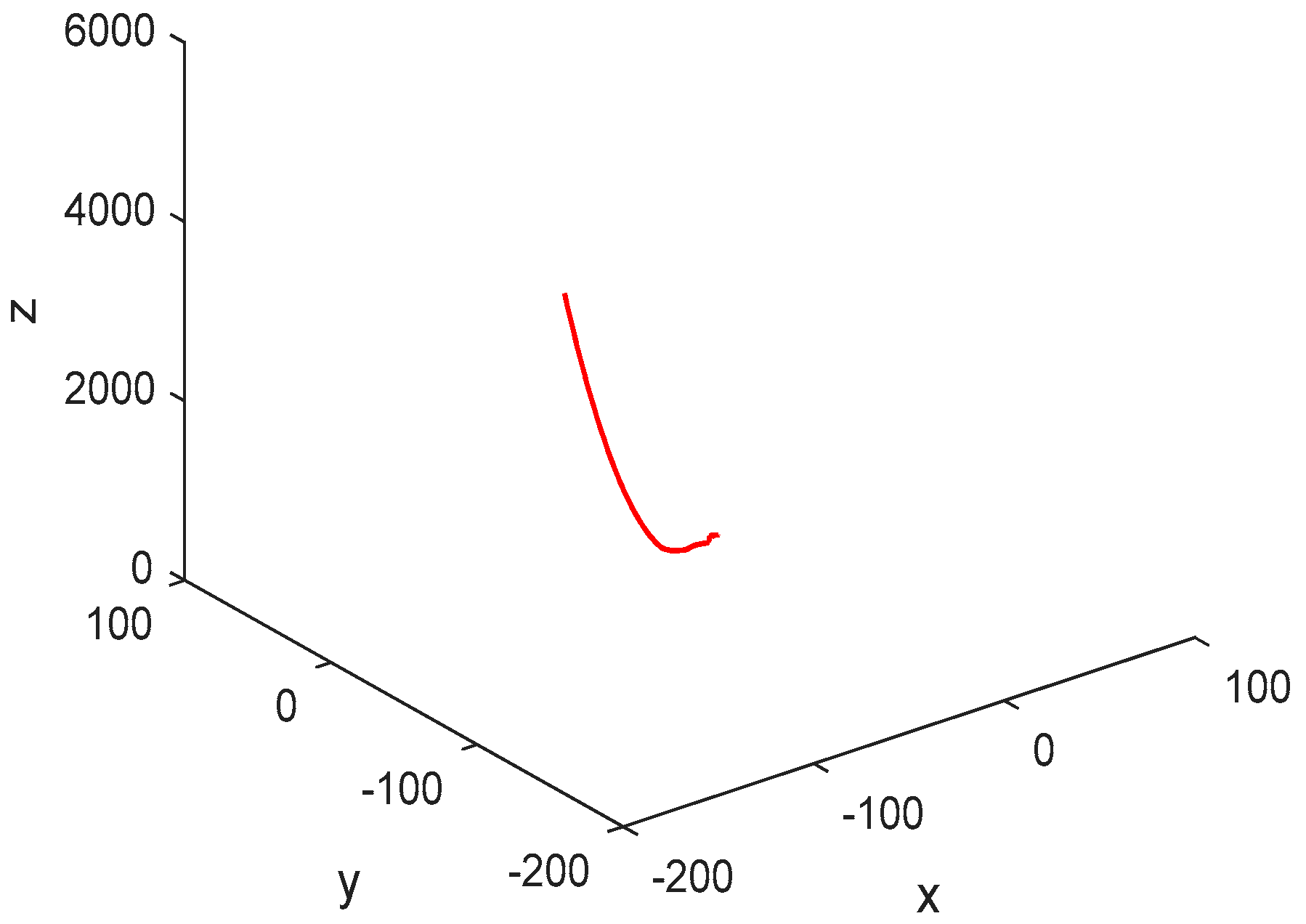
Figure 2 shows the response of the estimated matrix $\widehat{Z}$ with the adaptive law (12), which implies that the estimated parameter converges to the true value $Z$. In order to further verify the effectiveness of the proposed technology, the estimation error $\tilde{Z}$ of $Z$ is displayed in Figure 3, which indicates that the estimation error $\tilde{Z}$ converges to zero in about $3$ seconds. The flight trajectory of the quadrotor is also given in Figure 4. Figure 2 and Figure 3 show that the proposed online adaptive estimation method is very effective, and the estimated parameters converge to their true values faster, which can contribute to enhancing the system stability and robustness of quadrotors.

4. Experimental Verification

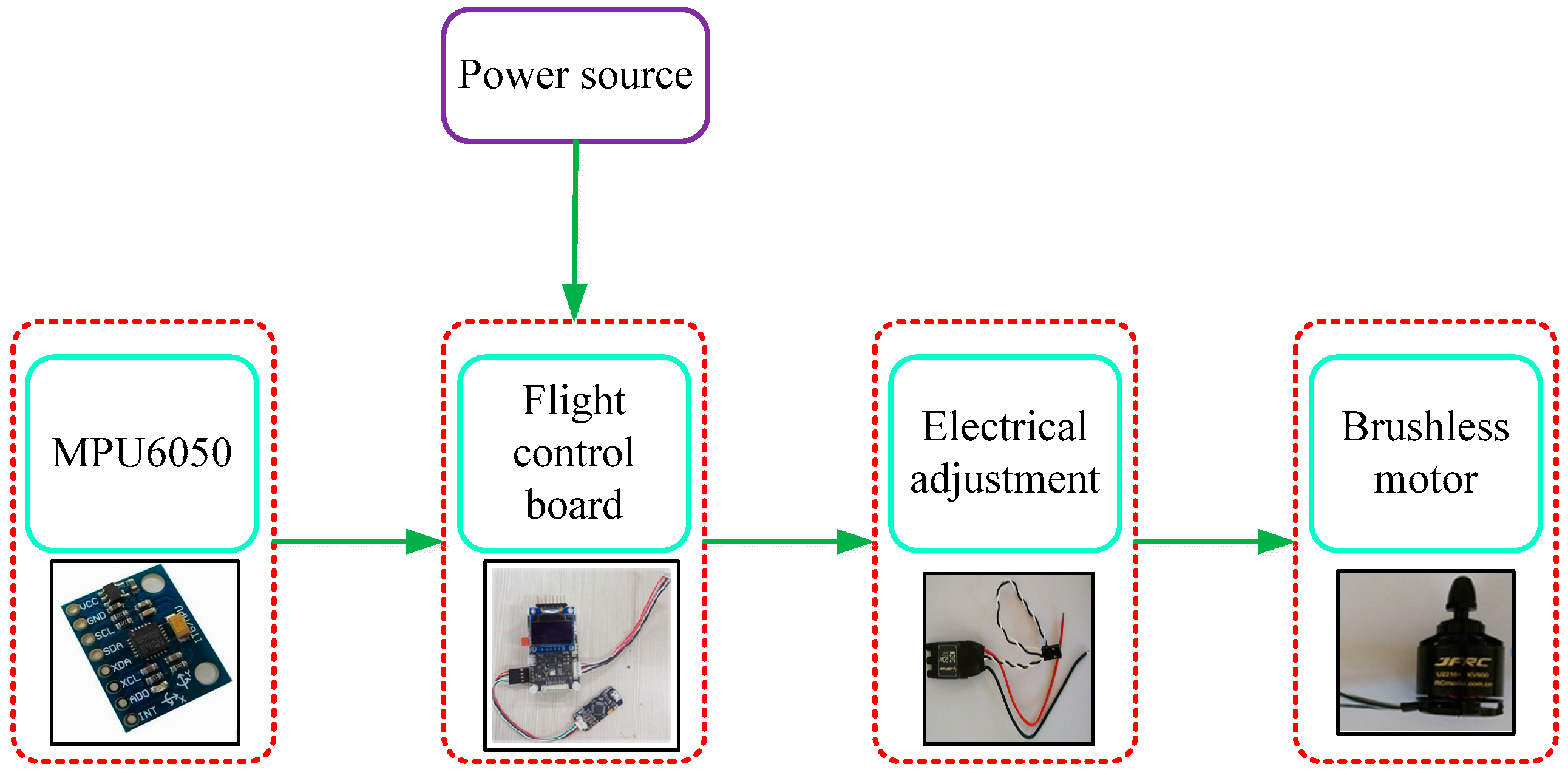
In this section, experiments are conducted to validate the proposed method. The experimental equipment is shown in Figure 5. In this case, the wireless serial port communication module and the serial port receiving terminal of the host computer are used to collect the attitude angle data. The main hardware components of the quadrotor include: a microcontroller (flying control board), a brushless motor, electrical adjustment (ESC), a propeller, a lithium battery, an MPU6050 (an acceleration sensor, a gyroscope, and a barometer, produced by InvenSense, Sunnyvale, CA, USA) receiver, a rack, and other components. The diagram of the structure of the adopted quadrotor is given in Figure 6.

In this experimental study, we collected 977 groups of data for the control actions of the vertical direction $U_1$, roll direction $U_2$, pitch direction $U_3$, and the yaw direction $U_4$ to validate the proposed method. The test environment’s temperature is $20\pm 2$ °C, and the environment humidity is about 30%. The sampling time is 0.005 ms. The parameters that need to be estimated are the same as those shown in Table 1.

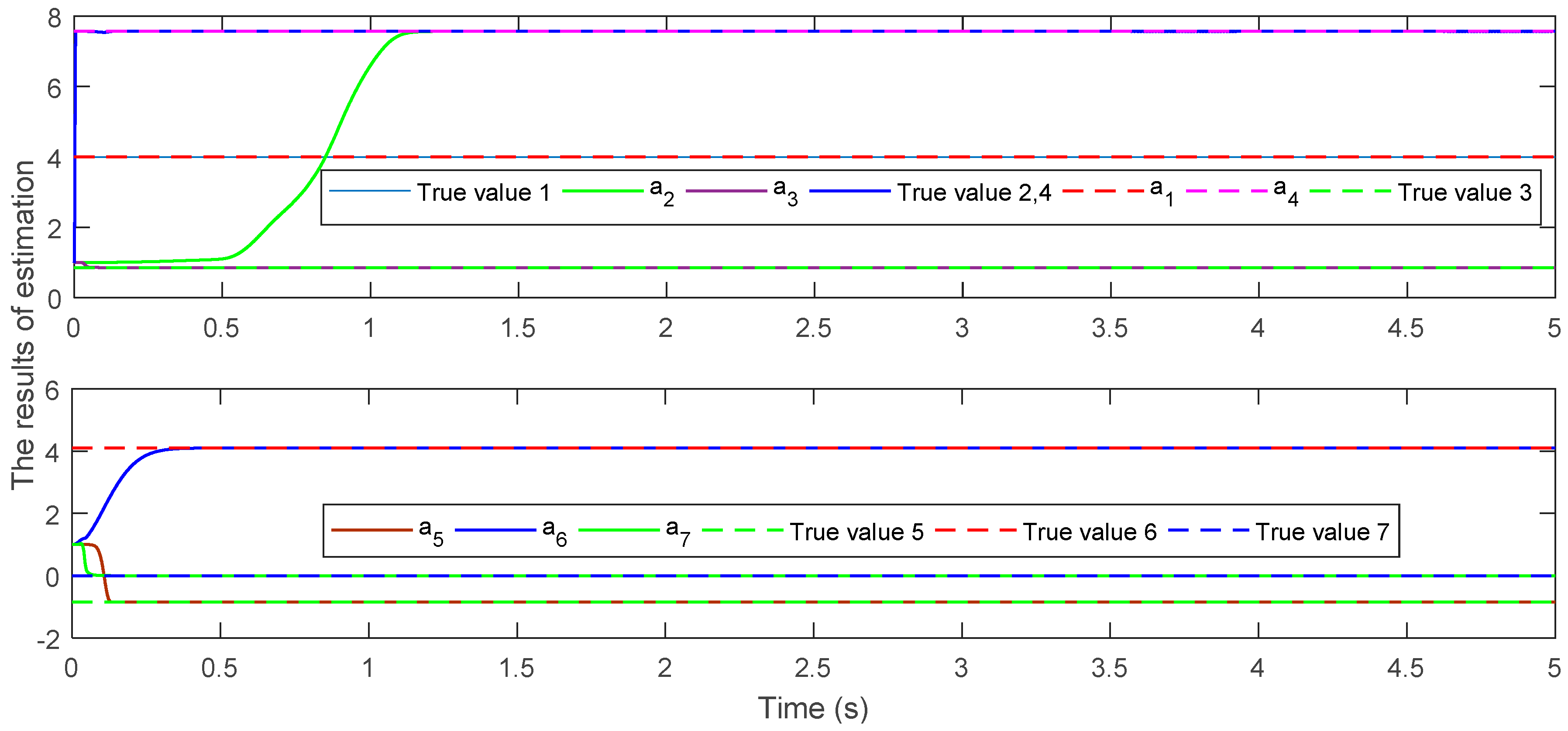
We can obtain the vertical direction, roll direction, pitch direction, and the yaw direction data via the wireless serial port communication module and the serial port receiving terminal of the host computer. Then, the obtained data is input into the proposed estimator to conduct the parameter estimation. The response of the estimated matrix $\widehat{Z}$ with the adaptive law (12) is given in Figure 7, which shows that the estimated parameter converges to the true value $Z$. 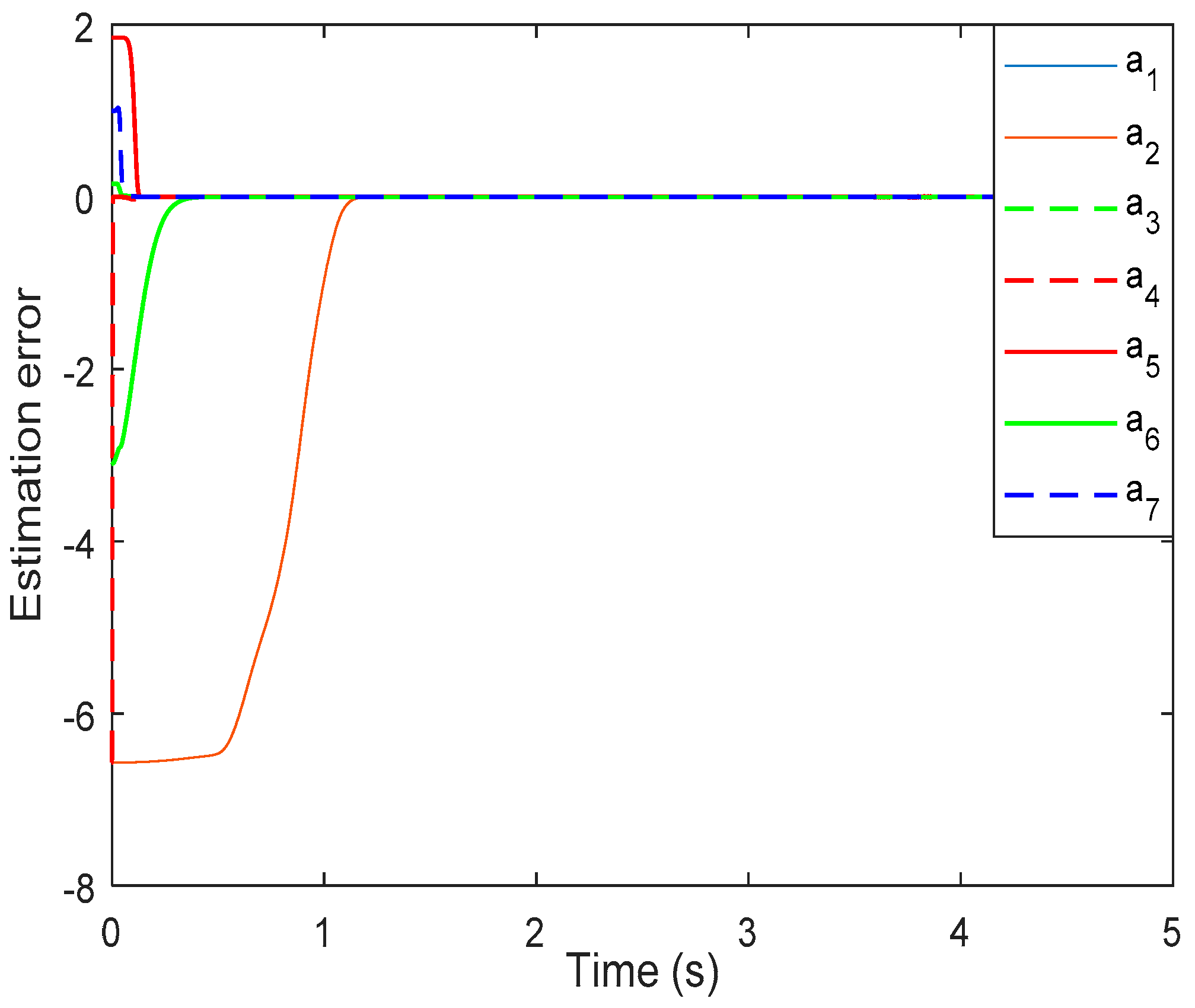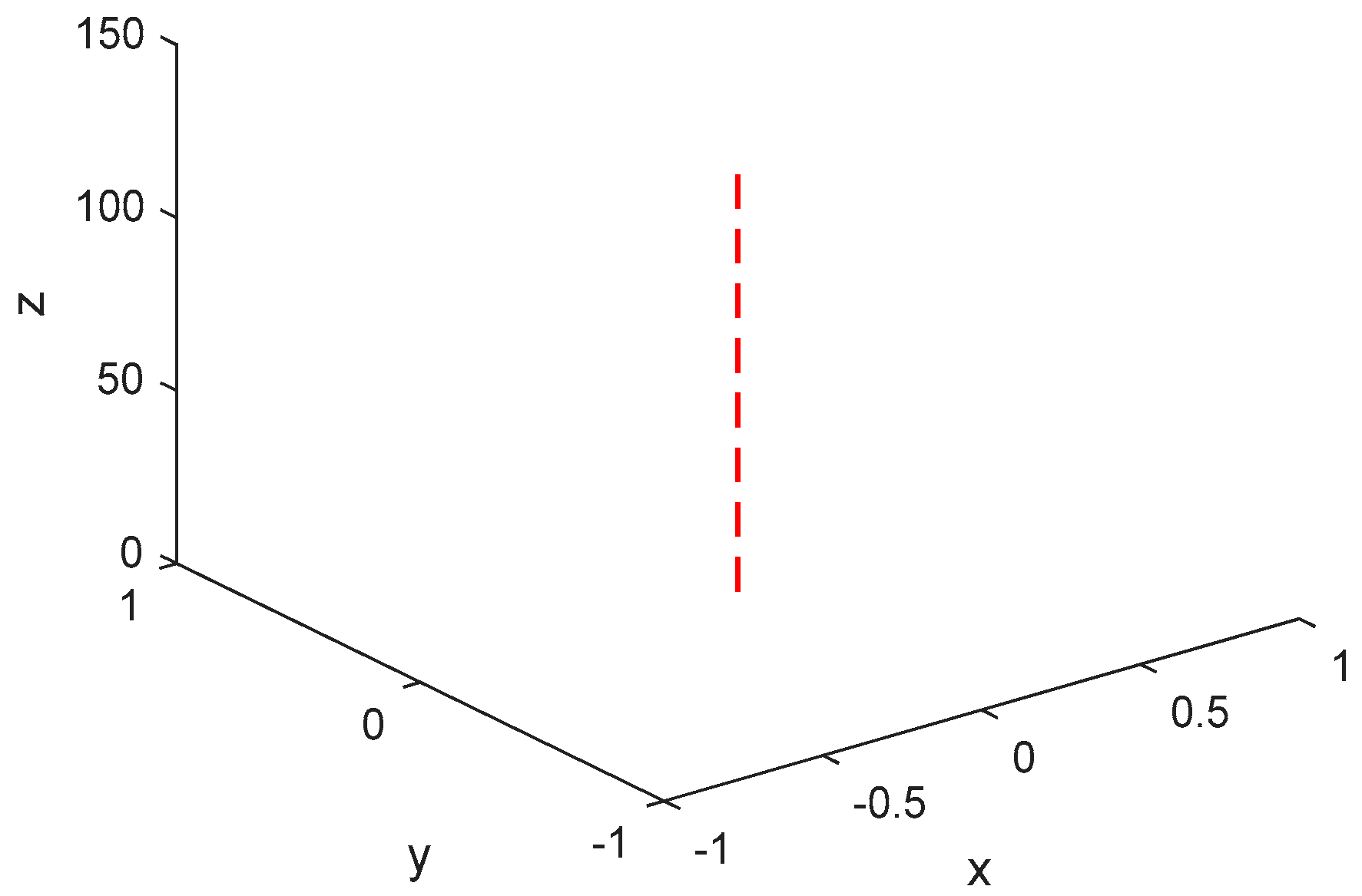In order to further verify the effectiveness of the proposed adaptive law, the estimation error $\tilde{Z}$ of $Z$ is given in Figure 8, which indicates that the estimation error $\tilde{Z}$ converges to zero in about 1.2 s. Nevertheless, the flight trajectory of the quadrotor is given in Figure 9, which indicates that the quadrotor is taking-off.

5. Conclusions

In this paper, an online adaptive parameter estimation method for quadrotors is proposed to improve the accuracy of the parameter estimation, which contributes to improving the stability and robustness of control systems for quadrotors. A scheme to obtain an expression of the estimation error is derived by introducing auxiliary filtered variables, and then an augmented matrix is constructed based on the derived filtered variables, which is further used to design the adaptive law to achieve convergence under the standard persistent excitation (PE) condition. Finally, a simulation example and experimental verification for quadrotors are displayed to indicate the effectiveness of the proposed method. Future work will focus on the estimation of time-varying parameters involved in the system.