Learning Heterogeneous Knowledge Base Embeddings for Explainable Recommendation
Abstract
1. Introduction
- We propose to integrate heterogeneous multi-type user behaviors and knowledge of the items into a unified graph structure for recommendation.
- Based on the user-item knowledge graph, we extend traditional CF to learn over the heterogeneous knowledge for recommendation, which helps to capture the user preferences more comprehensively.
- We further propose a soft matching algorithm to construct explanations regarding the recommended items by searching over the paths in the graph embedding space.
2. Related Work
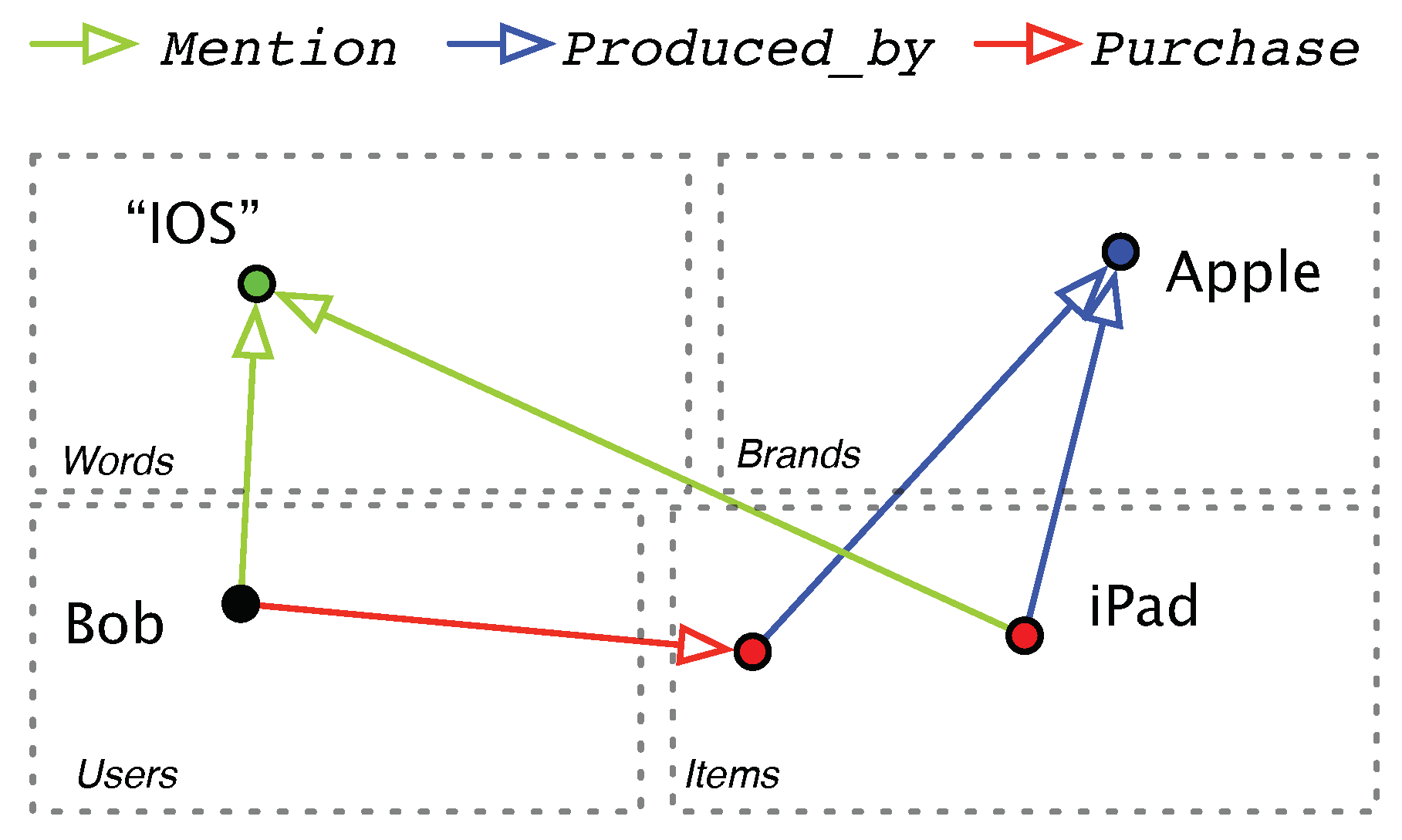
3. Problem Formulation
- user: the users of the recommender system.
- item: the products in the system to be recommended.
- word: the words in product names, descriptions or reviews.
- brand: the brand/producers of the product.
- category: the categories that a product belongs to.
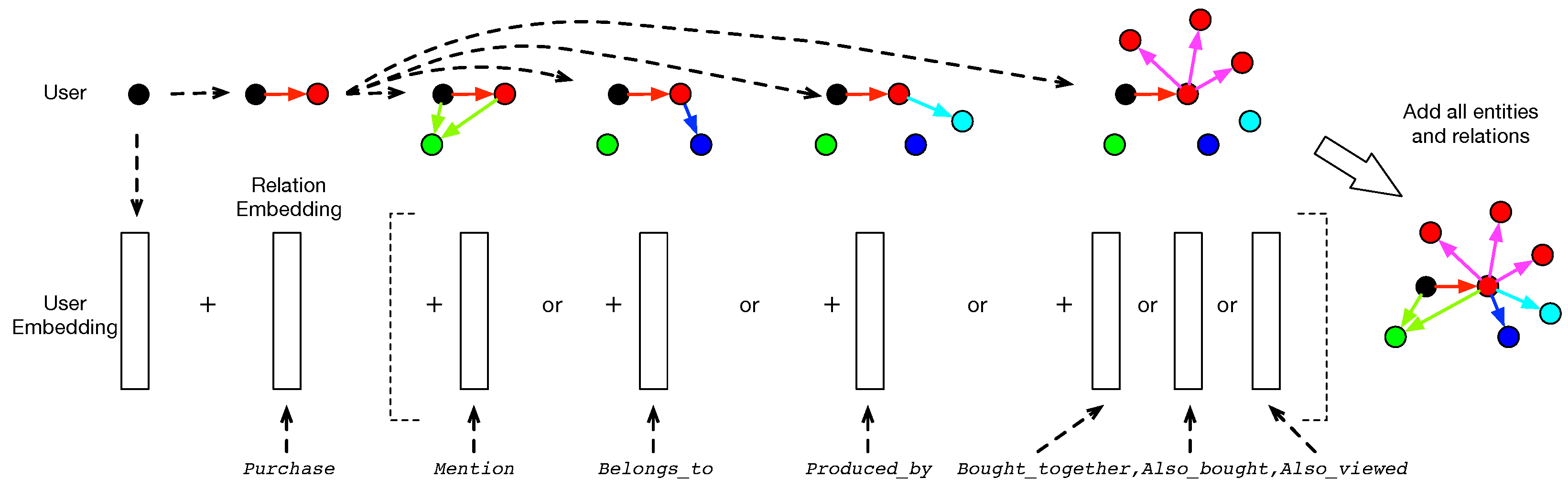
- Purchase: the relation from a user to an item, which means that the user has bought the item.
- Mention: the relation from a user or an item to a word, which means the word is mentioned in the user’s or item’s reviews.
- Belongs_to: the relation from an item to a category, which means that the item belongs to the category.
- Produced_by: the relation from an item to a brand, which means that the item is produced by the brand.
- Bought_together: the relation from an item to another item, which means that the items have been purchased together in a single transaction.
- Also_bought: the relation from an item to another item, which means the items have been purchased by same users.
- Also_viewed: the relation from an item to another item, which means that the second item was viewed before or after the purchase of the first item in a single session.
4. Collaborative Filtering on Knowledge Graphs
4.1. Relation Modeling as Entity Translations
4.2. Optimization Algorithm
5. Recommendation Explanation with Knowledge Reasoning
5.1. Explanation Path
| Algorithm 1: Recommendation Explanation Extraction |
 |
5.2. Entity Soft Matching
6. Experimental Setup
6.1. Datasets
6.2. Evaluation
- BPR: The Bayesian personalized ranking [38] model is a popular method for top-N recommendation that learns latent representations of users and items by optimizing the pairwise preferences between different user-item pairs. In this paper, we adopt matrix factorization as the prediction component for BPR.
- BPR-HFT: The hidden factors and topics (HFT) model [39] integrates latent factors with topic models for recommendation. The original HFT model is optimized for rating prediction tasks. For fair comparison, we learn the model parameters under the pairwise ranking framework of BPR for top-N recommendation.
- VBPR: The visual Bayesian personalized ranking [40] model is a state-of-the-art method that incorporate product image features into the framework of BPR for recommendation.
- TransRec: The translation-based recommendation approach proposed in [25], which takes items as entities and users as relations, and leveraged translation-based embeddings to learn the similarity between user and items for personalized recommendation. We adopted loss function, which was reported to have better performance in [25]. Notice that TransRec is different from our model because our model treats both items and users as entities, and learns embedding representations for different types of knowledge (e.g., brands, categories) as well as their relationships.
- DeepCoNN: The Deep Cooperative Neural Networks model for recommendation [32] is a neural model that applies a convolutional neural network (CNN) over the textual reviews to jointly model users and items for recommendation.
- CKE: The collaborative KBE model is a state-of-the-art neural model [24] that integrates text, images, and knowledge base for recommendation. It is similar to our model as they both use text and structured product knowledge, but it builds separate models on each type of data to construct item representations while our model constructs a knowledge graph that jointly embeds all entities and relations.
- JRL: The joint representation learning model [31] is a state-of-the-art neural recommender, which leverage multi-model information including text, images and ratings for Top-N recommendation.
6.3. Parameter Settings
7. Results and Discussion
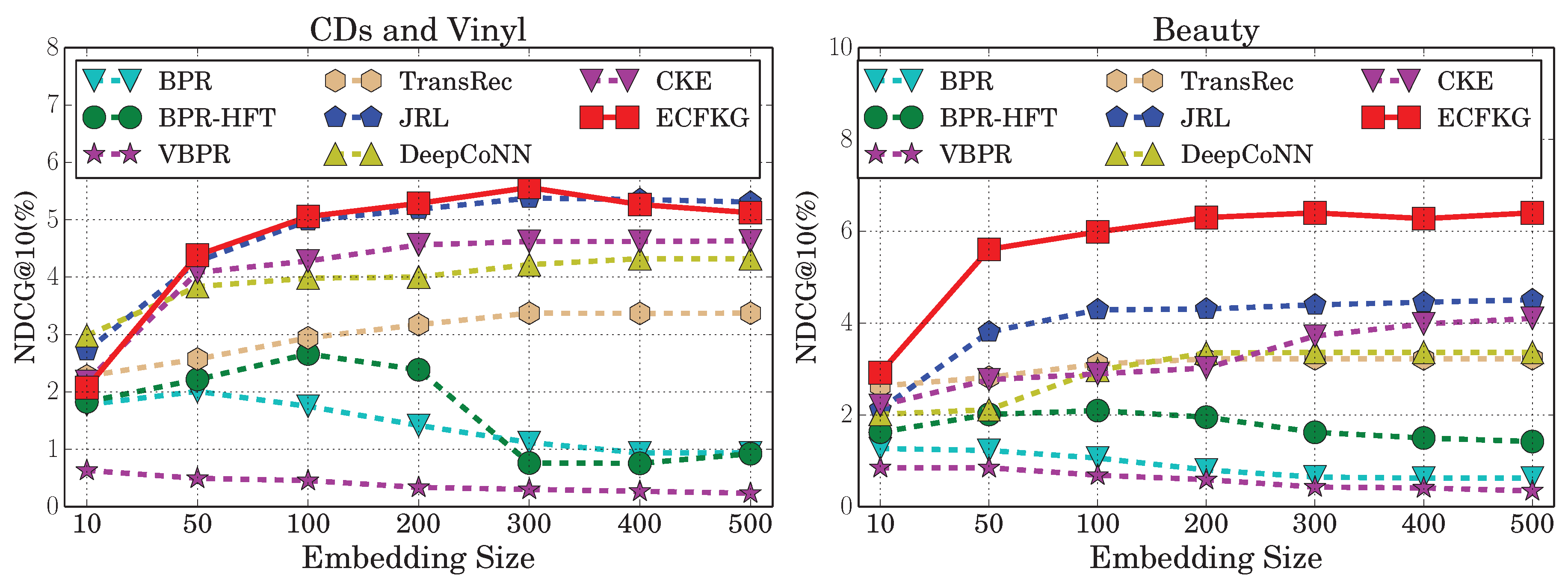
7.1. Recommendation Performance
- RQ1: Does incorporating knowledge-base in our model produce better recommendation performance?
- RQ2: Which types of product knowledge are most useful for top-N recommendation?
- RQ3: What is the computational efficiency of our model compared to other recommendation algorithms?
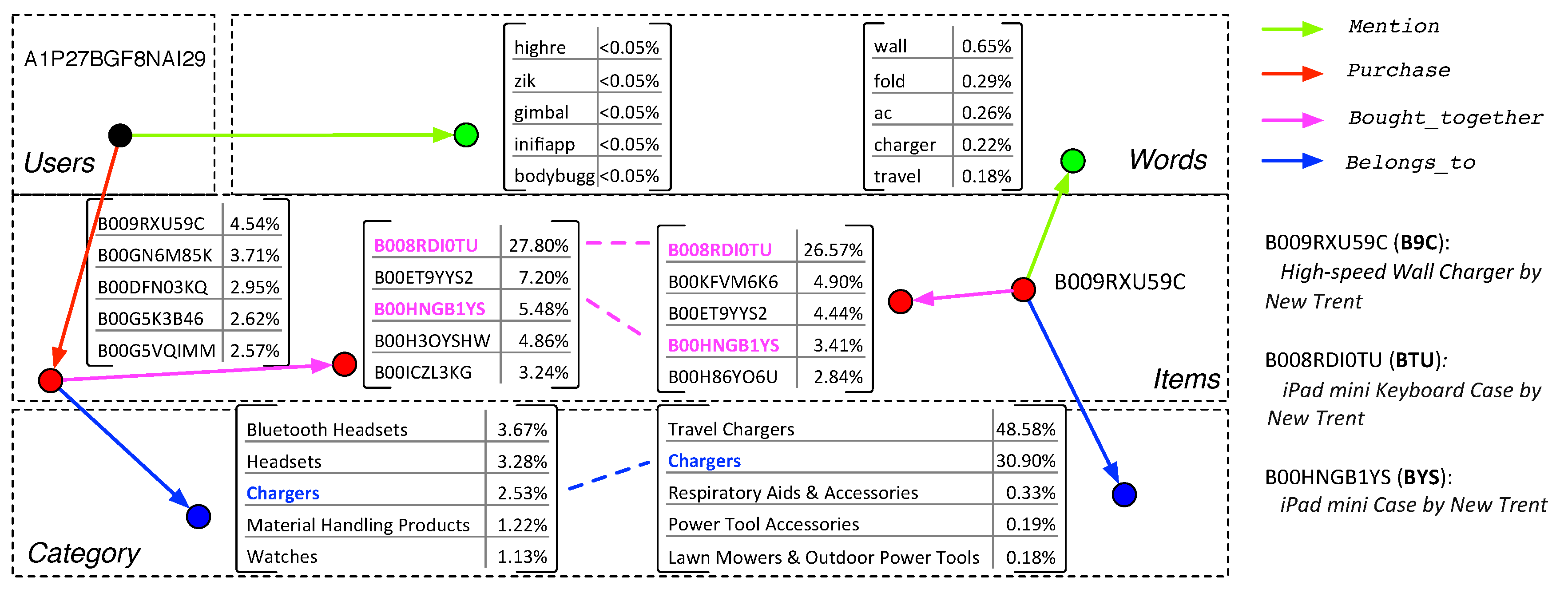
7.2. Case Study for Explanation Generation
- B9C is recommended because the user often purchases items that are bought with BTU together, and B9C is also frequently bought with BTU together ().
- B9C is recommended because the user often purchases items that are bought with BYS together, and B9C is also frequently bought with BYS together ().
- B9C is recommended because the user often purchases items related to the category Chargers, and B9C belongs to the category Chargers ().
8. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, Y.; Chen, X. Explainable Recommendation: A Survey and New Perspectives. arXiv, 2018; arXiv:1804.11192. [Google Scholar]
- Zhang, Y.; Lai, G.; Zhang, M.; Zhang, Y.; Liu, Y.; Ma, S. Explicit factor models for explainable recommendation based on phrase-level sentiment analysis. In Proceedings of the 37th International ACM SIGIR Conference on Research & Development in Information Retrieval, Gold Coast, Australia, 6–11 July 2014; pp. 83–92. [Google Scholar]
- Herlocker, J.L.; Konstan, J.A.; Riedl, J. Explaining collaborative filtering recommendations. In Proceedings of the 2000 ACM Conference on Computer Supported Cooperative Work, Philadelphia, PA, USA, 2–6 December 2000; pp. 241–250. [Google Scholar]
- Tintarev, N.; Masthoff, J. A survey of explanations in recommender systems. In Proceedings of the 2007 IEEE 23rd International Conference on Data Engineering Workshop, Istanbul, Turkey, 11–15 April 2007; pp. 801–810. [Google Scholar]
- Bilgic, M.; Mooney, R.J. Explaining recommendations: Satisfaction vs. promotion. In Proceedings of the Beyond Personalization 2005: A Workshop on the Next Stage of Recommender Systems Research at the 2005 International Conference on Intelligent User Interfaces, San Diego, CA, USA, 9 January 2005; p. 153. [Google Scholar]
- Cramer, H.; Evers, V.; Ramlal, S.; Van Someren, M.; Rutledge, L.; Stash, N.; Aroyo, L.; Wielinga, B. The effects of transparency on trust in and acceptance of a content-based art recommender. UMUAI 2008, 18, 455. [Google Scholar] [CrossRef]
- Tintarev, N.; Masthoff, J. Designing and Evaluating Explanations for Recommender Systems; Springer Press: Boston, MA, USA, 2011; pp. 479–510. [Google Scholar]
- Burke, R. Integrating knowledge-based and collaborative-filtering recommender systems. In Proceedings of the Workshop on AI and Electronic Commerce, Orlando, FL, USA, 18–19 July 1999; pp. 69–72. [Google Scholar]
- Shari, T. Knowledge-based recommender systems. Encycl. Libr. Inf. Sci. 2000, 69, 180. [Google Scholar]
- Ghani, R.; Fano, A. Building recommender systems using a knowledge base of product semantics. In Proceedings of the Workshop on Recommendation and Personalization in ECommerce at the 2nd International Conference on Adaptive Hypermedia and Adaptive Web based Systems, Malaga, Spain, 29–31 May 2002; pp. 27–29. [Google Scholar]
- Heitmann, B. An open framework for multi-source, cross-domain personalisation with semantic interest graphs. In Proceedings of the Sixth ACM Conference on Recommender Systems, Dublin, Ireland, 9–13 September 2012; pp. 313–316. [Google Scholar]
- Musto, C.; Lops, P.; Basile, P.; de Gemmis, M.; Semeraro, G. Semantics-aware graph-based recommender systems exploiting linked open data. In Proceedings of the 2016 Conference on User Modeling Adaptation and Personalization, Halifax, NS, Canada, 13–17 July 2016; pp. 229–237. [Google Scholar]
- Noia, T.D.; Ostuni, V.C.; Tomeo, P.; Sciascio, E.D. Sprank: Semantic path-based ranking for top-n recommendations using linked open data. ACM Trans. Intell. Syst. Technol. 2016, 8, 9. [Google Scholar] [CrossRef]
- Oramas, S.; Ostuni, V.C.; Noia, T.D.; Serra, X.; Sciascio, E.D. Sound and music recommendation with knowledge graphs. ACM Trans. Intell. Syst. Technol. 2017, 8, 21. [Google Scholar] [CrossRef]
- Catherine, R.; Mazaitis, K.; Eskenazi, M.; Cohen, W. Explainable Entity-based Recommendations with Knowledge Graphs. arXiv, 2017; arXiv:1707.05254. [Google Scholar]
- Nickel, M.; Tresp, V.; Kriegel, H.P. A Three-Way Model for Collective Learning on Multi-Relational Data. In Proceedings of the 28th International Conference on Machine Learning, Bellevue, WA, USA, 28 June–2 July 2011; pp. 809–816. [Google Scholar]
- Singh, A.P.; Gordon, G.J. Relational learning via collective matrix factorization. In Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Las Vegas, NV, USA, 24–27 August 2008; pp. 650–658. [Google Scholar]
- Miller, K.; Jordan, M.I.; Griffiths, T.L. Nonparametric latent feature models for link prediction. In Proceedings of the Advances in neural information processing systems, Vancouver, BC, Canada, 7–10 December 2009; pp. 1276–1284. [Google Scholar]
- Zhu, J. Max-margin nonparametric latent feature models for link prediction. In Proceedings of the 29th International Conference on Machine Learning, Edinburgh, UK, 27 June–3 July 2012. [Google Scholar]
- Bordes, A.; Weston, J.; Collobert, R.; Bengio, Y.; others. Learning Structured Embeddings of Knowledge Bases. In Proceedings of the 25th AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 9–10 August 2011; p. 6. [Google Scholar]
- Bordes, A.; Usunier, N.; Garcia-Duran, A.; Weston, J.; Yakhnenko, O. Translating embeddings for modeling multi-relational data. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–10 December 2013; pp. 2787–2795. [Google Scholar]
- Wang, Z.; Zhang, J.; Feng, J.; Chen, Z. Knowledge Graph Embedding by Translating on Hyperplanes. In Proceedings of the 28th AAAI Conference on Artificial Intelligence, Quebec, QC, Canada, 27–31 July 2014; pp. 1112–1119. [Google Scholar]
- Lin, Y.; Liu, Z.; Sun, M.; Liu, Y.; Zhu, X. Learning Entity and Relation Embeddings for Knowledge Graph Completion. In Proceedings of the 29th AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; p. 2181. [Google Scholar]
- Zhang, F.; Yuan, N.J.; Lian, D.; Xie, X.; Ma, W.Y. Collaborative knowledge base embedding for recommender systems. In Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining, San Francisco, CA, USA, 13–17 August 2016; pp. 353–362. [Google Scholar]
- He, R.; Kang, W.C.; McAuley, J. Translation-based Recommendation. In Proceedings of the 11th ACM Conference on Recommender Systems, Como, Italy, 27 –31 August 2017; pp. 161–169. [Google Scholar]
- Li, S.; Kawale, J.; Fu, Y. Deep Collaborative Filtering via Marginalized Denoising Auto-encoder. In Proceedings of the 24th ACM Conference on Information and Knowledge Management, Melbourne, Australia, 19–23 October 2015; pp. 811–820. [Google Scholar]
- Wang, H.; Wang, N.; Yeung, D.Y. Collaborative Deep Learning for Recommender Systems. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 1235–1244. [Google Scholar]
- Li, X.; She, J. Collaborative Variational Autoencoder for Recommender Systems. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 305–314. [Google Scholar]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.S.; Dean, J. Distributed representations of words and phrases and their compositionality. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–10 December 2013; pp. 3111–3119. [Google Scholar]
- Le, Q.; Mikolov, T. Distributed representations of sentences and documents. In Proceedings of the International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 1188–1196. [Google Scholar]
- Zhang, Y.; Ai, Q.; Chen, X.; Croft, W.B. Joint representation learning for top-n recommendation with heterogeneous information sources. In Proceedings of the 2017 ACM Conference on Information and Knowledge Management, Singapore, 6–10 November 2017; pp. 1449–1458. [Google Scholar]
- Zheng, L.; Noroozi, V.; Yu, P.S. Joint deep modeling of users and items using reviews for recommendation. In Proceedings of the Tenth ACM International Conference on Web Search and Data Mining, Cambridge, UK, 6–10 February 2017; pp. 425–434. [Google Scholar]
- Ai, Q.; Yang, L.; Guo, J.; Croft, W.B. Analysis of the paragraph vector model for information retrieval. In Proceedings of the 2016 ACM International Conference on the Theory of Information Retrieval, Newark, DE, USA, 12–16 September 2016; pp. 133–142. [Google Scholar]
- Ai, Q.; Zhang, Y.; Bi, K.; Chen, X.; Croft, W.B. Learning a hierarchical embedding model for personalized product search. In Proceedings of the 40th International ACM SIGIR Conference on Research and Development in Information Retrieval, Shinjuku, Tokyo, Japan, 7–11 August 2017; pp. 645–654. [Google Scholar]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient estimation of word representations in vector space. arXiv, 2013; arXiv:1301.3781. [Google Scholar]
- Levy, O.; Goldberg, Y. Neural word embedding as implicit matrix factorization. In Proceedings of the Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 2177–2185. [Google Scholar]
- McAuley, J.; Targett, C.; Shi, Q.; Van Den Hengel, A. Image-based recommendations on styles and substitutes. In Proceedings of the 38th International ACM SIGIR Conference on Research and Development in Information Retrieval, Santiago, Chile, 9–13 August 2015; pp. 43–52. [Google Scholar]
- Rendle, S.; Freudenthaler, C.; Gantner, Z.; Schmidt-Thieme, L. BPR: Bayesian personalized ranking from implicit feedback. In Proceedings of the Twenty-Fifth Conference on Uncertainty in Artificial Intelligence, Montreal, QC, Canada, 18–21 June 2009; pp. 452–461. [Google Scholar]
- McAuley, J.; Leskovec, J. Hidden factors and hidden topics: understanding rating dimensions with review text. In Proceedings of the 7th ACM Conference on Recommender Systems, Hong Kong, China, 12–16 October 2013; pp. 165–172. [Google Scholar]
- He, R.; McAuley, J. VBPR: Visual Bayesian Personalized Ranking from Implicit Feedback. In Proceedings of the 30th AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; pp. 144–150. [Google Scholar]
- Smucker, M.D.; Allan, J.; Carterette, B. A comparison of statistical significance tests for information retrieval evaluation. In Proceedings of the Sixteenth ACM Conference on Information and Knowledge Management, Lisbon, Portugal, 6–10 November 2007; pp. 623–632. [Google Scholar]
| CDs & Vinyl | Clothing | Cell Phones & Accessories | Beauty | |
|---|---|---|---|---|
| Entities | ||||
| #Reviews | 1,097,591 | 278,677 | 194,439 | 198,502 |
| #Words per review | 174.57 ± 177.05 | 62.21 ± 60.16 | 93.50 ±131.65 | 90.90 ± 91.86 |
| #Users | 75,258 | 39,387 | 27,879 | 22,363 |
| #Items | 64,443 | 23,033 | 10,429 | 12,101 |
| #Brands | 1414 | 1182 | 955 | 2077 |
| #Categories | 770 | 1,193 | 206 | 248 |
| Density | 0.023% | 0.031% | 0.067% | 0.074% |
| Relations | ||||
| #Purchase per user | 14.58 ± 39.13 | 7.08 ± 3.59 | 6.97 ± 4.55 | 8.88 ± 8.16 |
| #Mention per user | 2545.92 ± 10,942.31 | 440.20 ± 452.38 | 652.08 ± 1335.76 | 806.89 ± 1344.08 |
| #Mention per item | 2973.19 ± 5490.93 | 752.75 ± 909.42 | 1743.16 ± 3482.76 | 1491.16 ± 2553.93 |
| #Also_bought per item | 57.28 ± 39.22 | 61.35 ± 32.99 | 56.53 ± 35.82 | 73.65 ± 30.69 |
| #Also_viewed per item | 0.27 ± 1.86 | 6.29 ± 6.17 | 1.24 ± 4.29 | 12.84 ± 8.97 |
| #Bought_together per item | 0.68 ± 0.80 | 0.69 ± 0.90 | 0.81 ± 0.77 | 0.75 ± 0.72 |
| #Produced_by per item | 0.21 ± 0.41 | 0.17 ± 0.38 | 0.52 ± 0.50 | 0.83 ± 0.38 |
| #Belongs_to per item | 7.25 ± 3.13 | 6.72 ± 2.15 | 3.49 ± 1.08 | 4.11 ± 0.70 |
| Dataset | CDs and Vinyl | Clothing | Cell Phones | Beauty | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Measures (%) | NDCG | Recall | HR | Prec. | NDCG | Recall | HR | Prec. | NDCG | Recall | HR | Prec. | NDCG | Recall | HR | Prec. |
| BPR | 2.009 | 2.679 | 8.554 | 1.085 | 0.601 | 1.046 | 1.767 | 0.185 | 1.998 | 3.258 | 5.273 | 0.595 | 2.753 | 4.241 | 8.241 | 1.143 |
| BPR-HFT | 2.661 | 3.570 | 9.926 | 1.268 | 1.067 | 1.819 | 2.872 | 0.297 | 3.151 | 5.307 | 8.125 | 0.860 | 2.934 | 4.459 | 8.268 | 1.132 |
| VBPR | 0.631 | 0.845 | 2.930 | 0.328 | 0.560 | 0.968 | 1.557 | 0.166 | 1.797 | 3.489 | 5.002 | 0.507 | 1.901 | 2.786 | 5.961 | 0.902 |
| TransRec | 3.372 | 5.283 | 11.956 | 1.837 | 1.245 | 2.078 | 3.116 | 0.312 | 3.361 | 6.279 | 8.725 | 0.962 | 3.218 | 4.853 | 9.867 | 1.285 |
| DeepCoNN | 4.218 | 6.001 | 13.857 | 1.681 | 1.310 | 2.332 | 3.286 | 0.229 | 3.636 | 6.353 | 9.913 | 0.999 | 3.359 | 5.429 | 9.807 | 1.200 |
| CKE | 4.620 | 6.483 | 14.541 | 1.779 | 1.502 | 2.509 | 4.275 | 0.388 | 3.995 | 7.005 | 10.809 | 1.070 | 3.717 | 5.938 | 11.043 | 1.371 |
| JRL | 5.378 * | 7.545 * | 16.774 * | 2.085 * | 1.735 * | 2.989 * | 4.634 * | 0.442 * | 4.364 * | 7.510 * | 10.940 * | 1.096 * | 4.396 * | 6.949 * | 12.776 * | 1.546 * |
| Our model | 5.563 | 7.949 | 17.556 | 2.192 | 3.091 | 5.466 | 7.972 | 0.763 | 5.370 | 9.498 | 13.455 | 1.325 | 6.399 | 10.411 | 17.498 | 1.986 |
| Improvement | 3.44 | 5.35 | 4.66 | 5.13 | 78.16 | 82.87 | 72.03 | 72.62 | 23.05 | 26.47 | 22.99 | 20.89 | 45.56 | 49.82 | 36.96 | 28.46 |
| Relations | CDs and Vinyl | Clothing | Cell Phones | Beauty | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Measures(%) | NDCG | Recall | HT | Prec | NDCG | Recall | HT | Prec | NDCG | Recall | HT | Prec | NDCG | Recall | HT | Prec |
| Purchaseonly | 1.725 | 2.319 | 7.052 | 0.818 | 0.974 | 1.665 | 2.651 | 0.254 | 2.581 | 4.526 | 6.611 | 0.649 | 2.482 | 3.834 | 7.432 | 0.948 |
| +Also_view | 1.722 | 2.356 | 6.967 | 0.817 | 1.800 | 3.130 | 4.672 | 0.448 | 2.555 | 4.367 | 6.417 | 0.630 | 4.592 | 7.505 | 12.901 | 1.511 |
| +Also_bought | 3.641 | 5.285 | 12.332 | 1.458 | 1.352 | 2.419 | 3.580 | 0.343 | 4.095 | 7.129 | 10.051 | 0.986 | 4.301 | 6.994 | 11.908 | 1.408 |
| +Bought_together | 1.962 | 2.712 | 7.473 | 0.861 | 0.694 | 1.284 | 2.026 | 0.189 | 3.173 | 5.572 | 7.952 | 0.784 | 3.341 | 5.337 | 9.556 | 1.181 |
| +Produced_by | 1.719 | 2.318 | 6.842 | 0.792 | 0.579 | 1.044 | 1.630 | 0.155 | 2.852 | 4.982 | 7.274 | 0.719 | 3.707 | 5.939 | 10.660 | 1.287 |
| +Belongs_to | 2.799 | 4.028 | 10.297 | 1.200 | 1.453 | 2.570 | 3.961 | 0.376 | 2.807 | 4.892 | 7.242 | 0.717 | 3.347 | 5.382 | 9.994 | 1.193 |
| +Mention | 3.822 | 5.185 | 12.828 | 1.628 | 1.019 | 1.754 | 2.780 | 0.265 | 3.387 | 5.806 | 8.548 | 0.848 | 3.658 | 5.727 | 10.549 | 1.305 |
| +all(our model) | 5.563 | 7.949 | 17.556 | 2.192 | 3.091 | 5.466 | 7.972 | 0.763 | 5.370 | 9.498 | 13.455 | 1.325 | 6.370 | 10.341 | 17.131 | 1.959 |
| Review of Jabra VOX Corded Stereo Wired Headsets |
| ... I like to listen to music at work, but I must wear some sort of headset so that I do not create a disturbance. So, I have a broad experience in headsets ... |
| Review of OXA Juice Mini M1 2600mAh |
| ... I recently had an experience, where I was about town and need to recharge my iPad , and so I tried this thing out. I plugged in the iPad , and it quickly charged it up, and at my next destination it was ready to go ... |
| Review of OXA 8000mAh Solar External Battery Pack Portable |
| ... This amazing gadget is a solar powered charger for your small electronic device. This charger is (according to my ruler) 5-1/4 inches by 3 inches by about 6 inches tall. So, it is a bit big to place in the pocket ... |
| Review of OXA Bluetooth Wristwatch Bracelet |
| ... I was far from thrilled with Bluetooth headset that I had, so I decided to give this device a try. Pros: The bracelet is not bad looking, ... |
| Review of OXA Mini Portable Wireless Bluetooth Speaker |
| ... This little gadget is a Bluetooth speaker. It’s fantastic! This speaker fits comfortably in the palm of your hand, ... |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ai, Q.; Azizi, V.; Chen, X.; Zhang, Y. Learning Heterogeneous Knowledge Base Embeddings for Explainable Recommendation. Algorithms 2018, 11, 137. https://doi.org/10.3390/a11090137
Ai Q, Azizi V, Chen X, Zhang Y. Learning Heterogeneous Knowledge Base Embeddings for Explainable Recommendation. Algorithms. 2018; 11(9):137. https://doi.org/10.3390/a11090137
Chicago/Turabian StyleAi, Qingyao, Vahid Azizi, Xu Chen, and Yongfeng Zhang. 2018. "Learning Heterogeneous Knowledge Base Embeddings for Explainable Recommendation" Algorithms 11, no. 9: 137. https://doi.org/10.3390/a11090137
APA StyleAi, Q., Azizi, V., Chen, X., & Zhang, Y. (2018). Learning Heterogeneous Knowledge Base Embeddings for Explainable Recommendation. Algorithms, 11(9), 137. https://doi.org/10.3390/a11090137






