An Effective Data Transmission Algorithm Based on Social Relationships in Opportunistic Mobile Social Networks
Abstract
:1. Introduction
- In opportunistic social networks, we propose an effective data transmission algorithm based on social relationships, which divides the network into several communities. By forwarding data through the community structures, the information transfer is faster and safer.
- After dividing the nodes in the opportunistic social network into communities, we propose a method to reduce the community structure according to the features of nodes, to maintain the cohesion of the community and the high efficiency of data transmission.
- According to the reduced community structure, we copy the information that needs to be transmitted several times and distribute different numbers of copies to different communities, which can reduce routing overhead while ensuring packet delivery ratio and transmission delay.
- Using the simulation tool OMNET++, we analyze the performance of the ESR algorithm and compared it with some other algorithms. Our algorithm proposed in this paper has a higher packet delivery ratio, with lower transmission delay and routing overhead.
2. Related Works
3. System Model Design
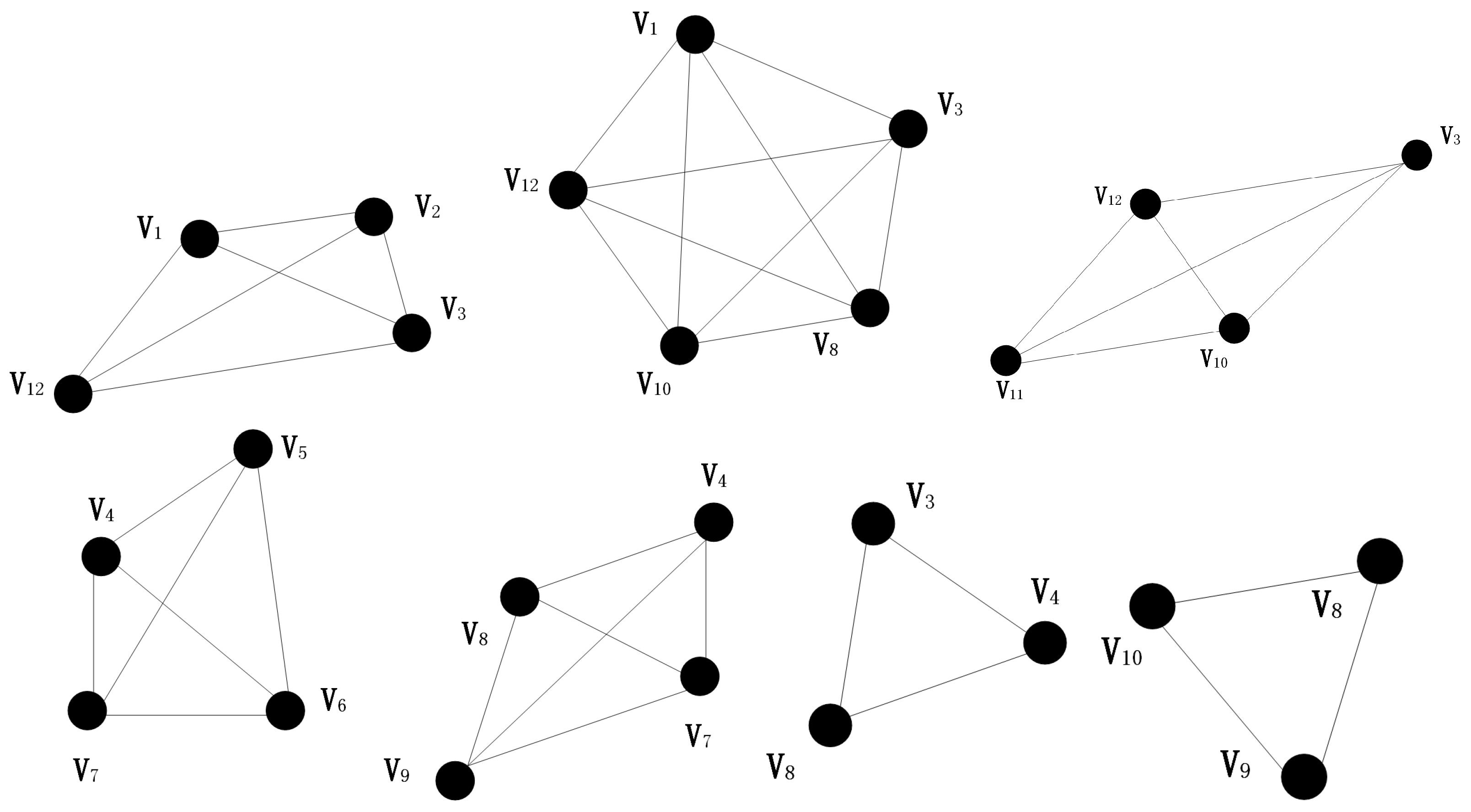
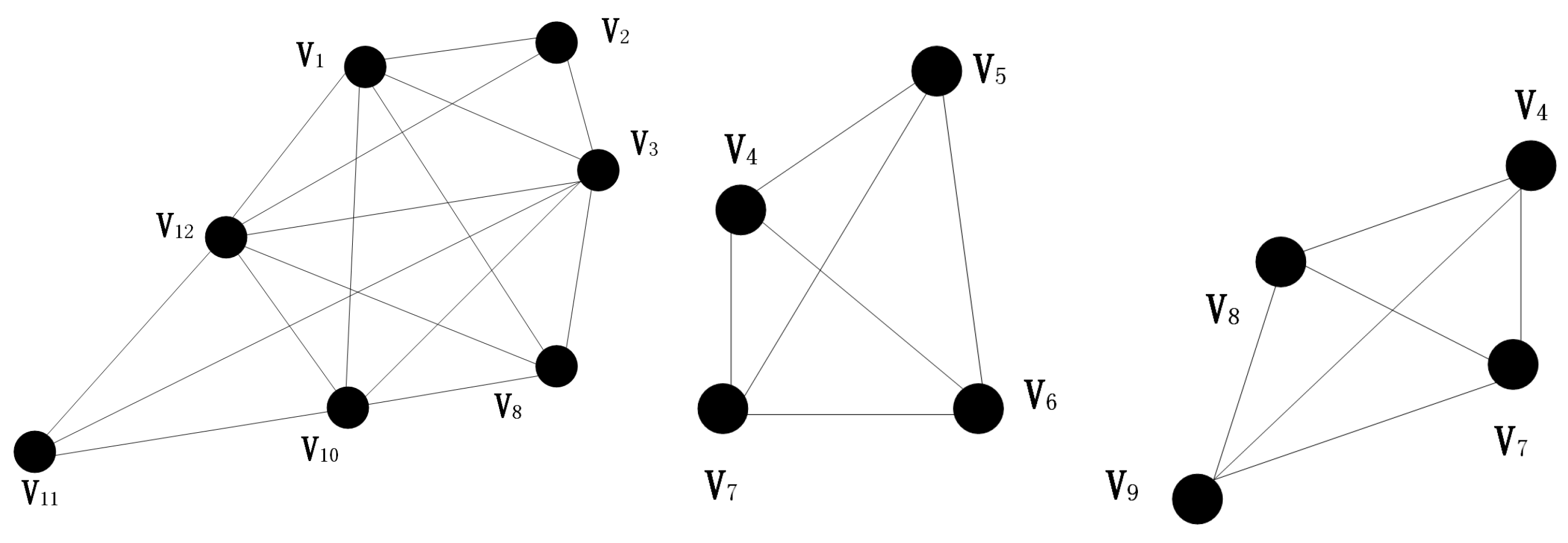
3.1. Community Division Strategy
3.2. Community Structure Contraction Strategy
| Algorithm 1 Community structure contraction algorithm |
|
3.3. Community-Based Data-Forwarding Algorithm
| Algorithm 2 Community based data-forwarding algorithm |
|
4. Simulation
4.1. Community Division Interval
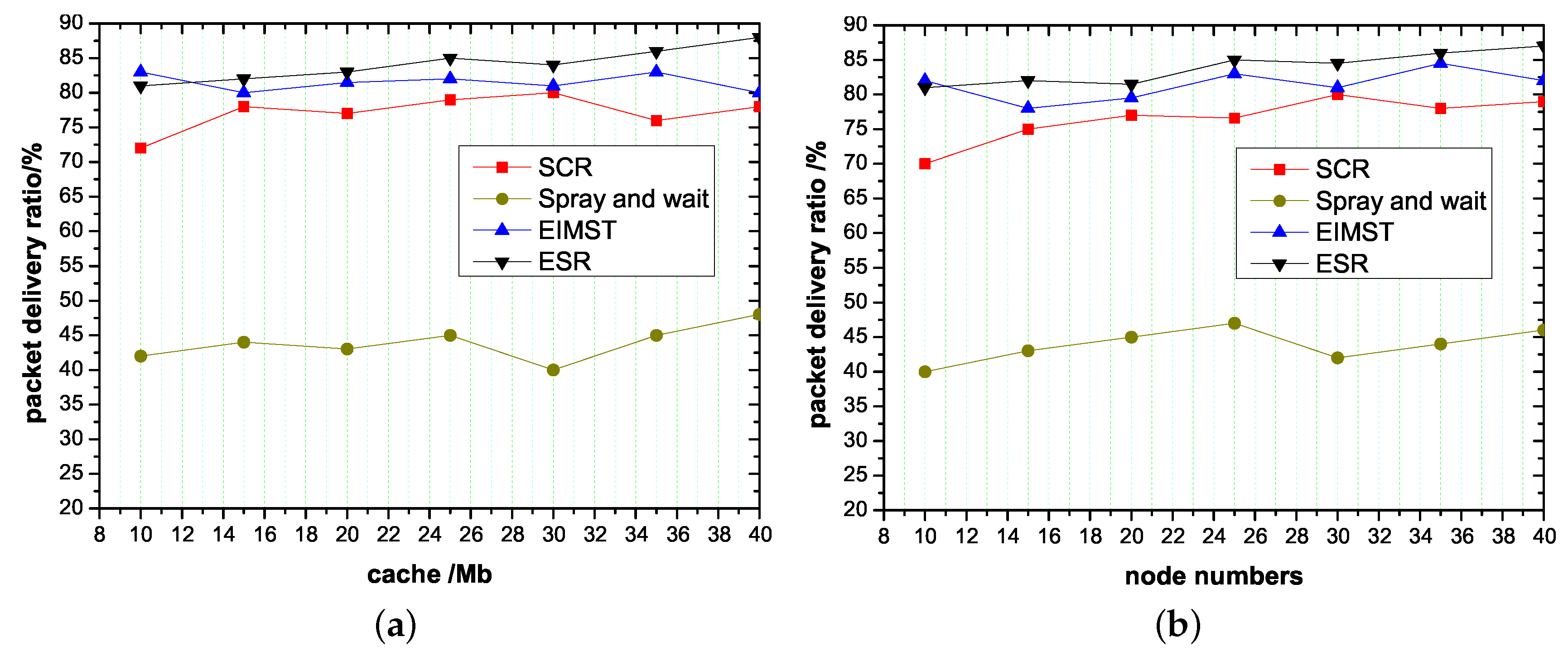
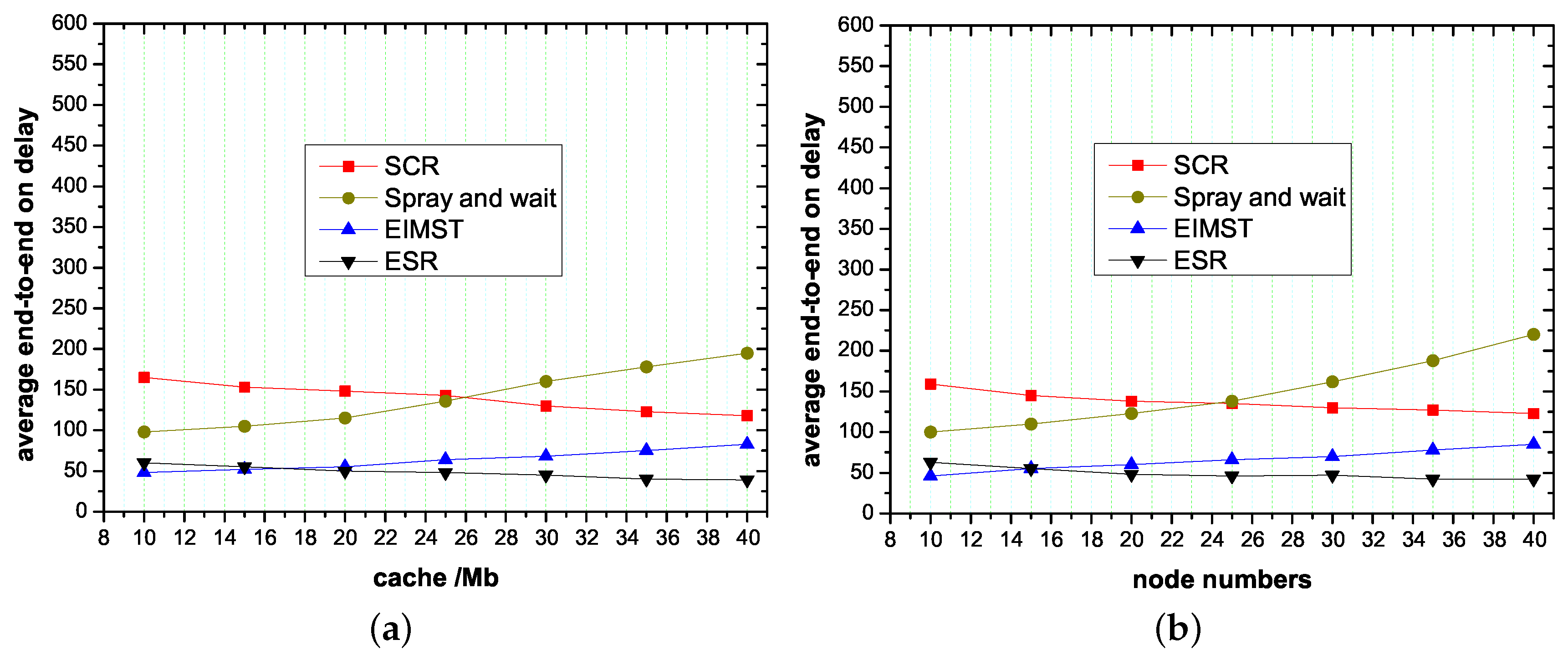
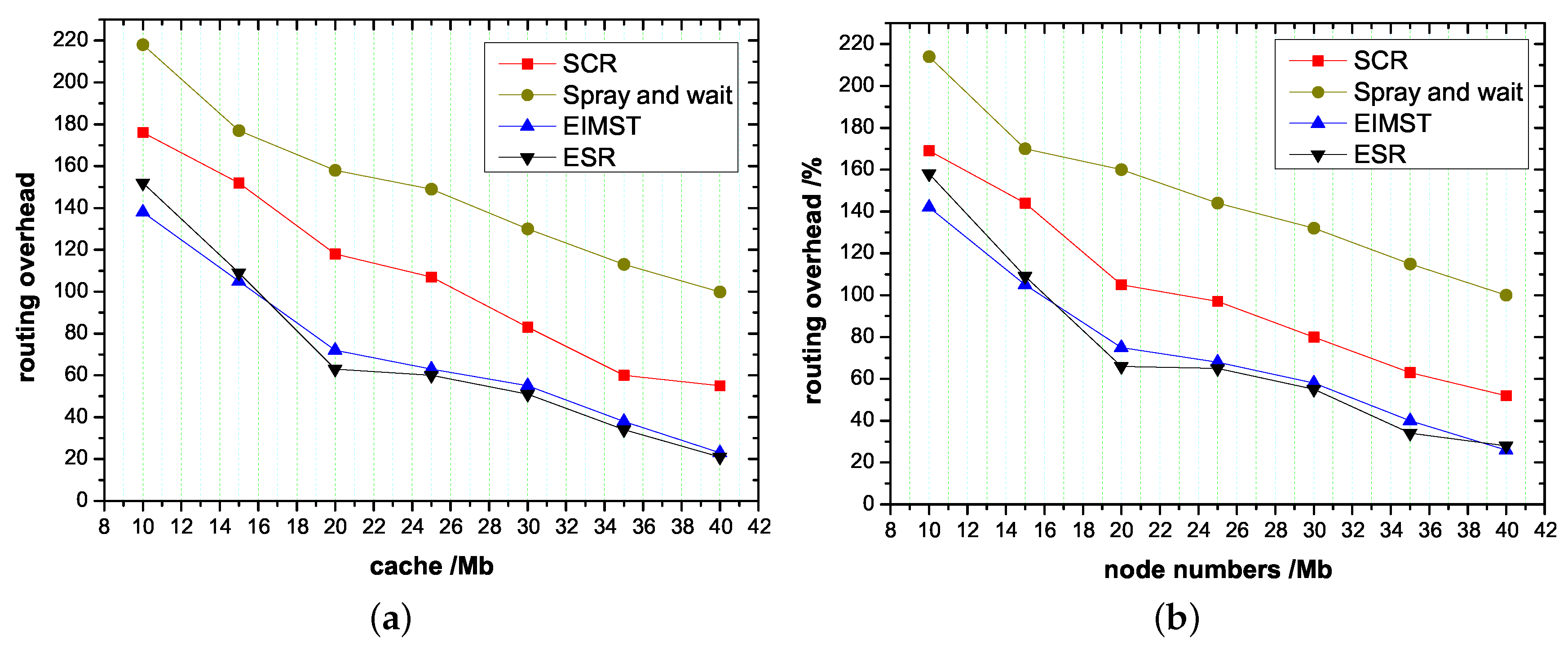
4.2. Effect of Node Cache and Node Numbers on Routing Algorithms
- Packet delivery ratio: This parameter refers to the probability that a packet sent from the source successfully reaches the target within a certain time.
- Average end-to-end on delay: This parameter comprehensively evaluates the delay caused by packet routing, waiting delay and transmission delay.
- Routing overhead: This parameter shows the overhead between two nodes when information is transmitted.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wu, J.; Chen, Z. Sensor communication area and node extend routing algorithm in opportunistic networks. Peer-to-Peer Netw. Appl. 2016, 11, 90–100. [Google Scholar] [CrossRef]
- Roy, A.; Deb, T. Performance Comparison of Routing Protocols in Mobile Ad Hoc Networks. Int. J. Eng. Sci. Technol. 2018, 2, 279. [Google Scholar]
- Mukherjee, A.; Basu, S.; Roy, S.; Bandyopadhyay, S. Developing a coherent global view for post disaster situation awareness using opportunistic network. In Proceedings of the 2015 7th International Conference on Communication Systems and Networks, Bangalore, India, 6–10 January 2015; pp. 1–8. [Google Scholar]
- Ghumare, S.S.; Labade, R.P.; Gagare, S.R. Rare Wild Animal Tracking in the Forest area with Wireless Sensor Network in Network Simulator-2. Int. J. Comput. Appl. 2016, 133, 1–4. [Google Scholar]
- Kaiwartya, O.; Abdullah, A.H.; Cao, Y.; Altameem, A.; Prasad, M.; Lin, C.T.; Liu, X. Internet of Vehicles: Motivation, Layered Architecture, Network Model, Challenges, and Future Aspects. IEEE Access 2017, 4, 5356–5373. [Google Scholar] [CrossRef]
- Jia, W.U.; Chen, Z.; Zhao, M. Effective information transmission based on socialization nodes in opportunistic networks. Comput. Netw. 2017, 129, 297–305. [Google Scholar]
- Zeng, F.; Zhao, N.; Li, W. Effective Social Relationship Measurement and Cluster Based Routing in Mobile Opportunistic Networks. Sensors 2017, 17, 1109. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Chen, Z. Human Activity Optimal Cooperation Objects Selection Routing Scheme in Opportunistic Networks Communication. Wirel. Pers. Commun. 2017, 95, 3357–3375. [Google Scholar] [CrossRef]
- Ciobanu, R.I.; Marin, R.C.; Dobre, C.; Cristea, V.; Mavromoustakis, C.X. ONSIDE: Socially-aware and Interest-based dissemination in opportunistic networks. In Network Operations and Management Symposium; IEEE: Piscataway, NJ, USA, 2014; pp. 1–6. [Google Scholar]
- Socievole, A.; Yoneki, E.; De Rango, F.; Crowcroft, J. ML-SOR: Message routing using multi-layer social networks in opportunistic communications. Comput. Netw. 2015, 81, 201–219. [Google Scholar] [CrossRef]
- Kumiawan, Z.H.; Yovita, L.V.; Wibowo, T.A. Performance analysis of dLife routing in a delay tolerant networks. In Proceedings of the 2016 International Conference on International Conference on Control, Electronics, Renewable Energy and Communications, Bandung, Indonesia, 13–15 September 2017; pp. 41–46. [Google Scholar]
- Wang, X.; Chen, M.; Kwon, T.; Jin, L.; Leung, V. Mobile traffic offloading by exploiting social network services and leveraging opportunistic device-to-device sharing. Wirel. Commun. IEEE 2014, 21, 28–36. [Google Scholar] [CrossRef]
- Wu, J.; Chen, Z.; Zhao, M. Weight distribution and community reconstitution based on communities communications in social opportunistic networks. Peer-to-Peer Netw. Appl. 2018, 1–12. [Google Scholar] [CrossRef]
- Yuan, L.; Qin, L.; Zhang, W.; Chang, L.; Yang, J. Index-based Densest Clique Percolation Community Search In Networks. IEEE Trans. Knowl. Data Eng. 2018, 30, 922–935. [Google Scholar] [CrossRef]
- Neena, V.V.; Rajam, V.M.A. Performance analysis of epidemic routing protocol for opportunistic networks in different mobility patterns. In Proceedings of the 2013 International Conference on International Conference on Computer Communication and Informatics, Coimbatore, India, 4–6 January 2013; pp. 1–5. [Google Scholar]
- Kim, J.B.; Lee, I.H. Non-Orthogonal Multiple Access in Coordinated Direct and Relay Transmission. IEEE Commun. Lett. 2015, 19, 2037–2040. [Google Scholar] [CrossRef]
- Wan, B. An optimized Prophet delay tolerant network routing algorithm based on social environment. Wirel. Internet Technol. 2017. [Google Scholar]
- Sisodiya, S.; Sharma, P.; Tiwari, S.K. A new modified spray and wait routing algorithm for heterogeneous delay tolerant network. In Proceedings of the 2017 International Conference on International Conference on I-Smac, Coimbatore, India, 10–11 February 2017; pp. 843–848. [Google Scholar]
- Han, X.; Yun, L.; Zhang, Z.; Li, J.; Xiong, F. A multi-label community discovery algorithm based on the community kernel. In Proceedings of the 11th International Knowledge Management in Organizations Conference on The changing face of Knowledge Management Impacting Society, Hagen, Germany, 25–28 July 2016; pp. 1–5. [Google Scholar]
- Jaimini, P.; Patel, R. Efficient Routing using Bubble Rap in Delay Tolerant Network. Int. J. Comput. Appl. 2016, 137, 16–19. [Google Scholar] [CrossRef]
- Du, W. Research on Individual Influence in Social Networking Services Based on MapReduce. J. Inf. Comput. Sci. 2015, 12, 4715–4723. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, X.; Zhang, J. Social-aware relay selection for cooperative networking: An optimal stopping approach. In Proceedings of the 2014 IEEE International Conference on Communications, Sydney, Australia, 10–14 June 2014; pp. 2257–2262. [Google Scholar]
- Cao, Y.; Han, C.; Zhang, X.; Kaiwartya, O.; Zhuang, Y.; Aslam, N.; Dianati, M. A Trajectory-Driven Opportunistic Routing Protocol for VCPS. IEEE Trans. Aerosp. Electron. Syst. 2018. [CrossRef]
- Kasana, R.; Kumar, S.; Kaiwartya, O.; Yan, W.; Cao, Y.; Abdullah, A.H. Location error resilient geographical routing for vehicular ad-hoc networks. IET Intell. Transp. Syst. 2017, 11, 450–458. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.K.; Ren, J.; Song, C.; Jia, J.; Zhang, Q. Label propagation algorithm for community detection based on node importance and label influence. Phys. Lett. A 2017, 381, 2691–2698. [Google Scholar] [CrossRef]
- Spyropoulos, T.; Psounis, K.; Raghavendra, C.S. Spray and wait: An efficient routing scheme for intermittently connected mobile networks. In Proceedings of the 2005 ACM SIGCOMM Workshop on Delay-Tolerant Networking, Philadelphia, PA, USA, 22–26 August 2005; pp. 252–259. [Google Scholar]
- Hornig, R. An overview of the OMNeT++ simulation environment. In Proceedings of the International Conference on Simulation TOOLS and Techniques for Communications, Networks and Systems & Workshops, Marseille, France, 3–7 March 2008; p. 60. [Google Scholar]
- Wu, J.; Chen, Z.; Zhao, M. Information Transmission Probability and Cache Management Method in Opportunistic Networks. Wirel. Commun. Mob. Comput. 2018. [Google Scholar] [CrossRef]


| Environmental Parameter | Settings |
|---|---|
| Simulation time/h | 12 |
| Simulation area | 4300 × 1200 m |
| Background city | St Paul |
| Number of nodes | 1000 |
| Velcocity of a node/(m/s) | 0.5 1.5 |
| Transmit speed(KB/s) | 250 |
| Maximum transmission distance/m | 10 |
| Transmission mode | broadcast |
| Buffer size/MB | 10 |
| Packet size | 500 KB 1 MB |
| Packet sending intervals/s | 25 35 |
| Parameter | Value | Description |
|---|---|---|
| N | 16 | Faction setting parameter |
| 0.17 | A threshold value that measures whether a node is important within a controllable range | |
| 0.42 | Parameter decides whether the community structure needs to shrink |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Y.; Chen, Z.; Wu, J.; Wang, L. An Effective Data Transmission Algorithm Based on Social Relationships in Opportunistic Mobile Social Networks. Algorithms 2018, 11, 125. https://doi.org/10.3390/a11080125
Yan Y, Chen Z, Wu J, Wang L. An Effective Data Transmission Algorithm Based on Social Relationships in Opportunistic Mobile Social Networks. Algorithms. 2018; 11(8):125. https://doi.org/10.3390/a11080125
Chicago/Turabian StyleYan, Yeqing, Zhigang Chen, Jia Wu, and Leilei Wang. 2018. "An Effective Data Transmission Algorithm Based on Social Relationships in Opportunistic Mobile Social Networks" Algorithms 11, no. 8: 125. https://doi.org/10.3390/a11080125
APA StyleYan, Y., Chen, Z., Wu, J., & Wang, L. (2018). An Effective Data Transmission Algorithm Based on Social Relationships in Opportunistic Mobile Social Networks. Algorithms, 11(8), 125. https://doi.org/10.3390/a11080125






