Stacked-GRU Based Power System Transient Stability Assessment Method
Abstract
1. Introduction
2. Methodology
2.1. Gated Recurrent Unit
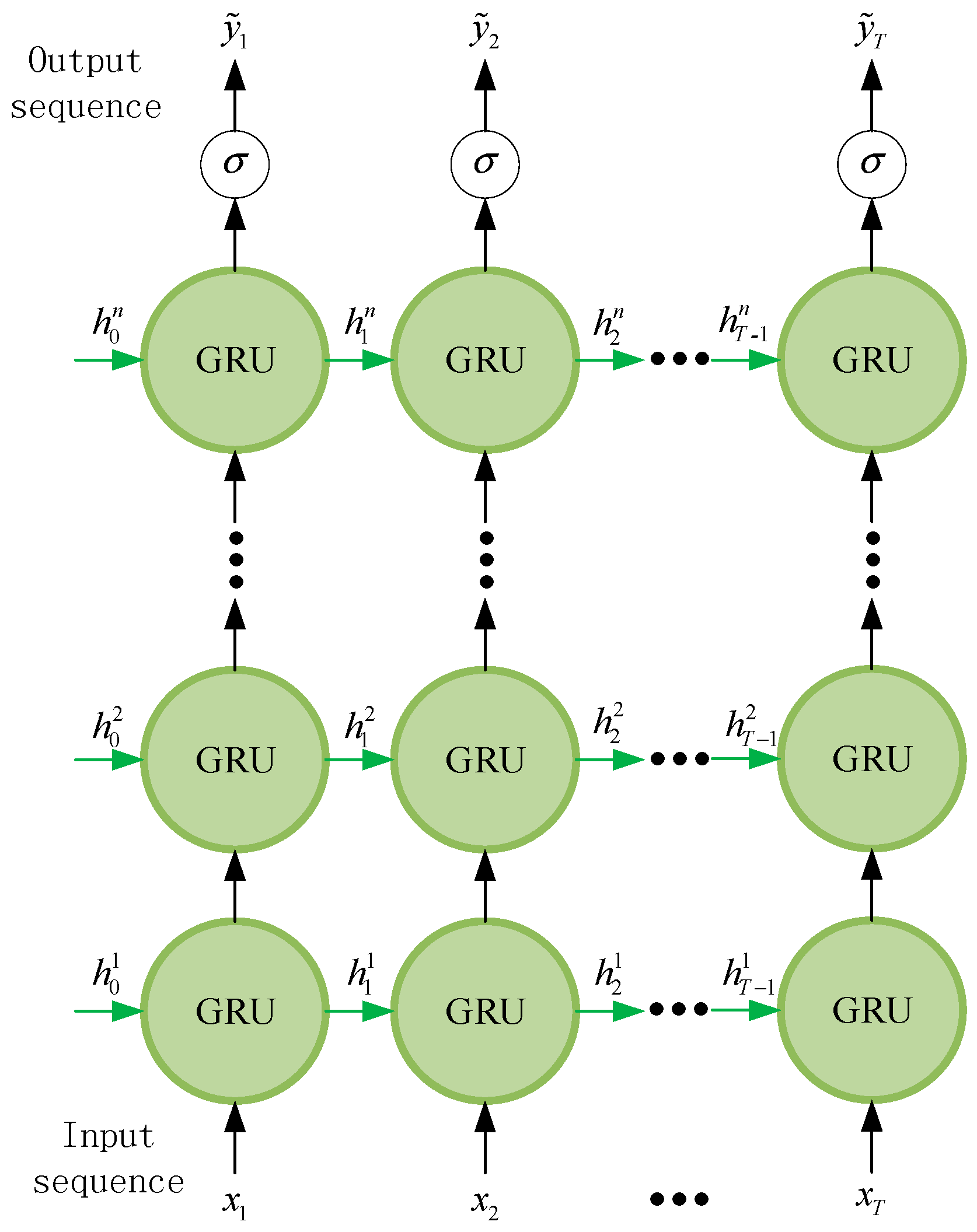
2.2. Stacked-GRU
3. Transient Stability Intelligent Assessment Method
3.1. Offline Training
3.2. Online Application
4. Case Studies
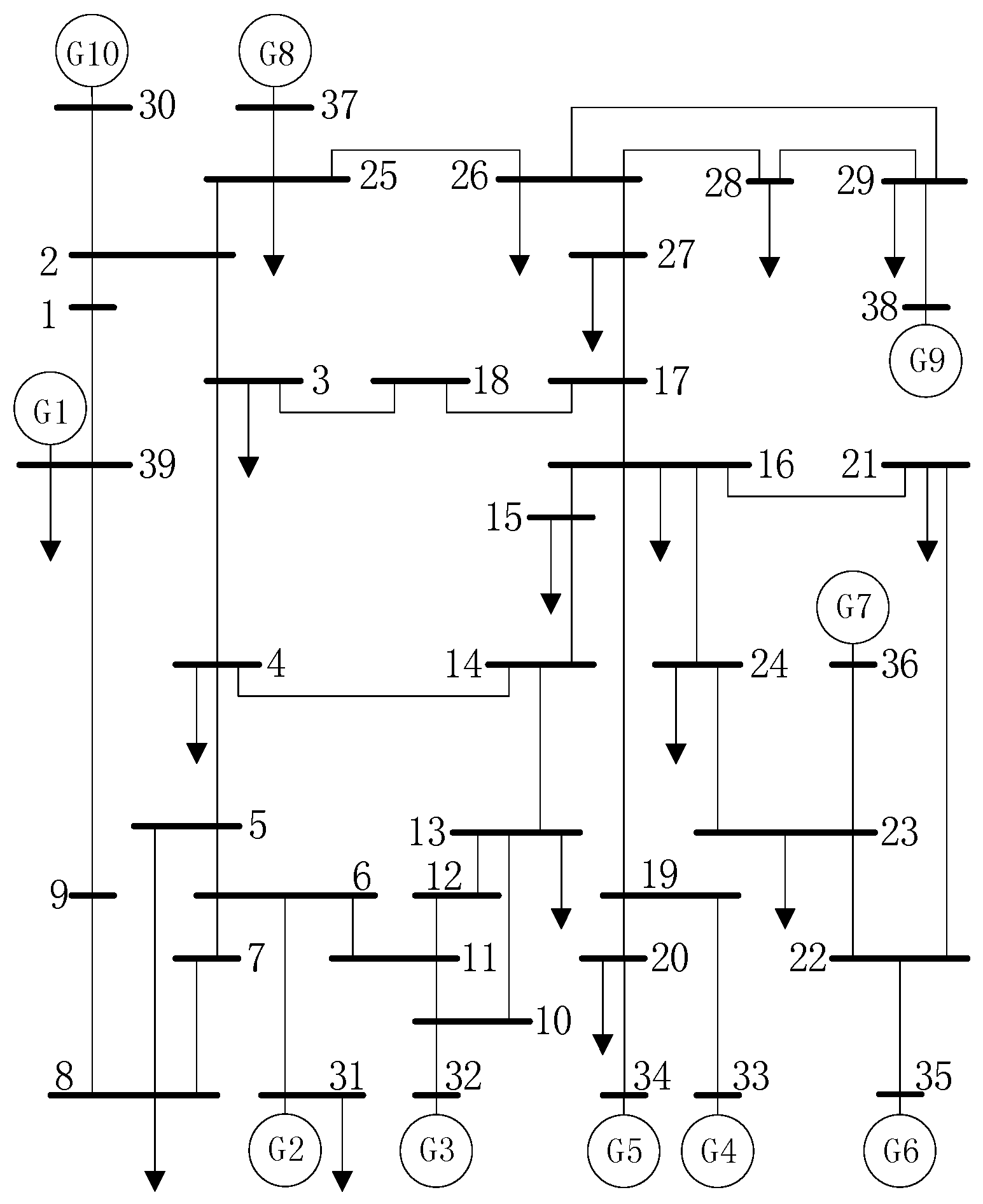
4.1. Data Generation
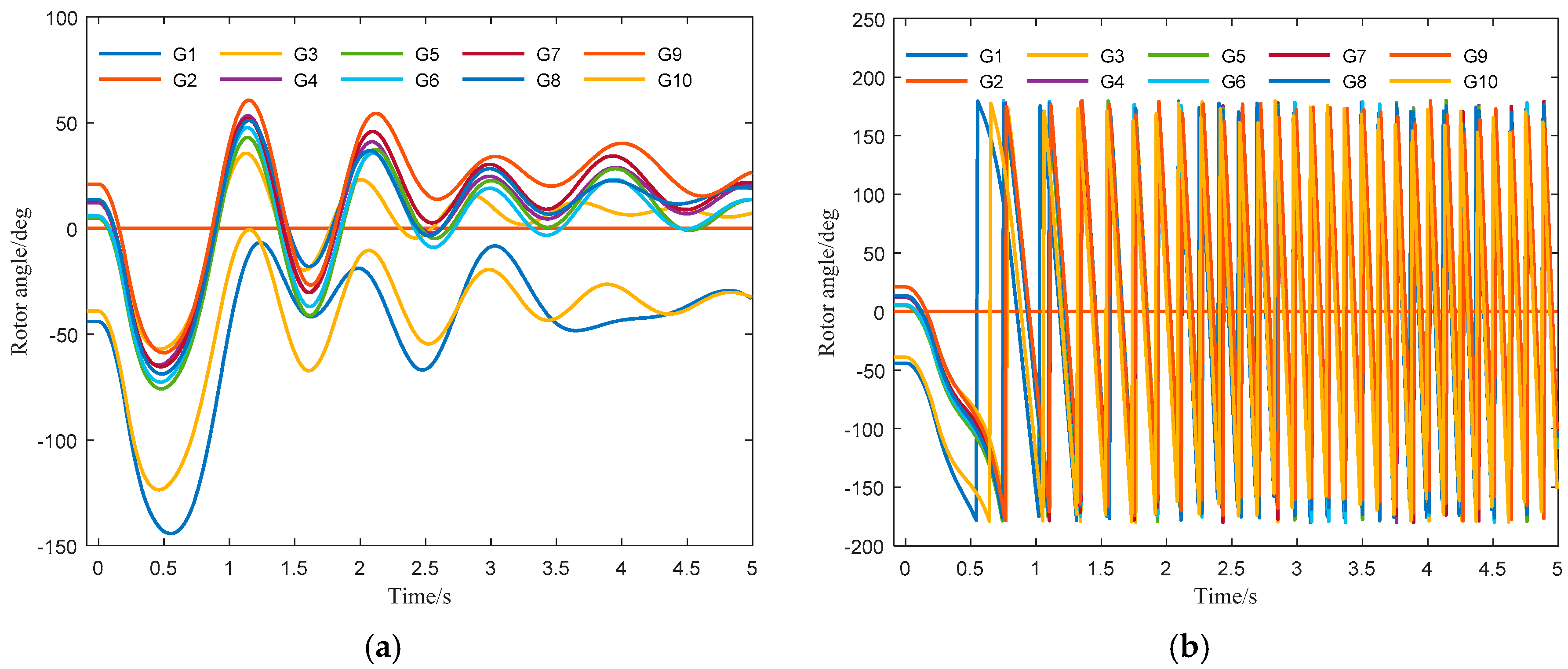
4.2. Discussion
4.2.1. Different Layers of Stacked-GRU Performance Assessment
4.2.2. Performance Comparison of Different Models
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhou, Y.Z.; Wu, J.Z.; Yu, Z.H.; Ji, L.Y.; Hao, L.L. Support vector machine ensemble classifier and its confidence evaluation for transient stability prediction of power systems. Power Syst. Technol. 2017. [Google Scholar] [CrossRef]
- Mei, S.W. Half-Volume Product Method in Power System Transient Analysis; Tsinghua University Press: Beijing, China, 2010; pp. 142–144. [Google Scholar]
- Wang, X.F. Modern Power System Analysis; Science Press: Beijing, China, 2003; pp. 354–362. [Google Scholar]
- Xue, Y.; Van Cutsem, T.; Ribbens-Pavella, M. A simple direct method for fast transient stability assessment of large power systems. IEEE Trans. Power Syst. 1988, 3, 400–412. [Google Scholar] [CrossRef]
- Ye, S. Study on Power Systems Transient Stability Assessment Based on Machine Learning Method. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, China, June 2010. [Google Scholar]
- Liu, L. Power System Transient Stability Assessment Based on Machine Learning. Master’s Thesis, North China Electric Power University, Beijing, China, March 2017. [Google Scholar]
- Yu, Y.X. Review of study on methodology of security regions of power system. J. Tianjin Univ. 2008, 6, 635–646. [Google Scholar] [CrossRef]
- Xi, X.F.; Zhou, G.D. A survey on deep learning for natural language processing. Acta Autom. Sin. 2008, 41, 635–646. [Google Scholar]
- Zhang, R.; Xu, Y.; Dong, Z.Y.; Wong, K.P. Post-disturbance transient stability assessment of power systems by a self-adaptive intelligent system. Gener. Trans. Distrib. IET 2015, 9, 296–305. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Z. Application of EOS-ELM with Binary Jaya- Based Feature Selection to Real-Time Transient Stability Assessment Using PMU Data. IEEE Access 2017, 5, 23092–23101. [Google Scholar] [CrossRef]
- James, J.Q.; Lam, A.Y.; Hill, D.J.; Li, V.O. Delay aware intelligent transient stability assessment system. IEEE Access 2017, 5, 17230–17239. [Google Scholar] [CrossRef]
- Yu, J.L.; Guo, Z.Z. Neural-network based transient security assessment for electrical power systems. Autom. Electr. Power Syst. 1991, 15, 44–50. [Google Scholar]
- Gomez, F.R.; Rajapakse, A.D.; Annakkage, U.D.; Fernando, I.T. Support vector machine-based algorithm for post-fault transient stability status prediction using synchronized measurements. IEEE Trans. Power Syst. 2011, 26, 1474–1483. [Google Scholar] [CrossRef]
- Ai, Y.D.; Chen, L.; Zhang, W.L. Power system transient stability assessment based on multi-support vector machines. Proc. CSEE 2016, 36, 1173–1180. [Google Scholar]
- Guo, T.; Milanovic, J.V. Probabilistic framework for assessing the accuracy of data mining tool for online prediction of transient stability. IEEE Trans. Power Syst. 2013, 29, 377–385. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Y.; Yu, Z.; Tian, F. A weighted random forest approach to improve predictive performance for power system transient stability assessment. In Proceedings of the 2016 IEEE PES Asia-Pacific Power & Energy Engineering Conference (APPEEC), Xi’an, China, 25–30 October 2016; pp. 1259–1263. [Google Scholar] [CrossRef]
- Liao, R.J.; Wang, Q.; Luo, S.; Liao, Y.X.; Sun, C.X. Condition assessment model for power transformer in service based on fuzzy synthetic evaluation. Autom. Electr. Power Syst. 2008, 32, 18–21. [Google Scholar]
- James, J.Q.; Hill, D.J.; Lam, A.Y.; Gu, J.; Li, V.O. Intelligent Time-Adaptive Transient Stability Assessment System. IEEE Trans. Power Syst. 2018, 33, 1049–1058. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; pp. 331–372. [Google Scholar]
- Olah, C. Understanding-LSTMs. Available online: http://colah.github.io/posts/2015-08-Understanding-LSTMs (accessed on 11 July 2018).
- Jozefowicz, R.; Zaremba, W.; Sutskever, I. An empirical exploration of recurrent network architectures. In Proceedings of the 32nd International Conference on Machine Learning (ICML 2015), Lille, France, 6–11 July 2015; pp. 2342–2350. [Google Scholar]
- Bianchini, M.; Maggini, M. Handbook on Neural Information Processing; Jain, L.C., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 29–65. [Google Scholar] [CrossRef]
- Cheng, Y. The Identification of Fault Type in Transmission Lines Based on Neural Network. Master’s Thesis, Dalian University of Technology, Dalian, China, January 2011. [Google Scholar]
- Tian, Z. Research on Sentiment Analysis Based on Deep Feature Representation. Master’s Thesis, Shandong University, Shandong, China, May 2017. [Google Scholar]
- Bersini, H.; Gorrini, V. A simplification of the backpropagation-through-time algorithm for optimal neurocontrol. IEEE Trans. Neural Netw. 1997, 8, 437–441. [Google Scholar] [CrossRef] [PubMed]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devil, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. Available online: https://arxiv.org/abs/1606.04467 (accessed on 11 July 2018).
- Pai, M.A. Energy Function Analysis for Power System Stability; Springer Science & Business Media: New York, NY, USA, 2012; pp. 223–227. [Google Scholar]
- Grubb, A.; Bagnell, J.A. Stacked training for overfitting avoidance in deep networks. In Proceedings of the ICML 2013 Workshop on Representation Learning, Atlanta, GA, USA, 21 June 2013. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]



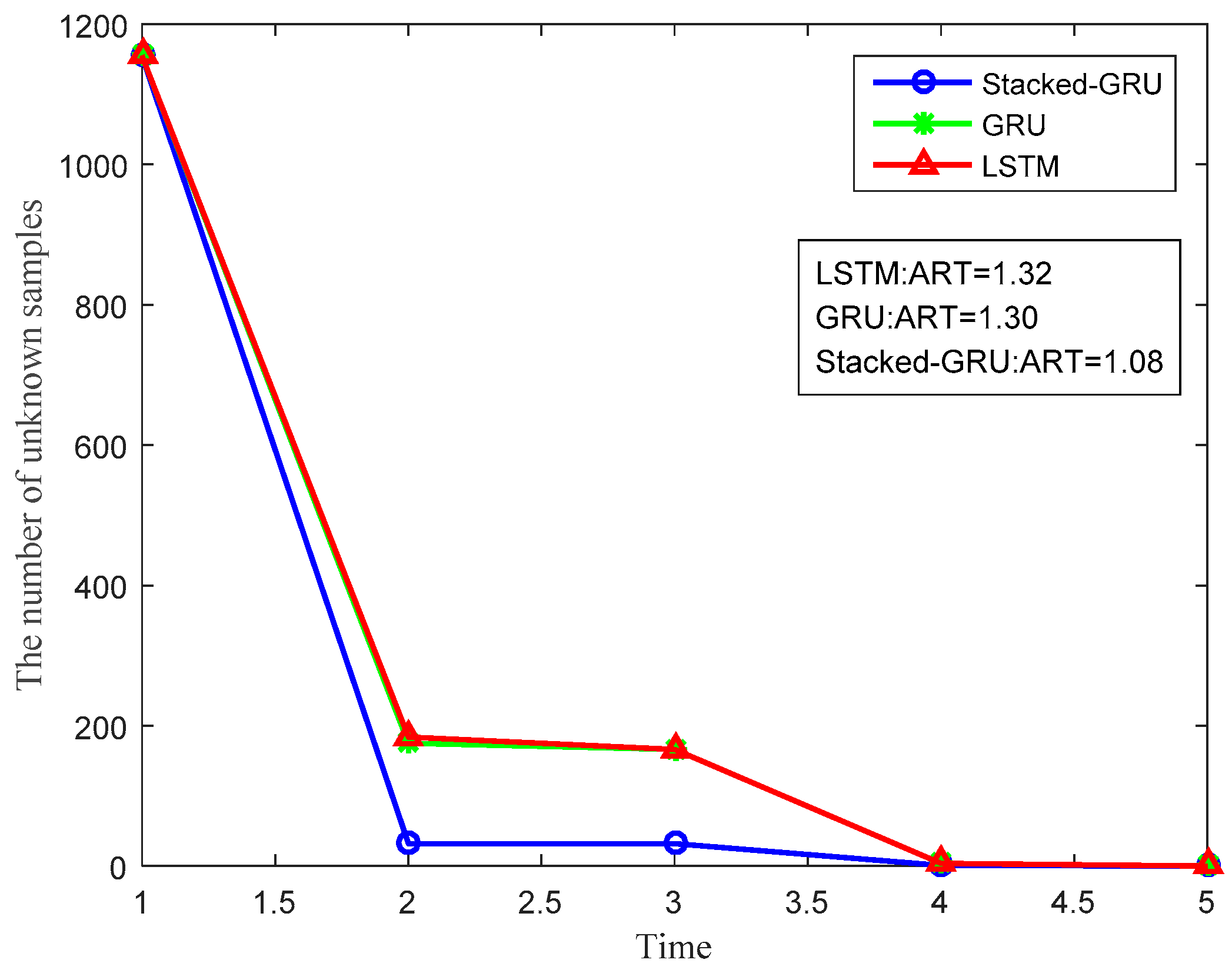
| Time | Number of Unknown Samples | Number of Known Samples | Accuracy |
|---|---|---|---|
| 1 | 1155 | 1123 | 100% |
| 2 | 32 | 1 | 100% |
| 3 | 31 | 30 | 100% |
| 4 | 1 | 0 | 100% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, F.; Li, J.; Tan, B.; Zeng, C.; Jiang, X.; Liu, L.; Yang, J. Stacked-GRU Based Power System Transient Stability Assessment Method. Algorithms 2018, 11, 121. https://doi.org/10.3390/a11080121
Pan F, Li J, Tan B, Zeng C, Jiang X, Liu L, Yang J. Stacked-GRU Based Power System Transient Stability Assessment Method. Algorithms. 2018; 11(8):121. https://doi.org/10.3390/a11080121
Chicago/Turabian StylePan, Feilai, Jun Li, Bendong Tan, Ciling Zeng, Xinfan Jiang, Li Liu, and Jun Yang. 2018. "Stacked-GRU Based Power System Transient Stability Assessment Method" Algorithms 11, no. 8: 121. https://doi.org/10.3390/a11080121
APA StylePan, F., Li, J., Tan, B., Zeng, C., Jiang, X., Liu, L., & Yang, J. (2018). Stacked-GRU Based Power System Transient Stability Assessment Method. Algorithms, 11(8), 121. https://doi.org/10.3390/a11080121




