emgr—The Empirical Gramian Framework
Abstract
Code Meta Data
| name (shortname) | EMpirical GRamian Framework (emgr) |
| version (release-date) | 5.4 (2018-05-05) |
| identifier (type) | doi:10.5281/zenodo.1241532 (doi) |
| authors (ORCIDs) | Christian Himpe (0000-0003-2194-6754) |
| topic (type) | Model Reduction (toolbox) |
| license (type) | 2-Clause BSD (open) |
| repository (type) | git:github.com/gramian/emgr (git) |
| languages | Matlab |
| dependencies | OCTAVE >= 4.2, MATLAB >= 2016b |
| systems | Linux, Windows |
| website | http://gramian.de |
| keywords | empirical-gramians, cross-gramian, combined-reduction |
1. Introduction
1.1. Aim
- Non-symmetric cross Gramian variant,
- linear cross Gramian variant,
- distributed cross Gramian variant and interface,
- inner product kernel interface,
- time-integrator interface,
- time-varying system compatibility,
- tensor-based trajectory storage,
- functional paradigm software design.
1.2. Outline
2. Mathematical Preliminaries
Model Reduction
- Projection-Based Combined Reduction
- Gramian-Based Model Reduction
3. Empirical Gramians
3.1. State-Space Empirical Gramians
3.1.1. Empirical Controllability Gramian
3.1.2. Empirical Observability Gramian
3.1.3. Empirical Linear Cross Gramian
3.1.4. Empirical Cross Gramian
3.1.5. Empirical Non-Symmetric Cross Gramians
3.2. Parameter-Space Empirical Gramians
3.2.1. Empirical Sensitivity Gramian
3.2.2. Empirical Identifiability Gramian
3.2.3. Empirical Cross-Identifiability Gramian
3.3. Notes on Empirical Gramians
4. Implementation Details
4.1. Design Principles
4.2. Parallelization
4.2.1. Shared Memory Parallelization
4.2.2. Heterogeneous Parallelization
4.2.3. Distributed Memory Parallelization
5. Interface
5.1. Mandatory Arguments
- f
- handle to a function with the signature xdot = f(x,u,p,t) representing the system’s vector-field and expecting the arguments: current state x, current input u, (current) parameter p and current time t.
- g
- handle to a function with the signature y = g(x,u,p,t) representing the system’s output functional and expecting the arguments: current state x, current input u, (current) parameter p and current time t.If g = 1, the identity output functional is assumed.
- s
- three component vector s = [M,N,Q] setting the dimensions of the input , state and output .
- t
- two component vector t = [h,T] specifying the time-step width h and time horizon T.
- w
- character selecting the empirical Gramian type; for details see Section 5.2.
5.2. Features
- ′c′
- Empirical controllability Gramian (see Section 3.1.1),emgr returns a matrix:
- empirical controllability Gramian matrix .
- ′o′
- Empirical observability Gramian (see Section 3.1.2),emgr returns a matrix:
- empirical observability Gramian matrix .
- ′x′
- Empirical cross Gramian (see Section 3.1.4),emgr returns a matrix:
- empirical cross Gramian matrix .
- ′y′
- Empirical linear cross Gramian (see Section 3.1.3),emgr returns a matrix:
- empirical linear cross Gramian matrix .
- ′s′
- Empirical sensitivity Gramian (see Section 3.2.1),emgr returns a cell array. holding:
- empirical controllability Gramian matrix ,
- empirical sensitivity Gramian diagonal .
- ′i′
- Empirical identifiability Gramian (see Section 3.2.2),emgr returns a cell array holding:
- empirical observability Gramian matrix ,
- empirical identifiability Gramian matrix .
- ′j′
- Empirical joint Gramian (see Section 3.2.3),emgr returns a cell array holding:
- empirical cross Gramian matrix ,
- empirical cross-identifiability Gramian matrix .
5.2.1. Non-Symmetric Cross Gramian
5.2.2. Parametric Systems
5.2.3. Time-Varying Systems
5.3. Optional Arguments
- pr system parameters (Default value: 0)
- vector a column vector holding the parameter components,
- matrix a set of parameters, each column holding one parameter.
- nf twelve component vector encoding the option flags, for details see Section 5.4.
- ut input function (Default value: 1)
- handle function handle expecting a signature u_t = u(t),
- 0 pseudo-random binary input,
- 1 delta impulse input,
- ∞ decreasing frequency exponential chirp.
- us steady-state input (Default value: 0)
- scalar set all M steady-state input components to argument,
- vector set steady-state input to argument of expected dimension .
- xs steady-state (Default value: 0)
- scalar set all N steady-state components to argument,
- vector set steady-state to argument of expected dimension .
- um input scales (Default value: 1)
- scalar set all M maximum input scales to argument,
- vector set maximum input scales to argument of expected dimension ,
- matrix set scales to argument with M rows; used as is.
- xm initial state scales (Default value: 1)
- scalar set all N maximum initial state scales to argument,
- vector set maximum steady-state scales to argument of expected dimension ,
- matrix set scales to argument with N rows; used as is.
- dp inner product interface via a handle to a function with the signature z = dp(x,y) defining the dot product for the Gramian matrix computation (Default value: []).
Inner Product Interface
- x
- matrix of dimension ,
- y
- matrix of dimension for .
5.4. Option Flags
- nf(1)
- Time series centering:
- = 0
- No centering,
- = 1
- Steady-state (for empirical covariance matrices),
- = 2
- Final state,
- = 3
- Arithmetic average over time (for empirical Gramians),
- = 4
- Root-mean-square over time,
- = 5
- Mid-range over time.
- nf(2)
- Input scale sequence:
- = 0
- Single scale: um ← um,
- = 1
- Linear scale subdivision: um ← um * [0.25, 0.5, 0.75, 1.0],
- = 2
- Geometric scale subdivision: um ← um * [0.125, 0.25, 0.5, 1.0],
- = 3
- Logarithmic scale subdivision: um ← um * [0.001, 0.01, 0.1, 1.0],
- = 4
- Sparse scale subdivision: um ← um * [0.01, 0.5, 0.99, 1.0].
- nf(3)
- Initial state scale sequence:
- = 0
- Single scale: xm ← xm,
- = 1
- Linear scale subdivision: xm ← xm * [0.25, 0.5, 0.75, 1.0],
- = 2
- Geometric scale subdivision: xm ← xm * [0.125, 0.25, 0.5, 1.0],
- = 3
- Logarithmic scale subdivision: xm ← xm * [0.001, 0.01, 0.1, 1.0],
- = 4
- Sparse scale subdivision: xm ← xm * [0.01, 0.5, 0.99, 1.0].
- nf(4)
- Input directions:
- = 0
- Positive and negative: um ← [-um, um],
- = 1
- Only positive: um ← um.
- nf(5)
- Initial state directions:
- = 0
- Positive and negative: xm ← [-xm, xm],
- = 1
- Only positive: xm ← xm.
- nf(6)
- Normalizing:
- nf(7)
- Non-Symmetric Cross Gramian, only , , :
- = 0
- Regular cross Gramian,
- = 1
- Non-symmetric cross Gramian.
- nf(8)
- Extra input for state and parameter perturbation trajectories, only , , , , :
- = 0
- No extra input,
- = 1
- Apply extra input (see [83]).
- nf(9)
- Center parameter scales, only , , :
- = 0
- No centering,
- = 1
- Center around arithmetic mean,
- = 2
- Center around logarithmic mean.
- nf(10)
- Parameter Gramian variant, only , , :
- = 0
- Average input-to-state (), detailed Schur-complement (, ),
- = 1
- Average input-to-output (), approximate Schur-complement (, ).
- nf(11)
- Empirical cross Gramian partition width, only , :
- = 0
- Full cross Gramian computation, no partitioning.
- < N
- Maximum partition size in terms of cross Gramian columns.
- nf(12)
- Partitioned empirical cross Gramian running index, only , :
- = 0
- No partitioning.
- > 0
- Index of the set of cross Gramian columns to be computed.
5.4.1. Schur-Complement
5.4.2. Partitioned Computation
5.5. Solver Configuration
- f
- handle to a function with the signature xdot = f(x,u,p,t) representing the system’s vector-field and expecting the arguments: current state x, current input u, (current) parameter p and current time t.
- g
- handle to a function with the signature y = g(x,u,p,t) representing the system’s output functional and expecting the arguments: the current state x, current input u, (current) parameter p and current time t.
- t
- two component vector t = [h,T] specifying the time-step width h and time horizon T.
- x0
- column vector of dimension N setting the initial condition.
- u
- handle to a function with the signature u_t = u(t).
- p
- column vector of dimension P holding the (current) parameter.
5.6. Sample Usage
6. Numerical Examples
6.1. Linear Verification
6.2. Hyperbolic Evaluation
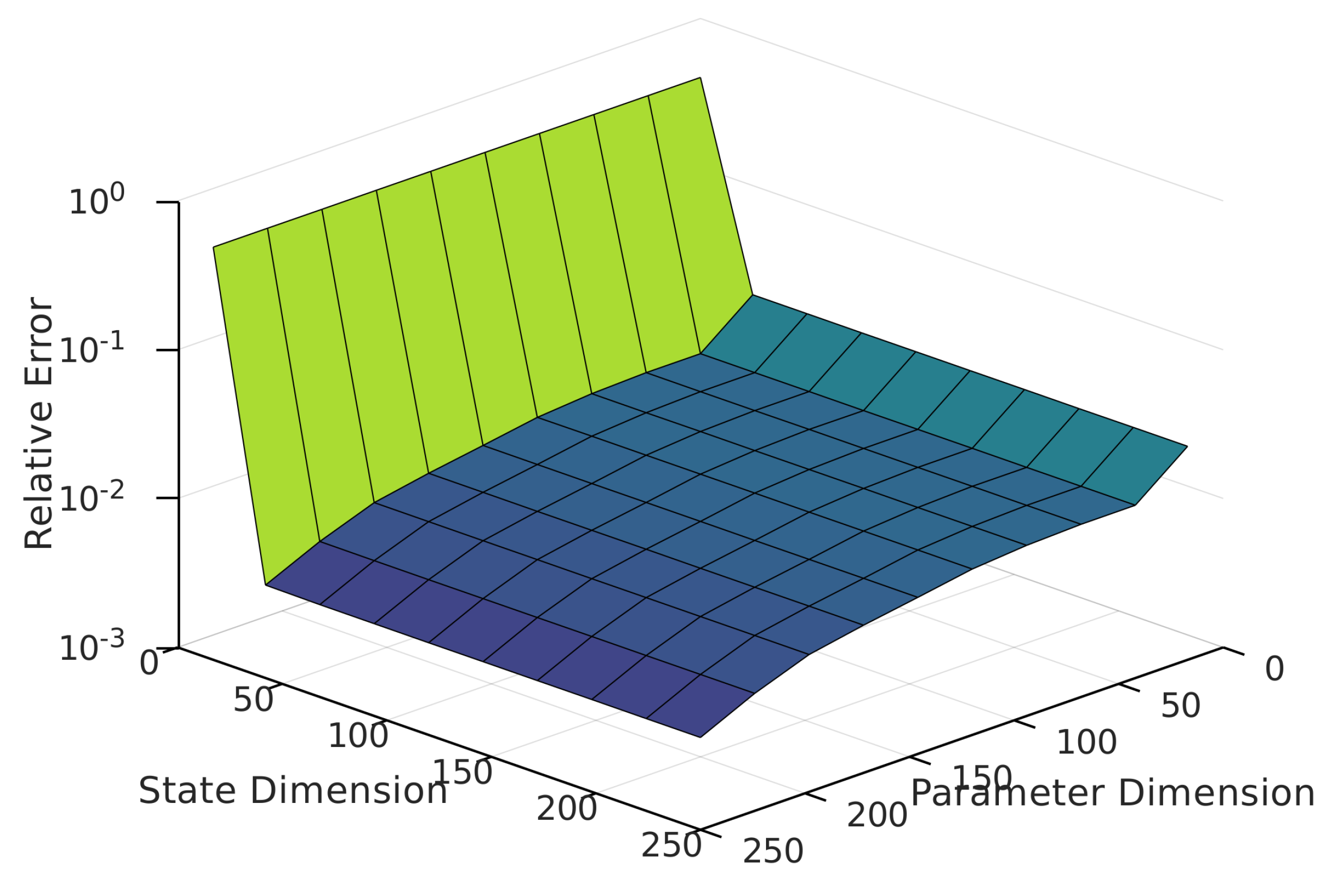
6.3. Nonlinear Validation
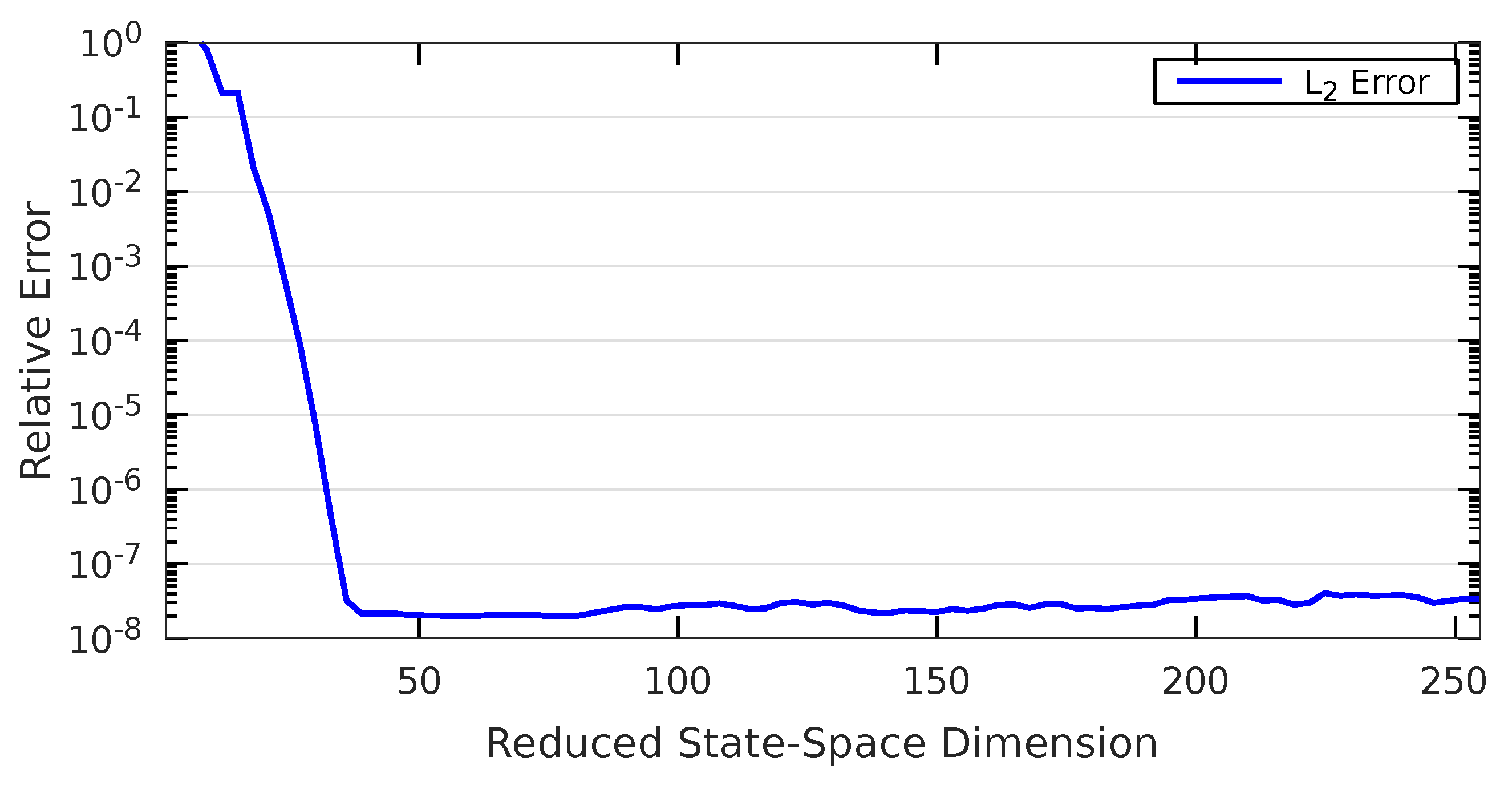
6.4. On Hyper-Reduction
7. Concluding Remark
Code Availability
Funding
Conflicts of Interest
Abbreviations
| PDE | Partial Differential Equation |
| ODE | Ordinary Differential Equation |
| MOR | Model Order Reduction |
| pMOR | parametric Model Order Reduction |
| nMOR | nonlinear Model Order Reduction |
| POD | Proper Orthogonal Decomposition |
| bPOD | balanced Proper Orthogonal Decomposition |
| SVD | Singular Value Decomposition |
| HSV | Hankel Singular Values |
| EVD | Eigenvalue Decomposition |
| SISO | Single-Input-Single-Output |
| MIMO | Multiple-Input-Multiple-Output |
| BLAS | Basic Linear Algebra System |
| LoC | Lines of Code |
| SIMD | Single Instruction Multiple Data |
| UMA | Unified Memory Access |
| GPGPU | General Purpose Graphics Processing Unit |
| GPU | Graphics Processing Unit |
| UMM | Unified Memory Model |
| hUMA | heterogeneous Unified Memory Access |
| CPU | Central Processing Unit |
| GEMM | GEneralized Matrix Multiplication |
| HAPOD | Hierarchical Approximate Proper Orthgoonal Decomposition |
| RKHS | Reproducing Kernel Hilbert Spaces |
| SSP | Strong Stability Preserving |
| SIMO | Single-Input-Multiple-Output |
| MPE | Missing Point Estimation |
| DEIM | Discrete Empirical Interpolation Method |
| DMD | Dynamic Mode Decomposition |
References
- Kalman, R.E. Mathematical description of linear dynamical systems. SIAM J. Control Optim. 1963, 1, 182–192. [Google Scholar] [CrossRef]
- Lall, S.; Marsden, J.E.; Glavaški, S. Empirical model reduction of controlled nonlinear systems. IFAC Proc. Vol. 1999, 32, 2598–2603. [Google Scholar] [CrossRef]
- Himpe, C. emgr—EMpirical GRamian Framework (Version 5.4). Available online: http://gramian.de (accessed on 26 June 2018).
- Moore, B.C. Principal component analysis in linear systems: Controllability, observability, and model reduction. IEEE Trans. Autom. Control 1981, 26, 17–32. [Google Scholar] [CrossRef]
- Sun, C.; Hahn, J. Model reduction in the presence of uncertainty in model parameters. J. Process Control 2006, 16, 645–649. [Google Scholar] [CrossRef]
- Himpe, C.; Ohlberger, M. The Empirical Cross Gramian for Parametrized Nonlinear Systems. IFAC-PapersOnLine 2015, 48, 727–728. [Google Scholar] [CrossRef]
- Hahn, J.; Edgar, T.F. Reduction of nonlinear models using balancing of empirical Gramians and Galerkin projections. In Proceedings of the 2000 American Control Conference, Chicago, IL, USA, 28–30 June 2000; Volume 4, pp. 2864–2868. [Google Scholar]
- Condon, M.; Ivanov, R. Model reduction of nonlinear systems. Compel-Int. J. Comp. Math. Electr. Electron. Eng. 2004, 23, 547–557. [Google Scholar] [CrossRef]
- Yao, S.; Deng, Y.; Yu, Z. Balanced Truncation on Empirical Gramians for Model-Order-Reduction of Non-Quasi-Static Effects in MOSFETs. In Proceedings of the 9th International Conference on Solid-State and Integrated-Circuit Technology, Beijing, China, 20–23 October 2008; pp. 309–312. [Google Scholar]
- Zhanfeng, M.; Chao, H. Structure-preserving balanced truncation for flexible spacecraft using cross Gramian. J. Beijing Univ. Aeronaut. Astronaut. 2008, 34, 1437–1440. [Google Scholar]
- Himpe, C.; Ohlberger, M. Cross-Gramian Based Combined State and Parameter Reduction for Large-Scale Control Systems. Math. Probl. Eng. 2014, 2014, 1–13. [Google Scholar] [CrossRef]
- Streif, S.; Findeisen, R.; Bullinger, E. Relating Cross Gramians and Sensitivity Analysis in Systems Biology. Theory Netw. Syst. 2006, 10, 437–442. [Google Scholar]
- Lystianingrum, V.; Hredzak, B.; Agelidis, V.G. Abnormal overheating detectability analysis based on cross Gramian for a supercapacitors string. In Proceedings of the Power and Energy Society General Meeting, Boston, MA, USA, 17–21 July 2016. [Google Scholar]
- Geffen, D.; Findeisen, R.; Schliemann, M.; Allgöwer, F.; Guay, M. Observability Based Parameter Identifiability for Biochemical Reaction Networks. In Proceedings of the 2008 American Control Conference, Seattle, WA, USA, 11–13 June 2008; pp. 2130–2135. [Google Scholar]
- Tolks, C.; Ament, C. Model Order Reduction of Glucose-Insulin Homeostasis Using Empirical Gramians and Balanced Truncation. IFAC-PapersOnline 2017, 50, 14735–14740. [Google Scholar] [CrossRef]
- Moaveni, B.; Khaki-Sedigh, A. Input-Output Pairing based on Cross-Gramian Matrix. In Proceedings of the International Joint Conference SICE-ICAS, Busan, Korea, 18–21 October 2006; pp. 2378–2380. [Google Scholar]
- Shaker, H.R.; Komareji, M. Control Configuration Selection for Multivariable Nonlinear Systems. Ind. Eng. Chem. Res. 2012, 51, 8583–8587. [Google Scholar] [CrossRef]
- Shaker, H.R.; Stoustrup, J. An interaction measure for control configuration selection for multivariable bilinear systems. Nonlinear Dyn. 2013, 72, 165–174. [Google Scholar] [CrossRef]
- Singh, A.K.; Hahn, J. Determining Optimal Sensor Locations for State and Parameter Estimation for Stable Nonlinear Systems. Ind. Eng. Chem. Res. 2005, 44, 5645–5659. [Google Scholar] [CrossRef]
- Saltik, M.B.; Özkan, L.; Weiland, S.; van den Hof, P.M.J. Sensor Configuration Problem: Application to a Membrane Separation Unit. IFAC-PapersOnLine 2016, 49, 189–194. [Google Scholar] [CrossRef]
- Summers, T.H.; Cortesi, F.L.; Lygeros, J. On Submodularity and Controllability in Complex Dynamical Networks. IEEE Trans. Control Netw. Syst. 2016, 3, 91–101. [Google Scholar] [CrossRef]
- Lawrence, D.; Myatt, J.H.; Camphouse, R.C. On Model Reduction via Empirical Balanced Truncation. In Proceedings of the American Control Conference, Portland, OR, USA, 8–10 June 2005; Volume 5, pp. 3139–3144. [Google Scholar]
- Hahn, J.; Kruger, U.; Edgar, T.F. Application of Model Reduction for Model Predictive Control. IFAC Proc. Vol. 2002, 15, 393–398. [Google Scholar] [CrossRef]
- Hahn, J.; Edgar, T.F. A Gramian Based Approach to Nonlinearity Quantification and Model Classification. Ind. Eng. Chem. Res. 2001, 40, 5724–5731. [Google Scholar] [CrossRef]
- Jiang, M.; Wu, J.; Jiang, L.; Li, X. A Gramians Based Method for Nonlinearity Quantification of Spatio-Temporal Systems. In Advanced Science and Technology Letters; SERSC: Haikou, China, 2016; Volume 121, pp. 38–42. [Google Scholar]
- Fernando, K.V.; Nicholson, H. On the Cauchy Index of Linear Systems. IEEE Trans. Autom. Control 1983, 28, 222–224. [Google Scholar] [CrossRef]
- Fortuna, L.; Fransca, M. Optimal and Robust Control: Advanced Topics with MATLAB; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Fu, J.; Zhong, C.; Ding, Y.; Zhou, J.; Zhong, C. An Information Theoretic Approach to Model Reduction based on Frequency-domain Cross-Gramian Information. In Proceedings of the 8th World Congress on Intelligent Control and Automation, Jinan, China, 7–9 July 2010; pp. 3679–3683. [Google Scholar]
- Halvarsson, B.; Castaño, M.; Birk, W. Uncertainty Bounds for Gramian-Based Interaction Measures. In Proceedings of the 14th WSEAS international conference on Systems: part of the 14th WSEAS CSCC multiconference, Corfu Island, Greece, 22–24 July 2010; Volume 2, pp. 393–398. [Google Scholar]
- Hrishikeshavan, V.; Humbert, J.S.; Chopra, I. Gramian Analysis of a Shrouded Rotor Micro Air Vehicle in Hover. J. Guid. Control Dyn. 2014, 37, 1684–1690. [Google Scholar] [CrossRef]
- Gugercin, S.; Antoulas, A.C.; Beattie, C. H2 Model Reduction for Large-Scale Linear Dynamical Systems. SIAM J. Matrix Anal. Appl. 2008, 30, 609–638. [Google Scholar] [CrossRef]
- Willcox, K.; Peraire, J. Balanced Model Reduction via the Proper Orthogonal Decomposition. AIAA J. 2002, 40, 2323–2330. [Google Scholar] [CrossRef]
- Rowley, C.W. Model reduction for fluids, using balanced proper orthogonal decomposition. Int. J. Bifurcat. Chaos 2005, 15, 997–1013. [Google Scholar] [CrossRef]
- Sun, C.; Hahn, J. Nonlinear Model Reduction Routines for MATLAB; Technical Report; Rensselaer Polytechnic Institute: Troy, NY, USA, 2006. [Google Scholar]
- Hahn, J.; Edgar, T.F. Balancing Approach to Minimal Realization and Model Reduction of Stable Nonlinear Systems. Ind. Eng. Chem. Res. 2002, 41, 2204–2212. [Google Scholar] [CrossRef]
- Choroszucha, R.B.; Sun, J.; Butts, K. Nonlinear Model Order Reduction for Predictive Control of the Diesel Engine Airpath. In Proceedings of the American Control Conference, Boston, MA, USA, 6–8 July 2016; pp. 5081–5086. [Google Scholar]
- Krener, A.; Ide, K. Measures of Unobservability. In Proceedings of the 48th IEEE Conference on Decision and Control, 2009 held jointly with the 2009 28th Chinese Control Conference, Shanghai, China, 16–18 December 2009; pp. 6401–6406. [Google Scholar]
- Himpe, C.; Ohlberger, M. A Unified Software Framework for Empirical Gramians. J. Math. 2013, 2013, 1–6. [Google Scholar] [CrossRef]
- Himpe, C.; Ohlberger, M. A note on the cross Gramian for non-symmetric systems. Syst. Sci. Control Eng. 2016, 4, 199–208. [Google Scholar] [CrossRef]
- Garcia, J.S.; Basilio, J.C. Computation of reduced-order models of multivariable systems by balanced truncation. Int. J. Syst. Sci. 2002, 33, 847–854. [Google Scholar] [CrossRef]
- Antoulas, A.C. Approximation of Large-Scale Dynamical Systems Volume 6 Advances in Design and Control; SIAM Publications: Philadelphia, PA, USA, 2005. [Google Scholar]
- Aldhaheri, R.W. Model order reduction via real Schur-form decomposition. Int. J. Control 1991, 53, 709–716. [Google Scholar] [CrossRef]
- Baur, U.; Benner, P. Gramian-Based Model Reduction for Data-Sparse Systems. SIAM J. Sci. Comput. 2008, 31, 776–798. [Google Scholar] [CrossRef]
- Sorensen, D.C.; Antoulas, A.C. The Sylvester equation and approximate balanced reduction. Numer. Linear Algebra Appl. 2002, 671–700. [Google Scholar] [CrossRef]
- Hahn, J.; Edgar, T.F. An improved method for nonlinear model reduction using balancing of empirical Gramians. Comput. Chem. Eng. 2002, 26, 1379–1397. [Google Scholar] [CrossRef]
- Sun, C.; Hahn, J. Parameter reduction for stable dynamical systems based on Hankel singular values and sensitivity analysis. Chem. Eng. Sci. 2006, 61, 5393–5403. [Google Scholar] [CrossRef]
- Himpe, C. Combined State and Parameter Reduction for Nonlinear Systems with an Application in Neuroscience. Ph.D. Thesis, Westfälische Wilhelms-Universität Münster, Münster, Germany, 2017. [Google Scholar]
- Keil, A.; Gouz;, J.L. Model Reduction of Modular Systems Using Balancing Methods; Technical Report; Technische Universität München: München, Germany, 2003. [Google Scholar]
- Stigter, J.D.; van Willigenburg, L.G.; Molenaar, J. An Efficient Method to Assess Local Controllability and Observability for Non-Linear Systems. IFAC-PapersOnLine 2018, 51, 535–540. [Google Scholar] [CrossRef]
- Hespanha, J. Linear Systems Theory; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Ma, X.; De Abreu-Garcia, J.A. On the Computation of Reduced Order Models of Nonlinear Systems using Balancing Technique. In Proceedings of the 27th IEEE Conference on Decision and Control, Austin, TX, USA, 7–9 December 1988; Volume 2, pp. 1165–1166. [Google Scholar]
- Singh, A.K.; Hahn, J. On the Use of Empirical Gramians for Controllability and Observability Analysis. In Proceedings of the 2005 American Control Conference, Portland, OR, USA, 8–10 June 2005; Volume 2005, pp. 140–141. [Google Scholar]
- Dones, I.; Skogestad, S.; Preisig, H.A. Application of Balanced Truncation to Nonlinear Systems. Ind. Eng. Chem. Res. 2011, 50, 10093–10101. [Google Scholar] [CrossRef]
- Scherpen, J.M.A. Balancing for nonlinear systems. Syst. Control Lett. 1993, 21, 143–153. [Google Scholar] [CrossRef]
- Hahn, J.; Edgar, T.F.; Marquardt, W. Controllability and observability covariance matrices for the analysis and order reduction of stable nonlinear systems. J. Process Control 2003, 13, 115–127. [Google Scholar] [CrossRef]
- Fernando, K.V.; Nicholson, H. On the Structure of Balanced and Other Principal Representations of SISO Systems. IEEE Trans. Autom. Control 1983, 28, 228–231. [Google Scholar] [CrossRef]
- Fernando, K.V. Covariance and Gramian Matrices in Control and Systems Theory. Ph.D. Thesis, University of Sheffield, Sheffield, UK, 1982. [Google Scholar]
- Fernando, K.V.; Nicholson, H. On the Cross-Gramian for Symmetric MIMO Systems. IEEE Trans. Circuits Syst. 1985, 32, 487–489. [Google Scholar] [CrossRef]
- Shaker, H.R. Generalized Cross-Gramian for Linear Systems. In Proceedings of the 7th IEEE Conference on Industrial Electronics and Applications (ICIEA), Singapore, 18–20 July 2012; pp. 749–751. [Google Scholar]
- Baur, U.; Benner, P.; Haasdonk, B.; Himpe, C.; Martini, I.; Ohlberger, M. Comparison of Methods for Parametric Model Order Reduction of Time-Dependent Problems. In Model Reduction and Approximation: Theory and Algorithms; Benner, P., Cohen, A., Ohlberger, M., Willcox, K., Eds.; SIAM: Philadelphia, PA, USA, 2017; pp. 377–407. [Google Scholar]
- Barbagallo, A.; De Felice, V.F.; Nagarajan, K.K. Reduced Order Modelling of a Couette Flow Using Balanced Proper Orthogonal Decomposition. In Proceedings of the 2nd Young ERCOFTAC Workshop, Montestigliano, Italy, 10 March 2008. [Google Scholar]
- Ionescu, T.C.; Fujimoto, K.; Scherpen, J.M.A. Singular Value Analysis of Nonlinear Symmetric Systems. IEEE Trans. Autom. Control 2011, 56, 2073–2086. [Google Scholar] [CrossRef]
- Fujimoto, K.; Scherpen, J.M.A. On balanced truncation for symmetric nonlinear systems. In Proceedings of the International Symposium on Mathematical Theory of Networks and Systems, Groningen, The Netherlands, 7–11 July 2014; Volume 21, pp. 1498–1502. [Google Scholar]
- Constantine, P. Active Subspaces: Emerging Ideas for Dimension Reduction in Parameter Studies; SIAM Spotlights, SIAM: Philadelphia, PA, USA, 2015. [Google Scholar]
- Lieberman, C.E.; Fidkowski, K.; Willcox, K.; van Bloemen Waanders, B. Hessian-based model reduction: Large-scale inversion and prediction. Int. J. Numer. Methods Fluids 2013, 71, 135–150. [Google Scholar] [CrossRef]
- Jazlan, A.; Sreeram, V.; Togneri, R. Cross Gramian Based Time Interval Model Reduction. In Proceedings of the 5th Australien Control Conference (AUCC), Gold Coast, Australia, 5–6 November 2015; pp. 274–276. [Google Scholar]
- The MathWorks, Inc. MATLAB. Available online: http://www.matlab.com (accessed on 26 June 2018).
- The Octave Developers. GNU Octave. Available online: http://octave.org (accessed on 26 June 2018).
- Johnson, R.K. The Elements of MATLAB Style; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Altman, Y.M. Accelerating MATLAB Performance: 1001 Tips to Speed up MATLAB Programs; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Rogers, P.; Marci, J.; Marinkovic, S. Heterogeneous Uniform Memory Access; AMD: Santa Clara, CA, USA, 2013. [Google Scholar]
- Himpe, C.; Leibner, T.; Rave, S. Hierarchical Approximate Proper Orthogonal Decomposition. arXiv, 2018; arXiv:1607.05210. [Google Scholar]
- Himpe, C.; Leibner, T.; Rave, S.; Saak, J. Fast Low-Rank Empirical Cross Gramians. Proc. Appl. Math. Mech. 2017, 17, 841–842. [Google Scholar] [CrossRef]
- Condon, M.; Ivanov, R. Empirical Balanced Truncation of Nonlinear Systems. J. Nonlinear Sci. 2004, 14, 405–414. [Google Scholar] [CrossRef]
- Nilsson, O.; Rantzer, A. A novel approach to balanced truncation of nonlinear systems. In Proceedings of the 2009 European Control Conference (ECC), Budapest, Hungary, 23–26 August 2009. [Google Scholar]
- Nikiforuk, P.N.; Gupta, M.M. On stochastic perturbation theory for linear systems. In Proceedings of the 1969 IEEE Symposium on Adaptive Processes (8th) Decision and Control, University Park, PA, USA, 17–19 November 1969. [Google Scholar]
- Bouvrie, J.; Hamzi, B. Kernel Methods for the Approximation of Nonlinear Systems. SIAM J. Control Optim. 2017, 55, 2460–2492. [Google Scholar] [CrossRef]
- Fasshauer, G.; McCourt, M. Kernel-Based Approximation Methods Using MATLAB Volume 19 Interdisciplinary Mathematical Sciences; World Scientific: Singapore, 2015. [Google Scholar]
- Kalashnikova, I.; Barone, M.; Arunajatesan, S.; van Bloemen Waanders, B. Construction of energy-stable projection-based reduced order models. Appl. Math. Comput. 2014, 249, 569–596. [Google Scholar] [CrossRef]
- Schelfhout, G.; de Moor, B. Time-Domain Weighted Balanced Truncation. In Proceedings of the 3rd European Control Conference, Rome, Italy, 5–8 September 1995; pp. 1–4. [Google Scholar]
- Snowden, T.J.; van der Graaf, P.H.; Tindall, M.J. A combined model reduction algorithm for controlled biochemical systems. BMC Syst. Biol. 2017, 11, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Eberle, C.; Ament, C. Identifiability and online estimation of diagnostic parameters with in the glucose insulin homeostasis. Biosystems 2012, 107, 135–141. [Google Scholar] [CrossRef] [PubMed]
- Powel, N.D.; Morgansen, K.A. Empirical Observability Gramian Rank Condition for Weak Observability of Nonlinear Systems with Control. In Proceedings of the 54th Annual Conference on Decision and Control, Osaka, Japan, 15–18 December 2015; pp. 6342–6348. [Google Scholar]
- Wu, M.; Yin, B.; Vosoughi, A.; Studer, C.; Cavallaro, J.R.; Dick, C. Approximate Matrix Inversion for High-Throughput Data Detection in the Large-Scale MIMO Uplink. In Proceedings of the 2013 IEEE International Symposium on Circuits and Systems (ISCAS2013), Beijing, China, 19–23 May 2013; pp. 2155–2158. [Google Scholar]
- Ketcheson, D.I. Highly Efficient Strong Stability-Preserving Runge-Kutta Methods with Low-Storage Implementations. SIAM J. Sci. Comput. 2008, 30, 2113–2136. [Google Scholar] [CrossRef]
- Eaton, J.W.; Bateman, D.; Hauberg, S.; Wehbring, R. GNU Octave Version 4.4.0 Manual: A High-Level Interactive Language for Numerical Computations. Available online: https://octave.org/octave.pdf (accessed on 26 June 2018).
- The MORwiki Community. MORwiki-Model Order Reduction Wiki. Available online: http://modelreduction.org (accessed on 26 June 2018).
- Himpe, C.; Ohlberger, M. Cross-Gramian-Based Model Reduction: A Comparison. In Model Reduction of Parametrized Systems; Benner, P., Ohlberger, M., Patera, A., Rozza, G., Urban, K., Eds.; Springer: Cham, Switzerland, 2017; Volume 17, pp. 271–283. [Google Scholar]
- Liu, W.Q.; Sreeram, V.; Teo, K.L. Model reduction for state-space symmetric systems. Syst. Control Lett. 1998, 34, 209–215. [Google Scholar] [CrossRef]
- Quan, Y.; Zhang, H.; Cai, L. Modeling and Control Based on a New Neural Network Model. In Proceedings of the American Control Conference, Arlington, VA, USA, 25–27 June 2001; Volume 3, pp. 1928–1929. [Google Scholar]
- Everson, R.; Sirovich, L. Karhunen-Loéve Procedure for Gappy Data. J. Opt. Soc. Am. A 1995, 12, 1657–1664. [Google Scholar] [CrossRef]
- Astrid, P. Fast Reduced Order Modeling Technique for Large Scale LTV Systems. In Proceedings of the American Control Conference, Boston, MA, USA, 30 June–2 July 2004; pp. 762–767. [Google Scholar]
- Chaturantabut, S.; Sorensen, D.C. Nonlinear model reduction via discrete empirical interpolation. SIAM J. Sci. Comput. 2010, 32, 2737–2764. [Google Scholar] [CrossRef]
- Williams, M.O.; Schmid, P.J.; Kutz, J.N. Hybrid Reduced-Order Integration with Proper Orthogonal Decomposition and Dynamic Mode Decomposition. Multiscale Model. Simul. 2013, 11, 522–544. [Google Scholar] [CrossRef]
- Moore, B.C. Principal Component Analysis in Nonlinear Systems: Preliminary Results. In Proceedings of the 18th IEEE Conference on Decision and Control including the Symposium on Adaptive Processes, Fort Lauderdale, FL, USA, 12–14 December 1979; Volume 2, pp. 1057–1060. [Google Scholar]
- Dimitriu, G.; Ştefănescu, R.; Navon, I.M. Comparative numerical analysis using reduced-order modeling strategies for nonlinear large-scale systems. J. Comput. Appl. Math. 2017, 310, 32–42. [Google Scholar] [CrossRef]
- Melchior, S.; Legat, V.; van Dooren, P. Gramian Based Model Reduction of Nonlinear MIMO Systems. In Proceedings of the Mathematical Theory of Networks and Systems, Melbourne, Australia, 9–13 July 2012. [Google Scholar]
- Yeung, E.; Liu, Z.; Hodas, N.O. A Koopman Operator Approach for Computing and Balancing Gramians for Discrete Time Nonlinear Systems. arXiv, 2017; arXiv:1709.08712. [Google Scholar]
- Choroszucha, R.B.; Sun, J. Empirical Riccati covariance matrices for closed-loop model order reduction of nonlinear systems by balanced truncation. In Proceedings of the American Control Conference, Seattle, WA, USA, 24–26 May 2017; pp. 3476–3482. [Google Scholar]
- Kawano, Y.; Scherpen, J.M.A. Empirical Differential Balancing for Nonlinear Systems. IFAC-PapersOnLine 2017, 50, 6326–6331. [Google Scholar] [CrossRef]


© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Himpe, C. emgr—The Empirical Gramian Framework. Algorithms 2018, 11, 91. https://doi.org/10.3390/a11070091
Himpe C. emgr—The Empirical Gramian Framework. Algorithms. 2018; 11(7):91. https://doi.org/10.3390/a11070091
Chicago/Turabian StyleHimpe, Christian. 2018. "emgr—The Empirical Gramian Framework" Algorithms 11, no. 7: 91. https://doi.org/10.3390/a11070091
APA StyleHimpe, C. (2018). emgr—The Empirical Gramian Framework. Algorithms, 11(7), 91. https://doi.org/10.3390/a11070091




