An Ensemble Extreme Learning Machine for Data Stream Classification
Abstract
1. Introduction
- An ensemble extreme learning machine algorithm is presented. In the data stream environment, the performance of ensemble classifiers is better than that of single classifier [38], so CELM employs ensemble learning method and improves the performance of ELMs.
- Because data stream classification is very demanding for real time and the high dimensions of data tend to reduce the efficiency of algorithm, CELM introduces a manifold learning method to reducing the dimension of data which reduces the time consumption of CELM.
- Concept drift detection is incorporated into the training process of ELM classifiers. The change of data stream is divided into three categories: normal condition, warning level and concept drift. Different from the traditional ELMs, CELM not only can detect gradual concept drift, but also can handle abrupt concept drift.
2. Background Knowledge
2.1. Data Stream Classification
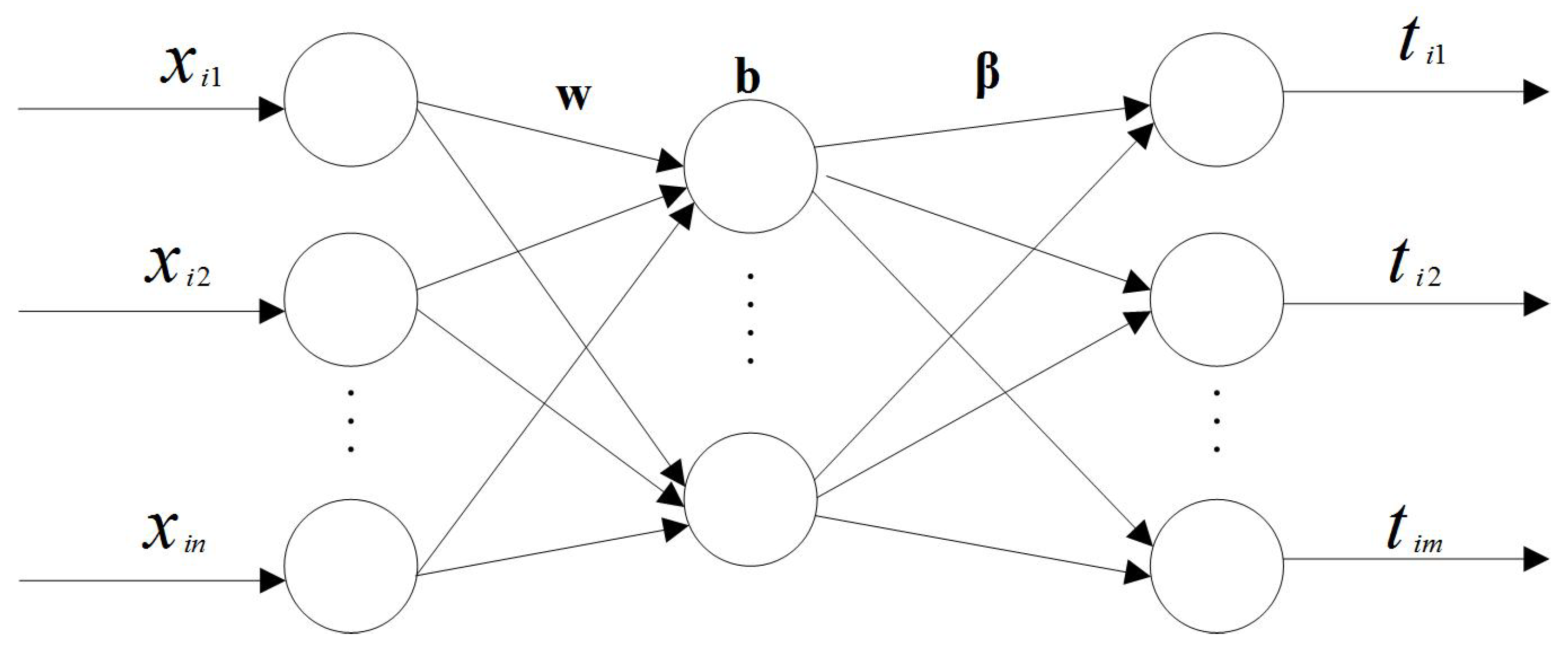
2.2. Extreme Learning Machine
| Algorithm 1 ELM. |
| Input: a training data ; the number of hidden nodes L; the activation function ; Output: ELM classifier. Step 1: Randomly generate the input weights and biases Step 2: Calculate the output matrix of hidden layer for dataset Step 3: Obtain the output weights according to Equation (6) or Equation (8); |
3. The Basic Principles of CELM
3.1. The Method of Dimensionality Reduction for Data Stream
| Algorithm 2 Dimension-reduction of data stream. |
| Input: Data stream , the size of data block : winsize, k and d; Output: . while do Get a data block with N samples from sliding window; Calculate ; Calculate ; Calculate d+1 eigenvectors of the matrix ; Get the low dimensional matrix ; |
3.2. The Data Stream Classification and Concept Drift Detection of CELM
| Algorithm 3 CELM. |
| Input: Data stream , the size of data block : winsize, k and d, , K classifiers; Output: An ensemble classifiers system. while do Get a data from sliding window; Use Algorithm 2 to descend dimension for ; if then The data stream is stable and directly uses classifier to finish classification task; else if then Uses online learning mechanism to update classifiers as Equations (21)–(27); else if then Concept drift has happened; Delete all classifiers and retrain each classifier as Algorithm 1; |
4. Experiments and Data Analysis
4.1. Datasets
4.2. The Comparison Results of CELM and Comparison Algorithms on the Test Datasets
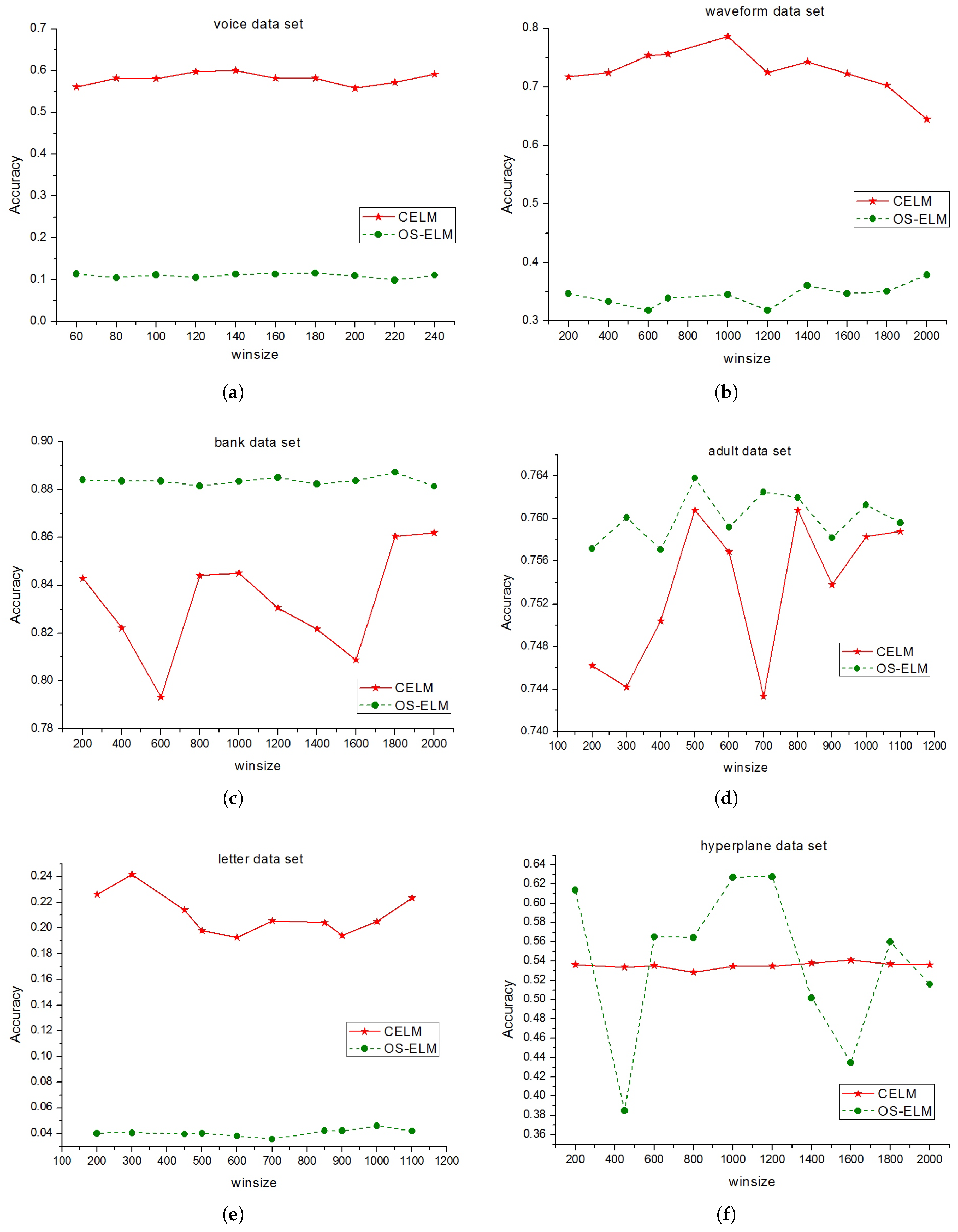
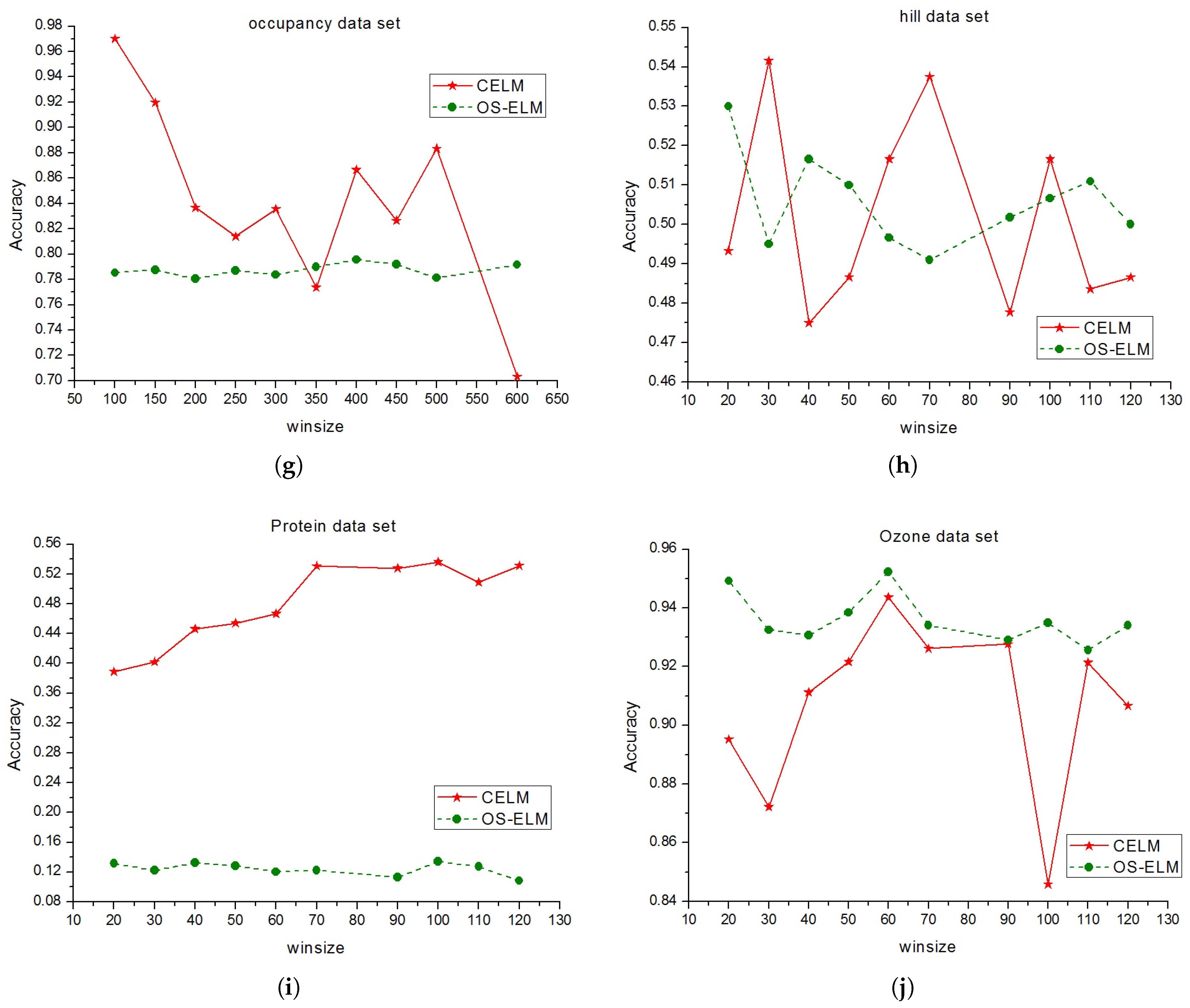
4.3. The Effect of Sliding Window on the Performance of CELM
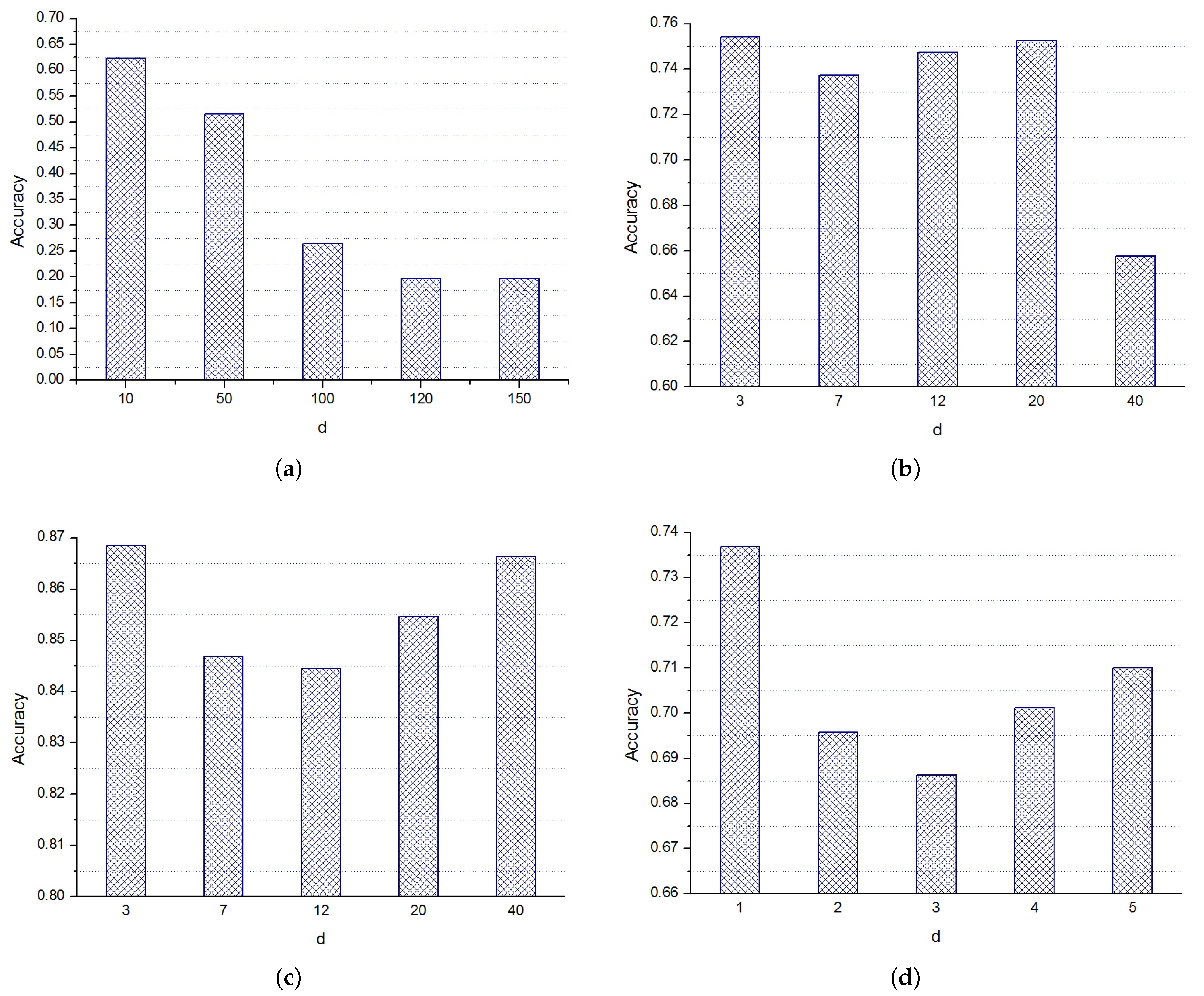
4.4. The Effect of the Values of d on the Performance of CELM
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gedik, B.; Schneider, S.; Hirzel, M.; Wu, K.L. Elastic Scaling for Data Stream Processing. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 1447–1463. [Google Scholar] [CrossRef]
- Krempl, G.; Last, M.; Lemaire, V.; Noack, T.; Shaker, A.; Sievi, S.; Spiliopoulou, M. Open challenges for data stream mining research. ACM SIGKDD Explor. Newsl. 2014, 16, 1–10. [Google Scholar] [CrossRef]
- Xu, S.; Wang, J. Classification Algorithm Combined with Unsupervised Learning for Data Stream. Pattern Recognit. Artif. Intell. 2016, 29, 665–672. [Google Scholar]
- Ramirez-Gallego, S.; Krawczyk, B.; Garcia, S.; Woźniak, M.; Herrera, F. A survey on data preprocessing for data stream mining: Current status and future directions. Neurocomputing 2017, 239, 39–57. [Google Scholar] [CrossRef]
- Sun, D.; Zhang, G.; Yang, S.; Zheng, W.; Khan, S.U.; Li, K. Re-Stream: Real-time and energy-efficient resource scheduling in big data stream computing environments. Inf. Sci. 2015, 319, 92–112. [Google Scholar] [CrossRef]
- Xu, S.; Wang, J. Dynamic extreme learning machine for data stream classification. Neurocomputing 2017, 238, 433–449. [Google Scholar] [CrossRef]
- Puthal, D.; Nepal, S.; Ranjan, R.; Chen, J. DLSeF: A Dynamic Key-Length-Based Efficient Real-Time Security Verification Model for Big Data Stream. ACM Trans. Embed. Comput. Syst. 2017, 16, 51. [Google Scholar] [CrossRef]
- Pan, S.; Wu, K.; Zhang, Y.; Li, X. Classifier ensemble for uncertain data stream classification. In Proceedings of the Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining, Hyderabat, India, 21–24 June 2010; pp. 488–495. [Google Scholar]
- Xu, S.; Wang, J. A Fast Incremental Extreme Learning Machine Algorithm for Data Streams Classification. Expert Syst. Appl. 2016, 65, 332–344. [Google Scholar] [CrossRef]
- Brzezinski, D.; Stefanowski, J. Combining block-based and online methods in learning ensembles from concept drifting data streams. Inf. Sci. 2014, 265, 50–67. [Google Scholar] [CrossRef]
- Farid, D.M.; Li, Z.; Hossain, A.; Rahman, C.M.; Strachan, R.; Sexton, G.; Dahal, K. An adaptive ensemble classifier for mining concept drifting data streams. Expert Syst. Appl. 2013, 40, 5895–5906. [Google Scholar] [CrossRef]
- Bifet, A. Adaptive learning from evolving data streams. In International Symposium on Intelligent Data Analysis: Advances in Intelligent Data Analysis VIII; Springer: Berlin/Heidelberg, Germany, 2009; pp. 249–260. [Google Scholar]
- Schmidt, J.P.; Siegel, A.; Srinivasan, A. Chernoff-Hoeffding Bounds for Applications with Limited Independence. SIAM J. Discret. Math. 1995, 8, 223–250. [Google Scholar] [CrossRef]
- Xu, S.; Wang, J. Data Stream Classification Algorithm Based on Kappa Coefficient. Comput. Sci. 2016, 43, 173–178. [Google Scholar]
- Domingos, P.M.; Hulten, G. Mining high-speed data streams. In Proceedings of the Sixth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Boston, MA, USA, 20–23 August 2000; pp. 71–80. [Google Scholar]
- Hulten, G.; Spencer, L.; Domingos, P.M. Mining time-changing data streams. In Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 26–29 August 2001; pp. 97–106. [Google Scholar]
- Wu, X.; Li, P.; Hu, X. Learning from concept drifting data streams with unlabeled data. Neurocomputing 2012, 92, 145–155. [Google Scholar] [CrossRef]
- Li, P.; Wu, X.; Hu, X.; Wang, H. Learning concept-drifting data streams with random ensemble decision trees. Neurocomputing 2015, 166, 68–83. [Google Scholar] [CrossRef]
- Brzezinski, D.; Stefanowski, J. Prequential AUC for classifier evaluation and drift detection in evolving data streams. In Proceedings of the 3rd International Conference on New Frontiers in Mining Complex Patterns (NFMCP’14), Nancy, France, 19 September 2014; pp. 87–101. [Google Scholar]
- Rutkowski, L.; Pietruczuk, L.; Duda, P.; Jaworski, M. Decision Trees for Mining Data Streams Based on the McDiarmid’s Bound. IEEE Trans. Knowl. Data Eng. 2013, 25, 1272–1279. [Google Scholar] [CrossRef]
- Ghazikhani, A.; Monsefi, R.; Yazdi, H.S. Online neural network model for non-stationary and imbalanced data stream classification. Int. J. Mach. Learn. Cybern. 2014, 5, 51–62. [Google Scholar] [CrossRef]
- Jain, V. Perspective analysis of telecommunication fraud detection using data stream analytics and neural network classification based data mining. Int. J. Inf. Technol. 2017, 9, 303–310. [Google Scholar] [CrossRef]
- Gao, M.; Yang, X.; Jain, R.; Ooi, B.C. Spatio-temporal event stream processing in multimedia communication systems. In Proceedings of the Scientific and Statistical Database Management, International Conference (SSDBM), Heidelberg, Germany, 30 June– 2 July 2010; pp. 602–620. [Google Scholar]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhou, H.; Ding, X.; Zhang, R. Extreme learning machine for regression and multiclass classification. IEEE Trans. Syst. Man Cybern. B 2012, 42, 513–529. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: A new learning scheme of feedforward neural networks. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks (IEEE Cat. No. 04CH37541), Budapest, Hungary, 25–29 July 2004; Volume 2, pp. 985–990. [Google Scholar]
- Lu, S.; Qiu, X.; Shi, J.; Li, N.; Lu, Z.H.; Chen, P.; Yang, M.M.; Liu, F.Y.; Jia, W.J.; Zhang, Y. A Pathological Brain Detection System based on Extreme Learning Machine Optimized by Bat Algorithm. CNS Neurol. Disord.-Drug Target 2017, 16, 23–29. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.H.; Muhammad, K.; Phillips, P.; Dong, Z.; Zhang, Y.D. Ductal carcinoma in situ detection in breast thermography by extreme learning machine and combination of statistical measure and fractal dimension. J. Ambient Intell. Humaniz. Comput. 2017, 1–11. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, F.; Yuan, Y. A study on effectiveness of extreme learning machine. Neurocomputing 2014, 74, 2483–2490. [Google Scholar] [CrossRef]
- Liang, N.Y.; Huang, G.B.; Saratchandran, P.; Sundararajan, N. A fast and accurate online sequential learning algorithm for feedforward networks. IEEE Trans. Neural Netw. 2006, 17, 1411–1423. [Google Scholar] [CrossRef] [PubMed]
- Gu, Y.; Liu, J.; Chen, Y.; Jiang, X.; Yu, H. TOSELM: Timeliness Online Sequential Extreme Learning Machine. Neurocomputing 2014, 128, 119–127. [Google Scholar] [CrossRef]
- Shao, Z.; Meng, J.E. An online sequential learning algorithm for regularized Extreme Learning Machine. Neurocomputing 2016, 173, 778–788. [Google Scholar] [CrossRef]
- Yangjun, R.; Xiaoguang, S.; Huyuan, S.; Lijuan, S.; Xin, W. Boosting ridge extreme learning machine. In Proceedings of the 2012 IEEE Symposium on Robotics and Applications (ISRA), Kuala Lumpur, Malaysia, 3–5 June 2012; pp. 881–884. [Google Scholar]
- Zhao, J.; Wang, Z.; Dong, S.P. Online sequential extreme learning machine with forgetting mechanism. Neurocomputing 2012, 87, 79–89. [Google Scholar] [CrossRef]
- Mirza, B.; Lin, Z.; Liu, N. Ensemble of subset online sequential extreme learning machine for class imbalance and concept drift. Neurocomputing 2015, 149, 316–329. [Google Scholar] [CrossRef]
- Vanli, N.D.; Sayin, M.O.; Delibalta, I.; Kozat, S.S. Sequential Nonlinear Learning for Distributed Multiagent Systems via Extreme Learning Machines. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 546–558. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.; Kumar, H.; Singla, R.K. An intrusion detection system using network traffic profiling and online sequential extreme learning machine. Expert Syst. Appl. 2015, 42, 8609–8624. [Google Scholar] [CrossRef]
- Wang, H.; Fan, W.; Yu, P.S.; Han, J. Mining concept-drifting data streams using ensemble classifiers. In Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washingto, DC, USA, 24–27 August 2003; pp. 226–235. [Google Scholar]
- Han, J.; Kamber, M.; Pei, J. Data Mining: Concepts and Techniques; Morgan Kaufmann: Burlington, MA, USA, 2012. [Google Scholar]
- Feng, L.; Xu, S.; Wang, F.; Liu, S. Rough extreme learning machine: A new classification method based on uncertainty measure. arXiv, 2017; arXiv:1710.10824. [Google Scholar]
- Wang, J.; Xu, S.; Duan, B.; Liu, C.; Liang, J. An Ensemble Classification Algorithm Based on Information Entropy for Data Streams. arXiv, 2017; arXiv:1708.03496. [Google Scholar]
- Zhang, X. Matrix Analysis and Application, 2nd ed.; Tsinghua University Press: Beijing, China, 2013. [Google Scholar]
- Roweis, S.T.; Saul, L.K. Nonlinear Dimensionality Reduction by Locally Linear Embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef] [PubMed]
- Gama, J.; Medas, P.; Castillo, G.; Rodrigues, P. Learning with Drift Detection. In Advances in Artificial Intelligence—Sbia 2004, Proceedings of the Brazilian Symposium on Artificial Intelligence, Sao Luis, Maranhao, Brazil, 29 September–1 October 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 286–295. [Google Scholar]
- Gama, J.; Castillo, G. Learning with local drift detection. In Proceedings of the International Conference on Advanced Data Mining and Applications, Xi’an, China, 14–16 August 2006; pp. 42–55. [Google Scholar]
- Street, W.N.; Kim, Y. A streaming ensemble algorithm (SEA) for large-scale classification. In Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA; 2001; pp. 377–382. [Google Scholar]
- Zhang, P.; Zhu, X.; Shi, Y.; Wu, X. An aggregate ensemble for mining concept drifting data streams with noise. In Proceedings of the 13th Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining (PAKDD ’09), Bangkok, Thailand, 27–30 April 2009; pp. 1021–1029. [Google Scholar]
- Sun, Y.; Mao, G.J.; Liu, X.; Liu, C.N. Mining Concept Drifts from Data Streams Based on Multi-classifiers. Acta Autom. Sin. 2008, 34, 2323–2326. [Google Scholar] [CrossRef]
- Bifet, A.; Holmes, G.; Kirkby, R.; Pfahringer, B. MOA: Massive Online Analysis. J. Mach. Learn. Res. 2010, 11, 1601–1604. [Google Scholar]
| Dataset | Size | Attributes | Classes | Types |
|---|---|---|---|---|
| voice | 7614 | 385 | 12 | Numeric |
| waveform | 50,000 | 21 | 3 | Numeric |
| bank | 45,211 | 16 | 2 | Mixed |
| adult | 32,561 | 13 | 2 | Mixed |
| letter | 20,000 | 16 | 26 | Categorical |
| hyperplane | 50,000 | 40 | 2 | Numeric |
| occupancy | 8143 | 5 | 2 | Numeric |
| hill | 1212 | 100 | 2 | Numeric |
| Protein | 1080 | 80 | 8 | Mixed |
| Ozone | 2534 | 72 | 2 | Numeric |
| Dataset | CELM | SEA | AE | OS-ELM | M_ID4 | winsize | d | L |
|---|---|---|---|---|---|---|---|---|
| voice | 0.6511 ± 0.1786 | 0.3357 ± 0.0651 | 0.4155 ± 0.0737 | 0.2808 ± 0.0429 | 0.6029 ± 0.1033 | 100 | 5 | 20 |
| waveform | 0.6619 ± 0.0119 | 0.6329 ± 0.0136 | 0.6374 ± 0.0204 | 0.6856 ± 0.0134 | 0.6205 ± 0.0195 | 1000 | 200 | 200 |
| bank | 0.8863 ± 0.0094 | 0.8841 ± 0.0088 | 0.8843 ± 0.0084 | 0.8812 ± 0.0087 | 0.8269 ± 0.0196 | 1200 | 13 | 5 |
| adult | 0.7596 ± 0.0135 | 0.8119 ± 0.0168 | 0.8156 ± 0.0117 | 0.7569 ± 0.0177 | 0.7501 ± 0.0235 | 1000 | 5 | 5 |
| letter | 0.4930 ± 0.0581 | 0.0361 ± 0.0096 | 0.3617 ± 0.0597 | 0.0418 ± 0.0046 | 0.6818 ± 0.1368 | 1000 | 13 | 2000 |
| hyperplane | 0.5812 ± 0.0205 | 0.5761 ± 0.0164 | 0.5758 ± 0.0182 | 0.5796 ± 0.0306 | 0.5385 ± 0.0199 | 1000 | 30 | 2000 |
| occupancy | 0.9670 ± 0.0294 | 0.9882 ± 0.0111 | 0.9788 ± 0.0191 | 0.7835 ± 0.0291 | 0.9640 ± 0.0182 | 100 | 5 | 10 |
| hill | 0.5517 ± 0.0659 | 0.5643 ± 0.0813 | 0.4833 ± 0.0491 | 0.4900 ± 0.0344 | 0.5283 ± 0.0369 | 60 | 80 | 100 |
| Protein | 0.6354 ± 0.0599 | 0.5750 ± 0.1578 | 0.6583 ± 0.1532 | 0.1354 ± 0.0348 | 0.5854 ± 0.1125 | 80 | 50 | 1000 |
| Ozone | 0.9408 ± 0.0107 | 0.9396 ± 0.0251 | 0.9392 ± 0.0131 | 0.9408 ± 0.0107 | 0.7692 ± 0.1018 | 120 | 30 | 200 |
| Average | 0.7128 ± 0.0297 | 0.6344 ± 0.0406 | 0.6750 ± 0.0424 | 0.5576 ± 0.0227 | 0.6868 ± 0.0592 | – | – | – |
| Dataset | CELM | SEA | AE | OS-ELM | M_ID4 |
|---|---|---|---|---|---|
| voice | 2.0433 | 2401.3555 | 291.9706 | 0.1160 | 5234.9994 |
| waveform | 82.9626 | 1523.1448 | 172.0207 | 0.1480 | >20,000 |
| bank | 10.8994 | 573.6019 | 63.8236 | 0.1100 | 2392.9633 |
| adult | 6.1201 | 279.0587 | 37.7094 | 0.0566 | 2830.5794 |
| letter | 70.0543 | 248.7848 | 29.8872 | 0.0865 | 3638.3141 |
| hyperplane | 27.5537 | 1558.7989 | 160.4245 | 0.2402 | 3486.1807 |
| occupancy | 1.2085 | 15.4485 | 2.3894 | 0.0632 | 75.3053 |
| hill | 0.5319 | 59.4144 | 8.9018 | 0.0548 | 75.0302 |
| Protein | 4.2500 | 40.2288 | 6.3598 | 0.0426 | 14.2372 |
| Ozone | 0.4528 | 64.5923 | 6.0510 | 0.0739 | 32.7597 |
| Dataset | The Number of Original Features | After Dimension Reduction | Decrement | Reduction Rate |
|---|---|---|---|---|
| voice | 385 | 5 | 380 | 0.9870 |
| adult | 13 | 5 | 7 | 0.5384 |
| letter | 16 | 13 | 3 | 0.1875 |
| hyperplane | 40 | 30 | 10 | 0.2500 |
| occupancy | 5 | 5 | 0 | 0.0000 |
| hill | 100 | 80 | 20 | 0.2000 |
| Protein | 80 | 50 | 30 | 0.3750 |
| Ozone | 72 | 30 | 42 | 0.5833 |
| Dataset | Voice | Waveform | Bank | Adult | Letter | Hyperplane | Occupancy | Hill | Protein | Ozone |
|---|---|---|---|---|---|---|---|---|---|---|
| Standard deviation | 0.1971 | 0.0409 | 0.0109 | 0.0193 | 0.0816 | 0.0112 | 0.0373 | 0.0222 | 0.1992 | 0.0045 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, R.; Xu, S.; Feng, L. An Ensemble Extreme Learning Machine for Data Stream Classification. Algorithms 2018, 11, 107. https://doi.org/10.3390/a11070107
Yang R, Xu S, Feng L. An Ensemble Extreme Learning Machine for Data Stream Classification. Algorithms. 2018; 11(7):107. https://doi.org/10.3390/a11070107
Chicago/Turabian StyleYang, Rui, Shuliang Xu, and Lin Feng. 2018. "An Ensemble Extreme Learning Machine for Data Stream Classification" Algorithms 11, no. 7: 107. https://doi.org/10.3390/a11070107
APA StyleYang, R., Xu, S., & Feng, L. (2018). An Ensemble Extreme Learning Machine for Data Stream Classification. Algorithms, 11(7), 107. https://doi.org/10.3390/a11070107





