Optimal Control Algorithms and Their Analysis for Short-Term Scheduling in Manufacturing Systems
Abstract
1. Introduction
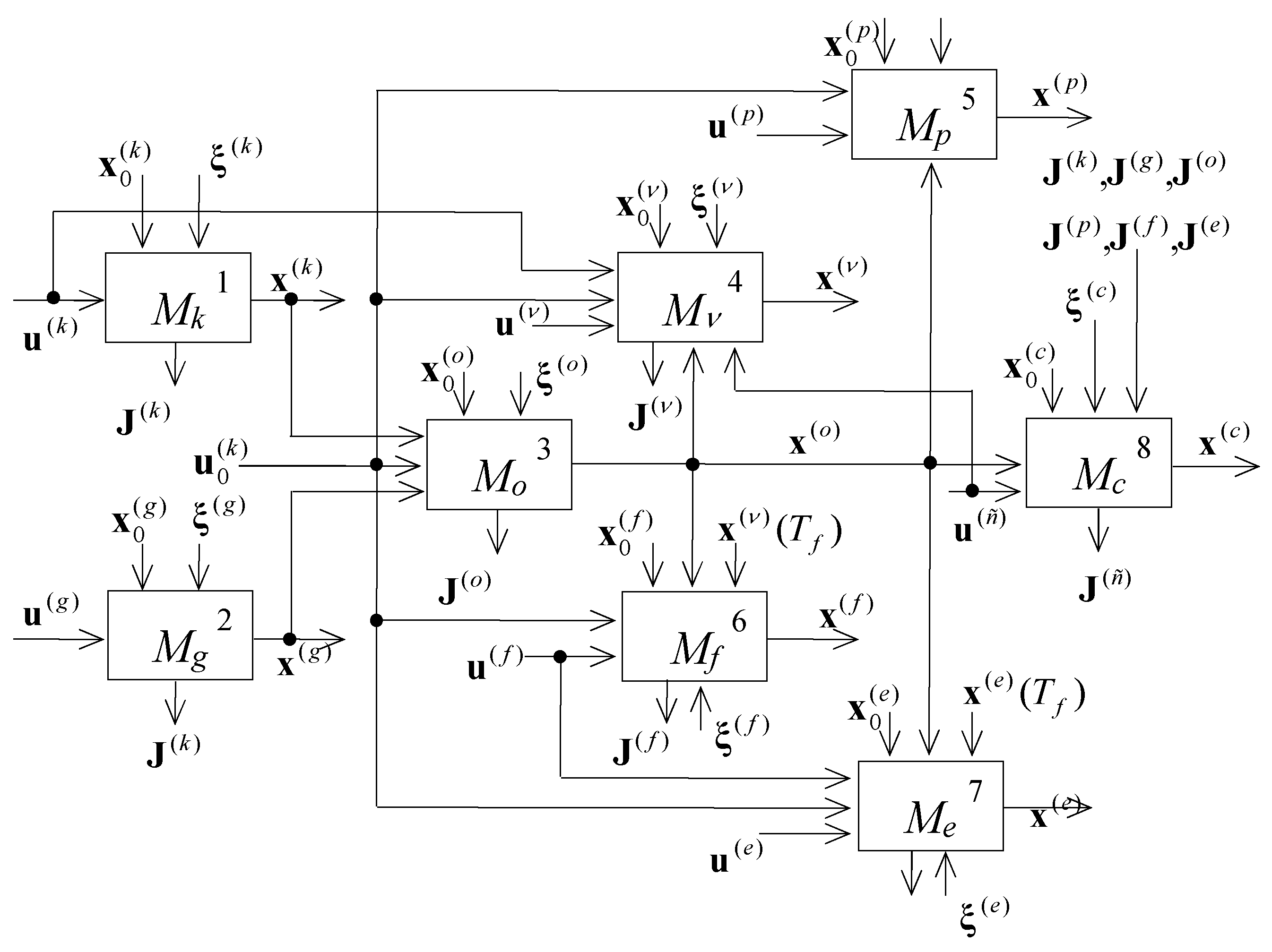
2. Optimal Control Applications to Scheduling in Manufacturing Systems
- —dynamic model of MS elements and subsystems motion control;
- —dynamic model of MS channel control;
- —dynamic model of MS operations control;
- —dynamic model of MS flow control;
- —dynamic model of MS resource control;
- —dynamic model of MS operation parameters control;
- —dynamic model of MS structure dynamic control;
- —dynamic model of MS auxiliary operation control.
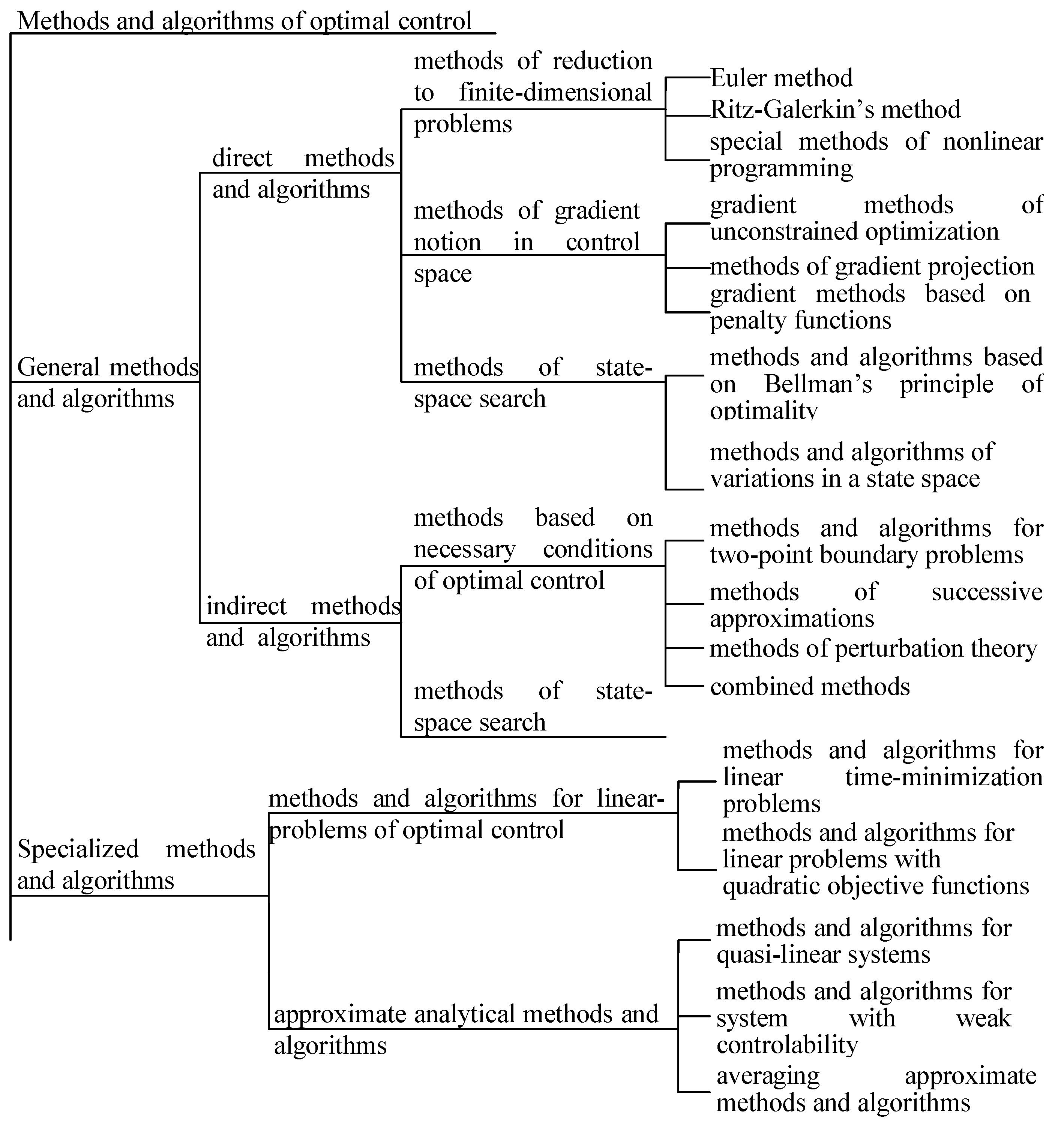
3. Classification and Analyses of Optimal Control Computational Algorithms for Short-Term Scheduling in MSs
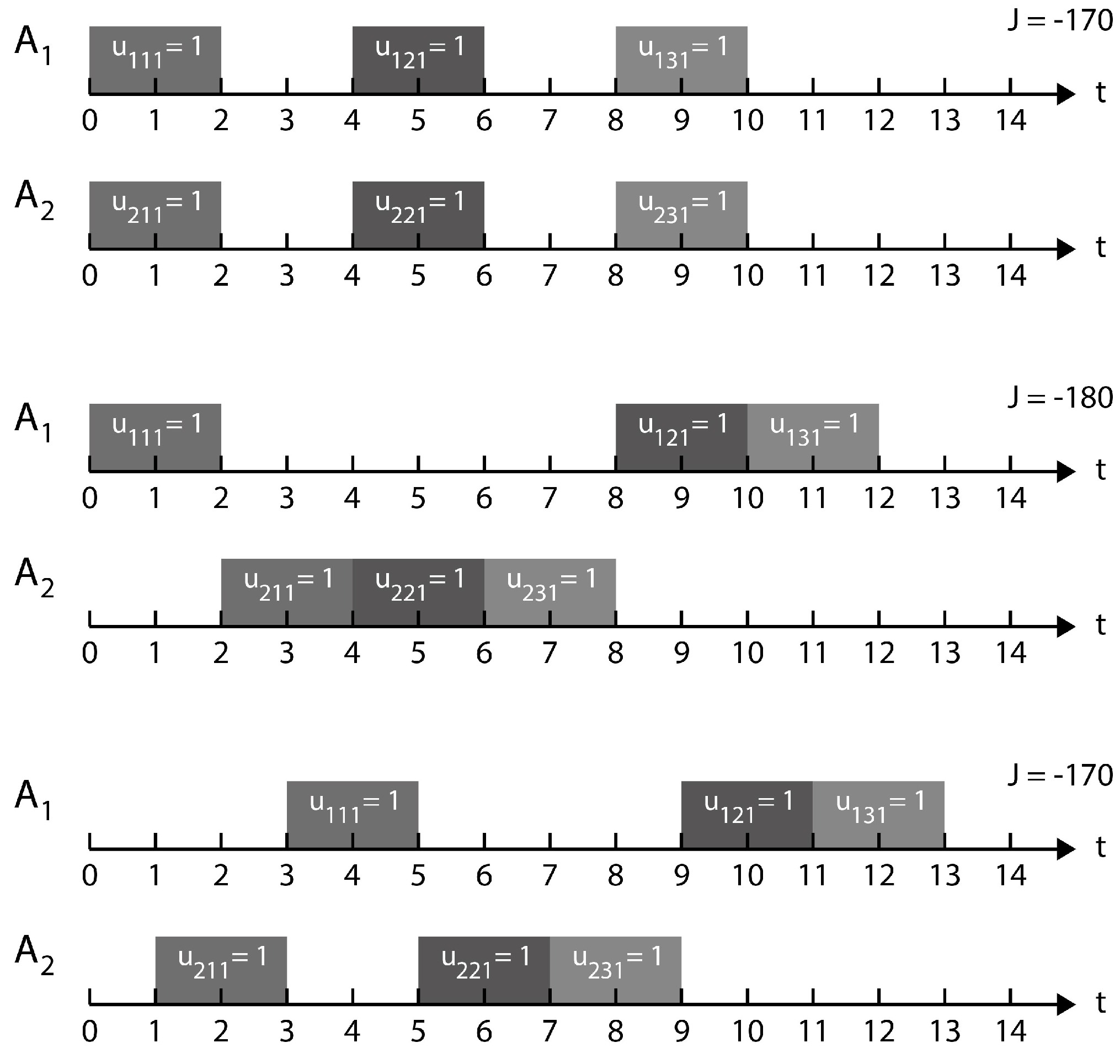
4. Combined Method and Algorithm for Short-Term Scheduling in MSs
- models M<o> of operation program control;
- models M<ν> of auxiliary operations program control.
- (a)
- If the problem P does not have allowable solutions, then this is true for the problem Г as well.
- (b)
- The minimal value of the goal function in the problem P is not greater than the one in the problem Г.
- (c)
- If the optimal program control of the problem P is allowable for the problem Г, then it is the optimal solution for the problem Г as well.
- (a)
- If the problem P does not have allowable solutions, then a control transferring dynamic system (1) from a given initial state to a given final state does not exist. The same end conditions are violated in the problem Г.
- (b)
- It can be seen that the difference between the functional Jp in (23) and the functional Job in the problem P is equal to losses caused by interruption of operation execution.
- (c)
- Let , ∀ t ∈ (T0, Tf] be an MS optimal program control in P and an allowable program control in Г; let be a solution of differential equations of the models M<o>, M<ν> subject to =. If so, then meets the requirements of the local section method (maximizes Hamilton’s function) for the problem Г. In this case, the vectors , return the minimum to the functional (1).
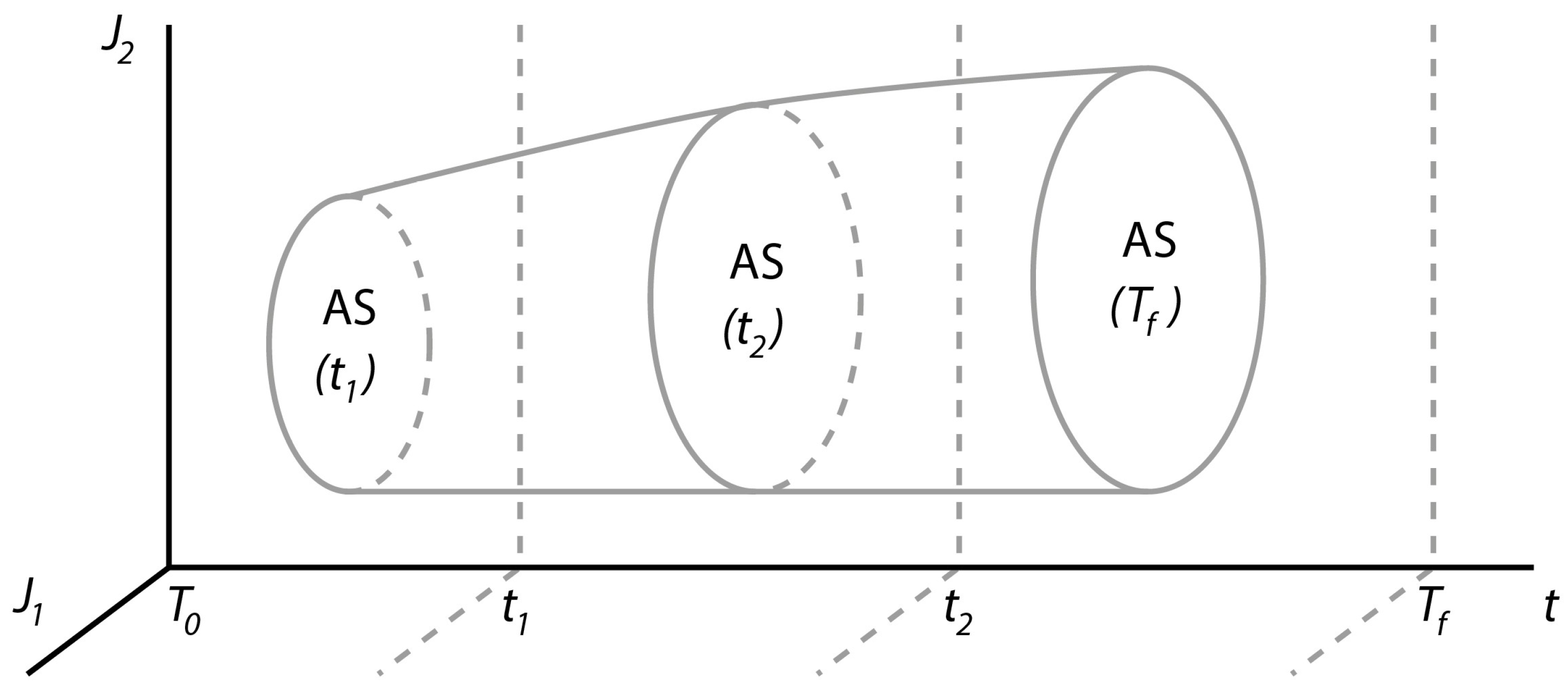
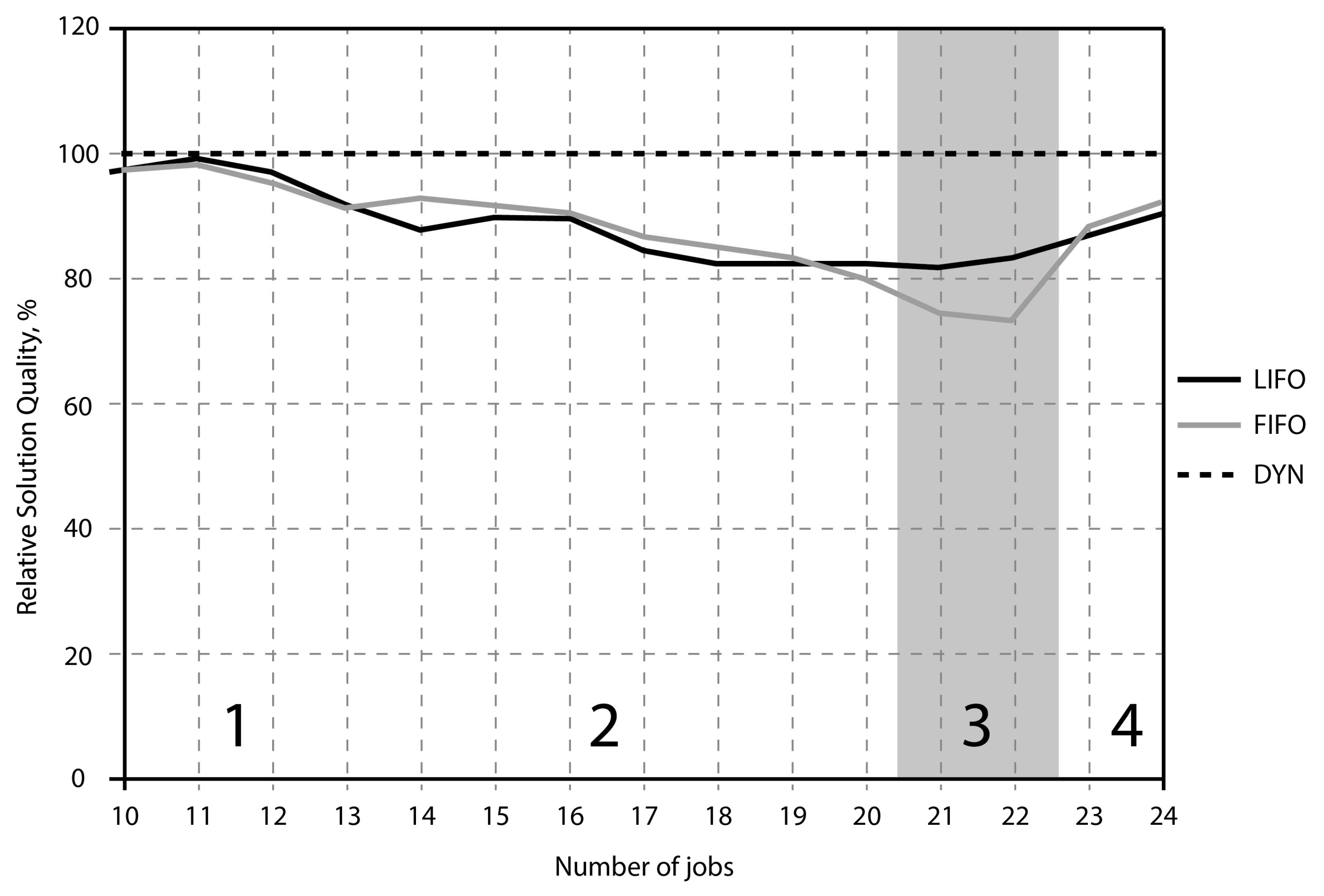
5. Qualitative and Quantitative Analysis of the MS Scheduling Problem
- the total number of operations on a planning horizon;
- a dispersion of volumes of operations;
- a ratio of the total volume of operations to the number of processes;
- a ratio of the amount of data of operation to the volume of the operation (relative operation density).
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| AS | Attainability Sets |
| OPC | Optimal Program Control |
| MS | Manufacturing System |
| SSAM | Successive Approximations Method |
Appendix A. List of Notations
References
- Blazewicz, J.; Ecker, K.; Pesch, E.; Schmidt, G.; Weglarz, J. Scheduling Computer and Manufacturing Processes, 2nd ed.; Springer: Berlin, Germany, 2001. [Google Scholar]
- Pinedo, M. Scheduling: Theory, Algorithms, and Systems; Springer: New York, NY, USA, 2008. [Google Scholar]
- Dolgui, A.; Proth, J.-M. Supply Chains Engineering: Useful Methods and Techniques; Springer: Berlin, Germany, 2010. [Google Scholar]
- Werner, F.; Sotskov, Y. (Eds.) Sequencing and Scheduling with Inaccurate Data; Nova Publishers: New York, NY, USA, 2014. [Google Scholar]
- Lauff, V.; Werner, F. On the Complexity and Some Properties of Multi-Stage Scheduling Problems with Earliness and Tardiness Penalties. Comput. Oper. Res. 2004, 31, 317–345. [Google Scholar] [CrossRef]
- Jungwattanakit, J.; Reodecha, M.; Chaovalitwongse, P.; Werner, F. A comparison of scheduling algorithms for flexible flow shop problems with unrelated parallel machines, setup times, and dual criteria. Comput. Oper. Res. 2009, 36, 358–378. [Google Scholar] [CrossRef]
- Dolgui, A.; Kovalev, S. Min-Max and Min-Max Regret Approaches to Minimum Cost Tools Selection 4OR-Q. J. Oper. Res. 2012, 10, 181–192. [Google Scholar] [CrossRef]
- Dolgui, A.; Kovalev, S. Scenario Based Robust Line Balancing: Computational Complexity. Discret. Appl. Math. 2012, 160, 1955–1963. [Google Scholar] [CrossRef]
- Sotskov, Y.N.; Lai, T.-C.; Werner, F. Measures of Problem Uncertainty for Scheduling with Interval Processing Times. OR Spectr. 2013, 35, 659–689. [Google Scholar] [CrossRef]
- Choi, T.-M.; Yeung, W.-K.; Cheng, T.C.E. Scheduling and co-ordination of multi-suppliers single-warehouse-operator single-manufacturer supply chains with variable production rates and storage costs. Int. J. Prod. Res. 2013, 51, 2593–2601. [Google Scholar] [CrossRef]
- Harjunkoski, I.; Maravelias, C.T.; Bongers, P.; Castro, P.M.; Engell, S.; Grossmann, I.E.; Hooker, J.; Méndez, C.; Sand, G.; Wassick, J. Scope for industrial applications of production scheduling models and solution methods. Comput. Chem. Eng. 2014, 62, 161–193. [Google Scholar] [CrossRef]
- Bożek, A.; Wysocki, M. Flexible Job Shop with Continuous Material Flow. Int. J. Prod. Res. 2015, 53, 1273–1290. [Google Scholar] [CrossRef]
- Ivanov, D.; Dolgui, A.; Sokolov, B. Robust dynamic schedule coordination control in the supply chain. Comput. Ind. Eng. 2016, 94, 18–31. [Google Scholar] [CrossRef]
- Giglio, D. Optimal control strategies for single-machine family scheduling with sequence-dependent batch setup and controllable processing times. J. Sched. 2015, 18, 525–543. [Google Scholar] [CrossRef]
- Lou, S.X.C.; Van Ryzin, G. Optimal control rules for scheduling job shops. Ann. Oper. Res. 1967, 17, 233–248. [Google Scholar] [CrossRef]
- Maimon, O.; Khmelnitsky, E.; Kogan, K. Optimal Flow Control in Manufacturing Systems; Springer: Berlin, Germany, 1998. [Google Scholar]
- Ivanov, D.; Sokolov, B. Dynamic coordinated scheduling in the manufacturing system under a process modernization. Int. J. Prod. Res. 2013, 51, 2680–2697. [Google Scholar] [CrossRef]
- Pinha, D.; Ahluwalia, R.; Carvalho, A. Parallel Mode Schedule Generation Scheme. In Proceedings of the 15th IFAC Symposium on Information Control Problems in Manufacturing INCOM, Ottawa, ON, Canada, 11–13 May 2015. [Google Scholar]
- Ivanov, D.; Sokolov, B. Structure dynamics control approach to supply chain planning and adaptation. Int. J. Prod. Res. 2012, 50, 6133–6149. [Google Scholar] [CrossRef]
- Ivanov, D.; Sokolov, B.; Dolgui, A. Multi-stage supply chains scheduling in petrochemistry with non-preemptive operations and execution control. Int. J. Prod. Res. 2014, 52, 4059–4077. [Google Scholar] [CrossRef]
- Pontryagin, L.S.; Boltyanskiy, V.G.; Gamkrelidze, R.V.; Mishchenko, E.F. The Mathematical Theory of Optimal Processes; Pergamon Press: Oxford, UK, 1964. [Google Scholar]
- Athaus, M.; Falb, P.L. Optimal Control: An Introduction to the Theory and Its Applications; McGraw-Hill: New York, NY, USA; San Francisco, CA, USA, 1966. [Google Scholar]
- Lee, E.B.; Markus, L. Foundations of Optimal Control Theory; Wiley & Sons: New York, NY, USA, 1967. [Google Scholar]
- Moiseev, N.N. Element of the Optimal Systems Theory; Nauka: Moscow, Russia, 1974. (In Russian) [Google Scholar]
- Bryson, A.E.; Ho, Y.-C. Applied Optimal Control; Hemisphere: Washington, DC, USA, 1975. [Google Scholar]
- Gershwin, S.B. Manufacturing Systems Engineering; PTR Prentice Hall: Englewood Cliffs, NJ, USA, 1994. [Google Scholar]
- Sethi, S.P.; Thompson, G.L. Optimal Control Theory: Applications to Management Science and Economics, 2nd ed.; Springer: Berlin, Germany, 2000. [Google Scholar]
- Dolgui, A.; Ivanov, D.; Sethi, S.; Sokolov, B. Scheduling in production, supply chain Industry 4.0 systems by optimal control: fundamentals, state-of-the-art, and applications. Int. J. Prod. Res. 2018. forthcoming. [Google Scholar]
- Bellmann, R. Adaptive Control Processes: A Guided Tour; Princeton University Press: Princeton, NJ, USA, 1972. [Google Scholar]
- Maccarthy, B.L.; Liu, J. Addressing the gap in scheduling research: A review of optimization and heuristic methods in production scheduling. Int. J. Prod. Res. 1993, 31, 59–79. [Google Scholar] [CrossRef]
- Sarimveis, H.; Patrinos, P.; Tarantilis, C.D.; Kiranoudis, C.T. Dynamic modeling and control of supply chains systems: A review. Comput. Oper. Res. 2008, 35, 3530–3561. [Google Scholar] [CrossRef]
- Ivanov, D.; Sokolov, B. Dynamic supply chains scheduling. J. Sched. 2012, 15, 201–216. [Google Scholar] [CrossRef]
- Ivanov, D.; Sokolov, B. Adaptive Supply Chain Management; Springer: London, UK, 2010. [Google Scholar]
- Ivanov, D.; Sokolov, B.; Käschel, J. Integrated supply chain planning based on a combined application of operations research and optimal control. Central. Eur. J. Oper. Res. 2011, 19, 219–317. [Google Scholar] [CrossRef]
- Ivanov, D.; Dolgui, A.; Sokolov, B.; Werner, F. Schedule robustness analysis with the help of attainable sets in continuous flow problem under capacity disruptions. Int. J. Prod. Res. 2016, 54, 3397–3413. [Google Scholar] [CrossRef]
- Kalinin, V.N.; Sokolov, B.V. Optimal planning of the process of interaction of moving operating objects. Int. J. Differ. Equ. 1985, 21, 502–506. [Google Scholar]
- Kalinin, V.N.; Sokolov, B.V. A dynamic model and an optimal scheduling algorithm for activities with bans of interrupts. Autom. Remote Control 1987, 48, 88–94. [Google Scholar]
- Ohtilev, M.Y.; Sokolov, B.V.; Yusupov, R.M. Intellectual Technologies for Monitoring and Control of Structure-Dynamics of Complex Technical Objects; Nauka: Moscow, Russia, 2006. [Google Scholar]
- Krylov, I.A.; Chernousko, F.L. An algorithm for the method of successive approximations in optimal control problems. USSR Comput. Math. Math. Phys. 1972, 12, 14–34. [Google Scholar] [CrossRef]
- Chernousko, F.L.; Lyubushin, A.A. Method of successive approximations for solution of optimal control problems. Optim. Control Appl. Methods 1982, 3, 101–114. [Google Scholar] [CrossRef]
- Ivanov, D.; Sokolov, B.; Dolgui, A.; Werner, F.; Ivanova, M. A dynamic model and an algorithm for short-term supply chain scheduling in the smart factory Industry 4.0. Int. J. Prod. Res. 2016, 54, 386–402. [Google Scholar] [CrossRef]
- Hartl, R.F.; Sethi, S.P.; Vickson, R.G. A survey of the maximum principles for optimal control problems with state constraints. SIAM Rev. 1995, 37, 181–218. [Google Scholar] [CrossRef]
- Chernousko, F.L. State Estimation of Dynamic Systems; Nauka: Moscow, Russia, 1994. [Google Scholar]
- Gubarev, V.A.; Zakharov, V.V.; Kovalenko, A.N. Introduction to Systems Analysis; LGU: Leningrad, Russia, 1988. [Google Scholar]
| Results and Their Implementation | The Main Results of Qualitative Analysis of MS Control Processes | The Directions of Practical Implementation of the Results | |
|---|---|---|---|
| No | |||
| 1 | Analysis of solution existence in the problems of MS control | Adequacy analysis of the control processes description in control models | |
| 2 | Conditions of controllability and attainability in the problems of MS control | Analysis MS control technology realizability on the planning interval. Detection of main factors of MS goal and information-technology abilities. | |
| 3 | Uniqueness condition for optimal program controls in scheduling problems | Analysis of possibility of optimal schedules obtaining for MS functioning | |
| 4 | Necessary and sufficient conditions of optimality in MS control problems | Preliminary analysis of optimal control structure, obtaining of main expressions for MS scheduling algorithms | |
| 5 | Conditions of reliability and sensitivity in MS control problems | Evaluation of reliability and sensitivity of MS control processes with respect to perturbation impacts and to the alteration of input data contents and structure | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sokolov, B.; Dolgui, A.; Ivanov, D. Optimal Control Algorithms and Their Analysis for Short-Term Scheduling in Manufacturing Systems. Algorithms 2018, 11, 57. https://doi.org/10.3390/a11050057
Sokolov B, Dolgui A, Ivanov D. Optimal Control Algorithms and Their Analysis for Short-Term Scheduling in Manufacturing Systems. Algorithms. 2018; 11(5):57. https://doi.org/10.3390/a11050057
Chicago/Turabian StyleSokolov, Boris, Alexandre Dolgui, and Dmitry Ivanov. 2018. "Optimal Control Algorithms and Their Analysis for Short-Term Scheduling in Manufacturing Systems" Algorithms 11, no. 5: 57. https://doi.org/10.3390/a11050057
APA StyleSokolov, B., Dolgui, A., & Ivanov, D. (2018). Optimal Control Algorithms and Their Analysis for Short-Term Scheduling in Manufacturing Systems. Algorithms, 11(5), 57. https://doi.org/10.3390/a11050057






