Abstract
To enhance the convergence speed and calculation precision of the grey wolf optimization algorithm (GWO), this paper proposes a dynamic generalized opposition-based grey wolf optimization algorithm (DOGWO). A dynamic generalized opposition-based learning strategy enhances the diversity of search populations and increases the potential of finding better solutions which can accelerate the convergence speed, improve the calculation precision, and avoid local optima to some extent. Furthermore, 23 benchmark functions were employed to evaluate the DOGWO algorithm. Experimental results show that the proposed DOGWO algorithm could provide very competitive results compared with other analyzed algorithms, with a faster convergence speed, higher calculation precision, and stronger stability.
1. Introduction
Many methods have been proposed to solve varied optimization problems. Exact optimization approaches (i.e., approaches guaranteeing the convergence to an optimal solution) have been proved to be valid and useful, but many still experience considerable difficulties when dealing with complex and large-scale optimization problems. Therefore, numerous meta-heuristics have been proposed to deal with these problems. Among meta-heuristics, hybrid meta-heuristics combining exact and heuristic approaches have been successfully developed and applied to many optimization problems such as C. Blum et al., G.R. Raidl et al., C. Blum et al., F. D’Andreagiovanni et al., F. D’Andreagiovanni et al, and J.A. Egea et al. [1,2,3,4,5,6].
As a result of their superior optimization performance and simplicity, meta-heuristic optimization algorithms have recently become very popular and are currently applied in a variety of fields. Meta-heuristic algorithms predominantly benefit from stochastic operators which can avoid local optima as opposed to traditional deterministic approaches [7,8,9]. Among them, nature-inspired meta-heuristic optimization algorithms are widely used in this field because of their flexibility, simplicity, good performance, and robustness. Nature-inspired meta-heuristic algorithms are predominantly used to solve optimization problems by mimicking not only physical phenomena but also biological or social behaviors. They can be classified into three categories: evolution-based, physics-based, and swarm-based approaches.
Evolution-based algorithms are inspired by evolutionary processes found in nature. Genetic algorithm (GA) [10], biogeography-based Optimization (BBO) [11] and differential evolution (DE) [12] are the most popular evolution-based algorithms. In addition, a new evolution-based polar bear optimization algorithm (PBO) [13] has been proposed which imitates the survival and hunting behaviors of polar bears and presents a novel birth and death mechanism to control the population. Physics-based algorithms are inspired by natural physical phenomena. The most popular algorithms are simulated annealing (SA) [14] and gravitational search algorithm (GSA) [15]. Moreover, some new physics-based algorithms, such as the black hole algorithm (BH) [16] and ray optimization (RO) [17], have recently been proposed. Swarm-based algorithms which mimic the biological behaviors of animals are very popular. The most well-known swarm-based algorithm is the particle swarm optimization (PSO) [18] which was inspired by the social behavior of birds. Two additional classic swarm-based algorithms are the ant colony optimization (ACO) [19] and the artificial bee colony algorithm (ABC) [20] which imitate the behaviors of ant and bee colonies, respectively. Recently, many novel swarm-based algorithms imitating different population behaviors have been proposed, including the firefly algorithm (FA) [21], the bat algorithm (BA) [22], the cuckoo search (CS) [23], the social spider optimization algorithm (SSO) [24], the grey wolf optimizer (GWO) [25], the dragonfly algorithm (DA) [26], the ant lion optimizer (ALO) [27], the moth-flame optimization algorithm (MFO) [28] and the whale optimization algorithm (WOA) [29]. Swarm-based optimization algorithms have been widely used in engineering, industry and other fields as a result of their excellent optimization performance and simplicity.
Proposed by Seyedali Mirjalili in 2014, the Grey Wolf Optimizer algorithm (GWO) is a swarm-based meta-heuristic optimization algorithm and was inspired by the hunting and search behaviors of grey wolves [25]. Thanks to its easy implementation, minor parameters, and good optimization performance, the GWO has been applied to various optimization problems and many engineering projects, such as power systems, photovoltaic systems, automated offshore crane design, feature selection in neural networks, etc. [30,31,32,33,34,35]. Moreover, many researchers have attempted different strategies to enhance the performance of GWO [36,37,38,39,40,41,42,43]. In this article, we will present a novel enhanced GWO optimization algorithm known as EOGWO by using a dynamic generalized opposition-based learning strategy (DGOBL). The crux of the DGOBL strategy is to increase the diversity of a population, a significant goal for a meta-heuristic optimization algorithm. Moreover, the DGOBL strategy uses a dynamic search interval instead of a fixed search interval which can improve the likelihood of finding solutions closer to global optimum in a short time. We validate the proposed DOGWO algorithm on 23 benchmark functions. The results show that the proposed DOGWO algorithm outperforms other algorithms mentioned in this paper with fast convergence speed, high calculation precision, and strong stability.
The rest of the paper is organized as follows. In Section 2, the standard GWO algorithm is briefly introduced. The dynamic generalized opposition-based learning strategy is introduced in detail and a new dynamic generalized opposition-based Grey Wolf Optimization algorithm (DOGWO) is presented in Section 3. Several simulation experiments are conducted in Section 4 and a comparative study on DOGWO and other optimization algorithms with various benchmarks is also presented. Section 4 also describes the results and gives a detailed analysis about the results. Finally, the work is concluded in Section 5.
2. The Grey Wolf Optimizer
Proposed by S. Mirjalilli in 2014, the GWO algorithm was inspired by the grey wolf’s unique hunting strategies, notably prey searching. A typical social hierarchy within grey wolf packs is shown in Figure 1.

Figure 1.
Social hierarchy of grey wolves.
The GWO algorithm assumes the grey wolf pack presents four levels: alpha (α) at the first level, beta (β) at the second level, delta (δ) at the third level, and omega (ω) at the last level. α wolves are leaders of wolf packs; they are responsible for making decisions that concern the whole pack. β wolves are subordinate wolves that help α in pack activities. δ wolves are designated to specific tasks such as sentinels, scouts, caretakers and so on; they submit to α and β wolves but dominate the ω wolves. ω wolves which are the lowest ranking wolves in a pack; they exist to maintain and support the dominance structure and satisfy the entire pack.
To mathematically describe the GWO algorithm, we consider α as the fittest solution and β and δ as the second and third best solutions, respectively. Other solutions represent ω wolves. In the GWO algorithm, hunting activities are guided by α, β and δ wolves; ω wolves obey wolves of the other three social levels.
According to C. Muro [44], the main phases of grey wolf hunting are:
- Tracking, chasing, and approaching the prey.
- Pursuing, encircling, and harassing the prey until it stops moving.
- Attacking towards the prey.
2.1. Encircling Prey
To mathematically model the encircling behavior of grey wolves according to one dimension, the following equations are proposed:
where t is the current iteration, is the position vector of the prey, and is the position of a grey wolf. A and C are coefficient vectors which can be calculated as follows:
where a is the convergence factor which will decrease from 2 to 0 linearly over the iteration. rand1 and rand2 are two random numbers in the range [0, 1] that play a significant role in the free derivation of the algorithm.
A = 2a × rand1 − a
C = 2 × rand2
2.2. Hunting
In many situations, we have no idea about the location of the optimum (prey). In the GWO algorithm, the author presumes that α, β, and δ have better knowledge about the possible location of prey. Therefore, these three wolves are responsible for guiding other wolves to search for the prey. To mathematically simulate the hunting behavior, the distances of α, β, and δ to the prey are calculated by Equation (5); these three wolves will decide with respect to their hierarchical ranking about the potential position of prey which is described by Equation (6). Finally, other wolves will update their positions according to the command of α, β, and δ, which is shown by Equation (7).
Dα(t) = |Cα∙Xα(t) − X(t)|, Dβ(t) = |Cβ∙Xβ(t) − X(t)|, Dδ(t) = |Cδ∙Xδ(t) − X(t)|
X1(t) = Xα(t) − A1∙Dα(t), X2(t) = Xβ(t) − A2∙Dβ(t), X3(t) = Xδ(t) − A3∙Dδ(t)
X(t + 1) = [X1(t) + X2(t) + X3(t)]/3
2.3. Attacking
In the GWO algorithm, the varied parameter A dominates the pack to either diverge from the prey or gather to the prey. This can be regarded as exploitation and exploration behavior in the process of searching for the optimum. It is defined as follows:
when |A| < 1, the wolves pack will gather to attack the prey;
when |A| > 1, the wolves pack will diverge and search for the new potential prey.
3. Dynamic Generalized Opposition-Based Learning Grey Wolf Optimizer (DOGWO)
To enhance the global search ability and accuracy of the GWO algorithm, the dynamic generalized opposition-based learning strategy (DGOBL) is appended to GWO. In this section, we will introduce the DGOBL strategy and present an enhanced GWO algorithm referred to as DOGWO.
3.1. Opposition-Based Learning (OBL)
Opposition-based Learning (OBL) is a computational intelligence strategy which was first proposed by Tizhoosh [45]. The OBL has proved to be an effective strategy to enhance the meta-heuristic optimization algorithms; it has been applied to many optimization algorithms such as the differential evolution algorithm, the genetic algorithm, the particle swarm optimization algorithm, the ant colony optimization algorithm, etc. [46,47,48,49,50,51,52,53,54]. According to OBL, the probability that the opposite individual is closer to the optimum than the current individual is 50%. Therefore, it will generate the opposite individual of the current individual, evaluate the fitness of both individuals, and select the better one as a new individual which can consequently improve the quality of the search population.
3.1.1. Opposite Number
Let x ∈ [lb, ub] be a real number. The opposite number of x is defined by:
x* = lb + ub − x
3.1.2. Opposite Point
Opposite definition in high-dimension can be described similarly as follows:
Let X = (x1, x2, x3, …, xD) be a point in a D-dimensional space, where x1, x2, x3, …, xD ∈ R, where xj ∈ [lbj + ubj], j ∈ 1, 2, …, D. The opposite point X* = (x1*, x2*, x3*, …, xD*) is defined by:
xj* = lbj + ubj − xj
3.2. Region Transformation Search Strategy (RTS)
3.2.1. Region Transformation Search
Let X be a search agent and X ∈ P(t) where P(t) is the current population and t indicates the iteration. If Ф transform is applied to X, then X will become X*. The transformation can be defined by:
X* = Ф(X)
After the Ф transform, the search space of X will altered from S(t) to a new search space S′(t), which can be defined as follows:
S′(t) = Ф(S(t))
3.2.2. RTS-Based Optimization
Iterative optimization process can be treated as the process of region transformation search in which the solution will transform from the current search space to a new search space after each iteration.
Let P(t) be the current search population of which the search space is S(t) and the population number is N. If Ф transform is applied to every search agent in P(t), then the transformed search agents will compose a new population P′(t).
The central tenet of RTS-based optimization is that if we choose the best N search agents between P(t) and the transformed P′(t) to form a new population P(t + 1) for the next generation, then we can easily know that x ∈ P(t + 1) which is better than x ∈ {P(t)∪P′(t) − P(t+1)} [55].
3.3. Dynamic Generalized Opposition-Based Learning Strategy (DGOBL)
3.3.1. The Concept of DGOBL
The focus of dynamic generalized opposition-based learning strategy (DGOBL) is to transform the fixed search space of individuals to a dynamic search space which can provide more chances to find solutions closer to the optimum. The DGOBL can be explained as follows:
Let x be an individual in current search space S, where x ∈ [lb, ub]. The opposite point x* in the transformed space S* can then be defined by:
where R is the transforming factor which is a random number in the range [0, 1].
x* = R(lbj + ubj ) − x
According to the definition, x ∈ [lb, ub], then x* ∈ [R(lb + ub) − lb, R(lb + ub) − ub]. The center of search space will transform from a fixed position to a random position in range [−, ].
If the current population number is N and dimension of individual is D, for an individual Xi = (Xi1, Xi2, …, XiD), the generalized opposition-based individual can be described as Xi* = (Xi1*, Xi2*, …, XiD*) which can be calculated by:
where R is a random number in range [0, 1], t indicates the iteration, and lbj(t), ubj(t) are dynamic boundaries which can be obtained by the following equation:
Xi,j* = R[lbj(t) + ubj(t)] − Xij, i = 1, 2, …, N; j = 1, 2,…, D
lbj(t) = min(Xi,j); ubj(t) = max(Xi,j)
It may be possible that the transformed individual Xi,j* jumps out of the boundary [Xmin, Xmax]. In this case, the transformed individual will be reset to be a random value in the interval as follows:
Xi,j* = rand(lbj(t), ubj(t)), if Xi,j* < Xmin or Xi,j* > Xmax
3.3.2. Optimization Mechanism Based on DGOBL and RTS
To both avoid the randomness of Region Tranformation Search (RTS) and to take advantage of Dynamic Generalized Opposition-based Learning (DGOBL), an effective optimization mechanism based on DGOBL and RTS is proposed.
Let X = (x1, x2, x3, …, xD) be a point in a D-dimensional space and F(x) is an optimization function. According to the definition above, X* = (x1*, x2*, x3*, …, xD*) is the opposite point of X = (x1, x2, x3, …, xD). Then, the fitness of individual xj and xj* is evaluated respectively and denoted as F(xj) and F(xj*). Finally, the superior one is chosen as a new point by comparing the value of F(xj) and F(xj*) [56,57].
The optimization mechanism based on DGOBL and RTS is shown in Figure 2. The current population P(t) has three individuals x1, x2, x3 where t indicates the iteration. According to the dynamic generalized opposition-based learning strategy, three transformed individuals x1*, x2*, x3* compose the opposite population OP(t). By using the optimization mechanism, three fittest individuals x1, x2*, x3* are chosen as a new population P′(t).

Figure 2.
The optimization mechanism based on Dynamic Generalized Opposition-based Learning (DGOBL) and Region Tranformation Search (RTS).
3.4. Enhancing GWO with DGOBL Strategy (DOGWO)
Applying DGOBL to GWO can increase the number of potential points and, accordingly, expand the search area. It also will help to improve the robustness of the modified algorithm. Moreover, DGOBL can provide a better population to search for the optimum. Consequently, this can increase the convergence speed. In addition, the pseudo code of the improved DOGWO is shown as follows (Algorithm 1):
| Algorithm 1: Dynamic Generalized Opposition-Based Grey Wolf Optimizer. |
| 1 Initialize the original position of alpha, beta and delta |
| 2 Randomly initialize the positions of search agents |
| 3 set loop counter L = 0 |
| 4 While L ≤ Max_iteration do |
| 5 Update the dynamic interval boundaries according to Equation (14) |
| 6 Set the DGOBL jumping strategy according to Equation (15) |
| 7 for i = 1 to Searchagent_NO do |
| 8 for j = 1 to Dim do |
| 9 OPij = r*[aj(t) + bj(t)] − Pij |
| 10 end |
| 11 end |
| 12 Calculate the fitness value of Pij and OPij |
| 13 if fitness of OPij < Pij |
| 14 Pij = OPij; |
| 15 else |
| 16 Pij = Pij; |
| 17 end |
| 18 Choose alpha, beta, delta according to the fitness value |
| 19 Xα = the best search agent |
| 20 Xβ = the second best search agent |
| 21 Xδ = the third best search agent |
| 22 for each search agent do |
| 23 Update the position of current search according to Equation (7) |
| 24 end |
| 25 Calculate the fitness value of all search agents |
| 26 Update Xα, Xβ, and Xδ |
| 27 L = L + 1; |
| 28 end |
| 29 return Xα |
4. Experiments and Discussion
4.1. Benchmark Functions
In this section, 23 benchmark functions commonly used in research were applied to evaluate the optimal performance of the proposed DOGWO algorithm [25,26,27,28,29,37,42,43]. The benchmark functions used were all minimization functions which can be divided into three categories: unimodal, multimodal, and fixed-dimension multimodal. According to S. Mirjalili et al. [25], the unimodal functions are suitable for benchmarking optimum exploitation ability of an algorithm; similarly, the multimodal functions are suitable for benchmarking the ability of optimum exploration of an algorithm. These benchmark functions are listed in Table 1 where F1–F6 are unimodal functions, F7–F12 are multimodal functions, and F13–F23 are fixed-dimension multimodal benchmark functions. Moreover, the 2-D versions of these 23 benchmark functions are presented in Figure 3 for a better analysis of the form and search space.

Table 1.
Benchmark functions.
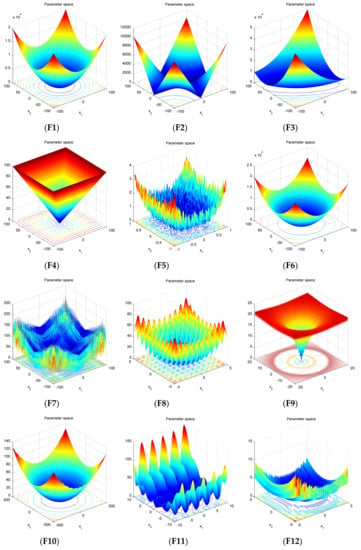

Figure 3.
2-D versions of the 23 benchmark functions.
4.2. Simulation Experiments
To verify the optimization performance of the proposed DOGWO algorithm, it was compared with several famous and recent algorithms: BA, ABC, PSO, MFO, ALO, and GWO by using the average and standard deviation. All the algorithms were run 30 times independently on each of the benchmark functions with the population size set as 50 and the iteration number as 1000. The parameters settings of the aforementioned algorithms are given in Table 2. Experiments were conducted in MATLAB R2012b of which the runtime environment was Intel(R) Corel(TM) i7-3770 CPU, 3.5 GB memory.

Table 2.
The parameters setting for seven algorithms.
The experiment results obtained by seven algorithms are shown in Table 3 where “Function” represents test function; “Best”, “Worst”, “Mean”, and “Std.” represent the best, worst, average global optimum, and standard deviation of 30 experiments, respectively. For F1–F12 of which the optimal solutions were zero, bold values indicate that the performance of DOGWO was better than other algorithms. For fixed-dimension functions in which the optimal solutions were fixed values, bold values indicate that the DOGWO was able to find the optimal solution.

Table 3.
Experiment results of benchmark functions.
The variation of fitness function value with the increase of iteration is denoted by convergence curve. Convergence curves of the partial benchmark functions are presented in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18. The ANOVA(Analysis of Variance) test, which was developed by R. Fisher, is a useful statistic test for comparing three or more samples for statistical significance. Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27, Figure 28, Figure 29, Figure 30, Figure 31 and Figure 32 show the ANOVA test of global optimum for several test functions.

Figure 4.
Convergence curves for F1.

Figure 5.
Convergence curves for F2.

Figure 6.
Convergence curves for F3.

Figure 7.
Convergence curves for F4.

Figure 8.
Convergence curves for F5.

Figure 9.
Convergence curves for F6.

Figure 10.
Convergence curves for F7.

Figure 11.
Convergence curves for F8.

Figure 12.
Convergence curves for F9.

Figure 13.
Convergence curves for F10.

Figure 14.
Convergence curves for F11.

Figure 15.
Convergence curves for F12.

Figure 16.
Convergence curves for F14.

Figure 17.
Convergence curves for F19–F20.

Figure 18.
Convergence curves for F21–F23.

Figure 19.
ANOVA test of global minimum for F1.

Figure 20.
ANOVA test of global minimum for F2.

Figure 21.
ANOVA test of global minimum for F3.

Figure 22.
ANOVA test of global minimum for F4.

Figure 23.
ANOVA test of global minimum for F5.

Figure 24.
ANOVA test of global minimum for F6.

Figure 25.
ANOVA test of global minimum for F7.

Figure 26.
ANOVA test of global minimum for F8.

Figure 27.
ANOVA test of global minimum for F9.

Figure 28.
ANOVA test of global minimum for F10.

Figure 29.
ANOVA test of global minimum for F11.

Figure 30.
ANOVA test of global minimum for F12.

Figure 31.
ANOVA test of global minimum for F14.

Figure 32.
ANOVA test of global minimum for F21.
Moreover, Figure 33 depicts the search history of 10 search agents with 500 iterations for several benchmark functions.
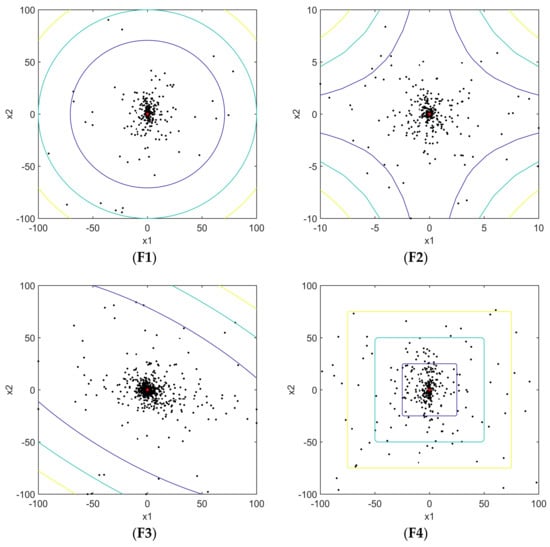

Figure 33.
Search history of benchmark functions where N = 10, Iterations = 500.
4.3. Analysis and Discussion
Table 3 shows the mean, best, worst, and standard deviation fitness function values obtained by seven algorithms. From Table 3, the results of the proposed DOGWO are very competitive. It can be observed that for the 23 benchmark functions, DOGWO was superior in performance in the worst, best, mean optimal values, and standard deviation as compared to the original GWO. This indicates that the DGOBL strategy is very effective to increase the population diversity which, consequently, can enhance the performance of the GWO. Moreover, the DOGWO provided a better performance on unimodal benchmark functions F1, F2, F3, F4 as well as the multimodal benchmark functions F7, F8, F10 in comparison to other algorithms. When the DOGWO converged to the global optimum accurately, the standard deviations of these functions were also zeros. For F5 and F9, the precision of best optimal value, worst optimal value, mean optimal value, and standard deviation of DOGWO were collectively better than other algorithms. In addition, for fixed-dimension multimodal functions F14, F15, F16, F17, F18, F19, F21, F22, and F23, DOGWO could find the optimum with small standard deviations. This shows that the proposed DOGWO algorithm performed well in both exploitation and exploration. Its exploitation ability helped to converge to the optimum and the exploration ability assisted with local optima avoidance. The DOGWO also had very competitive optimization ability with high calculation precision and strong robustness for these test functions. It should be mentioned that the enhanced performance of DOGWO took advantages of the dynamic generalized opposition-based learning strategy, as the DGOBL strategy enhanced the population diversity, assisted the algorithm to explore more promising regions of the search space, and helped with local optima avoidance. For F6 and F12, ALO achieved a better calculation value than DOGWO; ABC showed better performance for F13. However, DOGWO presented a promising performance for the majority of the benchmark functions. Hence, a conclusion can be easily drawn that the DOGWO has a great potential for solving diverse optimization problems from the results in Table 3.
Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 show the convergence curves of F1–F12, F14, F19, and F23. Red and blue asterisked dotted curves were plotted by DOGWO and GWO. Brown, green, and cyan-dotted curves were drawn by ABC, BA, and PSO, respectively. From these figures, it was demonstrated that DOGWO converged rapidly towards the optimum and exploited the optimum accurately for most of benchmark functions. It can also be concluded from the figures that DOGWO had a faster convergence rate and a better calculation precision in contrast to other algorithms. Moreover, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27, Figure 28, Figure 29, Figure 30, Figure 31 and Figure 32 depict the box plot of ANOVA tests of global optimum for F1–F12, F14, and F21. It can be easily determined that the fluctuate of global optimum of DOGWO was much smaller than other algorithms for most test functions, and the number of outlier was less than other algorithms. This suggests that the proposed DOGWO exhibited strong stability and robustness.
Furthermore, another test was conducted to draw the search history of search agents by which we could easily perceive the search process of DOGWO. Note that the search population number was 10 and the figures were drawn after 500 iterations. It can be observed from Figure 33 that the search agents of DOGWO tended to extensively search for promising regions of the search space and exploit the best solution. We found that most of candidate search agents were concentrated in the optimum area and other search agents were evenly dispersed in various regions of the search space. Hence, it can be stated that DOGWO had a strong ability of searching for the global optimum and avoiding the local optimum.
5. Conclusions and Future Works
This paper presents a novel GWO algorithm known as DOGWO through the use of a dynamic generalized opposition-based learning strategy (DGOBL). The DGOBL may enhance the likelihood of finding better solutions by transforming the fixed search space to a dynamic search space. The strategy also enhances the diversity of a search population which can accelerate the convergence speed, improve the calculation precision, and avoid local optima to some extent. From the results of the 23 benchmark functions, the proposed DOGWO outperformed other optimization algorithms mentioned in this paper on most benchmark functions and was comparable with partial functions. DOGWO exhibited a fast convergence speed, high precision, and a relatively high robustness and stability.
In the future, there remain questions that need to be addressed. To further test the performance of the proposed algorithm, its application to a well-known NP-hard problem, namely the resource constrained project scheduling problem (RCPSP), could be investigated. Moreover, the proposed algorithm could be applied to various practical engineering design problems, such as optimal task scheduling in cloud environments.
Acknowledgments
This work is supported by the National Science Foundation of China under Grants No. 61274025 and the Program for Youth Talents of Institute of Acoustics, Chinese Academy of Sciences No: QNYC201622. Special thanks to reviewers and editors for their constructive suggestions and work.
Author Contributions
Y.X. designed the algorithm, performed the experiments, and made the analysis; D.W. contribute materials and analysis tools; L.W. provided suggestions about both the algorithm and the experiment.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Blum, C.; Aguilera, M.J.B.; Roli, A.; Sampels, M. Hybrid Metaheuristics, an Emerging Approach to Optimization; Springer: Berlin, Germany, 2008. [Google Scholar]
- Raidl, G.R.; Puchinger, J. Combining (Integer) Linear Programming Techniques and Metaheuristics for Combinatorial Optimization; Springer: Berlin/Heidelberg, Germany, 2008; pp. 31–62. [Google Scholar]
- Blum, C.; Cotta, C.; Fernández, A.J.; Gallardo, J.E.; Mastrolilli, M. Hybridizations of Metaheuristics with Branch & Bound Derivates; Springer: Berlin/Heidelberg, Germany, 2008; pp. 85–116. [Google Scholar]
- D’Andreagiovanni, F. On Improving the Capacity of Solving Large-scale Wireless Network Design Problems by Genetic Algorithms. In Applications of Evolutionary Computation. EvoApplications. Lecture Notes in Computer Science; Di Chio, C., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6625, pp. 11–20. [Google Scholar]
- D’Andreagiovanni, F.; Krolikowski, J.; Pulaj, J. A fast hybrid primal heuristic for multiband robust capacitated network design with multiple time periods. Appl. Soft. Comput. 2015, 26, 497–507. [Google Scholar] [CrossRef]
- Egea, J.A.; Banga, J.R. Extended ant colony optimization for non-convex mixed integer nonlinear programming. Comput. Oper. Res. 2009, 36, 2217–2229. [Google Scholar]
- Bianchi, L.; Dorigo, M.; Gambardella, L.M.; Gutjahr, W.J. A survey on optimization metaheuristics for stochastic combinatorial optimization. Nat. Comput. 2009, 8, 239–287. [Google Scholar] [CrossRef]
- Cornuéjols, G. Valid inequalities for mixed integer linear programs. Math. Program. 2008, 112, 3–44. [Google Scholar] [CrossRef]
- Murty, K.G. Nonlinear Programming Theory and Algorithms: Nonlinear Programming Theory and Algorithms, 3rd ed.; Wiley: New York, NY, USA, 1979. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley Publishing Company: Boston, MA, USA, 1989; pp. 2104–2116. [Google Scholar]
- Simon, D. Biogeography-Based Optimization. IEEE Trans. Evolut. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Połap, D.; Woz´niak, M. Polar Bear Optimization Algorithm: Meta-Heuristic with Fast Population Movement and Dynamic Birth and Death Mechanism. Symmetry 2017, 9, 203. [Google Scholar] [CrossRef]
- Bertsimas, D.; Tsitsiklis, J. Simulated Annealing. Stat. Sci. 1993, 8, 10–15. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi, P.H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Intell. Inf. Manag. 2012, 4, 390–395. [Google Scholar] [CrossRef]
- Farahmandian, M.; Hatamlou, A. Solving optimization problem using black hole algorithm. J. Comput. Sci. Technol. 2015, 4, 68–74. [Google Scholar] [CrossRef]
- Kaveh, A.; Khayatazad, M. A new meta-heuristic method: Ray Optimization. Comput. Struct. 2012, 112–113, 283–294. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant Colony Optimization. IEEE Comput. Intell. Mag. 2007, 1, 28–39. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Yang, X.S. Firefly Algorithms for Multimodal Optimization. Mathematics 2010, 5792, 169–178. [Google Scholar]
- Yang, X.S. A New Metaheuristic Bat-Inspired Algorithm. Comput. Knowl. Technol. 2010, 284, 65–74. [Google Scholar]
- Yang, X.S.; Deb, S. Cuckoo Search via Levy Flights. In Proceedings of the World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Cuevas, E.; Cienfuegos, M.; Zaldívar, D. A swarm optimization algorithm inspired in the behavior of the social-spider. Expert Syst. Appl. 2014, 40, 6374–6384. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Mirjalili, S. The Ant Lion Optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Shayeghi, H.; Asefi, S.; Younesi, A. Tuning and comparing different power system stabilizers using different performance indices applying GWO algorithm. In Proceedings of the International Comprehensive Competition Conference on Engineering Sciences, Iran, Anzali, 8 September 2016. [Google Scholar]
- Mohanty, S.; Subudhi, B.; Ray, P.K. A Grey Wolf-Assisted Perturb & Observe MPPT Algorithm for a PV System. IEEE Trans. Energy Conv. 2017, 32, 340–347. [Google Scholar]
- Hameed, I.A.; Bye, R.T.; Osen, O.L. Grey wolf optimizer (GWO) for automated offshore crane design. In Proceedings of the IEEE Symposium Series on Computational Intelligence (SSCI), Athens, Greece, 6–9 December 2017. [Google Scholar]
- Siavash, M.; Pfeifer, C.; Rahiminejad, A. Reconfiguration of Smart Distribution Network in the Presence of Renewable DG’s Using GWO Algorithm. IOP Conf. Ser. Earth Environ. Sci. 2017, 83, 012003. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M.; Grosan, C. Experienced Grey Wolf Optimizer through Reinforcement Learning and Neural Networks. IEEE Trans. Neural Netw. Learn. 2018, 29, 681–694. [Google Scholar] [CrossRef] [PubMed]
- Zawbaa, H.M.; Emary, E.; Grosan, C.; Snasel, V. Large-dimensionality small-instance set feature selection: A hybrid bioinspired heuristic approach. Swarm. Evol. Comput. 2018. [Google Scholar] [CrossRef]
- Faris, H.; Aljarah, I.; Al-Betar, M.A. Grey wolf optimizer: A review of recent variants and applications. Neural Comput. Appl. 2017, 22, 1–23. [Google Scholar] [CrossRef]
- Rodríguez, L.; Castillo, O.; Soria, J. A Fuzzy Hierarchical Operator in the Grey Wolf Optimizer Algorithm. Appl. Soft Comput. 2017, 57, 315–328. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M.; Hassanien, A.E. Binary Grey Wolf Optimization Approaches for Feature Selection. Neurocomputing 2016, 172, 371–381. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M. Impact of chaos functions on modern swarm optimizers. PLoS ONE 2016, 11, e0158738. [Google Scholar] [CrossRef] [PubMed]
- Kohli, M.; Arora, S. Chaotic grey wolf optimization algorithm for constrained optimization problems. J. Comput. Des. Eng. 2017, 1–15. [Google Scholar] [CrossRef]
- Malik, M.R.S.; Mohideen, E.R.; Ali, L. Weighted distance Grey wolf optimizer for global optimization problems. In Proceedings of the 18th IEEE/ACIS International Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing (SNPD), Kanazawa, Japan, 26–28 June 2017; pp. 1–6. [Google Scholar]
- Heidari, A.A.; Pahlavani, P. An efficient modified grey wolf optimizer with Lévy flight for optimization tasks. Appl. Soft Comput. 2017, 60, 115–134. [Google Scholar] [CrossRef]
- Mittal, N.; Sohi, B.S.; Sohi, B.S. Modified Grey Wolf Optimizer for Global Engineering Optimization. Appl. Comput. Intell. Soft Comput. 2016, 4598, 1–16. [Google Scholar] [CrossRef]
- Muro, C.; Escobedo, R.; Spector, L. Wolf-pack (Canis lupus) hunting strategies emerge from simple rules in computational simulations. Behav. Process. 2011, 88, 192–197. [Google Scholar] [CrossRef] [PubMed]
- Tizhoosh, H.R. Opposition-based learning: A new scheme for machine intelligence. In Proceedings of the International Conference on Computation Intelligence on Modeling Control Automation and International Conference on Intelligent Agents, Web Technologies Internet Commerce, Vienna, Austria, 28–30 November 2005; pp. 695–701. [Google Scholar]
- Rahnamayan, S.; Tizhoosh, H.R.; Salama, M.M.A. Opposition-based differential evolution algorithms. In Proceedings of the IEEE Congress on Evolutionary Computation, Vancouver, BC, Canada, 16–21 July 2006; pp. 2010–2017. [Google Scholar]
- Rahnamayan, S.; Tizhoosh, H.R.; Salama, M.M.A. Opposition-based differential evolution for optimization of noisy problems. In Proceedings of the IEEE Congress on Evolutionary Computation, Vancouver, BC, Canada, 16–21 July 2006; pp. 1865–1872. [Google Scholar]
- Wang, H.; Li, H.; Liu, Y.; Li, C.; Zeng, S. Opposition based particle swarm algorithm with Cauchy mutation. In Proceedings of the IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 4750–4756. [Google Scholar]
- Rahnamayan, S.; Tizhoosh, H.R.; Salama, M.M.A. Opposition-based differential evolution. IEEE Trans. Evol. Comput. 2008, 2, 64–79. [Google Scholar] [CrossRef]
- Haiping, M.; Xieyong, R.; Baogen, J. Oppositional ant colony optimization algorithm and its application to fault monitoring. In Proceedings of the 29th Chinese Control Conference (CCC), Beijing, China, 29–31 July 2010; pp. 3895–3903. [Google Scholar]
- Lin, Z.Y.; Wang, L.L. A new opposition-based compact genetic algorithm with fluctuation. J. Comput. Inf. Syst. 2010, 6, 897–904. [Google Scholar]
- Shaw, B.; Mukherjee, V.; Ghoshal, S.P. A novel opposition-based gravitational search algorithm for combined economic and emission dispatch problems of power systems. Int. J. Electr. Power Energy Syst. 2012, 35, 21–33. [Google Scholar] [CrossRef]
- Wang, S.W.; Ding, L.X.; Xie, C.W.; Guo, Z.L.; Hu, Y.R. A hybrid differential evolution with elite opposition-based learning. J. Wuhan Univ. (Nat. Sci. Ed.) 2013, 59, 111–116. [Google Scholar]
- Zhao, R.X.; Luo, Q.F.; Zhou, Y.Q. Elite opposition-based social spider optimization algorithm for global function optimization. Algorithms 2017, 10, 9. [Google Scholar] [CrossRef]
- Wang, H.; Wu, Z.; Liu, Y. Space transformation search: A new evolutionary technique. In Proceedings of the First ACM/SIGEVO Summit on Genetic and Evolutionary Computation Conference, Shanghai, China, 12–14 June 2009; pp. 537–544. [Google Scholar]
- Wang, H.; Wu, Z.; Rahnamayan, S. Enhancing particle swarm optimization using generalized opposition-based learning. Inf. Sci. 2011, 181, 4699–4714. [Google Scholar] [CrossRef]
- Wang, H.; Rahnamay, S.; Wu, Z. Parallel differential evolution with self-adapting control parameters and generalized opposition-based learning for solving high-dimensional optimization problems. J. Parallel Distrib. Comput. 2013, 73, 62–73. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).