Modified Cuckoo Search Algorithm with Variational Parameters and Logistic Map

Abstract

Cuckoo Search (CS) is a Meta-heuristic method, which exhibits several advantages such as easier to application and fewer tuning parameters. However, it has proven to very easily fall into local optimal solutions and has a slow rate of convergence. Therefore, we propose Modified cuckoo search algorithm with variational parameter and logistic map (VLCS) to ameliorate these defects. To balance the exploitation and exploration of the VLCS algorithm, we not only use the coefficient function to change step size $\alpha$ and probability of detection $p_a$ at next generation, but also use logistic map of each dimension to initialize host nest location and update the location of host nest beyond the boundary. With fifteen benchmark functions, the simulations demonstrate that the VLCS algorithm can over come the disadvantages of the CS algorithm.In addition, the VLCS algorithm is good at dealing with high dimension problems and low dimension problems.

1. Introduction

Optimization problems are prevalent in society, such as profit maximization, minimum error, and so on [1,2]. To solve this kind of problems, many Meta-heuristic algorithms have been proposed, such as genetic algorithms (GA) [3,4,5], tabu search [6,7,8], simulated annealing [9,10,11], particle swarm optimization [12,13,14], ant colony optimization [15,16,17], etc. Cuckoo search (CS) [18] is inspired by nature, which is a concise method and easy to implement. Cuckoo search is widely used in the real world. For example, Shair et al. [19] developed a new approach which is CS algorithm in cutting stock problem. Medjahed et al. [20] proposed a new framework for band selection problem based on binary cuckoo search. However, CS method is not perfect, the main drawbacks being it easily falls into the local optimal solution and the slow rate of convergence [21]. Li and Yin [22] used self adaptive parameter method to improve CS. Wang et al. [23] presented a novel cuckoo search based on chaos theory and elitism. Huang et al. [24] proposed a Chaos-enhanced cuckoo search that use logistic map to ameliorate CS. Liu and Fu [25] proposed a cuckoo search algorithm based on frog leaping local search and chaos theory. Zheng and Zhou [26] used Gaussian distribution to initiate the CS algorithm, which only considered the initial part was not comprehensive. Li and Cao [27] used a DE algorithm and a CS algorithm to propose a new hybrid optimization algorithm. These algorithms actually have some improvement; however, some of the them make the CS become difficult to implement, while others increase the complexity of the CS. Therefore, many future studies are necessary to develop new effective cuckoo search algorithms for optimization problems [22].

Chiroma et al. [28] found that the population reduction and usage of biased random walk are the most frequently used modifications. To improve the CS algorithm, this paper chooses a different method. This paper proposes modified cuckoo search algorithm with variational parameters and logistic sequences (VLCS). VLCS uses logistic map of each dimension to initialize host nest location and update the location of host nest beyond the boundary, which can guarantee that the location of the nest is only calculated once. VLCS also uses coefficient function to change $\alpha$ and $p_a$ at next generation, which greatly accelerates the convergence rate.

The rest of this paper is organized as follows. Section 2 describes the CS algorithm and analyzes the defects of CS algorithm. Section 3 proposes the corresponding solution for the drawbacks of CS algorithm and the VLCS algorithm. Simulation experiments are presented in Section 4. Finally, conclusions are presented in Section 5.

2. Preliminary

2.1. Cuckoo Search Algorithm

Some cuckoos have an aggressive and complicated reproduction strategy. Yang and Deb imitated the strategy and proposed the CS algorithm. The CS [18] obeys three rules: (1) Each cuckoo lays one egg at a time, and dumps its egg in randomly chosen nest. (2) The best nests with high quality of eggs will carry over to the next generations. (3) The number of available host nests is fixed, and the egg laid by a cuckoo is discovered by the host bird with a probability $p_a$∈ [0, 1]. Based on these rules, the pseudo code of CS is shown in Algorithm 1.

Algorithm 1: Cuckoo Search via Lévy Flights

2.2. The Disadvantages of the Cuckoo Search Algorithm

Cuckoo search algorithm has three major drawbacks.

• Initialization
  Cuckoo search algorithm uses the random number to initiate these location of nests. Sometimes, the location of these nests will be the same, and sometimes the location of these nests are not properly dispersed in a defined area. Therefore, it causes repeated calculations and the easy chance to fall into local optimal solution [24].
• Parameters $\alpha$ and $p_a$
  In most cases, Yang and Deb used $\alpha =O(L/10)$ or $\alpha =O(L/100)$, where L is the characteristic scale of the problem of interest [29]. Yang and Deb also suggested $p_a$ = 0.25 [18]. In other words, $\alpha$ and $p_a$ are fixed number. The properties of the two parameters are the shortcomings of the algorithm, because $p_a$ and $\alpha$ should be changed with the progress of iterator, when CS algorithm search a local optimal solution and the global optimal solution.
• Boundary issue
  CS algorithm uses Lévy flights and random walk to find nest location [18,30]. The locations of some nests may be out of the boundary; when this happens CS algorithm uses the boundary value to replace these location. The bound dealing method will result in a lot of nests at the same location on the boundary, which is inefficient.

3. Modified Cuckoo Search Algorithm: VLCS

This section puts forward the corresponding solution for the drawbacks of the CS algorithm.

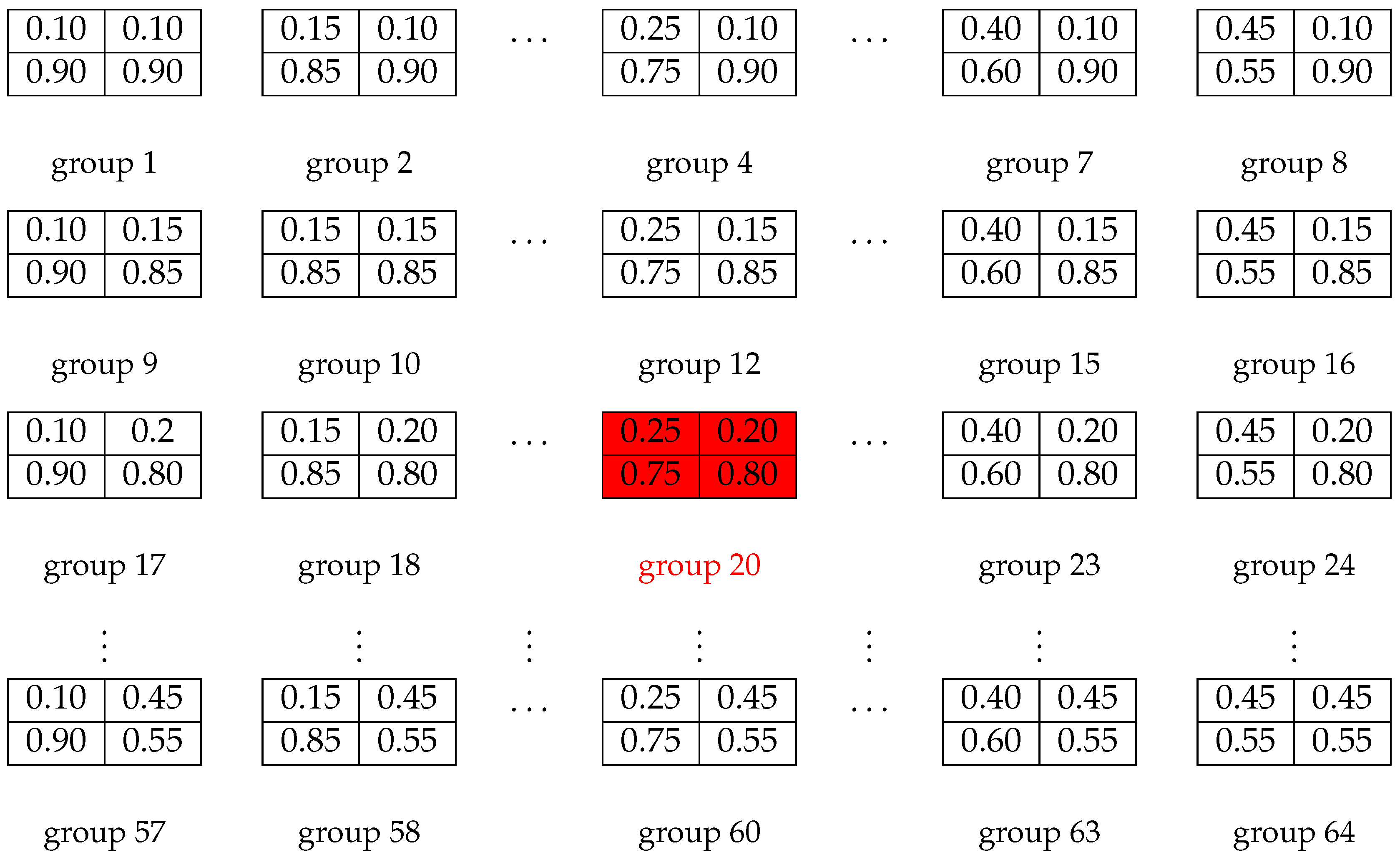
3.1. Nest Location of Each Host Are Initialized by Logistic Map of Each Dimension

In this paper, the nest location of each host is initialized by logistic map of each dimension for four reasons. Firstly, the location $x_d$ is found by the logistic map and will not repeat. This means that the speed of convergence can be accelerated. Secondly, logistic map is simple and easy to implement. Thirdly, logistic map is easy to embed into every part of the CS algorithm. Fourthly, since each dimension requires a chaotic map, using other chaotic maps will increase the complexity of the CS algorithm. Logistic map [31] is defined as:

$$x_{n+1}=\mu x_n(1-x_n),n=0,1,2,3,\dots$$

(1)

where $x_n\in (0,1)$, the control parameter $\mu \in [0,4]$ and n represents the n-th iteration. Chaos phenomenon occurs when $\mu =4$ [32]. The pseudo code of initialization is shown in Algorithm 2.

Algorithm 2: Nest location of each host is initialized by logistic map of each dimension

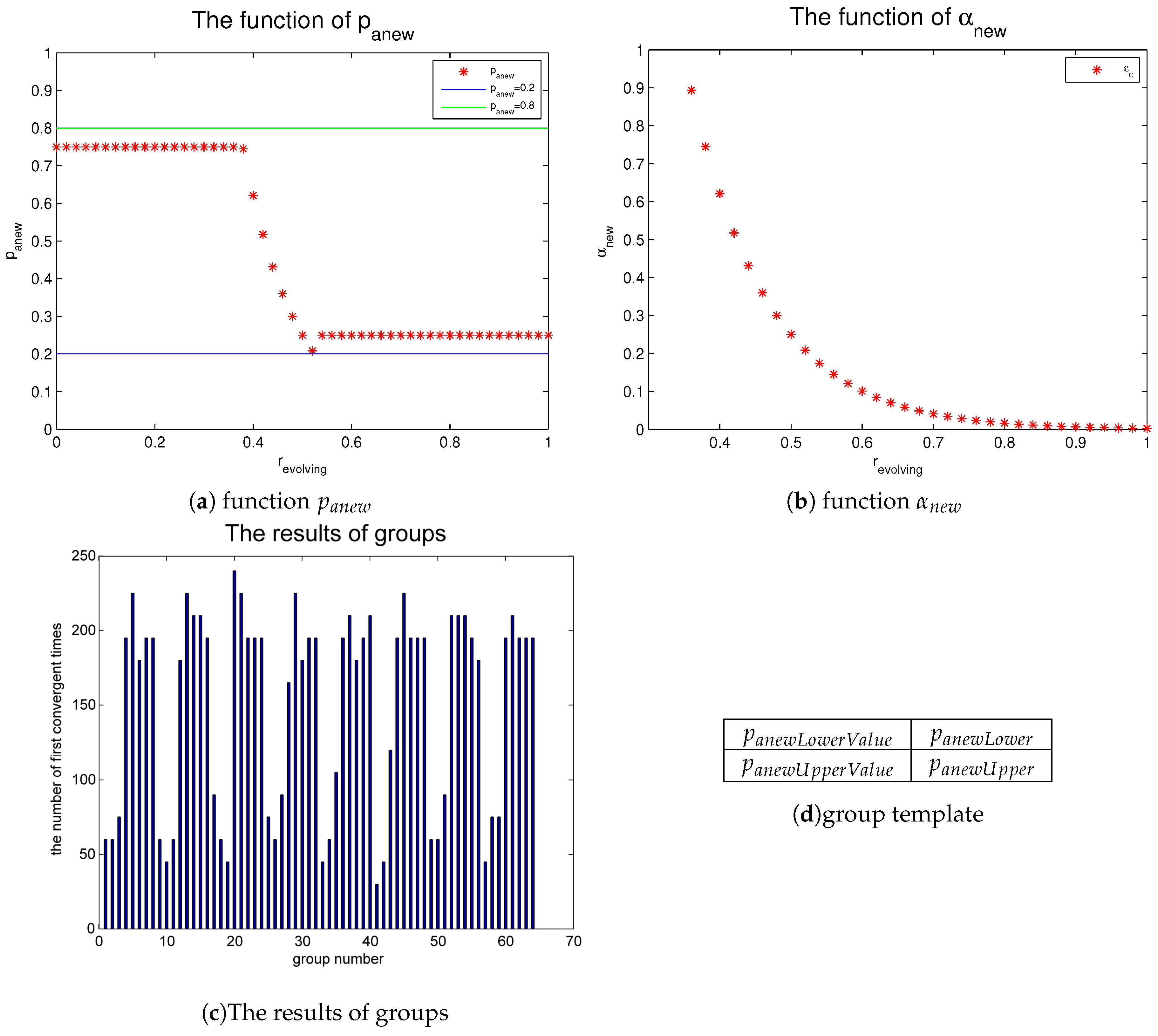
3.2. Step Size and $p_a$ Are Changed by Coefficient Function

This article uses the coefficient function to overcome the second disadvantage in Section 2. The coefficient function [33] is defined as:

$${\epsilon }_{\alpha }={10}^{(10\ast tan(arctan(0.2)\ast (2\ast r_{evolving}-1)))}$$

(2)

$$r_{evolving}=cur\_iteration/total\_iteration$$

(3)

In Equation (3), the cur_iteration means the current number of iteration and the total_iteration means the total number of iteration. The coefficient function in Equation (2) is used to adjust $\alpha$ and $p_a$ (Equation (4)).

$$\begin{array}{cc}\hfill {\alpha }_{new}& =\alpha /{\epsilon }_{\alpha }\hfill \\ \hfill p_{anew}& =\left\{\begin{array}{cc}{p}_{anewLowerValue}\hfill & \mathrm{if}{p}_{\alpha }/\epsilon <p_{anewLower}\hfill \\ p_{anewUpperValue}\hfill & \mathrm{else}\mathrm{if}{p}_{\alpha }\epsilon >p_{anewUpper}\hfill \\ p_{\alpha }/\epsilon \hfill & \mathrm{else}\hfill \end{array}\right.\hfill \end{array}$$

(4)

$p_{anewLowerValue}\in (0,1)$, $p_{anewLower}\in (0,1)$, $p_{anewUpperValue}\in (0,1)$ and $p_{anewUpper}\in (0,1)$. To find the optimal parameters, this paper use a template to group parameters and set the change size to 0.5. The template shown in Figure 1d and groups shown in

Table 1. Parameters groups.

. In Table 1, each row changes $p_{anewLowerValue}$ and $p_{anewUpperValue}$, and each column changes $p_{anewLower}$ and $p_{anewUpper}$. This paper selects $\alpha =1$ and $p_a=0.25$, which are mentioned by Yang and Deb [18] and recent literature [28]. With functions of

Table 2. benchmark function.

Test Function	Dimension	Range	Optimum
$f_{01}={\sum }_{i=1}^d{x}_i^2$	15	$x_i\in [-5.12,5.12]$	0
$f_{02}=-cos(x)cos(y)exp[-{(x-\pi )}^2-{(y-\pi )}^2]$	2	$x,y\in [-100,100]$	−1
$f_{03}={\sum }_{i=1}^{n-1}[100{(x_{i+1}-x_i^2)}^2+{(x_i-1)}^2]$	15	$x\in [-5,5]$	0
$f_{03}=-{\sum }_{i=1}^{5}cos[(i+1)x+1]{\sum }_{i=1}^{5}cos[(i+1)y+1]$	2	$x,y\in [-10,10]$	−186.7309
$f_{04}=\frac{1}{4000}{\sum }_{i=1}^d{x}^2-{\prod }_{i=0}^{d}cos(\frac{x_i}{\sqrt{i}})+1$	15	$x\in [-600,600]$	0
$f_{05}=\begin{array}{c}-20exp[-20\sqrt{\frac{1}{d}{\sum }_{i=1}^d{x}_i^2}]\hfill \\ -exp[\frac{1}{d}{\sum }_{i=1}^{d}cos(2\pi x_i)]+(20+e)\hfill \end{array}$	15	$x\in [-32.768,32.768]$	0
$f_{06}={\sum }_{i=1}^{d-1}[{(1-x_i)}^2+100{(x_{i+1}-x_i^2)}^2]$	16	$x\in [-10,10]$	0
$f_{07}={\sum }_{i=1}^d[-x_{i}sin(\sqrt{|x_i|})]$	10	$x\in [-500,500]$	−4189.829
$f_{08}=10d+{\sum }_{i=1}^d[x_i^2-10cos(2\pi x_i)]$	10	$x\in [-5.12,5.12]$	0
$f_{09}=-{\sum }_{i=1}^{d}sin(x_i){[sin(\frac{i{x}_i^2}{\pi })]}^{2m}$	5	$m=10,x\in [0,\pi ]$	−4.6877
$f_{10}=10\ast d+{\sum }_{i=1}^d(x_i^2-10cos(2\pi x_i))$	20	$x\in [-10,10]$	−654.6
$f_{11}={\sum }_{i=1}^d{({\sum }_{j=1}^i{x}_j)}^2$	30	$x\in [-100,100]$	0
$f_{12}={\sum }_{i=1}^d{(x_i+0.5)}^2$	30	$x\in [-100,100]$	0
$f_{13}={\sum }_{i=1}^{d}i{x}_i^4+random[0,1)$	30	$x\in [-1.28,1.28]$	0
$f_{14}={\sum }_{i=1}^d[x_i^2-10cos(2\pi x_i)+10]$	30	$x\in [-5.12,5.12]$	0
$f_{15}={(x_2-\frac{5.1}{4{\pi }^2}{x}_1^2+\frac{5}{\pi }-6)}^2+10(1-\frac{1}{8\pi })cos{x}_1+10$	2	$x_1,x_2\in [-5,15]$	0.398

, we did 9600 experiments, and the results are shown in Figure 1c. Then, we selects the optimal parameters from those experiments, which are red group 20 in Table 1. These parameters are $p_{anewLowerValue}=0.25$, $p_{anewLower}=0.2$, $p_{anewUpperValue}=0.75$ and $p_{anewUpper}=0.8$. Then, these values are used to draw Figure 1a. In Figure 1a, at the beginning of the $r_{evolving}$, the $p_{anew}=0.75$ can guarantee that the VLCS algorithm can jump out of the local optimal solution. At middle of the $r_{evolving}$, the change value of $p_{anew}$ can improve the convergence rate. At the end of the $r_{evolving}$, the $p_{anew}=0.25$ can guarantee the accuracy of the VLCS algorithm convergence. In Figure 1b, the interval of ${\alpha }_{new}$ decreases as $r_{revolving}$ increases. The ${\alpha }_{new}$ replaces the fixed step size of $\alpha$ and the $p_{anew}$ replaces the fixed $p_a$, which accelerate convergence of cuckoo search algorithm.

3.3. Boundary Is Constrained by Logistic Map of Each Dimension

For the boundary issue, the paper also uses the global random number r, which is changed by logistic map.The reason for using logistic map is the same as in Section 3.1. Algorithms 2 and 3 use the same r. This r can guarantee that the location of each nest is calculated only once.That means the r reduces repeated calculations and accelerates the convergence process. The pseudo code of boundary processing is shown in Algorithm 3.

Algorithm 3: Boundary is constrained by logistic map of each dimension

3.4. Proposed VLCS algorithm

This paper proposes VLCS algorithm to balance the exploitation and exploration. The VLCS algorithm uses logistic map of each dimension to handle global random $\mathit{r}$, which is used in initiation and boundary issue. Logistic map can guarantee that the location of each nest will only be calculated once. The VLCS algorithm uses ${\alpha }_{new}$ and $p_{anew}$ to replace the fixed parameters of the CS algorithm and improve the performance of CS algorithm. The pseudo code of VLCS algorithm is shown in Algorithm 4.

Algorithm 4: VLCS algorithm

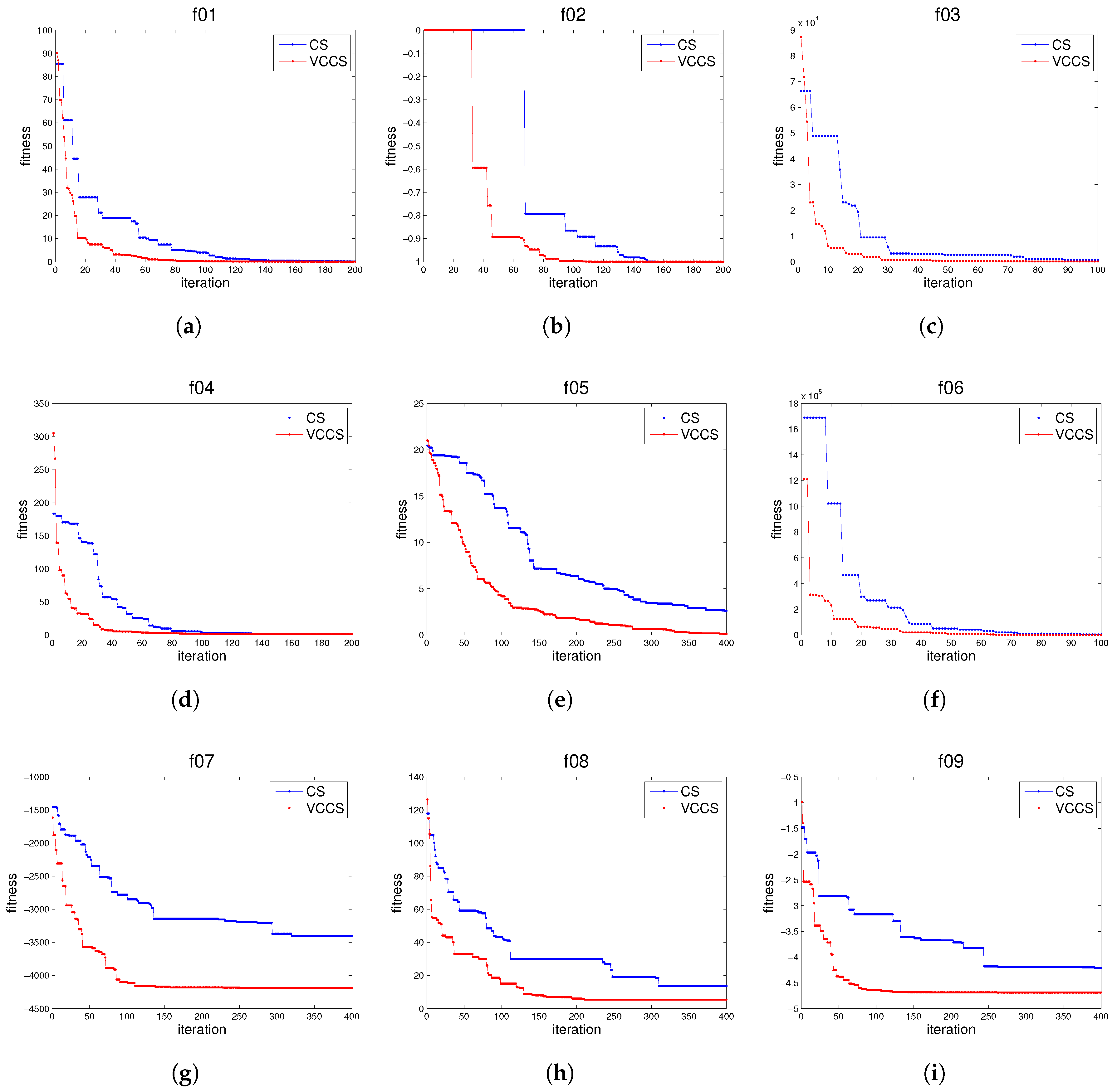
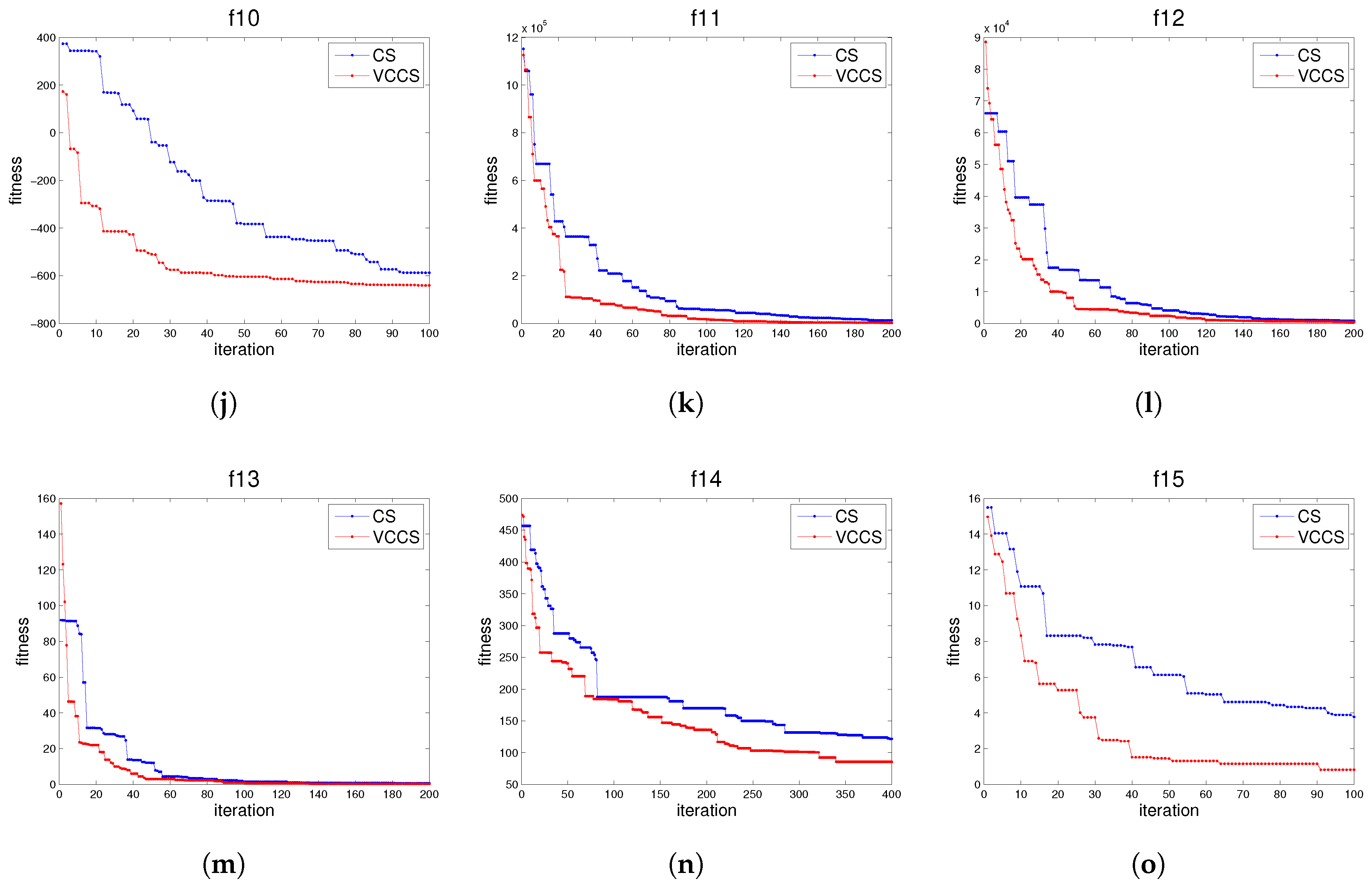
4. Simulation Experiments

This paper selects 15 benchmark functions [34,35,36] to prove that the VLCS algorithm is better than the CS algorithm.The simulation environment is Matlab R2014a. The ${\alpha }_{new}$ and $p_{anew}$ are shown in Equation (4). The benchmark functions and conditions are shown in Table 2. In Table 2, the dimensions of f02, f08 and f15 are two, and the others’ dimensions are not less than ten. To compare with other algorithms, the nest number of n is 15 [18,24]. If the number of nest is changed, the relative convergence rates of the VLCS algorithm and the CS algorithm do not change. Of course, if n is increased, the VLCS algorithm and the CS algorithm will converge faster than other meta-heuristic algorithms. The CS [18] was proposed by Xin She Yang, who has already attested that it is better than other meta-heuristic algorithms. Section 3.1 illustrates the benefits of logistic map. Most of modified CS algorithms are mainly focused on choosing chaotic maps (e.g., [23,24,25]). These studies do not mention how to reduce repeated calculation in each dimension. This means the VLCS algorithm converges faster than most of other modified CS algorithms, because the VLCS algorithm uses logistic map of each dimension to initialize host nest location and update the location of host nest beyond the boundary. Therefore, this paper compares the CS algorithm and the VLCS algorithm, and shows the results in Figure 2. There is little difference between the VLCS algorithm and the CS algorithm in the function f04, f13 and f14 because the three functions are simpler than other functions in Figure 2 and do not need to carry out complex calculations. From the results, f07, f08, f09, f10 and f14 show two things clearly. Firstly, the convergence speed of the VLCS algorithm is faster than the CS algorithm, because, at the middle of the iteration, the CS algorithm easily falls into the local optimal solution and needs time to jump out of the local optimal solution. Secondly, the convergence accuracy of the VLCS algorithm is better than the CS algorithm because the VLCS algorithm does not do redundant calculations in the same place, even in the same dimension. Actually, if the other pictures in Figure 2 are enlarged, it is easy to get the same conclusion. The VLCS algorithm solves the three disadvantages of the CS algorithm mentioned in Section 2.2. In addition, Table 2 contains high-dimensional and low-dimensional test functions. This means the VLCS algorithm applies not only to low-dimensional problems but also to high-dimensional problems.

5. Conclusions

In this paper, the VLCS algorithm consists of coefficient function, the standard CS algorithm and each dimension with one logistic map. The logistic map is used to handle the initial problem and boundary issue. Using the logistic map guarantees to reduce the complexity of the VLCS algorithm and improve the computational efficiency. The reasons are analyzed in Section 3.1. The coefficient function is used to calculate ${\alpha }_{new}$ and $p_{anew}$. The coefficient function is used to change ${\alpha }_{new}$ and $p_{anew}$ when the iteration increases. That is why the VLCS algorithm not only can reduce repeated calculation, but also can accelerate the speed of convergence. Furthermore, the VLCS algorithm can prevent itself from falling into a local optimum. The coefficient function is analyzed in Section 3.2. After the analysis of Section 4 simulation experiments, the VLCS algorithm is good at dealing with high dimension problems and low dimension problems.

In the future, we will come up with a more precise way to deal with $\alpha$ and $p_a$ and use the VLCS algorithm to solve other practical engineering problems and real-world problems such as image hiding, power distribution, AODV routing protocol and so on. We believe that the VLCS will promote the development of the algorithm and be very useful in real-world problems.