Abstract
Cognitive radio is a promising technology for improving spectrum utilization, which allows cognitive users access to the licensed spectrum while primary users are absent. In this paper, we design a resource allocation framework based on graph theory for spectrum assignment in cognitive radio networks. The framework takes into account the constraints that interference for primary users and possible collision among cognitive users. Based on the proposed model, we formulate a system utility function to maximize the system benefit. Based on the proposed model and objective problem, we design an improved ant colony optimization algorithm (IACO) from two aspects: first, we introduce differential evolution (DE) process to accelerate convergence speed by monitoring mechanism; then we design a variable neighborhood search (VNS) process to avoid the algorithm falling into the local optimal. Simulation results demonstrate that the improved algorithm achieves better performance.
1. Introduction
With the development of wireless technology, the massive growth of wireless products increases the demand for spectrum resources [1]. The fixed spectrum allocation policy limits the utilization of aspectrum that is one of the non-renewable natural resources, which leads to underutilization for a licensed spectrum and overutilization for unlicensed bands [2,3]. According to a report by the Federal Communications Commission [4], the spatial and temporal variations in the licensed spectrum utilization range from 15 to 85%. Therefore, achieving high utilization for licensed bands is one of the most critical approaches to solving the spectrum-scarcity problem in the next generation wireless systems. Cognitive radio (CR) [5] is a promising technology for dynamic spectrum management, which can achieve better exploitation for spectrum resources. CR is able to intelligently detect ‘spectrum holes’ (which means available licensed spectrum) and effectively allocate them to cognitive users (who can also be named as secondary users or unlicensed users) in accordance with the distribution objective. The main objective of spectrum allocation is to maximize spectrum utilization while avoiding the possible interference to authorized users (who are referred to as primary users). Thus, how to perform spectrum allocation to achieve maximization objectives while guarantee fairness constraints for cognitive users and interference constraints for primary users become the main question in dynamic spectrum assignment.
To address the spectrum allocation problem, we need to formulate a framework to guarantee interference protection for primary users and build a relationship among cognitive users. Scholars have done a lot of research about the mathematical model for spectrum allocation. In [6], Lu focuses on using bipartite graphs to solve the resource allocation problem, in which cognitive users and primary users are treated as two partite sets and an allocation scheme can be seen as a matching of the corresponding bipartite graph. A mathematical cross-layered model for the cognitive radio network link scheduling problem under the interference temperature model is presented in [7], which maximizes the number of scheduled links within a time frame while satisfying interference temperature constraints. In [8], Changyan integrates an auction model and Stackelberg game theory to deal with the different stage issues for spectrum sharing in CR networks. Game theory is adopted in [9] to reduce power waste caused by some cognitive users’ SINR over the target value. To maximize system utility in this paper, we perform spectrum allocation based on graph theory. However, the graph-theory-based allocation issue is a nondeterministic polynomial (NP) problem whose solution can be found in polynomial time on a non-deterministic machine. Intelligent optimization algorithms are effective methods to find a close-to-optimal solution for NP-hard issues.
In this paper, we adopt the ant colony optimization algorithm (ACO) for available licensed spectrum allocation. ACO [10] was first introduced by Dorigo in 1992, which is a popular means of dealing with assignment issues. The basic idea of ACO comes from the natural phenomena that ants can find the shortest path between nest and food efficiently due to their positive feedback attribute [11]. However, ACO is prone to being premature and stagnate when the problem scale is too big. These flaws would certainly drag the effectiveness of the algorithm down [12]. Based on the above, we design a novel spectrum allocation algorithm (IACO) based on ACO, which introduces the differential evolution (DE) [13] process to accelerates convergence speed by the monitoring mechanism, in addition, we employ a variable neighborhood search (VNS) process [14] to avoid falling into the local optimum. We can see from the simulation results that either the system utility or the other performance of IACO are greatly promoted.
2. System Model and Problem Formulation
In this framework, we consider the three matters of spectrum allocation issue as suggested in [15]: (a) possible interference to primary users; (b) collision with cognitive users; (c) system utility and the fairness of spectrum access. We build a graph-based mathematical model [16] to demonstrate the spectrum allocation problem, as shown in Figure 1, where represents the primary user who has the authority using a certain licensed spectrum channel, and denotes the cognitive user who can only access to ‘spectrum holes’ in an opportunistic manner. Each user has coverage area with radius or on channel m, where indicates the protection radius of the primary user p on channel m, whereas represents the interference radius of the cognitive user n with access to channel m. cannot access the licensed band that overlays with in some area to avoid interfering with primary user, meanwhile, any two cognitive users cannot use the same band if they overlap in some area to diminish collision with each other.
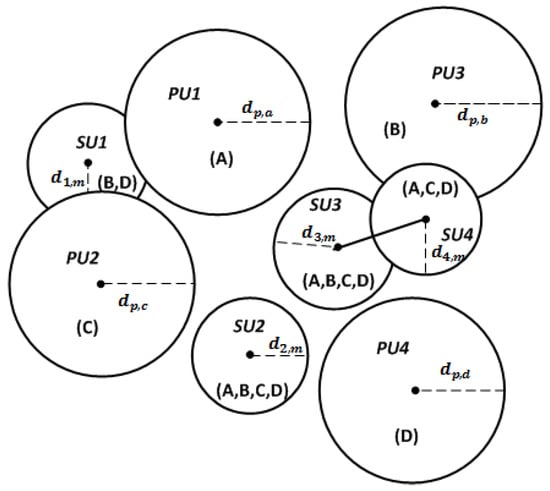
Figure 1.
Graph-based System Model.
We define a graph , where V is a set of vertices representing the cognitive users that compete for the licensed spectrum, E is a set of undirected edges between vertices denoting interference between any two vertices. For any two vertices , an edge exists between n and k if . The existence of the edge depends on the interference constraint C (see Section 2.1).
2.1. Matrices for Spectrum Allocation
Matrices Definition (See Table 1).

Table 1.
Matrices Definition.
Explanation for Matrices
- Available matrix L. The matrix represents the availability of licensed bands for cognitive users. If , user n can access spectrum m without interference to primary users, otherwise . As shown in Figure 1, spectrum channel B is available for , then .
- Benefit matrix B. The matrix indicates the benefit that a cognitive user gets by successful access to a licensed spectrum band, where only if .
- Interference matrix C. The three-axis matrix describes the interference relationship of any two vertices n and k when they access spectrum m. As shown in Figure 1, and overlap in some area, then , , .
- Allocation matrix A. The matrix is a spectrum allocation result which is interference free. If , cognitive user n can access spectrum m and transmission data in this band. A conflict free allocation needs to satisfy the interference constraints: .
- Degree matrix for cognitive users Z. The matrix represents the available spectrum number for each cognitive users. In Figure 1, .
- Degree ascending matrix K. The matrix is another representation of the available matrix, which incrementally orders the rows according to the degree matrix Z.
2.2. Problem Formulation and Measure Functions
Given the model above, we formulate the spectrum allocation problem by the following optimization function:
where is the set of interference free spectrum assignments for a given set of N cognitive users and M spectrum bands and constraints C.
There is always more than one allocation solution that would satisfy all the constraints. In order to choose the optimum solution in terms of different applications and measure the algorithm thoroughly, we use three different measure functions that already exist in the literature [17] to evaluate the solution.
- (1)
- Max-Sum-Reward-Mean (MSRM): This function is used to measure the average of total spectrum utilization in the system, which is the average of the sum user rewards.
- (2)
- Max-Proportional-Fair (MPF): The function is to measure the fairness among cognitive users accessing the spectrum in the system, which is driven by .
- (3)
- Max-Min-Reward (MMR): The function is to maximize the spectrum utilization at the bottleneck cognitive users who receive the lowest reward, which is a simple notion of fairness.
3. The IACO-Based Spectrum Allocation Method
3.1. The Basic Idea
In nature, ants usually find the shortest route paths from their nest to food efficiently even though obstacles exists in the path. It was found that there is an important medium used to communicate information among individuals regarding paths, and it is called the pheromone. On the one hand, a moving ant lays pheromone on the ground to mark the path, and the pheromone concentration on the path gets reinforced; on the other hand, the path with a greater concentration of pheromones will attract more ants to detect and select it with a greater probability. Based on the intelligence-ability of an ant colony, some scholars propose the ant colony optimization (ACO) algorithm and try to solve combinatorial optimization problems by mimicking the ants’ behavior [18].
ACO simulates the process of ants finding the shortest paths to obtain the close-to-optimal solution for NP-hard issues. The positive feedback mechanism is the drive of the algorithm, the process of which can be explained by two steps: first, each ant selects the path with the maximum pheromone concentration and releases its pheromone to this path while it moves; then, more ants are attracted to select the path. This not only accounts for the rapid discovery of good solutions but facilitates the process of finding the optimal solution.
However, ACO is slow to converge while problem scale is large, and also it is prone to be trapped in a local optimum in the later evolution. Based on these deficiencies of ACO, we design an improved ant colony optimization IACO for spectrum allocation, which employs DE and VNS for performance improvement. DE is a greedy genetic algorithm with retained thought, which evolves by mutation, crossover, and selection in the population. In this paper, we adopt DE to optimize the moving mode of the ants to improve the global convergence ability of the algorithm and maintain diversity of the population. Besides, VNS is a local search metaheuristic employing a set of neighborhood search methods to find the local optimum in each neighborhood iteratively and finally to reach the global optimum at the end. In this paper, we design a set of neighborhoods for VNS to improve the local searchability of the algorithm.
3.2. Transform for the Spectrum Allocation Problem
The graph-theoretic model based spectrum allocation problem is NP-hard, so we introduce the IACO to obtain the efficient assignment for cognitive users. We convert the assignment issue into the shortest paths finding in a special undirected graph using IACO, for example, the model in Figure 1 is transformed into an undirected graph (Figure 2d) by the transform process shown in Figure 2.
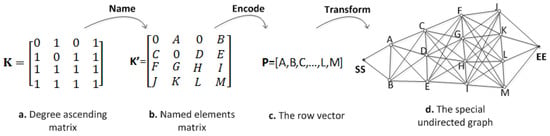
Figure 2.
Transform Process.
The transform process takes three steps: first, given the high computational complexity of resources allocation, IACO names only the non-zero elements in matrix K into binary sequences (the process of a to b in Figure 2); second, according to the row-major principle, we encode all letters into a row vector with the length of l that is the non-zero elements in K or (the process of b to c in Figure 2); third, based on the row vector P, we transform the letters into vertices of a special undirected graph except for the starting point and the ending point (the process of c to d in Figure 2). The ants move back and forth between to in the special graph to obtain the shortest paths (the optimal assignment scheme).
3.3. Differential Evolution Process in IACO
DE generate new individuals by cooperation and competition among populations to guide the direction for optimization searching. It is operated by three stochastic steps: mutation and crossover as well as selection. The DE process in IACO with l-dimensional space, and N is the number of individuals. In IACO, we use DE to generate a new individual to optimize the convergence speed. Specifically, we use the following steps to get the new individual of generation i. Firstly, mutate the population to get the variant :
where are three individuals randomly selected from current population, the mutation factor K is a real parameter in . We choose to mutation the population instead of [19]. Next, crossover is applied to generate vector by crossing element and variant with a certain probability, which is used to increase the diversity of the trial vector , as shown:
where is a uniform random number in , means crossover probability in and is a random quantity in . Finally, the new individual is selected from and based on the greedy thought, and the selection operation can be expressed as:
3.4. Variable Neighborhood Search Process in IACO
The DE-based ACO is a good way for seeking large search spaces. On the other hand, the combined algorithm has a weakness in which it fails to intensify the search in the promising area. Thus, we use VNS to enhance the local searchability of the improved algorithm. The VNS process in IACO has l-dimensional solution space, and is the set of neighborhood space for solution s. The process of VNS for local search is shown as follows:
Construct the neighborhood . The main objective of the improved algorithm is to maximize the spectrum utilization. To achieve this we first randomly choose a user , and get a benefit list according to matrix B, where m is the available channel number. Then, we assign the channel with the highest reward to user . Using this procedure, a new set of neighborhoods is constructed. Local search. In order to search around the initial solution s, we construct the neighborhood for local search. If the neighborhood search obtains a better fitness value, then the initial solution s is replaced by . Finally, the global optimum with the highest system utility is obtained after finishing the local search.
3.5. The Process and Description of IACO
The process of IACO-based spectrum allocation is described as below (see Algorithm 1):
Step 1: Initialization. Generate the initial vector and initialize pheromone of each path with (the edge between vertices is connected) or (the edge between vertices is available). Set the maximum evolution time , the maximum evolution time with low convergence speed , the number of population .
Step 2: Interference removal. The spectrum allocation scheme A must be interference free, and therefore A needs to satisfy the interference constraints from matrix C. Based on this, we would remove the interference-path to correct the solution. While A does not satisfy constraints defined by C, it is necessary to equiprobably set one value to 0.
Step 3: Fitness evaluation. Calculating fitness value is a way to convert binary sequence solutions into real space R, which can be expressed as: . Get the best path sequence and the highest fitness value .
Step 4: Monitor convergence rate. The monitoring mechanism is designed in IACO to detect the rate-of-change in fitness. If the growth rate stays slow and meets Equation (8) during , then turn to the 7th step to accelerate convergence speed of IACO by employing DE, otherwise, go to the 5th step for ACO traversing.
where is the fitness value of , is the evolution times, indicates the rate-of-change.
Step 5: Ants traversal. All ants move back and forth between the starting point and the ending point. As described below in Figure 3, spectrum allocation can be seen as row traversal, where row and column represent cognitive users and bands, respectively. In this row traversal, if the available channel number and , then band j is available for user i, that is to say node i in column j is visitable for ants, otherwise the ants skip the node. Then the evolution time .
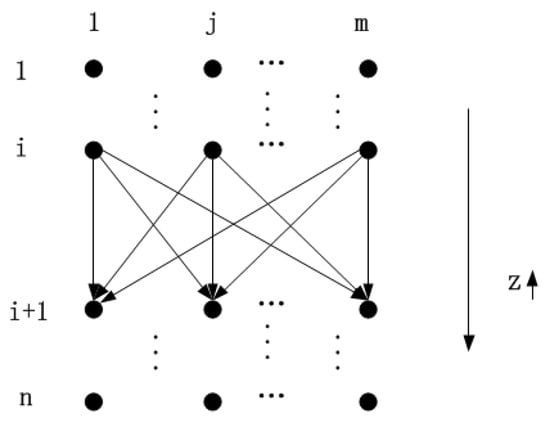
Figure 3.
The way of IACO for spectrum allocation.
- (1)
- Path selection. The transfer probability between node i and s in the choice process is presented as follows:where is a constant in the scope , and J is a random variable generated by the following formula:where and are the weighted factor of information and expectation heuristic respectively. is the available node-set for ant l at node i, is the infeasible node-set for ant l and it would be cleared after l finishes traversal.
- (2)
- Update pheromone. Using an elitist strategy to update pheromone. The pheromone concentration on path is updated as the following rules:where is the pheromone evaporation coefficient, is the residual factor of pheromone. Q is a constant of total pheromone released from all ants in each traversal, is the cost calculated by fitness function.
Step 6: Termination judgment. If reach the maximum iteration times , the solving process is over. Then map the best solution to allocation matrix A. If and the convergence speed is slow and and satisfy , then go to the 7th step, otherwise, go to the 8th.
Step 7: Accelerate the convergence speed. Adopting DE to accelerate the global convergence speed by optimizing the searching mode of the ants and guaranteeing the diversity of the population. Initialize DE with the subpopulation of ACO, .
Step 8: Local search. Employing VNS to improve the local searchability of the improved algorithm by searching around the initial solution.
3.6. Pseudocode of IACO
| Algorithm 1: An Improved Ant Colony Optimization Algorithm |
 |
4. Simulation Results and Discussion
To validate the performance of the IACO, we compare IACO with the ACO, GA, and PSO [15] from four aspects: convergence speed, MSRM, MMR and MPF in this section. We use the topology structure of the cognitive radio system as suggested in [6]. The user nodes are randomly generated in the rectangle region of . The number of primary users M is equal to orthogonal available spectrum number; the number of cognitive users is N.
Initialize IACO and ACO with ; In GA, the crossover rate , mutation rate ; In PSO, two acceleration coefficients , inertia weight , maximum speed . The population sizes are all N in IACO, ACO, PSO and GA, the maximum evolution generation is 200. The four algorithms use the same topology, the iteration times in the convergence experiment are 500 while others are 50, finally taking the mean of the result.
Experiment 1.
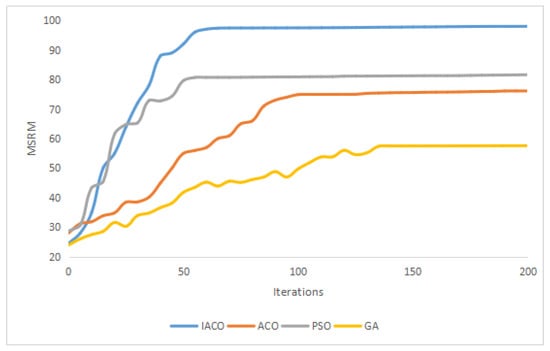
Figure 4 shows the MSRM trend with the increasing times of iteration under for different algorithms. In the first 50 iterations, GA is the slowest, ACO speeds up all the time but still inferior to PSO, and IACO is the best due to DE accelerating its convergence speed. At the later iteration, although PSO reaches the optimum firstly, its MSRM is lower than IACO; IACO has the highest MSRM in the end, because it adopts the VNS process to jump out of the local optimum.

Figure 4.
The average system benefit with increasing of iterations.
Experiment 2.
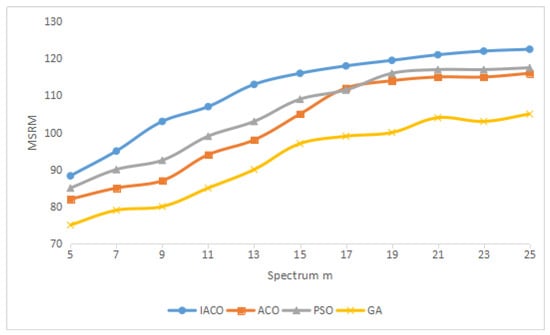
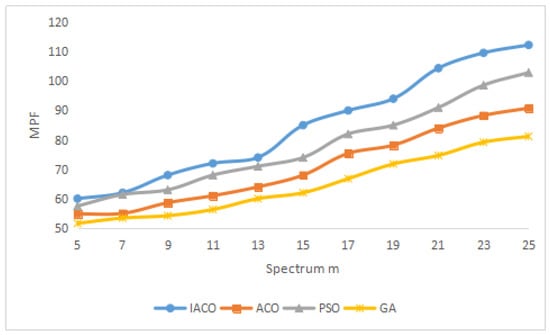
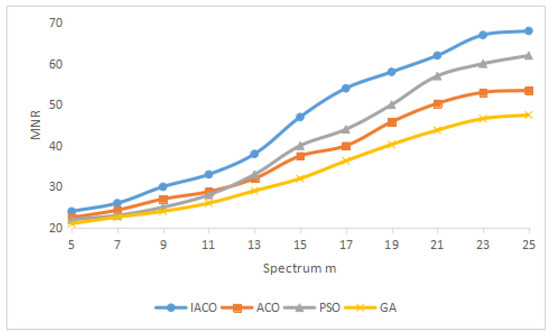
In this experiment, we show the MSRM, MPF and MMR trends with the increasing number of available licensed spectrum for different algorithms in Figure 5, Figure 6 and Figure 7, where the number of cognitive users is fixed on . In Figure 5, Figure 6 and Figure 7, all curves increase all the time. It can be seen that, if , MSRM grows quickly whereas MPF and MMR increase slowly because of the competition for access to spectrum in cognitive users. If , with the increasing of licensed spectrum number, MPF and MMR grow rapidly. Also, IACO is the best all the time.

Figure 5.
MSRM change with .

Figure 6.
MPF change with .

Figure 7.
MMR change with .
Finally, we fix the cognitive user on , available spectrum and use exhaustive method to obtain the optimal solution. The relative difference between each algorithm and the highest ideal value is obtained from , where b is the efficiency value of algorithms, B is the highest ideal value. This experiment is based on MSRM, MMR, MPF. As shown in Table 2, IACO is already close to the optimal value at the 100 iterations, only MPF has a slight relative difference. IACO has the advantage of convergence and can reach the optimal value quickly.

Table 2.
Optimal Value.
5. Conclusions
In this paper, we developed an efficient method IACO for available licensed spectrum allocation. The main target is to maximize the system utility by using IACO. In IACO, the monitoring mechanism detects the convergence speed for the algorithm to introduce DE in a timely manner. Besides, VNS is employed to help IACO get rid of the local optimum. Therefore, the new allocation algorithm IACO conquers the limits of ACO, and not only achieves high convergence speed but reduces the risk of trapping to the local maximum. The results show that the IACO-based spectrum allocation achieves the best performance in MSRM, MPF and MMR.
Acknowledgments
This work is supported by the Research Fund for Research of Method and Mechanism on Resisting Hole Attack for Wireless Sensor of China (Grant No. 61379110). This work is supported by the Fundamental Research Funds for the Central Universities of the Central South University (Grant No. 2017zzts733).
Author Contributions
L.L. and N.W. conceived and designed the experiments; N.W. performed the experiments; L.G. analyzed the data; Z.C. contributed reagents/materials/analysis tools; N.W. wrote the paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, D.; Chen, Z.; Awad, M.K.; Zhang, N.; Zhou, H.; Shen, X.S. Utility-Optimal Resource Management and Allocation Algorithm for Energy Harvesting Cognitive Radio Sensor Networks. IEEE J. Sel. Areas Commun. 2016, 34, 3552–3565. [Google Scholar] [CrossRef]
- Sharma, S.K.; Bogale, T.E.; Chatzinotas, S.; Ottersten, B.; Le, L.B.; Wang, X. Cognitive Radio Techniques Under Practical Imperfections: A Survey. IEEE Commun. Surv. Tutor. 2015, 17, 1858–1884. [Google Scholar] [CrossRef]
- Niyato, D.; Hossain, E. Cognitive radio for next-generation wireless networks: An approach to opportunistic channel selection in ieee 802.11-based wireless mesh. IEEE Wirel. Commun. 2009, 16, 46–54. [Google Scholar] [CrossRef]
- Akyildiz, I.F.; Lee, W.Y.; Vuran, M.C.; Mohanty, S. NeXt generation/dynamic spectrum access/cognitive radio wireless networks: A survey. Comput. Netw. 2006, 50, 2127–2159. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, Z.; Ren, J.; Zhang, N.; Awad, M.K.; Zhou, H.; Shen, X.S. Energy-Harvesting-Aided Spectrum Sensing and Data Transmission in Heterogeneous Cognitive Radio Sensor Network. IEEE Trans. Veh. Technol. 2017, 66, 831–843. [Google Scholar] [CrossRef]
- Lu, L.; He, D.; Li, G.Y.; Yu, X. Graph-Based Robust Resource Allocation for Cognitive Radio Networks. IEEE Trans. Signal Process. 2015, 63, 3825–3836. [Google Scholar] [CrossRef]
- Jalaeian, B.; Zhu, R.; Samani, H.; Motani, M. An Optimal Cross-Layer Framework for Cognitive Radio Network Under Interference Temperature Model. IEEE Syst. J. 2016, 10, 293–301. [Google Scholar] [CrossRef]
- Yi, C.; Cai, J. Two-Stage Spectrum Sharing With Combinatorial Auction and Stackelberg Game in Recall-Based Cognitive Radio Networks. IEEE Trans. Commun. 2014, 62, 3740–3752. [Google Scholar] [CrossRef]
- Yang, G.; Li, B.; Tan, X.; Wang, X. Adaptive power control algorithm in cognitive radio based on game theory. IET Commun. 2015, 9, 1807–1811. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. The Ant System: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man. Cybern. 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Song, X.O. Utilization and Fairness in Spectrum Assignment for Cognitive Radio Networks: An Ant Colony Optimization’s Perspective. In Proceedings of the 2014 International Conference on Wireless Communication and Sensor Network, Wuhan, China, 13–14 December 2014; pp. 42–45. [Google Scholar]
- Luo, W.; Lin, D.; Feng, X. An Improved Ant Colony Optimization and Its Application on TSP Problem. In Proceedings of the 2016 IEEE International Conference on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData), Chengdu, China, 15–18 December 2016; pp. 136–141. [Google Scholar]
- Li, H.; Zhang, L.; Jiao, Y. Discrete differential evolution algorithm for integer linear bilevel programming problems. J. Syst. Eng. Electron. 2016, 27, 912–919. [Google Scholar]
- Herremans, D.; Sörensen, K.; Martens, D. Classification and Generation of Composer-Specific Music Using Global Feature Models and Variable Neighborhood Search. Comput. Music J. 2015, 39, 71–91. [Google Scholar] [CrossRef]
- Zhao, Z.; Peng, Z.; Zheng, S.; Shang, J. Cognitive radio spectrum allocation using evolutionary algorithms. IEEE Trans. Wirel. Commun. 2009, 8, 4421–4425. [Google Scholar] [CrossRef]
- He, D. A Novel Spectrum Sensing Method in Cognitive Radio Networks Based on Graph Theory. In Proceedings of the 2015 IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015; pp. 1–6. [Google Scholar]
- Peng, C.; Zheng, H.; Zhao, B.Y. Utilization and Fairness in Spectrum Assignment for Opportunistic Spectrum Access; Springer: New York, NY, USA, 2006. [Google Scholar]
- Wajeed, M.A.; Adilakshmi, T. Adopting ant colony optimization for supervised text classification. In Proceedings of the 2016 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Jaipur, India, 21–24 September 2016; pp. 2562–2566. [Google Scholar]
- Das, S.; Suganthan, P.N. Differential Evolution: A Survey of the State-of-the-Art. IEEE Trans. Evolut. Comput. 2011, 15, 4–31. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).