Common Nearest Neighbor Clustering—A Benchmark
Abstract
:1. Introduction
2. Molecular Dynamics Simulations
3. Materials and Methods
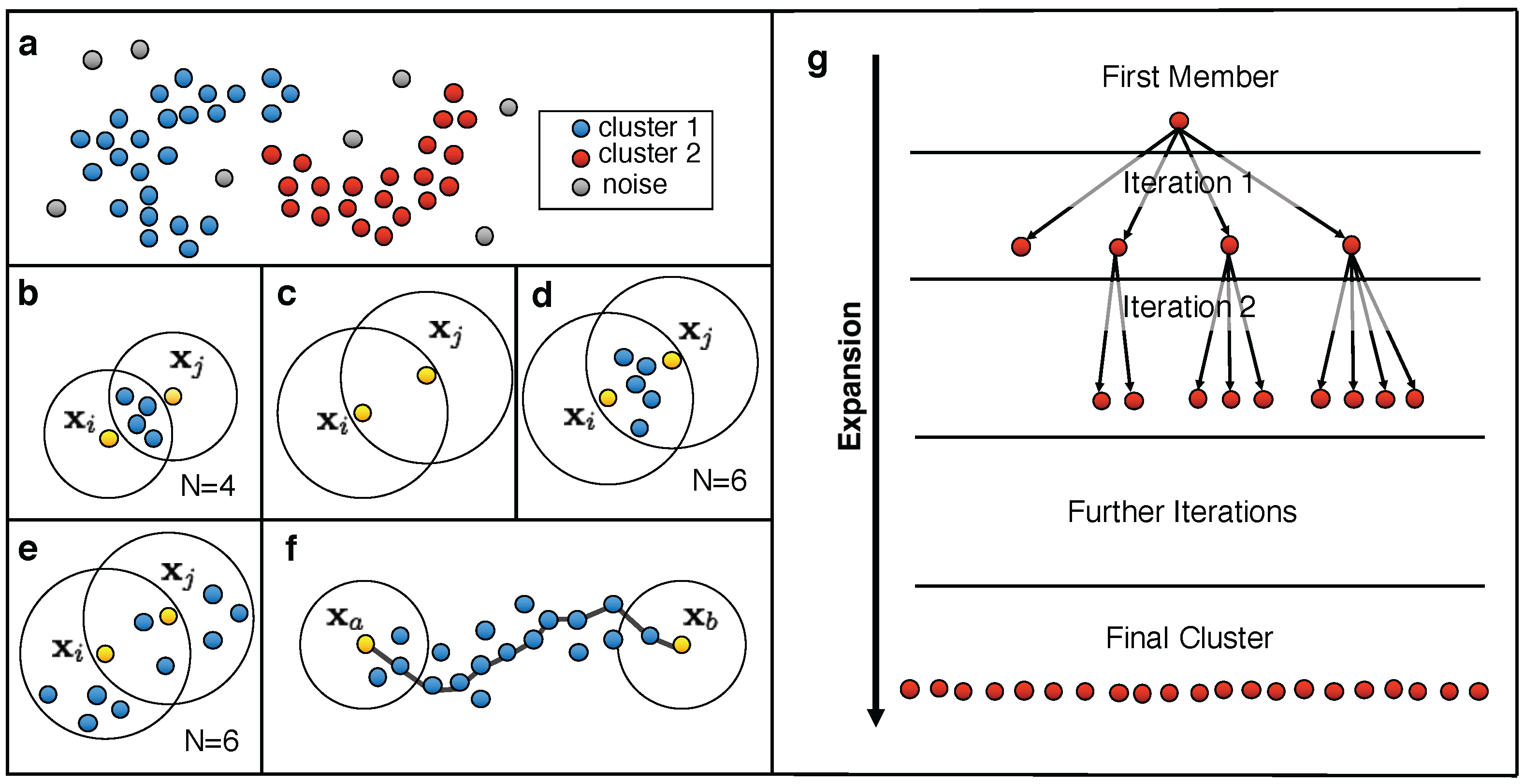
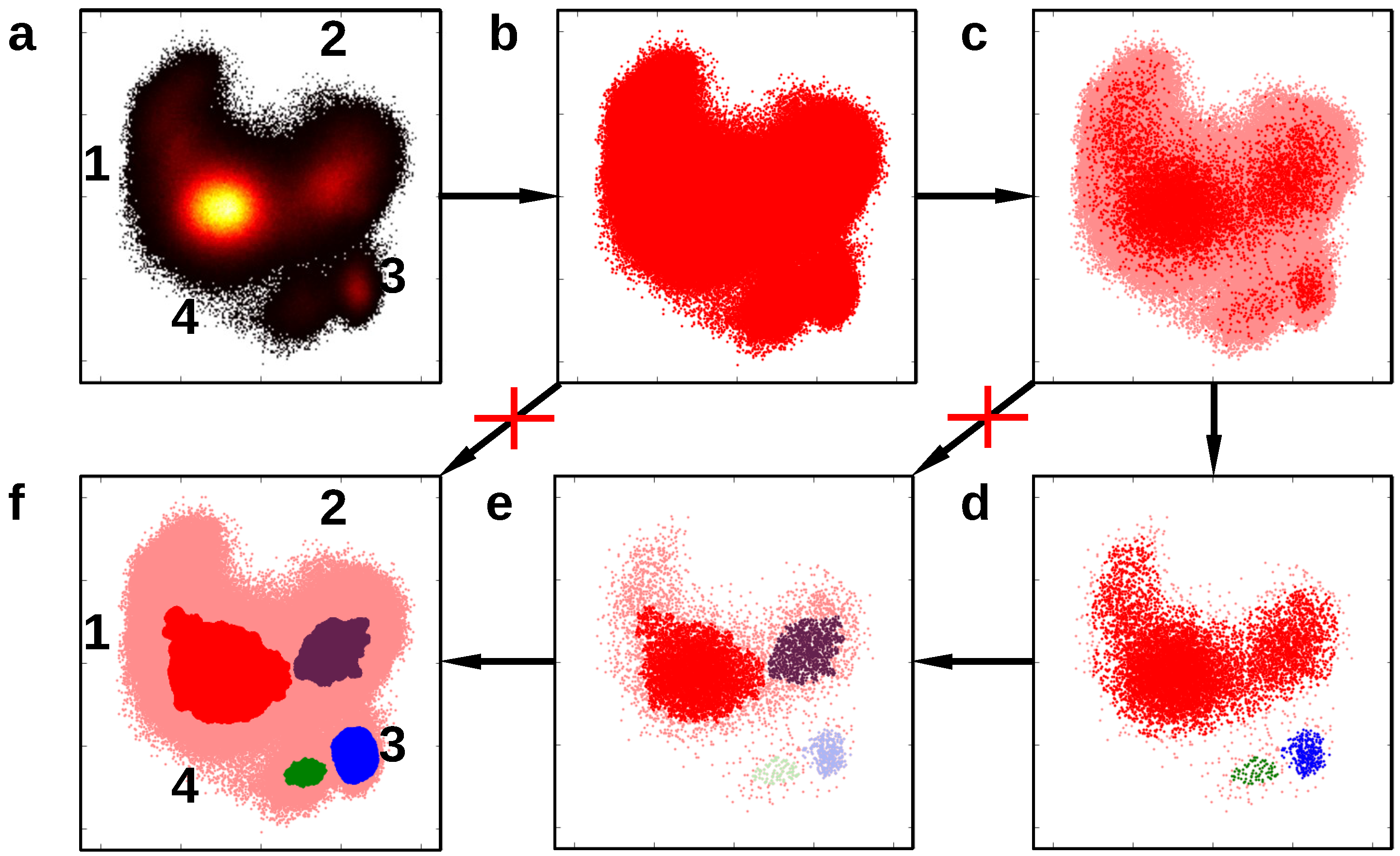
3.1. Common Nearest Neighbor Algorithm
- 0.
- Choose R and N.
- 1.
- Cluster initialization: Choose an arbitrary data point from the set of unclustered data points U as the first member of the cluster C. Set to (first line in Figure 4g).
- 2.
- Cluster expansion:
- (a)
- Add any unclustered data point within of , which fulfils the density criterion with respect to , to the cluster C (second line in Figure 4g) and remove it from U. Keep a list L of the newly added data points.
- (b)
- Choose a data point from L and set to .
- (c)
- Repeat steps (a) and (b) until no further data point can be added to C (third and fourth line in Figure 4g).
- (d)
- Save C to file and reset C to an empty list .
- 3.
- Repeat steps 1 and 2 until all data points are assigned to a cluster.
3.2. Hierarchical Clustering
3.3. Dataset Reduction
3.4. Centroid Index at Cluster Level
3.5. Markov Chain Monte Carlo Sampling
4. Results
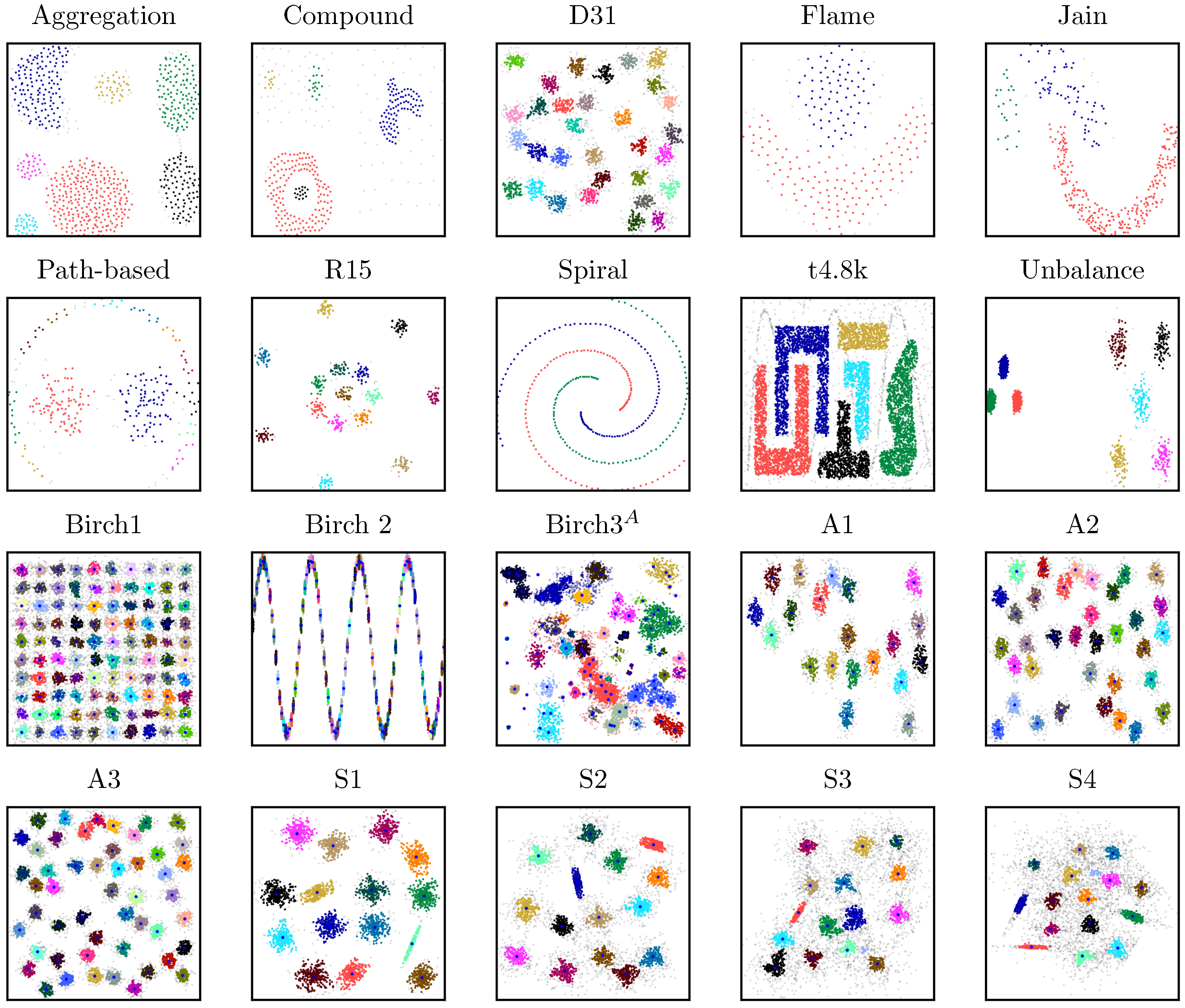
4.1. Benchmark
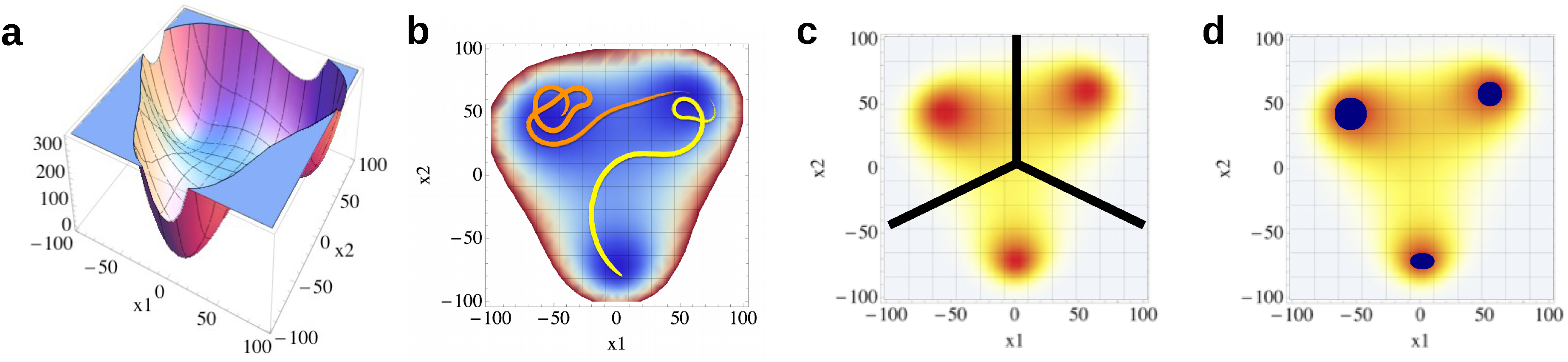
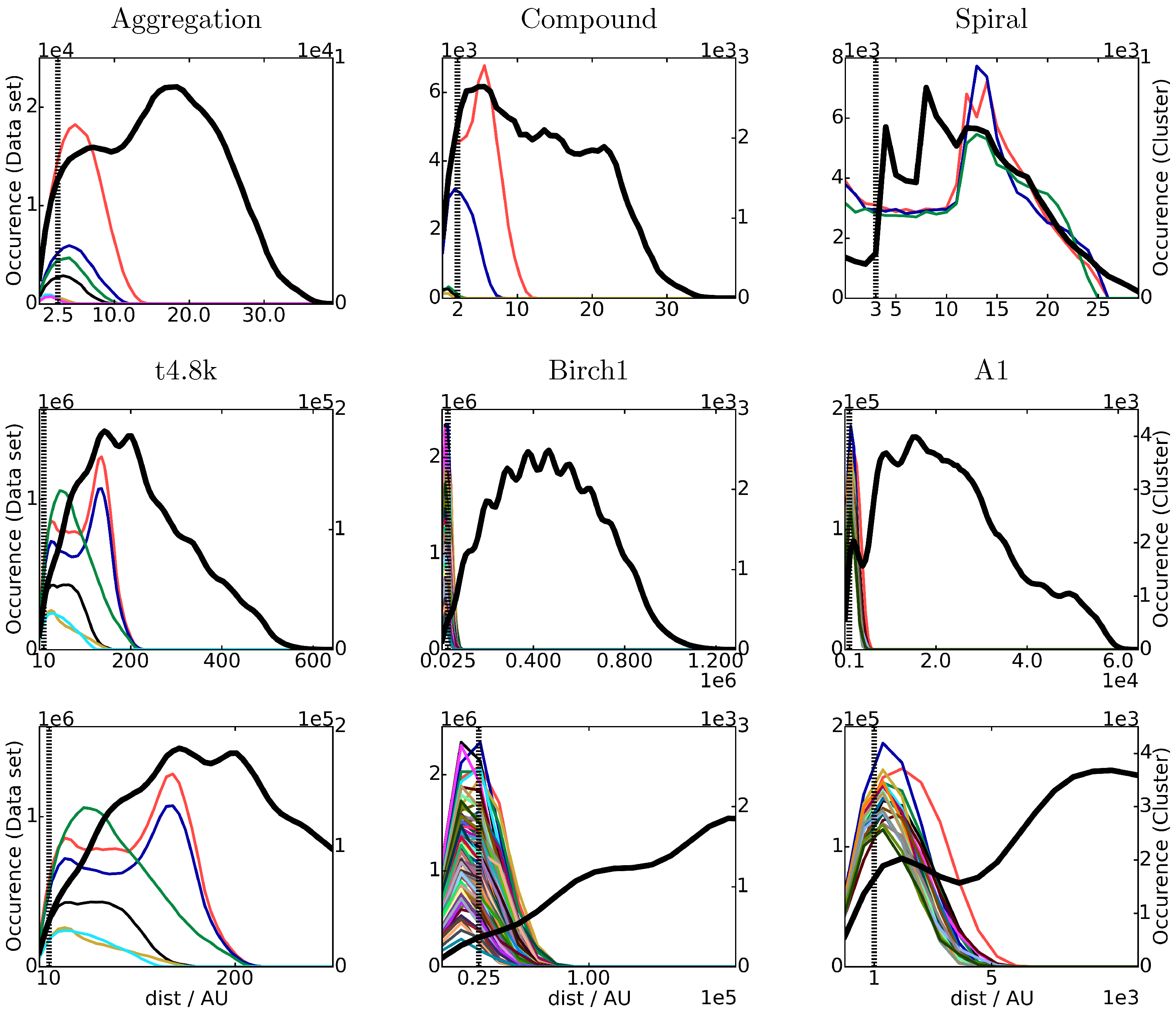
4.1.1. Cluster Size and Shape
4.1.2. Number of Clusters
4.1.3. Unbalanced Data-Point Density
4.1.4. Cluster Overlap
4.1.5. Dimensionality
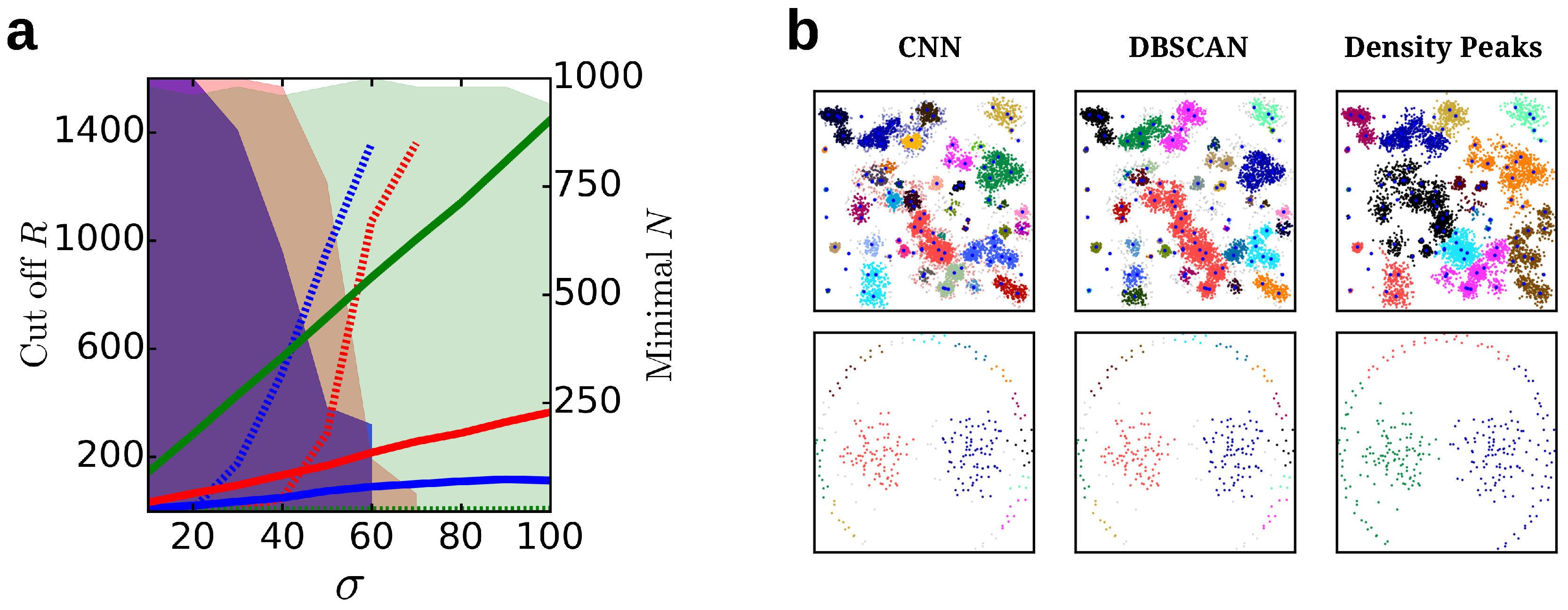
4.1.6. Comparison to Other Cluster Algorithms
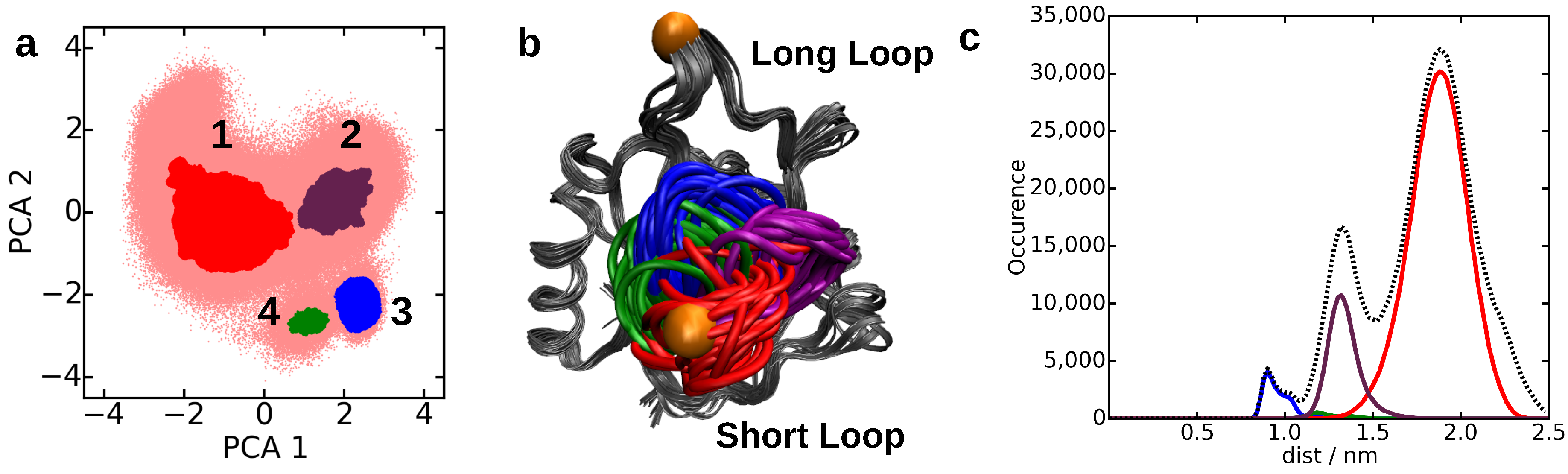
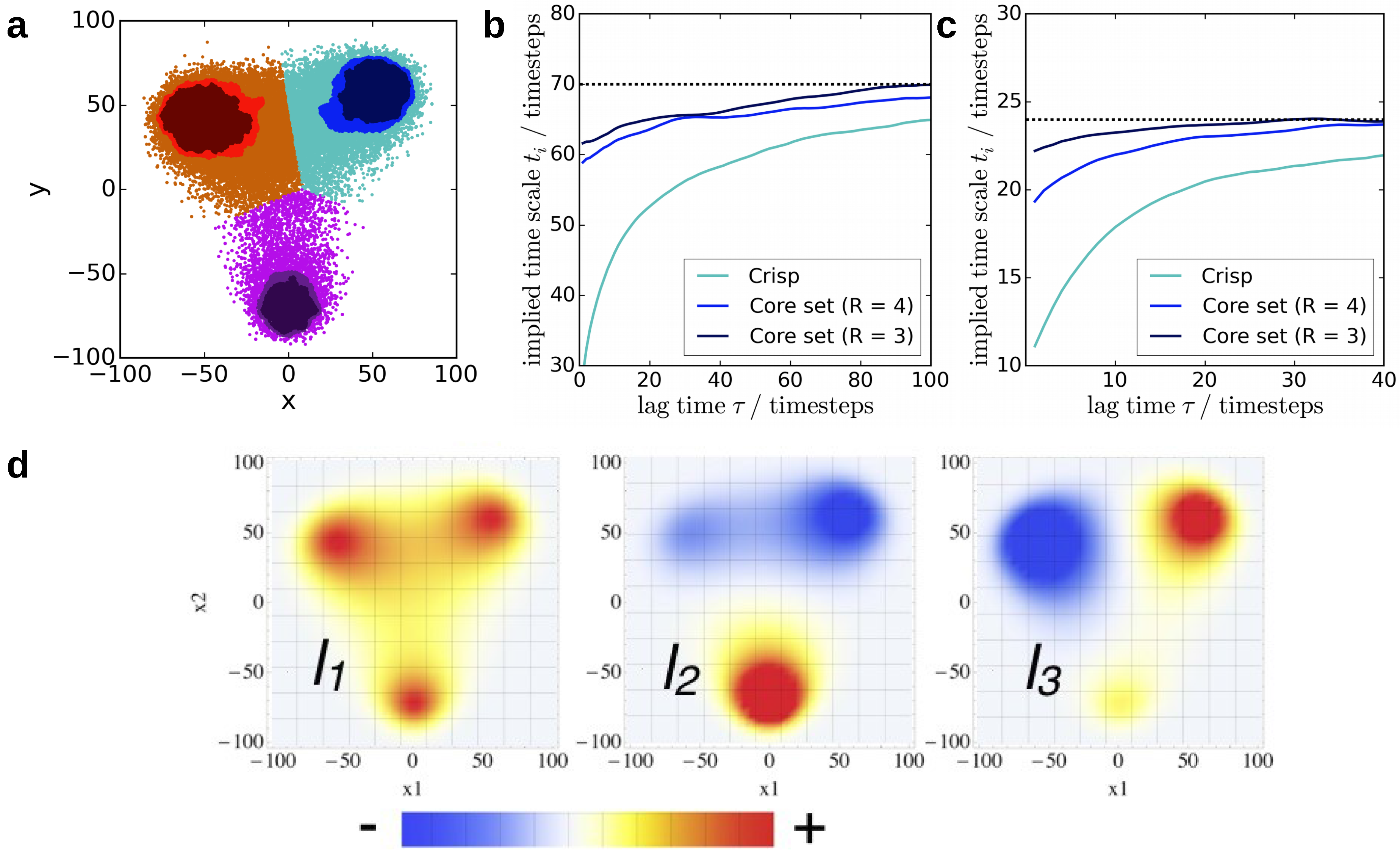
4.2. Core-Set Models of Molecular Dynamics
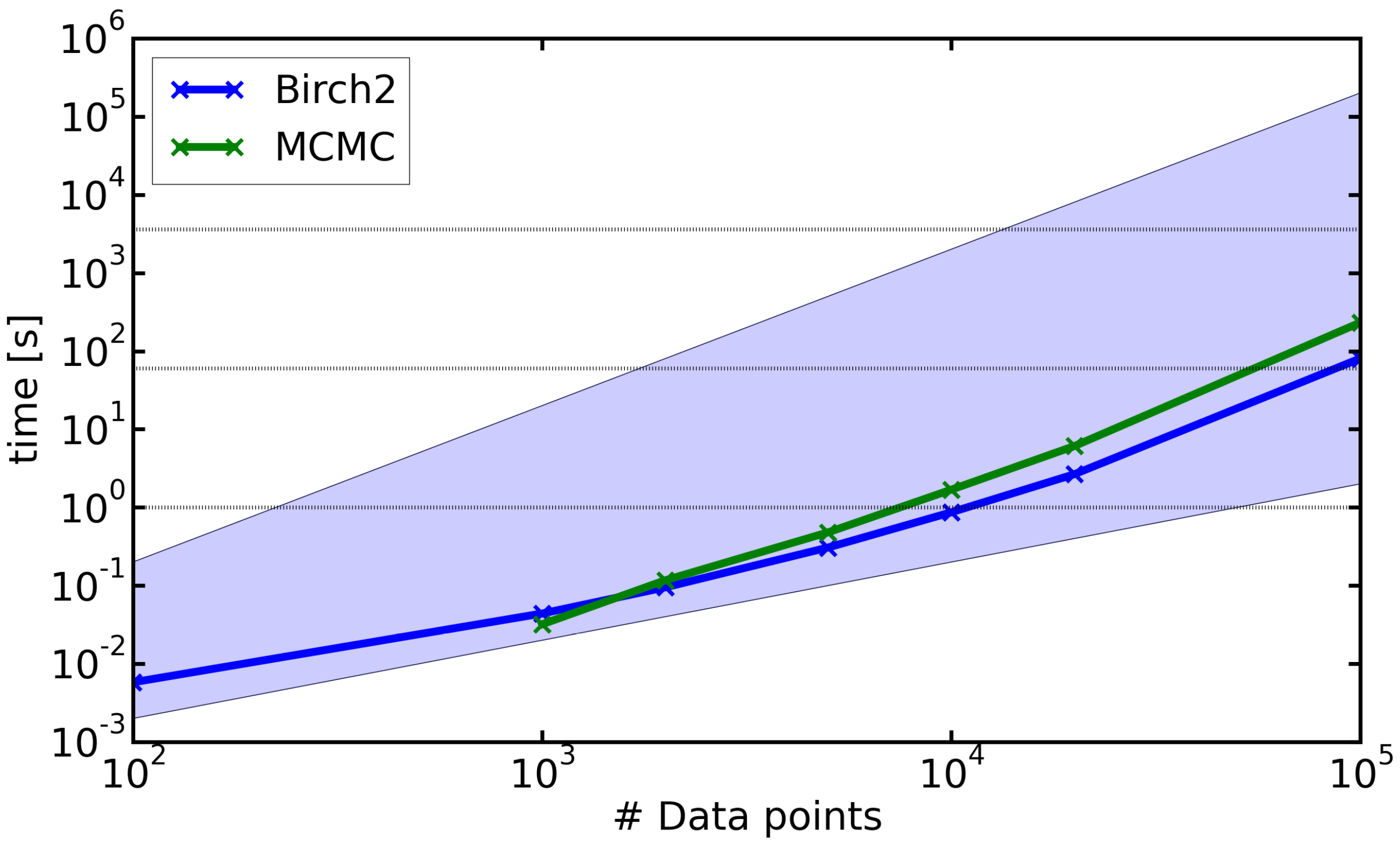
4.3. Run-Time Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| CI | Centroid Index at Cluster Level |
| CNN | Common nearest neighbor |
| DBSCAN | Density-Based Spatial Clustering of Applications with Noise |
| kM | kMeans algorithm |
| Max | Further point heuristic |
| MCMC | Markov chain Monte Carlo |
| MD | Molecular dynamics |
| MSM | Markov state model |
| PCA | Principle component analysis |
| PES | Potential energy surface |
References
- JeraldBeno, T.R.; Karnan, M. Dimensionality Reduction: Rough Set Based Feature Reduction. Int. J. Sci. Res. Publ. 2012, 2, 1–6. [Google Scholar]
- Karypis, G.; Han, E.H.; Kumar, V. CHAMELEON: A hierarchical 765 clustering algorithm using dynamic modeling. IEEE Trans. Comput. 1999, 32, 68–75. [Google Scholar]
- Fu, L.; Medico, E. FLAME, a novel fuzzy clustering method for the analysis of DNA microarray data. BMC Bioinform. 2007, 8, 3. [Google Scholar] [CrossRef] [PubMed]
- Keller, B.; Daura, X.; van Gunsteren, W.F. Comparing geometric and kinetic cluster algorithms for molecular simulation data. J. Chem. Phys. 2010, 132, 074110. [Google Scholar] [CrossRef] [PubMed]
- Jarvis, R.A.; Patrick, E.A. Clustering Using a Similarity Measure Based on Shared Near Neighbors. IEEE Trans. Comp. 1973, C-22, 1025–1034. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the KDD-96 the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Comaniciu, D.; Meer, P. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 603–619. [Google Scholar] [CrossRef]
- Ankerst, M.; Breuning, M.M.; Kriegel, H.P.; Sander, J. OPTICS: Ordering Points To Identify the Clustering Structure. In Proceedings of the ACM SIGMOD International Conference on Management of Data, Philadelphia, PA, USA, 1–3 June 1999; pp. 49–60. [Google Scholar]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Zhu, L.; Sheong, F.K.; Wang, W.; Huang, X. Adaptive partitioning by local density-peaks: An efficient density-based clustering algorithm for analyzing molecular dynamics trajectories. J. Comput. Chem. 2016, 38, 152–160. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.K.; Topchy, A.; Law, M.H.C.; Buhmann, J.M. Landscape of Clustering Algorithms. In Proceedings of the ICPR’04 17th International Conference on Pattern Recognition, Cambridge, UK, 23–26 August 2004; Volume 1, pp. 260–263. [Google Scholar]
- Kärkkäinen, I.; Fränti, P. Dynamic Local Search Algorithm for the Clustering Problem; Technical Report A-2002-6; University of Joensuu: Joensuu, Finland, 2002. [Google Scholar]
- Fränti, P.; Virmajoki, O. Iterative shrinking method for clustering problems. Pattern Recognit. 2006, 39, 761–765. [Google Scholar] [CrossRef]
- Zhang, T.; Ramakrishnan, R.; Livny, M. BIRCH: A new data clustering algorithm and its applications. Data Min. Knowl. Discov. 1997, 1, 141–182. [Google Scholar] [CrossRef]
- Kärkkäinen, I.; Fränti, P. Gradual model generator for single-pass clustering. Pattern Recognit. 2007, 40, 784–795. [Google Scholar] [CrossRef]
- Fränti, P.; Virmajoki, O.; Hautamäki, V. Fast agglomerative clustering using a k-nearest neighbor graph. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1875–1881. [Google Scholar] [CrossRef] [PubMed]
- Rezaei, M.; Fränti, P. Set-matching methods for external cluster validity. IEEE Trans. Knowl. Data Eng. 2016, 28, 2173–2186. [Google Scholar] [CrossRef]
- Gionis, A.; Mannila, H.; Tsaparas, P. Clustering aggregation. ACM Trans. Knowl. Discov. Data 2007, 1, 1–30. [Google Scholar] [CrossRef]
- Zahn, C.T. Graph-theoretical methods for detecting and describing gestalt clusters. IEEE Trans. Comput. 1971, 100, 68–86. [Google Scholar] [CrossRef]
- Veenman, C.J.; Reinders, M.J.T.; Backer, E. A maximum variance cluster algorithm. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 1273–1280. [Google Scholar] [CrossRef]
- Jain, A.K.; Law, M.H.C. Data Clustering: A User’s Dilemma. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2005; pp. 1–10. [Google Scholar]
- Chang, H.; Yeung, D.Y. Robust path-based spectral clustering. Pattern Recognit. 2008, 41, 191–203. [Google Scholar] [CrossRef]
- Lemke, O.; Keller, B.G. CNNClustering. Available online: https://github.com/BDGSoftware/CNNClustering (accessed on 6 January 2017).
- Lemke, O.; Keller, B.G. Density-based cluster algorithms for the identification of core sets. J. Chem. Phys. 2016, 145, 164104. [Google Scholar] [CrossRef] [PubMed]
- Sarich, M.; Banisch, R.; Hartmann, C.; Schütte, C. Markov State Models for Rare Events in Molecular Dynamics. Entropy 2014, 16, 258–286. [Google Scholar] [CrossRef]
- Vanden-Eijnden, E.; Venturoli, M.; Ciccotti, G.; Elber, R. On the assumptions underlying milestoning. J. Chem. Phys. 2008, 129, 174102. [Google Scholar] [CrossRef] [PubMed]
- Schütte, C. Conformational Dynamics: Modelling, Theory, Algorithm, and Application to Biomolecules. Habilitation Thesis, Konrad-Zuse-Zentrum für Informationstechnik, Berlin, Germany, 1999. [Google Scholar]
- Schütte, C.; Noé, F.; Lu, J.; Sarich, M.; Vanden-Eijnden, E. Markov state models based on milestoning. J. Chem. Phys. 2011, 134, 204105. [Google Scholar] [CrossRef] [PubMed]
- Schütte, C.; Sarich, M. A critical appraisal of Markov state models. Eur. Phys. J. Spec. Top. 2015, 224, 2445. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understanding Molecular Simulations; Academic Press: San Diego, CA, USA, 1996. [Google Scholar]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: New York, NY, USA, 1987. [Google Scholar]
- Leach, A.R. Molecular Modelling; Addison Wesley Longman: Essex, UK, 1996. [Google Scholar]
- Hanske, J.; Aleksić, S.; Ballaschk, M.; Jurk, M.; Shanina, E.; Beerbaum, M.; Schmieder, P.; Keller, B.G.; Rademacher, C. Intradomain Allosteric Network Modulates Calcium Affinity of the C-Type Lectin Receptor Langerin. J. Am. Chem. Soc. 2016, 138, 12176–12186. [Google Scholar] [CrossRef] [PubMed]
- Witek, J.; Keller, B.G.; Blatter, M.; Meissner, A.; Wagner, T.; Riniker, S. Kinetic Models of Cyclosporin a in Polar and Apolar Environments Reveal Multiple Congruent Conformational States. J. Chem. Inf. Model. 2016, 56, 1547–1562. [Google Scholar] [CrossRef] [PubMed]
- Tsai, C.J.; Nussinov, R. A Unified View of “How Allostery Works”. PLoS Comput. Biol. 2014, 10, e1003394. [Google Scholar] [CrossRef] [PubMed]
- Ball, G.H.; Hall, D.J. A clustering technique for summarizing multivariate data. Behav. Sci. 1967, 12, 153–155. [Google Scholar] [CrossRef] [PubMed]
- Fränti, P.; Rezaei, M.; Zhao, Q. Centroid index: Cluster level similarity measure. Pattern Recognit. 2014, 47, 3034–3045. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Fränti, P.; Sieranoja, S. Clustering datasets. Algorithms 2017. submitted. [Google Scholar]
- Arthur, D.; Vassilvitskii, S. K-means++: The advantages of careful seeding. In Proceedings of the ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–9 January 2007; pp. 1027–1035. [Google Scholar]
- Scherer, M.K.; Trendelkamp-Schroer, B.; Paul, F.; Pérez-Hernández, G.; Hoffmann, M.; Plattner, N.; Wehmeyer, C.; Prinz, J.H.; Noé, F. PyEMMA 2: A Software Package for Estimation, Validation, and Analysis of Markov Models. J. Chem. Theory Comput. 2015, 11, 5525–5542. [Google Scholar] [CrossRef] [PubMed]
- Lloyd, S.P. Least squares quantization in pcm. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Gonzalez, T.F. Clustering to minimize the maximum intercluster distance. Theor. Comput. Sci. 1985, 38, 293–306. [Google Scholar] [CrossRef]
- Fränti, P.; Mariescu-Istodor, R.; Zhong, C. XNN graph. Joint Int. Workshop Struct. Syntactic Stat. Pattern Recognit. 2016, LNCS 10029, 207–217. [Google Scholar]
- Schwantes, C.R.; Pande, V.S. Modeling Molecular Kinetics with tICA and the Kernel Trick. J. Chem. Theory Comput. 2015, 11, 600–608. [Google Scholar] [CrossRef] [PubMed]
- Aghabozorgi, S.; Shirkhorshidi, A.S.; Wah, T.Y. Time-series clustering—A decade review. Inf. Syst. 2015, 53, 16–38. [Google Scholar] [CrossRef]
- Mariescu-Istodor, R.; Fränti, P. Grid-Based Method for GPS Route Analysis for Retrieval. ACM Trans. Algorithm 2017, 3, 1–28. [Google Scholar] [CrossRef]
- Chandrakala, S.; Sekhar, C.C. A density based method for multivariate time series clustering in kernel feature space. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 June 2008. [Google Scholar]
- Hamprecht, F.A.; Peter, C.; Daura, X.; Thiel, W.; van Gunsteren, W.F. A strategy for analysis of (molecular) equilibrium simulations: Configuration space density estimation, clustering, and visualization. J. Chem. Phys. 2001, 114, 2079–2089. [Google Scholar] [CrossRef]
- Schütte, C.; Fischer, A.; Huisinga, W.; Deuflhard, P. A Direct Approach to Conformational Dynamics Based on Hybrid Monte Carlo. J. Comput. Phys. 1999, 151, 146–168. [Google Scholar] [CrossRef]
- Swope, W.C.; Pitera, J.W.; Suits, F. Describing Protein Folding Kinetics by Molecular Dynamics Simulations. J. Phys. Chem. B 2004, 108, 6571–6581. [Google Scholar] [CrossRef]
- Chodera, J.D.; Singhal, N.; Pande, V.S.; Dill, K.A.; Swope, W.C. Automatic discovery of metastable states for the construction of Markov models of macromolecular conformational dynamics. J. Chem. Phys. 2007, 126, 155101. [Google Scholar] [CrossRef] [PubMed]
- Buchete, N.V.; Hummer, G. Coarse Master Equations for Peptide Folding Dynamics. J. Phys. Chem. B 2008, 112, 6057–6069. [Google Scholar] [CrossRef] [PubMed]
- Keller, B.; Hünenberger, P.; van Gunsteren, W.F. An Analysis of the Validity of Markov State Models for Emulating the Dynamics of Classical Molecular Systems and Ensembles. J. Chem. Theory Comput. 2011, 7, 1032–1044. [Google Scholar] [CrossRef] [PubMed]
- Prinz, J.H.; Wu, H.; Sarich, M.; Keller, B.; Senne, M.; Held, M.; Chodera, J.D.; Schütte, C.; Noé, F. Markov models of molecular kinetics: Generation and validation. J. Chem. Phys. 2011, 134, 174105. [Google Scholar] [CrossRef] [PubMed]
- Sarich, M.; Noé, F.; Schütte, C. On the Approximation Quality of Markov State Models. Multisc. Model. Simul. 2010, 8, 1154–1177. [Google Scholar] [CrossRef]
- Nüske, F.; Keller, B.G.; Pérez-Hernández, G.; Mey, A.S.J.S.; Noé, F. Variational Approach to Molecular Kinetics. J. Chem. Theory Comput. 2014, 10, 1739–1752. [Google Scholar] [CrossRef] [PubMed]
- Vitalini, F.; Noé, F.; Keller, B.G. A Basis Set for Peptides for the Variational Approach to Conformational Kinetics. J. Chem. Theory Comput. 2015, 11, 3992–4004. [Google Scholar] [CrossRef] [PubMed]
- Fackeldey, K.; Röblitz, S.; Scharkoi, O.; Weber, M. Soft Versus Hard Metastable Conformations in Molecular Simulations; Technical Report 11-27; ZIB: Berlin, Germany, 2011. [Google Scholar]
- Weber, M.; Fackeldey, K.; Schütte, C. Set-free Markov state model building. J. Chem. Phys. 2017, 146, 124133. [Google Scholar] [CrossRef] [PubMed]
| Dataset | CNN Parameter | DBSCAN Parameter | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Name | |||||||||
| A sets [12] | |||||||||
| A1 | 3000 | 2 | 20 | 1 | 9 | 10 | 800 | 9 | 10 |
| A2 | 5200 | 2 | 35 | 1 | 9 | 10 | 800 | 9 | 10 |
| A3 | 7500 | 2 | 50 | 1 | 9 | 10 | 800 | 9 | 10 |
| S sets [13] | |||||||||
| S1 | 5000 | 2 | 15 | 2.5 | 5 | 10 | 2.0 | 9 | 10 |
| S2 | 5000 | 2 | 15 | 2.5 | 17 | 10 | 2.0 | 9 | 10 |
| S3 | 5000 | 2 | 15 | 2.5 | 25 | 10 | 1.7 | 9 | 10 |
| S4 | 5000 | 2 | 15 | 2.5 | 30 | 10 | 1.7 | 9 | 10 |
| Birch sets [14] | |||||||||
| Birch1 | 10,000 | 2 | 100 | 2.5 | 23 | 10 | 1.5 | 9 | 10 |
| Birch2 | 10,000 | 2 | 100 | 2.5 | 20 | 10 | 1.5 | 9 | 10 |
| Birch3 | 10,000 | 2 | 100 | 3 | 10 | 10 | --- | --- | --- |
| --- | --- | --- | --- | 2 | 10 | 10 | --- | --- | --- |
| --- | --- | --- | --- | 1.5 | 10 | 10 | 1.5 | 9 | 10 |
| Dim sets [15,16] | |||||||||
| Dim-32 | 1024 | 32 | 16 | 10 | 5 | 10 | 15 | 9 | 10 |
| Dim-64 | 1024 | 64 | 16 | 10 | 5 | 10 | 15 | 9 | 10 |
| Dim-128 | 1024 | 128 | 16 | 10 | 5 | 10 | 15 | 9 | 10 |
| Dim-256 | 1024 | 256 | 16 | 10 | 5 | 10 | 15 | 9 | 10 |
| Dim-512 | 1024 | 512 | 16 | 10 | 5 | 10 | 20 | 9 | 10 |
| Dim-1024 | 1024 | 1024 | 16 | 10 | 5 | 10 | 20 | 9 | 10 |
| Unbalance [17] | |||||||||
| Unbalance | 6500 | 2 | 8 | 1 | 5 | 10 | 6 | 9 | 10 |
| Shape sets | |||||||||
| Aggregation [18] | 788 | 2 | 7 | 2.50 | 17 | 10 | --- | --- | --- |
| Compound [19] | 399 | 2 | 6 | 2.00 | 15 | 10 | --- | --- | --- |
| D31 [20] | 3100 | 2 | 31 | 0.45 | 4 | 10 | --- | --- | --- |
| Flame [3] | 240 | 2 | 2 | 2.00 | 15 | 10 | --- | --- | --- |
| Jain [21] | 373 | 2 | 2 | 2.50 | 3 | 10 | --- | --- | --- |
| Path-based [22] | 300 | 2 | 3 | 1.40 | 2 | 5 | 1.4 | 2 | 5 |
| R15 [20] | 600 | 2 | 15 | 0.60 | 9 | 10 | --- | --- | --- |
| Spiral [22] | 312 | 2 | 3 | 3.00 | 3 | 10 | --- | --- | --- |
| t4.8k [2] | 8000 | 2 | 6 | 10.00 | 15 | 10 | --- | --- | --- |
| i | |||||
|---|---|---|---|---|---|
| 1 | 0.8 | −45 | 0.9 | 40 | 10 |
| 2 | 0.8 | 0 | 0.9 | −65 | 0 |
| 3 | 0.8 | 45 | 0.9 | 55 | 10 |
| Dataset | CNN | DBSCAN | CI | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Name | Noise | Noise | CNN | DBSCAN | kM(++) | kM [39] | kM (Max) [39] | |||
| A sets [12] | ||||||||||
| A1 | 20 | 20 | 22% | 19 | 19% | 0 | 1 | 1 | 2.5 | 1.0 |
| A2 | 35 | 35 | 22% | 34 | 18% | 0 | 1 | 1 | 4.5 | 2.6 |
| A3 | 50 | 50 | 22% | 50 | 18% | 0 | 1 | 2 | 6.6 | 2.9 |
| S sets [13] | ||||||||||
| S1 | 15 | 15 | 4% | 16 | 6% | 0 | 1 | 0 | 1.8 | 0.7 |
| S2 | 15 | 15 | 28% | 14 | 12% | 0 | 2 | 1 | 1.4 | 1.0 |
| S3 | 15 | 16 | 46% | 15 | 20% | 1 | 5 | 0 | 1.3 | 0.7 |
| S4 | 15 | 16 | 48% | 12 | 14% | 1 | 4 | 1 | 0.9 | 1.0 |
| Birch sets [14] | ||||||||||
| Birch1 | 100 | 100 | 34% | 95 | 14% | 0 | 9 | 4 | 6.6 | 5.5 |
| Birch2 | 100 | 100 | 9% | 100 | 3% | 0 | 0 | 0 | 16.6 | 7.3 |
| Birch3 | 100 | 21 | 2% | |||||||
| 35 | 11% | |||||||||
| 42 | 32% | 41 | 6% | 58 | 59 | 16 | --- | --- | ||
| Dim sets [15,16] | ||||||||||
| Dim-32 | 16 | 16 | 50% | 16 | 29% | 0 | 0 | 0 | 3.6 | 0.0 |
| Dim-64 | 16 | 16 | 47% | 16 | 27% | 0 | 0 | 0 | 3.7 | --- |
| Dim-128 | 16 | 16 | 51% | 16 | 32% | 0 | 0 | 0 | 3.8 | --- |
| Dim-256 | 16 | 16 | 60% | 16 | 34% | 0 | 0 | 0 | 3.9 | --- |
| Dim-512 | 16 | 15 | 71% | 16 | 25% | 1 | 0 | 0 | 4.1 | --- |
| Dim-1024 | 16 | 16 | 78% | 16 | 26% | 0 | 0 | 0 | 3.8 | --- |
| Unbalance [17] | ||||||||||
| Unbalance | 8 | 8 | 1 % | 8 | 4 % | 0 | 0 | 0 | 3.6 | 0.9 |
| Shape sets | ||||||||||
| Aggregation [18] | 7 | 7 | 9% | --- | --- % | --- | --- | --- | --- | --- |
| Compound [19] | 6 | 5 | 27% | --- | --- % | --- | --- | --- | --- | --- |
| D31 [20] | 31 | 31 | 17% | --- | --- % | --- | --- | --- | --- | --- |
| Flame [3] | 2 | 2 | 15% | --- | --- % | --- | --- | --- | --- | --- |
| Jain [21] | 2 | 3 | 1% | --- | --- % | --- | --- | --- | --- | --- |
| Path-based [22] | 3 | 13 | 3% | 13 | 3% | --- | --- | --- | --- | --- |
| R15 [20] | 15 | 15 | 5% | --- | --- % | --- | --- | --- | --- | --- |
| Spiral [22] | 3 | 3 | 0% | --- | --- % | --- | --- | --- | --- | --- |
| t4.8k [2] | 6 | 6 | 13% | --- | --- % | --- | --- | --- | --- | --- |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lemke, O.; Keller, B.G. Common Nearest Neighbor Clustering—A Benchmark. Algorithms 2018, 11, 19. https://doi.org/10.3390/a11020019
Lemke O, Keller BG. Common Nearest Neighbor Clustering—A Benchmark. Algorithms. 2018; 11(2):19. https://doi.org/10.3390/a11020019
Chicago/Turabian StyleLemke, Oliver, and Bettina G. Keller. 2018. "Common Nearest Neighbor Clustering—A Benchmark" Algorithms 11, no. 2: 19. https://doi.org/10.3390/a11020019
APA StyleLemke, O., & Keller, B. G. (2018). Common Nearest Neighbor Clustering—A Benchmark. Algorithms, 11(2), 19. https://doi.org/10.3390/a11020019




