Vertex Cover Reconfiguration and Beyond ^†

Abstract

In the Vertex Cover Reconfiguration (VCR) problem, given a graph G, positive integers k and ℓ and two vertex covers S and T of G of size at most k, we determine whether S can be transformed into T by a sequence of at most ℓ vertex additions or removals such that every operation results in a vertex cover of size at most k. Motivated by results establishing the $\mathsf{W}\left[\mathsf{1}\right]$-hardness of VCR when parameterized by ℓ, we delineate the complexity of the problem restricted to various graph classes. In particular, we show that VCR remains $\mathsf{W}\left[\mathsf{1}\right]$-hard on bipartite graphs, is $\mathsf{NP}$-hard, but fixed-parameter tractable on (regular) graphs of bounded degree and more generally on nowhere dense graphs and is solvable in polynomial time on trees and (with some additional restrictions) on cactus graphs.

1. Introduction

Under the reconfiguration framework, we consider structural and algorithmic questions related to the solution space of a search problem $\mathcal{Q}$. Given an instance $\mathcal{I}$, an optional range $[r_l,r_u]$ bounding a numerically-quantifiable property $\mathsf{\Psi }$ of feasible solutions for $\mathcal{Q}$ and a symmetric adjacency relation (usually polynomially-testable) $\mathcal{A}$ on the set of feasible solutions, we can construct a reconfiguration graph ${\mathcal{R}}_{\mathcal{Q}}(\mathcal{I},r_l,r_u)$ for each instance $\mathcal{I}$ of $\mathcal{Q}$. The nodes of ${\mathcal{R}}_{\mathcal{Q}}(\mathcal{I},r_l,r_u)$ correspond to the feasible solutions of $\mathcal{I}$ having $r_l\le \mathsf{\Psi }\le r_u$, and there is an edge between two nodes whenever the corresponding solutions are adjacent under $\mathcal{A}$. An edge can be seen as a reconfiguration step transforming one solution into the other. Given two feasible solutions for $\mathcal{I}$, S and T, one can ask if there exists a walk (reconfiguration sequence) in $R_{\mathcal{Q}}(\mathcal{I},r_l,r_u)$ from S to T, or for the shortest such walk. On the structural side, one can ask about the diameter of reconfiguration graph ${\mathcal{R}}_{\mathcal{Q}}(\mathcal{I},r_l,r_u)$ or whether it is connected with respect to some or any $\mathcal{I}$, fixed $\mathcal{A}$ and fixed $\mathsf{\Psi }$.

These types of reconfiguration questions have received considerable attention in recent years [1,2,3,4,5] and are interesting for a variety of reasons. From an algorithmic standpoint, reconfiguration problems model dynamic situations in which we seek to transform a solution into a more desirable one, maintaining feasibility during the process. Reconfiguration also models questions of evolution; it can represent the evolution of a genotype where only individual mutations are allowed and all genotypes must satisfy a certain fitness threshold, i.e., be feasible. Moreover, the study of reconfiguration yields insights into the structure of the solution space of the underlying problem, crucial for the design of efficient algorithms. In fact, one of the initial motivations behind such questions was to study the performance of heuristics [2] and random sampling methods [6], where connectivity and other properties of the solution space play a crucial role.

Reconfiguration problems have been studied mainly under classical complexity assumptions, with most work devoted to determining the existence of a reconfiguration sequence between two given solutions. For most $\mathsf{NP}$-complete problems, this question has been shown to be $\mathsf{PSPACE}$-complete [3,7,8], while for some problems in $\mathsf{P}$, the reconfiguration question could be either in $\mathsf{P}$ [3] or $\mathsf{PSPACE}$-complete [9]. As $\mathsf{PSPACE}$-completeness implies that the number of vertices in reconfiguration graphs, and therefore the length of reconfiguration sequences, can be superpolynomial in the number of vertices in the input graph, it is natural to ask whether we can achieve tractability if we restrict the length of the sequence or other properties of the problem to a fixed constant. These results motivated Mouawad et al. [10] to study reconfiguration under the parameterized complexity framework [11,12].

The Vertex Cover Reconfiguration (VCR) problem was shown to be fixed-parameter tractable when parameterized by k and $\mathsf{W}\left[\mathsf{1}\right]$-hard when parameterized by ℓ [10]; in ${\mathcal{R}}_{\mathsf{VC}}(G,0,k)$, each feasible solution for instance G is a vertex cover of size at most k (a subset $S\subseteq V\left(G\right)$ such that each edge of the graph has at least one endpoint in S) and two solutions are adjacent if one can be obtained from the other by the addition or removal of a single vertex of G. Motivated by these results, we embark on a systematic investigation of the parameterized complexity of the problem restricted to various graph classes.

In Section 4, we start by showing that the VCR problem parameterized by ℓ remains $\mathsf{W}\left[\mathsf{1}\right]$-hard when restricted to bipartite graphs. To obtain this result, we introduce the $(t,d)$-bipartite constrained crown problem and show that it plays a central role for determining the complexity of the reconfiguration problem. As the vertex cover is solvable in polynomial time on bipartite graphs, this result provides an example of a search problem in $\mathsf{P}$ whose reconfiguration version is $\mathsf{W}\left[\mathsf{1}\right]$-hard parameterized by ℓ, answering a question left open by Mouawad et al. [10]. In Section 5, we characterize instances of the VCR problem solvable in time polynomial in $|V(G)|$ and apply this characterization to trees, graphs with no even cycles and (with some additional restrictions) to cactus graphs (we incorrectly claimed to have proved the result for cactus graphs in its full generality in an earlier version of this paper [13]). We note that a polynomial-time algorithm for even-hole-free graphs was also independently obtained by Kamiński et al. [8] for solving several variants of the closely-related independent set reconfiguration problem. Moreover, VCR is known to be $\mathsf{PSPACE}$-complete on graphs of bounded treewidth [14] (for some constant value of treewidth), but it remains open whether the problem is $\mathsf{PSPACE}$-complete already for graphs of treewidth at most two, or even outerplanar graphs. Our result on cactus graphs is a first step towards settling these questions. In Section 6, we present the first fixed-parameter tractable algorithm for VCR parameterized by ℓ on graphs of bounded degree after establishing the $\mathsf{NP}$-hardness of the problem on four-regular graphs. Finally, we show using completely different techniques, and at the cost of a much worse running time, that VCR, as well as a host of other reconfiguration problems are fixed-parameter tractable on nowhere dense classes of graphs.

2. Preliminaries

For general graph theoretic definitions, we refer the reader to the book of Diestel [15]. Unless otherwise stated, we assume that each graph G is a simple undirected graph with vertex set $V\left(G\right)$ and edge set $E\left(G\right)$, where $|V(G)|=n$ and $|E(G)|=m$. The open neighbourhood of a vertex v is denoted by $N_G\left(v\right)=\{u\mid uv\in E\left(G\right)\}$ and the closed neighbourhood by $N_G\left[v\right]=N_G\left(v\right)\cup \left\{v\right\}$. For a set of vertices $A\subseteq V\left(G\right)$, we define $N_G\left(A\right)=\{v\notin A\mid uv\in E\left(G\right),u\in A\}$ and $N_G\left[A\right]=N_G\left(A\right)\cup A$. The subgraph of G induced by A is denoted by $G\left[A\right]$, where $G\left[A\right]$ has vertex set A and edge set $\{uv\in E(G)\mid u,v\in A\}$.

A walk of length q from $v_0$ to $v_q$ in G is a vertex sequence $v_0,\dots ,v_q$ such that, for all $i\in \{0,\dots ,q-1\}$, $v_i{v}_{i+1}\in E\left(G\right)$. It is a path if all vertices are distinct and a cycle if $q\ge 3$, $v_0=v_q$, and $v_0,\dots ,v_{q-1}$ is a path. A matching $\mathcal{M}\left(G\right)$ on a graph G is a set of edges of G such that no two edges share a vertex; we use $V\left(\mathcal{M}\right(G\left)\right)$ to denote the set of vertices incident to edges in $\mathcal{M}\left(G\right)$. A set of vertices $A\subseteq V\left(G\right)$ is said to be saturated by $\mathcal{M}\left(G\right)$ if $A\subseteq V\left(\mathcal{M}\right(G\left)\right)$.

To avoid confusion, we refer to nodes in reconfiguration graphs, as distinguished from vertices in the input graph. We denote an instance of the vertex cover reconfiguration problem by $(G,S,T,k,\ell )$, where G is the input graph, S and T are the source and target vertex covers, respectively, k is the maximum allowed capacity and ℓ is an upper bound on the length of the reconfiguration sequence we seek. By a slight abuse of notation, we use upper case letters to refer to both a node in the reconfiguration graph, as well as the corresponding vertex cover. For any node $S\in V\left({\mathcal{R}}_{\mathsf{VC}}(G,0,k)\right)$, the quantity $k-|S|$ corresponds to the available capacity at S. We partition $V\left(G\right)$ into the sets $C_{ST}=S\cap T$ (vertices common to S and T), $S_R=S\backslash C_{ST}$ (vertices to be removed from S in the course of reconfiguration), $T_A=T\backslash C_{ST}$ (vertices to be added to form T) and $O_{ST}=V\left(G\right)\backslash (S\cup T)=V\left(G\right)\backslash (C_{ST}\cup S_R\cup T_A)$ (all other vertices). To simplify notation, we sometimes use $G_{\Delta }$ to denote the graph induced by the vertices in the symmetric difference of S and T, i.e., $G_{\Delta }=G[S\Delta T]=G[S_R\cup T_A]$. We say a vertex is touched in the course of a reconfiguration sequence from S to T if v is either added or removed at least once. We say a vertex v, in a vertex cover S, is removable if and only if $v\in S$ and $N_G\left(v\right)\subseteq S$.

Proposition 1.

For any graph G and any two vertex covers S and T of G, $G_{\Delta }=G[S_R\cup T_A]$ is bipartite. Moreover, there are no edges between vertices in $S_R\cup T_A$ and vertices in $O_{ST}$.

Proof. 

None of the vertices in $S_R$ are included in T. Since T is a vertex cover of G, each edge of G must have an endpoint in T, and hence, $G\left[S_R\right]$ must be an independent set. Similar arguments apply to $G\left[T_A\right]$ and to show that there are no edges between vertices in $S_R\cup T_A$ and vertices in $O_{ST}$. ☐

Proposition 2.

For a graph G and any two vertex covers S and T of G, any vertex in $S_R\cup T_A$ must be touched an odd number of times and any vertex not in $S_R\cup T_A$ must be touched an even number of times in any reconfiguration sequence of length at most ℓ from S to T. Moreover, any vertex can be touched at most $\ell -|S_R\cup T_A|+1$ times.

Throughout this work, we implicitly consider the vertex cover reconfiguration problem as a parameterized problem with ℓ as the parameter. The reader is referred to the books of Downey and Fellows for more on parameterized complexity [11,12].

3. Representing Reconfiguration Sequences

There are multiple ways of representing a reconfiguration sequence between two vertex covers of a graph G. In Section 4 and Section 5, we focus on a representation that consists of an ordered sequence of vertex covers or nodes in the reconfiguration graph. Given a graph G and two vertex covers of G, $A_0$ and $A_j$, we denote a reconfiguration sequence from $A_0$ to $A_j$ by $\alpha =(A_0,A_1,\dots ,A_j)$, where $A_i$ is a vertex cover of G and $A_i$ is obtained from $A_{i-1}$ by either the removal or the addition of a single vertex from $A_{i-1}$ for all $0<i\le j$. For any pair of consecutive vertex covers ($A_{i-1}$, $A_i$) in $\alpha$, we say $A_i$ ($A_{i-1}$) is the successor (predecessor) of $A_{i-1}$ ($A_i$). A reconfiguration sequence $\beta =(A_0,A_1,\dots ,A_i)$ is a prefix of $\alpha =(A_0,A_1,\dots ,A_j)$ if $i<j$.

In Section 6, we use the notion of edit sequences. We assume all vertices of G are labelled from one to n, i.e., $V\left(G\right)=\{v_1,v_2,\dots ,v_n\}$. We let ${\mathcal{E}}_a=\{a_1,\dots ,a_n\}$ and ${\mathcal{E}}_r=\{r_1,\dots ,r_n\}$ denote the sets of addition markers and removal markers, respectively. An edit sequence $\alpha$ is an ordered sequence of elements obtained from the full set of markers $\mathcal{E}={\mathcal{E}}_a\cup {\mathcal{E}}_r$, where $a_i$ stands for the addition of vertex $v_i$, $r_j$ stands for the removal of vertex $v_j$ and $1\le i,j\le n$. The length of $\alpha$, $|\alpha |$, is equal to the total number of markers in $\alpha$. We let $\alpha \left[p\right]\in \mathcal{E}$, $1\le p\le |\alpha |$, denote the marker at position p in $\alpha$. We say $\beta$ is a segment of $\alpha$ whenever $\beta$ consists of a subsequence of $\alpha$ with no gaps. The length of a segment is defined as the total number of markers it contains. We use the notation $\alpha [p_1,p_2]$, $1\le p_1,p_2\le |\alpha |$, to denote the segment starting at position $p_1$ and ending at position $p_2$. Two segments $\beta$ and ${\beta }^{\prime }$ are consecutive whenever ${\beta }^{\prime }$ occurs later than $\beta$ in $\alpha$ and there are no gaps between $\beta$ and ${\beta }^{\prime }$. For any pair of consecutive segments $\beta$ and ${\beta }^{\prime }$ in $\alpha$, we say ${\beta }^{\prime }$ ($\beta$) is the successor (predecessor) of $\beta$ (${\beta }^{\prime }$). Given an edit sequence $\alpha$, a segment $\beta$ of $\alpha$ is a maximal addition segment if $\beta$ is a maximal subsequence of $\alpha$ consisting of only addition markers and no gaps. Similarly, $\beta$ is a maximal removal segment if $\beta$ is a maximal subsequence of $\alpha$ consisting of only removal markers and no gaps.

We now discuss how edit sequences relate to reconfiguration sequences. Given a graph G and an edit sequence $\alpha$, we use $V\left(\alpha \right)$ to denote the set of vertices touched in $\alpha$, i.e., $V\left(\alpha \right)=\{v_i\mid a_i\in \alpha \vee r_i\in \alpha \}$. We let $V(S,\alpha )$ denote the set of vertices obtained after executing all reconfiguration steps in $\alpha$ on G starting from some vertex cover S of G. We say $\alpha$ is valid whenever every set $V(S,\alpha [1,p\left]\right)$, $1\le p\le |\alpha |$, is a vertex cover of G, and we say $\alpha$ is invalid otherwise. Note that even if $|S|\le k$, $\alpha$ is not necessarily a walk in the reconfiguration graph ${\mathcal{R}}_{\mathsf{VC}}(G,0,k)$, as $\alpha$ might violate the maximum allowed capacity constraint k. Hence, we let $\mathsf{cap}\left(\alpha \right)={\mathsf{max}}_{1\le p\le |\alpha |}(|V(S,\alpha [1,p])|)$, and we say $\alpha$ is tight whenever it is valid and $\mathsf{cap}\left(\alpha \right)\le k$.

Proposition 3.

Given a graph G and two vertex covers S and T of G, an edit sequence α is a reconfiguration sequence from S to T if and only if α is a tight edit sequence from S to T.

4. Hardness Results

In earlier work establishing the $\mathsf{W}\left[\mathsf{1}\right]$-hardness of the VCR problem parameterized by ℓ on general graphs, it was also shown that the problem becomes fixed-parameter tractable whenever $\ell =|S_R\cup T_A|$ [10] (as we know exactly which vertices have to be touched, it is only a question of finding the right order of additions and removals). When $|S_R\cup T_A|=n$, we know from Proposition 2 that $\ell \ge n$, since every vertex in $S_R\cup T_A$ must be touched at least once. Moreover, Proposition 1 implies that whenever $|S_R\cup T_A|=n$, the input graph must be bipartite. It is thus natural to ask about the complexity of the problem when $\ell <n$ and the input graph is restricted to be bipartite. Since the vertex cover problem is known to be solvable in time polynomial in n on bipartite graphs, our result is, to the best of our knowledge, the first example of a problem solvable in polynomial time whose reconfiguration version is $\mathsf{W}\left[\mathsf{1}\right]$-hard.

For a graph G, a crown is a pair $(W,H)$ satisfying the following properties: (i) $W\ne Ø$ is an independent set of G; (ii) $N_G\left(W\right)=H$; and (iii) there exists a matching in $G[W\cup H]$ that saturates H [16,17]. H is called the head of the crown, and the width of the crown is $|H|$. Crown structures have played a central role in the development of efficient kernelization algorithms for the vertex cover problem [16,17]. We define the closely-related notion of $(t,d)$-constrained crowns and show in the remainder of this section that the complexity of finding such structures in a bipartite graph is central for determining the complexity of the reconfiguration problem.

We define a $(t,d)$-constrained crown as a pair $(W,H)$ satisfying all properties of a regular crown with the additional constraints that $|H|\le t$ and $|W|-|H|\ge d\ge 0$. We are now ready to introduce the $(t,d)$-Bipartite Constrained Crown problem, or $(t,d)$-BCC, which is formally defined as follows:

$(t,d)$-bipartite constrained crown
Input:	A bipartite graph $G=(A\cup B,E)$ and two positive integers t and d
Parameters:	t and d
Question:	Does G have a $(t,d)$-constrained crown $(W,H)$ such that $W\subseteq A$ and $H\subseteq B$?

Lemma 1.

The $(t,d)$-bipartite constrained crown is $\mathsf{W}\left[\mathsf{1}\right]$-hard even when the input graph, $G=(A\cup B,E)$, is $C_4$-free and all vertices in A have degree at most two.

Proof. 

We give a reduction from the k-clique, known to be $\mathsf{W}\left[\mathsf{1}\right]$-hard, to the $(k,(\genfrac{}{}{0pt}{}{k}{2}))$-bipartite constrained crown. For $(G,k)$ an instance of k-clique, we let $V\left(G\right)=\{v_1,\dots ,v_n\}$ and $E\left(G\right)=\{e_1,\dots ,e_m\}$.

We first form a bipartite graph $G^{\prime }=((X\cup Z)\cup Y,E_1\cup E_2)$, where vertex sets X and Y contain one vertex for each vertex in $V\left(G\right)$ and Z contains one vertex for each edge in $E\left(G\right)$. More formally, we set $X=\{x_1,\dots ,x_n\}$, $Y=\{y_1,\dots ,y_n\}$, and $Z=\{z_1,\dots ,z_m\}$. The edges in $E_1$ join each pair of vertices $x_i$ and $y_i$ for $1\le i\le n$ and the edges in $E_2$ join each vertex z in Z to the two vertices $y_i$ and $y_j$ corresponding to the endpoints of the edge in $E\left(G\right)$ to which z corresponds. Since each edge either joins vertices in X and Y or vertices in Y and Z, it is not difficult to see that the vertex sets $X\cup Z$ and Y form a bipartition.

By our construction, $G^{\prime }$ is $C_4$-free; vertices in X have degree one, and since there are no double edges in G, i.e., two edges between the same pair of vertices, no pair of vertices in Y can have more than one common neighbour in Z. For $(G^{\prime },k,(\genfrac{}{}{0pt}{}{k}{2}))$ an instance of $(k,(\genfrac{}{}{0pt}{}{k}{2}))$-BCC, $A=X\cup Z$ and $B=Y$, we claim that G has a clique of size k if and only if $G^{\prime }$ has a $(k,(\genfrac{}{}{0pt}{}{k}{2}))$-constrained crown $(W,H)$ such that $W\subseteq A$ and $H\subseteq B$.

If G has a clique K of size k, we set $H=\{y_i\mid v_i\in V\left(K\right)\}$, namely the vertices in Y corresponding to the vertices in the clique. To form W, we choose $\{x_i\mid v_i\in V\left(K\right)\}\cup \{z_i\mid e_i\in E\left(K\right)\}$, that is the vertices in X corresponding to the vertices in the clique and the vertices in Z corresponding to the edges in the clique. Clearly, H is a subset of size k of B, and W is a subset of size $k+(\genfrac{}{}{0pt}{}{k}{2})$ of A; this implies that $|W|-|H|\ge d=(\genfrac{}{}{0pt}{}{k}{2})$, as required. To see why $N_{G^{\prime }}\left(W\right)=H$, it suffices to note that every vertex $x_i\in W$ is connected to exactly one vertex $y_i\in H$, and every degree-two vertex $z_i\in W$ corresponds to an edge in K whose endpoints $v_i{v}_j$ must have corresponding vertices in H. Moreover, due to $E_1$, there is a matching between the vertices of H and the vertices of W in X and, hence, a matching in $G^{\prime }[W\cup H]$ that saturates H.

We now assume that $G^{\prime }$ has a $(k,(\genfrac{}{}{0pt}{}{k}{2}))$-constrained crown $(W,H)$ such that $W\subseteq X\cup Z$ and $H\subseteq Y$. It suffices to show that $|H|$ must be equal to k, $|W\cap Z|$ must be equal to $($ and, hence, $|W\cap X|$ must be equal to k; from this, we can conclude that the vertices in $\{v_i\mid y_i\in H\}$ form a clique of size k in G as $|W\cap Z|=(\genfrac{}{}{0pt}{}{k}{2})$, requiring that edges exist between each pair of vertices in the set $\{v_i\mid y_i\in H\}$. Moreover, since $|W\cap X|=k$ and $N_{G^{\prime }}\left(W\right)=H$, a matching that saturates H can be easily found by simply picking all edges $x_i{y}_i$ for $y_i\in H$.

To prove the sizes of H and W, we first observe that since $|H|\le k$, $N_{G^{\prime }}\left(W\right)=H$, and each vertex in Y has exactly one neighbour in X, we know that $|W\cap X|\le |H|\le k$. Moreover, since $|W|=|W\cap X|+|W\cap Z|$ and $|W|-|H|\ge (\genfrac{}{}{0pt}{}{k}{2})$, we know that $|W\cap Z|=|W|-|W\cap X|\ge (\genfrac{}{}{0pt}{}{k}{2})+|H|-|W\cap X|\ge (\genfrac{}{}{0pt}{}{k}{2})$. If $|W\cap Z|=(\genfrac{}{}{0pt}{}{k}{2})$, our proof is complete, since by our construction of $G^{\prime }$, H is a set of at most k vertices in the original graph G, and the subgraph induced by those vertices in G has $(\genfrac{}{}{0pt}{}{k}{2})$ edges. Hence, $|H|$ must be equal to k. Suppose instead that $|W\cap Z|>(\genfrac{}{}{0pt}{}{k}{2})$. In this case, since each vertex of Z has degree two, the number of neighbours of $W\cap Z$ in Y is greater than k, violating the assumptions that $N_{G^{\prime }}\left(W\right)=H$ and $|H|\le k$. ☐

We can now show the main result of this section:

Theorem 1.

VCR parameterized by ℓ and restricted to bipartite graphs is $\mathsf{W}\left[\mathsf{1}\right]$-hard.

Proof. 

We give a reduction from the $(t,d)$-bipartite constrained crown to vertex cover reconfiguration in bipartite graphs. For $(G=(A\cup B,E),t,d)$, an instance of the $(t,d)$-bipartite constrained crown, $A=\{a_1,\dots ,a_{|A|}\}$ and $B=\{b_1,\dots ,b_{|B|}\}$, we form $G^{\prime }=(X\cup Y\cup U\cup V,E_1\cup E_2)$ such that X and Y correspond to the vertex sets A and B, $E_1$ connects vertices in X and Y corresponding to vertices in A and B joined by edges in G and U, V and $E_2$ form a complete bipartite graph $K_{d+t,d+t}$. More formally, $X=\{x_1,\dots ,x_{|A|}\}$, $Y=\{y_1,\dots ,y_{|B|}\}$, $U=\{u_1,\dots ,u_{d+t}\}$, $V=\{v_1,\dots ,v_{d+t}\}$, $E_1=\{x_i{y}_j\mid a_i{b}_j\in E\left(G\right)\}$ and $E_2=\{u_i{v}_j\mid 1\le i\le d+t,1\le j\le d+t\}$.

We let $(G^{\prime },S,T,k=|A|+d+2t,\ell =4d+6t)$ be an instance of VCR, where $S=X\cup U$ and $T=X\cup V$. Clearly, $|S|=|T|=|A|+d+t$. We claim that G has a $(k,d)$-constrained crown $(W,H)$ such that $W\subseteq A$ and $H\subseteq B$ if and only if there is a path of length at most $4d+6t$ from S to T.

If G has such a pair $(W,H)$, we form a reconfiguration sequence of length at most $4d+6t$ as follows:

(1)

Add each vertex $y_i$ such that $b_i\in H$. The resulting vertex cover size is $|A|+d+t+|H|$.

(2)

Remove $d+|H|$ vertices $x_i$ such that $a_i\in W$. The resulting vertex cover size is $|A|+t$.

(3)

Add each vertex from V. The resulting vertex cover size is $|A|+d+2t$.

(4)

Remove each vertex from U. The resulting vertex cover size is $|A|+t$.

(5)

Add each vertex removed in Phase 2. The resulting vertex cover size is $|A|+d+t+|H|$.

(6)

Remove each vertex added in Phase 1. The resulting vertex cover size is $|A|+d+t$.

The length of the sequence follows from the fact that $|H|\le t$: Phases 1 and 6 consist of at most t steps each and Phases 2, 3, 4 and 5 of at most $d+t$ steps each. The fact that each set forms a vertex cover is a consequence of the fact that $N_G\left(W\right)=H$.

For the converse, we observe that before removing any vertex $u_i$, $1\le i\le d+t$, from U, we first need to add all $d+t$ vertices from V. Therefore, if there is a path of length at most $4d+6t$ from S to T, then we can assume without loss of generality that there exists a node Q (i.e., a vertex cover) along this path such that:

$$|Q|\le |A|+t\mathrm{and},$$

all vertices that were touched in order to reach node Q belong to $X\cup Y$.

In other words, at node Q, the available capacity is greater than or equal to $d+t$, and all edges in $G[U\cup V]$ are still covered by U. We let $Q_{\mathrm{IN}}=Q\backslash S$ and $Q_{\mathrm{OUT}}=S\backslash Q$. Since $S=X\cup U$, $Q_{\mathrm{IN}}\subseteq Y$ and $Q_{\mathrm{OUT}}\subseteq X$. Moreover, since $|Q|=|S|+|Q_{\mathrm{IN}}|-|Q_{\mathrm{OUT}}|=|A|+d+t+|Q_{\mathrm{IN}}|-|Q_{\mathrm{OUT}}|\le |A|+t$, we know that $|Q_{\mathrm{OUT}}|-|Q_{\mathrm{IN}}|$ must be greater than or equal to d. Given that $\ell \le 4d+6t$ and we need exactly $2d+2t$ steps to add all vertices in V and remove all vertices in U, we have $2d+4t$ remaining steps to allocate elsewhere. Therefore, $|Q_{\mathrm{OUT}}|+|Q_{\mathrm{IN}}|\le d+2t$ as $Q_{\mathrm{IN}}\subseteq Y$, $Q_{\mathrm{OUT}}\subseteq X$, and every vertex in $Q_{\mathrm{IN}}\cup Q_{\mathrm{OUT}}$ must be touched at least twice (i.e., added and then removed). Combining those observations, we get:

$$\begin{gathered} |Q_{\mathrm{OUT}}|+|Q_{\mathrm{IN}}|\le d+2t \\ |Q_{\mathrm{IN}}|-|Q_{\mathrm{OUT}}|\le -d \\ |Q_{\mathrm{IN}}|\le t \end{gathered}$$

We have just shown that G has a pair $(Q_{\mathrm{OUT}},Q_{\mathrm{IN}})$ such that $Q_{\mathrm{OUT}}\subseteq X$, $Q_{\mathrm{IN}}\subseteq Y$, $|Q_{\mathrm{IN}}|\le t$, $|Q_{\mathrm{OUT}}|-|Q_{\mathrm{IN}}|\ge d\ge 0$, and $N_G\left(Q_{\mathrm{OUT}}\right)=Q_{\mathrm{IN}}$, as otherwise some edge is not covered. The remaining condition for $(Q_{\mathrm{OUT}},Q_{\mathrm{IN}})$ to satisfy is for $G[Q_{\mathrm{OUT}}\cup Q_{\mathrm{IN}}]$ to have a matching that saturates $Q_{\mathrm{IN}}$. Hall’s marriage theorem [18] states that such a saturating matching exists if and only if for every subset P of $Q_{\mathrm{IN}}$, $|P|\le |N_{G[Q_{\mathrm{OUT}}\cup Q_{\mathrm{IN}}]}\left(P\right)|$. By a simple application of Hall’s theorem, if no such matching exists, then there exists a subgraph Z of $G[Q_{\mathrm{OUT}}\cup Q_{\mathrm{IN}}]$ such that $|V\left(Z\right)\cap Q_{\mathrm{OUT}}|<|V\left(Z\right)\cap Q_{\mathrm{IN}}|$. By deleting this subgraph from $Q_{\mathrm{OUT}}\cup Q_{\mathrm{IN}}$, we can get a new pair $(Q_{\mathrm{OUT}}^{\prime },Q_{\mathrm{IN}}^{\prime })$, which must still satisfy $Q_{\mathrm{OUT}}^{\prime }\subseteq X$, $Q_{\mathrm{IN}}^{\prime }\subseteq Y$, $|Q_{\mathrm{IN}}^{\prime }|\le t$, $|Q_{\mathrm{OUT}}^{\prime }|-|Q_{\mathrm{IN}}^{\prime }|\ge d\ge 0$ and $N_G\left(Q_{\mathrm{OUT}}^{\prime }\right)=Q_{\mathrm{IN}}^{\prime }$, since we delete more vertices from $Q_{\mathrm{IN}}$ than we do from $Q_{OUT}$ and $N_{G[Q_{\mathrm{OUT}}\cup Q_{\mathrm{IN}}]}(V\left(Z\right)\cap Q_{\mathrm{IN}})=V\left(Z\right)\cap Q_{\mathrm{OUT}}$. Finally, if $(Q_{\mathrm{OUT}}^{\prime },Q_{\mathrm{IN}}^{\prime })$ does not have a matching that saturates $Q_{\mathrm{IN}}^{\prime }$, we can repeatedly apply the same rule until we reach a pair that satisfies all the required properties. Since $|Q_{\mathrm{OUT}}|\ge |Q_{\mathrm{IN}}|$, such a pair is guaranteed to exist, as otherwise every subset P of $Q_{\mathrm{IN}}$ would satisfy $|P|>|N_{G[Q_{\mathrm{OUT}}\cup Q_{\mathrm{IN}}]}\left(P\right)|$ and hence $|Q_{\mathrm{OUT}}|<|Q_{\mathrm{IN}}|$, a contradiction. ☐

5. Polynomial-Time Algorithms

In this section, we present a characterization of instances of the VCR problem solvable in time polynomial in n, and apply this characterization to trees, graphs with no even cycles (as subgraphs) and to cactus graphs (with some additional restrictions). We show how to find reconfiguration sequences of the shortest possible length and therefore ignore the parameter ℓ. Unless stated otherwise, reconfiguration sequences are represented as ordered sequences of vertex covers or nodes in the reconfiguration graph.

Definition 1.

Given two vertex covers of G, A and B, a reconfiguration sequence β from A to some vertex cover $A^{\prime }$ is a c-bounded prefix of a reconfiguration sequence α from A to B, if and only if all of the following conditions hold:

(1) 

$|A^{\prime }|\le |A|$;

(2) 

For every node $A^{″}$ in β, $|A^{″}|\le |A|+c$;

(3) 

For every node $A^{″}$ in β, $A^{″}$ is obtained from its predecessor by either the removal or the addition of a single vertex in the symmetric difference of the predecessor and B;

(4) 

No vertex is touched more than once in the course of β.

We write $A\stackrel{c,B}{\leftrightarrow }{A}^{\prime }$ when such a c-bounded prefix exists.

Proposition 4.

Given two vertex covers S and T of G, if G has a vertex cover $S^{\prime }$ such that $S\stackrel{c,T}{\leftrightarrow }{S}^{\prime }$, then $S\stackrel{d,T}{\leftrightarrow }{S}^{\prime }$ for all $d>c$.

Lemma 2.

Given two vertex covers S and T of G and two positive integers k and c such that $|S|,|T|\le k$, a reconfiguration sequence α of length $|S_R|+|T_A|=|S\Delta T|$ from S to T exists if:

(1) 

$|S|\le k-c$;

(2) 

$|T|\le k-c$; and

(3) 

For any two vertex covers A and B of G such that $|A|\le k-c$ and $|B|\le k-c$, either $A\stackrel{c,B}{\leftrightarrow }{A}^{\prime }$ or $B\stackrel{c,A}{\leftrightarrow }{B}^{\prime }$, where $A^{\prime }$ and $B^{\prime }$ are vertex covers of G.

Moreover, if c-bounded prefixes can be found in time polynomial in n, then α can be found in time polynomial in n.

Proof. 

We prove the lemma by induction on $|S\Delta T|$. When $|S\Delta T|=0$, S is equal to T, and the claim holds trivially since $|\alpha |=0$.

When $|S\Delta T|>0$, we know that either $S\stackrel{c,T}{\leftrightarrow }{S}^{\prime }$ or $T\stackrel{c,S}{\leftrightarrow }{T}^{\prime }$. Without loss of generality, we assume $S\stackrel{c,T}{\leftrightarrow }{S}^{\prime }$ and let $\beta$ denote the c-bounded prefix from S to $S^{\prime }$. From Definition 1, we know that the size of every node in $\beta$ is no greater than $|S|+c\le k$. Therefore, the maximum allowed capacity constraint is never violated.

Since $|S^{\prime }|\le |S|$ (Definition 1), by the induction hypothesis, there exists a reconfiguration sequence from $S^{\prime }$ to T whose length is $|S^{\prime }\Delta T|$. By appending the reconfiguration sequence from $S^{\prime }$ to T to the reconfiguration sequence from S to $S^{\prime }$, we obtain a reconfiguration sequence $\alpha$ from S to T.

To show that $|\alpha |=|S\Delta T|$, it suffices to show that $|\beta |+|S^{\prime }\Delta T|=|S\Delta T|$. We know that no vertex is touched more than once in $\beta$, and every touched vertex belongs to $S\Delta T$ (Definition 1). We let $H\subseteq S\Delta T$ denote the set of touched vertices in $\beta$, and we subdivide H into two sets $H_S=H\cap S=H\cap S_R$ and $H_T=H\cap T=H\cap T_A$. It follows that $|\beta |=|H_S|+|H_T|$ and $|S^{\prime }\Delta T|=|S_R\backslash H_S|+|T_A\backslash H_T|$. Therefore, $|\beta |+|S^{\prime }\Delta T|=|H_S|+|H_T|+|S_R\backslash H_S|+|T_A\backslash H_T|=|S_R|+|T_A|=|S\Delta T|$ as needed.

When c-bounded prefixes can be found in time polynomial in n, the proof gives an algorithm for constructing the full reconfiguration sequence from S to T in time polynomial in n. ☐

5.1. Trees

Theorem 2.

Vertex cover reconfiguration restricted to trees can be solved in time polynomial in n.

Proof. 

We let $(G,S,T,k,\ell )$ be an instance of vertex cover reconfiguration. The proof proceeds in two stages. We start by showing that when G is a tree and S and T are of size at most $k-1$, we can always find one-bounded prefixes $S\stackrel{1,T}{\leftrightarrow }{S}^{\prime }$ or $T\stackrel{1,S}{\leftrightarrow }{T}^{\prime }$ in time polynomial in n. Therefore, we can apply Lemma 2 with $c=1$ to find a reconfiguration sequence of length $|S\Delta T|$ from S to T in time polynomial in n. In the second part of the proof, we show how to handle the remaining cases where S, T or both S and T are of a size greater than $k-1$.

First, we note that every forest either has a degree-zero or a degree-one vertex. Hence, trees and forests are one-degenerate graphs. Since G is a tree, $G[S_R\cup T_A]$ is a forest and is therefore one-degenerate. To find one-bounded prefixes in $G[S_R\cup T_A]$, it is enough to find a vertex of degree at most one, which can clearly be done in time polynomial in n: For any two vertex covers S and T of a tree G such that $S,T\le k-1$, we can always find a vertex $v\in S_R\cup T_A$ having degree at most one in $G[S_R\cup T_A]$. The existence of v guarantees the existence of a one-bounded prefix from either S to some vertex cover $S^{\prime }$ or from T to some vertex cover $T^{\prime }$. When $v\in S_R$ and $|N_{G[S_R\cup T_A]}\left(v\right)|=0$, we have $S\stackrel{0,T}{\leftrightarrow }{S}^{\prime }$, since $S^{\prime }$ is obtained from S by simply removing v. When $v\in S_R$ and $|N_{G[S_R\cup T_A]}\left(v\right)|=1$, we have $S\stackrel{1,T}{\leftrightarrow }{S}^{\prime }$, since $S^{\prime }$ is obtained from S by first adding the unique neighbour of v and then removing v. Similar arguments hold when $v\in T_A$.

Therefore, combining Lemma 2 and the fact that $G[S_R\cup T_A]$ is one-degenerate, we know that if $|S|\le k-1$ and $|T|\le k-1$, a reconfiguration sequence of length $|S_R|+|T_A|$ from S to T can be found in time polynomial in n. Furthermore, since the length of a reconfiguration sequence can never be less than $|S_R|+|T_A|$, the reconfiguration sequence given by Lemma 2 is the shortest path from S to T in the reconfiguration graph.

When S (or T) has size k and is minimal, then we have a no-instance, since neither removing, nor adding a vertex results in a k-vertex cover, and hence, S (or T) will be an isolated node in the reconfiguration graph, with no path to T (or S).

When S, T or both S and T are of size k and are non-minimal, there always exists a reconfiguration sequence from S to T, since S and T can be reconfigured to solutions $S^{\prime }$ and $T^{\prime }$, respectively, of size less than k, to which Lemma 2 can be applied. The only reconfiguration steps from S (or T) of size k are to subsets of S of size $k-1$ (or to subsets of T of size $k-1$); the reconfiguration sequence obtained from Lemma 2 is thus a shortest path. Therefore, we can obtain a shortest path from S to T through a careful selection of $S^{\prime }$ and $T^{\prime }$. There are two cases to consider:

Case (1): $|S|=k$, $|T|=k$, S is non-minimal and T is non-minimal. When both S and T are of size k and are non-minimal, then each must contain at least one removable vertex. Hence, by removing such vertices, we can transform S and T into vertex covers $S^{\prime }$ and $T^{\prime }$, respectively, of size $k-1$. We let u and v be removable vertices in S and T, respectively, and we set $S^{\prime }=S\backslash \left\{u\right\}$ and $T^{\prime }=T\backslash \left\{v\right\}$.

• If $u\in S_R$ and $v\in T_A$, then the length of a shortest reconfiguration sequence from $S^{\prime }$ to $T^{\prime }$ will be $|S^{\prime }\Delta T^{\prime }|=|S\Delta T|-2$. Therefore, accounting for the two additional removals, the length of a shortest path from S to T will be equal to $|S\Delta T|$.
• If $u\in S_R$ and $v\in C_{ST}$, then the length of a shortest reconfiguration sequence from $S^{\prime }$ to $T^{\prime }$ will be $|S^{\prime }\Delta T^{\prime }|=|S\Delta T|-1$. Since v is in $C_{ST}$, it must be removed and added back. Therefore, the length of a shortest path from S to T will be equal to $|S\Delta T|+2$. The same is true when $u\in C_{ST}$ and $v\in T_A$ or when $u=v$ and $u\in C_{ST}$.
• Otherwise, when $u\in C_{ST}$, $v\in C_{ST}$ and $u\ne v$, the length of a shortest path from S to T will be $|S\Delta T|+4$, since we have to touch two vertices in $C_{ST}$ (i.e., two extra additions and two extra removals).

Case (2): $|S|=k$, $|T|=k-1$ and S is non-minimal (similar arguments hold for the symmetric case where $|S|=k-1$, $|T|=k$, and T is non-minimal). Since $|T|=k-1$, we only need to reduce the size of S to $k-1$ in order to apply Lemma 2. Since S is non-minimal, it must contain at least one removable vertex. We let u be a removable vertex in S, and we set $S^{\prime }=S\backslash \left\{u\right\}$.

• If $u\in S_R$, then the length of a shortest reconfiguration sequence from $S^{\prime }$ to T will be $|S^{\prime }\Delta T|=|S\Delta T|-1$. Therefore, accounting for the additional removal, the length of a shortest path from S to T will be equal to $|S\Delta T|$.
• If $u\in C_{ST}$, then the length of a shortest reconfiguration sequence from $S^{\prime }$ to T will be $|S^{\prime }\Delta T|=|S\Delta T|$. Since v is in $C_{ST}$, it must be removed and added back. Therefore, the length of a shortest path from S to T will be equal to $|S\Delta T|+2$.

As there are at most $k^2$ pairs of removable vertices in S and T to check for Case (1), we can exhaustively try all pairs and choose one that minimizes the length of a reconfiguration sequence. Similarly, there are at most k removable vertices to check in Case (2). Consequently, vertex cover reconfiguration on trees can be solved in time polynomial in n. ☐

5.2. Cactus Graphs

A cactus graph G [19] is a connected graph in which every edge belongs to at most one cycle. We let $\mathcal{C}\left(G\right)$ denote the set of all cycles in G. We say vertex $v\in V\left(G\right)$ is a join vertex if v belongs to a cycle and $N_G\left(v\right)\ge 3$.

The following proposition is a consequence of the fact that a maximal matching $\mathcal{M}\left(G\right)$ of a cactus graph G can contain an edge from each cycle in $\mathcal{C}\left(G\right)$.

Proposition 5.

For a cactus graph G, the number of cycles in G is bounded above by the size of a maximum matching $\mathcal{M}\left(G\right)$, i.e., $|\mathcal{C}(G)|\le |\mathcal{M}(G)|$.

The next proposition is a consequence of the fact that for any cactus graph G, we can obtain a spanning tree of G by removing a single edge from every cycle in G.

Proposition 6.

For a cactus graph G and $T_G$ a spanning tree of G, the total number of edges in G is equal to the number of edges in $T_G$ plus the total number of cycles in G, i.e., $|E\left(G\right)|=|E\left(T_G\right)|+|\mathcal{C}\left(G\right)|=|V\left(T_G\right)|-1+|\mathcal{C}\left(G\right)|$.

Any graph with no even cycles (as subgraphs) is a cactus graph [20]. For a graph G with no even cycles and any two vertex covers, S and T, of G, we know that $G[S_R\cup T_A]$ must be a forest, i.e., a bipartite graph with no even cycles (Proposition 1). Proposition 7 follows from the fact that in the proof of Theorem 2, the fact that G is a tree is used only to determine that $G[S_R\cup T_A]$ must be a forest. Therefore, using the same proof as in Theorem 2, we can show:

Proposition 7.

Vertex cover reconfiguration on graphs with no even cycles can be solved in time polynomial in n.

In the remainder of this section, we generalize Proposition 7 to all cactus graphs assuming that the given vertex covers S and T are of size at most $k-2$. To do so, we first show, in Lemmas 3 and 4, that the third condition of Lemma 2 is satisfied for cactus graphs with $c=2$. In Lemma 5, we show how two-bounded prefixes can be found in time polynomial in n, which leads to Theorem 3. We note that a similar result was proven independently by Ito et al. [21] via completely different methods.

Lemma 3.

Given two vertex covers S and T of G, there exists a vertex cover $S^{\prime }$ (or $T^{\prime }$) of G such that $S\stackrel{2,T}{\leftrightarrow }{S}^{\prime }$ (or $T\stackrel{2,S}{\leftrightarrow }{T}^{\prime }$) if one of the following conditions holds:

(1) 

$G[S_R\cup T_A]$ has a vertex $v\in S_R$ ($v\in T_A$) such that $|N_{G[S_R\cup T_A]}\left(v\right)|\le 1$; or

(2) 

there exists a cycle Y in $G[S_R\cup T_A]$ such that all vertices in $Y\cap S_R$ ($Y\cap T_A$) have degree exactly two in $G[S_R\cup T_A]$.

Moreover, both conditions can be checked in time polynomial in n, and when one of them is true, the corresponding two-bounded prefix can be found in time polynomial in n.

Proof. 

First, we note that checking for Condition (1) can be accomplished in time polynomial in n by simply inspecting the degree of every vertex in $G[S_R\cup T_A]$. The total number of cycles satisfying condition (2) is linear in the number of degree-two vertices in $G[S_R\cup T_A]$. Therefore, we can check for Condition (2) in time polynomial in n by a simple breadth-first search starting from every degree-two vertex in $G[S_R\cup T_A]$.

If $G[S_R\cup T_A]$ has a vertex $v\in S_R$ of degree zero, we let $S^{\prime }$ denote the vertex cover obtained by simply removing v from S. It is easy to see that the reconfiguration sequence from S to $S^{\prime }$ is a zero-bounded prefix and can be found in time polynomial in n.

Similarly, if $G[S_R\cup T_A]$ has a vertex $v\in S_R$ of degree one, we let $S^{\prime }$ denote the node obtained by the addition of the single vertex in $N_{G[S_R\cup T_A]}\left(v\right)$ followed by the removal of v. The reconfiguration sequence from S to $S^{\prime }$ is a one-bounded prefix and can be found in time polynomial in n.

For the second case, we let Y be a cycle in $G[S_R\cup T_A]$, and we partition the vertices of the cycle into two sets; $Y_S=Y\cap S_R$ and $Y_T=Y\cap T_A$. Since $G[S_R\cup T_A]$ is bipartite, we know that $|Y_S|=|Y_T|$. Since all vertices in $Y_S$ have degree exactly two in $G[S_R\cup T_A]$, it follows that $N_{G[S_R\cup T_A]}\left(Y_S\right)\subseteq Y_T$. Therefore, a reconfiguration sequence from S to some vertex cover $S^{\prime }$ that adds all vertices in $Y_T$ (one by one) and then removes all vertices in $Y_S$ (one by one) will satisfy Conditions (1), (3) and (4) from Definition 1 for any value of c. For $c=2$, such a sequence will not satisfy Condition (2) if the cycle has at least six vertices (i.e., $|Y_T|\ge 3$). However, using the fact that every vertex in $Y_S$ has degree exactly two in $G[S_R\cup T_A]$, we can find a reconfiguration sequence from S to $S^{\prime }$ in which no vertex cover has a size greater than $|S|+2$. To do so, we restrict our attention to $G[Y_S\cup Y_T]$. Since Y is an even cycle, we can label all the vertices of Y in clockwise order from zero to $|Y|-1$ such that all vertices in $Y_S$ receive even labels. The reconfiguration sequence from S to $S^{\prime }$ starts by adding the two vertices labelled 1 and $|Y|-1$. After doing so, the vertex labelled 0 is removed. Next, to remove the vertex labelled 2, we only need to add the vertex labelled 3. The same process is repeated for all vertices with even labels up to $|Y|-4$. Finally, when we reach the vertex labelled $|Y|-2$, both of its neighbours will have already been added, and we can simply remove it. Hence, we have a two-bounded prefix from S to $S^{\prime }$, and it is not hard to see that finding this reconfiguration sequence can be accomplished in time polynomial in n.

When the appropriate assumptions hold, we can show the symmetric case $T\stackrel{2,S}{\leftrightarrow }{T}^{\prime }$ using similar arguments. ☐

Lemma 4.

If G is a cactus graph and S and T are two vertex covers of G, then there exists a vertex cover $S^{\prime }$ (or $T^{\prime }$) of G such that $S\stackrel{2,T}{\leftrightarrow }{S}^{\prime }$ (or $T\stackrel{2,S}{\leftrightarrow }{T}^{\prime }$).

Proof. 

We assume that $|S_R|\ge |T_A|$, as we can swap the roles of S and T whenever $|S_R|<|T_A|$. We observe that every connected component of $G[S_R\cup T_A]$ is a cactus graph since every induced subgraph of a cactus graph is also a cactus graph. Since we assume $|S_R|\ge |T_A|$, at least one connected component X of $G[S_R\cup T_A]$ must satisfy $|V\left(X\right)\cap S_R|\ge |V\left(X\right)\cap T_A|$.

To prove the lemma, we show that if neither condition of Lemma 3 applies to X, it must be the case that $|V\left(X\right)\cap S_R|<|V\left(X\right)\cap T_A|$, contradicting our assumption. To simplify the notation, we assume without loss of generality that $G[S_R\cup T_A]$ is connected, as we can otherwise set $G[S_R\cup T_A]=X$. The proof proceeds in two steps. First, we show that if Condition (1) of Lemma 3 is not satisfied, then $G[S_R\cup T_A]$ must have at least one vertex $u\in S_R$ of degree at most two in $G[S_R\cup T_A]$. In the second step, we show that if both Conditions (1) and (2) of Lemma 3 are not satisfied, then $|S_R|<|T_A|$, which completes the proof by contradiction.

Since $G[S_R\cup T_A]$ is a cactus graph, we can apply Propositions 5 and 6 to get:

$$\begin{array}{cc}\hfill |E(G[S_R\cup T_A])|& =|S_R|+|T_A|-1+|\mathcal{C}\left(G[S_R\cup T_A]\right)|\hfill \\ & \le |S_R|+|T_A|-1+|\mathcal{M}\left(G[S_R\cup T_A]\right)|\hfill \end{array}$$

(1)

Moreover, since $G[S_R\cup T_A]$ is bipartite (Proposition 1), the size of a maximum matching in $G[S_R\cup T_A]$ is less than or equal to $m\mathrm{IN}(|S_R|,|T_A|)$. Therefore:

$$\begin{array}{c}\hfill |\mathcal{C}\left(G[S_R\cup T_A]\right)|\le |\mathcal{M}\left(G[S_R\cup T_A]\right)|\le |S_R|\end{array}$$

(2)

Combining (1) and (2), we get:

$$\begin{array}{cc}\hfill |E(G[S_R\cup T_A])|& =|S_R|+|T_A|-1+\mathcal{C}\left(G[S_R\cup T_A]\right)\hfill \\ & \le 2|S_R|+|T_A|-1\hfill \end{array}$$

(3)

If the minimum degree in $G[S_R\cup T_A]$ of any vertex in $S_R$ is three or more, then $3|S_R|\le |E\left(G[S_R\cup T_A]\right)|\le 2|S_R|+|T_A|-1$ and thus $|S_R|\le |T_A|-1$, contradicting our assumption that $|S_R|\ge |T_A|$. Hence, $G[S_R\cup T_A]$ must have at least one vertex of degree two in $S_R$.

Next, we show that if $G[S_R\cup T_A]$ has no vertex $v\in S_R$ such that $|N_{G[S_R\cup T_A]}\left(v\right)|\le 1$ and no cycle Y such that all vertices in $Y\cap S_R$ have degree exactly two in $G[S_R\cup T_A]$, then $|S_R|<|T_A|$. We let $S^x$ denote the set of vertices in $S_R$ having degree x in $G[S_R\cup T_A]$. Since $G[S_R\cup T_A]$ has no vertex $v\in S_R$ such that $|N_{G[S_R\cup T_A]}\left(v\right)|\le 1$, we know that $S^2$ cannot be empty. In addition, since there is no cycle Y in $G[S_R\cup T_A]$ such that all vertices in $Y\cap S_R$ have degree exactly two in $G[S_R\cup T_A]$, any cycle involving a vertex in $S^2$ must also include a vertex from ${\bigcup }_{i\ge 3}{S}^i$. It follows that ${\bigcup }_{i\ge 3}{S}^i$ is a feedback vertex set (a set whose removal destroys all cycles) of $G[S_R\cup T_A]$, and $G[S^2\cup T_A]$ is a forest.

We let $m_s$ denote the maximum degree in $G[S_R\cup T_A]$ of any vertex in $S_R$. Since each edge in $G[S_R\cup T_A]$ has one endpoint in $S_R$,

$$\begin{array}{cc}\hfill \sum _{i=2}^{m_s}i|S^i|& \le |E(G[S_R\cup T_A])|\hfill \end{array}$$

(4)

and since each vertex in $S_R$ is in some $S^i$ and using (1), we can rewrite (4) as:

$$\begin{array}{cc}\hfill \sum _{i=2}^{m_s}i|S^i|& \le \left(\sum _{i=2}^{m_s}|S^i|\right)+|T_A|-1+|\mathcal{C}\left(G[S_R\cup T_A]\right)|.\hfill \end{array}$$

(5)

To bound $|\mathcal{C}(G[S_R\cup T_A])|$, we note that since no edge can belong to more than one cycle in a cactus graph, any vertex $v\in S^x$ can be involved in at most $\lfloor \frac{x}{2}\rfloor$ cycles. Combining this observation with the fact that any cycle involving a vertex in $S^2$ must also include a vertex from ${\bigcup }_{i\ge 3}{S}^i$, we have:

$$\begin{array}{cc}\hfill \sum _{i=2}^{m_s}i|S^i|& \le \left(\sum _{i=2}^{m_s}|S^i|\right)+|T_A|-1+\left(\sum _{i=3}^{m_s}\lfloor \frac{i}{2}\rfloor |S^i|\right)\hfill \\ & \le |S^2|+\left(\sum _{i=3}^{m_s}(1+\lfloor \frac{i}{2}\rfloor )|S^i|\right)+|T_A|-1\hfill \end{array}$$

(6)

Finally, by rewriting ${\sum }_{i=2}^{m_s}i|S^i|$ as $2|S^2|+{\sum }_{i=3}^{m_s}i|S^i|$ and given that $i-(1+\lfloor \frac{i}{2}\rfloor )\ge 1$ for $i\ge 3$, we obtain the desired bound:

$$\begin{array}{cc}\hfill 2|S^2|+\sum _{i=3}^{m_s}i|S^i|& \le |S^2|+\left(\sum _{i=3}^{m_s}(1+\lfloor \frac{i}{2}\rfloor )|S^i|\right)+|T_A|-1\hfill \\ \hfill |S^2|+\sum _{i=3}^{m_s}i|S^i|& \le \left(\sum _{i=3}^{m_s}(1+\lfloor \frac{i}{2}\rfloor )|S^i|\right)+|T_A|-1\hfill \\ \hfill |S^2|+\sum _{i=3}^{m_s}(i-(1+\lfloor \frac{i}{2}\rfloor ))|S^i|& \le |T_A|-1\hfill \\ \hfill |S_R|=\sum _{i=2}^{m_s}|S^i|& \le |T_A|-1\hfill \end{array}$$

(7)

This completes the proof. ☐

Lemma 5.

If G is a cactus graph and S and T are vertex covers of G, then finding a two-bounded prefix from S to some vertex cover $S^{\prime }$ (or from T to some vertex cover $T^{\prime }$) of G can be accomplished in time polynomial in n.

Proof. 

To find a two-bounded prefix from S to some vertex cover $S^{\prime }$ (or from T to some vertex cover $T^{\prime }$), we simply need to satisfy one of the conditions of Lemma 3, which can both be checked in time polynomial in n. Since $G[S_R\cup T_A]$ is a cactus graph, we know from Lemma 4 that one of them must be true. ☐

Theorem 3.

If S and T are of size at most $k-2$, then vertex cover reconfiguration on cactus graphs can be solved in time polynomial in n.

Proof. 

From Lemma 4, we know that for any cactus graph G and two vertex covers S and T of G, then either $S\stackrel{2,T}{\leftrightarrow }{S}^{\prime }$ or $T\stackrel{2,S}{\leftrightarrow }{T}^{\prime }$, where $S^{\prime }$ and $T^{\prime }$ are some vertex covers of G. In addition, Lemma 5 shows that such two-bounded prefixes can be found in time polynomial in n. By combining these facts, we can now apply Lemma 2. That is, if $|S|\le k-2$ and $|T|\le k-2$, a reconfiguration sequence of length $|S_R|+|T_A|$ from S to T can be found in time polynomial in n. ☐

It remains open whether we can solve the VCR problem in polynomial time on cactus graphs without any restrictions on the size of S and T. For instance, it is unclear if we can always determine (in polynomial time) whether a vertex cover of size $k-1$ can be transformed into a vertex cover of size $k-2$ and, if so, whether we can find the shortest reconfiguration sequence.

6. $\mathsf{FPT}$ Algorithms

In this section, we first focus on vertex cover reconfiguration on graphs of bounded degree. We start by showing that vertex cover reconfiguration is $\mathsf{NP}$-hard on graphs of degree at most d, for any $d\ge 4$, by proving $\mathsf{NP}$-hardness on 4-regular graphs. The proof is based on the observation that the reconfiguration version of the problem is at least as hard as the compression version:

Vertex cover compression
Input:	A graph $G=(V,E)$ and a vertex cover C of G such that $|C|=k\ge 1$
Parameters:	k
Question:	Does G have a vertex cover $C^{\prime }$ of size $k-1$?

The $\mathsf{NP}$-hardness result relies on the representation of reconfiguration sequences as edit sequences. Next, we give an $\mathsf{FPT}$ algorithm for vertex cover reconfiguration on graphs of bounded degree. Finally, we show that a host of graph reconfiguration problems definable in first-order logic is fixed-parameter tractable on nowhere dense classes of graphs.

6.1. Compression via Reconfiguration

Theorem 4.

Vertex cover reconfiguration is at least as hard as vertex cover compression.

Proof. 

We give a reduction from the latter to the former. For $(G,C,k)$, an instance of vertex cover compression, we let $V\left(G\right)=\{v_1,\dots ,v_n\}$ and form $G^{\prime }=(V_G\cup V_A\cup V_B,E_G\cup E_J)$, where $G^{\prime }$ consists of the disjoint union of a copy of G and a biclique $K_{k,k}$. Formally, we have:

$$\begin{array}{c}\hfill V_G=\{g_1,\dots ,g_n\}\\ \hfill V_A=\{a_1,\dots ,a_k\}\\ \hfill V_B=\{b_1,\dots ,b_k\}\\ \hfill E_G=\{g_i{g}_j\mid g_i\in V_G,g_j\in V_G,v_i{v}_j\in E\left(G\right)\}\\ \hfill E_J=\{a_i{b}_j\mid a_i\in V_A,b_j\in V_B,1\le i\le k,1\le j\le k\}.\end{array}$$

We let $(G^{\prime },S,T,3k-1,6k-2)$ be an instance of vertex cover reconfiguration, where $S=V_A\cup \{g_i\mid v_i\in C\}$ and $T=V_B\cup \{g_i\mid v_i\in C\}$. Clearly, $|S|=|T|=2k$ and both S and T are vertex covers of $G^{\prime }$. We claim that G has a vertex cover of size $k-1$ if and only if there is a reconfiguration sequence of length $6k-2$ or less from S to T.

Before we can remove any vertex from $V_A$, we need to add all k vertices from $V_B$. However, $2k+k=3k>3k-1$, which violates the maximum allowed capacity. Therefore, if there is a reconfiguration sequence from S to T, then one of the vertex covers in the sequence must contain at most $2k-1$ vertices. Of those $2k-1$ vertices, k vertices correspond to the vertices in $V_A$ and cover only the edges in $E_J$. Thus, the remaining $k-1$ vertices must be in $V_G$ and should cover all the edges in $E_G$. By our construction of $G^{\prime }$, these $k-1$ vertices correspond to a vertex cover of G.

Similarly, if G has a vertex cover $\widehat{C}$ such that $|\widehat{C}|=k-1$, then the following reconfiguration sequence transforms S to T: add all vertices of $\widehat{C}$, remove all vertices of C, add all vertices of $V_B$, remove all vertices from $V_A$ and finally add back all vertices of C and remove those of $\widehat{C}$. The length of this sequence is equal to $6k-2$ whenever $C\cap \widehat{C}=Ø$ and is shorter otherwise. ☐

6.2. $\mathsf{NP}$-Hardness on Four-Regular Graphs

We are now ready to show that vertex cover reconfiguration remains $\mathsf{NP}$-hard even if the input graph is restricted to be four-regular. We use the same ideas as we did in the previous section. Since vertex cover remains $\mathsf{NP}$-hard on four-regular graphs [22] and any algorithm that solves the vertex cover compression problem can be used to solve the vertex cover problem, we get the desired result. The main difference here is that we need to construct a gadget, $W_k$, that is also four-regular. We describe $W_k$ in terms of several component subgraphs, each playing a role in forcing the reconfiguration of vertex covers.

A k-necklace, $k\ge 4$, is a graph obtained by replacing every edge in a cycle on k vertices by two vertices and four edges. For convenience, we refer to every vertex on the original cycle as a bead and every new vertex in the resulting graph as a sequin. The resulting graph has k beads each of degree four and $2k$ sequins each of degree two. Every two sequins that share the same neighbourhood in a k-necklace are called a sequin pair. We say two beads are adjacent whenever they share exactly two common neighbours. Similarly, we say two sequin pairs are adjacent whenever they share exactly one common neighbour. Every two adjacent beads (sequin pairs) are linked by a sequin pair (bead).

The graph $W_k$ consists of $2k$ copies of a k-necklace. We let $U=\{U_1,\dots U_k\}$ and $L=\{L_1,\dots L_k\}$ denote the first and second k copies, respectively; for convenience, we use the terms “upper” and “lower” to mean “in U” and “in L”, respectively. We let $b_{i,j}^u$ and $b_{i,j}^l$ denote the j-th beads of necklace $U_i$ and $L_i$, respectively, where $1\le i\le k$ and $1\le j\le k$. Beads on each necklace in $W_k$ are numbered consecutively in “clockwise order” from one to k. For every two adjacent beads $b_{i,j}^x$ and $b_{i,j+1}^x$, where $x\in \{u,l\}$, we let $p_{i,j}^x$ denote the sequin pair that links both beads.

For each sequin pair $p_{i,j}^l$, we add four edges to form a $K_{2,2}$ (a joining biclique) with the pair $p_{j,i}^u$, for all $1\le i,j\le k$ (Figure 1); we say that sequin pairs $p_{i,j}^l$ and $p_{j,i}^u$ are joined. All $k^2$ joining bicliques in $W_k$ are vertex disjoint. The total number of vertices in $W_k$ is $6k^2$. Every vertex has degree exactly four; every bead is connected to four sequins from the same necklace, and every sequin is connected to two beads from the same necklace and two other sequins from a different necklace. We let S be the set containing all upper beads and lower sequins, whereas T contains all lower beads and upper sequins. Formally, $S=\{b_{i,j}^u\mid 1\le i,j\le k\}\cup \{v\in p_{i,j}^l\mid 1\le i,j\le k\}$ and $T=\{b_{i,j}^l\mid 1\le i,j\le k\}\cup \{v\in p_{i,j}^u\mid 1\le i,j\le k\}$. Each set contains $3k^2$ vertices, that is half the vertices in $W_k$.

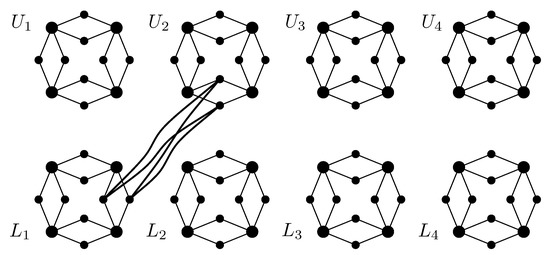
Figure 1. The graph $W_4$ (the edges of only one of the $k^2$ joining bicliques is shown).

Proposition 8.

S and T are minimum vertex covers of $W_k$.

Proof. 

We need at least $2k^2$ vertices to cover the edges in the $k^2$ vertex disjoint joining bicliques contained in $W_k$. Moreover, any minimal vertex cover C of $W_k$ that includes a vertex v from a sequin pair $p_{i,j}^x=\{v,w\}$, where $x\in \{u,l\}$, must also include w. Otherwise, the two beads linking $p_{i,j}^x$ to its adjacent sequin pairs must be in C to cover the edges incident on w, making v removable. Hence, any minimal vertex cover C of $W_k$ must include either one or both sequin pairs in a joining biclique. We let x denote the number of joining bicliques from which two sequin pairs are included in C. Similarly, we let y denote the number of joining bicliques from which only one sequin pair is included in C. Hence, $x+y=k^2$ and $|C|\ge 4x+2y$. When $y=0$, $|C|\ge 4k^2$ and C cannot be a minimum vertex cover, as S and T are both vertex covers of $W_k$ of size $3k^2$. When $y\ge 1$, we are left with at least y uncovered edges incident to the sequin pairs not in C. Those edges must be covered using at least y beads and, hence, $|C|\ge 4x+3y$. If we assume $4x+3y<3k^2$, we get a contradiction since $4x+4y=4k^2<3k^2+y$ and $k^2<y$. Therefore, S and T must be minimum vertex covers of $W_k$. ☐

To prove the next two results, we consider the representation of reconfiguration sequences as edit sequences. Since S is a minimal vertex cover of $W_k$, $\alpha$ cannot start with a vertex removal. Since $V(S,\alpha [1,|\alpha |-1\left]\right)$ is a vertex cover of $W_k$, $|S|=|T|$ and S and T are minimum vertex covers of $W_k$, $\alpha$ cannot end with a vertex addition. Moreover, if $|\alpha |=6k^2$, then $\alpha$ must touch every vertex in $W_k$ exactly once.

Proposition 9.

Any (valid) edit sequence ${\alpha }^{\prime }$ of length $6k^2$ from S to T can be converted into a (valid) edit sequence α from S to T such that $|\alpha |=|{\alpha }^{\prime }|=6k^2$, $|V(S,\alpha [1,p])|\le |V(S,{\alpha }^{\prime }[1,p])|$, for all $1\le p\le |\alpha |$, and any two vertices u and v from the same sequin pair in $W_k$ are either added in the same maximal addition segment or removed in the same maximal removal segment of α. Consequently, $\mathsf{cap}\left(\alpha \right)\le \mathsf{cap}\left({\alpha }^{\prime }\right)$.

Proof. 

Both vertices in a sequin pair share the same neighbourhood. Hence, when u is removed, all of its neighbours must have been added, making v also removable. Moreover, since every vertex is touched exactly once in ${\alpha }^{\prime }$, none of the neighbours of u and v will be touched in ${\alpha }^{\prime }$ after the removal of u. Therefore, if v is not removed in the same maximal removal segment as u, then we obtain $\alpha$ by shifting the removal of v, so that it happens immediately after the removal of u. It is not hard to see that $|\alpha |=|{\alpha }^{\prime }|=6k^2$ and $|V(S,\alpha [1,p])|\le |V(S,{\alpha }^{\prime }[1,p])|$, for all $1\le p\le |\alpha |$.

For the case of additions, if only u is added in some maximal addition segment $\beta$, then none of its neighbours can yet be removed. Let $\gamma$ be the maximal addition segment in which v is added (which occurs after $\beta$ in ${\alpha }^{\prime }$). We obtain $\alpha$ by shifting the addition of u from $\beta$ to $\gamma$. ☐

Lemma 6.

There exists a function of k, $f\left(k\right)$, such that $(W_k,S,T,3k^2+f\left(k\right),\ell )$ is a yes-instance and $(W_k,S,T,3k^2+f\left(k\right)-1,\ell )$ is a no-instance of vertex cover reconfiguration for $\ell =6k^2$. Moreover, $k-2\le f\left(k\right)\le k+3$.

Proof. 

To show that such an $f\left(k\right)$ exists, we first prove the $k-2$ lower bound by showing that any valid edit sequence $\alpha$ of length $6k^2$ from S to T must have some prefix where the number of vertex additions $\#a$ minus the number of vertex removals $\#r$ is at least $k-2$, i.e., $\#a-\#r\ge k-2$. In fact, we will show that the aforementioned property holds for any valid edit sequence $\alpha$ of length $6k^2$ in which two vertices from the same sequin pair are always added or removed in the same maximal addition or removal segment, respectively. Considering only such sequences is sufficient because, from Proposition 9, we know that any sequence ${\alpha }^{\prime }$ of length $6k^2$ can be transformed into such a sequence $\alpha$ so that $|V(S,\alpha [1,p])|\le |V(S,{\alpha }^{\prime }[1,p])|$, for all $1\le p\le |\alpha |$. In other words, if ${\alpha }^{\prime }$ has no prefix with $\#a-\#r\ge k-2$ (but $\alpha$ does), then $\mathsf{cap}\left({\alpha }^{\prime }\right)<\mathsf{cap}\left(\alpha \right)$, a contradiction.

We let position x, $1\le x\le |\alpha |$, be the smallest position such that $\alpha [1,x]$ contains exactly $5k$ vertex removals. Those $5k$ vertices correspond to a set $S^{\prime }\subset S$, as $\alpha$ touches every vertex exactly once. The claim is that $\alpha [1,x]$ must contain at least $6k-2$ vertex additions. We let $T^{\prime }\subset T$ denote the set of added vertices in $\alpha [1,x]$. Since $N_{W_k}\left(S^{\prime }\right)\subseteq T^{\prime }$, we complete the proof of the lower bound by showing that $|T^{\prime }|\ge |N_{W_k}\left(S^{\prime }\right)|\ge \frac{6}{5}|S^{\prime }|-2\ge 6k-2$. To do so, we show that for any $S^{\prime }\subset S$ of size $5k$, $N_{W_k}\left(S^{\prime }\right)\subseteq T^{\prime }$ contains at least $\frac{6}{5}|S^{\prime }|-2=6k-2$ vertices.

In what follows, we restrict our attention to the bipartite graph $Z=W_k[S^{\prime }\cup T^{\prime }]$, and we let $S^{\prime }$ and $T^{\prime }$ denote the two partitions of Z. We subdivide $S^{\prime }$ into two sets: $S_b^{\prime }$ contains upper beads, and $S_s^{\prime }$ contains lower sequins. Since every vertex in $S_b^{\prime }$ has four neighbours in $T^{\prime }$ and adjacent beads share exactly two neighbours, we have $|N_Z\left(S_b^{\prime }\right)|\ge 2|S_b^{\prime }|$, and equality occurs whenever $S_b^{\prime }$ contains $2k$ beads from the same two upper necklaces. Whenever $S_b^{\prime }$ contains fewer than $2k$ beads and $Z[S_b^{\prime }\cup N_Z\left(S_b^{\prime }\right)]$ consists of $t_b\ge 1$ connected components, at least one bead from each component (except possibly the first) will be adjacent to at most one other bead in the same component. Therefore, $|N_Z\left(S_b^{\prime }\right)|\ge 2|S_b^{\prime }|+2(t_b-1)$.

Proposition 9 implies that $T^{\prime }$ will always contain both vertices of any sequin pair. Since we are only considering vertices in $V\left(\alpha \right[1,x\left]\right)$, some sequins in $S_s^{\prime }$ might be missing the other sequin in the corresponding pair. However, all the neighbours of the sequin pair have to be in $T^{\prime }$, so we assume without loss of generality that vertices in $S_s^{\prime }$ can be grouped into sequin pairs. Every sequin pair in $S_s^{\prime }$ has four neighbours in $T^{\prime }$. Adjacent sequin pairs share exactly one neighbour. Hence, $|N_Z\left(S_s^{\prime }\right)|\ge \frac{3}{2}|S_s^{\prime }|$, and equality occurs whenever $S_s^{\prime }$ contains k sequin pairs of a single lower necklace. Whenever $S_s^{\prime }$ contains fewer than k sequin pairs and $Z[S_s^{\prime }\cup N_Z\left(S_s^{\prime }\right)]$ consists of $t_s\ge 1$ connected components, at least one sequin pair from each component will be adjacent to at most one other sequin pair in the same component. Therefore, $|N_Z\left(S_s^{\prime }\right)|\ge \frac{3}{2}|S_s^{\prime }|+t_s$.

Combining the previous observations, we know that when either $S_b^{\prime }$ or $S_s^{\prime }$ is empty, $|N_Z\left(S^{\prime }\right)|\ge \frac{6}{5}|S^{\prime }|$, as needed. When both are not empty, we let $I=N_Z\left(S_b^{\prime }\right)\cap N_Z\left(S_s^{\prime }\right)$. Hence, $|N_Z\left(S_b^{\prime }\right)|+|N_Z\left(S_s^{\prime }\right)|-|I|\ge 2|S_b^{\prime }|+2(t_b-1)+\frac{3}{2}|S_s^{\prime }|+t_s-|I|$, and we rewrite it as:

$$\begin{array}{cc}\hfill |N_Z\left(S^{\prime }\right)|+2& \ge \frac{100}{50}|S_b^{\prime }|+\frac{75}{50}|S_s^{\prime }|+2(t_b-1)+t_s-(|I|-2)\hfill \end{array}$$

(8)

We now bound the size of I. Note that I can only contain upper sequin pairs joined with sequin pairs in $S_s^{\prime }$. As every sequin pair in $S_s^{\prime }$ has either zero or two neighbours in I, $|S_s^{\prime }|\ge |I|$. Moreover, for every two sequin pairs in $S_s^{\prime }$ having two neighbours in I, there must exist at least one vertex in $S_b^{\prime }$, which implies $|S_b^{\prime }|\ge \frac{|I|}{4}$. Finally, whenever a sequin pair $p\in S_s^{\prime }$ has two neighbours in I, then $t_b,t_s\ge 1$, as at least one bead neighbouring the sequin pair joined with p must be in $S_b^{\prime }$. Every other sequin pair $p^{\prime }\in S_s^{\prime }$, $p^{\prime }\ne p$, with two neighbours in I will force at least one additional connected component in either $Z[S_b^{\prime }\cup N_Z\left(S_b^{\prime }\right)]$ or $Z[S_s^{\prime }\cup N_Z\left(S_s^{\prime }\right)]$ since $W_k$ contains a single joining biclique between any two necklaces. Therefore, the total number of connected components is $t_b+t_s\ge \frac{|I|}{2}$. Putting it all together, we get:

$$\begin{array}{cc}\hfill \frac{40}{50}|S_b^{\prime }|+\frac{15}{50}|S_s^{\prime }|+2(t_b-1)+t_s& \ge \frac{2}{10}|I|+\frac{3}{10}|I|+\frac{5}{10}|I|+t_b-2\hfill \\ & \ge |I|-2\hfill \end{array}$$

(9)

Combining Equations (8) and (9), we get:

$$\begin{array}{cc}\hfill |N_Z\left(S^{\prime }\right)|+2& \ge \frac{6}{5}|S^{\prime }|+\frac{40}{50}|S_b^{\prime }|+\frac{15}{50}|S_s^{\prime }|+2(t_b-1)+t_s-(|I|-2)\hfill \\ & \ge \frac{6}{5}|S^{\prime }|\hfill \end{array}$$

(10)

Therefore, $V(S,\alpha [1,x\left]\right)$ is a vertex cover of $W_k$ of size at least $3k^2+k-2$, as needed.

To show the $f\left(k\right)\le k+3$ upper bound, we show that $(W_k,S,T,3k^2+k+3,6k^2)$ is a yes-instance by providing an actual reconfiguration sequence:

(1)

Add all k beads in $L_1$. Since S is a vertex cover of $W_k$, we know that the additional k beads will result in a vertex cover of size $3k^2+k$.

(2)

Add both vertices in $p_{1,1}^u$, and remove both vertices in $p_{1,1}^l$. The removal of both vertices in $p_{1,1}^l$ is possible since we added all their neighbours in $L_1$ (Step (1)) and $U_1$. The size of a vertex cover reaches $3k^2+k+2$ after the additions and then drops back to $3k^2+k$.

(3)

Repeat Step (2) for all sequin pairs $p_{i,1}^u$ and $p_{1,i}^l$ for $2\le i\le k$. The size of a vertex cover is again $3k^2+k$ once Step (3) is completed. Step (2) is repeated a total of k times. After every repetition, we have a vertex cover of $W_k$ since all beads in $L_1$ were added in Step (1), and the remaining neighbours of each sequin pair in $U_i$ are added prior to the removals.

(4)

Add both vertices in $p_{1,2}^u$, and remove vertex $b_{1,2}^u$.

(5)

Add $b_{2,1}^l$ and $b_{2,2}^l$. At this point, the size of a vertex cover is $3k^2+k+3$.

(6)

Remove both vertices in $p_{2,1}^l$.

(7)

Repeat Steps (4), (5) and (6) until all beads in $L_2$ have been added and the sequin pairs removed. When we reach the last sequin pair in $L_2$, $b_{2,1}^l$ was already added, and hence, we gain a surplus of one, which brings the vertex cover size back to $3k^2+k$.

(8)

Repeat Steps (4) to (7) for every remaining necklace in L.

Since every vertex in $W_k$ is touched exactly once, we know that $\ell =6k^2$. In the course of the described reconfiguration sequence, the maximum size of any vertex cover is $3k^2+k+3$. Hence, $f\left(k\right)\le k+3$. This completes the proof. ☐

It would be interesting to close the gap on $f\left(k\right)$, but the existence of such a value is enough to prove the main theorem of this section.

Theorem 5.

Vertex cover reconfiguration is $\mathsf{NP}$-hard on four-regular graphs.

Proof. 

We prove the result by a reduction from vertex cover compression to vertex cover reconfiguration where the input graph is restricted to be four-regular in both cases. For $(G,C,k)$, an instance of vertex cover compression, we form $G^{\prime }=(V\left(G\right)\cup V\left(W_k\right),E\left(G\right)\cup E\left(W_k\right))$. We let $(G^{\prime },S,T,3k^2+k+f\left(k\right)-1,6k^2+4k-2)$ be an instance of vertex cover reconfiguration, where $S=\{e_{i,j}^u\mid 1\le i,j\le k\}\cup \{p_{i,j}^l\mid 1\le i,j\le k\}\cup C$ and $T=\{e_{i,j}^l\mid 1\le i,j\le k\}\cup \{p_{i,j}^u\mid 1\le i,j\le k\}\cup C$, and $f\left(k\right)$ is the value whose existence was shown in Lemma 6.

Clearly, $|S|=|T|=3k^2+k$ and both S and T are vertex covers of $G^{\prime }$. We claim that G has a vertex cover of size $k-1$ if and only if there is a reconfiguration sequence of length $6k^2+4k-2$ or less from S to T.

We know from Lemma 6 that the reconfiguration of $W_k$ requires at least $f\left(k\right)$ available capacity. However, $3k^2+k+f\left(k\right)>3k^2+k+f\left(k\right)-1$, which violates the maximum allowed capacity. Therefore, if there is a reconfiguration sequence from S to T, then one of the vertex covers in the sequence must contain at most $3k^2+k-1$ vertices. By Proposition 8, we know that $3k^2$ of those $3k^2+k-1$ vertices are needed to cover the edges in $E\left(W_k\right)$. Thus, the remaining $k-1$ vertices must be in $V\left(G\right)$ and should cover all edges in $E\left(G\right)$. By construction of $G^{\prime }$, these $k-1$ vertices correspond to a vertex cover of G.

Similarly, if G has a vertex cover $\widehat{C}$ such that $|\widehat{C}|=k-1$, then the following reconfiguration sequence transforms S to T: add all vertices of $\widehat{C}$, remove all vertices of C, apply the reconfiguration sequence whose existence was shown in Lemma 6 to $G^{\prime }\left[V\left(W_k\right)\right]$ and finally add back all vertices of C and remove those of $\widehat{C}$. The length of this sequence is equal to $6k^2+4k-2$ whenever $C\cap \widehat{C}=Ø$ and is shorter otherwise. ☐

6.3. $\mathsf{FPT}$ Algorithm for Graphs of Bounded Degree

In this section, we prove that vertex cover reconfiguration parameterized by ℓ is fixed-parameter tractable for graphs of degree at most d. Our algorithm is randomized and based on a variant of the colour-coding technique [23] that is particularly useful in designing parameterized algorithms on graphs of bounded degree. The technique, known in the literature as random separation [24], boils down to a simple, but fruitful observation that in some cases, if we randomly colour the vertex set of a graph using two colours, the solution or vertices we are looking for are appropriately coloured with high probability. In our case, we want to make sure that the set of touched vertices gets highlighted. We note that our algorithm can easily be derandomized using standard techniques [25].

We start with an instance $(G,S,T,k,\ell )$ of VCR, with G having degree at most d. Recall that we partition $V\left(G\right)$ into the sets $C_{ST}=S\cap T$, $S_R=S\backslash C_{ST}$, $T_A=T\backslash C_{ST}$, and the independent set $O_{ST}=V\left(G\right)\backslash (S\cup T)=V\left(G\right)\backslash (C_{ST}\cup S_R\cup T_A)$. We colour independently every vertex of G using one of two colours, say red and blue (denoted by $\mathcal{R}$ and $\mathcal{B}$), with probability $\frac{1}{2}$. We let $\chi :V\left(G\right)\to \{\mathcal{R},\mathcal{B}\}$ denote the resulting random colouring. Suppose that $(G,S,T,k,\ell )$ is a yes-instance, and let $\sigma$ denote a reconfiguration sequence from S to T of length at most ℓ. We say that the colouring $\chi$ is successful if both of the following conditions hold:

• Every vertex in $V\left(\sigma \right)$ is coloured red; and
• Every vertex in $N_G\left(V\left(\sigma \right)\right)$ is coloured blue.

Observe that $V\left(\sigma \right)$ and $N_G\left(V\left(\sigma \right)\right)$ are disjoint. Therefore, the two aforementioned conditions are independent. Moreover, since the maximum degree of G is d, we have $|V\left(\sigma \right)|+|N_G\left(V\left(\sigma \right)\right)|\le (\ell +1)d$. Consequently, the probability that $\chi$ is successful is at least:

$$\begin{array}{c}\hfill \frac{1}{2^{|V\left(\sigma \right)|+|N_G\left(V\left(\sigma \right)\right)|}}\ge \frac{1}{2^{(\ell +1)d}}.\end{array}$$

Let $V_{\mathcal{R}}$ denote the set of vertices coloured red and $V_{\mathcal{B}}$ denote the set of vertices coloured blue. Moreover, we let $C_1$, …, $C_q$ denote the set of connected components of $G\left[V_{\mathcal{R}}\right]$. The main observation now is the following:

Proposition 10.

If χ is successful, then $N_G\left(V\left(\sigma \right)\right)\subseteq C_{ST}$, $V\left(\sigma \right)$ has a non-empty intersection with at most ℓ connected components of $G\left[V_{\mathcal{R}}\right]$, and each one of those components consists of at most ℓ vertices.

Proof. 

The fact that $N_G\left(V\left(\sigma \right)\right)\subseteq C_{ST}$ follows from the observation that every vertex in $V\left(\sigma \right)$ must be added or removed at least once and no vertex in $N_G\left(V\left(\sigma \right)\right)$ is ever added or removed. In other words, if $v\in V\left(\sigma \right)$ is removed, then all of its untouched neighbours must be in $C_{ST}$. Similarly, if $v\in V\left(\sigma \right)$ is added, then prior to being added, all of its untouched neighbours must be in $C_{ST}$.

Since $|V(\sigma )|\le \ell$, we know that $G[V\left(\sigma \right)\cup N_G\left(V\left(\sigma \right)\right)]$ consists of at most ℓ connected components (each of size at most $(\ell +1)d$) and $G\left[V\right(\sigma \left)\right]$ consists of at most ℓ components (each of size at most ℓ). Let C be a connected component of $G\left[V_{\mathcal{R}}\right]$ such that $|V(C)|>\ell$. We claim that we can safely ignore (and hence delete) this component when $\chi$ is successful. Suppose to the contrary that $V\left(\sigma \right)\cap V\left(C\right)=Q\ne Ø$. Since $\chi$ is successful, it must be the case that every vertex in $N_G\left(Q\right)$ is coloured blue. However, we know that there exists at least one vertex in $N_G\left(Q\right)$ that is coloured red (since C is a connected component of $G\left[V_{\mathcal{R}}\right]$ and all vertices in C are coloured red). As we have obtained a contradiction, we can conclude that when $\chi$ is successful, $V\left(\sigma \right)$ can intersect at most ℓ connected components of $G\left[V_{\mathcal{R}}\right]$, and none of those components can be of a size greater than ℓ, as claimed. ☐

Given Proposition 10, we can safely assume that every connected component of $G\left[V_{\mathcal{R}}\right]$ consists of at most ℓ vertices (as the remaining components can be ignored when $\chi$ is successful). For simplicity, let us first assume that $G\left[V\right(\sigma \left)\right]$ is connected. Thus, if $\chi$ is successful, then there exists a single component in $G\left[V_{\mathcal{R}}\right]$, say $C^{★}$, such that $V(\sigma )\subseteq V(C^{★})$, $|V(C^{★})|\le \ell$ and $S_R\cup T_A\subseteq V(C^{★})$. Therefore, we can simply enumerate all possible sequences of length at most ℓ and make sure that at least one of them is the required reconfiguration sequence from S to T. This brute-force testing can be accomplished in time $2^{\mathcal{O}(\ell log\ell )}·n^{\mathcal{O}\left(1\right)}$.

Let us now consider the general case when $G\left[V\right(\sigma \left)\right]$ is not necessarily connected. We say a component C of $G\left[V_{\mathcal{R}}\right]$ is important if $V\left(C\right)\cap (S_R\cup T_A)\ne Ø$. There are at most ℓ important components. Hence, we only need to bound the number of unimportant components. To that end, we partition the unimportant components of $G\left[V_{\mathcal{R}}\right]$ into equivalence classes with respect to the following relation ≃:

$$C\simeq C^{\prime }\iff C\mathrm{is}\mathrm{isomorphic}\mathrm{to}{C}^{\prime }.$$

Proposition 11.

The total number of graphs with at most ℓ vertices is at most $2^{\mathcal{O}\left({\ell }^2\right)}$, and therefore, the equivalence relation ≃ has at most $2^{\mathcal{O}\left({\ell }^2\right)}$ equivalence classes.

Assume that some equivalence class contains more than ℓ unimportant components. We claim that retaining only ℓ of them is enough. To see why, it is enough to note that $V\left(\sigma \right)$ intersects with at most ℓ of those components; they are all isomorphic; and the neighbours of any such component are contained in $C_{ST}$. Putting it all together, we know that we have at most $2^{\mathcal{O}\left({\ell }^2\right)}$ equivalence classes, each with at most ℓ components, and each component is of size at most ℓ. Hence, we can guess the sequence from S to T in time $2^{\mathcal{O}({\ell }^{3}log\ell )}·n^{\mathcal{O}\left(1\right)}$ (testing whether two graphs with ℓ vertices are isomorphic can be accomplished naively in time $2^{\ell log\ell }$).

We have proven that the probability that $\chi$ is successful is at least $2^{-(\ell +1)d}$. Hence, to obtain a Monte Carlo algorithm with false negatives, we repeat the above procedure $2^{(\ell +1)d}$ times and obtain the following result:

Theorem 6.

There exists a one-sided error Monte Carlo algorithm with false negatives that solves the vertex cover reconfiguration problem on graphs of degree at most d in time $2^{(\ell +1)d}·2^{\mathcal{O}({\ell }^{3}log\ell )}·n^{\mathcal{O}\left(1\right)}$.

6.4. $\mathsf{FPT}$ Algorithm for Nowhere Dense Graphs

In this section, we present a more general result, showing that the reconfiguration variant of every first-order definable optimization problem parameterized by ℓ is fixed-parameter tractable on every fixed nowhere dense class of graphs.

Let us quickly recall the necessary definitions from logic. For our purpose, it suffices to consider first-order logic over the vocabulary of coloured graphs. We refer to the textbook [26] for extensive background on logic.

Let $A,B$ be two unary relation symbols and E a binary relation symbol. We call $\{E,A,B\}$ the vocabulary of graphs with two colours A and B. First-order formulas over the vocabulary of coloured graphs are formed from atomic formulas $x=y$, $E(x,y)$, $A\left(x\right)$ and $B\left(x\right)$, where $x,y$ are variables (we assume that we have an infinite supply of variables), by the usual Boolean connectives ¬ (negation), ∧ (conjunction) and ∨ (disjunction) and existential and universal quantification $\exists x,\forall x$, respectively. The free variables of a formula are those not in the scope of a quantifier, and we write $\phi (x_1,\dots ,x_k)$ to indicate that the free variables of the formula $\phi$ are among $x_1,\dots ,x_k$. To define the semantics, we inductively define a satisfaction relation ⊨. Let G be a graph and $A,B\subseteq V\left(G\right)$. For simplicity, we do not distinguish between A as a symbol and A as a set. For a formula $\phi (x_1,\dots ,x_k)$, and $v_1,\dots ,v_k\in V\left(G\right)$, $G\models \phi (v_1,\dots ,v_k)$ means that G satisfies $\phi$ if the free variables $x_1,\dots ,x_k$ are interpreted by $v_1,\dots ,v_k$. If $\phi (x_1,x_2)=E(x_1,x_2)$ is atomic, then $G\models \phi (v_1,v_2)$ if $(v_1,v_2)\in E\left(G\right)$. Similarly, if $\phi \left(x\right)=A\left(x\right)$, then $G\models \phi \left(v\right)$ if $v\in A$. The meanings of the equality symbol, the Boolean connectives and the quantifiers are the usual ones.

Let $\phi \left(X\right)$ be a first-order formula that has a free set variable X. For example, the vertex cover problem is defined by the formula:

$$\phi \left(X\right)=\forall x\forall y(\neg E(x,y)\vee X(x)\vee X(y\left)\right).$$

As another example, we can define dominating sets by the formula:

$$\phi \left(X\right)=\forall x\left(X\right(x)\vee \exists y(X\left(y\right)\wedge E(x,y))$$

and independent sets by the formula:

$$\phi \left(X\right)=\forall x\forall y\left(\right(X\left(x\right)\wedge X\left(y\right)\wedge x\ne y)\to \neg E(x,y\left)\right).$$

Naturally, we can define a reconfiguration variant for each such formula $\phi$. Given two sets $S,T\subseteq V\left(G\right)$, we ask for a sequence $S_1,\dots ,S_t$, $S_1=S$ and $S_t=T$ such that $G\models \phi \left(S_i\right)$ for all intermediate configurations $S_i$. We call the corresponding decision problem $\phi$-reconfiguration, and we refer to a solution of a problem instance as a $\phi$-reconfiguration sequence.

Nowhere dense graph classes were introduced by Nešetřil and Ossona de Mendez [27] as a very general model of uniform sparseness in graphs. We refer to the textbook [28] for the formal definition of the notion of nowhere denseness and for more background on its theory. For our purpose, it is sufficient to note that most familiar classes of sparse graphs are nowhere dense, e.g., every proper minor closed class and every class of bounded degree is nowhere dense. We will prove the following theorem.

Theorem 7.

Let $\phi \left(X\right)$ be a first-order formula over the vocabulary of graphs with a free set variable; let $\mathcal{C}$ be a nowhere dense class of graphs; let $ϵ>0$ be a real; and let $\ell \ge 1$ be an integer. Then, there exists a constant $f(|\phi |,\ell ,ϵ)$ and an algorithm that, given an n-vertex graph $G\in \mathcal{C}$ and two sets $S,T\subseteq V\left(G\right)$ with $G\models \phi \left(S\right)$, $G\models \phi \left(T\right)$, decides whether there exists a φ-reconfiguration sequence of length at most ℓ in time $f(|\phi |,\ell ,ϵ)·n^{1+ϵ}$.

Proof. 

Our proof is based on a result of Grohe, Kreutzer and Siebertz [29], which states that for every first-order formula $\psi$ (without free variables), every nowhere dense class $\mathcal{C}$ of graphs and every real $ϵ>0$, there exists a constant $f(|\psi |,ϵ)$, such that given an n-vertex graph $G\in \mathcal{C}$, one can decide in time $f(|\psi |,ϵ)·n^{1+ϵ}$ whether $\psi$ holds in G.

In order to approach the $\phi$-reconfiguration problem, we want to write a formula $\psi$ over the vocabulary of graphs with two colours S and T without free variables, which expresses the existence of a $\phi$-reconfiguration sequence of length at most ℓ. We will guarantee that the length of $\psi$ is bounded by a function depending only on ℓ (and on $\phi$, though only as a fixed constant). Then, by fixing any $ϵ>0$ and using the result of [29], we conclude that $\phi$-Reconfiguration is fixed-parameter tractable parameterized by ℓ on every nowhere dense class $\mathcal{C}$.

The formula $\psi$ simply states the existence of a sequence of ℓ elements that will be added or removed in the course of the reconfiguration. For each initial sequence of length $i=1,\dots ,\ell$ of these ℓ guesses, we state in $\psi$ that the formula $\phi \left(X\right)$ is satisfied for the set S modified according to the first i operations. Finally, we state that the reconfiguration leads to the set T. The precise formula is cumbersome to write; however, we expect that the reader is convinced that we can express the desired statement in first-order logic once we have stated how to handle a single addition and removal of a vertex. To state that a vertex is added to the set S, we write the formula:

$$\exists x_1\left({\phi }^{\prime }(S,x_1)\right),$$

where ${\phi }^{\prime }\left(X\right)$ is obtained from $\phi \left(X\right)$ by replacing every atom $X\left(x\right)$ for a variable x by the formula $X\left(x\right)\vee x=x_1$. If we now want to remove a vertex, we extend the formula to the formula:

$$\exists x_2\exists x_1\left(\left((x_1\ne x_2)\to {\phi }^{″}(S,x_1,x_2)\right)\wedge \left((x_1=x_2)\to {\phi }^{‴}(S,x_2)\right)\right),$$

where ${\phi }^{″}(X,x_1,x_2)$ is the formula obtained from $\phi \left(X\right)$ by replacing every atom $X\left(x\right)$ by the formula $(X\left(x\right)\vee x=x_1)\wedge x\ne x_2$, and ${\phi }^{‴}(X,x_2)$ is obtained from $\phi \left(X\right)$ by replacing $X\left(x\right)$ by $X\left(x\right)\wedge x\ne x_2$. Similarly, we can handle any sequence of additions and removals of vertices of length at most ℓ and form a big disjunction over all such sequences to obtain the final formula $\psi$. ☐

7. Conclusions

To the best of our knowledge, our results constitute the first in-depth study of the VCR problem parameterized by the length of a reconfiguration sequence. We showed that even though the vertex cover problem is solvable in polynomial time on bipartite graphs, VCR remains $\mathsf{W}\left[\mathsf{1}\right]$-hard. On the tractable side, we showed that VCR is solvable in polynomial time for trees, as well as graphs with no even cycles and is fixed-parameter tractable for graphs of bounded degree. It remains open whether we can solve VCR in polynomial time on cactus graphs without any restrictions on the size of S and T. Finally, we believe that the techniques used in both our hardness proofs and positive results can be extended to cover a host of graph deletion problems defined in terms of hereditary graph properties [10]. It also remains to be seen whether our $\mathsf{FPT}$ results can be extended to a larger class of sparse graphs, e.g., biclique-free graphs.