Abstract
Cluster analyses are often conducted with the goal to characterize an underlying probability density, for which the data-point density serves as an estimate for this probability density. We here test and benchmark the common nearest neighbor (CNN) cluster algorithm. This algorithm assigns a spherical neighborhood R to each data point and estimates the data-point density between two data points as the number of data points N in the overlapping region of their neighborhoods (step 1). The main principle in the CNN cluster algorithm is cluster growing. This grows the clusters by sequentially adding data points and thereby effectively positions the border of the clusters along an iso-surface of the underlying probability density. This yields a strict partitioning with outliers, for which the cluster represents peaks in the underlying probability density—termed core sets (step 2). The removal of the outliers on the basis of a threshold criterion is optional (step 3). The benchmark datasets address a series of typical challenges, including datasets with a very high dimensional state space and datasets in which the cluster centroids are aligned along an underlying structure (Birch sets). The performance of the CNN algorithm is evaluated with respect to these challenges. The results indicate that the CNN cluster algorithm can be useful in a wide range of settings. Cluster algorithms are particularly important for the analysis of molecular dynamics (MD) simulations. We demonstrate how the CNN cluster results can be used as a discretization of the molecular state space for the construction of a core-set model of the MD improving the accuracy compared to conventional full-partitioning models. The software for the CNN clustering is available on GitHub.
1. Introduction
A data point is a vector in a (high-dimensional) state space (or feature space) . A dataset is a set of n data points. The task of cluster algorithms is to partition the dataset into meaningful subsets , …, where the subsets … are called clusters.
In many practical cases, the dataset S represents a sample of a probability density , and the true goal of the analysis is to characterize this density. There are several reasons why one would take the detour via a cluster analysis of the sample rather than by analyzing the probability density directly. For example, the probability density might not be known analytically, or the state space might be too high dimensional to allow for an analytical or numerical analysis of the probability density. If the goal is to characterize a probability density, then the clusters are often interpreted as discretizations of the state space , where we denote the state associated to cluster by , with .
Cluster algorithms can be classified according to a wide range of categories. A very basic categorization is according to whether or not the cluster algorithm enforces a one-to-one mapping of each data point to a specific cluster [1]. In strict partitioning clustering, each data point is assigned to exactly one cluster. By contrast, in overlapping clustering, each data point belongs to one or more clusters. Finally, in strict partitioning clustering with outliers, any given data point can either belong to exactly one cluster or to no cluster at all. The data points that are not assigned to a cluster are called outliers. Strict partitioning clustering yields a discretization of the state space into crisp, non-overlapping states , and for all (Figure 1c). By contrast, strict partitioning clustering with outliers yields a discretization that does not fully partition the state space , and for all . That is, there is a region that is not covered by the cluster states. This is the region in which the outliers are located (Figure 1d).
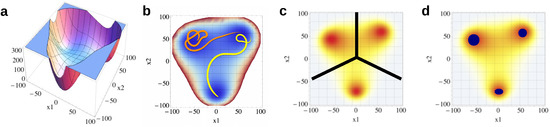
Figure 1.
(a) Potential energy surface (PES) spanned by two coordinates and ; (b) trajectories within the PES (projection onto and ); (c) Boltzmann distribution of the PES divided into three states; (d) core sets (blue) within the Boltzmann distribution; all non-assigned data points are outside the core sets.
An alternative way to categorize cluster algorithms is according to the criterion the algorithms uses to assign a data point to a cluster [1]. Many commonly used cluster algorithms assign an objective function or a cost function to each possible partitioning of the dataset and aim to optimize the objective function by modifying the partitioning. For example, k-means clustering aims to minimize the sum of the squared deviations of the cluster members to the cluster center. Because their objective function is based on the relation of each single data point to the cluster center, these algorithms tend to yield spherically shaped clusters. However, shapes in a dataset that we intuitively recognize as clusters are in fact defined by a sudden change in the data-point density at the rims of the cluster, rather than by how distant its members are to the cluster center. This can for example be seen in the t4.8k [2] and Flame datasets [3] (Figure 2). Thus, cluster algorithms that are based on such distance-based objective functions are poorly suited to identify clusters with complex shapes or to characterize an underlying probability density [4]. Unfortunately, measuring the data-point density, that is, the number of data points per volume element, is often not possible, because calculating the volume of a state with irregular borders in a high-dimensional and sometimes non-linear state space is extremely difficult. Density-based clustering algorithms [4,5,6,7,8,9,10] circumvent this problem by using the number of data points in the neighborhood of a data point as a proxy for the data-point density. As a consequence, the objective function of these algorithms is often only given implicitly [11].
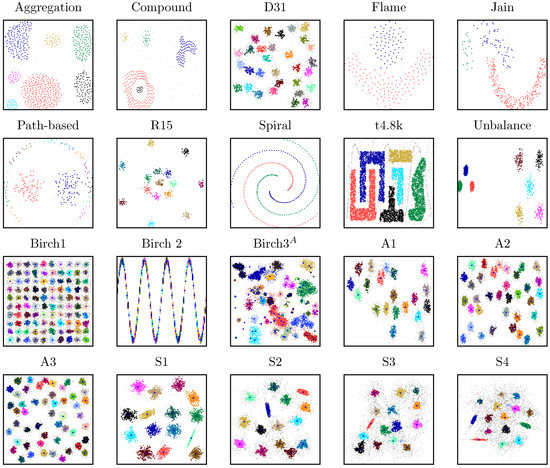
Figure 2.
Performance of the common nearest neighbor (CNN) algorithm on a variety of different two-dimensional (2D) datasets; the parameter sets are presented in Table 1; non-assigned data points (noise) are highlighted in light gray; if accessible, the true centroids are highlighted blue. For the Birch3 dataset, a three-step hierarchical clustering approach was applied. The original clusters after the first step are highlighted in light red and light blue.
When the goal of the cluster analysis is to characterize an underlying probability density, one would ideally like to partition the state space along iso-density lines. We have developed the common nearest neighbor (CNN) clustering for this purpose [4,23]. The algorithm defines a small spherical neighborhood around each data point and approximates the data-point density between two data points and as the number of data points within the overlapping region of the two neighborhoods. If the data-point density in the overlap region exceeds a threshold value, the two data points are assigned to the same cluster. Thus, CNN clustering is a density-based clustering that yields a strict partitioning with outliers. We refer to the clusters from such a strict partitioning with outliers, which are interpreted as designating peaks in the underlying probability density, as core sets. In [24], the algorithm has been extended to a hierarchical cluster algorithm.
The initial purpose of the CNN algorithms was to analyze molecular dynamics (MD) simulations, which yield a sample of a particularly high-dimensional and complicated probability distribution, the Boltzmann distribution. The CNN algorithm successfully processes MD data without prior dimensionality reduction of the dataset [4,24]. It also compares favorably to other density-based cluster algorithms for the analysis of MD data [24]. The CNN algorithm has been used to characterize the molecular ensemble as well as to discretize the molecular state space for the construction of a core-set model of MD [24,25,26,27,28,29].
In this contribution, we ask whether the CNN algorithm is limited to MD datasets, or whether it can successfully cluster a diverse benchmark dataset with challenges that are unlikely to occur in the context of MD simulations. We analyze the performance of the CNN algorithm with respect to general properties of datasets, such as the cluster size, cluster shape or cluster overlap, in Section 4.1. A characterization of a probability density by a partitioning into core sets and an intermediate region seems insufficient at first glance, because, particularly for high-dimensional probability densities, the vast majority of the state space tends to be assigned to the intermediate region. We demonstrate why such a partitioning is in fact often preferable to a strict partitioning when it comes to characterizing high-dimensional probability densities in Section 4.2. Section 2 contains a brief review of MD simulations. The CNN algorithm is explained in Section 3.1.
2. Molecular Dynamics Simulations
Molecules are not rigid entities but fluctuate between different three-dimensional shapes, called conformations. To understand the properties and functions of complex molecules, such as, for example, proteins, one often needs to have a detailed understanding of their conformational dynamics.
These conformational changes are difficult to characterize by experiments, but they can be simulated by classical MD simulations [30,31,32]. In these simulations, a conformation is represented by a position vector , where N is the number of atoms in the system, and each atom is assigned a position in the three-dimensional space. The interactions between the atoms are represented by a predefined potential energy function (Figure 1a). The dynamics are generated by assigning initial velocities to each atom and integrating Newton’s equations of motion numerically on the potential energy surface (PES) . This yields a trajectory, that is, a sequence of positional vectors , where n is the number of time steps in the simulations. The trajectory can be visualized as a trace in the conformational space (Figure 1b).
If the system is coupled to a heat bath by a thermostat algorithm, the trajectory represents a sample of the Boltzmann probability density:
where T denotes the absolute temperature, and is the Boltzmann constant (Figure 1c). Equation (1) implies that regions with low energy are sampled much more frequently than regions with high potential energy. Of particular importance are the minima in the potential energy functions, which correspond to regions with a high data-point density that are separated from other frequently sampled regions (other minima) by regions of significantly low data-point density (transition states). In a simulation of the MD, a trajectory will stay for a long time within one minimum before it transitions to another minimum. Thus, the minima do not only correspond to frequently sampled conformations but concomitantly to long-lived conformations (metastable states).
Figure 3 shows an example: the conformations of the C-type lectin receptor Langerin. Langerin is a mostly rigid protein (gray parts in Figure 3b), but it has a flexible short loop that assumes several distinct conformations (colored parts in Figure 3b). For details of the simulation protocol, see [33]. Figure 3a shows a projection of the Boltzmann distribution on a two-dimensional (2D) reduced space (obtained by principle component analysis of the trajectory). The conformations correspond to highly populated regions in this space. Figure 3a also shows that, in this reduced space, the conformations partially overlap. Knowing the core sets of these regions is thus much more useful for the characterization of the conformations than knowing the exact boundaries. In this case, the gap between the short loop and the long loop can open and close (Figure 3b), and the conformations are distinct states along this reaction coordinate (Figure 3c). Finally, changes in the environment or interactions with other molecules, for example, ligands, can induce shifts in the Boltzmann distribution of a molecule, which are critical to its functions [33,34,35]. For the analysis of simulations and the elucidation of MD, it is therefore of supreme importance that we can accurately identify the regions of high probability density (core sets).
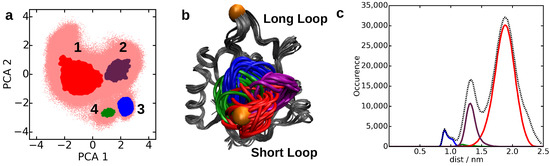
Figure 3.
Molecular dynamics (MD) simulation trajectory of Langerin [33] (a) projected onto the first two principle components. Each core set (highlighted in different colors) represents a minimum of the potential energy surface spanned by the principle components and is linked to (b) a metastable state. (The core sets were identified by common nearest neighbor clustering, where the distance metric was the Euclidean distance in the space spanned by the first two principle components. A preprocessing of the MD dataset by principle component analysis is however not strictly necessary [4,24]). (c) Distance distribution of the distance Met260-Gly290 (highlighted in (b) by orange spheres).
3. Materials and Methods
3.1. Common Nearest Neighbor Algorithm
The CNN algorithm [4] is a density-based cluster algorithm that yields a strict partitioning with outliers. CNN clustering depends on two parameters: the radius of the neighborhood R and the number of common nearest neighbors N. R determines the neighborhood of a data point ; that is, all data points that are closer than this distance are the nearest neighbors of (Figure 4). Two data points and are density-reachable if they share at least N nearest neighbors. This condition serves as an approximation of the local data-point density in the region between the two data points (Figure 4b). Data points that are density-reachable from each other always belong to the same cluster. It is important to point out that not all nearest neighbors of are necessarily density-reachable from . This is, for example, the case if no data points are located in the overlapping region of the two neighborhoods (Figure 4c).
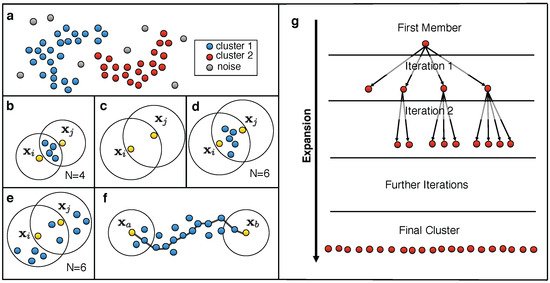
Figure 4.
Clustering process using the common nearest neighbor (CNN) algorithm: (a) A dataset that consists of two clusters and several noise points. (b–e) Depiction of the density criteria that determine whether two data points and belong to the same cluster: (b) The first density criterion, N shared nearest neighbors, is fulfilled. (c) The second density criterion, and are nearest neighbors with respect to the other data point, is fulfilled. (d) Both criteria (b,c) are fulfilled at the same time. Hence, and belong to the same cluster. (e) One criterion is fulfilled, the other is not. Hence, and do not belong to the same cluster. (f) and fulfil no density criteria but belong to the same cluster as they are density-connected (reproduced from Lemke, O.; Keller, B.G. “Density-based cluster algorithms for the identification of core sets”, J. Chem. Phys. 2016, 145, 164104, with the permission of AIP Publishing). (g) Depiction of a clustering process over several cluster expansion steps (iterations). We note that the cluster is expanded by adding single data points to the current cluster that fulfil the density criterion with respect to a data point within the cluster.
We consider a situation in which data point is density-reachable from and data point is density-reachable from but data points and are not density-reachable from each other. In CNN clustering, all three data points belong to the same cluster. In fact, the cluster is iteratively extended by adding data points that are density-reachable by at least one of the current cluster members. Thus, a given cluster member is not necessarily density-reachable from all other cluster members, but it must be density-connected to all other cluster members. Two data points are density-connected if they are connected via a sequence of density-reachable data points (Figure 4f). As a consequence, the algorithm can identify clusters of arbitrary shapes and sizes.
The following is the CNN cluster algorithm:
- 0.
- Choose R and N.
- 1.
- Cluster initialization: Choose an arbitrary data point from the set of unclustered data points U as the first member of the cluster C. Set to (first line in Figure 4g).
- 2.
- Cluster expansion:
- (a)
- Add any unclustered data point within of , which fulfils the density criterion with respect to , to the cluster C (second line in Figure 4g) and remove it from U. Keep a list L of the newly added data points.
- (b)
- Choose a data point from L and set to .
- (c)
- Repeat steps (a) and (b) until no further data point can be added to C (third and fourth line in Figure 4g).
- (d)
- Save C to file and reset C to an empty list .
- 3.
- Repeat steps 1 and 2 until all data points are assigned to a cluster.
We note that the CNN algorithm is not an optimization algorithm; it is a cluster growing algorithm [36]. The cluster memberships are completely defined by the parameters R and N, which stay constant over the complete clustering. All data points that are density-connected will be assigned to one cluster (steps 1 and 2 in the described procedure). Thus, the number of clusters is also defined by these parameters. Additionally, the cluster result is completely independent of the choice for the initial cluster member. The CNN algorithm merely extracts the cluster memberships from the datasets by checking the density criterion. Starting from an initial cluster member, it grows a specific cluster by adding members one-by-one (single-link). A data point becomes a cluster member if it is density-connected to any of the current cluster members. Unclustered points are checked several times until the cluster cannot be extended any further. The remaining unclustered data points belong to either another cluster or are outliers. The cluster is thus removed from the dataset and a new cluster is initialized. That is, the clusters are sequentially “cut out” from the dataset.
The algorithm can yield clusters with only a single member. These clusters are labeled as noise points and are combined into a single set. Alternatively, one can assign all clusters with less than M members to the set of noise points. The parameter M then represents the minimal cluster size, for which the default value is .
The parameters R and N together represent a data-point density threshold. They thus have to be adapted to the data-point density of the dataset at hand. The neighborhood radius R is chosen to be smaller than the position of the first peak in the histogram of pairwise distances. For the benchmark datasets, we chose (see Section 4.1 and Figure 5 for more details and an illustration). N is chosen by reclustering the dataset with different values of N and plotting the number of clusters as a function of N. Usually one finds a plateau region in this plot, which then determines the value for N (see [4]). Alternatively, one can analyze the distance distribution within the clusters to decide on the value of N (see Section 4.1 and Figure 5 for more details and an illustration). At the moment, there is no scheme to choose the parameters R and N automatically. However, following the schemes described above, it is very easy to find a good parameter set manually. For the benchmark datasets, the parameter M has been set to 10. For MD datasets, we find that , where n is the size of the dataset, is a useful heuristic.
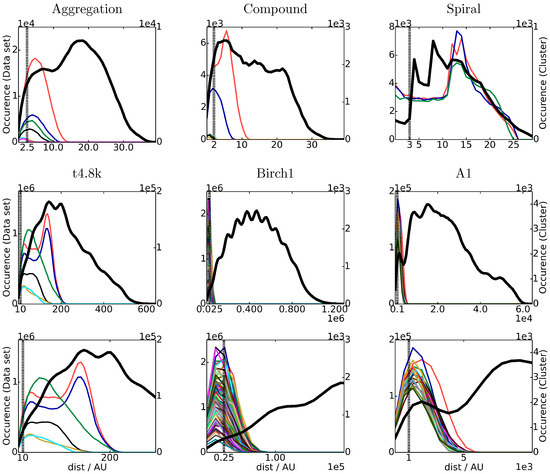
Figure 5.
Distance distribution of different datasets (left axis, black). Distance distribution of the isolated clusters (right axis, colored according to the clusters in Figure 2). In the third row, a zoom into the datasets of the second row is shown. The dashed line denotes the chosen cutoff distance R for each dataset.
We note that in each cluster extraction step (steps 1 and 2), the algorithm identifies a single cluster, which is then removed from the set of unclustered data points. There are two modifications that decrease the run-time of the algorithm. First, the first member of each new cluster is chosen to be the data point that has the greatest number of nearest neighbors in the set of unclustered data points. Second, the current cluster criterion data points, which are potentially density-reachable from a given cluster member, lie within a radius of from this data point. If one additionally requires that density-reachable data points have to be neighbors of each other (i.e., they are members of each other’s neighbor list), the search radius reduces to R (Figure 4d), and all data points that are potentially density-reachable from are members of its neighbor list.
The software for the algorithm is available on GitHub [23].
3.2. Hierarchical Clustering
The CNN algorithm aims to define clusters along iso-surfaces of the underlying probability density. If the dataset contains clusters with varying data-point densities, which are however well separated from each other by regions of very low data-point density, a single parameter set (R and N) is usually sufficient to extract all clusters in a single clustering step. For this, one chooses the parameters such that they correspond to the low data-point density in the intervening space between the clusters, and the CNN algorithm identifies all regions with higher density as separate clusters. In some cases it might, however, be necessary to characterize local density peaks within a single cluster. Achieving this with only a single set of parameters is often not possible, because the data-point density between two local peaks is often higher than the data-point density in some of the other clusters in the dataset. Such a situation is shown for the dataset of the simulation of Langerin (Figure 6a). The region between clusters 1 and 2 has a higher data-point density than clusters 3 and 4. Yet, one would not like to categorize clusters 3 and 4 as noise points because they represent distinct states (Figure 3), which might be relevant to the function of the molecule. The solution is to apply a hierarchical approach [24]. First, the dataset (Figure 6c) is partitioned into clusters 3 and 4 and a large cluster that combines clusters 1 and 2 (Figure 6d) using a set of clustering parameters, which represents a very low data-point density, that is, either large R or small N. The large cluster is then partitioned into clusters 1 and 2 by clustering with a parameter set that represents a higher data-point density (Figure 6e), decreasing R and/or increasing N. Reclustering clusters 3 and 4 with these “harsher” parameters partitions these clusters into only noise points, which shows that these clusters do not exhibit any local structure. The procedure can be repeated iteratively until no further substructures can be identified.
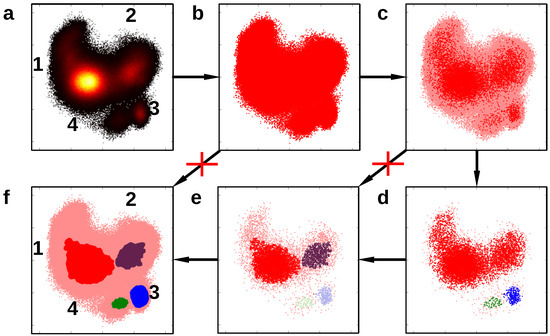
Figure 6.
Hierarchical clustering: (a) the density of a molecular dynamics simulation trajectory projected onto two meaningful coordinates; (b) the dataset of the trajectory; (c) a reduced dataset (red) for the clustering; (d) outcome of the first clustering step; (e) outcome of the second clustering step; (f) final core sets. A direct step from (b–f) is not possible because of the dataset size. A direct step from (c–e) is not possible because of the high difference in the cluster density.
3.3. Dataset Reduction
For large datasets, the most computationally expensive step in the CNN clustering is the calculation of the pairwise distances ( complexity). The true clustering step scales much faster, and its computational costs are typically negligible compared to the construction of the distance matrix (see Section 4.3). This is particularly true for datasets from simulations, because (i) the state space is high dimensional, and (ii) each distance calculation is preceded by a rotational and translational alignment of the two conformations. Thus, in practice, the full dataset (Figure 6b) is reduced by, for example, extracting every nth data point from the full dataset (Figure 6c). The clustering is then carried out on the reduced dataset (Figure 6d–e). In the final step, the full dataset is mapped onto the clusters using, for each cluster, the parameter set that was used for its isolation (Figure 6f).
3.4. Centroid Index at Cluster Level
In benchmark sets for which a set of reference centroids was given , we used the centroid index at cluster level (CI) [37] to estimate the quality of the CNN cluster results. For each CNN cluster , we calculated a centroid as the arithmetic mean over all cluster members and obtained a set of cluster centroids . We note that if the CNN cluster algorithm identified a different number of clusters than the reference partition contained. The CI maps each onto its closest reference centroid and counts the number of reference orphans, that is, reference centroids to which no cluster centroid was mapped. The reverse CI maps each onto its closest cluster centroid and counts the number of cluster orphans, that is, cluster centroids to which no reference centroid was mapped. In Table 1, we report the maximum of these two numbers.

Table 1.
Properties of the benchmark datasets: n: dataset size; d: dimensionality; : reference number of clusters. Parameters for the common nearest neighbor (CNN) algorithm: R and N: cluster parameter set; M: minimal cluster size. Parameter for the Density based spatial clustering of applications with noise DBSCAN algorithm: : cutoff distance; : minimum number of neighbors; M: minimal cluster size. Hierarchical clustering was necessary. The size was reduced from 100,000 extracting every 10th data point.
3.5. Markov Chain Monte Carlo Sampling
We used the Markov chain Monte Carlo (MCMC) algorithm [38] to generate pseudo-dynamics in the potential energy function:
with . All other parameters are shown in Table 2 and the potential energy function is depicted in Figure 1a.

Table 2.
Parameters used for the construction of a generated potential energy surface as shown in Figure 1a.
In MCMC sampling, a random position is drawn from a normal distribution centered at the current position . The new position is accepted with a probability of . By setting
the resulting dataset represents a sample of the Boltzmann distribution. The starting point was set to , and , where T denotes the absolute temperature and denotes the Boltzmann constant. The sampling was performed over iterations.
4. Results
4.1. Benchmark
The CNN algorithm was evaluated using different 2D datasets, which showed regions of different data-point density (Table 1). These datasets were chosen to cover several typical challenges for cluster algorithms: the dataset containing clusters in a variety of sizes and shapes (shape sets); the centroids of the clusters being aligned along a specific pattern (Birch sets); the number of clusters varying between different datasets (A sets); the dataset containing overlapping clusters (S sets). The datasets were obtained from [39]. The clustering results are presented in Figure 2 and Table 3. The parameters are recorded in Table 1. The cluster parameters were determined by the following procedure: we plotted the histogram of the pairwise distances in the dataset and chose R to be smaller than the distance for which the first maximum in the histogram appeared (Figure 5). The first peak in this histogram often represents the average distance between data points within a cluster. With a larger value of R, the neighborhood of a data point is so large that the boundary between the cluster and noise region is often not accurately resolved. A second advantage of a small value for R is that the neighbor lists are short, which keeps the run-time of the CNN algorithm small. Once R was set, the neighborhood parameter N was varied from small to large values, and the best clustering results from this scan are reported in Figure 2 and Table 1. This procedure is possible because the CNN clustering is, as far as the distances are calculated once, computationally inexpensive. The choice of the cluster parameters can in principle be automized by numerically identifying the peak in the histogram of the pairwise distances to determine R and by numerically identifying the plateau region in the number of clusters during the scan of the neighborhood parameter N. However, this has not been implemented yet because the procedure can be carried out manually very quickly. For all datasets, which could be resolved with a single parameter set, the hierarchical variant of the algorithm was not applied, as every single step involved the definition of a new parameter set.

Table 3.
Clustering results for different datasets. The left part shows the number of isolated clusters for the common nearest neighbor (CNN) and the DBSCAN algorithm (compared to the reference number of cluster ) as well as the percentage of data points declared as noise. The right part shows the centroid index at cluster level (CI) [37] using the CNN algorithm, the DBSCAN-algorithm and the kMeans(++) algorithm () [40] as implemented in [41]. The CI values are compared to reference values provided by the authors of [39] for the kMeans algorithm [42] using a random initialization (kM) and using a further point heuristic (Max) [43] initialization. The reference data were averaged over 5,000 runs. Hierarchical clustering was necessary. After the last clustering step.
To determine the quality of the clustering, we visually inspected the results (Figure 2). Additionally, we used the CI [37]. This measure maps the original centroids of the dataset (if available) to the centroids obtained by the clustering algorithm and counts mismatches. A perfect clustering has a CI of zero. As a third criterion, we analyzed the distribution of pairwise distances within each cluster (Figure 5). For datasets without any nested clusters, the distance distribution within each cluster should show a single maximum. Otherwise, the cluster can be split into two separate clusters. This is even true for datasets with convex but well-separated clusters; see, for example, datasets Compound [19] and Spiral [22]. However, if the dataset contains convex clusters that are nested at a very small distance, the rule does not apply. This is shown for the dataset t4.8k [2].
CNN clustering correctly partitioned the vast majority of the benchmark datasets (Figure 2 and Table 3). To obtain a deeper insight into the performance of the CNN algorithm as well as the dependency on the choice of parameters, we analyzed the clustering results with respect to five main challenges of typical datasets: (1) differences in cluster size and shape; (2) number of clusters; (3) unbalanced data-point density; (4) cluster overlap; (5) dimensionality of the dataset.
4.1.1. Cluster Size and Shape
Analyzing the cluster results of the Shape sets, we observe that CNN clustering can extract clusters with different sizes and shapes without prior knowledge of the exact number of clusters (see, e.g., the t4.8k [2] (shape) and the Aggregation (size) datasets [18]). Only for two datasets was the reference solution not found. In the Jain dataset [21], the green and the blue clusters are aligned along the same curved line and thus visually appear to be linked. However, there is a clear gap in the data-point density between these two clusters. Thus, classifying them as two different clusters seems to be justified. Therefore, the only Shape set that could not be clustered satisfactorily by the CNN algorithm was the Path-based dataset [22]. The data-point densities between the two central clusters and between the clusters and the outer ring were comparable to or even higher than the data-point density within the outer ring. Thus, we could extract the two central clusters using a small neighborhood distance R (i.e., targeting a high data-point density). This parameter setting split the outer ring into seven separate clusters (M was reduced to five for this case to highlight the splitting). Even with hierarchical clustering, the outer ring could not be separated from the noise points.
4.1.2. Number of Clusters
To investigate, the influence of varying the cluster number on the A sets was analyzed. These datasets had the property that the smaller sets were subsets of the larger sets. Hence, only one parameter set should have been needed to resolve all three datasets. As shown in Table 1, this was the case for the CNN algorithm, as it could perfectly resolve all three datasets with one parameter set. In addition, it has to be remembered that the cluster number is not predefined and is an outcome of the algorithm.
4.1.3. Unbalanced Data-Point Density
Differences in data-point density were analyzed by clustering the Unbalance dataset [17]. The results show that the CNN algorithm can handle datasets for which the clusters have different data-point density. If the clusters are well separated, this is even possible with a single set of parameters (i.e., without hierarchical clustering). However, if the clusters overlap, the CNN algorithm can fail, as was observed for the Birch3 dataset [14]. This dataset was particularly challenging because the clusters had vastly different data-point densities and because the overlap between the clusters in the reference solution was so strong that no drop in the data-point density occurred. The latter problem cannot be counteracted using the CNN algorithm, as a density drop between two clusters is essential for the definition of clusters within CNN clustering. However, applying a hierarchical clustering approach, as described in Section 3.2, results in a better cluster identification (compared to one-step clustering) and can solve the first issue. We used three rounds of hierarchical clustering to highlight the optimization. Further rounds would have yielded an even more detailed resolution of the dataset. At this point it has to be remembered that each hierarchical step is done separately, and a parameter set has to be selected manually for each single step.
4.1.4. Cluster Overlap
As shown in the former section, the CNN algorithm fails if overlapping clusters of different data-point density are clustered. Therefore, it is of interest to investigate the influence of the overlap for clusters of equal data-point density. Increasing cluster overlap was tested using the S sets [13]. The datasets with a small overlap (S1 and S2) were clustered correctly. In the datasets S3 and S4, CNN identified 16 instead of 15 clusters, as in the reference solution. The additional cluster, however, had a similar data-point density compared to the 15 reference clusters. From the viewpoint of density-based clustering, there was thus no reason to declare the data points in the additional cluster as noise. To further evaluate how the overlap influences the clustering results (depending on the chosen parameter set), the G2 datasets [44] were also tested. The G2 datasets consisted of two Gaussian-distributed clusters in 1–1024 dimensions. For every dimension, 10 datasets were present, where the standard deviation differed between 10 and 100. The distance between the maxima was . The CNN algorithm was probed on the datasets of 2, 8 and 128 dimensions. To gain useful information out of these 30 datasets, three parameters were recorded: The distance cutoff R (0.9 of the position of the first maximum in the distance distribution), the minimal value of N needed to separate the two clusters, and the maximal relative cluster size that could be obtained with the resulting parameter set (the maximal cluster size for each cluster was 50%). The results are summarized in Figure 7a. Figure 7a shows that with an increasing standard deviation (i.e., increasing overlap), the chosen cut-off parameter R also increased as the maxima of the distance distribution merged, as shown in [39]. The CNN algorithm could separate the clusters in two dimensions until a standard deviation of 60 was reached. For higher standard deviations, no separation could be observed using this algorithm. Additionally, with increasing overlap, the density parameter N had to also be increased, resulting in a decrease of the maximal cluster size from 50% () to 10% (). The effects of increasing dimensionality are discussed in the next paragraph.
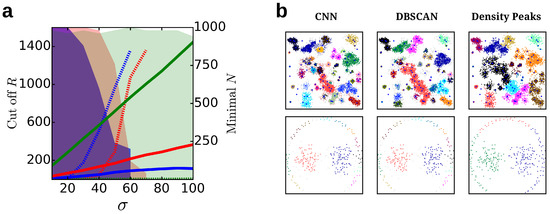
Figure 7.
Further evaluation of the clustering: (a) Parameters R (solid, left axis) and N (dashed, right axis) for the clustering of the G2 datasets for 2 (blue), 8 (red) and 128 (green) dimensions. For N the minimal value is reported for which a split of the two clusters is observed. The colored region highlights the cluster sizes that are possible to extract. We note that beyond for two dimensions and for eight dimensions, no split of the clusters is observed. (b) Clustering for the Birch3 (upper) and the Path-based (lower) datasets using the common nearest neighbor (CNN), the DBSCAN and the density peaks algorithms.
4.1.5. Dimensionality
In the previous paragraphs, it is shown that the CNN algorithm can handle 2D datasets, consisting of clusters of different sizes, shapes and densities, quite well. However, many problems cannot be represented as a 2D dataset and show a higher dimensionality (e.g., protein dynamics). We therefore applied the CNN algorithm to high-dimensional datasets (Dim [16] and G2 datasets [44]). The Dim datasets consist of 16 Gaussian functions in 32 to 1024 dimensions (Dim-32 to Dim-1024 [16]). For all datasets, a clear separation of the Gaussians was achieved. This proves that the CNN algorithm can also resolve higher-dimensional datasets. However, for 512 dimensions, one cluster became lost. Additionally, the number of noise points increased with increasing dimensionality. Both observations came into play as a result of the vastness of the high-dimensional space. However, for the G2 datasets, the advantages of a higher dimensionality can also be observed (Figure 7a). With each additional dimension, the distance between the maxima increased. Hence, with constant standard deviation, the overlap decreased. As a consequence, the density parameter N could be kept small over a long range of standard deviations, resulting in larger clusters.
4.1.6. Comparison to Other Cluster Algorithms
To evaluate the obtained results discussed in the former chapters, other cluster algorithms were also tested. One algorithm is the kMeans(++) algorithm [40,42], as implemented in the MD analysis package pyEMMA [41], which is often applied for the analysis of MD simulations. This algorithm shows satisfactory partition for datasets consisting of well-separated spherical clusters such as the Dim sets. However, the more the clusters overlap, the worse the results of the kMeans++ algorithm become. For convex clusters (Shape sets), the algorithm fails completely. Hence, a highly increased cluster number is needed to apply to real data, such as MD data. Additionally, the kMeans(++) algorithm is not capable of extracting only the cores and also yields, for most cases, bad boundaries. For further comparison, the results for other kMeans variants are also added to Table 3. The results were taken from [39] and are therefore not further discussed. In [24], we showed that other density-based cluster algorithms are also capable of extracting core sets in MD data. One of these algorithms is the DBSCAN algorithm [6]. There are two main differences between CNN and DBSCAN: (1) The CNN algorithm estimates the data-point density in the region between two data points, whereas DBSCAN estimates the data-point density for which a single data point merges this data point with its neighbors independent of whether there is dip in the data-point density or not. (2) The results of DBSCAN depend on the initialization, whereas with CNN, the cluster results depend only on the parameters R, N, and M. For the DBSCAN algorithm, the sorted-9-dist graph as proposed by [6] was applied to determine the cut-off parameter. To make this algorithm comparable to the CNN algorithm, a minimal cluster size of 10 was added. The results of the DBSCAN algorithm show that using this scheme, for most datasets, only worse results compared to the CNN algorithm were obtained. Only for the Dim datasets [16] were better results observed. However, in [24] we showed that using a comparable scheme for the parameter selection as presented in this paper for the CNN algorithm, better results for the DBSCAN algorithm were observed. It has to be remembered that if the noise level of the dataset is not known in both parameter selection schemes, at least one parameter is chosen manually by the user. For two datasets, the CNN algorithm failed completely: the Pathbased and the Birch3 dataset. To check if other density-based cluster algorithms could handle these datasets besides the DBSCAN algorithm, the density peaks algorithm [9,10] was also evaluated. For the reduced Birch3 dataset, both algorithms failed, resulting in a CI of 59 for DBSCAN and a CI of 87 for the density peaks algorithm (; 13 clusters isolated). The Pathbased dataset could also not be resolved as a result of the reasons explained above (DBSCAN: 13 clusters; density peaks (): three clusters, but not perfectly resolved). The results for the two datasets are shown in Figure 7b.
4.2. Core-Set Models of Molecular Dynamics
MD simulations are not only used to sample and analyze the Boltzmann distribution, but also to extract and analyze the slow dynamic processes of the system. The slow dynamic processes of pseudo-dynamics (i.e., generated by a MCMC algorithm) on the PES in Figure 1 are shown in Figure 8d. The first process is the stationary process and is equal to the Boltzmann distribution. Formally, it is associated to a time scale of infinity. The slowest dynamic process with a finite time scale is and represents the dynamic exchange between the minimum at the bottom and the two minima at the top, that is, across the largest barrier. Its time scale is ≈70 time steps, where each iteration of the MCMC algorithm is interpreted as a time step. The next slowest process, , represents the dynamic exchange between the two minima at the top and is associated to a time scale of ≈24 time steps.
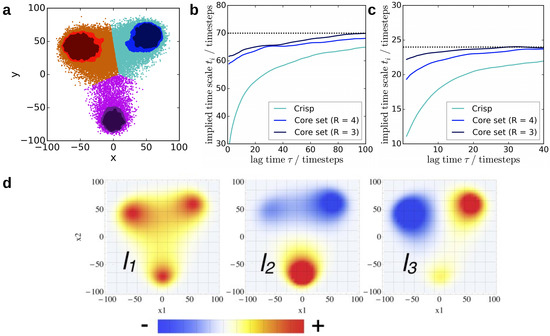
Figure 8.
(a) Core sets of the two-dimensional (2D) potential energy surface (PES) using different parameter sets. A smaller core set corresponds to a smaller cutoff radius. Implied time scales (colored according to the upper right cluster in (a)) of the slower process (b) and the faster process (c). The black dashed line denotes the convergence limit. (d) Corresponding eigenvectors to the slow processes: Stationary distribution (left), slower process (middle), and faster process (right). The eigenvectors describe transitions of probability density between states with different sign (highlighted by the color).
There are several methods known that can extract information from such a trajectory, such as sequence kernels and support vector machines [45,46,47,48,49]. However, most of these are currently not applied to MD data, as these data are described in terms of non-linear internal coordinates in a high-dimensional conformational space. The most commonly used method to extract the slow dynamic processes from a trajectory are Markov state models [50,51,52,53,54,55] (MSM). They represent a discretization of the dynamical propagator [50,55] and are based on a discretization of the molecular state space into crisp non-overlapping states. The dynamics are approximated as a jump process (Markov process) between pairs of states within a time lag (Figure 8a), which yields a matrix of pairwise transition probabilities, the transition matrix . The transition probabilities can be estimated from a trajectory. The transition matrix is however only a model of the true dynamics, and the approximation error depends sensitively on the discretization [56]. Recently, methods to discretize the dynamical propagator with respect to arbitrary ansatz functions have emerged [29,57,58,59,60]. In core-set models [24,25,26,28], the state space is discretized into core sets, which do not fully partition the state space. Associated to each core set is a committor function , which represents the probability that the dynamic process will reach before it reaches any of the other core sets. Thus, if , if , and otherwise. If the core sets represent long-lived conformations (which usually coincide with maxima in the Boltzmann distribution), discretizing the dynamical propagator with respect to the associated committor functions yields models with a very small approximation error.
The approximation error of a model is usually judged by the drift of the implied time scale as a function of the time lag (Figure 8b,c):
where is the time lag of the model and is the eigenvalue associated to the kth eigenvector of the discretized propagator [51]. If the dynamics were fully Markovian within the chosen discretization, the implied time scale would be constant, that is, independent of . However, even for models with a discretization error, the implied time scales typically reach a plateau region for large . However, large values of also imply a low time resolution of the model. In general, the smaller the value of for which the drift of the implied time scale becomes negligible, the smaller the approximation error. At time lags shorter than this , the implied time scales are typically underestimated.
Figure 8b,c shows the implied time scale test for the slow dynamic processes and in the three-well potential energy function. We used a crisp discretization (cyan lines) and two different core-set discretizations (blue and black lines) and estimated the models from the same MCMC trajectory. The crisp discretization was obtained by kMeans(++) clustering [40,41,42], where the number of clusters was set to three (Figure 8a). The core-set discretization was obtained by CNN clustering with and , where the smaller cutoff radius corresponded to the smaller core sets (Figure 8a). Both core-set models yielded a much smaller discretization error than the crisp discretization. The two core-set models had a similar discretization error. However, the model with the smaller core sets was slightly more accurate. At a time lag of time steps, at the time lag at which both processes could be resolved, the slowest implied time scale was estimated to be 64 time steps and 62 time steps by the two core-set models, which was relatively close to the limit value of ≈70 time steps. By contrast, the crisp discretization yields a value of 46 time steps. For the implied time scale , the estimates were 23 time steps and 22 time steps for the core-set model, and 18 time steps for the crisp discretization, where the limit value was ≈24 time steps.
4.3. Run-Time Analysis
The input of the CNN algorithm is a distance matrix of the dataset. For most practical applications, the computational cost of calculating the distance matrix from a set of data points in a often high-dimensional feature space by far outweighs the computational cost of the clustering. This is particularly true for MD data, for which each distance calculation is preceded by a translational and rotational fit. The complexity of calculating the distance matrix is .
Figure 9 shows the run-time analysis of the CNN clustering, that is, the computational cost of the clustering, excluding the cost for the calculation of the distance matrix. The run-time of the CNN algorithm depends on the size of the neighbor lists, which in turn depends on the structure of the dataset. We therefore tested two different datasets. The Birch2 set (blue line) showed a high number of well-separated clusters, which resulted in a short neighbor list and thus a fast run-time. By contrast, the sample of the 2D Boltzmann distribution (Section 4.2), called MCMC, consisted of three strongly overlapping clusters, which yielded large neighbor lists. The full datasets consisted of (Birch2) and data points (MCMC) and were downsampled to test the run-time on smaller datasets. We chose the neighborhood radii R using the procedure described in Section 3.1. The value of N was set to 0.2% of the dataset size (e.g., N = 20 for 10,000 data points). The run-times for both systems were far from a quadratic scaling. Datasets with data points could be clustered within a few minutes on an Intel(R) Core(TM) i5-4590 CPU with 3.30 GHz and 16 GB of RAM. We might be able to further reduce the run-time of the algorithm by adopting a more efficient neighbor-search strategy, which has recently been proposed in [10].
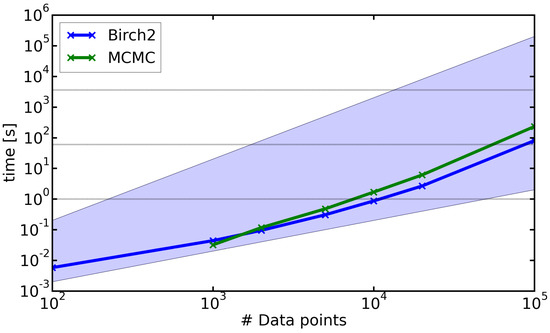
Figure 9.
Run-time of the clustering step (without calculation of the distance matrix) for different dataset sizes for the (blue) Birch2 and (green) sample of the two-dimensional Boltzmann distribution (Section 4.2). The blue area highlights the scaling of the clustering step between linear (lower bound) and quadratic (upper bound) behavior. The dashed lines represent 1 h, 1 min and 1 s respectively. All calculations were performed on an Intel(R) Core(TM) i5-4590 CPU with 3.30 GHz and 16 GB of RAM.
5. Conclusions
We have previously shown that cluster algorithms that base their clustering criterion on a distance-based objective function are poorly suited to characterize probability density, because the distance to a centroid is not distinctive for features in the probability density [4]. By contrast, changes in data-point density are. Thus, density-based cluster algorithms, which aim to estimate the data-point density, are well suited for this task. Characterizing the underlying probability density often means finding its peaks or finding a set of data points that are representative for these peaks. Thus, one is interested in identifying a core set. The term core set corresponds to a strict partitioning with outliers of a sample of the underlying probability density. Algorithms that yield such a partitioning are much more suited for the identification of core sets than cluster algorithms that yield a full partitioning of the dataset. This is particularly true for high-dimensional datasets, for which the data points at the rim of the peak can easily outnumber the data points within the core. We have illustrated this for the conformations of the protein Langerin. Finally, the characterization of the underlying probability density sometimes serves as a preliminary step for a discretization of the state space. Using a model of the dynamics on a 2D PES as an example (Section 4.2), we have shown that a core-set discretization yields more accurate models than a full partitioning discretization (i.e., strict partitioning without outliers).
The CNN cluster algorithm assigns cluster membership according to an estimate of the data-point density in between two closely spaced points (maximum distance 2R, where R is set to a small value). In this way, it aims at cutting out clusters from the state space along iso-density lines. Hierarchical clustering to subdivide clusters and to identify local density peaks is possible, but this was not needed for most of the test datasets. Other density-based cluster algorithms, such as DBSCAN [6] and the density peak algorithm [9,10], use similar strategies to extract the clusters from a dataset. For MD datasets, the CNN algorithm and the DBSCAN algorithm yield similar results [24]. A comparison of CNN with density peaks for MD data will be part of future work.
We have successfully applied CNN clustering to a series of test datasets, including datasets with cluster overlap, datasets with a very high dimensional state space and datasets in which the cluster centroids are aligned along an underlying structure (Birch sets). CNN successfully clustered 24 of 26 benchmark datasets (3 out of 24 with small deviations), when the value R was set by visual inspection of the pairwise distance histogram and N was determined as described in Section 3.1. Success was defined by calculating the CI and, for the 2D datasets, by visual inspection of the cluster results. We highlighted that no problems regarding cluster size, cluster shape or cluster number were present for the CNN algorithm. However, cluster overlap in combination with unbalanced cluster sizes (Birch3) can challenge the algorithm, as the required drop-in data-point density vanishes. In addition to this, we showed that an increasing overlap makes it harder to find a suitable set of parameters (G2), as the number of parameter sets that can resolve the clusters decreases.
In conclusion, CNN clustering was originally developed for the analysis of MD data. The positive benchmark results indicate that CNN clustering is not limited to this setting but that it is likely to be useful for datasets from a wide range of sources. If the dataset resembles dynamic processes, we showed that the dynamics can be described more accurately using core sets instead of a strict clustering without outliers.
Acknowledgments
This research has been funded by Deutsche Forschungsgemeinschaft (DFG) through CRC765 “Multivalency as chemical organization and action principle: New architectures, functions and applications”, Project C10.
Author Contributions
O.L. and B.G.K. conceived and designed the experiments; O.L. performed the experiments and analyzed the data; O.L. and B.G.K. wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CI | Centroid Index at Cluster Level |
| CNN | Common nearest neighbor |
| DBSCAN | Density-Based Spatial Clustering of Applications with Noise |
| kM | kMeans algorithm |
| Max | Further point heuristic |
| MCMC | Markov chain Monte Carlo |
| MD | Molecular dynamics |
| MSM | Markov state model |
| PCA | Principle component analysis |
| PES | Potential energy surface |
References
- JeraldBeno, T.R.; Karnan, M. Dimensionality Reduction: Rough Set Based Feature Reduction. Int. J. Sci. Res. Publ. 2012, 2, 1–6. [Google Scholar]
- Karypis, G.; Han, E.H.; Kumar, V. CHAMELEON: A hierarchical 765 clustering algorithm using dynamic modeling. IEEE Trans. Comput. 1999, 32, 68–75. [Google Scholar]
- Fu, L.; Medico, E. FLAME, a novel fuzzy clustering method for the analysis of DNA microarray data. BMC Bioinform. 2007, 8, 3. [Google Scholar] [CrossRef] [PubMed]
- Keller, B.; Daura, X.; van Gunsteren, W.F. Comparing geometric and kinetic cluster algorithms for molecular simulation data. J. Chem. Phys. 2010, 132, 074110. [Google Scholar] [CrossRef] [PubMed]
- Jarvis, R.A.; Patrick, E.A. Clustering Using a Similarity Measure Based on Shared Near Neighbors. IEEE Trans. Comp. 1973, C-22, 1025–1034. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the KDD-96 the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Comaniciu, D.; Meer, P. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 603–619. [Google Scholar] [CrossRef]
- Ankerst, M.; Breuning, M.M.; Kriegel, H.P.; Sander, J. OPTICS: Ordering Points To Identify the Clustering Structure. In Proceedings of the ACM SIGMOD International Conference on Management of Data, Philadelphia, PA, USA, 1–3 June 1999; pp. 49–60. [Google Scholar]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Zhu, L.; Sheong, F.K.; Wang, W.; Huang, X. Adaptive partitioning by local density-peaks: An efficient density-based clustering algorithm for analyzing molecular dynamics trajectories. J. Comput. Chem. 2016, 38, 152–160. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.K.; Topchy, A.; Law, M.H.C.; Buhmann, J.M. Landscape of Clustering Algorithms. In Proceedings of the ICPR’04 17th International Conference on Pattern Recognition, Cambridge, UK, 23–26 August 2004; Volume 1, pp. 260–263. [Google Scholar]
- Kärkkäinen, I.; Fränti, P. Dynamic Local Search Algorithm for the Clustering Problem; Technical Report A-2002-6; University of Joensuu: Joensuu, Finland, 2002. [Google Scholar]
- Fränti, P.; Virmajoki, O. Iterative shrinking method for clustering problems. Pattern Recognit. 2006, 39, 761–765. [Google Scholar] [CrossRef]
- Zhang, T.; Ramakrishnan, R.; Livny, M. BIRCH: A new data clustering algorithm and its applications. Data Min. Knowl. Discov. 1997, 1, 141–182. [Google Scholar] [CrossRef]
- Kärkkäinen, I.; Fränti, P. Gradual model generator for single-pass clustering. Pattern Recognit. 2007, 40, 784–795. [Google Scholar] [CrossRef]
- Fränti, P.; Virmajoki, O.; Hautamäki, V. Fast agglomerative clustering using a k-nearest neighbor graph. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1875–1881. [Google Scholar] [CrossRef] [PubMed]
- Rezaei, M.; Fränti, P. Set-matching methods for external cluster validity. IEEE Trans. Knowl. Data Eng. 2016, 28, 2173–2186. [Google Scholar] [CrossRef]
- Gionis, A.; Mannila, H.; Tsaparas, P. Clustering aggregation. ACM Trans. Knowl. Discov. Data 2007, 1, 1–30. [Google Scholar] [CrossRef]
- Zahn, C.T. Graph-theoretical methods for detecting and describing gestalt clusters. IEEE Trans. Comput. 1971, 100, 68–86. [Google Scholar] [CrossRef]
- Veenman, C.J.; Reinders, M.J.T.; Backer, E. A maximum variance cluster algorithm. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 1273–1280. [Google Scholar] [CrossRef]
- Jain, A.K.; Law, M.H.C. Data Clustering: A User’s Dilemma. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2005; pp. 1–10. [Google Scholar]
- Chang, H.; Yeung, D.Y. Robust path-based spectral clustering. Pattern Recognit. 2008, 41, 191–203. [Google Scholar] [CrossRef]
- Lemke, O.; Keller, B.G. CNNClustering. Available online: https://github.com/BDGSoftware/CNNClustering (accessed on 6 January 2017).
- Lemke, O.; Keller, B.G. Density-based cluster algorithms for the identification of core sets. J. Chem. Phys. 2016, 145, 164104. [Google Scholar] [CrossRef] [PubMed]
- Sarich, M.; Banisch, R.; Hartmann, C.; Schütte, C. Markov State Models for Rare Events in Molecular Dynamics. Entropy 2014, 16, 258–286. [Google Scholar] [CrossRef]
- Vanden-Eijnden, E.; Venturoli, M.; Ciccotti, G.; Elber, R. On the assumptions underlying milestoning. J. Chem. Phys. 2008, 129, 174102. [Google Scholar] [CrossRef] [PubMed]
- Schütte, C. Conformational Dynamics: Modelling, Theory, Algorithm, and Application to Biomolecules. Habilitation Thesis, Konrad-Zuse-Zentrum für Informationstechnik, Berlin, Germany, 1999. [Google Scholar]
- Schütte, C.; Noé, F.; Lu, J.; Sarich, M.; Vanden-Eijnden, E. Markov state models based on milestoning. J. Chem. Phys. 2011, 134, 204105. [Google Scholar] [CrossRef] [PubMed]
- Schütte, C.; Sarich, M. A critical appraisal of Markov state models. Eur. Phys. J. Spec. Top. 2015, 224, 2445. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understanding Molecular Simulations; Academic Press: San Diego, CA, USA, 1996. [Google Scholar]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: New York, NY, USA, 1987. [Google Scholar]
- Leach, A.R. Molecular Modelling; Addison Wesley Longman: Essex, UK, 1996. [Google Scholar]
- Hanske, J.; Aleksić, S.; Ballaschk, M.; Jurk, M.; Shanina, E.; Beerbaum, M.; Schmieder, P.; Keller, B.G.; Rademacher, C. Intradomain Allosteric Network Modulates Calcium Affinity of the C-Type Lectin Receptor Langerin. J. Am. Chem. Soc. 2016, 138, 12176–12186. [Google Scholar] [CrossRef] [PubMed]
- Witek, J.; Keller, B.G.; Blatter, M.; Meissner, A.; Wagner, T.; Riniker, S. Kinetic Models of Cyclosporin a in Polar and Apolar Environments Reveal Multiple Congruent Conformational States. J. Chem. Inf. Model. 2016, 56, 1547–1562. [Google Scholar] [CrossRef] [PubMed]
- Tsai, C.J.; Nussinov, R. A Unified View of “How Allostery Works”. PLoS Comput. Biol. 2014, 10, e1003394. [Google Scholar] [CrossRef] [PubMed]
- Ball, G.H.; Hall, D.J. A clustering technique for summarizing multivariate data. Behav. Sci. 1967, 12, 153–155. [Google Scholar] [CrossRef] [PubMed]
- Fränti, P.; Rezaei, M.; Zhao, Q. Centroid index: Cluster level similarity measure. Pattern Recognit. 2014, 47, 3034–3045. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Fränti, P.; Sieranoja, S. Clustering datasets. Algorithms 2017. submitted. [Google Scholar]
- Arthur, D.; Vassilvitskii, S. K-means++: The advantages of careful seeding. In Proceedings of the ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–9 January 2007; pp. 1027–1035. [Google Scholar]
- Scherer, M.K.; Trendelkamp-Schroer, B.; Paul, F.; Pérez-Hernández, G.; Hoffmann, M.; Plattner, N.; Wehmeyer, C.; Prinz, J.H.; Noé, F. PyEMMA 2: A Software Package for Estimation, Validation, and Analysis of Markov Models. J. Chem. Theory Comput. 2015, 11, 5525–5542. [Google Scholar] [CrossRef] [PubMed]
- Lloyd, S.P. Least squares quantization in pcm. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Gonzalez, T.F. Clustering to minimize the maximum intercluster distance. Theor. Comput. Sci. 1985, 38, 293–306. [Google Scholar] [CrossRef]
- Fränti, P.; Mariescu-Istodor, R.; Zhong, C. XNN graph. Joint Int. Workshop Struct. Syntactic Stat. Pattern Recognit. 2016, LNCS 10029, 207–217. [Google Scholar]
- Schwantes, C.R.; Pande, V.S. Modeling Molecular Kinetics with tICA and the Kernel Trick. J. Chem. Theory Comput. 2015, 11, 600–608. [Google Scholar] [CrossRef] [PubMed]
- Aghabozorgi, S.; Shirkhorshidi, A.S.; Wah, T.Y. Time-series clustering—A decade review. Inf. Syst. 2015, 53, 16–38. [Google Scholar] [CrossRef]
- Mariescu-Istodor, R.; Fränti, P. Grid-Based Method for GPS Route Analysis for Retrieval. ACM Trans. Algorithm 2017, 3, 1–28. [Google Scholar] [CrossRef]
- Chandrakala, S.; Sekhar, C.C. A density based method for multivariate time series clustering in kernel feature space. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 June 2008. [Google Scholar]
- Hamprecht, F.A.; Peter, C.; Daura, X.; Thiel, W.; van Gunsteren, W.F. A strategy for analysis of (molecular) equilibrium simulations: Configuration space density estimation, clustering, and visualization. J. Chem. Phys. 2001, 114, 2079–2089. [Google Scholar] [CrossRef]
- Schütte, C.; Fischer, A.; Huisinga, W.; Deuflhard, P. A Direct Approach to Conformational Dynamics Based on Hybrid Monte Carlo. J. Comput. Phys. 1999, 151, 146–168. [Google Scholar] [CrossRef]
- Swope, W.C.; Pitera, J.W.; Suits, F. Describing Protein Folding Kinetics by Molecular Dynamics Simulations. J. Phys. Chem. B 2004, 108, 6571–6581. [Google Scholar] [CrossRef]
- Chodera, J.D.; Singhal, N.; Pande, V.S.; Dill, K.A.; Swope, W.C. Automatic discovery of metastable states for the construction of Markov models of macromolecular conformational dynamics. J. Chem. Phys. 2007, 126, 155101. [Google Scholar] [CrossRef] [PubMed]
- Buchete, N.V.; Hummer, G. Coarse Master Equations for Peptide Folding Dynamics. J. Phys. Chem. B 2008, 112, 6057–6069. [Google Scholar] [CrossRef] [PubMed]
- Keller, B.; Hünenberger, P.; van Gunsteren, W.F. An Analysis of the Validity of Markov State Models for Emulating the Dynamics of Classical Molecular Systems and Ensembles. J. Chem. Theory Comput. 2011, 7, 1032–1044. [Google Scholar] [CrossRef] [PubMed]
- Prinz, J.H.; Wu, H.; Sarich, M.; Keller, B.; Senne, M.; Held, M.; Chodera, J.D.; Schütte, C.; Noé, F. Markov models of molecular kinetics: Generation and validation. J. Chem. Phys. 2011, 134, 174105. [Google Scholar] [CrossRef] [PubMed]
- Sarich, M.; Noé, F.; Schütte, C. On the Approximation Quality of Markov State Models. Multisc. Model. Simul. 2010, 8, 1154–1177. [Google Scholar] [CrossRef]
- Nüske, F.; Keller, B.G.; Pérez-Hernández, G.; Mey, A.S.J.S.; Noé, F. Variational Approach to Molecular Kinetics. J. Chem. Theory Comput. 2014, 10, 1739–1752. [Google Scholar] [CrossRef] [PubMed]
- Vitalini, F.; Noé, F.; Keller, B.G. A Basis Set for Peptides for the Variational Approach to Conformational Kinetics. J. Chem. Theory Comput. 2015, 11, 3992–4004. [Google Scholar] [CrossRef] [PubMed]
- Fackeldey, K.; Röblitz, S.; Scharkoi, O.; Weber, M. Soft Versus Hard Metastable Conformations in Molecular Simulations; Technical Report 11-27; ZIB: Berlin, Germany, 2011. [Google Scholar]
- Weber, M.; Fackeldey, K.; Schütte, C. Set-free Markov state model building. J. Chem. Phys. 2017, 146, 124133. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).