An Improved Bacterial-Foraging Optimization-Based Machine Learning Framework for Predicting the Severity of Somatization Disorder
Abstract
:1. Introduction
- (a)
- First, in order to fully explore the potential of the KELM classifier, we introduce an opposition-based, learning-strategy-enhanced BFO to adaptively determine the two key parameters of KELM, which aided the KELM classifier in more efficiently achieving the maximum classification performance.
- (b)
- The resulting model, IBFO-KELM, is applied to serve as a computer-aided decision-making tool for predicting the severity of somatization disorder.
- (c)
- The proposed IBFO-KELM method achieves superior results, and offers more stable and robust results when compared to the four other KELM models.
2. Background Information
2.1. Kernel Extreme Learning Machine (KELM)
2.2. Bacterial Foraging Optimization (BFO)
- (1)
- Chemotaxis: Chemotaxis operation is the core of the algorithm, which simulates the foraging behavior of E. coli moving and tumbling. In poorer areas, the bacteria tumble more frequently, while bacteria move in areas where food is more abundant. The chemotaxis operation of the ith bacterium can be represented aswhere the represents the ith bacterium at the jth chemotactic, kth reproductive, and lth elimination–dispersal steps. C(i) is the trend step length of bacteria i in a random direction (dcti). Δ is a random vector between −1 and 1.
- (2)
- Swarming: In the chemotactic of bacteria to the foraging process, in addition to searching for food in their own way, there is both gravitation and repulsion among the individual bacteria. Bacteria will generate attractive information to allow individual bacteria to travel to the center of the population, bringing them together; at the same time, individual bacteria are kept at a distance based on their respective repulsion information.
- (3)
- Reproduction: According to the natural mechanism of survival of the fittest, after some time, bacteria with weak ability to seek food will eventually be eliminated, and bacteria with strong feeding ability will breed offspring to maintain the size of the population. By simulating this phenomenon, a reproduction operation is proposed. In S-sized populations, S/2 bacteria with poor fitness were eliminated and S/2 individuals with higher fitness self-replicated after the bacteria performed the chemotaxis operator. After the execution of the reproduction operation, the offspring will inherit the fine characteristics of the parent completely, protect the good individuals, and greatly accelerate the speed towards the global optimal solution.
- (4)
- Elimination–Dispersal: In the process of bacterial foraging, do not rule out the occurrence of unexpected conditions leading to the death of bacteria or causing them to migrate to another new area. By simulating this phenomenon, an elimination–dispersal operation has been proposed. This operation occurs with a certain probability Ped. When the bacterial individual satisfies the probability Ped, then the individual of the bacterial dies and randomly generates a new individual anywhere in the solution space. This bacterium may be different from the original bacterial, which helps to jump out of the local optimal solution and promote the search for the global optimal solution.
2.3. Improved Bacterial Foraging Optimization (IBFO)
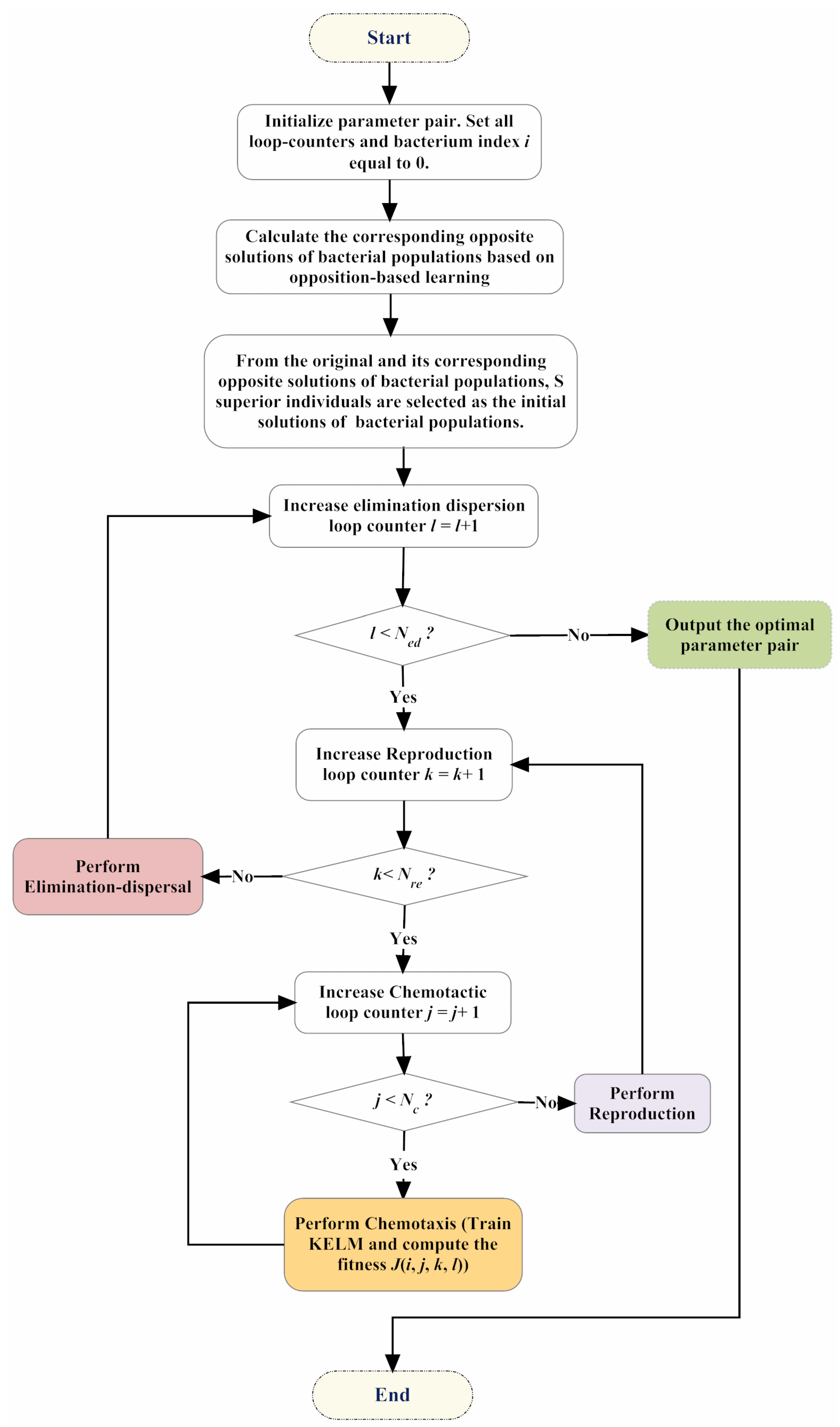
3. Proposed IBFO-KELM Model
| Algorithm 1. Pseudo-code of the improved bacterial foraging optimization (IBFO) strategy. |
| Begin Initialize dimension p, population S, chemotactic steps Nc, swimming length Ns, reproduction steps Nre, elimination-dispersal steps Ned, elimination-dispersal probability Ped, step size C(i). Calculate the corresponding opposite solutions of bacterial populations based on opposition-based learning. From the original and its corresponding opposite solutions of bacterial populations, S superior individuals are selected as the initial solutions of bacterial populations. for ell = 1:Ned for K = 1:Nre for j = 1:Nc Intertime = Intertime + 1; for i = 1:s J(i,j,K,ell) = fobj(P(:,i,j,K,ell)); Jlast = J(i,j,K,ell); Tumble according to Equation (5) m = 0; while m < Ns m = m + 1; if J(i,j + 1,K,ell) < Jlast Jlast = J(i,j + 1,K,ell); Tumble according to Equation (5) else m = Ns; End End End End /*Reprodution*/ Jhealth = sum(J(:,:,K,ell),2); [Jhealth,sortind] = sort(Jhealth); P(:,:,1,K + 1,ell) = P(:,sortind,Nc + 1,K,ell); for i = 1:Sr P(:,i + Sr,1,K + 1,ell) = P(:,i,1,K + 1,ell); End End /*Elimination-Dispersal*/ for m = 1:s if Ped > rand Reinitialize bacteria m End End End End |
4. Experimental Design
4.1. Somatization Disorder Data Description
4.2. Experimental Setup
5. Experimental Results and Discussion
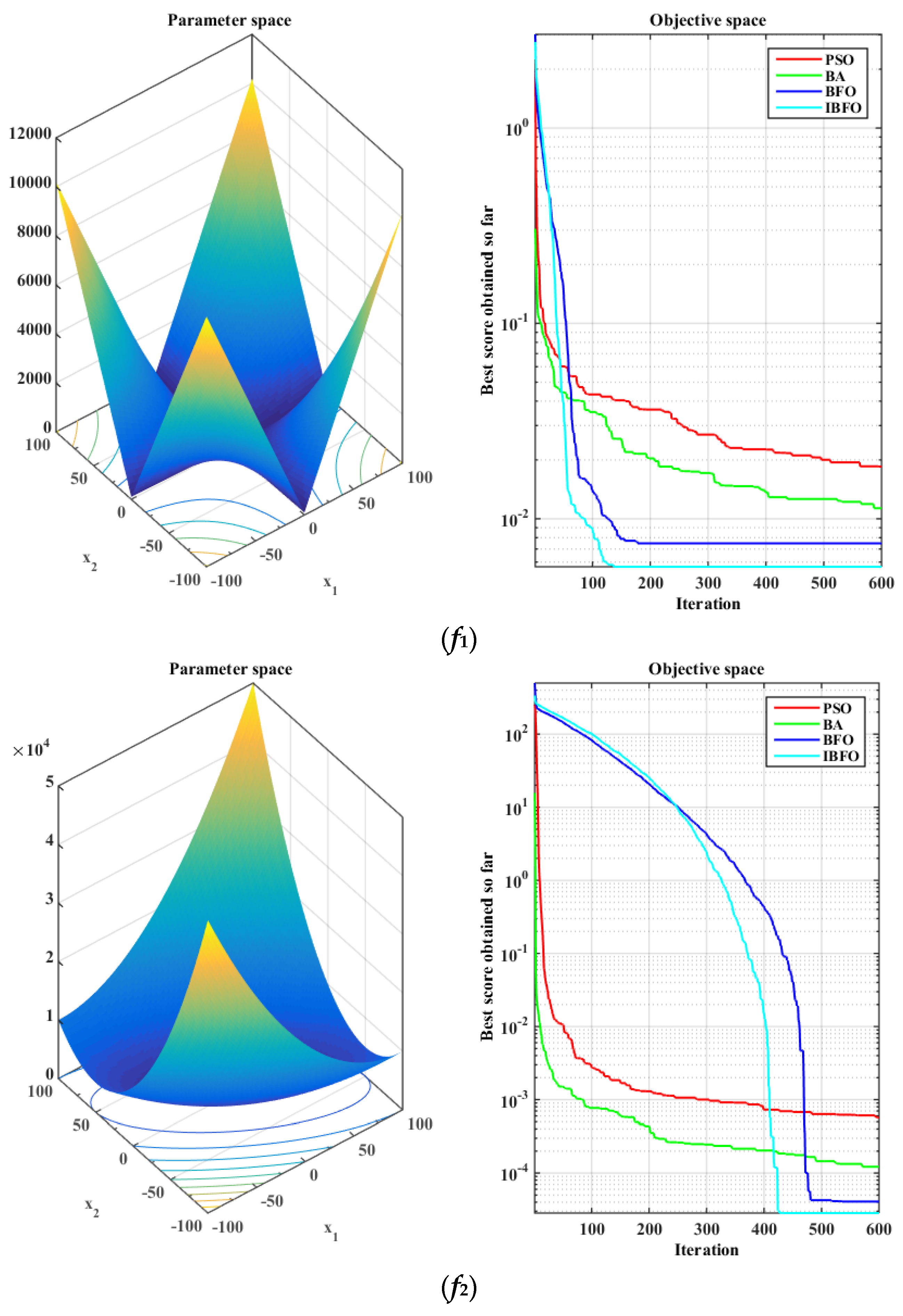
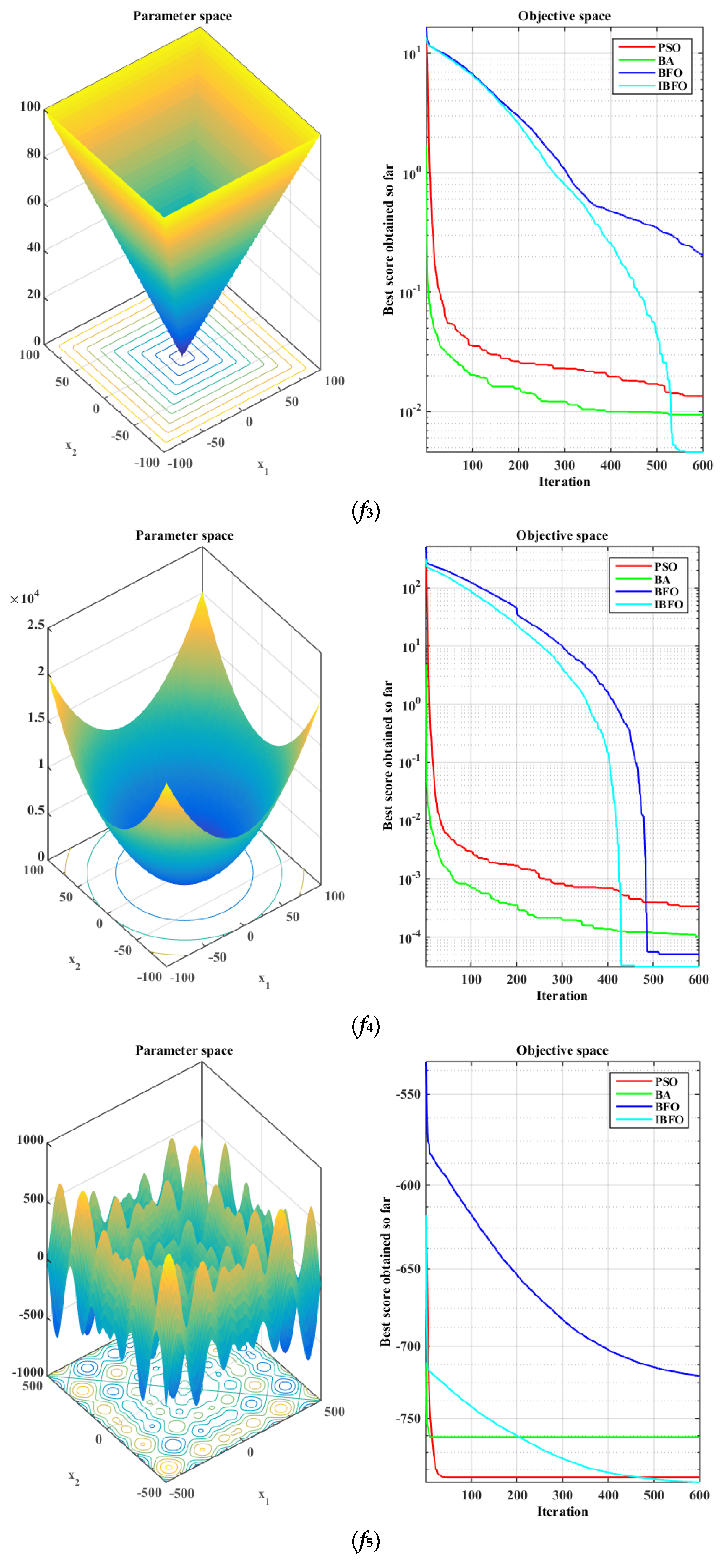
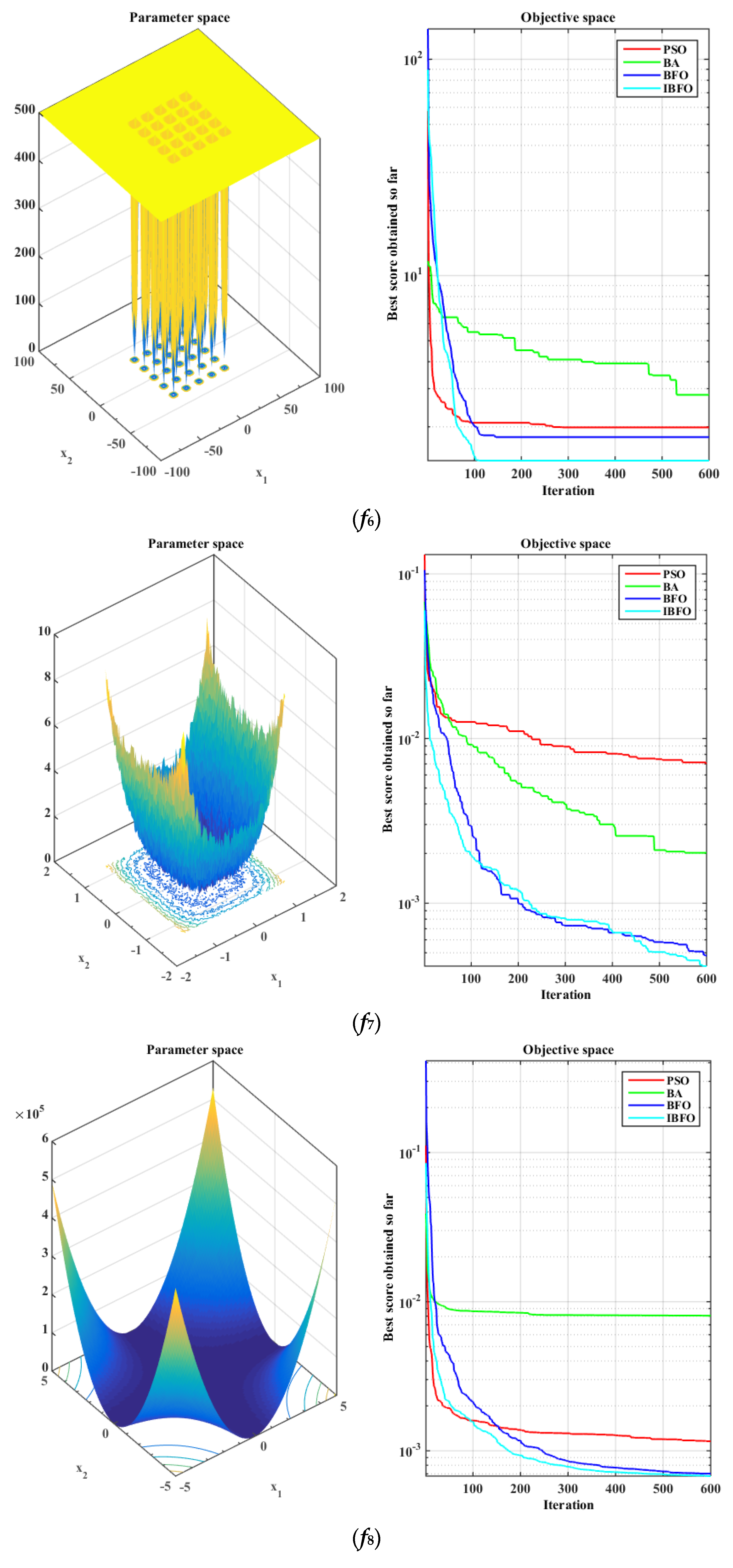
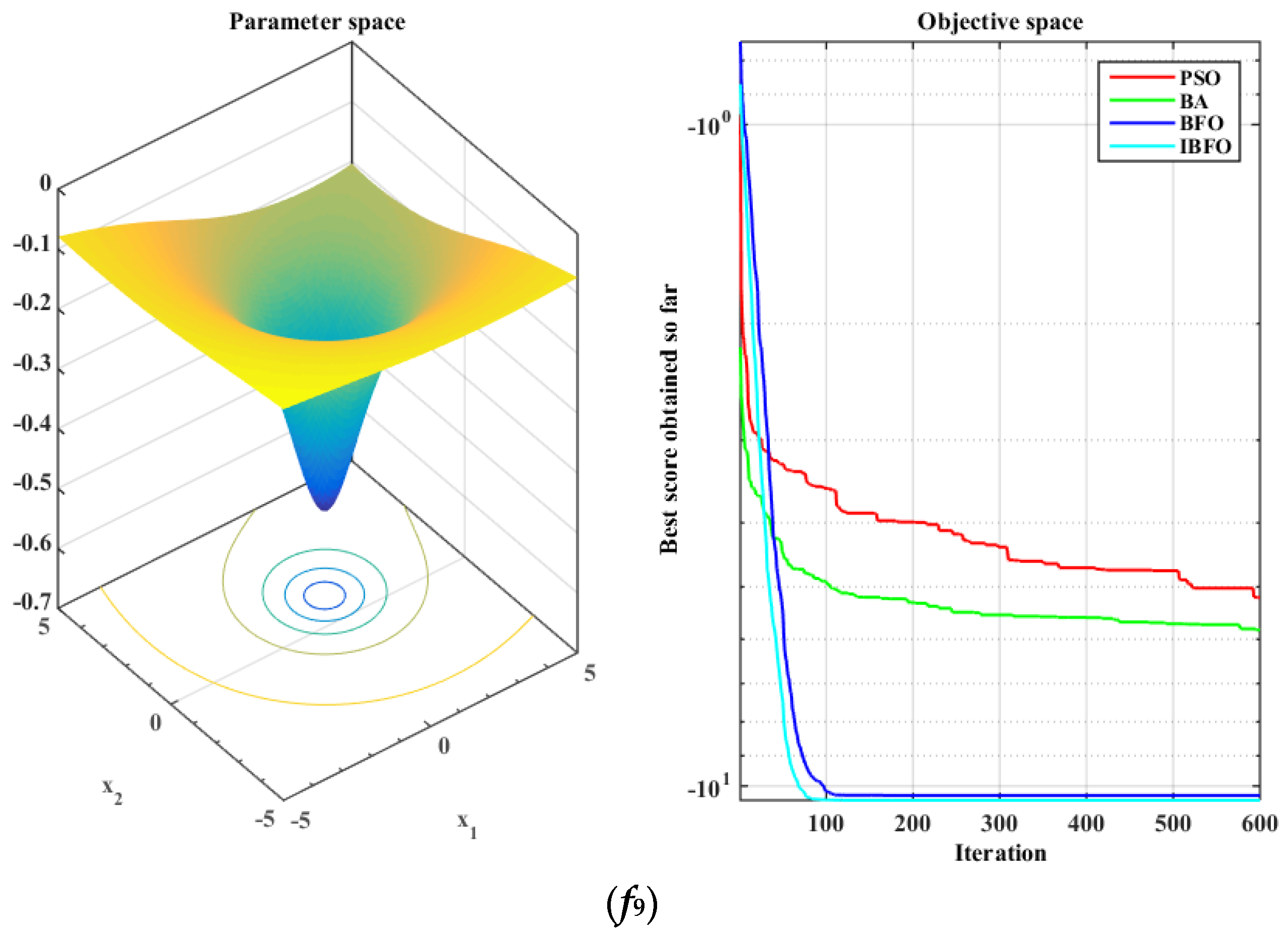
5.1. Benchmark Function Validation
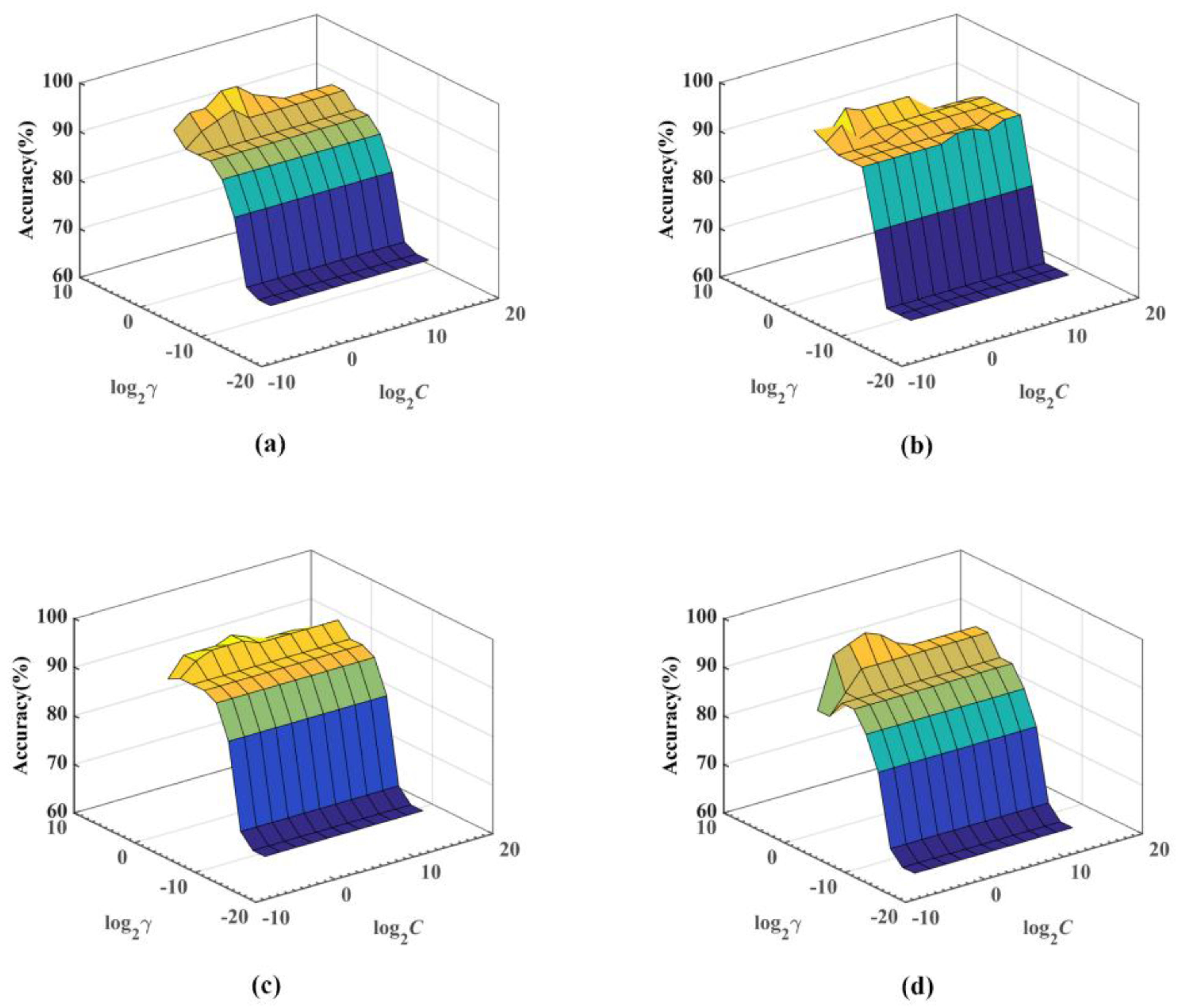
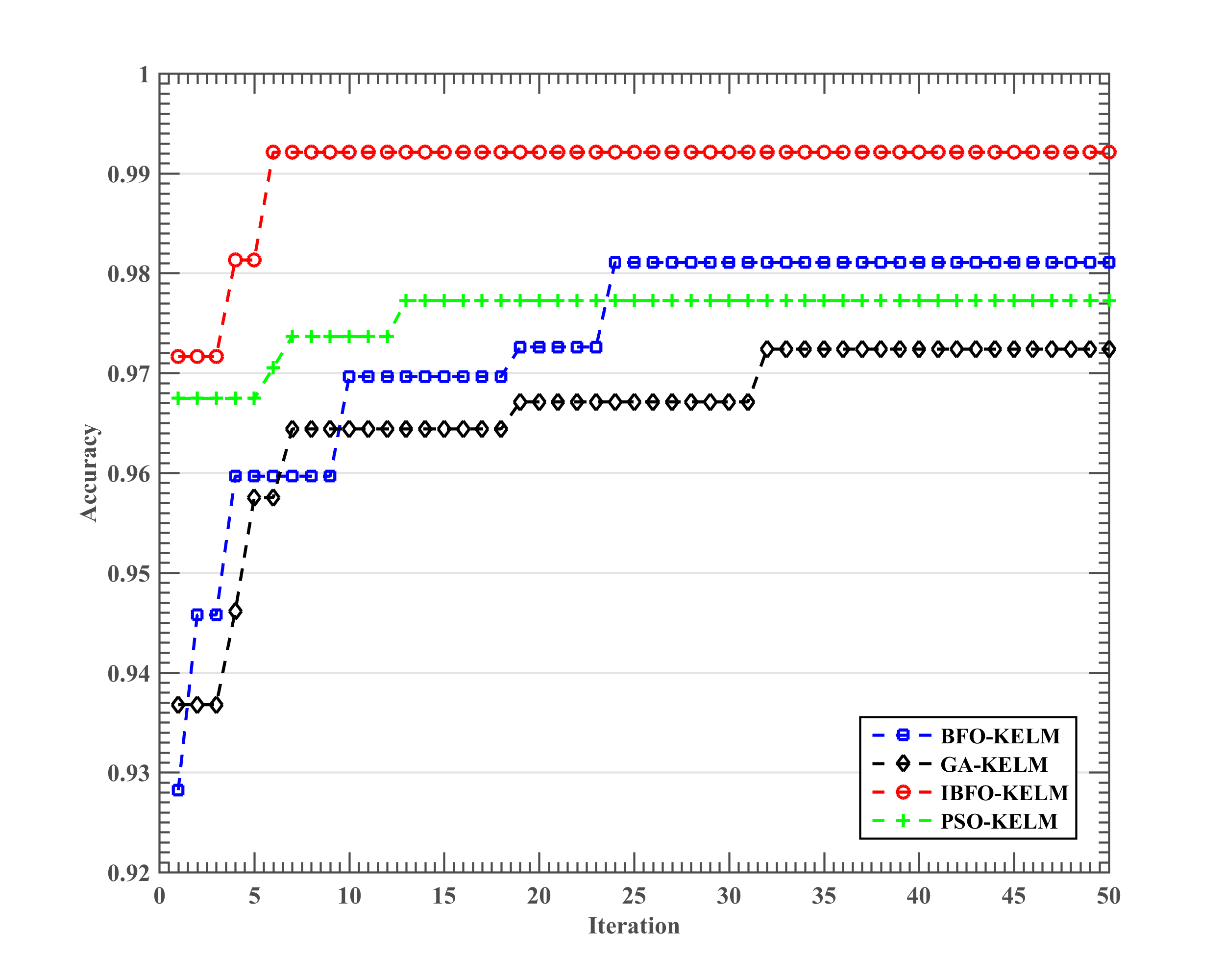
5.2. Results of the Somatization Disorder Diagnosis
6. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Holi, M.M.; Sammallahti, P.R.; Aalberg, V.A. A finnish validation study of the SCL-90. Acta Psychiatr. Scand. 1998, 97, 42–46. [Google Scholar] [CrossRef] [PubMed]
- Derogatis, L.R.; Lipman, R.S.; Covi, L. SCL-90: An outpatient psychiatric rating scale—Preliminary report. Psychopharmacol. Bull. 1973, 9, 13–28. [Google Scholar] [PubMed]
- Huang, G.-B.; Zhou, H.; Ding, X.; Zhang, R. Extreme learning machine for regression and multiclass classification. IEEE Trans. Syst. Man Cybern. Part B 2012, 42, 513–529. [Google Scholar] [CrossRef] [PubMed]
- Pal, M.; Maxwell, A.E.; Warner, T.A. Kernel-based extreme learning machine for remote-sensing image classification. Remote Sens. Lett. 2013, 4, 853–862. [Google Scholar] [CrossRef]
- Chen, C.; Li, W.; Su, H.; Liu, K. Spectral-spatial classification of hyperspectral image based on kernel extreme learning machine. Remote Sens. 2014, 6, 5795–5814. [Google Scholar] [CrossRef]
- Garea, A.S.; Heras, D.B.; Argüello, F. Gpu classification of remote-sensing images using kernel ELM and extended morphological profiles. Int. J. Remote Sens. 2016, 37, 5918–5935. [Google Scholar] [CrossRef]
- Liu, T.; Hu, L.; Ma, C.; Wang, Z.Y.; Chen, H.L. A fast approach for detection of erythemato-squamous diseases based on extreme learning machine with maximum relevance minimum redundancy feature selection. Int. J. Syst. Sci. 2015, 46, 919–931. [Google Scholar] [CrossRef]
- Ma, C.; Ouyang, J.; Chen, H.-L.; Zhao, X.-H. An efficient diagnosis system for parkinson’s disease using kernel-based extreme learning machine with subtractive clustering features weighting approach. Comput. Math. Methods Med. 2014, 2014, 985789. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Chen, H.; Huang, H.; Zhao, X.; Cai, Z.; Tong, C.; Liu, W.; Tian, X. An enhanced grey wolf optimization based feature selection wrapped kernel extreme learning machine for medical diagnosis. Comput. Math. Methods Med. 2017, 2017, 15. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.-L.; Wang, G.; Ma, C.; Cai, Z.-N.; Liu, W.-B.; Wang, S.-J. An efficient hybrid kernel extreme learning machine approach for early diagnosis of parkinson’s disease. Neurocomputing 2016, 184, 131–144. [Google Scholar] [CrossRef]
- Wang, M.; Chen, H.; Yang, B.; Zhao, X.; Hu, L.; Cai, Z.; Huang, H.; Tong, C. Toward an optimal kernel extreme learning machine using a chaotic moth-flame optimization strategy with applications in medical diagnoses. Neurocomputing 2017, 267, 69–84. [Google Scholar] [CrossRef]
- Zhao, D.; Huang, C.; Wei, Y.; Yu, F.; Wang, M.; Chen, H. An effective computational model for bankruptcy prediction using kernel extreme learning machine approach. Comput. Econ. 2017, 49, 325–341. [Google Scholar] [CrossRef]
- Wang, M.; Chen, H.; Li, H.; Cai, Z.; Zhao, X.; Tong, C.; Li, J.; Xu, X. Grey wolf optimization evolving kernel extreme learning machine: Application to bankruptcy prediction. Eng. Appl. Artif. Intell. 2017, 63, 54–68. [Google Scholar] [CrossRef]
- Deng, W.-Y.; Zheng, Q.-H.; Wang, Z.-M. Cross-person activity recognition using reduced kernel extreme learning machine. Neural Netw. 2014, 53, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Tang, L.; Wang, J.; Li, A.; Hao, Y. 2-D defect profile reconstruction from ultrasonic guided wave signals based on qga-kernelized elm. Neurocomputing 2014, 128, 217–223. [Google Scholar] [CrossRef]
- Zhao, X.; Li, D.; Yang, B.; Liu, S.; Pan, Z.; Chen, H. An efficient and effective automatic recognition system for online recognition of foreign fibers in cotton. IEEE Access 2016, 4, 8465–8475. [Google Scholar] [CrossRef]
- Uçar, A.; Özalp, R. Efficient android electronic nose design for recognition and perception of fruit odors using kernel extreme learning machines. Chemom. Intell. Lab. Syst. 2017, 166, 69–80. [Google Scholar] [CrossRef]
- Peng, C.; Yan, J.; Duan, S.; Wang, L.; Jia, P.; Zhang, S. Enhancing electronic nose performance based on a novel qpso-kelm model. Sensors 2016, 16, 520. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Y.; Xu, X.; Shen, D.; Fang, Y.; Xiao, Z. Traffic sign recognition using kernel extreme learning machines with deep perceptual features. IEEE Trans. Intell. Transp. Syst. 2017, 18, 1647–1653. [Google Scholar] [CrossRef]
- Li, J.; Li, D.C. Wind power time series prediction using optimized kernel extreme learning machine method. Acta Phys. Sin. 2016, 65, 130501. [Google Scholar]
- Avci, D.; Dogantekin, A. An expert diagnosis system for parkinson disease based on genetic algorithm-wavelet kernel-extreme learning machine. Park. Dis. 2016, 2016. [Google Scholar] [CrossRef] [PubMed]
- Veronese, N.; Luchini, C.; Nottegar, A.; Kaneko, T.; Sergi, G.; Manzato, E.; Solmi, M.; Scarpa, A. Prognostic impact of extra-nodal extension in thyroid cancer: A meta-analysis. J. Surg. Oncol. 2015, 112, 828–833. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Du, B.; Liu, J.; Xia, H.; Yeap, W.K. A kernel extreme learning machine algorithm based on improved particle swam optimization. Memet. Comput. 2017, 9, 121–128. [Google Scholar] [CrossRef]
- Passino, K.M. Biomimicry of bacterial foraging for distributed optimization and control. IEEE Control Syst. Mag. 2002, 22, 52–67. [Google Scholar] [CrossRef]
- Majhi, R.; Panda, G.; Majhi, B.; Sahoo, G. Efficient prediction of stock market indices using adaptive bacterial foraging optimization (ABFO) and bfo based techniques. Expert Syst. Appl. 2009, 36, 10097–10104. [Google Scholar] [CrossRef]
- Dasgupta, S.; Das, S.; Biswas, A.; Abraham, A. Automatic circle detection on digital images with an adaptive bacterial foraging algorithm. Soft Comput. 2010, 14, 1151–1164. [Google Scholar] [CrossRef]
- Mishra, S. A hybrid least square-fuzzy bacterial foraging strategy for harmonic estimation. IEEE Trans. Evol. Comput. 2005, 9, 61–73. [Google Scholar] [CrossRef]
- Mishra, S.; Bhende, C.N. Bacterial foraging technique-based optimized active power filter for load compensation. IEEE Trans. Power Deliv. 2007, 22, 457–465. [Google Scholar] [CrossRef]
- Ulagammai, M.; Venkatesh, P.; Kannan, P.S.; Prasad Padhy, N. Application of bacterial foraging technique trained artificial and wavelet neural networks in load forecasting. Neurocomputing 2007, 70, 2659–2667. [Google Scholar] [CrossRef]
- Wu, Q.; Mao, J.F.; Wei, C.F.; Fu, S.; Law, R.; Ding, L.; Yu, B.T.; Jia, B.; Yang, C.H. Hybrid BF-PSO and fuzzy support vector machine for diagnosis of fatigue status using emg signal features. Neurocomputing 2016, 173, 483–500. [Google Scholar] [CrossRef]
- Yang, C.; Ji, J.; Liu, J.; Liu, J.; Yin, B. Structural learning of bayesian networks by bacterial foraging optimization. Int. J. Approx. Reason. 2016, 69, 147–167. [Google Scholar] [CrossRef]
- Sivarani, T.S.; Joseph Jawhar, S.; Agees Kumar, C.; Prem Kumar, K. Novel bacterial foraging-based anfis for speed control of matrix converter-fed industrial bldc motors operated under low speed and high torque. Neural Comput. Appl. 2016, 1–24. [Google Scholar] [CrossRef]
- Cai, Z.; Gu, J.; Chen, H.L. A new hybrid intelligent framework for predicting parkinson’s disease. IEEE Access 2017, 5, 17188–17200. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L. An effective bacterial foraging optimizer for global optimization. Inf. Sci. 2016, 329, 719–735. [Google Scholar] [CrossRef]
- Panda, R.; Naik, M.K. A novel adaptive crossover bacterial foraging optimization algorithm for linear discriminant analysis based face recognition. Appl. Soft Comput. J. 2015, 30, 722–736. [Google Scholar] [CrossRef]
- Nasir, A.N.K.; Tokhi, M.O.; Ghani, N.M.A. Novel adaptive bacterial foraging algorithms for global optimisation with application to modelling of a trs. Expert Syst. Appl. 2015, 42, 1513–1530. [Google Scholar] [CrossRef]
- Tizhoosh, H.R. Opposition-based learning: A new scheme for machine intelligence. In Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation, CIMCA 2005 and International Conference on Intelligent Agents, Web Technologies and Internet, Vienna, Austria, 28–30 November 2005; pp. 695–701. [Google Scholar]
- Salzberg, S.L. On comparing classifiers: Pitfalls to avoid and a recommended approach. Data Min. Knowl. Discov. 1997, 1, 317–328. [Google Scholar] [CrossRef]
- Statnikov, A.; Tsamardinos, I.; Dosbayev, Y.; Aliferis, C.F. GEMS: A system for automated cancer diagnosis and biomarker discovery from microarray gene expression data. Int. J. Med. Inform. 2005, 74, 491–503. [Google Scholar] [CrossRef] [PubMed]
| Feature | Description |
|---|---|
| F1 | Headache |
| F2 | Dizzy or fainted |
| F3 | Chest pain |
| F4 | Low back pain |
| F5 | Nausea or upset stomach |
| F6 | Muscle soreness |
| F7 | Having breathe difficulty |
| F8 | A series of chills or fever |
| F9 | Body tingling or prickling |
| F10 | The throat is infarcted |
| F11 | Feeling that part of the body is weak |
| F12 | Feeling the weight of your hands or feet |
| F13 | Somatization severity |
| Function | Range | Minimum |
|---|---|---|
| [−10, 10] | 0 | |
| [−100, 100] | 0 | |
| [−100, 100] | 0 | |
| [−100, 100] | 0 | |
| [0,1] | [−1.28, 1.28] | 0 |
| [−500, 500] | −418.9829 × 5 | |
| [−65, 65] | 1 | |
| [−5, 5] | 0.00030 | |
| [0, 10] | −10.5363 |
| Methods | ||||||||
|---|---|---|---|---|---|---|---|---|
| PSO | BA | BFO | IBFO | |||||
| Ave | Std | Ave | Std | Ave | Std | Ave | Std | |
| f1 | 0.0185 | 0.0097 | 0.0113 | 0.0053 | 0.0075 | 0.0042 | 0.0057 | 0.0031 |
| f2 | 0.0006 | 0.0005 | 0.0001 | 0.0001 | 4.07 × 10−5 | 4.76 × 10−5 | 2.83 × 10−5 | 4.83 × 10−5 |
| f3 | 0.0135 | 0.0079 | 0.0095 | 0.0045 | 0.2072 | 1.1059 | 0.0046 | 0.0029 |
| f4 | 0.0003 | 0.0003 | 9.88 × 10−5 | 0.0001 | 5.11 × 10−5 | 0.0001 | 3.13 × 10−5 | 3.76 × 10−5 |
| f5 | 0.0070 | 0.0045 | 0.0020 | 0.0016 | 0.00045 | 0.0003 | 0.0004 | 0.0003 |
| f6 | −793.55 | 65.4056 | −763.56 | 77.9863 | −720.08 | 76.2664 | −797.41 | 56.1899 |
| f7 | 1.9873 | 1.5529 | 2.8100 | 1.9357 | 1.7915 | 1.0204 | 1.3947 | 0.8472 |
| f8 | 0.0012 | 0.0002 | 0.0081 | 0.0095 | 0.0007 | 0.0002 | 0.0007 | 0.0002 |
| f9 | −5.1904 | 1.9864 | −5.8112 | 3.1206 | −10.3323 | 0.9752 | −10.5104 | 0.0135 |
| Step Size | IBFO-KELM | |||
|---|---|---|---|---|
| ACC | MCC | Sensitivity | Specificity | |
| 0.05 | 0.9213 (0.0389) | 0.8227 (0.0903) | 0.9679 (0.035) | 0.8286 (0.0768) |
| 0.1 | 0.9402 (0.0362) | 0.8653 (0.0824) | 0.9713 (0.0282) | 0.8786 (0.0678) |
| 0.15 | 0.9697 (0.0351) | 0.9243 (0.0907) | 0.9729 (0.0351) | 0.9600 (0.0843) |
| 0.2 | 0.9476 (0.0512) | 0.8850 (0.1089) | 0.9679 (0.0544) | 0.9071 (0.0828) |
| 0.25 | 0.9378 (0.0427) | 0.8614 (0.0965) | 0.9786 (0.0301) | 0.8571 (0.1117) |
| 0.3 | 0.9211 (0.0377) | 0.8241 (0.0836) | 0.9675 (0.0365) | 0.8286 (0.1075) |
| Method | Metrics | |||
|---|---|---|---|---|
| ACC | MCC | Sensitivity | Specificity | |
| IBFO-KELM | 0.9697 ± 0.0351 | 0.9243 ± 0.0907 | 0.9729 ± 0.0351 | 0.9600 ± 0.0843 |
| BFO-KELM | 0.9329 ± 0.0362 | 0.8280 ± 0.0850 | 0.9586 ± 0.0491 | 0.8550 ± 0.1012 |
| PSO-KELM | 0.9282 ± 0.0266 | 0.8056 ± 0.0813 | 0.9657 ± 0.0362 | 0.8050 ± 0.1383 |
| GA-KELM | 0.9176 ± 0.0662 | 0.7775 ± 0.1879 | 0.9595 ± 0.0349 | 0.8000 ± 0.2494 |
| Grid-KELM | 0.9076 ± 0.0679 | 0.7592 ± 0.1637 | 0.9448 ± 0.0724 | 0.7900 ± 0.1647 |
| Method | p-Value | |||
|---|---|---|---|---|
| ACC | MCC | Sensitivity | Specificity | |
| BFO-KELM | 0.03 | 0.03 | 0.24 | 0.06 |
| PSO-KELM | 0.02 | 0.02 | 0.41 | 0.02 |
| GA-KELM | 0.03 | 0.04 | 0.61 | 0.08 |
| Grid-KELM | 0.02 | 0.02 | 0.23 | 0.02 |
| Method | Metrics | |||
|---|---|---|---|---|
| ACC | MCC | Sensitivity | Specificity | |
| NB | 0.9182 ± 0.0543 | 0.7766 ± 0.1495 | 0.9800 ± 0.0322 | 0.7350 ± 0.1634 |
| SVM | 0.8971 ± 0.0735 | 0.7122 ± 0.2148 | 0.9595 ± 0.0469 | 0.7100 ± 0.2601 |
| RF | 0.9382 ± 0.0405 | 0.8337 ± 0.1133 | 0.9652 ± 0.0367 | 0.8500 ± 0.1414 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, X.; Chen, H.; Zhang, Q.; Li, X.; Huang, H.; Wang, G. An Improved Bacterial-Foraging Optimization-Based Machine Learning Framework for Predicting the Severity of Somatization Disorder. Algorithms 2018, 11, 17. https://doi.org/10.3390/a11020017
Lv X, Chen H, Zhang Q, Li X, Huang H, Wang G. An Improved Bacterial-Foraging Optimization-Based Machine Learning Framework for Predicting the Severity of Somatization Disorder. Algorithms. 2018; 11(2):17. https://doi.org/10.3390/a11020017
Chicago/Turabian StyleLv, Xinen, Huiling Chen, Qian Zhang, Xujie Li, Hui Huang, and Gang Wang. 2018. "An Improved Bacterial-Foraging Optimization-Based Machine Learning Framework for Predicting the Severity of Somatization Disorder" Algorithms 11, no. 2: 17. https://doi.org/10.3390/a11020017
APA StyleLv, X., Chen, H., Zhang, Q., Li, X., Huang, H., & Wang, G. (2018). An Improved Bacterial-Foraging Optimization-Based Machine Learning Framework for Predicting the Severity of Somatization Disorder. Algorithms, 11(2), 17. https://doi.org/10.3390/a11020017






