A Novel Spectrum Scheduling Scheme with Ant Colony Optimization Algorithm
Abstract
:1. Introduction
2. System Model and Problem Formulation
2.1. Matrices for Spectrum Allocation
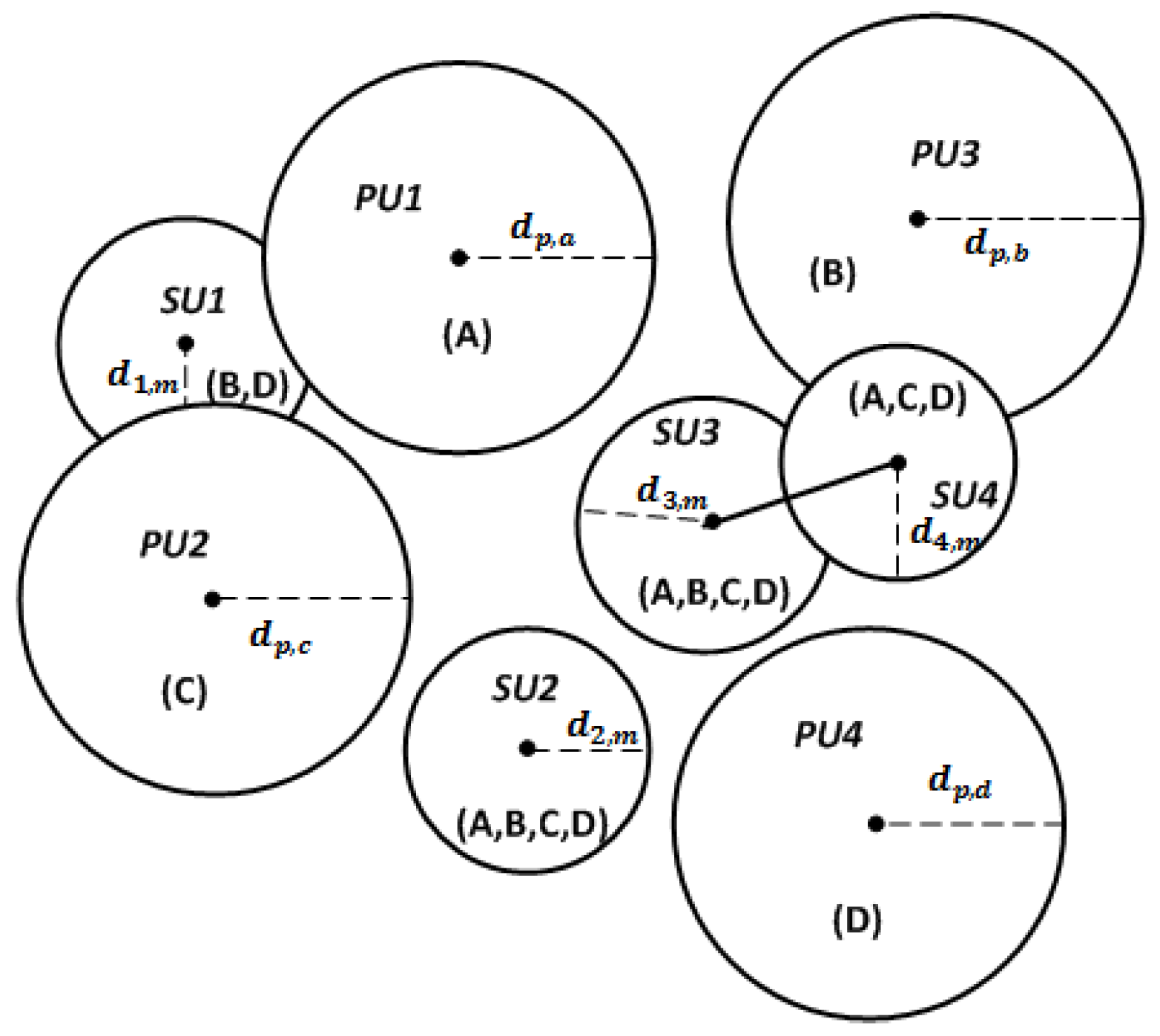
- Available matrix L. The matrix represents the availability of licensed bands for cognitive users. If , user n can access spectrum m without interference to primary users, otherwise . As shown in Figure 1, spectrum channel B is available for , then .
- Benefit matrix B. The matrix indicates the benefit that a cognitive user gets by successful access to a licensed spectrum band, where only if .
- Interference matrix C. The three-axis matrix describes the interference relationship of any two vertices n and k when they access spectrum m. As shown in Figure 1, and overlap in some area, then , , .
- Allocation matrix A. The matrix is a spectrum allocation result which is interference free. If , cognitive user n can access spectrum m and transmission data in this band. A conflict free allocation needs to satisfy the interference constraints: .
- Degree matrix for cognitive users Z. The matrix represents the available spectrum number for each cognitive users. In Figure 1, .
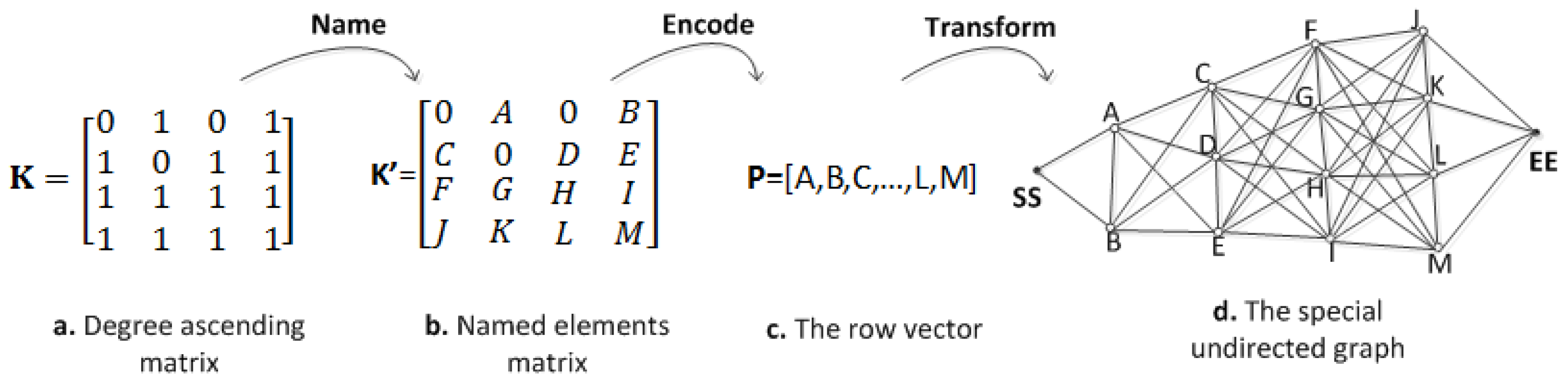
- Degree ascending matrix K. The matrix is another representation of the available matrix, which incrementally orders the rows according to the degree matrix Z.
2.2. Problem Formulation and Measure Functions
- (1)
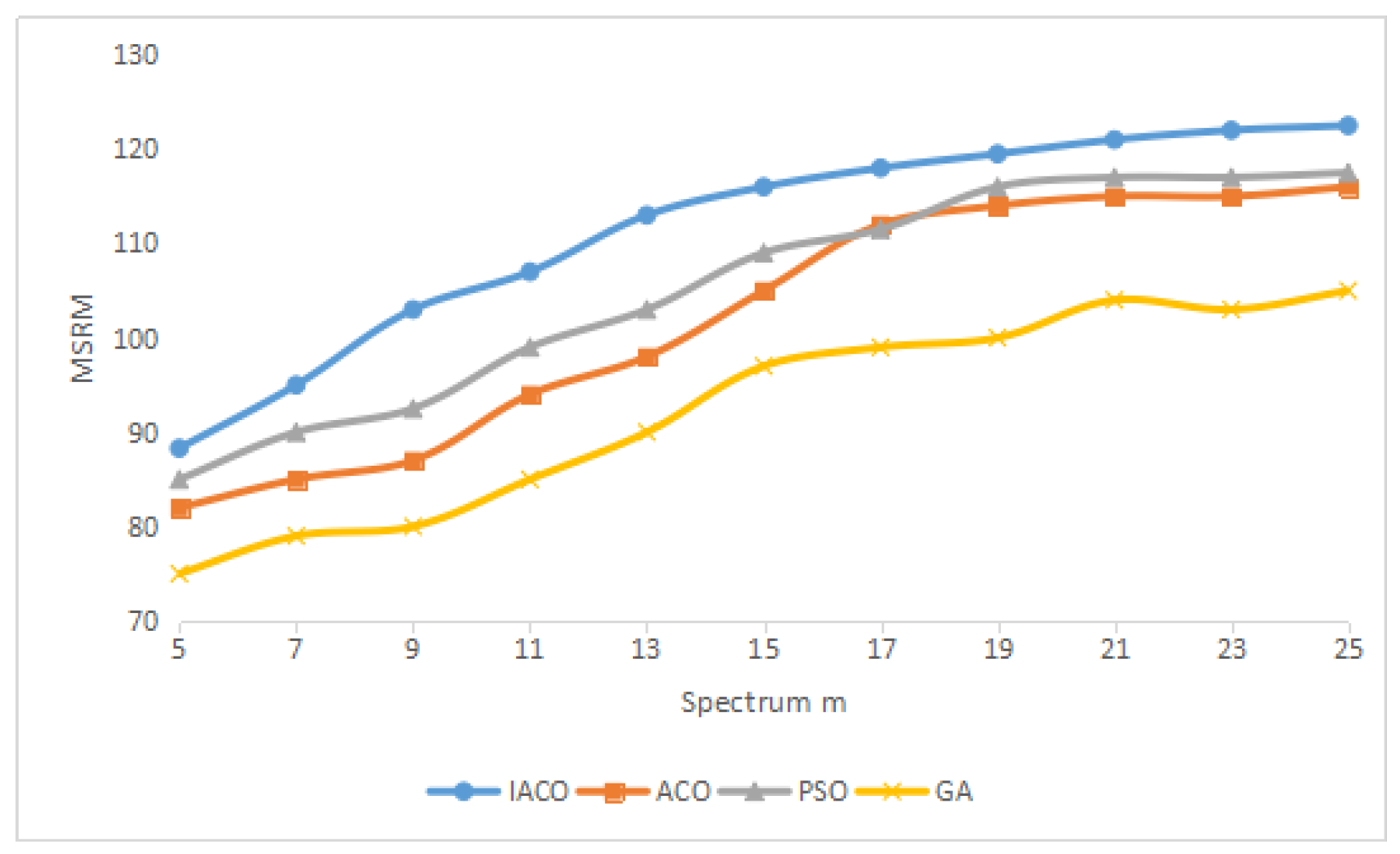
- Max-Sum-Reward-Mean (MSRM): This function is used to measure the average of total spectrum utilization in the system, which is the average of the sum user rewards.
- (2)
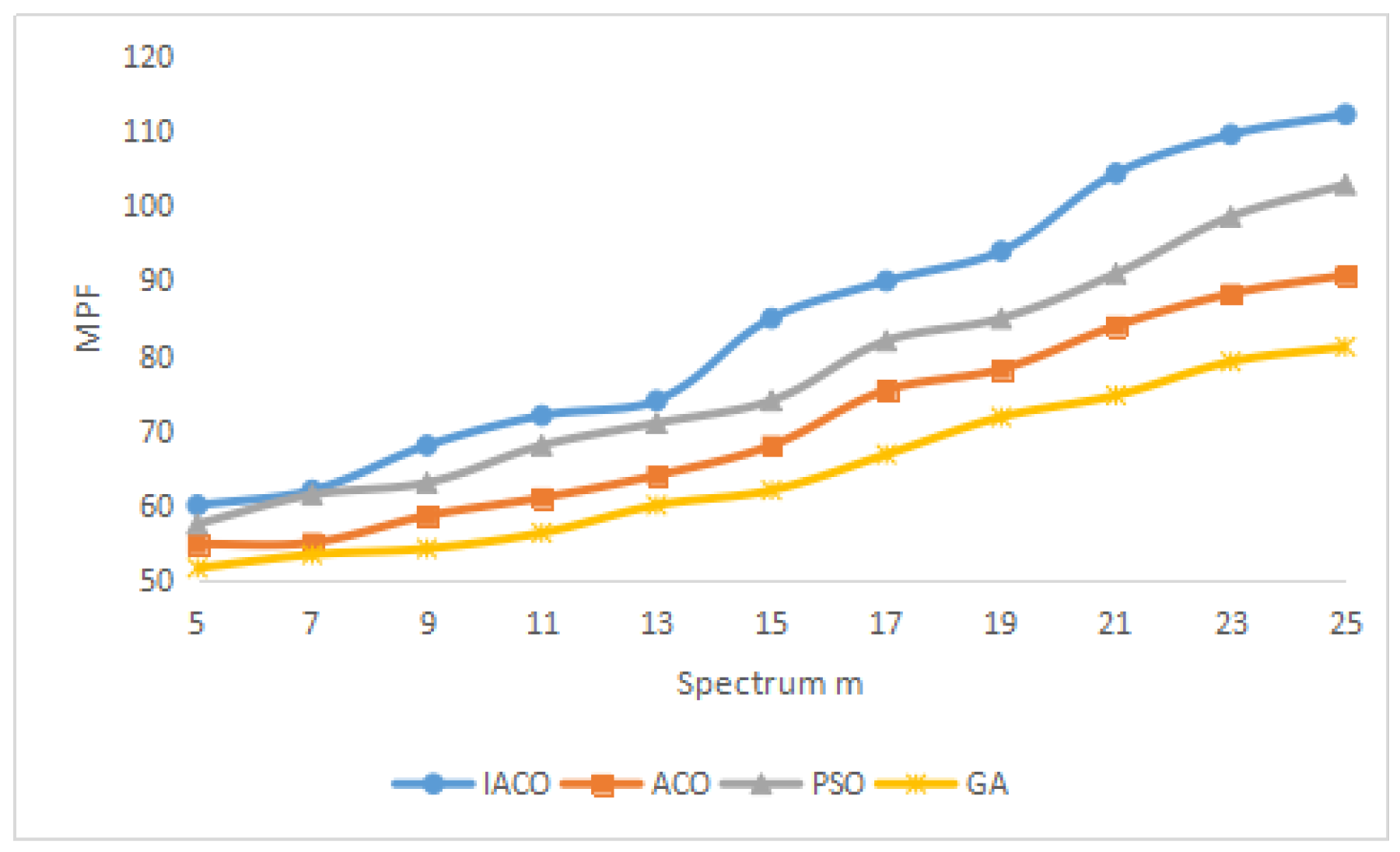
- Max-Proportional-Fair (MPF): The function is to measure the fairness among cognitive users accessing the spectrum in the system, which is driven by .
- (3)
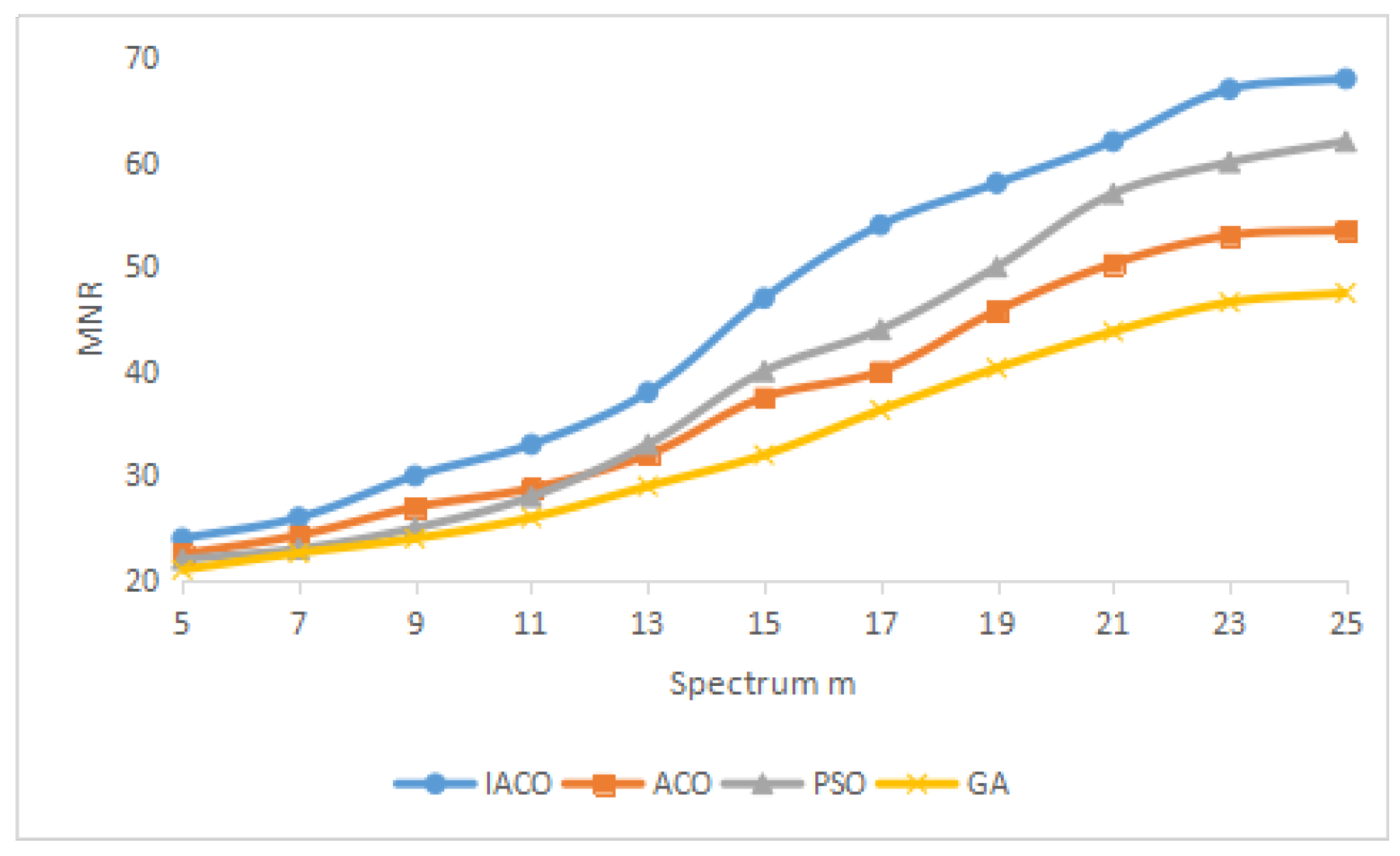
- Max-Min-Reward (MMR): The function is to maximize the spectrum utilization at the bottleneck cognitive users who receive the lowest reward, which is a simple notion of fairness.
3. The IACO-Based Spectrum Allocation Method
3.1. The Basic Idea
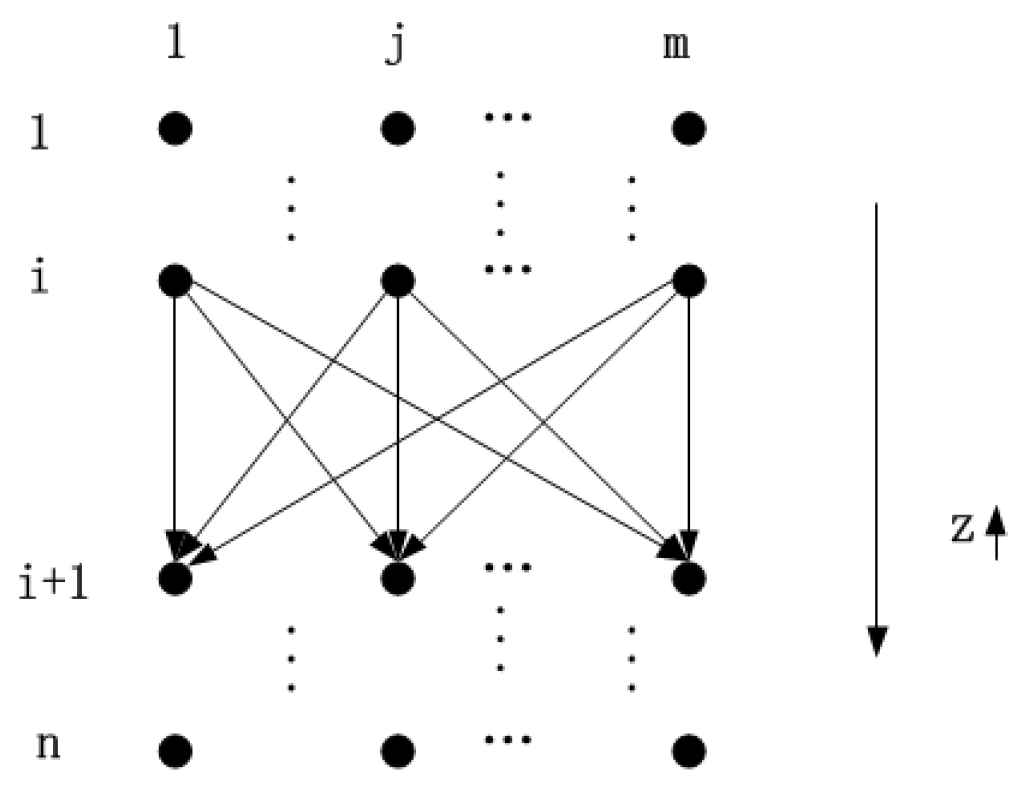
3.2. Transform for the Spectrum Allocation Problem
3.3. Differential Evolution Process in IACO
3.4. Variable Neighborhood Search Process in IACO
3.5. The Process and Description of IACO
- (1)
- Path selection. The transfer probability between node i and s in the choice process is presented as follows:where is a constant in the scope , and J is a random variable generated by the following formula:where and are the weighted factor of information and expectation heuristic respectively. is the available node-set for ant l at node i, is the infeasible node-set for ant l and it would be cleared after l finishes traversal.
- (2)
- Update pheromone. Using an elitist strategy to update pheromone. The pheromone concentration on path is updated as the following rules:where is the pheromone evaporation coefficient, is the residual factor of pheromone. Q is a constant of total pheromone released from all ants in each traversal, is the cost calculated by fitness function.
3.6. Pseudocode of IACO
| Algorithm 1: An Improved Ant Colony Optimization Algorithm |
 |
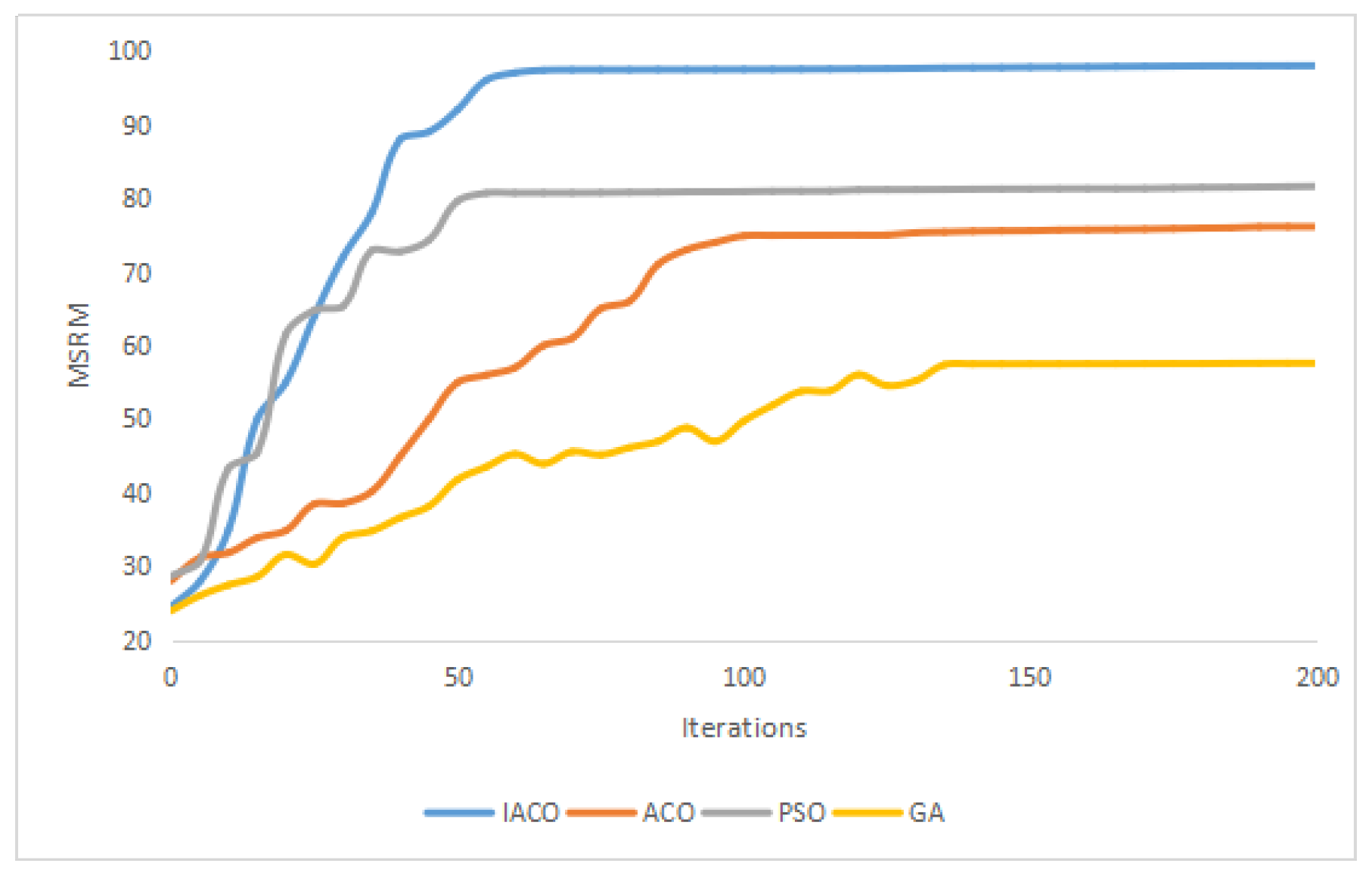
4. Simulation Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhang, D.; Chen, Z.; Awad, M.K.; Zhang, N.; Zhou, H.; Shen, X.S. Utility-Optimal Resource Management and Allocation Algorithm for Energy Harvesting Cognitive Radio Sensor Networks. IEEE J. Sel. Areas Commun. 2016, 34, 3552–3565. [Google Scholar] [CrossRef]
- Sharma, S.K.; Bogale, T.E.; Chatzinotas, S.; Ottersten, B.; Le, L.B.; Wang, X. Cognitive Radio Techniques Under Practical Imperfections: A Survey. IEEE Commun. Surv. Tutor. 2015, 17, 1858–1884. [Google Scholar] [CrossRef]
- Niyato, D.; Hossain, E. Cognitive radio for next-generation wireless networks: An approach to opportunistic channel selection in ieee 802.11-based wireless mesh. IEEE Wirel. Commun. 2009, 16, 46–54. [Google Scholar] [CrossRef]
- Akyildiz, I.F.; Lee, W.Y.; Vuran, M.C.; Mohanty, S. NeXt generation/dynamic spectrum access/cognitive radio wireless networks: A survey. Comput. Netw. 2006, 50, 2127–2159. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, Z.; Ren, J.; Zhang, N.; Awad, M.K.; Zhou, H.; Shen, X.S. Energy-Harvesting-Aided Spectrum Sensing and Data Transmission in Heterogeneous Cognitive Radio Sensor Network. IEEE Trans. Veh. Technol. 2017, 66, 831–843. [Google Scholar] [CrossRef]
- Lu, L.; He, D.; Li, G.Y.; Yu, X. Graph-Based Robust Resource Allocation for Cognitive Radio Networks. IEEE Trans. Signal Process. 2015, 63, 3825–3836. [Google Scholar] [CrossRef]
- Jalaeian, B.; Zhu, R.; Samani, H.; Motani, M. An Optimal Cross-Layer Framework for Cognitive Radio Network Under Interference Temperature Model. IEEE Syst. J. 2016, 10, 293–301. [Google Scholar] [CrossRef]
- Yi, C.; Cai, J. Two-Stage Spectrum Sharing With Combinatorial Auction and Stackelberg Game in Recall-Based Cognitive Radio Networks. IEEE Trans. Commun. 2014, 62, 3740–3752. [Google Scholar] [CrossRef]
- Yang, G.; Li, B.; Tan, X.; Wang, X. Adaptive power control algorithm in cognitive radio based on game theory. IET Commun. 2015, 9, 1807–1811. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. The Ant System: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man. Cybern. 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Song, X.O. Utilization and Fairness in Spectrum Assignment for Cognitive Radio Networks: An Ant Colony Optimization’s Perspective. In Proceedings of the 2014 International Conference on Wireless Communication and Sensor Network, Wuhan, China, 13–14 December 2014; pp. 42–45. [Google Scholar]
- Luo, W.; Lin, D.; Feng, X. An Improved Ant Colony Optimization and Its Application on TSP Problem. In Proceedings of the 2016 IEEE International Conference on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData), Chengdu, China, 15–18 December 2016; pp. 136–141. [Google Scholar]
- Li, H.; Zhang, L.; Jiao, Y. Discrete differential evolution algorithm for integer linear bilevel programming problems. J. Syst. Eng. Electron. 2016, 27, 912–919. [Google Scholar]
- Herremans, D.; Sörensen, K.; Martens, D. Classification and Generation of Composer-Specific Music Using Global Feature Models and Variable Neighborhood Search. Comput. Music J. 2015, 39, 71–91. [Google Scholar] [CrossRef]
- Zhao, Z.; Peng, Z.; Zheng, S.; Shang, J. Cognitive radio spectrum allocation using evolutionary algorithms. IEEE Trans. Wirel. Commun. 2009, 8, 4421–4425. [Google Scholar] [CrossRef]
- He, D. A Novel Spectrum Sensing Method in Cognitive Radio Networks Based on Graph Theory. In Proceedings of the 2015 IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015; pp. 1–6. [Google Scholar]
- Peng, C.; Zheng, H.; Zhao, B.Y. Utilization and Fairness in Spectrum Assignment for Opportunistic Spectrum Access; Springer: New York, NY, USA, 2006. [Google Scholar]
- Wajeed, M.A.; Adilakshmi, T. Adopting ant colony optimization for supervised text classification. In Proceedings of the 2016 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Jaipur, India, 21–24 September 2016; pp. 2562–2566. [Google Scholar]
- Das, S.; Suganthan, P.N. Differential Evolution: A Survey of the State-of-the-Art. IEEE Trans. Evolut. Comput. 2011, 15, 4–31. [Google Scholar] [CrossRef]
| Name of Matrix | Definition of Matrix |
|---|---|
| Available matrix | |
| Benefit matrix | |
| Interference matrix | |
| Allocation matrix | |
| Degree matrix for cognitive users | |
| Degree ascending matrix |
| Iteration | Algorithm | Relative Difference (%) | ||
|---|---|---|---|---|
| MSRM | MMR | MPF | ||
| 30 | IACO | 0.366 | 0.447 | 1.711 |
| ACO | 1.144 | 1.676 | 3.017 | |
| PSO | 0.324 | 1.275 | 2.083 | |
| GA | 1.033 | 2.876 | 3.496 | |
| 100 | IACO | 0 | 0 | 0.013 |
| ACO | 0 | 1.514 | 2.504 | |
| PSO | 0 | 1.309 | 0.952 | |
| GA | 0.472 | 2.666 | 3.224 | |
| 200 | IACO | 0 | 0 | 0.012 |
| ACO | 0 | 1.177 | 2.299 | |
| PSO | 0 | 0.616 | 0.564 | |
| GA | 0.063 | 2.282 | 2.71 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Wang, N.; Chen, Z.; Guo, L. A Novel Spectrum Scheduling Scheme with Ant Colony Optimization Algorithm. Algorithms 2018, 11, 16. https://doi.org/10.3390/a11020016
Liu L, Wang N, Chen Z, Guo L. A Novel Spectrum Scheduling Scheme with Ant Colony Optimization Algorithm. Algorithms. 2018; 11(2):16. https://doi.org/10.3390/a11020016
Chicago/Turabian StyleLiu, Liping, Ning Wang, Zhigang Chen, and Lin Guo. 2018. "A Novel Spectrum Scheduling Scheme with Ant Colony Optimization Algorithm" Algorithms 11, no. 2: 16. https://doi.org/10.3390/a11020016
APA StyleLiu, L., Wang, N., Chen, Z., & Guo, L. (2018). A Novel Spectrum Scheduling Scheme with Ant Colony Optimization Algorithm. Algorithms, 11(2), 16. https://doi.org/10.3390/a11020016





