Abstract
Parallel reservoir simulation is an important approach to solving real-time reservoir management problems. Recently, there is a new trend of using a graphics processing unit (GPU) to parallelize the reservoir simulations. Current GPU-aided reservoir simulations focus on compute unified device architecture (CUDA). Nevertheless, CUDA is not functionally portable across devices and incurs high amount of code. Meanwhile, domain decomposition is not well used for GPU-based reservoir simulations. In order to address the problems, we propose a parallel method with OpenACC to accelerate serial code and reduce the time and effort during porting an application to GPU. Furthermore, the GPU-aided domain decomposition is developed to accelerate the efficiency of reservoir simulation. The experimental results indicate that (1) the proposed GPU-aided approach can outperform the CPU-based one up to about two times, meanwhile with the help of OpenACC, the workload of the transplant code was reduced significantly by about 22 percent of the source code, (2) the domain decomposition method can further improve the execution efficiency up to 1.7×. The proposed parallel reservoir simulation method is a efficient tool to accelerate reservoir simulation.
1. Introduction
Numerical simulation of reservoirs is an integral part of geoscientific studies to optimize petroleum recovery. Modern petroleum reservoir simulation requires simulating detailed and computationally expensive geological and physical models. Parallel reservoir simulators have the potential to solve larger, more realistic problems than previously possible [1]. There has been considerable effort on parallel reservoir simulation with various high-performance techniques and platforms [2]. For example, since the 1990s multiple-core platforms, such as CRAY X-MP [3] and IBM SP2 [4], have been used to accelerate the reservoir simulation. Furthermore, modern high-performance computing platforms like GRID [5] and Cloud [6] were employed as well to address the issue of computing performance of reservoir simulations.
Recently, the modern graphics processing unit (GPU) [7] has evolved into a highly parallel, many-core processor far beyond a graphic engine. Thus, it is a new trend that GPU is exploited in parallel reservoir simulations. There has been some work about GPU-aided reservoir simulations, for instance in [8,9,10]. However, to the best of our knowledge, all GPU implementations for reservoir simulations do not consider the domain decomposition technique, which has been widely used in reservoir simulations [11]. Meanwhile, current GPU-based reservoir simulations are based on NVIDIA CUDA (compute unified device architecture) [12]. Unfortunately CUDA is not functionally portable across devices. Thus, programmers are forced to have multiple versions of the code for each device that they must maintain and validate, which is tedious, error prone, and generally unproductive [13]. To address the issue of CUDA, directive-based GPU programming is an emergent technique that has the potential to significantly reduce the time and effort required to port applications to the GPU by allowing the reuse of existing Fortran or C code bases [14]. OpenACC [15] is one representative among directive-based GPU programming ways and allows functional portability across various heterogeneous architectures and offers the benefit that programmers can incrementally offload and control computation. Currently OpenACC has widely been applied in computational fluid dynamics (CFD) such as solving incompressible Naviertokes (INS) equations [16], the spectral element method computing [17], Lattice Boltzmann (LB) [18] methods and so on.
Inspired by the successful application of domain decomposition in reservoir simulation and OpenACC in CFD, in this paper, we utilize GPU-aided domain decomposition method and OpenACC to parallelize a reservoir simulation based on the black-oil model. Since in the fully implicit black-oil simulation, the nonlinear solver often takes more than 90% of the total execution time [19], we focus on parallel nonlinear solvers in this paper. To achieve our goal, we first proposed one parallel algorithm with OpenACC so that each thread group can solve the linear equations in parallel. Furthermore, we proposed a data parallel scheme based on a domain decomposition method so that each GPU thread group gains load-balanced computing tasks. To the best of our knowledge, the proposed approach is the first massively GPU parallel for the reservoir simulation with OpenACC.
2. Related Work
In the past decade, numerous methods have emerged for parallelizing Reservoir Simulation. These methods can roughly be categorized into three kinds: (1) multiple-core platforms, (2) modern high-performance computing platforms and (3) many-core platforms. The approaches based on multiple-core platforms employ multiple CPUs or processes to, in parallel, execute the procedure of reservoir simulation. For instance, in [3], Chien et al proposed a vectorized, parallel-processed algorithm over one CRAY X-MP machine for the local grid refinement and adaptive implicit schemes in a general purpose reservoir simulator. As another example in [4], IBM SP2 machines with 32 processors have been used to achieve a scalable parallel multi-purpose reservoir simulator based on MPI techniques. Furthermore, in order to accelerate distributed reservoir simulators, modern high-performance computing platforms like GRID and Cloud were employed as well. For example in [5], a GRID computing platform was employed to manage computation procedures, data and workflow for distributed reservoir simulators. Similarly, in [6] an industry standard reservoir simulation software known as Eclipse has been used with Amazon Web Services (AWS). AWS is an Amazon’s cloud computing service platform.
Regarding the modern GPU, in [8] the authors analyzed the GPU-aided parallel methods for each step in reservoir simulation. In [9], the authors developed parallel preconditioners for iterative linear solvers in reservoir simulation using the NVIDIA Tesla GPU. In [10], GPU has been used to large-scale Bakken reservoir simulation with 10+ million cells. Different from the current GPU-aided reservoir simulations, we employ OpenACC rather than CUDA to parallelize a reservoir simulation to significantly reduce the time and effort required to port applications to the GPU by allowing the reuse of existing Fortran or C code.
Domain Decomposition Method (DDM) [20] solves a boundary value problem by splitting it into smaller boundary value problems in subdomains and iterating to coordinate to the solution between adjacent subdomians, which has been used widely in reservoir simulation to reduce the runtime. It can be categorized into the overlapping domain decomposition method and non-overlapping methods. Overlapping methods compute all subdomains in parallel then update the solution of the entire computational region, and repeats iterations until the solution converges. It does not need to wait for other regions’ boundaries values, and all subdomains are processed in parallel. Therefore its convergence speed is generally faster than that of non-overlapping methods. Note that the amount of computation fora subdomain depends on size of the overlap region, specifically if the overlapping area is large its computation is large and the global solution converges fast, on the other hand, when its overlap is small, the calculation amount is smaller, but the convergence speed of global solution is slow. The overlapping domain decomposition methods include the Schwarz alternating method and additive Schwarz method (ASM) [21]. ASM is more suitable for large-scale parallel methods compared with the Schwarz alternating method.
3. Materials and Methods
In this section, we first describe one black-oil model for reservoir simulation. Then, we introduce how to parallelize reservoir simulation with OpenACC. Finally, we propose a GPU-aided domain decomposition method for the reservoir simulation.
3.1. The Black-Oil Model Reservoir Simulation
The main task of reservoir simulation is to analyze the exact distribution of the underground remaining oil, more exactly adjusting the wells’ locations using simulating the fluid dynamics. The procedure of a reservoir simulation is illustrated in Figure 1. Noted that the reservoir simulation is based on the finite difference method (FDM). As we can see, the simulation procedure consists of three parts:
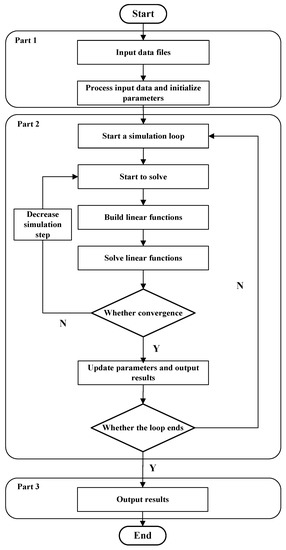
Figure 1.
The flowchat of reservoir simulation.
- (Initialization) This part inputs and initializes the raw data (i.e., oil reservoir data records) and parameters, it belongs to a preprocessing stage for black-oil reservoir simulation.
- (Computation) This part is the key of reservoir simulation which repeatedly builds a Jacobian matrix and solves the linear equation. One common method is using Newton’s method to convert the nonlinear equations into linear equations, then solve the linear equations. In each time step, the procedure of solving equations is performed first in the Jacobian matrix and solved until the computing result is convergent. Then the parameter is updated timely. The iteration mentioned above is carried out until the loop termination condition is satisfied.
- (Output) This part outputs the final computation results.
Considering a three-phase (oil, gas and water) black-oil system, assuming the gas component can exist in both the gas and the oil phases, and oil and water components can only exist in their own phases. The differential equations for oil, gas and water components can be respectively written as: Oil component:
where K is the absolute permeability, means the relative permeability of phase oil, is the density of phase oil, represents the viscosity of phase oil, p is the pressure of phase oil, is the unit weight, D is the depth, is the saturation of phase oil, and ∇ is the gradient operator.
Similarly, the differential equations for gas and water components can be respectively written as, Gas and Water component:
where , mean the relative permeability of phase gas and water, , and are respectively the density of gas component in oil phase, gas phase, water. , are the pressure of phase gas and water, , mean the saturation of phase gas and water.
In addition, the black-oil model involves 6 unknowns: , , , , , , but there are three equations above, so three auxiliary equations are introduced here.
This is the Saturation Constraint,
and the remaining two equations are the Capillary Pressures Constraint,
where is the capillary pressure of oil and water system, meanwhile notes the capillary pressure of oil and gas system.
The black-oil model is built, it is basis of reservoir simulation.
3.2. Parallel Nonlinear Equation Solver with OpenACC
As far as we concerned, there are currently two main ideas of parallel reservoir simulation (see Figure 2 ). The first method only parallelizes the linear equation solver, the main idea is that it solves the equations in parallel. It only involves decomposition of the math model rather than the physical model. There is an alternative way for a parallel reservoir simulation which solves the nonlinear equation in parallel. In this method, the physical simulation domain is decomposed to several subregions at the beginning, next, a local Jacobian matrix is built to form linear functions, and then multiple local linear equations are solved. It is easy to observe that the second method achieves a higher parallel degree. So, we aim at the problem of a parallel nonlinear solver in this paper. It mainly contains local Jacobian matrix assembly and a local linear equation solver. We respectively use the OpenACC directive clause to accelerate the two parts.
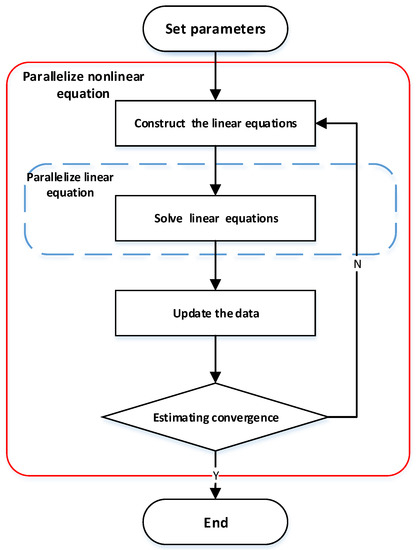
Figure 2.
Two parallel idea comparison.
OpenACC is a directive-based extension of languages designed to simplify parallel programming of heterogeneous CPU/GPU. Like OpenMP, its benchmark is for C/C++ and Fortran source code to identify the areas that should be accelerated using compiler directives and additional functions. A programmer only needs to add annotative directives to previous projects without modification. Then the compiler analyzes them and generates the procedures for offloading data and tasks to accelerators. The current standard 2.5 was released in October 2015. It is characterized by being maintainable, portable and scalable.
OpenACC assumes three levels in the processor: gang, worker and vector. In CUDA, these three levels correspond to grid, block and thread. In NVIDIA Tesla GPU, they respectively correspond to the streaming multi-processor, warp and thread. In the research work supporting by Fortran, a directive is inserted to a code as compiler instruction with a general syntax of
!$acc directive-name [clause[[,]clause]…]
There are three types of important directive constructs:
- Specification of a parallel region construct: Two kind of directive constructs, kernel and parallel, are defined in OpenACC to specify which part of the code is to be executed in parallel. While the kernels directive entrusts a compiler with responsibility of analyzing dependencies of variables, the parallel directive implies that responsibility to the user. We use the latter in our implementation.
- Memory allocation and data transfer data construct: Data directive is a representative example. In OpenACC2.5, enter and exit directives are added which allocate and free memory space on the device. Data transfer between host and device is executed by update directive. Then before the parallel region, the clause of the data directive is always present.
- Specification of parallelized loop: This is done by loop directive. In parallel regions, it is necessary to specify this. With this instruction, the user can directly determine the gang, worker and vector parameter. And variables are private to loop.
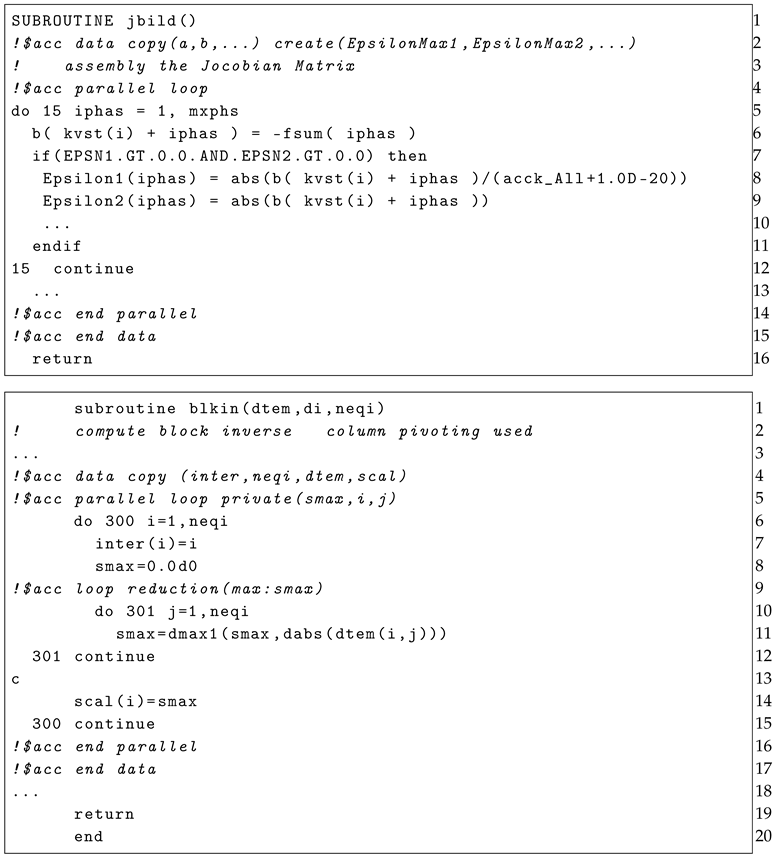
Our work is based on the fixed-style Fortran77 language, so the corresponding OpenACC clause is also subject to fixed style Fortran standard. As shown in the following two code examples belonging to the Jacobian matrix assembly and linear equation solver, we respectively introduce the application in different scenarios in detail.
The first code block (see SUBROUTINE jbild ()) is the example for parallel Jacobian matrix assembly. This part contains a group of judgment sentences, and fewer calculation statements distinguished from the linear equation solver. In line 2 of code block 1, this is a construct where the coefficient matrix and rhs (right hand side) matrix are copied to device memory, after the local work array and parameter are created. It massively reduces the data movement by explicitly declaring the data management rather than managed by compiler. In line 4 of code block 1, a construct added before a loop and a subclause is used here to tell the compiler that the following code contains a loop, and should be executed in device side. At the end of the Jacobian matrix assembly, we should exit the and construct. By adding these clauses, the coefficient matrix of each cell is built in parallel, so the run time is reduced significantly.
The second code block (see subroutine blkin (... )) belongs to the linear equation solver. As depicted above, the function of the subroutine is computing the inverse of the block matrix. Compared to code block 1, it contains many computation clauses (including multiplication, division, reduction and so on). As far as we know, a set of reduction operations and atomic operations is supported by OpenACC, so accuracy of parallel projects is guaranteed technically. In line 4 here, the construct is added to explicitly manage the data movement, then the construct is used to generate parallel code. It should be noted that some variables cause an access violation which is commonly used in serial execution. For programs that are working properly, these variables should be copied as private members in each thread, as a consequence the subclause is applied here, it tells the compiler to generate private variables i, j and in every execution unit. After the modification, the serial code is executed on the GPU efficiently and accurately.
The two examples help us to understand that OpenACC is high-level programming interface, the early project can be run in parallel easily on a GPU with a few code modifications. This is because OpenACC saves a great deal of code for device initialization compared to CUDA and OpenCL, the compiler does this work for us automatically. Developers only need to tell the compiler the code region which needs to be parallel and guarantee the data usage correctly. Compared to CUDA, OpenACC can significantly reduce the workload of porting code and acheive a good acceleration effect at the same time.
3.3. The GPU-Aided Domain Decomposition
The aforementioned parallel method is based on physical domain decomposing. Thus, we introduce our scheme of domain decomposing as following.
In this paper, domain decomposition method (DDM) is used as the method of parallel nonlinear equation Newton iteration which is frequently-used and effective in the serial software parallelization field. The basic point of DDM is that it divides the reservoir simulation domain into many small subdomains, each subdomain is assigned to a process to deal with. After calculation, processes communicate and update boundary data. Then we apply DDM on the GPU, and implement GPU-aided domain decomposition (GDDM). In Figure 3, GDDM divides reservoir domain into subdomain , , , , the same number CPU threads are launched, based on the GPU HypeQ feature, each CPU thread launches a group of GPU thread blocks to calculate the corresponding subdomain. The iteration repeats continuously until the global solution converges, i.e., , where is the linear model of F about x, is the relative error tolerance and means the absolute error tolerance.
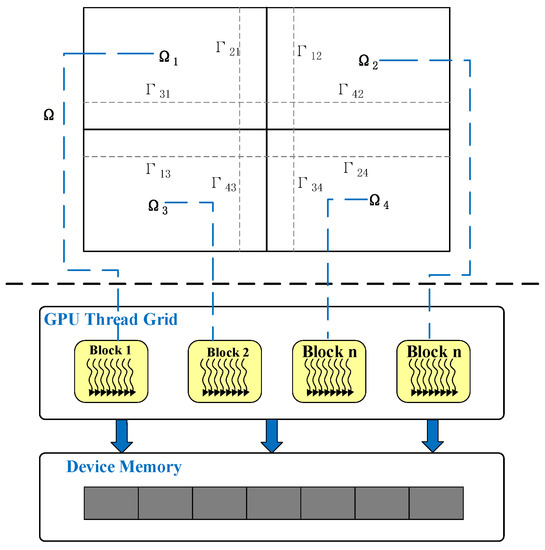
Figure 3.
GDDM method example.
Considering the influence of open boundary, we use the domain decomposition overlapping scheme, which uses the additive Schwarz method (ASM). In Figure 3, the simulation domain is divided into some subdomains which all contain a overlap part with other (for example is original boundary of , is boundary of in ). The mathematical model is assumed as:
Differential Operator as,
where , , and .
ASM is described as follows:
- Choose the approximate solution ,
- Parallel compute boundary value of subdomain,
- Extend to
- If it does not meet the convergence conditions, make , then go to step 2.
ASM is used as preprocessor to build a linear solver, and it is fully-parallel. Note that the number of overlaps is set as variable for considering its effect on iterative convergence.
4. Results and Discussion
We first provided an experimental setup, then evaluated and discussed the performances of proposed methods.
4.1. Experimental Setup
All experiments have been executed on work bench which is a single-node workstation, the configurations are presented in Table 1. As shown in Table 1, the main hardware platform is Intel i7 5820K CPU and Maxwell architecture GPU (GTX TITAN X), the host memory and device memory are respectively 32GB DDR4 and 12 GB DDR5, in software respect, the OS is Windows 10 (64-bit), the compiler is PGI Visual Fortran 16.9 where the latest OpenACC 2.5 is supported. In this paper the experimental datasets used are actual production data, which is composed of multiple data blocks organized by keywords and forms as a text file. For comparison, a CPU-based reservoir simulation project with Fortran is used in our following experiments. The reservoir simulation is based on a black-oil model, uses conjugate gradient as the linear solver, and employs the block triangular preconditioner. We used the Newton iteration method for simulations and the number of total time steps is up to 3000.

Table 1.
Configurations of the computer. Graphics processing unit (GPU).
The overall experimental plan is mentioned here. We evaluated performance of the parallel reservoir work by following three experiments: In the first experiment, we compare the parallel method with the serial in terms of simulation time, after that, we count the workload by computing the line number of OpenACC directive clauses added during the project modification, which is the evaluation of OpenACC’s availability. In last experiment, we compare two kinds of parallel reservoir simulation methods which differentiate from the other depending on whether the domain decomposition is used. The runtime is the performance merit here. The number of overlapping layers as another variable to influence reservoir time is also in consideration.
4.2. Evaluating and Discussing the Efficiency of OpenACC Parallel
In this section, we evaluated the efficiency of the parallel in term of runtime, essentially it could prove that the OpenACC was a powerful tool for developers to accelerate the previous project. In this experiment, the dataset was actual production data with more than 3000 nodes. Due to the Jacobian matrix assembly and linear equation solver taking more than 90% of the total runtime, we recorded the two parts’ runtime respectively and observed the acceleration effect in detail. For comparison, the serial is adopted as the standard to evaluate the efficiency of parallel simulation.
In the first experiment, the number of nodes was set ranging from 500, 1000, 1500, 2000, 2500 to 3000. This was the only factor and other variables were set as default, then the runtime of the Jacobian matrix assembly was collected as the experimental result. As shown in Figure 4, with the number of nodes increasing, the runtime of the jacobian matrix assembly from two methods gradually rose. The increasing of runtime from the serial method is massively quicker than the parallel one like linear increment, meanwhile the runtime of the parallel method accelerated by OpenACC slightly increased. When the node number was set to 500, the earlier serial was faster than the parallel. However with the node number increasing, the difference between runtimes continuously reduced, and when the node number was close to 1600, the runtime of the two methods were equivalent. After that, the parallel method outperformed the serial, when the node number equaled 3000, the parallel method was 1.68 times faster than the serial. So through experiment, we can see the OpenACC is similar to CUDA when the size of data is small, it takes a great deal of time to initial device and move data, but when the size becomes large, the OpenACC takes advantage of the GPU’s powerful computation capacity.
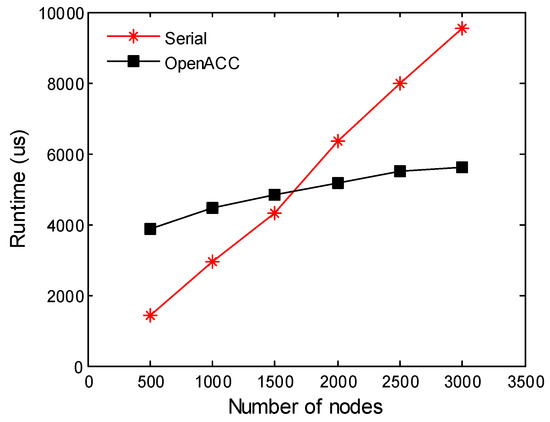
Figure 4.
Jacobian matrix assembly.
In the second experiment, we further compared the runtime of linear equation solvers from two methods. We also set the node number in the range from 500, 1000, 1500, 2000, 2500 to 3000, and other variables were set as default. As depicted in Figure 5, we observed that the timeline trend was similar to Figure 4, at the begining, the early vision serial code was faster. But while the node number increased, the proposed parallel started to outperform the other one. When the node number was set to 3000, the parallel was 2.1 times faster than the serial method. We thought the linear equation solver involved a large number of computation operation, so the GPU helped us to get better acceleration effect than the Jacobian matrix assembly.
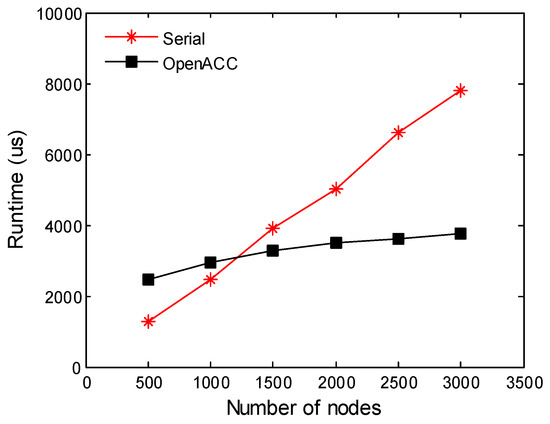
Figure 5.
Linear equations solver.
4.3. Evaluating and Discussing the Amount of Code During Project Modification
In this section, we evaluated the workload by calculating the line number of OpenACC directive clauses added during project migration, which was the experiment in term of OpenACC’s availability. As shown in Table 2, like the previous experiment, the experimental data of Jacobian matrix assembly and linear equations solver were collected separately in order to observe them in detail. Then the overall of the two parts was also displayed here.

Table 2.
Evaluating the workload of porting the application.
In Table 2, the experimental results showed that in Jacobian matrix assembly, the line amount of original code was 1703, the added directives was 307 lines and the increased ratio was 18%. In the linear equation solver, the raw code was 2073 lines, the incremental code was 520 lines and the ratio was 25.1%. In general, the total directives were 827 lines and the increased ratio was 21.9%. We can see that the increased ratio in the linear equations solver was higher than the ratio in the Jacobian matrix assembly, this was because the linear equation solver always contained a great deal of computation operations, so a set of workspace arrays would be allocated with frequent movement here, and many complex operations were also taken into consideration to guarantee the accuracy of reservoir simulation. The experiment demonstrated that with less time and acceptable effect to port application to GPU, OpenACC was able to speed up the traditional reservoir project.
4.4. Evaluating and Discussing the GPU-Aided Domain Decomposition Method
In this section, we evaluated the acceleration effect about the proposed above GPU-aided domain decomposition method. Here the variables were the number of subdomains and the number of overlapping layers from ASM. The total number of node was set to 3000, the sum time of the Jacobian matrix assembly and the linear solver was as the experimental result. In addition the method which only adopted OpenACC but not DDM was set as the baseline. Due to the limitation of the node number, the number of the subdomains was set to 9 and 25, the corresponding results were shown in Figure 6 and Figure 7 respectively. As a consequence, the other variable was set to related values, specifically, the number of overlapping layers was set ranging from 3, 5 to 7 in Figure 6 and from 2, 4, 6, 8, 10 to 12 in Figure 7. In these pictures, “O-number” was the number of overlapping layer where “O” representd the overlapping layer and “number” was the value, “NUDD” means that the GDDM was not used.
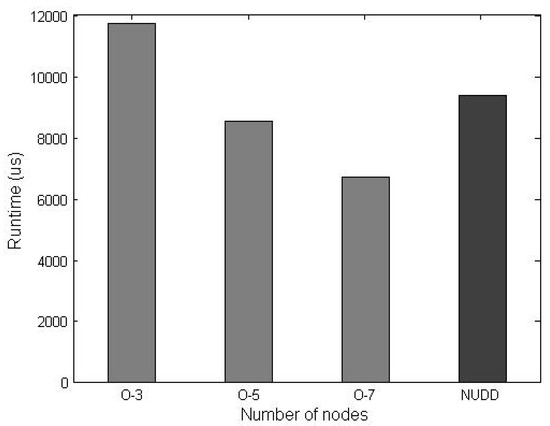
Figure 6.
The number of subdomains was set to 9.
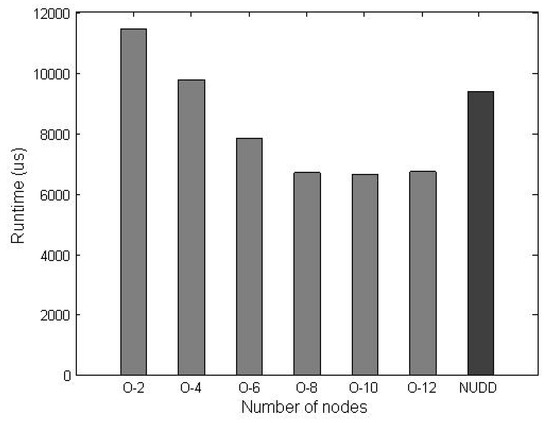
Figure 7.
The number of subdomains was set to 25.
As shown in Figure 6, the domain was divided into 9 subdomains, the number of overlapping layers were set as mentioned above. With the number of overlapping layers increasing, the runtime gradually reduced. When the overlapping layer was set to 3, the runtime was more than the baseline method, then when it was set to 7, the GDDM implemented a 1.4 times acceleration effect. We thought that when the number of the overlapping layers was set small, the local solution in subdomain contained large deviation compared to global solution, many iterative process would be performed to complete the convergence, with the number rising, the problem was solved. In Figure 7 the previous problem occurred again, when the number increased, the runtime was reduced by degrees. When the overlapping layer reached 10, the runtime was minimal, after that the runtime started to rise, therefore as the number of overlapping layers was set to 10, the GDDM achieved the best acceleration effect, 1.6 times faster than the baseline.
5. Conclusions
This paper addresses the problem of accelerating reservoir simulation by using a graphics processor unit (GPU). In order to convert traditional serial reservoir simulation to parallel reservoir simulation, OpenACC is used to keep a small amount of code modification while porting the code. In order to improve the acceleration effect further, we apply a GPU-aided domain decomposition method.
Author Contributions
Conceptualization, Z.D.; Formal analysis, W.H.; Funding acquisition, Z.K. and D.Z.; Methodology, Z.D.; Project administration, Z.K.; Software, Z.D. and W.H.
Funding
This work is supported in part by the National Natural Science Foundation of China (No. U1711266), the National Science and Technology Major Project of the Ministry of Science and Technology of China (2016ZX05014-003), the China Postdoctoral Science Foundation (2014M552112), the Fundamental Research Funds for the National University, China University of Geosciences (Wuhan).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this paper:
| CUDA | Compute Unified Device Architecture |
| GPU | Graphics processing unit |
| FDM | Finite difference method |
| AWS | Amazon Web Services |
| DDM | Domain decomposition method |
| GDDM | GPU-aided domain decomposition |
| ASM | Additive Schwarz Method |
References
- Maliassov, S.; Beckner, B.; Dyadechko, V. Parallel reservoir simulation using a specific software framework. In Proceedings of the Society of Petroleum Engineers-SPE Reservoir Simulation Symposium, The Woodlands, TX, USA, 3–5 February 2013; pp. 1062–1070. [Google Scholar]
- Guan, W.; Qiao, C.; Zhang, H.; Zhang, C.S.; Zhi, M.; Zhu, Z.; Zheng, Z.; Ye, W.; Zhang, Y.; Hu, X.; et al. On robust and efficient parallel reservoir simulation on tianhe-2. In Proceedings of the Society of Petroleum Engineers-SPE Reservoir Characterisation and Simulation Conference and Exhibition, Abu Dhabi, UAE, 27 May 2015; pp. 933–945. [Google Scholar]
- Chien, M.; Northrup, E. Vectorization and parallel processing of local grid refinement and adaptive implicit schemes in a general purpose reservoir simulator. In Proceedings of the SPE Symposium on Reservoir Simulation, New Orleans, LA, USA, 28 February–3 March 1993; pp. 279–290. [Google Scholar]
- Chien, M.C.; Tchelepi, H.A.; Yardumian, H.E.; Chen, W.H. A scalable parallel multi-purpose reservoir simulator. In Proceedings of the SPE Symposium on Reservoir Simulation, Dallas, TX, USA, 8–11 June 1997; pp. 17–30. [Google Scholar]
- Li, X.; Lei, Z.; Huang, D.; Khamra, Y.E.; Allen, G.; White, C.D.; Kim, J.G. Queues: Using grid computing for simulation studies. In Proceedings of the Digital Energy Conference and Exhibition, Houston, TX, USA, 11–12 April 2007; pp. 1–13. [Google Scholar]
- Eldred, M.E.; Orangi, A.; Al-Emadi, A.A.; Ahmad, A.; O’Reilly, T.J.; Barghouti, N. Reservoir simulations in a high performance cloud computing environment. In Proceedings of the SPE Intelligent Energy Conference & Exhibition, Utrecht, The Netherlands, 1–3 April 2014; pp. 1–8. [Google Scholar]
- Nickolls, J.; Dally, W.J. The gpu computing era. IEEE Micro 2010, 30, 56–69. [Google Scholar] [CrossRef]
- Klie, H.M.; Sudan, H.H.; Li, R.; Saad, Y. Exploiting capabilities of many core platforms in reservoir simulation. In Proceedings of the SPE Reservoir Simulation Symposium, The Woodlands, TX, USA, USA, 21–23 February 2011; pp. 1–12. [Google Scholar]
- Liu, H.; Yu, S.; Chen, Z.J.; Hsieh, B.; Shao, L. Parallel preconditioners for reservoir simulation on gpu. In Proceedings of the SPE Latin America and Caribbean Petroleum Engineering Conference, Mexico City, Mexico, 16–18 April 2012; pp. 1–5. [Google Scholar]
- Gilman, J.R.; Uland, M.; Angola, O.; Michelena, R.; Meng, H.; Esler, K.; Mukundakrishnan, K.; Natoli, V. Unconventional reservoir model predictions using massively-parallel gpu flow-simulation: Part-1 bakken reservoir characterization choices and parameter testing. In Proceedings of the Unconventional Resources Technology Conference, San Antonio, TX, USA, 20–22 July 2015; pp. 1–21. [Google Scholar]
- Beckner, B.L.; Haugen, K.B.; Maliassov, S.; Dyadechko, V.; Wiegand, K.D. General parallel reservoir simulation. In Proceedings of the International Petroleum Exhibition and Conference, Abu Dhabi, UAE, 9–12 November 2015; pp. 1–10. [Google Scholar]
- NVIDIA. NVIDIA CUDA C Programming Guide Version 6.0; NVIDIA: Santa Clara, CA, USA, 2014. [Google Scholar]
- Sabne, A.; Sakdhnagool, P.; Lee, S.; Vetter, J.S. Evaluating performance portability of openacc. LNCS 2015, 8967, 51–66. [Google Scholar]
- Lopez, I.; Fumero, J.J.; de Sande, F. Directive-based programming for gpus: A comparative study. In Proceedings of the IEEE 14th International Conference on High Performance Computing and Communications, Liverpool, UK, 25–27 June 2012; pp. 410–417. [Google Scholar]
- OpenACC: OpenACC Programming and Best Practices Guide. 2015. Available online: www.openacc.org (accessed on 18 December 2018).
- Pickering, B.P.; Jackson, C.W.; Scogland, T.R.; Feng, W.C.; Roy, C.J. Directive-based gpu programming for computational fluid dynamics. Comput. Fluids 2015, 114, 242–253. [Google Scholar] [CrossRef]
- Cebamanos, L.; Henty, D.; Richardson, H.; Hart, A. Auto-tuning an openacc accelerated version of nek5000. LNCS 2014, 8759, 69–81. [Google Scholar]
- Calore, E.; Kraus, J.; Schifano, S.F.; Tripiccione, R. Accelerating lattice boltzmann applications with openacc. LNCS 2015, 9233, 613–624. [Google Scholar]
- Wang, Y.; Killough, J.E. A new approach to load balance for parallel/compositional simulation based on reservoir-model overdecomposition. SPE J. 2014, 19, 304–315. [Google Scholar] [CrossRef]
- Have, P.; Masson, R.; Nataf, F.; Szydlarski, M.; Xiang, H.; Zhao, T. Algebraic domain decomposition methods for highly heterogeneous problems. SIAM J. Sci. Comput. 2013, 35, 284–302. [Google Scholar] [CrossRef]
- Fischer, P.F. An overlapping schwarz method for spectral element solution of the incompressible navier–stokes equations. J. Comput. Phys. 1997, 133, 84–101. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).