Evaluating Algorithm Efficiency for Optimizing Experimental Designs with Correlated Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Statistical Model for Randomized Complete Block Designs
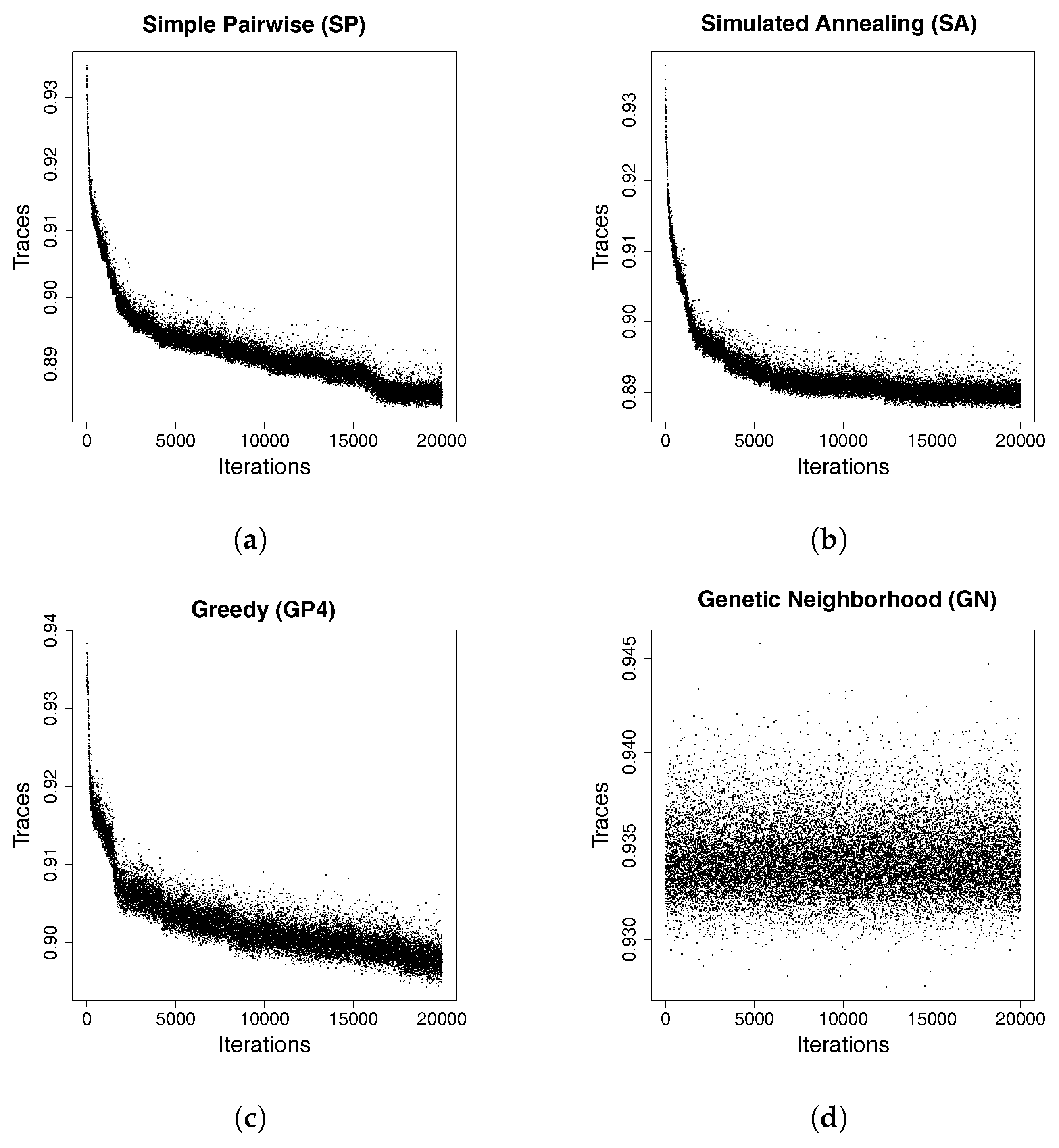
2.2. Algorithms
- Simple Pairwise (SP), that swaps a single pair of treatments at a time,
- Greedy Pairwise (GP), that swaps more than a single pair of treatments at a time,
- Genetic Neighbourhood (GN), that takes into consideration the genetic relatedness of the direct neighbouring of a experimental units to perform swaps, and
- Simulated Annealing (SA), that swaps a pair of treatments at a time, but accepts poor designs at random with a given probability which diminishes with time.
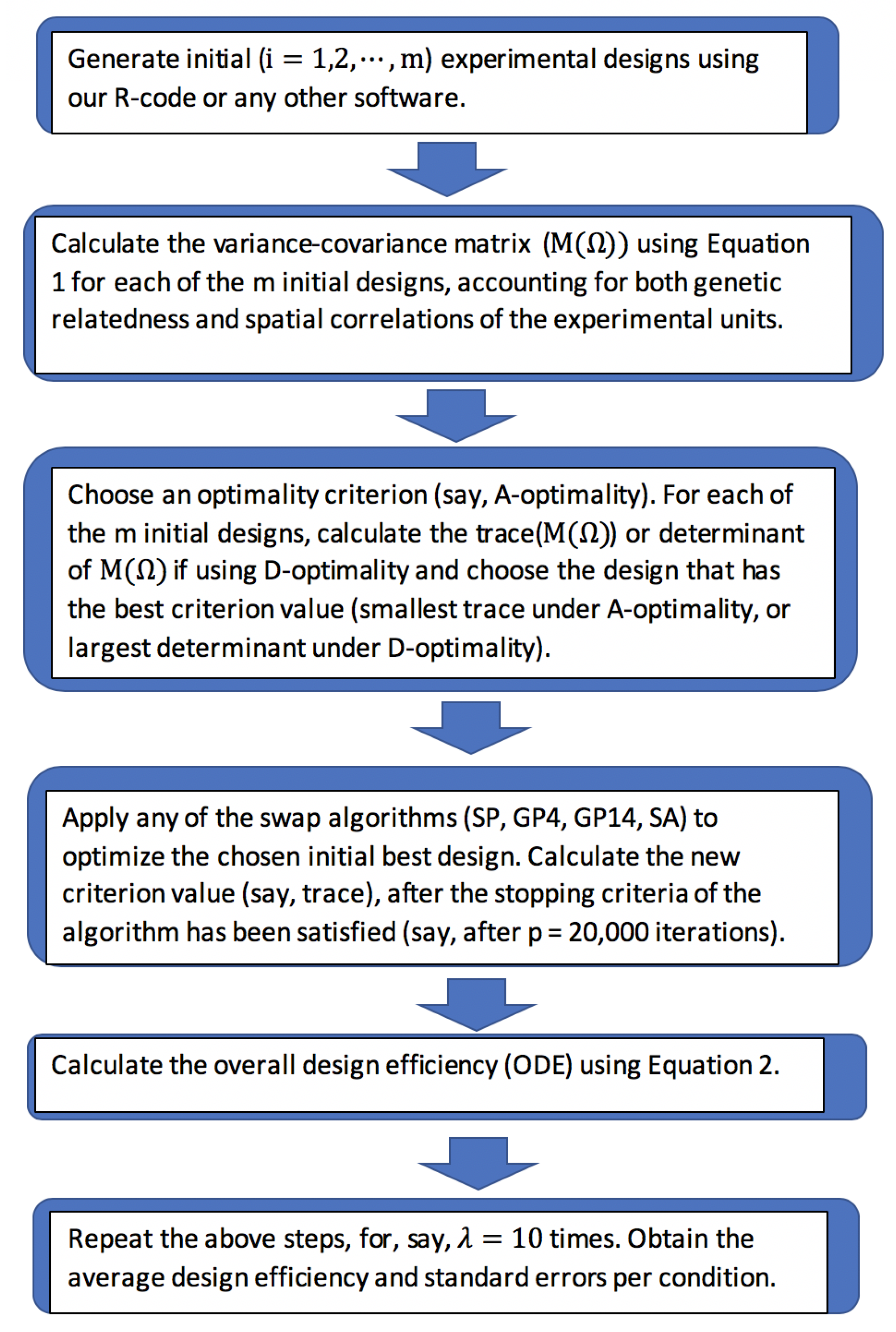
2.3. Evaluation of Algorithms
3. Results
4. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. R-Code for the Algorithms
Appendix A.1. Simple Pairwise Algorithm (SP)


Appendix A.2. Simulated Annealing Algorithm (SA)


Appendix A.3. Greedy Pairwise Algorithm (GP)


Appendix A.4. Genetic Neighborhood Algorithm (GN)


Appendix B. R-Code for Generating Initial Randomized Complete Block Design (RCBD)
Appendix B.1. Generate a RCBD


Appendix B.2. Generate Multiple RCBD

Appendix C. Generate a Numerator Relationship Matrix
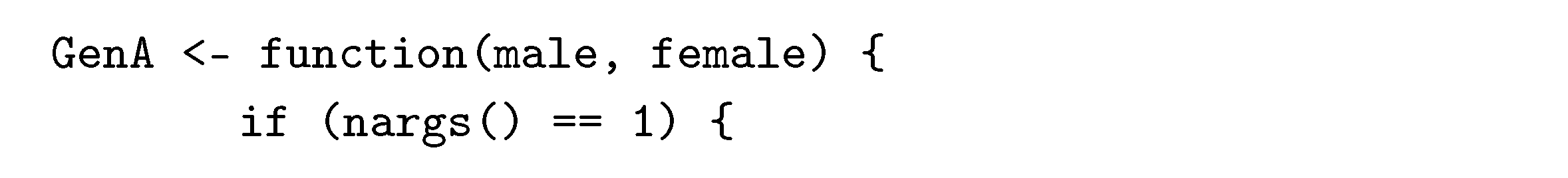

Appendix D. Calculate the Variance-Covariance Matrix


References
- Welham, S.J.; Gezan, S.A.; Clark, S.J.; Mead, A. Statistical Methods in Biology; Design and Analysis of Experiments and Regression; Chapman & Hall: Boca Raton, FL, USA, 2015. [Google Scholar]
- Piepho, H.P.; Möhring, J.; Melchinger, A.E.; Büchse, A. BLUP for phenotypic selection in plant breeding and variety testing. Euphytica 2008, 161, 209–228. [Google Scholar] [CrossRef]
- John, J.A.; Williams, E.R. Cyclic and Computer Generated Designs, 2nd ed.; Monographs of Statistics and Applied Probability 38; Chapman and Hall: London, UK, 1995. [Google Scholar]
- Williams, E.R.; John, J.A.; Whitaker, D. Construction of resolvable spatial row-column designs. Biometrics 2006, 62, 103–108. [Google Scholar] [CrossRef] [PubMed]
- Gezan, S.A.; White, T.L.; Huber, D.A. Accounting for spatial variability in breeding trials: A simulation study. Agronomy 2010, 102, 1562–1571. [Google Scholar] [CrossRef]
- Butler, D.G.; Smith, A.B.; Cullis, B.R. On the design of field experiments with correlated treatment effects. J. Agric. Biol. Environ. Stat. 2014, 19, 539–555. [Google Scholar] [CrossRef]
- Chernoff, H. Locally optimal designs for estimating parameters. Ann. Math. Stat. 1953, 24, 586–602. [Google Scholar] [CrossRef]
- Cullis, B.R.; Lill, W.; Fisher, J.; Read, B.; Gleeson, A. A new procedure for the analysis of early generation variety trials. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1989, 38, 361–375. [Google Scholar] [CrossRef]
- Cullis, B.R.; Smith, A.B.; Coombes, N.E. On the design of early generation variety trials with correlated data. J. Agric. Biol. Environ. Stat. 2006, 11, 381–393. [Google Scholar] [CrossRef]
- Mramba, L.K.; Peter, G.F.; Whitaker, V.M.; Gezan, S.A. Generating improved experimental designs with spatially and genetically correlated observations using mixed models. Agronomy 2018, 8, 40. [Google Scholar] [CrossRef]
- Kuhfeld, W.F. MR-2010C—Experimental Design: Efficiency, Coding, and Choice Designs; Technical Report; SAS Insitute Inc.: Cary, NC, USA, 2010. [Google Scholar]
- Wald, A. On the efficient design of statistical investigations. Ann. Math. Stat. 1943, 14, 134–140. [Google Scholar] [CrossRef]
- Das, A. An introduction to optimality criteria and some results on optimal block design. In Design Workshop Lecture Notes; Indian Statistical Institute: Kolkata, India; Theoretical Statistics and Mathematics Unit: New Delhi, India, 2002; pp. 1–21. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- VSN International. CycDesign 6.0: A Package for the Computer Generation of Experimental Designs; VSN International Ltd.: Hemel Hempstead, UK, 2018. [Google Scholar]
- VSN International. Genstat for Windows, 19th ed.; VSN International Ltd.: Hemel Hempstead, UK, 2017. [Google Scholar]
- Coombes, N.E. DiGGer: Design Search Tool in R. 2009. Available online: http://nswdpibiom.org/austatgen/software/ (accessed on 17 December 2018).
- Cressie, N.A.C. Statistics for Spatial Data, revised ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1993. [Google Scholar]
- Gilmour, A.R.; Gogel, B.J.; Cullis, B.R.; Thompson, R. ASReml User Guide Release 3.0; VSN International Ltd.: Hemel Hempstead, UK, 2009. [Google Scholar]
- Henderson, C.R. The estimation of genetic parameters. Ann. Math. Stat. 1950, 21, 309–310. [Google Scholar]
- Hooks, T.; Marx, D.; Kachman, S.; Pedersen, J. Optimality criteria for models with random effects. Revista Colombiana de Estadística 2009, 32, 17–31. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Borges, P.; Eid, T.; Bergseng, E. Applying simulated annealing using different methods for the neighborhood search in forest planning problems. Eur. J. Oper. Res. 2014, 233, 700–710. [Google Scholar] [CrossRef]
- Liu, G.; Han, S.; Zhao, X.; Nelson, J.D.; Wang, H.; Wang, W. Optimisation algorithms for spatially constrained forest planning. Ecol. Model. 2006, 194, 421–428. [Google Scholar] [CrossRef]
- Filho, J.S.B.; Gilmour, S.G. Planning incomplete block experiments when treatments are genetically related. Biometrics 2003, 59, 375–381. [Google Scholar] [CrossRef]
- Butler, D.G.; Eccleston, J.A.; Cullis, B.R. On an approximate optimality criterion for the design of field experiments under spatial dependence. Aust. N. Z. J. Stat. 2008, 50, 295–307. [Google Scholar] [CrossRef]

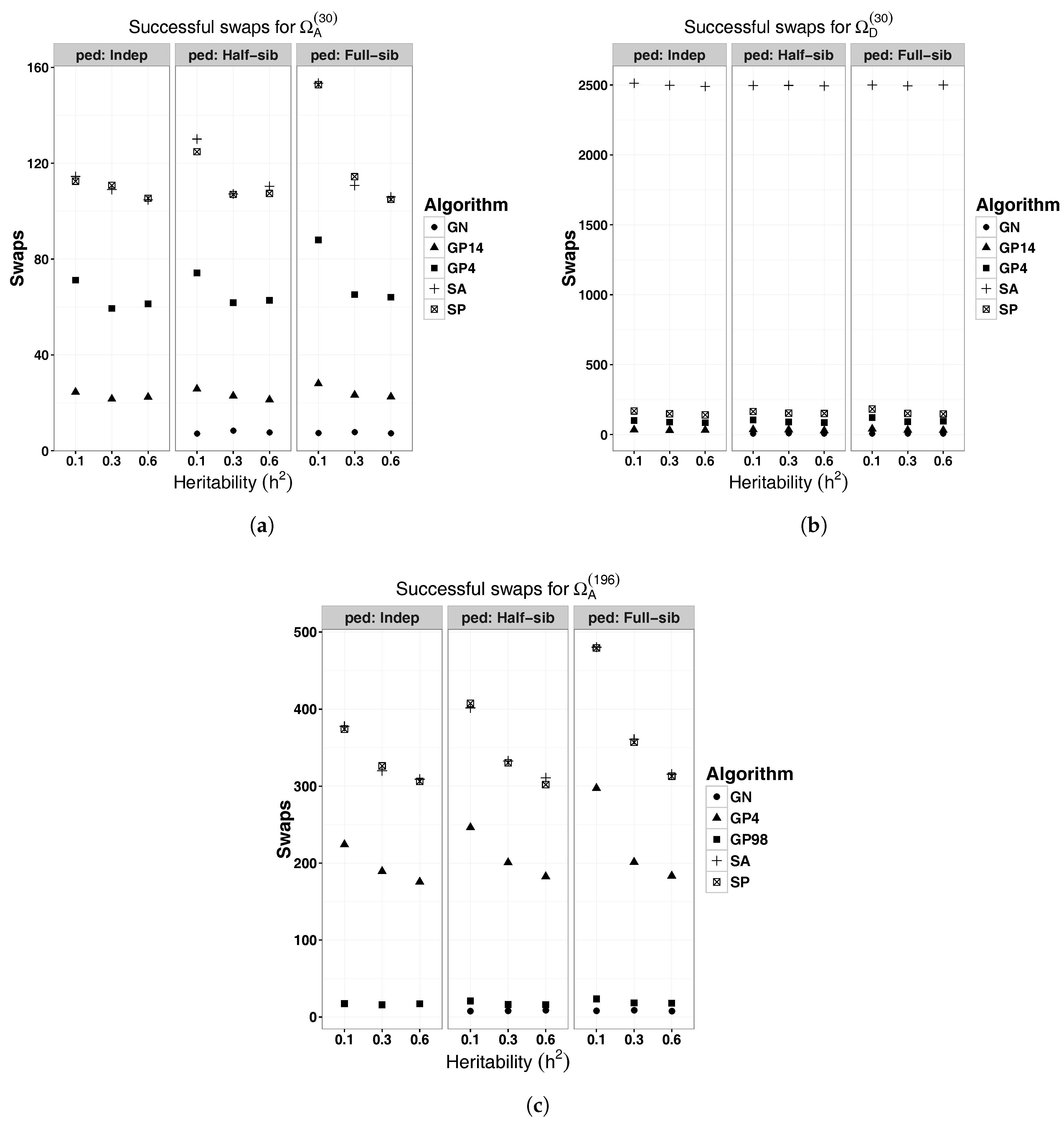
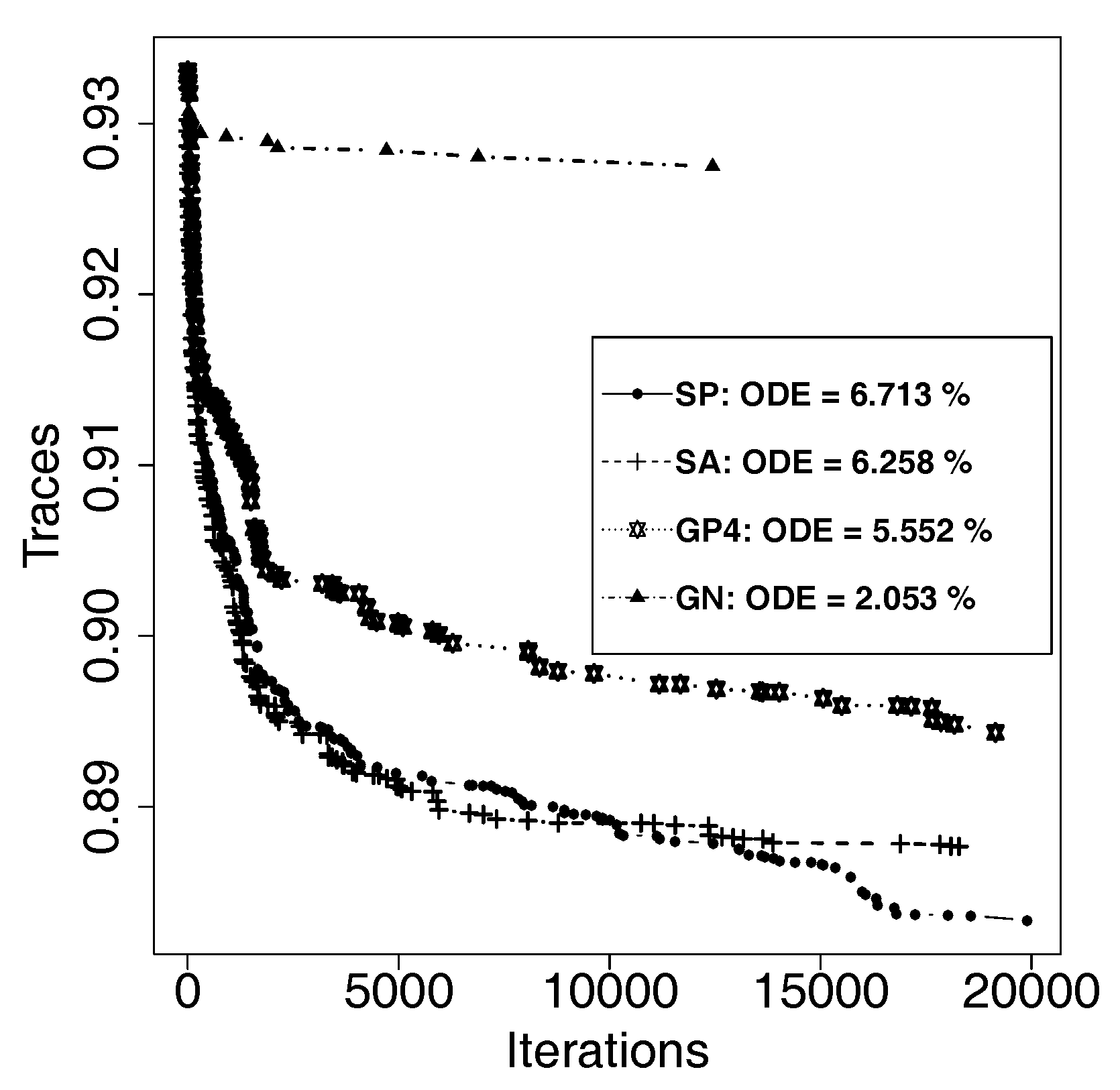
| Condition | Pedigree | |
|---|---|---|
| 1 | 0.1 | Indep |
| 2 | 0.3 | |
| 3 | 0.6 | |
| 4 | 0.1 | Half-sib |
| 5 | 0.3 | |
| 6 | 0.6 | |
| 7 | 0.1 | Full-sib |
| 8 | 0.3 | |
| 9 | 0.6 |
| Condition | SP | GP4 | GP14 | SA | GN | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pedigree | ODE % | S.E. | ODE % | S.E. | ODE % | S.E. | ODE % | S.E. | ODE % | S.E | ||||||
| Indep | 0.1 | 6.347 | 0.060 | 5.501 | 0.060 | 3.747 | 0.093 | 6.385 | 0.072 | - | - | |||||
| 0.3 | 7.398 | 0.066 | 6.194 | 0.080 | 4.371 | 0.053 | 7.403 | 0.063 | - | - | ||||||
| 0.6 | 5.109 | 0.044 | 4.414 | 0.057 | 3.110 | 0.054 | 5.222 | 0.064 | - | - | ||||||
| Half-sib | 0.1 | 5.826 | 0.026 | 5.082 | 0.055 | 3.610 | 0.065 | 5.781 | 0.045 | 1.853 | 0.042 | |||||
| 0.3 | 5.375 | 0.056 | 4.640 | 0.082 | 3.192 | 0.052 | 5.428 | 0.047 | 1.940 | 0.088 | ||||||
| 0.6 | 3.066 | 0.028 | 2.663 | 0.023 | 1.858 | 0.033 | 3.131 | 0.028 | 1.064 | 0.033 | ||||||
| Full-sib | 0.1 | 4.109 | 0.030 | 3.611 | 0.026 | 2.543 | 0.038 | 4.045 | 0.027 | 1.343 | 0.034 | |||||
| 0.3 | 2.656 | 0.029 | 2.265 | 0.021 | 1.601 | 0.034 | 2.667 | 0.032 | 0.920 | 0.027 | ||||||
| 0.6 | 1.247 | 0.006 | 1.065 | 0.009 | 0.755 | 0.012 | 1.247 | 0.013 | 0.460 | 0.011 | ||||||
| Condition | SP | GP4 | GP98 | SA | GN | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pedigree | ODE % | S.E. | ODE % | S.E. | ODE % | S.E. | ODE % | S.E. | ODE % | S.E | ||||||
| Indep | 0.1 | 1.633 | 0.013 | 1.354 | 0.018 | 0.481 | 0.008 | 1.629 | 0.015 | - | - | |||||
| 0.3 | 2.794 | 0.020 | 2.387 | 0.017 | 0.864 | 0.024 | 2.736 | 0.034 | - | - | ||||||
| 0.6 | 3.232 | 0.024 | 2.754 | 0.039 | 1.080 | 0.028 | 3.270 | 0.027 | - | - | ||||||
| Half-sib | 0.1 | 2.032 | 0.023 | 1.776 | 0.019 | 0.690 | 0.018 | 2.016 | 0.019 | 0.216 | 0.014 | |||||
| 0.3 | 2.684 | 0.018 | 2.269 | 0.009 | 0.851 | 0.024 | 2.670 | 0.019 | 0.381 | 0.013 | ||||||
| 0.6 | 2.801 | 0.027 | 2.402 | 0.029 | 0.890 | 0.025 | 2.818 | 0.009 | 0.351 | 0.020 | ||||||
| Full-sib | 0.1 | 2.813 | 0.018 | 2.471 | 0.022 | 0.888 | 0.025 | 2.827 | 0.014 | 0.324 | 0.015 | |||||
| 0.3 | 2.240 | 0.016 | 1.886 | 0.023 | 0.702 | 0.020 | 2.226 | 0.021 | 0.297 | 0.011 | ||||||
| 0.6 | 1.873 | 0.011 | 1.588 | 0.013 | 0.623 | 0.016 | 1.926 | 0.013 | 0.280 | 0.013 | ||||||
| Condition | SP | GP4 | GP14 | SA | GN | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pedigree | ODE % | S.E. | ODE % | S.E. | ODE % | S.E. | ODE % | S.E. | ODE % | S.E | ||||||
| Indep | 0.1 | 1.807 | 0.014 | 1.600 | 0.014 | 1.029 | 0.014 | 0.085 | 0.019 | - | - | |||||
| 0.3 | 2.324 | 0.017 | 1.993 | 0.013 | 1.335 | 0.030 | 0.104 | 0.025 | - | - | ||||||
| 0.6 | 2.247 | 0.021 | 1.930 | 0.021 | 1.265 | 0.032 | 0.178 | 0.027 | - | - | ||||||
| Half-sib | 0.1 | 1.766 | 0.012 | 1.576 | 0.015 | 1.115 | 0.015 | 0.130 | 0.034 | 0.446 | 0.015 | |||||
| 0.3 | 2.287 | 0.023 | 2.054 | 0.024 | 1.377 | 0.022 | 0.150 | 0.041 | 0.614 | 0.013 | ||||||
| 0.6 | 2.253 | 0.024 | 1.933 | 0.020 | 1.315 | 0.019 | 0.090 | 0.023 | 0.637 | 0.023 | ||||||
| Full-sib | 0.1 | 1.666 | 0.011 | 1.514 | 0.013 | 1.037 | 0.009 | 0.097 | 0.025 | 0.431 | 0.010 | |||||
| 0.3 | 2.168 | 0.013 | 1.935 | 0.025 | 1.307 | 0.026 | 0.119 | 0.025 | 0.634 | 0.017 | ||||||
| 0.6 | 2.225 | 0.027 | 1.913 | 0.023 | 1.316 | 0.025 | 0.125 | 0.019 | 0.669 | 0.022 | ||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mramba, L.K.; Gezan, S.A. Evaluating Algorithm Efficiency for Optimizing Experimental Designs with Correlated Data. Algorithms 2018, 11, 212. https://doi.org/10.3390/a11120212
Mramba LK, Gezan SA. Evaluating Algorithm Efficiency for Optimizing Experimental Designs with Correlated Data. Algorithms. 2018; 11(12):212. https://doi.org/10.3390/a11120212
Chicago/Turabian StyleMramba, Lazarus K., and Salvador A. Gezan. 2018. "Evaluating Algorithm Efficiency for Optimizing Experimental Designs with Correlated Data" Algorithms 11, no. 12: 212. https://doi.org/10.3390/a11120212
APA StyleMramba, L. K., & Gezan, S. A. (2018). Evaluating Algorithm Efficiency for Optimizing Experimental Designs with Correlated Data. Algorithms, 11(12), 212. https://doi.org/10.3390/a11120212






