Parametric Estimation in the Vasicek-Type Model Driven by Sub-Fractional Brownian Motion

Abstract

In the paper, we tackle the least squares estimators of the Vasicek-type model driven by sub-fractional Brownian motion:

$$d{X}_t=(\mu +\theta X_t)dt+d{S}_t^H,t\ge 0$$

with $X_0=0$, where $S^H$ is a sub-fractional Brownian motion whose Hurst index H is greater than $\frac{1}{2}$, and $\mu \in \mathbb{R}$, $\theta \in {\mathbb{R}}^{+}$ are two unknown parameters. Based on the so-called continuous observations, we suggest the least square estimators of $\mu$ and $\theta$ and discuss the consistency and asymptotic distributions of the two estimators.

1. Introduction

Statistical inference for stochastic equations is a main research direction in probability theory and its applications. When the noise is a standard Brownian motion or a Lévy process, such problems have been extensively studied. Some surveys and complete literature for this direction could be found in Bishwal [1], Iacus [2], Kutoyants [3], Liptser and Shiryaev [4], Prakasa Rao [5], and the references therein. However, in contrast to the extensive studies on semimartingale types, other statistical inferences associated with some Gaussian processes are very limited, and a common denominator in all these works is that it is assumed that the equation admits only an unknown parameter. Let us consider the parameter estimates of the Vasicek-type model driven by a Gaussian process G:

$$d{X}_t=(\mu +\theta X_t)dt+d{G}_t,t\ge 0,$$

(1)

where $\mu \in \mathbb{R}$, $\theta \in {\mathbb{R}}^{+}$ are two parameters.

When $\mu =0$ and G is a fractional Brownian motion with Hurst index $H\in (0,1)$, the question has been studied by many authors. We mention the works of Berzin et al. [6], Es-Sebaiy [7], Es-Sebaiy and Nourdin [8], Hu and Nualart et al. [9,10], Kleptsyna and Le Breton [11], Prakasa Rao [12], and the references therein for results on parameter estimation of stochastic equations driven by the fractional Brownian motion (fBm). When G is not a fractional Brownian motion, the research for this question is very limited. For $\mu =0$ and G a sub-fractional Brownian motion, Mendy [13] considered the least squares estimation of $\theta$ and studied the consistency and asymptotic behavior. For $\mu =0$ and G a Gaussian process, El Machkouri et al. [14] showed the strong consistency and the asymptotic distribution of the least squares estimator $\widehat{\theta }$ of $\theta$ based on the properties of G, and as some examples, the authors also studied the three Vasicek-type models driven by fractional Brownian motion, sub-fractional Brownian motion, and bi-fractional Brownian motion, respectively.

Motivated by these above results and for simplicity, in this paper, we consider the least squares estimation of Equation (1) when G is a sub-fractional Brownian motion $S^H$ with Hurst index $H\in (\frac{1}{2},1)$ and both $\mu$ and $\theta >0$ are unknown. That is, the parameter estimation of the so-called Vasicek-type model driven by sub-fractional Brownian motion:

$$d{X}_t=(\mu +\theta X_t)dt+d{S}_t^H,t\ge 0,$$

(2)

where $S^H$ is a sub-fractional Brownian motion and $\mu \in \mathbb{R}$, $\theta \in {\mathbb{R}}^{+}$ are two unknown parameters. On the other hand, there exists still a practical motivation for studying the parameter estimation, that is to provide optional tools to understand volatility modeling in finance. In fact, any mean-reverting model in continuous or discrete observations can be regarded as a model for stochastic volatility. We can consult the research monograph [15] for this modeling idea. Since stochastic volatility is not observed for many financial markets and the sub-fractional Brownian motion is a process without ergodicity, the discussions on the parameter estimation based on discrete observations are beyond the scope of this article. For the sake of simplicity, we focus on tackling the least squares estimation of Equation (2) based on the so-called continuous observations.

The so-called sub-fractional Brownian motion (sub-fBm in short) $S^H=\{S_t^H,t\ge 0\}$ with index $H\in (0,1)$ is introduced by Bojdecki et al. [16], which arises from occupation time fluctuations of branching particle systems with the Poisson initial condition. It is a mean zero Gaussian process with $S_0^H=0$ and:

$$R_H(t,s)\equiv E\left[S_t^H{S}_s^H\right]=s^{2H}+t^{2H}-\frac{1}{2}\left[{(s+t)}^{2H}+{|t-s|}^{2H}\right]$$

(3)

for all $s,t\ge 0$. For $H=1/2$, $S^H$ coincides with the standard Brownian motion B. Sub-fBm $S^H$ is neither a semimartingale nor a Markov process unless $H=1/2$. The sub-fBm has many properties analogous to those of fractional Brownian motion such as self-similarity, long/short-range dependence, and Hölder paths. However, it has no stationary increments. Moreover, it admits the estimates:

$$[(2-2^{2H-1})\wedge 1]{(t-s)}^{2H}\le E\left[{\left(S_t^H-S_s^H\right)}^2\right]\le [(2-2^{2H-1})\vee 1]{(t-s)}^{2H}.$$

(4)

More works for sub-fractional Brownian motion can be found in Bojdecki Y et al. [17,18], Li and Xiao [19], Shen and Yan [20], Sun and Yan [21,22], Tudor [23,24,25,26], Yan et al. [27,28], and the references therein. On the other hand, in contrast to the extensive studies on fractional Brownian motion, there has been little systematic investigation on other self-Gaussian processes. The main reason for this is the complexity of dependence structures, and in general, these Gaussian processes have no stationary increments and the representation based on Wiener integral with respect to a Brownian motion. Therefore, it seems interesting to study the asymptotic behavior associated with other self-Gaussian processes.

Now, we consider Equation (2) with $\frac{1}{2}<H<1$ and $\theta >0$. Clearly, we have:

$$X_t=\frac{\mu }{\theta }(e^{\theta t}-1)+e^{\theta t}{\int }_0^t{e}^{-\theta s}d{S}_s^H$$

for all $t\ge 0$, and the trajectory of X is $\gamma$-Hölder continuous for all $\gamma <H$ (see Section 3). As an immediate result, we see that the Young integral ${\int }_0^T{X}_{t}d{X}_t$ is well defined for all $\frac{1}{2}<H<1$. Let now the system Equation (2) be observed continuously, and let H be known. By using the least squares method due to Hu and Nualart [10], the least squares estimators of $\theta$ and $\mu$ can be motivated by minimizing the contrast function:

$$\rho (\mu ,\theta )={\int }_0^T{\left|\dot{X_t}-(\mu +\theta X_t)\right|}^{2}dt.$$

Minimizing the above contrast function $(\mu ,\theta )\mapsto \rho (\mu ,\theta )$, we introduce estimators of $\theta$ and $\mu$ as follows:

$${\widehat{\theta }}_T=\frac{T{\int }_0^T{X}_{s}d{X}_s-X_T{\int }_0^T{X}_{s}ds}{T{\int }_0^T{X_s}^{2}ds-{\left({\int }_0^T{X}_{s}ds\right)}^2}$$

(5)

and:

$${\widehat{\mu }}_T=\frac{1}{T}\left(X_T-{\widehat{\theta }}_T{\int }_0^T{X}_{s}ds\right)=\frac{X_T{\int }_0^T{X_s}^{2}ds-\frac{1}{2}{\left(X_T\right)}^2{\int }_0^T{X}_{s}ds}{T{\int }_0^T{X_s}^{2}ds-{\left({\int }_0^T{X}_{s}ds\right)}^2},$$

(6)

where the stochastic integral ${\int }_0^T{X}_{t}d{X}_t$ is a Young integral for $\frac{1}{2}<H<1$. Our main statement is as follows:

• The least squares estimators ${\widehat{\theta }}_T$ and ${\widehat{\mu }}_T$ are strong consistent, and we have:

$$e^{\theta T}({\widehat{\theta }}_T-\theta )⟶\frac{2\theta {\lambda }_H}{{\lambda }_H-{\vartheta }_H}·\frac{\xi }{\eta +\frac{\mu }{\theta }{({\lambda }_H-{\vartheta }_H)}^{-1}},$$

$$T\left({\widehat{\mu }}_T-\mu -\frac{1}{T}{S}_T^H\right)⟶2{\lambda }_H\xi ,$$

and:

$$T^{1-H}\left({\widehat{\mu }}_T-\mu \right)⟶\zeta$$

in distribution, as T tends to infinity, where $\xi ,\eta \sim N(0,1)$ are mutually independent, $\zeta \sim N(0,2-2^{2H-1})$, ${\lambda }_H=H\mathsf{\Gamma }\left(2H\right)$, and:

$${\vartheta }_H=H(2H-1){\int }_0^{\infty }{\int }_0^{\infty }{e}^{-(s+r)}{(s+r)}^{2H-2}dsdr.$$

This paper is organized as follows. In Section 2, we present some preliminaries for sub-fBm. In Section 3, we prove the consistence of ${\widehat{\mu }}_T$ and ${\widehat{\theta }}_T$. In Section 4, we investigate the asymptotic distribution of estimators ${\widehat{\mu }}_T$ and ${\widehat{\theta }}_T$.

2. Preliminaries

In this section, we briefly recall some basic definitions and results of sub-fBm. Throughout this paper, we assume that $0<H<1$ is arbitrary, but fixed, and let $S^H=\{S_t^H,0\le t\le T\}$ be a one-dimensional sub-fBm with Hurst index H and defined on $(\mathsf{\Omega },{\mathcal{F}}^H,P)$. $S^H$ can be written as a Volterra process, and it is also possible to construct a stochastic calculus of variations with respect to the Gaussian process $S^H$, which will be related to the Malliavin calculus. Some surveys and complete literature for Malliavin calculus of the Gaussian process could be found in Alòs et al. [29], Nualart [30], and Tudor [25,26].

Recall that a mean zero Gaussian process $S^H=\{S_t^H,t\ge 0\}$ with Hurst index $H\in (0,1)$ is called the sub-fractional Brownian motion (sub-fBm) if $S_0^H=0$ and the covariance:

$$R_H(t,s)\equiv E\left[S_t^H{S}_s^H\right]=s^{2H}+t^{2H}-\frac{1}{2}\left[{(s+t)}^{2H}+{|t-s|}^{2H}\right]$$

(7)

for all $s,t\ge 0$. Consider the kernel $Q_H(t,s)$ by:

$$Q_H(t,s)=\frac{\sqrt{\pi }}{2^{H-\frac{1}{2}}}{I}_{T-,2,\frac{3-2H}{4}}^{\frac{1}{2}-H}\left(u^{H-\frac{1}{2}}{1}_{[0,t)}\right)\left(s\right),$$

where $I_{T-,2,\frac{3-2H}{4}}^{H-\frac{1}{2}}$ denotes the Erdély–Kober-type fractional integral operator defined by:

$$(I_{T-,\sigma ,\eta }^{\alpha }f)\left(s\right)=\frac{\sigma s^{\sigma \eta }}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_s^T\frac{t^{\sigma (1-\alpha -\eta )-1}f\left(t\right)}{{(t^{\sigma }-s^{\sigma })}^{1-\alpha }}dt,s\in [0,T],\alpha >0,$$

(8)

$$(I_{T-,\sigma ,\eta }^{\alpha }f)\left(s\right)=s^{\sigma \eta }{\left(\frac{-d}{\sigma s^{\sigma -1}ds}\right)}^n{s}^{\sigma (n-\eta )}\left(I_{T-,\sigma ,\eta -n}^{\alpha +n}f\right)\left(s\right),s\in [0,T],\alpha >-n$$

(9)

for all measurable functions $f:[0,T]\mapsto \mathbb{R}$, $\alpha \in \mathbb{R}$, $\sigma ,\eta \in \mathbb{R}$. Some basic properties of this fractional integral can be found in Samko et al. [31]. By using the kernel $Q_H$, we have the Wiener integral representation (in distribution) of sub-fBm $S^H$ as follows:

$$S_t^H={\kappa }_H{\int }_0^1{Q}_H(t,s)d{B}_s,t\in [0,T]$$

(10)

for some standard Brownian motion, where:

$${\kappa }_H=\frac{1}{\pi }\mathsf{\Gamma }\left(2H\right)\sin H.$$

Let $\mathcal{E}$ be the family of elementary functions $f:[0,T]\mapsto \mathbb{R}$ of the form:

$$f=\sum _{j=1}^n{a}_j{1}_{[t_{j-1},t_j)},0=t_0<t_1<t_2<\cdots <t_n=T,a_j\in \mathbb{R}$$

(11)

and let $\mathcal{H}$ be the completion of the linear space $\mathcal{E}$ with respect to the inner product:

$${\langle 1_{[0,s]},1_{[0,t]}\rangle }_{\mathcal{H}}=R_H(t,s).$$

When $\frac{1}{2}<H<1$, we can characterize $\mathcal{H}$ as:

$$\mathcal{H}=\left\{{\phi |\parallel \phi \parallel }_{\mathcal{H}}^2:={\int }_0^T{\int }_0^T\phi \left(t\right)\phi \left(s\right)\varphi (t,s)dsdt<\infty \right\}$$

with $\varphi (t,s)=H(2H-1)\left({|t-s|}^{2H-2}-{|t+s|}^{2H-2}\right)$. When $0<H<\frac{1}{2}$, we have:

$$\mathcal{H}=\left\{f|\exists {\phi }_f\in L^2\left([0,T]\right),I_{T-,2,\frac{2H+1}{4}}^{\frac{1}{2}-H}\left(\frac{2^{H-\frac{1}{2}}}{\sqrt{\pi }}{\phi }_f\right)\left(t\right)=t^{H-\frac{1}{2}}f\left(t\right)\right\}$$

and ${\parallel f\parallel }_{\mathcal{H}}^2={\int }_0^T{\phi }_f{\left(t\right)}^{2}dt$, and:

$${\phi }_f\left(t\right)=I_{T-,2,\frac{3-2H}{4}}^{H-\frac{1}{2}}\left(\frac{\sqrt{\pi }}{2^{H-\frac{1}{2}}}{u}^{H-\frac{1}{2}}f\right)\left(t\right).$$

As usual, we define the linear mapping $\phi \mapsto S^H\left(f\right)$ on $\mathcal{E}$ by:

$$1_{[0,t]}\mapsto S^H\left(1_{[0,t]}\right)=S_t^H\equiv {\int }_0^T{1}_{[0,t]}\left(s\right)d{S}_s^H$$

for all $t\in [0,T]$. Then, the linear mapping is an isometry from $\mathcal{E}$ to the Gaussian space generated by $S^H$, and it can be extended to $\mathcal{H}$ and:

$${\parallel f\parallel }_{\mathcal{H}}^2=E{\left[S^H\left(f\right)\right]}^2$$

for any $f\in \mathcal{H}$, which is called the Wiener integral with respect to $S^H$, denoted by:

$$S^H\left(f\right)={\int }_0^{T}f\left(t\right)d{S}_t^H$$

(12)

for any $f\in \mathcal{H}$. If the Wiener integral ${\int }_0^{T}f\left(t\right)d{S}_t^H$ is well defined for every $T>0$, we then can define the integral:

$${\int }_0^{\infty }f\left(t\right)d{S}_t^H$$

for any $\phi$ satisfying:

$${\parallel f\parallel }_{\mathcal{H}}^2:={\int }_0^{\infty }{\int }_0^{\infty }f\left(t\right)f\left(s\right)\varphi (t,s)dsdt<\infty .$$

Thus, we can call Equation (12) the indefinite Wiener integral. Denote by $\mathcal{S}$ the set of smooth functionals of the form:

$$F=f(S^H\left({\phi }_1\right),S^H\left({\phi }_2\right),\dots ,S^H\left({\phi }_n\right)),$$

(13)

where $f\in C_b^{\infty }\left({\mathbb{R}}^n\right)$ (f and all its derivatives are bounded) and ${\phi }_i\in \mathcal{H}$. Denote by $D^H$ and ${\delta }^H$ the Malliavin derivative and divergence integral operator associated with sub-fractional Brownian motion $S^H$, respectively. Then, we have:

$$D^{H}F=\sum _{j=1}^n\frac{\partial f}{\partial x_j}(S^H\left({\phi }_1\right),S^H\left({\phi }_2\right),\dots ,S^H\left({\phi }_n\right)){\phi }_j.$$

We denote by ${\mathbb{D}}^{1,2}$ the closure of $\mathcal{S}$ with respect to the norm:

$${\parallel F\parallel }_{1,2}:=\sqrt{{E\left|F\right|}^2+E{\parallel D^{H}F\parallel }_{\mathcal{H}}^2}$$

for $F\in \mathcal{S}$. The divergence integral ${\delta }^H$ is the adjoint of derivative operator $D^H$ and:

$$E\left[F{\delta }^H\left(u\right)\right]=E\left[{\langle D^{H}F,u\rangle }_{\mathcal{H}}\right]=E\left[{\int }_0^T{\phi }_u\left(s\right){\phi }_{D^{H}F}\left(s\right)ds\right]$$

(14)

for $F\in {\mathbb{D}}^{1,2}$. We will use the notation:

$${\delta }^H\left(u\right)={\int }_0^T{u}_s\delta S_s^H$$

to express the Skorohod integral of an adapted process u, and the indefinite Skorohod integral is defined as ${\int }_0^t{u}_s\delta S_s^H={\delta }^H\left(u{1}_{[0,t]}\right)$. Clearly, the divergence integral is closed in $L^2$.

Finally, we recall Young’s integration and some results established in Bertoin [32] and Föllmer [33]. A Borel function f on $[a,b]$ is said to be of bounded p-variation with $p\ge 1$ if:

$$v_p(f,[a,b]):=\underset{{▵}_n}{\sup }\sum _{j=1}^n{|f\left(x_j\right)-f\left(x_{j-1}\right)|}^p<\infty ,$$

where the supremum is taken over all partitions ${▵}_n=\{a=x_0<x_1<\cdots <x_n=b\}$ of $[a,b]$. The estimates Equation (4) and the normality imply that the sub-fractional Brownian motion $t\mapsto S_t^H$ admits almost surely a bounded $\frac{1}{H-\theta }$-variation on any finite interval for any sufficiently small $\theta \in (0,H)$. That is, we have:

$$v_{p_H}(S^H,[0,t])<\infty$$

for all $t>0$ and $p_H>\frac{1}{H}$. The definition of p-variation for processes is slightly different. We say that the continuous adapted process Z has a locally-bounded p-variation if there exists an increasing sequence of stopping times $\{T_n,n\ge 0\}$ such that $T_n\uparrow \infty$, a.s., as $n\to \infty$ and $Z^{T_n}$ has a bounded p-variation for all n. It is easy to prove that if Y is an adapted continuous process, such that for P-a.s. $\omega \in \mathsf{\Omega }$ and all positive $t\ge 0$, the function $t\mapsto Y_t\left(\omega \right)$ has a bounded p-variation on $[0,t]$, then the process Y has a locally-bounded p-variation.

Let X and Y be two adapted continuous processed with locally-bounded p and q variations, respectively, such that $1/p+1/q>1$, then one can define (see, for example, Bertoin [32]):

$$Z_t:={\int }_0^t{Y}_{s}d{X}_s,t\ge 0,$$

as the limit in probability of a Riemann sum, which generalizes the usual integral when X or Y are semimartingales, and Z has a locally-bounded p-variation. Moreover, Bertoin [32] showed that $Y^{\prime }Y$ has a locally-bounded q-variation and:

$${\int }_0^t{Y}_s^{\prime }{Y}_{s}d{X}_s={\int }_0^t{Y}_s^{\prime }d{Z}_s,$$

provided $Y^{\prime }$ is an adapted continuous process with locally-bounded q-variation.

Lemma 1

(Föllmer [33]). Let U and V be two continuous adapted processes with locally-bounded p-variation ($1\le p<2$). Then, $\frac{\partial }{\partial x}f(U_s,V_s)$ and $\frac{\partial }{\partial y}f(U_s,V_s)$ have locally-bounded two-variations, and It’s formula:

$$f(U_t,V_t)=f(U_0,V_0)+{\int }_0^t\frac{\partial }{\partial x}f(U_s,V_s)d{U}_s+{\int }_0^t\frac{\partial }{\partial y}f(U_s,V_s)d{V}_s$$

(15)

holds for all $f\in C^{2\times 2}\left({\mathbb{R}}^2\right)$. In particular, we have the integration by parts formula:

$$U_t{V}_t-U_0{V}_0={\int }_0^t{U}_{s}d{V}_s+{\int }_0^t{V}_{s}d{U}_s$$

(16)

for all $t\ge 0$.

Corollary 1.

Let $\frac{1}{2}<H<1$. If u is a continuous adapted process with bounded q-variations with $1\le q<2$, then Young’s integral:

$${\int }_0^t{u}_{s}d{S}_s^H$$

is well-defined and:

$$u_t{S}_t^H={\int }_0^t{u}_{s}d{S}_s^H+{\int }_0^t{S}_s^{H}d{u}_s$$

for all $t\ge 0$.

Corollary 2

(Alós et al. [29]). Let $\frac{1}{2}<H<1$. If u is a continuous adapted process with bounded q-variations with $1\le q<2$ and $u\in \mathrm{Dom}\left({\delta }^H\right)$, we then have:

$${\int }_0^t{u}_{s}d{S}_s^H={\int }_0^t{u}_s\delta S_s^H+{\int }_0^t{\int }_0^t{D}_r^H{u}_s\varphi (s,r)drds$$

(17)

for all $t\ge 0$.

3. The Consistency of the Least Squares Estimator

In this section, our main objective is to expound and to prove the next theorem, which gives the consistency of the estimators given by Equations (5) and (6).

Theorem 1.

For $H\in (\frac{1}{2},1)$, we have:

(1) 

${\widehat{\theta }}_T\to \theta$, as T tends to infinity, almost surely.

(2) 

${\widehat{\mu }}_T\to \mu$, as T tends to infinity, almost surely.

From Equation (2), one can easily get:

$$X_t=\frac{\mu }{\theta }(e^{\theta t}-1)+e^{\theta t}{\int }_0^t{e}^{-\theta s}d{S}_s^H=\frac{\mu }{\theta }(e^{\theta t}-1)+S_t^H+\theta e^{\theta t}{Z}_t$$

(18)

for all $t\ge 0$, where $Z_t={\int }_0^t{e}^{-\theta s}{S}_s^{H}ds$. For convenience, we denote:

$$\begin{array}{c}\hfill f\left(t\right)=\frac{\mu }{\theta }(e^{\theta t}-1)\mathrm{and}{Y}_t={\int }_0^t{e}^{-\theta s}d{S}_s^H.\end{array}$$

Then, Equation (18) can be rewritten as below:

$$\begin{array}{c}\hfill X_t=f\left(t\right)+e^{\theta t}{Y}_t=f\left(t\right)+S_t^H+\theta e^{\theta t}{Z}_t.\end{array}$$

It follows from the above equation that:

$$Y_t=e^{-\theta t}{S}_t^H+\theta Z_t,$$

(19)

for all $t\ge 0$.

Lemma 2

(Lemma 2.1 in El Machkouri et al. [14]). Let $H\in (\frac{1}{2},1)$. Then, the sub-fractional OUprocess is γ-Hölder continuous for all $\gamma <H$, and the Young integral:

$${\int }_0^t{u}_{s}d{X}_s=u_t{X}_t-u_0{X}_0-{\int }_0^t{X}_{s}d{u}_s$$

is well-defined for all $t\ge 0$ if u is an adapted continuous process with bounded p-variation with $1\le p<\frac{1}{1-H+\vartheta }$ for any sufficiently small $ϵ\in (0,H)$. Moreover,

$$Z_T⟶Z_{\infty }={\int }_0^{\infty }{e}^{-\theta r}{S}_r^{H}dr$$

almost surely and in $L^2\left(\mathsf{\Omega }\right)$, as T tends to infinity. Thus, as $T\to \infty$,

$$Y_T⟶Y_{\infty }=\theta Z_{\infty }$$

almost surely and in $L^2\left(\mathsf{\Omega }\right)$.

Lemma 3

(Hu-Nualart [10]). For all $\frac{1}{2}<H<1$, we have:

$${\int }_0^{\infty }{\int }_0^{\infty }{e}^{-\theta (u+v)}{|u-v|}^{2H-2}dudv=\frac{{\theta }^{-2H}}{(2H-1)}\mathsf{\Gamma }\left(2H\right).$$

(20)

Lemma 4.

Let $H\in (\frac{1}{2},1)$. We then have that:

$$\underset{T\to \infty }{\lim }{e}^{-2\theta T}{\int }_0^T{f}^2\left(s\right)ds=\frac{{\mu }^2}{2{\theta }^3}$$

(21)

Proof of Lemma 4.

This is a simple calculus exercise.  ☐

Corollary 3.

Let $H\in (\frac{1}{2},1)$. We then have that:

$$\begin{array}{c}{e}^{-\theta T}{\int }_0^T{X}_{s}ds⟶\frac{\mu }{{\theta }^2}+\frac{1}{\theta }{Y}_{\infty }\hfill \end{array}$$

(22)

$$\begin{array}{c}{e}^{-2\theta t}{\int }_0^t{X}_s^{2}ds⟶\frac{1}{2\theta }{\left(\frac{\mu }{\theta }+Y_{\infty }\right)}^2\hfill \end{array}$$

(23)

almost surely, and in $L^2\left(\mathsf{\Omega }\right)$, as T tends to infinity.

Proof of Corollary 3.

By Lemma 2, Equation (21), and L’Hôpital’s rule, we get that:

$$\begin{array}{c}{e}^{-2\theta T}{\int }_0^T{e}^{2\theta s}{Y}_s^{2}ds⟶\frac{1}{2\theta }{\left(Y_{\infty }\right)}^2,\hfill \\ e^{-2\theta T}{\int }_0^T{e}^{\theta s}f\left(s\right)Y_{s}ds⟶\frac{\mu }{2{\theta }^2}{Y}_{\infty },\hfill \\ e^{-2\theta T}{\int }_0^T{X}_s^{2}ds⟶\frac{1}{2\theta }{\left(\frac{\mu }{\theta }+Y_{\infty }\right)}^2,\hfill \end{array}$$

almost surely, as T tends to infinity. Thus, the lemma follows from Equation (18).  ☐

Lemma 5.

Let $H\in (\frac{1}{2},1)$. Then, the convergence:

$$\frac{1}{T}{S}_T^H,\frac{1}{T}{e}^{-\theta T}{\int }_0^T{S}_t^H{Y}_t{e}^{\theta t}dt,\frac{1}{T}{e}^{-\theta T}{\int }_0^T{e}^{\theta t}d{S}_t^H⟶0$$

hold almost surely and in $L^2$, as T tends to infinity.

Proposition 1.

Let $H\in (\frac{1}{2},1)$. We have that:

$$\begin{array}{c}\hfill \frac{1}{T}{e}^{-\theta T}\left({\int }_0^T{X}_s^{2}ds-\frac{1}{2}{X}_T{\int }_0^T{X}_{s}ds\right)⟶\frac{{\mu }^2}{2{\theta }^2}+\frac{\mu }{2\theta }{Y}_{\infty }\end{array}$$

(24)

almost surely, as T tends to infinity.

Proof of Proposition 1.

By Equation (18) and Lemma 1, we have:

$$\begin{array}{cc}\hfill \frac{1}{T}& e^{-\theta T}\left({\int }_0^T{X}_t^{2}dt-\frac{1}{2}{X}_T{\int }_0^T{X}_{t}dt\right)\hfill \\ & =\frac{1}{T}{e}^{-\theta T}\left({\int }_0^T{\left(f\left(t\right)+e^{\theta t}{Y}_t\right)}^{2}dt-\frac{1}{2}\left(f\left(T\right)+e^{\theta T}{Y}_T\right){\int }_0^T\left(f\left(t\right)+e^{\theta t}{Y}_t\right)dt\right)\hfill \\ & =\frac{1}{T}{e}^{-\theta T}\left({\int }_0^{T}f{\left(t\right)}^{2}dt-\frac{1}{2}f\left(T\right){\int }_0^{T}f\left(t\right)dt\right)\hfill \\ & +\frac{1}{T}{e}^{-\theta T}\left({\int }_0^T{e}^{2\theta t}{Y}_t^{2}dt-\frac{1}{2}{e}^{\theta T}{Y}_T{\int }_0^T{e}^{\theta t}{Y}_{t}dt\right)\hfill \\ & +\frac{1}{T}{e}^{-\theta T}\left(2{\int }_0^{T}f\left(t\right)e^{\theta t}{Y}_{t}dt-\frac{1}{2}{e}^{\theta T}{Y}_T{\int }_0^{T}f\left(t\right)dt-\frac{1}{2}f\left(T\right){\int }_0^T{e}^{\theta t}{Y}_{t}dt\right)\hfill \\ & \equiv {\mathsf{\Lambda }}_1\left(T\right)+{\mathsf{\Lambda }}_2\left(T\right)+{\mathsf{\Lambda }}_3\left(T\right)\hfill \end{array}$$

(25)

for all $T>0$. Clearly, an elementary calculus can show that:

$$\begin{array}{cc}\hfill {\mathsf{\Lambda }}_1\left(T\right)& =\frac{1}{T}{e}^{-\theta T}\left({\int }_0^{T}f{\left(t\right)}^{2}dt-\frac{1}{2}f\left(T\right){\int }_0^{T}f\left(t\right)dt\right)\hfill \\ & =\frac{{\mu }^2}{{\theta }^{2}T}{e}^{-\theta T}\left({\int }_0^T{(e^{\theta t}-1)}^{2}dt-\frac{1}{2}(e^{\theta T}-1){\int }_0^T(e^{\theta t}-1)dt\right)\hfill \\ & =\frac{{\mu }^2}{{\theta }^{2}T}{e}^{-\theta T}\left(\frac{1}{\theta }-\frac{1}{\theta }{e}^{\theta T}+\frac{1}{2}T+\frac{1}{2}T{e}^{\theta T}\right)⟶\frac{{\mu }^2}{2{\theta }^2},\hfill \end{array}$$

as T tends to infinity. For ${\mathsf{\Lambda }}_2\left(T\right)$, we have:

$$\begin{array}{cc}\hfill {\int }_0^T{e}^{\theta t}{Y}_{t}dt& =\frac{1}{\theta }{\int }_0^T{Y}_{t}d{e}^{\theta t}\hfill \\ & =\frac{1}{\theta }\left(Y_T{e}^{\theta T}-{\int }_0^T{e}^{\theta t}d{Y}_t\right)=\frac{1}{\theta }\left(Y_T{e}^{\theta T}-S_T^H\right)\hfill \end{array}$$

by integration by parts, which gives:

$$\begin{array}{cc}\hfill {\int }_0^T{e}^{2\theta t}{Y}_t^{2}dt& ={\int }_0^T{e}^{\theta t}{Y}_{t}d\left({\int }_0^t{e}^{\theta s}{Y}_{s}ds\right)=\frac{1}{\theta }{\int }_0^T{e}^{\theta t}{Y}_{t}d\left(Y_t{e}^{\theta t}-S_t^H\right)\hfill \\ & =\frac{1}{\theta }{\int }_0^T{e}^{\theta t}{Y}_{t}d\left(Y_t{e}^{\theta t}\right)-{\int }_0^T{e}^{\theta t}{Y}_{t}d{S}_t^H\hfill \\ & =\frac{1}{2\theta }{\left(e^{\theta T}{Y}_T\right)}^2-e^{\theta T}{Y}_T{S}_T^H+{\int }_0^T{S}_t^{H}d\left(e^{\theta t}{Y}_t\right)\hfill \\ & =\frac{1}{2\theta }{\left(e^{\theta T}{Y}_T\right)}^2-e^{\theta T}{Y}_T{S}_T^H+\theta {\int }_0^T{S}_t^H{Y}_t{e}^{\theta t}dt+{\int }_0^T{S}_t^{H}d{S}_t^H\hfill \\ & =\frac{1}{2\theta }{\left(e^{\theta T}{Y}_T\right)}^2-e^{\theta T}{Y}_T{S}_T^H+\theta {\int }_0^T{S}_t^H{Y}_t{e}^{\theta t}dt+\frac{1}{2}{\left(S_T^H\right)}^2\hfill \end{array}$$

for all $T>0$ by integration by parts. It follows from Lemma 1 and Lemma 5 that:

$$\begin{array}{cc}\hfill {\mathsf{\Lambda }}_2\left(T\right)& =\frac{1}{T}{e}^{-\theta T}\left({\int }_0^T{e}^{2\theta t}{Y}_t^{2}dt-\frac{1}{2}{e}^{\theta T}{Y}_T{\int }_0^T{e}^{\theta t}{Y}_{t}dt\right)\hfill \\ & =\frac{1}{T}{e}^{-\theta T}\left(-e^{\theta T}{Y}_T{S}_T^H+\theta {\int }_0^T{S}_t^H{Y}_t{e}^{\theta t}dt+\frac{1}{2}{\left(S_T^H\right)}^2+\frac{1}{\theta }{S}_T^H{e}^{\theta T}{Y}_T\right)\hfill \\ & ⟶0,\hfill \end{array}$$

almost surely, as T tends to infinity. For ${\mathsf{\Lambda }}_3\left(T\right)$, we have:

$$\begin{array}{cc}\hfill {\mathsf{\Lambda }}_{31}\left(T\right):& =2{\int }_0^T\left(e^{\theta t}-1\right)e^{\theta t}{Y}_{t}dt=2{\int }_0^T{e}^{2\theta t}{Y}_{t}dt-2{\int }_0^T{e}^{\theta t}{Y}_{t}dt\hfill \\ & =\frac{1}{\theta }\left(e^{2\theta T}{Y}_T-{\int }_0^T{e}^{2\theta t}d{Y}_t\right)-2{\int }_0^T{e}^{\theta t}{Y}_{t}dt\hfill \\ & =\frac{1}{\theta }\left(e^{2\theta T}{Y}_T-{\int }_0^T{e}^{\theta t}d{S}_t^H\right)-2{\int }_0^T{e}^{\theta t}{Y}_{t}dt\hfill \end{array}$$

and:

$$\begin{array}{cc}\hfill {\mathsf{\Lambda }}_{32}\left(T\right):& =\frac{1}{2}{e}^{\theta T}{Y}_T{\int }_0^T\left(e^{\theta t}-1\right)dt+\frac{1}{2}{e}^{\theta T}{Y}_T{\int }_0^T\left(e^{\theta t}-1\right)dt\hfill \\ & =\left(\frac{1}{2\theta }{e}^{2\theta T}{Y}_T-\frac{T}{2}{e}^{\theta T}{Y}_T\right)+\left(\frac{1}{2}{e}^{\theta T}{\int }_0^T{e}^{\theta t}{Y}_{t}dt-\frac{1}{2}{\int }_0^T{e}^{\theta t}{Y}_{t}dt\right)\hfill \\ & =\left(\frac{1}{2\theta }{e}^{2\theta T}{Y}_T-\frac{T}{2}{e}^{\theta T}{Y}_T\right)+\left(\frac{1}{2\theta }{e}^{2\theta T}{Y}_T-\frac{1}{2\theta }{e}^{\theta T}{\int }_0^T{e}^{\theta t}d{Y}_t-\frac{1}{2}{\int }_0^T{e}^{\theta t}{Y}_{t}dt\right)\hfill \\ & =\frac{1}{\theta }{e}^{2\theta T}{Y}_T-\frac{T}{2}{e}^{\theta T}{Y}_T-\frac{1}{2\theta }{e}^{\theta T}{S}_T^H-\frac{1}{2}{\int }_0^T{e}^{\theta t}{Y}_{t}dt\hfill \end{array}$$

for all $T>0$ by integration by parts. It follows from Lemma 1 and Lemma 5 that:

$$\begin{array}{cc}\hfill {\mathsf{\Lambda }}_3\left(T\right)& =\frac{1}{T}{e}^{-\theta T}\left(2{\int }_0^{T}f\left(t\right)e^{\theta t}{Y}_{t}dt-\frac{1}{2}{e}^{\theta T}{Y}_T{\int }_0^{T}f\left(t\right)dt-\frac{1}{2}f\left(T\right){\int }_0^T{e}^{\theta t}{Y}_{t}dt\right)\hfill \\ & =\frac{\mu }{\theta T}{e}^{-\theta T}\left(2{\int }_0^T\left(e^{\theta t}-1\right)e^{\theta t}{Y}_{t}dt-\frac{1}{2}{e}^{\theta T}{Y}_T{\int }_0^T\left(e^{\theta t}-1\right)dt-\frac{1}{2}\left(e^{\theta T}-1\right){\int }_0^T{e}^{\theta t}{Y}_{t}dt\right)\hfill \\ & =\frac{\mu }{\theta T}{e}^{-\theta T}\left({\mathsf{\Lambda }}_{31}\left(T\right)-{\mathsf{\Lambda }}_{32}\left(T\right)\right)\hfill \\ & =\frac{\mu }{\theta T}{e}^{-\theta T}\left(-\frac{1}{\theta }{\int }_0^T{e}^{\theta t}d{S}_t^H-2{\int }_0^T{e}^{\theta t}{Y}_{t}dt+\frac{T}{2}{e}^{\theta T}{Y}_T+\frac{1}{2\theta }{e}^{\theta T}{S}_T^H+\frac{1}{2}{\int }_0^T{e}^{\theta t}{Y}_{t}dt\right)\hfill \\ & ⟶\frac{\mu }{2\theta }{Y}_{\infty },\hfill \end{array}$$

almost surely, as T tends to infinity. Thus, we have showed that:

$$\begin{array}{cc}\hfill \frac{1}{T}{e}^{-\theta T}\left({\int }_0^T{X}_t^{2}dt-\frac{1}{2}{X}_T{\int }_0^T{X}_{t}dt\right)& ={\mathsf{\Lambda }}_1\left(T\right)+{\mathsf{\Lambda }}_2\left(T\right)+{\mathsf{\Lambda }}_3\left(T\right)\hfill \\ & ⟶\frac{{\mu }^2}{2{\theta }^2}+\frac{\mu }{2\theta }{Y}_{\infty }\hfill \end{array}$$

by Equation (25), almost surely, as T tends to infinity.  ☐

Now, we can prove Theorem 1.

Proof of Theorem 1.

Denote:

$${\mathsf{\Psi }}_t=t{\int }_0^t{X_s}^{2}ds-{\left({\int }_0^t{X}_{s}ds\right)}^2$$

for $t>0$. By Equation (18) and Lemma 1, we obtain:

$$\begin{array}{c}{e}^{-\theta T}{X}_T=\frac{\mu }{\theta }{e}^{-\theta T}(e^{\theta T}-1)+{\int }_0^T{e}^{-\theta s}d{S}_s^H⟶\frac{\mu }{\theta }+Y_{\infty },\hfill \\ \frac{1}{T}{e}^{-2\theta T}{X}_T{\int }_0^T{X}_{s}ds=\frac{1}{T}\left(e^{-\theta T}{X}_T\right)\left(e^{-\theta T}{\int }_0^T{X}_{s}ds\right)⟶0\hfill \end{array}$$

and:

$$\frac{1}{T}{e}^{-2\theta T}{\mathsf{\Psi }}_T=e^{-2\theta T}{\int }_0^T{X_s}^{2}ds-\frac{1}{T}{e}^{-2\theta T}{\left({\int }_0^T{X}_{s}ds\right)}^2⟶\frac{1}{2\theta }{\left(\frac{\mu }{\theta }+Y_{\infty }\right)}^2$$

(26)

almost surely, as T tends to infinity, which imply that:

$${\widehat{\theta }}_T=\frac{\frac{1}{2}{e}^{-2\theta T}{\left(X_T\right)}^2-\frac{1}{T}{e}^{-2\theta T}{X}_T{\int }_0^T{X}_{s}ds}{\frac{1}{T}{e}^{-2\theta T}{\mathsf{\Psi }}_T}⟶\theta ,$$

(27)

almost surely, as T tends to infinity.

On the other hand, we have:

$$e^{-\theta T}{X}_T=e^{-\theta T}\left((e^{\theta T}-1)+e^{\theta T}{\int }_0^T{e}^{-\theta t}d{S}_t^H\right)⟶\frac{\mu }{\theta }+Y_{\infty },$$

almost surely, as T tends to infinity. Combining this with Proposition 1 and Equation (26), we get:

$$\begin{array}{cc}\hfill {\widehat{\mu }}_T& =\left(e^{-\theta T}{X}_T\right)\frac{\frac{1}{T}{e}^{-\theta T}\left({\int }_0^T{X_s}^{2}ds-\frac{1}{2}{X}_T{\int }_0^T{X}_{s}ds\right)}{\frac{1}{T}{e}^{-2\theta T}{\mathsf{\Psi }}_T}⟶\mu ,\hfill \end{array}$$

almost surely, as T tends to infinity. Thus, we have completed the proof.  ☐

4. Asymptotic Distribution of the Least Squares Estimator

In this section, we consider the asymptotic normality of the LSE $\widehat{\mu }$ and $\widehat{\theta }$. We start with some preliminaries and let $H>\frac{1}{2}$.

Lemma 6

(El Machkouri et al [14]). Let F be any ${\mathcal{F}}^H=\sigma \left(\{S_t^H,t\ge 0\}\right)$-measurable random variable such that $P(F<\infty )=1$. Then, we have:

$$\begin{array}{c}\hfill \left(F,e^{-\theta T}{\int }_0^T{e}^{\theta s}d{S}_s^H\right)\stackrel{law}{⟶}(F,{\theta }^{-2H}{\lambda }_H\xi ),\end{array}$$

as $T\to \infty$, where $\xi \sim \mathcal{N}(0,1)$ is independent of $S^H$ and ${\lambda }_H=H\mathsf{\Gamma }\left(2H\right)$.

Proof of Lemma 6.

The lemma is introduced in El Machkouri et al. [14]. In fact, we need to check that:

$$E{\left(e^{-\theta T}{\int }_0^T{e}^{\theta s}d{S}_s^H\right)}^2⟶\ell \left(H\right)={\theta }^{-2H}{\lambda }_H$$

and:

$$E{\left(e^{-\theta T}{S}_T^H{\int }_0^T{e}^{\theta s}d{S}_s^H\right)}^2⟶0$$

for all fixed $s\ge 0$, as T tends to infinity. However, the proof of the first convergence given by them is incomplete.

In order to introduce the first convergence, by Lemma 3, we have that:

$$\begin{array}{cc}\hfill \ell \left(H\right)& =H(2H-1)\underset{T\to \infty }{\lim }{\int }_0^T{\int }_0^T{e}^{-\theta (T-s)}{e}^{-\theta (T-r)}\left({|s-r|}^{2H-2}-{|s+r|}^{2H-2}\right)dsdr\hfill \\ & =H(2H-1)\underset{T\to \infty }{\lim }{\int }_0^T{\int }_0^T{e}^{-\theta (T-s)}{e}^{-\theta (T-r)}{|s-r|}^{2H-2}dsdr\hfill \\ & -H(2H-1)\underset{T\to \infty }{\lim }{\int }_0^T{\int }_0^T{e}^{-\theta (T-s)}{e}^{-\theta (T-r)}{|s+r|}^{2H-2}dsdr\hfill \\ & =H{\theta }^{-2H}\mathsf{\Gamma }\left(2H\right)-H(2H-1)\underset{T\to \infty }{\lim }{\int }_0^T{\int }_0^T{e}^{-\theta (T-s)}{e}^{-\theta (T-r)}{|s+r|}^{2H-2}dsdr.\hfill \end{array}$$

Notice that:

$$\begin{array}{cc}\hfill {\int }_0^T{\int }_0^T{e}^{-\theta (T-s)}& e^{-\theta (T-r)}{|s+r|}^{2H-2}dsdr={\int }_0^T{\int }_0^T{e}^{-\theta x}{e}^{-\theta y}{|2T-x-y|}^{2H-2}dxdy\hfill \\ & \le {\int }_0^T{\int }_0^T{e}^{-\theta x}{e}^{-\theta y}{(T-x)}^{2H-2}dxdy\hfill \\ & =\frac{1}{\theta }{\int }_0^T{e}^{-\theta x}{(T-x)}^{2H-2}dx\left(1-e^{-\theta T}\right)\le \frac{1}{\theta }{e}^{-\theta T}{\int }_0^T{e}^{\theta s}{s}^{2H-2}ds\hfill \\ & ⟶0,\hfill \end{array}$$

as T tends to infinity. We get $\ell \left(H\right)=H{\theta }^{-2H}\mathsf{\Gamma }\left(2H\right)={\theta }^{-2H}{\lambda }_H$, and the lemma follows.

Lemma 7

(I. Mendy [13]). Suppose that $H>\frac{1}{2}$. Then, as $t\to \infty$,

$$e^{\frac{-\theta T}{2}}{\int }_0^T\delta S_s^H{e}^{-\theta s}{\int }_0^s\delta S_r^H{e}^{\theta r}⟶0$$

(28)

in $L^2\left(\mathsf{\Omega }\right)$ and:

$$e^{\frac{-\theta T}{2}}{\int }_0^{T}ds{e}^{-\theta s}{\int }_0^{s}dr{e}^{\theta r}{\varphi }_H(s,r)⟶0,$$

(29)

as $T\to \infty$.

Theorem 2.

For $\frac{1}{2}<H<1$, the convergence:

$$e^{\theta T}({\widehat{\theta }}_T-\theta )⟶\frac{2\theta {\lambda }_H}{{\lambda }_H-{\vartheta }_H}·\frac{\xi }{\eta +\frac{\mu }{\theta }{({\lambda }_H-{\vartheta }_H)}^{-1}},$$

(30)

$$T\left({\widehat{\mu }}_T-\mu -\frac{1}{T}{S}_T^H\right)⟶2{\lambda }_H\xi$$

(31)

and:

$$T^{1-H}\left(\widehat{{\mu }_T}-\mu \right)⟶\zeta$$

(32)

hold in distribution, as T tends to infinity, where $\xi ,\eta \sim N(0,1)$ are mutually independent, $\zeta \sim N(0,2-2^{H-1})$, and:

$${\vartheta }_H=H(2H-1){\int }_0^{\infty }{\int }_0^{\infty }{e}^{-(s+r)}{(s+r)}^{2H-2}dsdr.$$

Remark 1.

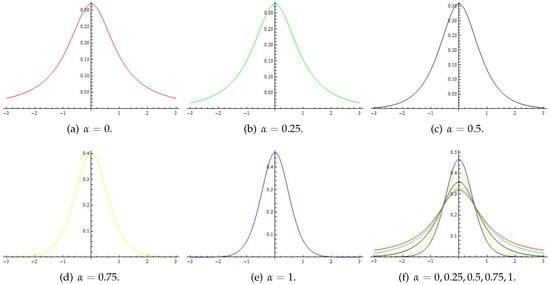
It is not difficult to show that the density of $\vartheta =\frac{\xi }{\eta +\alpha }$ is:

$$f_{\vartheta }(x,\alpha )=\frac{1}{2\pi }{e}^{-\frac{x^2}{2(1+x^2)}{\alpha }^2}{\int }_{\mathbb{R}}{e}^{-\frac{1}{2}(1+x^2)y^2}\left|y+\frac{\alpha }{1+x^2}\right|dy,$$

where $\xi ,\eta \sim N(0,1)$ are mutually independent and $\alpha \in \mathbb{R}$. In particular, as we know that $\frac{\xi }{\eta }$ admits a standard Cauchy distribution, provided $\alpha =0$, when $\alpha \ne 0$, we have:

$$f_{\vartheta }(x,\alpha )=\frac{{\alpha }^2}{2\pi {(1+x^2)}^2}{e}^{-\frac{x^2}{2(1+x^2)}{\alpha }^2}{\int }_{\mathbb{R}}{e}^{-\frac{{\alpha }^2}{2(1+x^2)}{y}^2}|1+y|dy.$$

The next figures give the plots of the density functions $f_{\vartheta }(x,\alpha )$ with $\alpha =0,0.25,0.5,0.75,1$, respectively, and in Figure 1f, we give the graphs of the five density functions in a common coordinate system.

Proof of Theorem 2.

We first introduce the convergence Equation (30). Recall that:

$${\mathsf{\Psi }}_t=t{\int }_0^t{X_s}^{2}ds-\left({\int }_0^t{X}_{s}ds\right)$$

for $t>0$. It follows from the identities:

$$X_T{\int }_0^T{X}_{s}ds=\left(S_T^H+\mu T+\theta {\int }_0^T{X}_{s}ds\right){\int }_0^T{X}_{s}ds$$

and:

$${\int }_0^T{X}_{s}d{X}_s={\int }_0^T{X}_{s}d{S}_s^H+\mu {\int }_0^T{X}_{s}ds+\theta {\int }_0^T{\left(X_s\right)}^{2}ds$$

that:

$$\begin{array}{cc}\hfill \widehat{\theta }-\theta & =\frac{T{\int }_0^T{X}_{s}d{X}_s-X_T{\int }_0^T{X}_{s}ds}{{\mathsf{\Psi }}_T}-\theta \hfill \\ & =\frac{1}{{\mathsf{\Psi }}_T}\left(T{\int }_0^T{X}_{s}d{X}_s-X_T{\int }_0^T{X}_{s}ds-\theta T{\int }_0^T{X}_s^{2}ds+\theta {\left({\int }_0^T{X}_{s}ds\right)}^2\right)\hfill \\ & =\frac{1}{{\mathsf{\Psi }}_T}\left(T{\int }_0^T{X}_{s}d{S}_s^H-S_T^H{\int }_0^T{X}_{s}ds\right)\hfill \\ & =\frac{1}{{\mathsf{\Psi }}_T}\left(T{\int }_0^T(f\left(s\right)+e^{\theta s}{Y}_s)d{S}_s^H-S_T^H{\int }_0^T{X}_{s}ds\right)\hfill \\ & =\frac{T}{{\mathsf{\Psi }}_T}{\int }_0^T\left(e^{\theta s}{Y}_s+f\left(s\right)\right)d{S}_s^H-\frac{1}{{\mathsf{\Psi }}_T}\left(S_T^H{\int }_0^T{X}_{s}ds\right)\hfill \\ & =\frac{T}{{\mathsf{\Psi }}_T}\left({\int }_0^T{e}^{\theta s}{Y}_{s}d{S}_s^H+\frac{\mu }{\theta }{\int }_0^T{e}^{\theta s}d{S}_s^H\right)-\frac{T}{{\mathsf{\Psi }}_T}{S}_T^H-\frac{1}{{\mathsf{\Psi }}_T}\left(S_T^H{\int }_0^T{X}_{s}ds\right)\hfill \\ & \equiv B_1\left(T\right)-B_2\left(T\right)-B_3\left(T\right)\hfill \end{array}$$

(33)

for all $T>0$. Clearly, we have $e^{-\theta T}{S}_T^H\to 0$ and:

$$\begin{array}{c}\hfill \frac{1}{T}{e}^{-\theta T}\left(S_T^H{\int }_0^T{X}_{s}ds\right)⟶0\end{array}$$

almost surely, as $T\to \infty$, by Lemma 5 and Equation (22), which imply that:

$$e^{\theta T}{B}_2\left(T\right)=\frac{1}{T^{-1}{e}^{-2\theta T}{\mathsf{\Psi }}_T}·e^{-\theta T}{S}_T^H⟶0$$

(34)

and:

$$e^{\theta T}{B}_3\left(T\right)=\frac{1}{T^{-1}{e}^{-2\theta T}{\mathsf{\Psi }}_T}·\frac{1}{T}{e}^{-\theta T}\left(S_T^H{\int }_0^T{X}_{s}ds\right)⟶0$$

(35)

almost surely, as $T\to \infty$ by Equation (26). To prove the statement Equation (30), we need to estimate:

$$\begin{array}{cc}\hfill e^{\theta T}{B}_1\left(T\right)& =\frac{T}{{\mathsf{\Psi }}_T}{e}^{\theta T}\left({\int }_0^T{e}^{\theta s}{Y}_{s}d{S}_s^H+\frac{\mu }{\theta }{\int }_0^T{e}^{\theta s}d{S}_s^H\right).\hfill \end{array}$$

Notice that:

$$\begin{array}{cc}\hfill {\int }_0^T& e^{\theta s}{Y}_{s}d{S}_s^H={\int }_0^T{e}^{\theta s}\left({\int }_0^s{e}^{-\theta r}d{S}_r^H\right)d{S}_s^H\hfill \\ & ={\int }_0^T{e}^{\theta s}\left({\int }_0^{T}d{S}_r^H{e}^{-\theta r}\right)d{S}_s^H-{\int }_0^T{e}^{\theta s}\left({\int }_0^s{e}^{-\theta r}d{S}_r^H\right)d{S}_s^H\hfill \\ & ={\int }_0^T{e}^{\theta s}\left({\int }_0^{T}d{S}_r^H{e}^{-\theta r}\right)d{S}_s^H\hfill \\ & -{\int }_0^T\left({\int }_0^s{e}^{-\theta r}\delta S_r^H\right)e^{\theta s}\delta S_s^H-{\int }_0^T{\int }_0^T{D}_r^H\left(e^{-\theta s}{\int }_0^s{e}^{\theta x}\delta S_x^H\right){\varphi }_H(r,s)drds\hfill \\ & =Y_T{\int }_0^T{e}^{\theta s}d{S}_s^H\hfill \\ & -{\int }_0^T\left({\int }_0^s{e}^{-\theta r}\delta S_r^H\right)e^{\theta s}\delta S_s^H-{\int }_0^T{e}^{-\theta s}ds{\int }_0^s{e}^{\theta r}{\varphi }_H(r,s)dr\hfill \end{array}$$

for every $T\ge 0$ by the relationship Equation (17). We see that:

$$\begin{array}{cc}\hfill e^{\theta T}{B}_1\left(T\right)& =\frac{e^{-\theta T}}{\frac{1}{T}{e}^{-2\theta T}{\mathsf{\Psi }}_T}\left({\int }_0^T{e}^{\theta s}{Y}_{s}d{S}_s^H+\frac{\mu }{\theta }{\int }_0^T{e}^{\theta s}d{S}_s^H\right)\hfill \\ & =\frac{e^{-\theta T}}{\frac{1}{T}{e}^{-2\theta T}{\mathsf{\Psi }}_T}\left(Y_T{\int }_0^T{e}^{\theta s}d{S}_s^H+\frac{\mu }{\theta }{\int }_0^T{e}^{\theta s}d{S}_s^H\right)\hfill \\ & -\frac{e^{-\theta T}}{\frac{1}{T}{e}^{-2\theta T}{\mathsf{\Psi }}_T}{\int }_0^T\left({\int }_0^s{e}^{-\theta r}\delta S_r^H\right)e^{\theta s}\delta S_s^H\hfill \\ & -\frac{e^{-\theta T}}{\frac{1}{T}{e}^{-2\theta T}{\mathsf{\Psi }}_T}{\int }_0^t{e}^{-\theta s}ds{\int }_0^s{e}^{\theta r}{\varphi }_H(r,s)dr\hfill \\ & \equiv B_{11}\left(T\right)-B_{12}\left(T\right)-B_{13}\left(T\right)\hfill \end{array}$$

(36)

for all $T\ge 0$. Clearly, Lemma 7 and Equation (26) imply that the convergence:

$$B_{12}\left(T\right),B_{13}\left(T\right)⟶0$$

(37)

holds almost surely, as $T\to \infty$. For $B_{11}\left(T\right)$, by Lemma 6, we have also that:

$$\begin{array}{cc}\hfill B_{11}\left(T\right)& =\frac{e^{-\theta T}}{\frac{1}{T}{e}^{-2\theta T}{\mathsf{\Psi }}_T}\left(Y_T+\frac{\mu }{\theta }\right){\int }_0^T{e}^{\theta s}d{S}_s^H\hfill \\ & =\left\{\frac{1}{\frac{1}{T}{e}^{-2\theta T}{\mathsf{\Psi }}_T}\left(Y_T+\frac{\mu }{\theta }\right)\left(Y_{\infty }+\frac{\mu }{\theta }\right)\right\}·\frac{e^{-\theta T}{\int }_0^T{e}^{\theta s}d{S}_s^H}{Y_{\infty }+\frac{\mu }{\theta }}\hfill \\ & ⟶2\theta \frac{{\lambda }_H}{{\lambda }_H-{\vartheta }_H}·\frac{\xi }{\eta +\frac{\mu }{\theta }{({\lambda }_H-{\vartheta }_H)}^{-1}}\hfill \end{array}$$

(38)

in distribution, as $T\to \infty$, where $\eta \sim N(0,1)$ is independent of $\xi \sim N(0,1)$. Combining this with Equations (33)–(36), and Slutsky’s theorem, we have introduced the desired conclusion:

$$e^{\theta T}\left({\widehat{\theta }}_T-\theta \right)⟶\frac{2\theta {\lambda }_H}{{\lambda }_H-{\vartheta }_H}·\frac{\xi }{\eta +\frac{\mu }{\theta }{({\lambda }_H-{\vartheta }_H)}^{-1}}$$

in distribution, as $T\to \infty$.

For the convergence Equation (31), we have:

$$\begin{array}{cc}\hfill {\widehat{\mu }}_T-\mu & =\frac{1}{T}\left(X_T-{\widehat{\theta }}_T{\int }_0^T{X}_{s}ds-\mu T\right)\hfill \\ & =\frac{1}{T}\left\{-\left({\widehat{\theta }}_T-\theta \right){\int }_0^T{X}_{s}ds+X_T-\theta {\int }_0^T{X}_{s}ds-\mu T\right\}\hfill \\ & =-\frac{1}{T}\left({\widehat{\theta }}_T-\theta \right){\int }_0^T{X}_{s}ds+\frac{1}{T}{S}_T^H\hfill \end{array}$$

for all $T>0$ and:

$$\begin{array}{cc}\hfill T\left({\widehat{\mu }}_T-\mu -\frac{1}{T}{S}_T^H\right)& =-\left(e^{\theta T}({\widehat{\theta }}_T-\theta )\right)·\left(e^{-\theta T}{\int }_0^T{X}_{s}ds\right)\hfill \\ & ⟶2{\lambda }_H\xi \hfill \end{array}$$

in distribution, as T tends to infinity, by the convergence Equation (30) and Slutsky’s theorem.

For the convergence Equation (32), noticing that the proof of the convergence Equation (31), we have:

$$\begin{array}{cc}\hfill T^{1-H}\left({\widehat{\mu }}_T-\mu \right)& =-\frac{1}{T^H}\left(e^{\theta T}({\widehat{\theta }}_T-\theta )\right)·\left(e^{-\theta T}{\int }_0^T{X}_{s}ds\right)+\frac{S_T^H}{T^H}\hfill \end{array}$$

for all $T>0$, and it is easy to see that:

$$D\left(T\right):=\frac{1}{T^H}\left(e^{\theta T}({\widehat{\theta }}_T-\theta )\right)·\left(e^{-\theta T}{\int }_0^T{X}_{s}ds\right)⟶0,$$

as T tends to infinity, in probability. In fact, by Equations (2), (18) and Lemma 2, we have:

$$\begin{array}{c}\hfill e^{-\theta T}{\int }_0^T{X}_{s}ds=\frac{1}{\theta }{e}^{-\theta T}f\left(T\right)+Z_T-\frac{\mu }{\theta }T{e}^{-\theta T}⟶\frac{\mu }{{\theta }^2}+Z_{\infty }\end{array}$$

almost surely, as T tends to infinity. Combining this with the convergence Equation (30), we have that $D\left(T\right)\to 0$ in probability, as T tends to infinity. Thus, the convergence Equation (32) follows from the fact:

$$\begin{array}{c}\hfill \frac{S_T^H}{T^H}\sim N\left(0,2-2^{2H-1}\right)\end{array}$$

for all $T>0$. This completes the proof of Theorem 2.  ☐

5. Conclusions

In this paper, we discuss the least squares estimation for the Vasicek-type model driven by a sub-fraction Brownian motion $S^H$ with Hurst index $H\in (\frac{1}{2},1)$. Based on the so-called continuous observation, we introduce the least squares estimators of the two unknown parameters $\mu$ and $\theta$ in the Vasicek-type model and prove in detail the consistency and asymptotic distributions of the two estimators. In general, however, there exists a gap between the results we introduce and their applicability. For instance, one must take into account the so-called discrete observations and then choose an observation frequency for any practical problem in finance. Hence, in our current study, we are considering the parametric estimation of the Vasicek-type model under the so-called discrete observations. Moreover, in the future, we will attempt to give the least squares estimators of the Vasicek-type model driven by a general Gaussian process.