Damage Identification Algorithm of Hinged Joints for Simply Supported Slab Bridges Based on Modified Hinge Plate Method and Artificial Bee Colony Algorithms
Abstract
:1. Introduction
2. Methods
2.1. Traditional Hinge Plate Method
2.2. Modified Hinge Plate Method
2.3. Artificial Bee Colony (ABC) Algorithm
2.3.1. Original ABC Algorithm
2.3.2. Improved ABC Algorithms
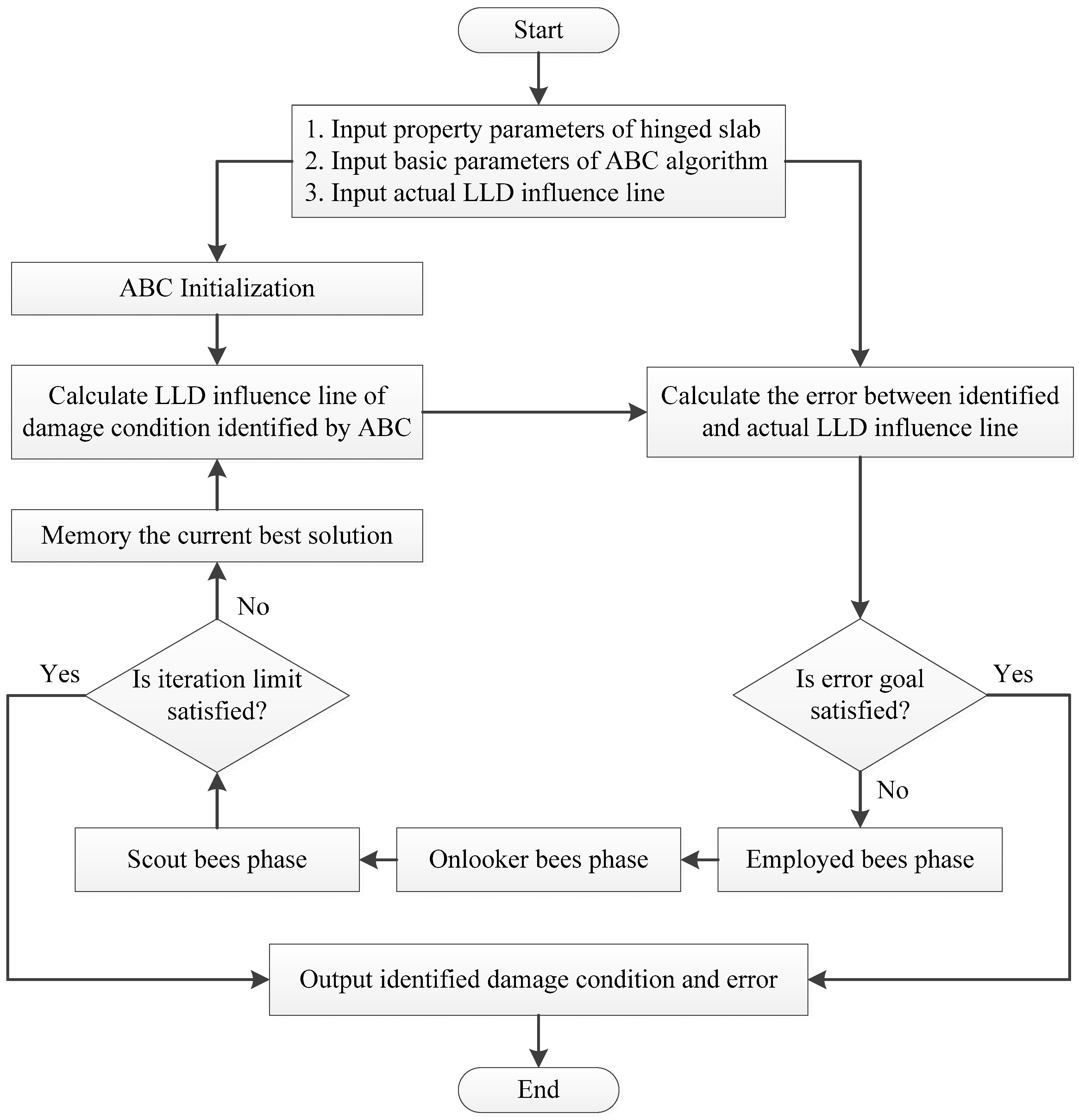
2.4. Methodology
- Firstly, each slab deflection of hinged bridges are measured through a static experiment with external loads and the corresponding parameters of the bridge should be obtained;
- Secondly, the actual LLD influence line can be calculated by the deflections in the first step;
- Thirdly, we can generate an ABC model, of which the objective function is the Euclidean distance between the actual LLD influence line and the one calculated by the MHPM method;
- Lastly, we can search the solution with the best fitness by original or improved ABC algorithm, and the best solution is the identified hinge joint damage degree and location of the hinged-slab bridge.
3. Results and Discussion
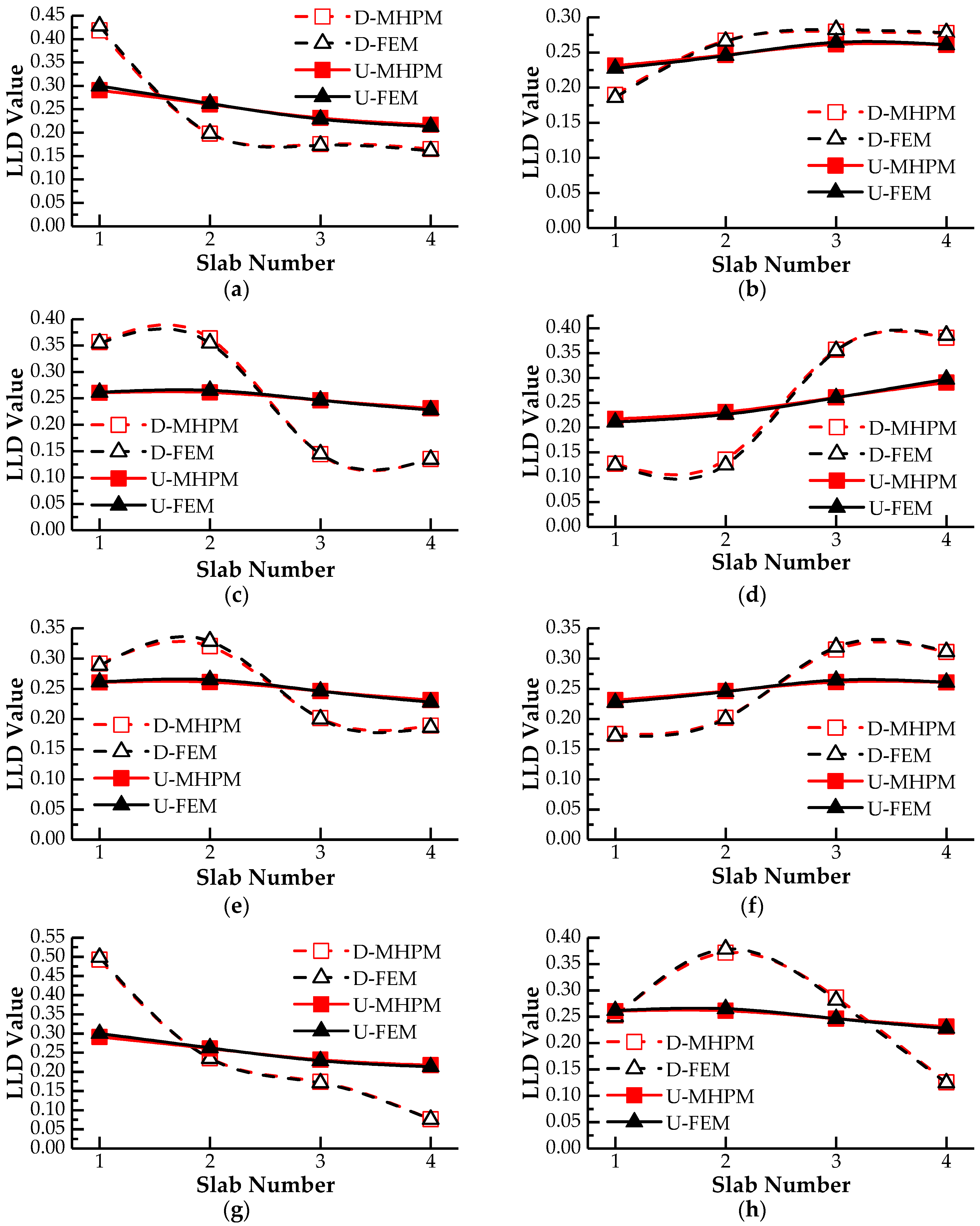
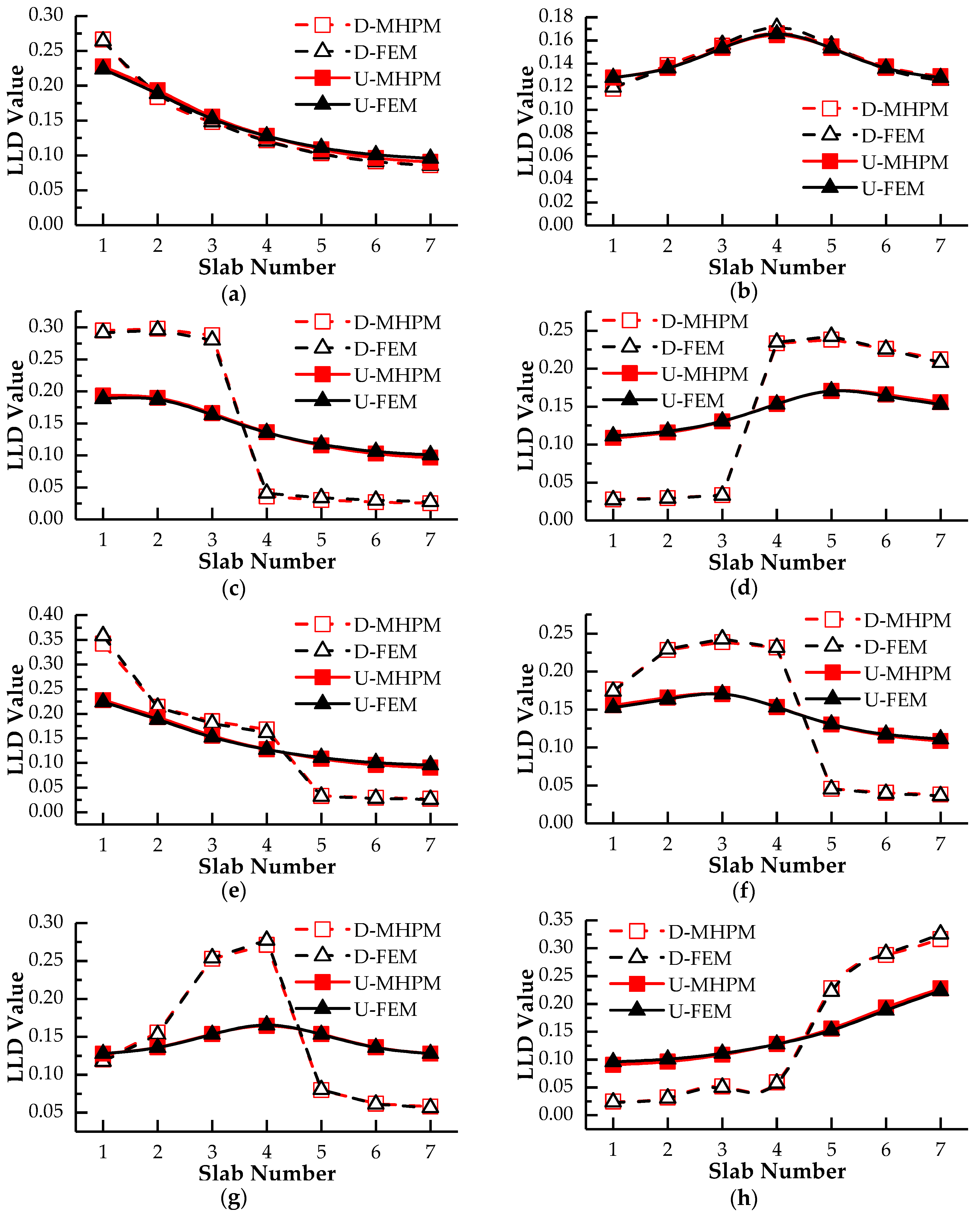
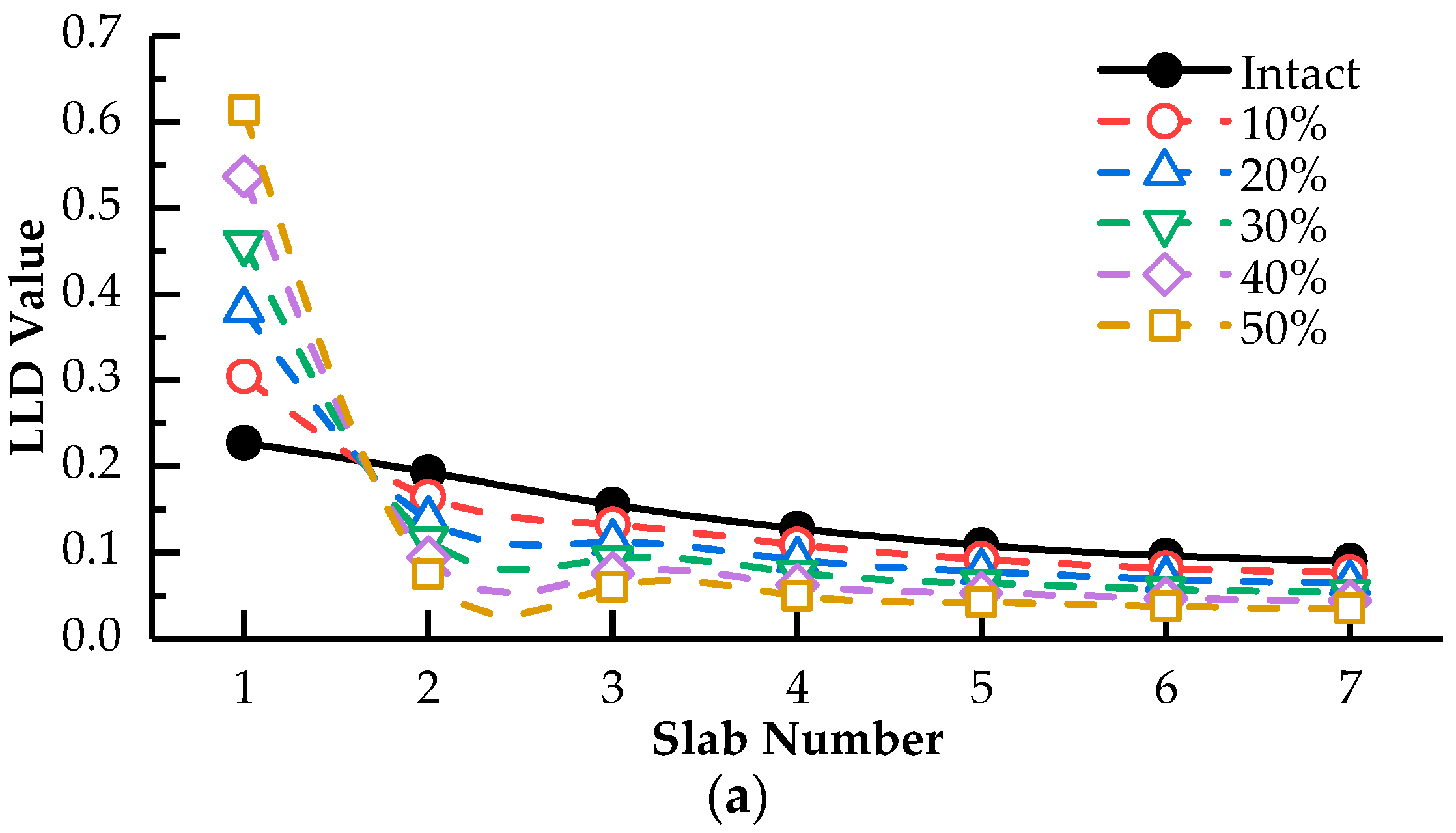
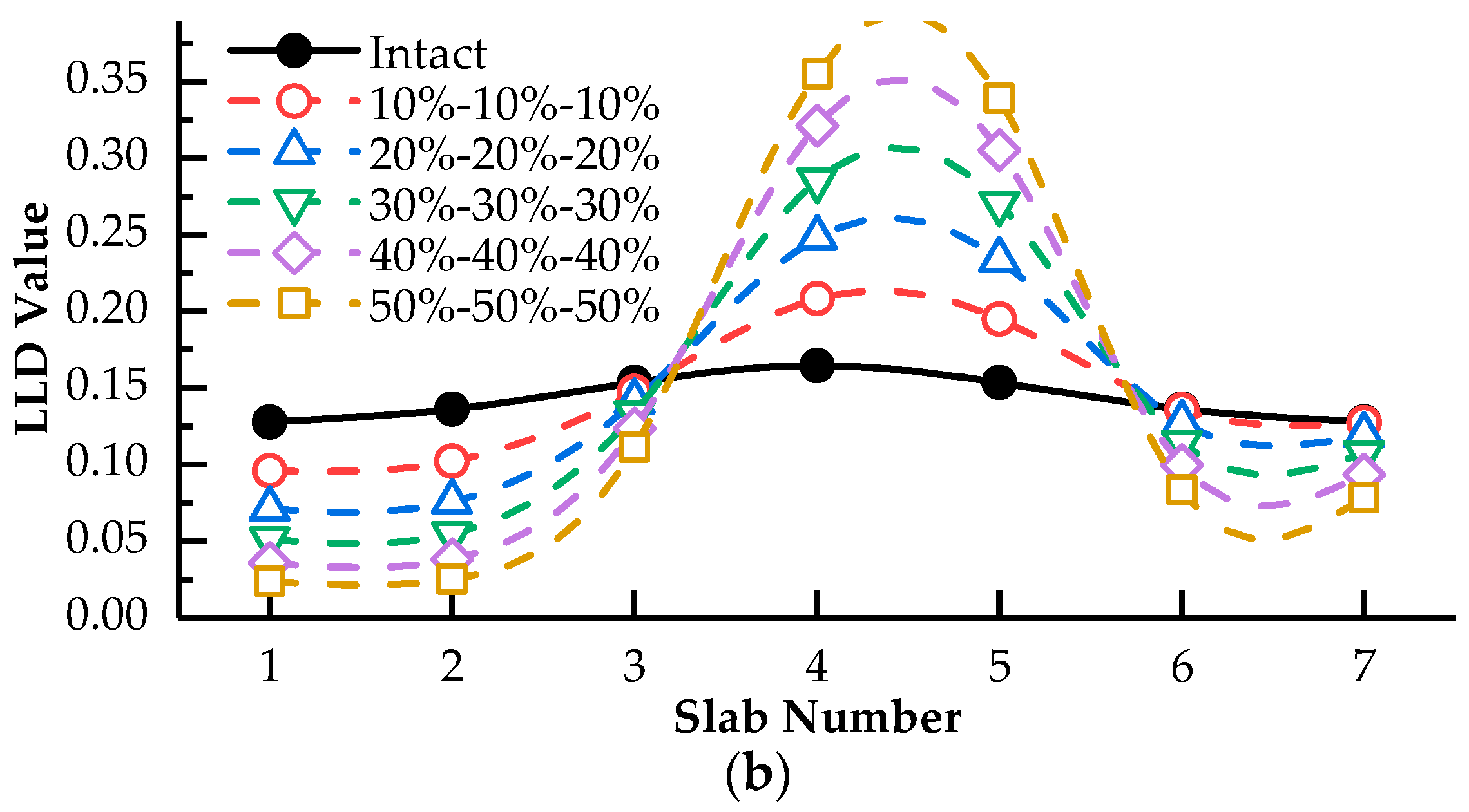
3.1. Lateral Load Distribution Evaluation Based on Modified Hinge Plate Method
3.2. Damage Severity Identification of Hinge Joint Based on Artificial Bee Colony
3.2.1. Damage Identification Process
3.2.2. Numerical Simulations
4. Conclusions
- (1)
- The damage factor through substitution of a relative displacement into the canonical equations can realize the simulation of hinge joint damage. The lateral load distribution influence line calculated by modified hinge plate method coincided with the result computed by the finite element method. The maximum error of damage cases in this study by modified hinge plate method was less than 1.9%.
- (2)
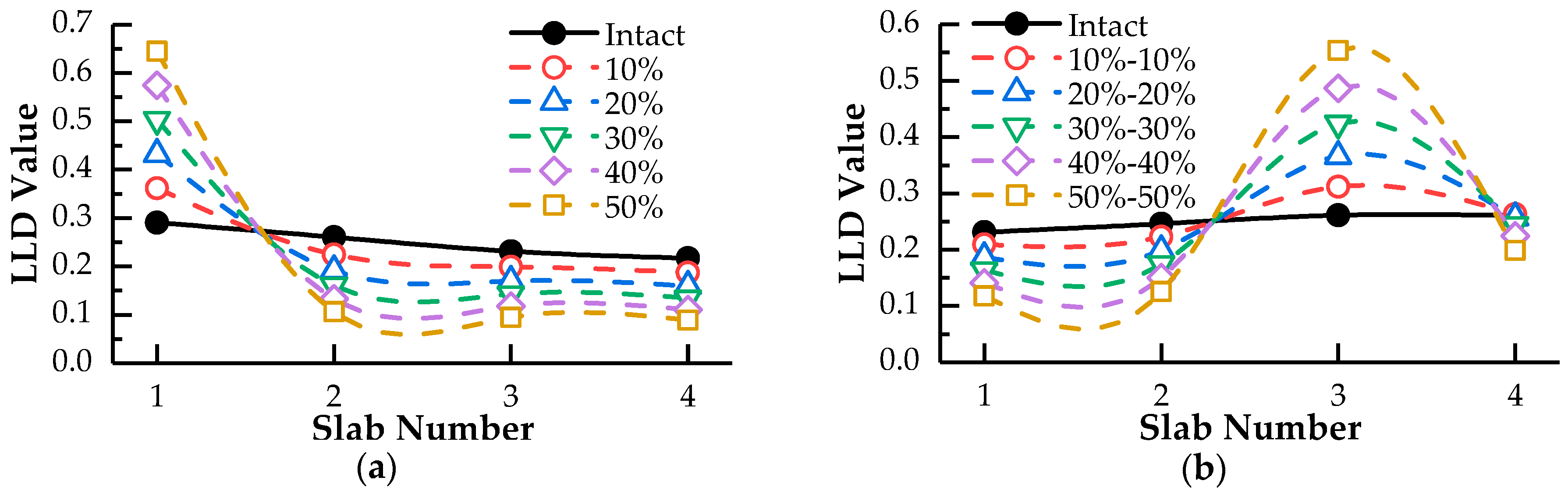
- Hinge joint damage can lead to cross phenomenon of lateral load distribution influence lines, which is suitable for the damage localization of hinged-slab bridges with single hinge damage. Moreover, the offset degree of lateral load distribution influence line is proportional to damage degrees, which can realize the qualitative assessment of hinge damage. However, cross phenomenon is not effective to identify the damage location with multiple hinge damages.
- (3)
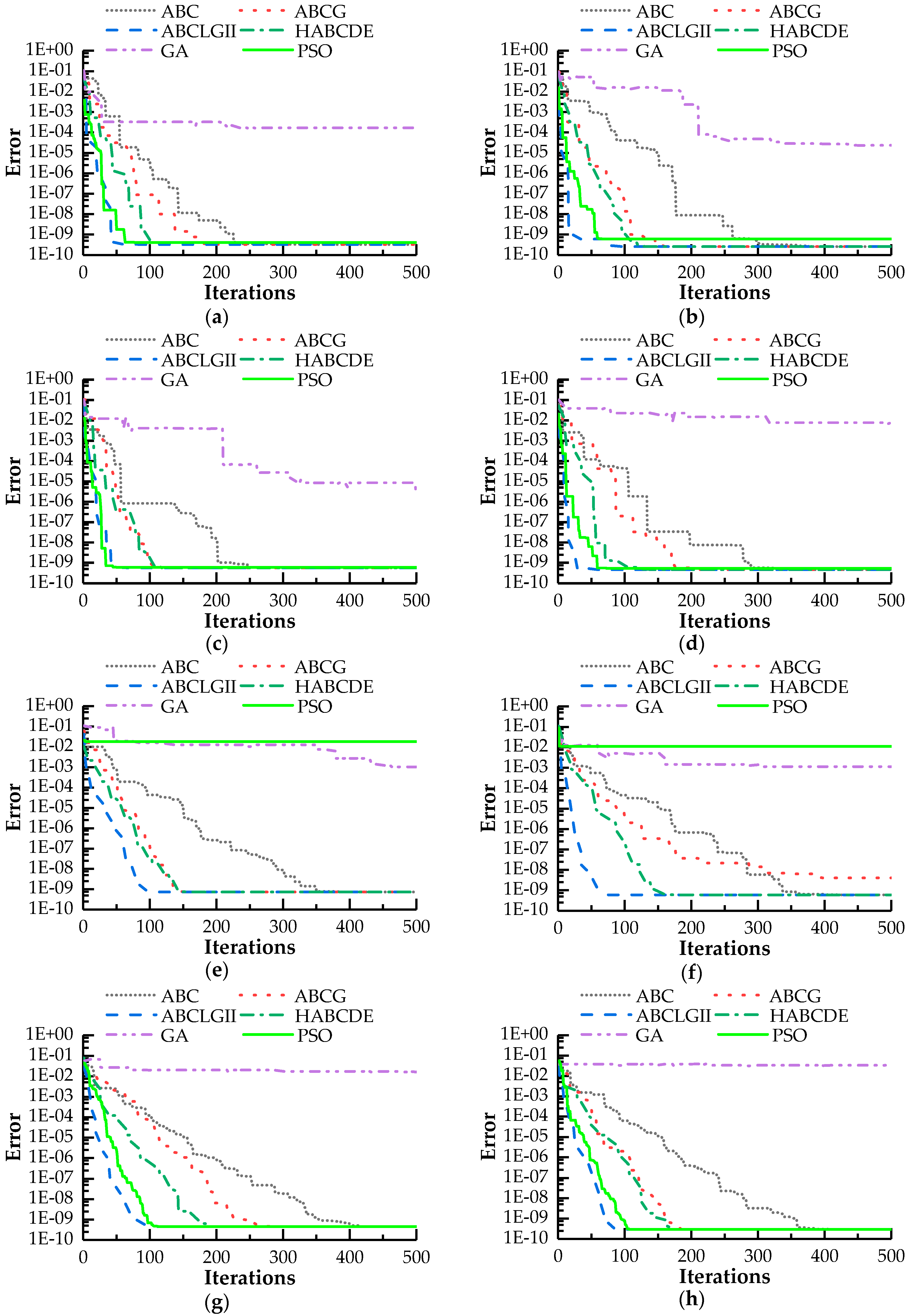
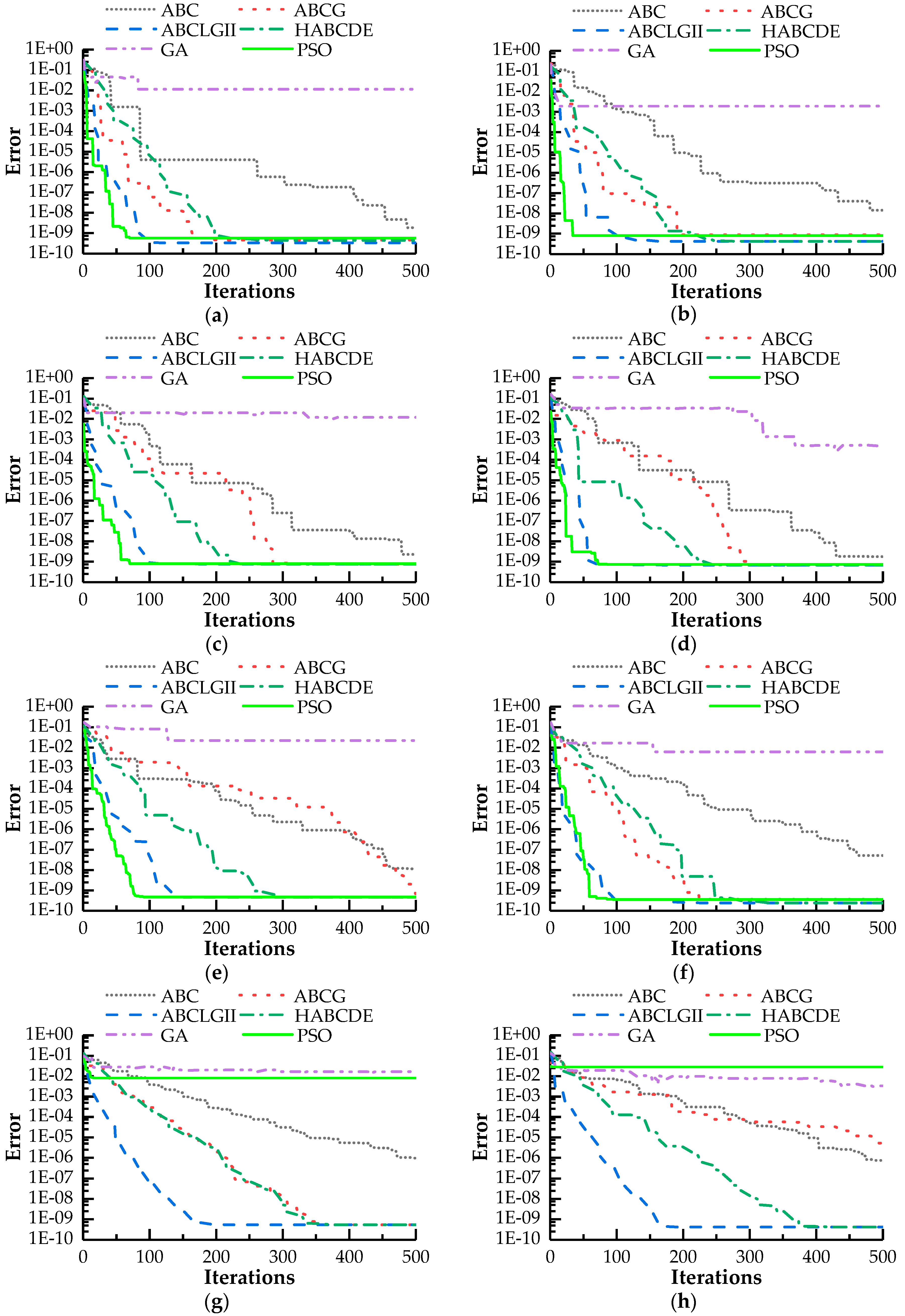
- Original and improved artificial bee colony algorithms successfully identified the location and degree of hinge joint damages, of which the maximum error did not exceed 4.72 × 10−6. Based on ABCLGII and HABCDE, the algorithms had the lowest time cost (less than 70 s). Moreover, ABCLGII converged after 100 iterations approximately, while the others did not. So ABCLGII is the most suitable for the proposed damage identification algorithm among artificial bee colony algorithms in this work.
- (4)
- The results of comparison with particle swarm optimization and genetic algorithm revealed that both PSO and GA converged after 100 iterations at most and the time costs of them were no more than 30 s, which presented satisfactory convergence speed and time cost. However, the accuracy of damage identification algorithm based on PSO was not stable; namely, the minimum and maximum errors were 1 × 10−9 for single damage condition and 0.028 for multiple hinge damages, respectively. As for GA, its error fluctuated between 0.0005 and 0.022, which demonstrated it had the most unsatisfactory identification results among these methods.
- (5)
- It demonstrated again that the proposed algorithm was accurate through comparison with methods in the literature [19,20]. The former algorithm had zero error while the latter ones had larger errors ranging from 0.003 to 0.164. Even the latter algorithms identified the damage degree and location improperly.
Author Contributions
Funding
Conflicts of Interest
References
- Heo, G.; Kim, C.; Jeon, S.; Jeon, J. An experimental study of a data compression technology-based intelligent data acquisition (IDAQ) system for structural health monitoring of a long-span bridge. Appl. Sci. 2018, 8, 361. [Google Scholar] [CrossRef]
- Amezquita-Sanchez, J.P.; Adeli, H. Signal processing techniques for vibration-based health monitoring of smart structures. Arch. Comput. Method Eng. 2016, 23, 1–15. [Google Scholar] [CrossRef]
- Satpal, S.B.; Guha, A.; Banerjee, S. Damage identification in aluminum beams using support vector machine: Numerical and experimental studies. Struct. Control Health 2016, 23, 446–457. [Google Scholar] [CrossRef]
- Fan, W.; Qiao, P.Z. Vibration-based damage identification methods: A review and comparative study. Struct. Health Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Qin, S.Q.; Zhang, Y.Z.; Zhou, Y.L.; Kang, J.T. Dynamic model updating for bridge structures using the kriging model and PSO algorithm ensemble with higher vibration modes. Sensors 2018, 18, 1879. [Google Scholar] [CrossRef] [PubMed]
- Blachowski, B.; An, Y.; Spencer, B.F., Jr.; Ou, J. Axial strain accelerations approach for damage localization in statically determinate truss structures. Comput.-Aided Civ. Inf. 2017, 32, 304–318. [Google Scholar] [CrossRef]
- Kim, C.-W.; Chang, K.-C.; Kitauchi, S.; McGetrick, P.J. A field experiment on a steel gerber-truss bridge for damage detection utilizing vehicle-induced vibrations. Struct. Health Monit. 2016, 15, 174–192. [Google Scholar] [CrossRef]
- Russo, F.M.; Wipf, T.J.; Klaiber, F.W.; Trb, T.R.B. Diagnostic load tests of a prestressed concrete bridge damaged by overheight vehicle impact. In Proceedings of the Fifth International Bridge Engineering Conference, TAMPA, FL, USA, 3–5 April 2000. [Google Scholar]
- Chung, W.; Liu, J.; Sotelino, E.D. Influence of secondary elements and deck cracking on the lateral load distribution of steel girder bridges. J. Bridge Eng. 2006, 11, 178–187. [Google Scholar] [CrossRef]
- Al-Saidy, A.H.; Klaiber, F.W.; Wipf, T.J.; Al-Jabri, K.S.; Al-Nuaimi, A.S. Parametric study on the behavior of short span composite bridge girders strengthened with carbon fiber reinforced polymer plates. Constr. Build. Mater. 2008, 22, 729–737. [Google Scholar] [CrossRef]
- Kim, Y.J.; Green, M.F.; Fallis, G.J. Repair of bridge girder damaged by impact loads with prestressed CFRP sheets. J. Bridge Eng. 2008, 13, 15–23. [Google Scholar] [CrossRef]
- Azimi, H.; Sennah, K. Parametric effects on evaluation of an impact-damaged prestressed concrete bridge girder repaired by externally bonded carbon-fiber-reinforced polymer sheets. J. Perform. Constr. Facil. 2015, 29, 1–12. [Google Scholar] [CrossRef]
- Yao, L.S. Bridge Engineering, 2nd ed.; China Communicaitons Press: Beijing, China, 2010; pp. 128–142. ISBN 978-7-114-07042-6. (In Chinese) [Google Scholar]
- American Association of State Highway and Transportation Officials (AASHTO). AASHTO Standard Specifications for Highway Bridges, 16th ed.; American Association of State Highway and Transportation Officials, Inc.: Washington, DC, USA, 1996; ISBN 1-56051-040-4. [Google Scholar]
- American Association of State Highway and Transportation Officials (AASHTO). AASHTO LRFD Bridge Design Specifications, 6th ed.; American Association of State Highway and Transportation Officials, Inc.: Washington, DC, USA, 2012; ISBN 978-1-56051-523-4. [Google Scholar]
- Huo, X.S.; Wasserman, E.P.; Iqbal, R.A. Simplified method for calculating lateral distribution factors for live load shear. J. Bridge Eng. 2005, 10, 544–554. [Google Scholar] [CrossRef]
- Wang, W.Y.; Zhang, C.; Wan, S. Study on transverse load distribution of hinged hollow beam. In Proceedings of the 2017 4th International Conference on Advanced Materials, Mechanics and Structural Engineering, Tianjin, China, 22–24 September 2017. [Google Scholar]
- Jiao, Y.B.; Liu, H.B.; Wang, X.Q.; Luo, G.B. Modal property-based approach for lateral distribution evaluation of intact and damaged reinforced concrete bridge. In Proceedings of the 10th International Workshop on Structural Health Monitoring, Stanford, CA, USA, 1–3 September 2015; pp. 2911–2918. [Google Scholar]
- Wei, B.L.; Deng, M.Y. Computional method analysis for transverse load distribution of damage bridge. J. Henan Polytech. Univ. 2015, 34, 102–108. [Google Scholar] [CrossRef]
- Cheng, C.; Shen, C.W.; Xu, L. The hinged-jointed plate method for calculating transverse load distribution on a damaged bridge. J. Wuhan Univ. Technol. 2004, 28, 229–231. (In Chinese) [Google Scholar]
- Conde, B.; Drosopoulos, G.A.; Stavroulakis, G.E.; Riveiro, B.; Stavroulaki, M.E. Inverse analysis of masonry arch bridges for damaged condition investigation: Application on kakodiki bridge. Eng. Struct. 2016, 127, 388–401. [Google Scholar] [CrossRef]
- Santos, A.; Silva, M.; Santos, R.; Figueiredo, E.; Sales, C.; Costa, J.C.W.A. A global expectation-maximization based on memetic swarm optimization for structural damage detection. Struct. Health Monit. 2016, 15, 610–625. [Google Scholar] [CrossRef]
- Wei, Z.T.; Liu, J.K.; Lu, Z.R. Structural damage detection using improved particle swarm optimization. Inverse Probl. Sci. Eng. 2018, 26, 792–810. [Google Scholar] [CrossRef]
- Yang, Z.B.; Chen, X.F.; Xie, Y.; Miao, H.H.; Gao, J.J.; Qi, K.Z. Hybrid two-step method of damage detection for plate-like structures. Struct. Control Health 2016, 23, 267–285. [Google Scholar] [CrossRef]
- Casciati, S.; Elia, L. Damage localization in a cable-stayed bridge via bio-inspired metaheuristic tools. Struct. Control Health 2017, 24. [Google Scholar] [CrossRef]
- Antonelli, A.; Giarnetti, S.; Leccese, F. Enhanced PLL system for harmonic analysis through genetic algorithm application. In Proceedings of the International Conference on Environment and Electrical Engineering, Venice, Italy, 18–25 May 2012; pp. 328–333. [Google Scholar] [CrossRef]
- Hou, W.; Jin, Y.; Zhu, C.; Li, G. A novel maximum power point tracking algorithm based on glowworm swarm optimization for photovoltaic systems. Int. J. Photoenergy 2016. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. On the performance of artificial bee colony (ABC) algorithm. Appl. Soft Comput. 2008, 8, 687–697. [Google Scholar] [CrossRef]
- Karaboga, D.; Akay, B. A comparative study of artificial bee colony algorithm. Appl. Math. Comput. 2009, 214, 108–132. [Google Scholar] [CrossRef]
- Pham, D.T.; Castellani, M. Benchmarking and comparison of nature-inspired population-based continuous optimisation algorithms. Soft Comput. 2014, 18, 871–903. [Google Scholar] [CrossRef]
- Sun, H.; Lus, H.; Betti, R. Identification of structural models using a modified artificial bee colony algorithm. Comput. Struct. 2013, 116, 59–74. [Google Scholar] [CrossRef]
- Xu, H.J.; Ding, Z.H.; Lu, Z.R.; Liu, J.K. Structural damage detection based on chaotic artificial bee colony algorithm. Struct. Eng. Mech. 2015, 55, 1223–1239. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization. Ph.D. Thesis, Erciyes University, Kayseri, Turkey, 2005. [Google Scholar]
- Gao, W.F.; Liu, S.Y.; Huang, L.L. Enhancing artificial bee colony algorithm using more information-based search equations. Inf. Sci. 2014, 270, 112–133. [Google Scholar] [CrossRef]
- Akay, B.; Karaboga, D. A modified artificial bee colony algorithm for real-parameter optimization. Inf. Sci. 2012, 192, 120–142. [Google Scholar] [CrossRef]
- Pang, B.; Song, Y.; Zhang, C.; Wang, H.; Yang, R. A modified artificial bee colony algorithm based on the self-learning mechanism. Algorithms 2018, 11, 78. [Google Scholar] [CrossRef]
- Karaboga, D.; Gorkemli, B. A quick artificial bee colony (QABC) algorithm and its performance on optimization problems. Appl. Soft Comput. 2014, 23, 227–238. [Google Scholar] [CrossRef]
- Jadon, S.S.; Tiwari, R.; Sharma, H.; Bansal, J.C. Hybrid artificial bee colony algorithm with differential evolution. Appl. Soft Comput. 2017, 58, 11–24. [Google Scholar] [CrossRef]
- Xiang, W.L.; Meng, X.L.; Li, Y.Z.; He, R.C.; An, M.Q. An improved artificial bee colony algorithm based on the gravity model. Inf. Sci. 2018, 429, 49–71. [Google Scholar] [CrossRef]
- Liu, Q.Z.; Zhu, M.M.; Li, G.H.; Wang, W.J.; Cui, L.Z.; Chen, J.Y.; Lu, J. A novel artificial bee colony algorithm with local and global information interaction. Appl. Soft Comput. 2018, 62, 702–735. [Google Scholar] [CrossRef]
- Yildiz, A.R. A new hybrid artificial bee colony algorithm for robust optimal design and manufacturing. Appl. Soft Comput. 2013, 13, 2906–2912. [Google Scholar] [CrossRef]
- Li, G.H.; Shi, D. Calculation of Lateral Load Distribution of Highway Bridges, 2nd ed.; China Communicaitons Press: Beijing, China, 1990; pp. 87–116. (In Chinese) [Google Scholar]
- Ravanfar, S.A.; Razak, H.A.; Ismail, Z.; Hakim, S.J.S. A two-step damage identification approach for beam structures based on wavelet transform and genetic algorithm. Meccanica 2016, 51, 635–653. [Google Scholar] [CrossRef]
- Liu, H.B.; Wang, X.Q.; Jiao, Y.B. Damage identification for irregular-shaped bridge based on fuzzy c-means clustering improved by particle swarm optimization algorithm. J. Vibroeng. 2016, 18, 2149–2166. [Google Scholar] [CrossRef]

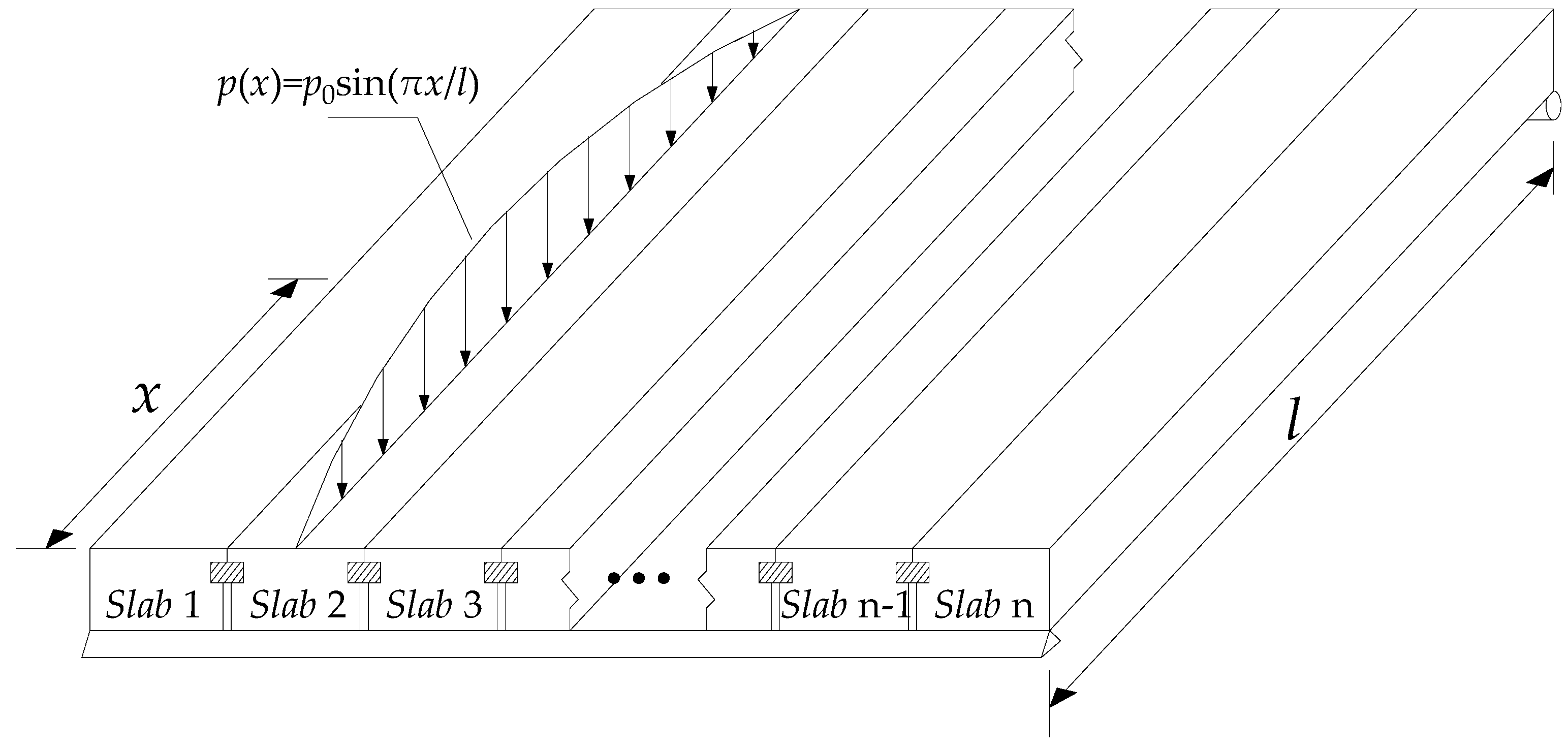
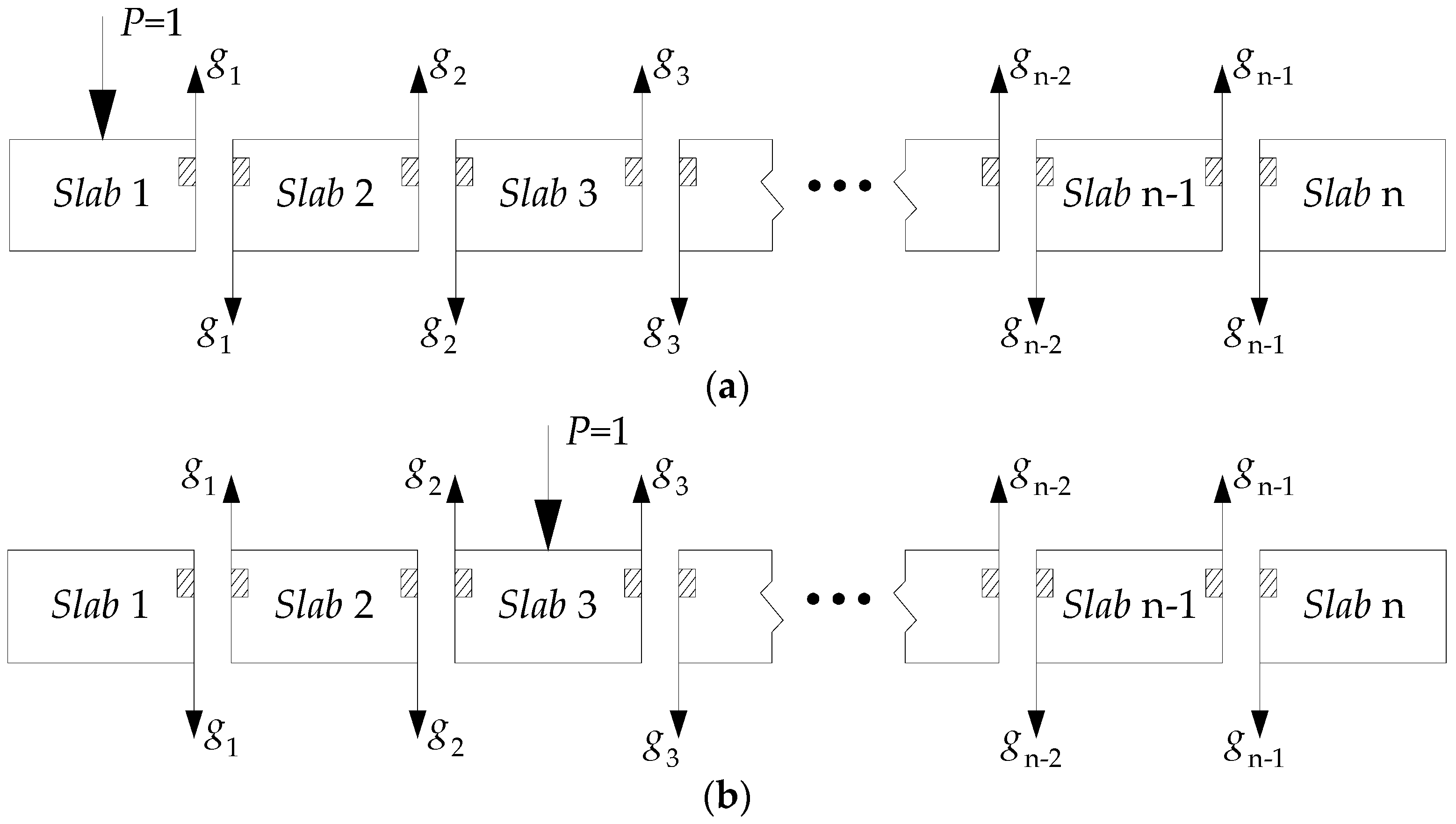
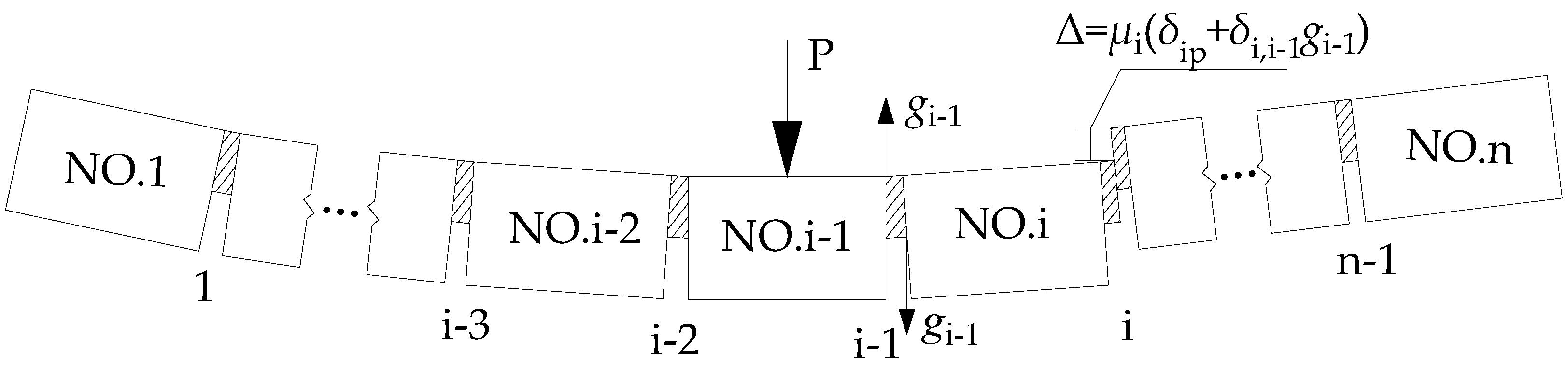

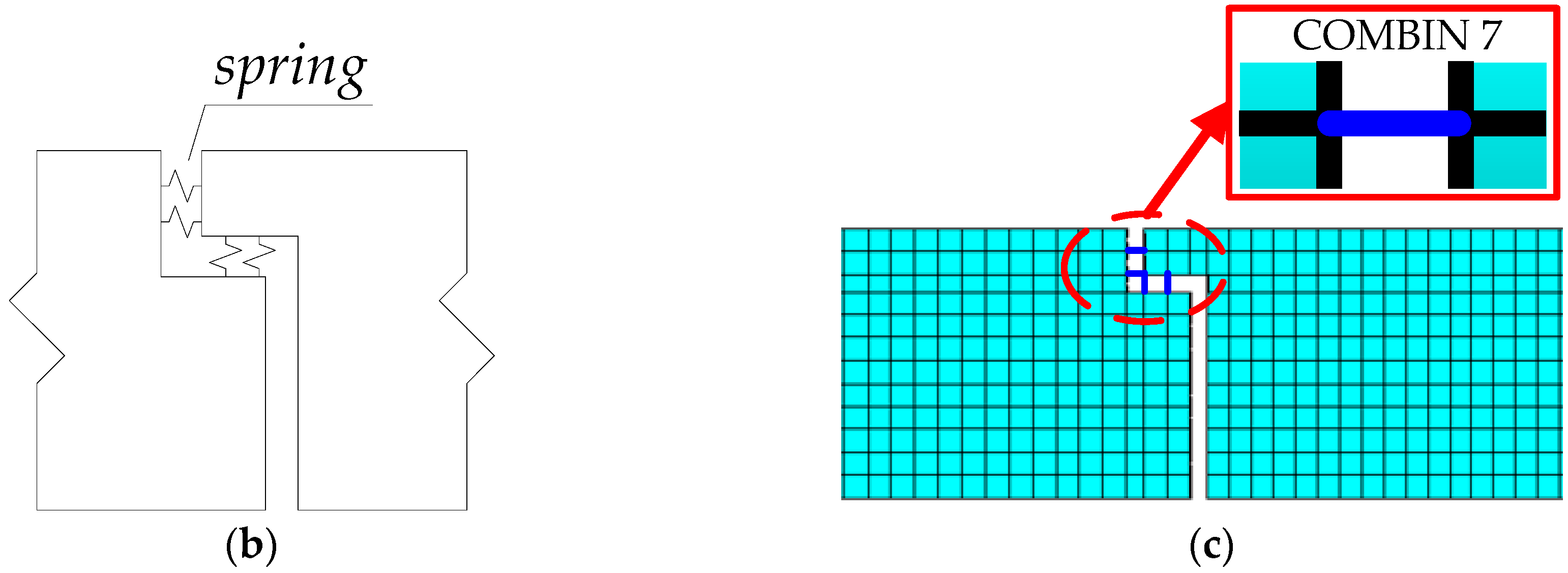
| Algorithm: The load lateral distribution influence line | |
| Input: the number of slabs: n; Young’s modulus vector: E; the slab number to be calculated: SN | |
| the three-dimensional geometry parameter of slab: l, b, h; the damage condition of hinged joints: μ | |
| 01 | Calculate and through the illustration of Equation (8) |
| 02 | for FP = 1: n |
| 03 | switch FP |
| 04 | case 1 |
| 05 | Calculate δij and δip by Equations (6) and (7), respectively |
| 06 | Calculate the relative displacement through the right side of Equation (10) |
| 07 | Solve Equation (10) and obtain g = [g1, …, gi, …, gn−1] |
| 08 | Calculate the load lateral distribution vertical value by Equation (2) |
| 09 | case n |
| 10 | Calculate δij and δip by Equations (6) and (7), respectively |
| 11 | Calculate the relative displacement through the right side of Equation (12) |
| 12 | Solve Equation (12) and obtain g = [g1, …, gi, …, gn−1] |
| 13 | Calculate the load lateral distribution vertical value by Equation (3) |
| 14 | otherwise |
| 15 | Calculate δij and δip by Equations (6) and (8), respectively |
| 16 | Calculate the relative displacement through the right side of Equation (11) |
| 17 | Solve Equation (11) and obtain g = [g1, …, gi, …, gn−1] |
| 18 | Calculate the lateral load distribution vertical value by Equation (4) |
| 19 | end switch |
| 20 | Memory the objective lateral load distribution vertical value |
| 21 | end for |
| Output: The load lateral distribution influence line of Slab SN: | |
| Algorithms | The Parameter Values |
|---|---|
| ABCG 1 | ; ; ; ; ; |
| ABCLGII 2 | ; ; |
| HABCDE 3 | ; ; |
| Case No. | Damage Location and Extent | Slab Nos. for LLD 1 |
|---|---|---|
| 1 | [0.18, 0, 0] | 1, 3 |
| 2 | [0, 0.33, 0] | 2, 4 |
| 3 | [0.05, 0.15, 0] | 2, 3 |
| 4 | [0.22, 0.10, 0.43] | 1, 2 |
| Case No. | Damage Location and Extent | Slab Nos. for LLD |
|---|---|---|
| 5 | [0.05, 0, 0, 0, 0, 0] | 1, 4 |
| 6 | [0, 0, 0.6, 0, 0, 0] | 2, 5 |
| 7 | [0.1, 0, 0, 0.5, 0, 0] | 1, 3 |
| 8 | [0.1, 0.15, 0, 0.4, 0.05, 0] | 4, 7 |
| Case No. | Slab No. | LLD Influence Line Vertical Value | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | 1 | 0.41844 | 0.19806 | 0.17576 | 0.16496 |
| 3 | 0.18972 | 0.26694 | 0.27956 | 0.27774 | |
| 2 | 2 | 0.35677 | 0.36376 | 0.14416 | 0.13531 |
| 4 | 0.12700 | 0.13531 | 0.35677 | 0.38093 | |
| 3 | 2 | 0.29225 | 0.32085 | 0.20157 | 0.18919 |
| 3 | 0.17522 | 0.20219 | 0.31539 | 0.31137 | |
| 4 | 1 | 0.49264 | 0.23551 | 0.17375 | 0.07614 |
| 2 | 0.25219 | 0.37177 | 0.28635 | 0.12548 | |
| Case No. | Slab No. | Algorithms | Hinge Joint No. | ||
|---|---|---|---|---|---|
| 1 | 2 | 3 | |||
| 1 | 1 | ABC | 0.18 | 5.643 × 10−10 | 0 |
| ABCG | 0.18 | 5.646 × 10−10 | 0 | ||
| ABCLGII | 0.18 | 5.641 × 10−10 | 0 | ||
| HABCDE | 0.18 | 0 | 0 | ||
| GA | 0.1802 | 7.630 × 10−6 | 4.252 × 10−9 | ||
| PSO | 0.18 | 0 | 0 | ||
| 3 | ABC | 0.18 | 3.512 × 10−10 | 1.724 × 10−9 | |
| ABCG | 0.18 | 3.504 × 10−10 | 1.725 × 10−9 | ||
| ABCLGII | 0.18 | 3.505 × 10−10 | 1.725 × 10−9 | ||
| HABCDE | 0.18 | 3.506 × 10−10 | 1.725 × 10−9 | ||
| GA | 0.1799 | 3.064 × 10−5 | 1.526 × 10−5 | ||
| PSO | 0.18 | 0 | 0 | ||
| 2 | 2 | ABC | 4.140 × 10−10 | 0.33 | 0 |
| ABCG | 4.142 × 10−10 | 0.33 | 0 | ||
| ABCLGII | 4.139 × 10−10 | 0.33 | 0 | ||
| HABCDE | 4.141 × 10−10 | 0.33 | 0 | ||
| GA | 2.998 × 10−8 | 0.33 | 6.199 × 10−6 | ||
| PSO | 0 | 0.33 | 0 | ||
| 4 | ABC | 1.753 × 10−9 | 0.33 | 0 | |
| ABCG | 1.753 × 10−9 | 0.33 | 0 | ||
| ABCLGII | 1.753 × 10−9 | 0.33 | 1.998 × 10−15 | ||
| HABCDE | 1.754 × 10−9 | 0.33 | 2.998 × 10−15 | ||
| GA | 0 | 0.3457 | 0 | ||
| PSO | 0 | 0.33 | 0 | ||
| 3 | 2 | ABC | 0.05 | 0.15 | 0 |
| ABCG | 0.05 | 0.15 | 0 | ||
| ABCLGII | 0.05 | 0.15 | 0 | ||
| HABCDE | 0.05 | 0.15 | 0 | ||
| GA | 0.0489 | 0.1485 | 0.0039 | ||
| PSO | 0 | 0.1377 | 0 | ||
| 3 | ABC | 0.05 | 0.15 | 0 | |
| ABCG | 0.0499 | 0.15 | 0 | ||
| ABCLGII | 0.05 | 0.15 | 0 | ||
| HABCDE | 0.05 | 0.15 | 0 | ||
| GA | 0.0547 | 0.1484 | 0 | ||
| PSO | 0 | 0.159 | 0 | ||
| 4 | 1 | ABC | 0.22 | 0.1 | 0.43 |
| ABCG | 0.22 | 0.1 | 0.43 | ||
| ABCLGII | 0.22 | 0.1 | 0.43 | ||
| HABCDE | 0.22 | 0.1 | 0.43 | ||
| GA | 0.2166 | 0.1261 | 0.501 | ||
| PSO | 0.22 | 0.1 | 0.43 | ||
| 2 | ABC | 0.22 | 0.1 | 0.43 | |
| ABCG | 0.22 | 0.1 | 0.43 | ||
| ABCLGII | 0.22 | 0.1 | 0.43 | ||
| HABCDE | 0.22 | 0.1 | 0.43 | ||
| GA | 0.1953 | 0.0525 | 0.5378 | ||
| PSO | 0.22 | 0.1 | 0.43 | ||
| Case No. | 1 | 2 | 3 | 4 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Slab No. | 1 | 3 | 2 | 4 | 2 | 3 | 1 | 2 | |
| Algorithms | ABC | 432 | 429 | 434 | 435 | 449 | 454 | 476 | 471 |
| ABCG | 435 | 430 | 432 | 431 | 453 | 451 | 475 | 473 | |
| ABCLGII | 53 | 49 | 51 | 54 | 52 | 51 | 54 | 56 | |
| HABCDE | 56 | 55 | 57 | 56 | 59 | 63 | 62 | 65 | |
| GA | 23 | 22 | 19 | 21 | 25 | 23 | 28 | 29 | |
| PSO | 20 | 21 | 20 | 22 | 21 | 22 | 26 | 24 | |
| Case No. | Slab No. | LLD Influence Line Vertical Value | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| 5 | 1 | 0.26629 | 0.18381 | 0.14782 | 0.12150 | 0.10314 | 0.09153 | 0.08590 |
| 4 | 0.11814 | 0.13872 | 0.15553 | 0.16616 | 0.15493 | 0.13749 | 0.12904 | |
| 6 | 2 | 0.29513 | 0.29808 | 0.28782 | 0.03595 | 0.03052 | 0.02708 | 0.02542 |
| 5 | 0.02767 | 0.02948 | 0.03322 | 0.23341 | 0.23824 | 0.22593 | 0.21205 | |
| 7 | 1 | 0.34244 | 0.21413 | 0.18510 | 0.16820 | 0.03313 | 0.02940 | 0.02760 |
| 3 | 0.17655 | 0.22862 | 0.23877 | 0.23183 | 0.04567 | 0.04053 | 0.03804 | |
| 8 | 4 | 0.12022 | 0.15568 | 0.25309 | 0.27135 | 0.07970 | 0.06187 | 0.05807 |
| 7 | 0.02463 | 0.03190 | 0.05186 | 0.05895 | 0.22806 | 0.28812 | 0.31649 | |
| Case No. | Slab No. | Algorithms | Hinge Joint No. | |||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |||
| 5 | 1 | ABC | 0.05 | 0 | 0 | 0 | 0 | 0 |
| ABCG | 0.05 | 5.740 × 10−10 | 0 | 0 | 0 | 0 | ||
| ABCLGII | 0.05 | 5.275 × 10−10 | 0 | 0 | 0 | 3.035 × 10−9 | ||
| HABCDE | 0.05 | 5.597 × 10−10 | 0 | 0 | 1.786 × 10−10 | 0 | ||
| GA | 0.0625 | 0 | 0 | 0 | 0 | 0 | ||
| PSO | 0.05 | 0 | 0 | 0 | 0 | 0 | ||
| 4 | ABC | 0.0500001 | 0 | 0 | 0 | 0 | 0 | |
| ABCG | 0.05 | 0 | 0 | 0 | 0 | 0 | ||
| ABCLGII | 0.05 | 1.384 × 10−9 | 0 | 1.050 × 10−9 | 1.486 × 10−10 | 3.510 × 10−10 | ||
| HABCDE | 0.05 | 1.386 × 10−9 | 0 | 1.049 × 10−9 | 2.280 × 10−10 | 0 | ||
| GA | 0.0626 | 0 | 0 | 0 | 4.768 × 10−7 | 0 | ||
| PSO | 0.05 | 0 | 0 | 0 | 0 | 0 | ||
| 6 | 2 | ABC | 0 | 0 | 0.6 | 0 | 0 | 0 |
| ABCG | 0 | 0 | 0.6 | 2.644 × 10−9 | 0 | 0 | ||
| ABCLGII | 0 | 0 | 0.6 | 2.640 × 10−9 | 0 | 0 | ||
| HABCDE | 0 | 0 | 0.6 | 2.644 × 10−9 | 0 | 0 | ||
| GA | 0 | 6.820 × 10−13 | 0.6441 | 2.980 × 10−8 | 0 | 7.629 × 10−6 | ||
| PSO | 0 | 0 | 0.6 | 0 | 0 | 0 | ||
| 5 | ABC | 0 | 0 | 0.6 | 0 | 0 | 2.514 × 10−10 | |
| ABCG | 0 | 0 | 0.6 | 0 | 0 | 0 | ||
| ABCLGII | 2.598 × 10−14 | 0 | 0.6 | 5.820 × 10−10 | 5.523 × 10−10 | 2.002 × 10−10 | ||
| HABCDE | 9.992 × 10−15 | 0 | 0.6 | 5.828 × 10−10 | 5.534 × 10−10 | 1.996 × 10−10 | ||
| GA | 3.074 × 10−8 | 0 | 0.5977 | 3.243 × 10−5 | 2.235 × 10−8 | 1.073 × 10−6 | ||
| PSO | 0 | 0 | 0.6 | 0 | 0 | 0 | ||
| 7 | 1 | ABC | 0.1 | 6.030 × 10−9 | 0 | 0.5 | 0 | 3.176 × 10−9 |
| ABCG | 0.1 | 0 | 0 | 0.5 | 0 | 0 | ||
| ABCLGII | 0.1 | 2.428 × 10−10 | 0 | 0.5 | 0 | 2.998 × 10−15 | ||
| HABCDE | 0.1 | 2.423 × 10−10 | 0 | 0.5 | 0 | 0 | ||
| GA | 0.1250 | 0 | 0 | 0.5002 | 1.513 × 10−8 | 0 | ||
| PSO | 0.1 | 0 | 0 | 0.5 | 0 | 0 | ||
| 3 | ABC | 0.1 | 0 | 0 | 0.5 | 0 | 0 | |
| ABCG | 0.1 | 0 | 0 | 0.5 | 0 | 0 | ||
| ABCLGII | 0.1 | 3.608 × 10−10 | 7.175 × 10−10 | 0.5 | 0 | 0 | ||
| HABCDE | 0.1 | 3.612 × 10−10 | 7.182 × 10−10 | 0.5 | 0 | 0 | ||
| GA | 0.1250 | 4.888 × 10−6 | 2.328 × 10−10 | 0.5010 | 2.384 × 10−7 | 1.197 × 10−7 | ||
| PSO | 0.1 | 0 | 0 | 0.5 | 0 | 0 | ||
| 8 | 4 | ABC | 0.0999 | 0.150002 | 0 | 0.400001 | 0.0499 | 2.300 × 10−6 |
| ABCG | 0.1 | 0.15 | 0 | 0.4 | 0.05 | 0 | ||
| ABCLGII | 0.1 | 0.15 | 0 | 0.4 | 0.05 | 0 | ||
| HABCDE | 0.1 | 0.15 | 0 | 0.4 | 0.05 | 0 | ||
| GA | 0.0625 | 0.1885 | 0 | 0.4119 | 1.967 × 10−6 | 0 | ||
| PSO | 0.1012 | 0.1505 | 0 | 0.4093 | 0 | 0 | ||
| 7 | ABC | 0.1 | 0.1499 | 0 | 0.4 | 0.0499 | 0 | |
| ABCG | 0.1001 | 0.1499 | 0 | 0.400004 | 0.050001 | 0 | ||
| ABCLGII | 0.1 | 0.15 | 0 | 0.4 | 0.05 | 6.652 × 10−10 | ||
| HABCDE | 0.1 | 0.15 | 0 | 0.4 | 0.05 | 6.656 × 10−10 | ||
| GA | 0.0674 | 0.1765 | 0 | 0.3988 | 0.0449 | 0.0019 | ||
| PSO | 0.2218 | 0 | 0.0397 | 0.4287 | 0 | 0 | ||
| Case No. | 5 | 6 | 7 | 8 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Slab No. | 1 | 4 | 2 | 5 | 1 | 3 | 4 | 7 | |
| Algorithms | ABC | 641 | 655 | 631 | 647 | 753 | 701 | 768 | 787 |
| ABCG | 660 | 673 | 666 | 628 | 740 | 724 | 747 | 753 | |
| ABCLGII | 59 | 53 | 59 | 61 | 58 | 58 | 60 | 62 | |
| HABCDE | 60 | 60 | 62 | 61 | 64 | 66 | 69 | 69 | |
| GA | 23 | 25 | 20 | 24 | 23 | 24 | 28 | 27 | |
| PSO | 22 | 23 | 22 | 25 | 24 | 25 | 29 | 28 | |
| Case No. | Slab No. | Algorithms | Damage Identification Results | Error |
|---|---|---|---|---|
| 2 | 2 | In this article | [4.139 × 10−10, 0.33, 0] | 0 |
| [19] | [0.04, 0.41, 0] | 0.079 | ||
| [20] | [0, 0.38, 0.03] | 0.063 | ||
| 3 | 3 | In this article | [0.05, 0.15, 0] | 0 |
| [19] | [0.033, 0.14, 0] | 0.017 | ||
| [20] | [0.046, 0.155, 0] | 0.014 | ||
| 5 | 1 | In this article | [0.05, 5.275 × 10−10, 0, 0, 0, 3.035 × 10−9] | 0 |
| [19] | [0.057, 0, 0, 0, 0, 0] | 0.005 | ||
| [20] | [0.048, 0, 0, 0, 0, 0] | 0.003 | ||
| 7 | 3 | In this article | [0.1, 3.608 × 10−10, 7.175 × 10−10, 0.5, 0, 0] | 0 |
| [19] | [0.15, 0.03, 0.12, 0.41, 0.07, 0] | 0.164 | ||
| [20] | [0.13, 0, 0.09, 0.54, 0.049, 0] | 0.118 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; He, X.; Jiao, Y. Damage Identification Algorithm of Hinged Joints for Simply Supported Slab Bridges Based on Modified Hinge Plate Method and Artificial Bee Colony Algorithms. Algorithms 2018, 11, 198. https://doi.org/10.3390/a11120198
Liu H, He X, Jiao Y. Damage Identification Algorithm of Hinged Joints for Simply Supported Slab Bridges Based on Modified Hinge Plate Method and Artificial Bee Colony Algorithms. Algorithms. 2018; 11(12):198. https://doi.org/10.3390/a11120198
Chicago/Turabian StyleLiu, Hanbing, Xin He, and Yubo Jiao. 2018. "Damage Identification Algorithm of Hinged Joints for Simply Supported Slab Bridges Based on Modified Hinge Plate Method and Artificial Bee Colony Algorithms" Algorithms 11, no. 12: 198. https://doi.org/10.3390/a11120198
APA StyleLiu, H., He, X., & Jiao, Y. (2018). Damage Identification Algorithm of Hinged Joints for Simply Supported Slab Bridges Based on Modified Hinge Plate Method and Artificial Bee Colony Algorithms. Algorithms, 11(12), 198. https://doi.org/10.3390/a11120198





