In this section, we describe how we implemented the convex-hull algorithms used in our workhorse experiments. Note that we have coded the algorithms by closely following the high-level descriptions given here. Therefore, an interested reader may want to read the source code alongside with the following text.
4.1. Plane Sweep
A sequence of points is monotone if the points are sorted according to their x-coordinates—in non-decreasing or non-increasing order. Let p, q, and r be three consecutive vertices on a monotone polygonal chain. Recall that a vertex q of such a chain is concave if there is a left turn or no turn (in the code the condition is not right_turn(p, q, r)) when moving from p to r via q. That is, the angle on the right-hand side with respect to the traversal order is greater than or equal to .
The
plane-sweep algorithm, proposed by Andrew [
3], computes the convex hull for a sequence of points as follows:
- (A)
Sort the input points in non-decreasing order according to their x-coordinates.
- (B)
Determine the leftmost point (west pole) and the rightmost point (east pole). If there are several pole candidates with the same x-coordinate, let the bottommost of them be the west pole; and on the other end, let the topmost one be the east pole.
- (C)
Partition the sorted sequence into two parts, the first containing those points that are above or on the line segment determined by the west pole and the east pole, and the second containing the points below that line segment.
- (D)
Scan the two monotone chains separately by eliminating all concave points that are not on the convex hull. For an early description of this backtracking procedure relying on cross-product computations, see [
33].
- (E)
Concatenate the computed convex chains to form the final answer.
It is worth mentioning that the backtracking procedure used in Step (D) does not work for all polygons as claimed in [
33] (for a bug report, see [
9]). What is important for our purposes is that it works for monotone polygonal chains provided that the poles are handled as discussed by Andrew [
3]: All other points that have the same
x-coordinate as the west pole (east pole) are eliminated, except the topmost (bottommost) one provided that it is not a duplicate of the pole. Furthermore, Andrew [
3] pointed out that in Step (C) it is only necessary to perform the orientation test for points whose
y-coordinate is between the
y-coordinates of the west and east poles. Usually, this will reduce the number of orientation tests performed by a significant fraction.
There is a catch hidden in the original description of the algorithm [
3]. In Step (C), the partitioning procedure must retain the sorted order of the points, i.e., it must be
stable. In Andrew’s description, it is not specified how this step is to be implemented. It is possible to do stable partitioning in place in linear time (see [
34]), but all linear-time algorithms developed for this purpose are considered to be galactic. That means they are known to have a wonderful asymptotic behaviour, but they are never used to actually compute anything [
35]. Therefore, it is understandable that Gomes’ implementation of
torch [
4] used extra arrays of indices to carry out multi-way grouping stably.
It is known that the
plane-sweep algorithm can be implemented in place. Unfortunately, the description given in [
15] does not lead to an efficient implementation; the goal of that article was to show that an in-place implementation is possible.
The problem with stable partitioning can be avoided by performing the computations in a different order: find the west and east poles before sorting. This way, when creating the two candidate collections, we can use unstable in-place partitioning employed in
quicksort—for example, the variant proposed by Lomuto ([
26], Section 7.1)—and sort the candidate collections separately after partitioning.
Let p and r be two points that are known to be on the convex hull. In our implementation of plane-sweep the key subroutine is chain: It takes an oriented line segment and a candidate collection C of points, which all lie on the left of , and computes the convex chain, i.e., part of the convex hull, from p to r via the points in C. The extreme points are specified by two iterators and the candidate collection is assumed to follow immediately after p in the input sequence. The past-the-end position of the candidate collection is yet another parameter. To make the function generic, so that it can compute both the upper hull and the lower hull, it has a comparator as its last parameter. This comparator specifies the sorting order of the points. As is customary in the C++ standard library, a less-than comparison function orders the points in non-decreasing order and a greater-than comparison function orders them in non-increasing order.
To accomplish its task,
chain works as follows: (a) If
C is empty, return the position of the successor of
p as the answer, i.e., the computed chain consists of
p. (b) Sort the candidates in the given order according to their
x-coordinates. As a result, the points with equal
x-coordinates can be arranged in any order. (c) If in
C there are points with the same
x-coordinate as
p, eliminate all the other except the one having the largest
y-coordinate—with respect to the given ordering—before any further processing. (d) Use the standard backtracking procedure [
33] to eliminate all concave points from the remaining candidates. The stack is maintained in place at the beginning of the zone occupied initially by
p and
C coming just after
p. This elimination process is semi-stable, meaning that it retains the sorted order of the points in the left part of partitioning; it may change the order of the eliminated points. (e) Return the position of the first eliminated point as the answer (or the past-the-end position of
C if all points are convex).
Thus, our in-place implementation of
plane-sweep processes any non-empty sequence of points as follows (for an illustration, see
Figure 2):
- (1)
Find the west and east poles by scanning the input sequence once. Place the poles at their respective ends of the input sequence. If the poles are the same point, stop and return the position of the successor of the west pole.
- (2)
Partition the input sequence into two parts: (a) the upper-hull candidates, i.e., the points that are above or on the line segment determined by the west pole and the east pole; and (b) the lower-hull candidates, i.e., the points below that line segment.
- (3)
Apply the function chain with the poles, the upper-hull candidates, and comparison function less than. This gives us the upper hull from the west pole to the east pole, excluding the east pole.
- (4)
Swap the east pole to the beginning of the lower-hull candidates, and apply the function chain with the two poles—this time giving the east pole first, the lower-hull candidates, and the comparison function greater than. After this we also have the lower hull, but it is not in its final place.
- (5)
Move the computed lower hull just after the computed upper hull (if it is not there already). This is a standard in-place block-swap computation. Finally, return the position of the first eliminated point (or the past-the-end position if all points are in the convex hull).
If
heapsort [
36] was used in the implementation of
chain, the whole algorithm would operate in place and run in
worst-case time. However, the C
++ standard-library
introsort [
27], which is a combination of
quicksort,
insertionsort, and
heapsort, is known to be more efficient in practice. Still, it guarantees the
worst-case running time and, because of careful programming, it operates in situ since the recursion stack is never allowed to become deeper than
.
4.2. Torch
The following definitions are from [
37]: (1) A
rectilinear line segment is a line segment oriented parallel to either the
x-axis or the
y-axis. (2) A point set is
rectilinear convex if for any two of its points which determine a rectilinear line segment, the line segment lies entirely in the given set. (3) Given a multiset
S of points, its (
connected)
rectilinear convex hull is the smallest connected rectilinear convex set enclosing all the points of
S. Roughly speaking, a rectilinear convex hull connects all the maximal points with four rectilinear curves.
At the abstract level,
torch [
2] operates in two stages: (1) Find the points on the rectilinear convex hull. (2) Refine this approximation by discarding all concave points from it. The correctness of this approach follows directly from the fact that the rectilinear convexity is a looser condition than the normal convexity. Ottmann et al. [
37] showed how to compute the rectilinear convex hull in
time and
space. If
plane-sweep is used to do the refinement, the overall running time of this procedure is
. A similar approach was proposed by Bentley et al. [
14] (see also [
38,
39])—they computed all maximal points; they were not interested in the rectilinear curvature. They proved that, under the assumption that the points are chosen from a probability distribution in which each coordinate of a point is chosen independently of all other coordinates, the number of maximal points is
. Using this fact, one can develop algorithms for computing maxima and convex hulls (for a historical review, see [
39]), for which the expected running time is
and the worst-case running time
.
Gomes [
2] combined the rectilinear-convex-hull algorithm by Ottmann et al. [
37] and the
plane-sweep algorithm [
3] as follows: (1) By integrating the two algorithms better, redundant sorting computations can be avoided. (2) By replacing lexicographic sorting with
x-sorting, a superset can be computed faster even though now it may include some extra maximal points that lie on the periphery of the rectilinear convex hull—i.e., the computation of the rectilinear convex hull is not fully accurate, but for our purpose these extra maximal points are by no means harmful. We call the points selected by Gomes’ heuristic algorithm
boundary points. In
torch, Steps (C) and (D) of the
plane-sweep algorithm are replaced with the following three steps (for an illustration, see
Figure 3):
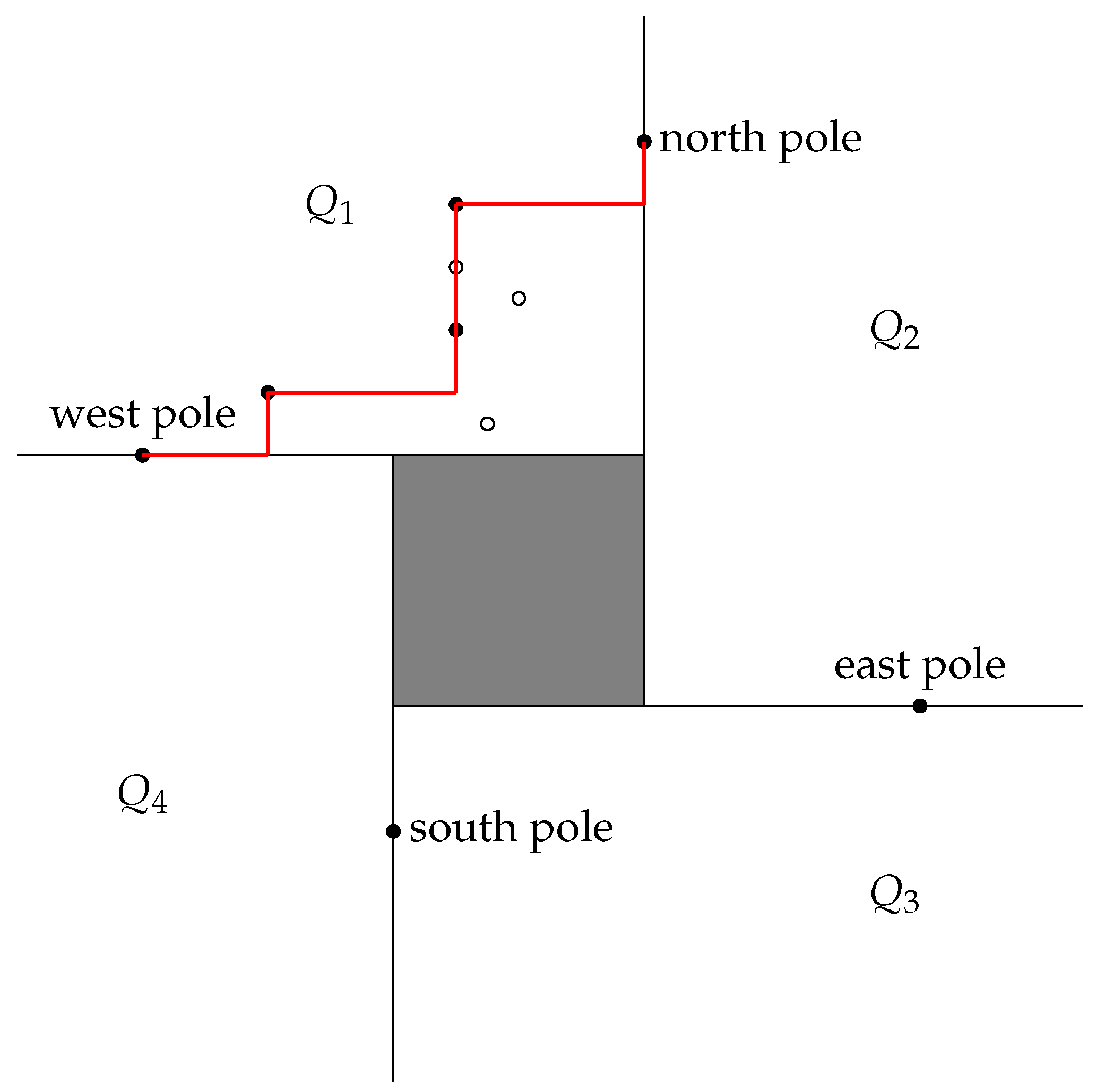
- (B’)
Find the topmost point (north pole) and the bottommost point (south pole) by one additional scan and resolve the ties in a similar fashion as in Step (B).
- (C’)
Group the input points into four (overlapping) candidate collections such that, for
, the
i’th collection contains the points that are not dominated by the adjacent poles in the respective direction (north-west, north-east, south-east, or south-west), i.e., these points are in the quadrant
of
Figure 3. Note that the quadrant includes the borders.
- (D’)
In each of the candidate collections, compute the boundary points before discarding the concave points that are not in the output polygon.
Let us look at Step (D’) a little more thoroughly by considering what is done in : (1) The points in are sorted according to their x-coordinates. (2) The sorted sequence is scanned from the west pole to the north pole and a point is selected as a boundary point if its y-coordinate is larger than or equal to the maximum y-coordinate seen so far. That is, the selected points form a monotonic sequence both with respect to their x-coordinates and y-coordinates; we call such a sequence a staircase. Since the points on the computed staircase are all maximal and only maximal points on a rectilinear line segment determined by two other points may be discarded, the staircase must contain all vertices of the convex hull that are in . (3) As the final step, the standard backtracking procedure is applied for the points in the staircase to get the part of the convex hull that is inside .
One should observe that the classification, whether a point is a boundary point or not, depends on the original order of the points. For example, consider a multiset of three points , , given in this order. All these points are dominant in the north-west direction, but the scan only selects the first two as the boundary points. If the order of the last two points had been the opposite, then all three would be classified as boundary points. Since it is unspecified, how a sorting algorithm will order points whose x-coordinates are equal, in our worst-case constructions we assume that such points are ordered so that all maximal points will be classified as boundary points.
The processing in the other quadrants is symmetric. In the points are scanned from the east pole to the north pole and the staircase goes upwards as in . In the processing is from the east pole to the south pole and we keep track of the current minimum with respect to the y-coordinates—so the staircase goes downwards. Finally, in the points are scanned from the west pole to the south pole and the staircase goes downwards as in .
In Step (C’), to do the grouping, it is only necessary to compare the coordinates, the orientation test is not needed. Also, in Step (D’), only coordinate comparisons are done, no arithmetic operations. In the original description [
2], the staircases were concatenated to form an approximation of the convex hull before the final elimination scan. However, doing so may cause the algorithm to malfunction—we will get back to the correctness of this approach in
Section 5.3.
The asymptotic running time of this algorithm is determined by the sorting steps, which require a total of
time in the worst case and in the average case for the best comparison-based sorting method. If the number of maximal points is small as the theory suggests [
14], the cost incurred by the evaluation of the orientation tests will be insignificant. Compared to other alternatives, this algorithm is important for two reasons:
- (1)
Only the x-coordinates are compared when sorting the points.
- (2)
The number of the orientation tests performed is proportional to the number of maximal points, the coefficient being at most two times the average number of directions the points are dominant in.
As to the use of memory, in the implementation of
torch [
4], Gomes used
four arrays of indices—implemented as std::vector—to keep track of the points in each of the four candidate collections,
an array of points—implemented as std::vector—to store the boundary points in the approximation, and
a stack—implemented as std::deque—to store the output.
Fact 1. In the worst-case scenario, Gomes’ implementation may require space for about indices and points for multiset data (or about indices and points for set data) for temporary arrays, or points and pointers for the output stack.
Proof. To verify this deficiency for multisets, consider a special input having four poles , , , and points at the origin. Since the duplicates are on the border, they should be placed in each of the four candidate collections. Hence, each of the index arrays will be of size . Since the origin is not dominated by any of the poles, none of the duplicates will be eliminated. Therefore, all the duplicates should be included in the approximation of the convex hull, which may contain about points. For sets, in a bad input all input points lie on a line. In this case, all points should be placed in the candidate collections for two of the four quadrants. Again, none of the points on the line are dominated by the poles. Therefore, the approximation may contain points.
For C
++ standard-library vectors, the total amount of space allocated can be two times larger than what is actually needed (see, for example, the benchmarks reported in [
40]). In the C
++ standard library, by default a stack is implemented as a deque which is realized by maintaining a vector of pointers to memory segments (of, say, 512 points). From this discussion, the stated bounds follow. □
It should be emphasized that this heuristic algorithm only reduces the number of orientation tests performed in the average case. There is no asymptotic improvement in the overall running time—in the worst case or in the average case—because the pruning is done after the sorting. The plane-sweep algorithm may perform the orientation test up to about times. For the special input described above, torch may perform the orientation test at least times, so in the worst case there is no improvement in this respect either. As we utilize an implementation improvement, where not all maximal points are computed, but only those that form a staircase in each of the four quadrants, some of the maximal points may be eliminated already during this staircase formation. Experimentally, the highest number of orientation tests observed to be performed by torch was .
Due to the correctness issues and excessive use of memory, we decided to implement our own version of
torch. Our corrected version requires
or
words of additional memory, depending on whether
heapsort [
36] or
introsort [
27] is used in sorting. After finding the poles, the algorithm processes the points in four phases:
- (1a)
Partition the input sequence such that the points in the north-west quadrant (
in
Figure 3) determined by the west and north poles are moved to the beginning and the remaining points to the end (normal two-way partitioning).
- (1b)
Sort the points in according to their x-coordinates in non-decreasing order.
- (1c)
Find the boundary points in and move the eliminated points at the end of the zone occupied by the points of . Here the staircase goes upwards.
- (1d)
Scan the boundary points in to determine the convex chain from the west pole to the north pole. Again, the eliminated points are put at the end of the corresponding zone.
- (2a)
Consider all the remaining points (also those eliminated earlier) and partition the zone occupied by them into two so that the points in become just after the west-north chain ending with the north pole.
- (2b)
Sort the points in according to their x-coordinates in non-increasing order.
- (2c)
Find the boundary points in as in Step (1c). Also here the staircase goes upwards.
- (2d)
Reverse the boundary points in place so that their x-order becomes non-decreasing.
- (2e)
Continue the scan that removes the concave points from the boundary points to get the convex chain from the north pole to the east pole.
- (3)
Compute the south-east chain of the convex hull for the points in as in Step (2), except that now the staircase goes downwards and the reversal of the boundary points is not necessary.
- (4)
Compute the south-west chain of the convex hull for the points in as in Step (2), except that now the sorting order is non-decreasing and the staircase goes downwards.
It is important to observe that any point in the middle of
Figure 3 is dominated by one of the poles in each of the four directions. Hence, these points are never moved to a candidate collection. However, if a point lies in two (or more) quadrants, it will take part in several sorting computations. (In
Figure 3, move the east pole up and see what happens.) To recover from this, it might be advantageous to use an adaptive sorting algorithm.
4.3. Quickhull
The
quickhull algorithm, which mimics
quicksort, has been reinvented several times (see, e.g., [
8,
9,
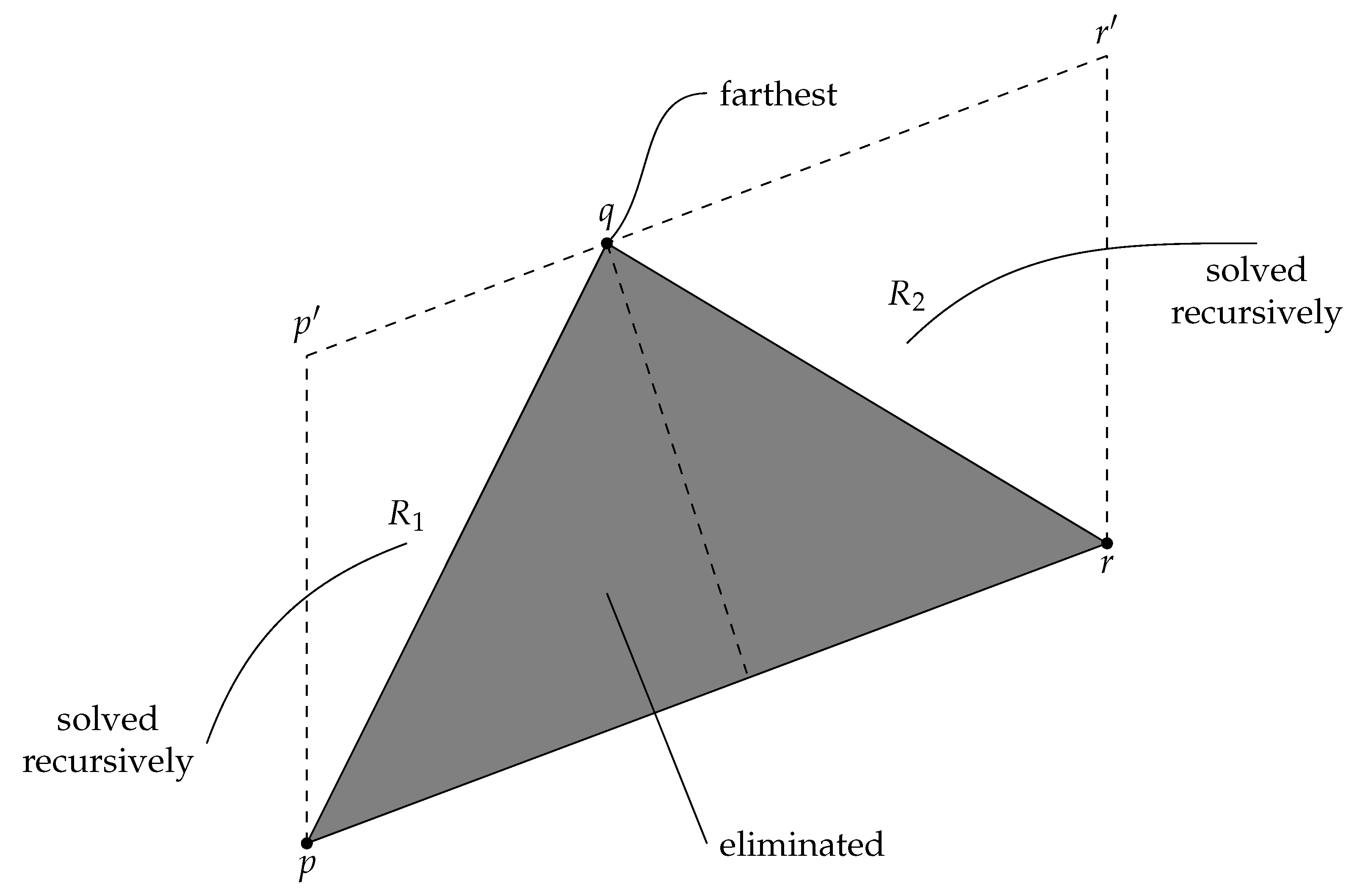
10]). The key subroutine is again the one that chains two extreme points together, but now it is implemented recursively (for a visualization, see
Figure 4). The parameters are an oriented line segment
determined by two extreme points
p and
r, and a collection
C of points on the left side of
. If the cardinality of
C is small, we can use any brute-force method to compute the convex chain from
p to
r, return that chain, and stop. Otherwise, of the points in
C, we find an extreme point
q in the direction orthogonal to
; in the case of ties, we select the leftmost extreme point. Then, we eliminate all the points inside or on the perimeter of the triangle
from further consideration by moving them away to the end of the zone occupied by
C. Finally, we invoke the recursive subroutine once for the points of
C that are on the left of
, and once for the points of
C that are on the left of
. An important feature of this algorithm is that the interior points are eliminated during sorting—full sorting may not be necessary. Therefore, we expect this algorithm to be fast.
Gomes used the
qhull program [
41] in his experiments. However, he did not give any details how he used this library routine so, unfortunately, we have not been able to repeat his experiments. From the
qhull manual [
42], one can read that the program is designed to
solve many geometric problems,
work in the d-dimensional space for any ,
be output sensitive,
reduce space requirements, and
handle most of the rounding errors caused by floating-point arithmetic.
Based on this description, we got a feeling that this is like using a sledgehammer to crack a nut. Simply, specialized code designed for finding the two-dimensional convex hull—and only that—should be faster. After doing the implementation work, the resulting code was less than 200 lines long. As an extra bonus,
we had full control over any further tuning and
we could be sure that the computed output was correct as, also here, we relied on exact integer arithmetic.
In our implementation of
quickhull we followed the guidelines given by Eddy [
8] (the space-efficient alternative): (1) As in
plane-sweep, find the two poles, the west pole
p and the east pole
r. Put
p first and
r last in the sequence. (2) Partition the remaining points between
p and
r into upper-hull and lower-hull candidates:
contains those points that lie above or on the line segment
and
those that lie below it. (3) Call the recursive elimination routine described above for the upper-hull candidates with the parameters
and
. (4) Move
r just after the upper chain computed and the eliminated points after the lower-hull candidates. (5) Apply the recursive elimination routine for the lower-hull candidates with the parameters
and
. (6) Now the point sequence is rearranged such that (a)
p comes first, (b) the computed upper chain follows it, (c)
r comes next, (d) then comes the computed lower chain, and (e) all the eliminated points are at the end. Lastly, return the position of the first eliminated point (or the past-the-end position if no such point exists) as the final answer.
As a matter of fact, the analogy with
quicksort [
16] is not entirely correct since it is a randomized algorithm—a random element is used as the pivot. Albeit, Barber et al. [
41] addressed both randomized and the non-randomized versions of
quickhull. Eddy [
8] made the analogy with
quickersort [
43], in which the middle element is used as the pivot and the stack size is kept logarithmic. In our opinion, this analogy is not quite correct either. It would be more appropriate to see the algorithm as an incarnation of the
middle-of-the-range quicksort where for each subproblem the minimum and maximum values are determined and their mean is used as the pivot. If the elements being sorted are integers drawn from a universe of size
U, the worst-case running time of this variant is
.
Eddy [
8] showed that the worst case of
quickhull is
. However, Overmars and van Leeuwen [
44] proved that in the average case the algorithm runs in
expected time. The result holds when the points are chosen uniformly and independently at random from a bounded convex region. Actually, their proof is stronger, because by exploiting the connection to
middle-of-the-range quicksort, it can be applied to get the following:
Fact 2. When the coordinates of the points are integers drawn from a bounded universe of size U, the worst-case running time ofquickhullis .
Proof. The key observation made by Overmars and van Leeuwen [
44] was that, if in the general recursive step the problem under consideration covers an area of size
A (the region of interest must be inside the parallelogram
in
Figure 4), then the total area covered by the two subproblems considered at the next level of recursion is bounded from above by
(some regions inside
and
in
Figure 4).
When this observation is applied to the bounded-universe case, we know that the area covered by the topmost recursive call is at most . That is, the depth of the recursion must be bounded by . In the recursion tree, since the subproblems are disjoint, the total work done at each level is at most . Thus, the running time must be bounded by . □
So, in the bounded-universe case, middle-of-the-range quicksort and quickhull cannot work tremendously badly. As an immediate consequence, if these algorithms are implemented recursively, the size of the recursion stack will be bounded by .
4.4. Other Elimination Heuristics
The
quickhull algorithm brings forth the important issue of eliminating interior points—if there are any—before sorting. When computing the convex hull, one has to consider all directions when finding the extreme points. A rough approximation of the convex hull is obtained by considering only a few specific directions. As discussed in several papers (see, for example, [
3,
11,
12]), by eliminating the points falling inside or on the boundary of such an approximation, the problem size can often be reduced considerably. After this kind of preprocessing, any of the algorithms mentioned earlier could be used to process the remaining points.
For a good elimination strategy two things are important: (1) speed and (2) effectiveness. To achieve high speed, the elimination procedure should be simple. With good elimination effectiveness, the cost of the main algorithm may become insignificant. So there is a trade-off between the two.
Akl and Toussaint [
11] found the extrema in four equispaced directions—those determined by the coordinate axes. Also, Andrew [
3] mentioned this as an option to achieve further saving in the average-case performance of the
plane-sweep algorithm. This
poles-first algorithm, as we name it, works as follows: (1) Compute the west, north, east, and south poles. (2) Eliminate the points inside or on the perimeter of the quadrilateral (or triangle or line segment) having these poles as its vertices. (3) Apply the
plane-sweep algorithm for the remaining points. The elimination overhead is two scans—so the elimination procedure is fast. Unfortunately, it is not always efficient. For example, in the case that the west and south poles coincide, and the north and east poles coincide, only the points on the line segment determined by the two poles will be eliminated.
Devroye and Toussaint [
12] used eight equispaced directions. We name this algorithm
throw-away; we implemented it as follows: (1) Find the extreme points in eight predetermined directions:
,
,
, and
. (2) Eliminate all the points inside or on the boundary of the convex polygon determined by the found points. (3) Apply the
plane-sweep algorithm for the remaining points. Also here, the elimination overhead is two scans: one max-finding scan to find the extrema and another partitioning scan to do the elimination. If the
plane-sweep algorithm used
heapsort, the whole algorithm would work in place; with
introsort it works in situ instead.
Devroye and Toussaint [
12] proved that for the square data set the number of points left after
throw-away preprocessing will be small. Unfortunately, as also pointed out by them, the result depends heavily on the shape of the region, from where the points are drawn randomly.
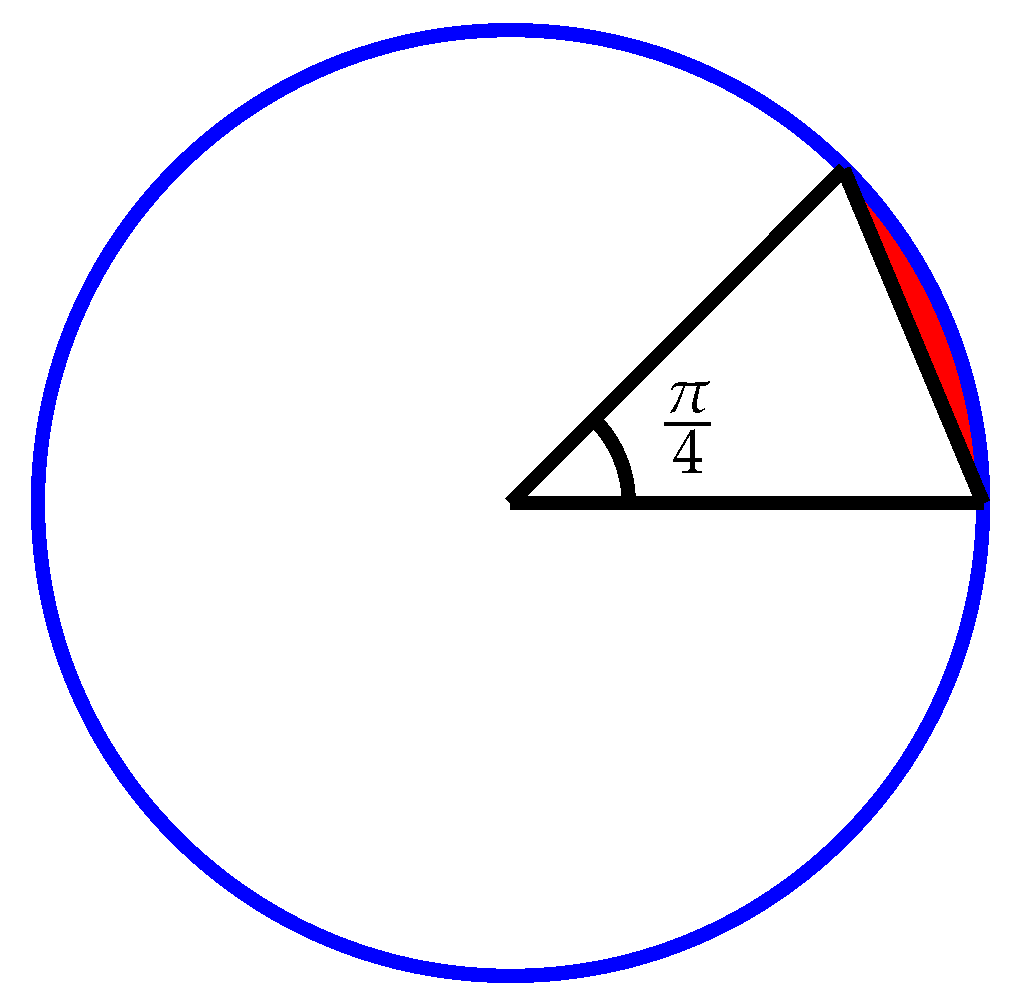
Fact 3. For the disc data set of size n, the expected number of points left afterthrow-awaypreprocessing is bounded from below by .
Proof. Let
r be the radius of the circle, in which the points lie. The preprocessing step finds (up to) eight points. Assume that the polygon determined by the found points covers the largest possible area inside the circle. Trivially, the shape that maximizes the covered area is an equal-sided octagon touching the circle at each of the vertices. Let us now consider one of the sectors defined by two consecutive vertices of such an octagon (see
Figure 5). The inside angle of this sector is
. Hence, the area of the sector is
. The area of the triangle inside this sector is
. Since
, the area of the top of the sector inside the circle that is not covered (the red area in
Figure 5) is
. Summing this over all eight sectors, the fraction of the circle that is not covered is
. This is about
%. From this it follows that the expected number of points left after elimination must be larger than
, as claimed. □
An implementation of the
throw-away algorithm was described in [
18]. The authors tried to make the integration between the preprocessing step and the
plane-sweep algorithm smooth to prevent repetitive work in the latter (recomputation of the poles and orientation tests in partitioning). However, the linear space needed for this integration was a high price to pay because, after elimination, the main bulk of the work is done in sorting.
Yet another alternative is to see quickhull as an elimination algorithm. To integrate quickhull with plane-sweep, we reimplemented it in an introspective way. When the recursion depth reached some predetermined threshold, we stopped the recursion and solved the subproblem at hand using plane-sweep. For integer k, let k-introhull be the member of the family of quickhull algorithms for which the threshold is k. For example, 3-introhull is quite similar to throw-away elimination. The member -introhull is significant, because the amount of work done at the top portion of the recursion tree will be bounded by and the amount of the work done when solving the subproblems at the leaves will also sum up to . For this variant, the worst-case running time is as for the plane-sweep algorithm. Still, the average-case running time is since the expected number of points left decreases geometrically with recursion depth. From this it follows that the expected number of points left at recursion level is .
By the observation of Overmars and van Leeuwen [
44], for
k-
introhull, the expected number of points left after the elimination should at most be around
for both of our data sets. To verify this bound in practice, we measured the expected number of points left after elimination for the two data sets. To understand how
k-
introhull works compared to the other elimination heuristics, we made the same experiments for them, too.
The numbers in
Table 3 are the averages of many repetitions, except those on the last row. The elimination effectiveness of
poles-first is not impressive—although there are no surprises in the numbers. The
throw-away algorithm works better; it is designed for the square data set, but the limit
in the elimination effectiveness for the disc data set leaves some shadows for this algorithm. The numbers for 3-
introhull are basically the same as those for
throw-away. Roughly speaking, in
quickhull all the work is done at a few first recursion levels. Compared to the static
throw-away algorithm, the elimination strategy applied in
quickhull is adaptive, and it can be made finer by increasing
k. If good worst-case efficiency is important and one wants to use
quickhull, we can warmly recommend
-
introhull. The overhead compared to the standard set-up is one if statement in each recursive call to check if the leaf level has been reached. So the worst-case performance of
quickhull can be reduced from
to
if wanted.