New and Efficient Algorithms for Producing Frequent Itemsets with the Map-Reduce Framework

Abstract

The Map-Reduce (MR) framework has become a popular framework for developing new parallel algorithms for Big Data. Efficient algorithms for data mining of big data and distributed databases has become an important problem. In this paper we focus on algorithms producing association rules and frequent itemsets. After reviewing the most recent algorithms that perform this task within the MR framework, we present two new algorithms: one algorithm for producing closed frequent itemsets, and the second one for producing frequent itemsets when the database is updated and new data is added to the old database. Both algorithms include novel optimizations which are suitable to the MR framework, as well as to other parallel architectures. A detailed experimental evaluation shows the effectiveness and advantages of the algorithms over existing methods when it comes to large distributed databases.

1. Introduction

The amount of information generated in our world has grown in the last few decades at an exponential rate. The rise of the internet, growth of the number of internet users, social networks with user generated data and other digital processes contributed to petabytes of data being generated and analyzed. This process resulted in a new term: Big Data. Classical databases (DB) are unable to handle such size and velocity of data. Therefore, special tools were developed for this task. One of the common tools that is in use today is the Map-Reduce (MR) framework [1]. It was originally developed by Google, but currently the most researched version is an open source project called Hadoop [2]. MR provides a parallel distributed model and framework that scales to thousands of machines.

While today there are more recent parallel architectures like Spark [3], arguably, in terms of developed algorithms, MR is the most popular framework for contemporary large-scale data analytics [4]. The MR original paper has been cited more than twenty-five thousand times. Therefore, MR is the focus of the present paper. In addition, the algorithms presented in this paper include optimizations which can be applied to any parallel architecture that processes large distributed databases where each node processes one chunk of data; thus, their applicability is beyond the MR framework.

Association Rules Mining (ARM) is an important problem in Data Mining and has been heavily researched since the 1990s. It is being solved in two steps: firstly, by finding all Frequent Itemsets (FI) by a process called Frequent Itemsets Mining (FIM), and then generating the rules themselves from FI. FIM is the most computationally intensive part of ARM [5,6,7]. Solving FIM efficiently allows for efficient solving of the ARM problem. Most of the studies were done thoroughly in centralized static dataset [8] and data stream [9] settings. With data growth, classical FIM/ARM algorithms that were designed to be used on a single machine had to be adapted to a parallel environment. Recently, a few solutions were proposed for running classical FIM/ARM algorithms in the Map-Reduce framework [10,11,12,13]. These algorithms find frequent itemsets for a given static database. Our goal in this paper is to improve these algorithms in some common and important scenarios.

There are several strategies to handle FIM more efficiently. One of the strategies, which is a major branch in this research field, is mining closed frequent itemsets instead of frequent itemsets in order to discover non-redundant association rules. A set of closed frequent itemsets is proven to be a complete yet compact representation of the set of all frequent itemsets [14]. Mining closed frequent itemsets instead of frequent itemsets saves computation time and memory usage, and produces a compacted output. Many algorithms, like Closet, Closet+, CHARM and FP-Close [8], have been presented for mining closed frequent itemsets in centralized datasets. Handling very large databases is more challenging than mining centralized data in the following aspects: (1) the distributed settings are in a shared-nothing environment (one can of course share data, however it is very expensive in terms of communication), meaning that assumptions like shared memory and shared storage, that lie at the base of most algorithms, no longer apply; (2) data transfer is more expensive than data processing, meaning that performance measurements change; (3) the data is huge and cannot reside on a single node. This paper will describe our scheme for distributed mining of closed frequent itemsets which overcomes the drawbacks of existing algorithms.

Another strategy for efficiently handling FI is to mine FI and then always keep FI up-to-date. There is a need for an algorithm that will be able to update the FI effectively when the database is updated, instead of re-running the full FIM algorithm on the whole DB from scratch. There are incremental versions of FIM and ARM algorithms [15,16] for single machine execution. Some of these algorithms can even suit a distributed environment [17], but not the MR model. Because the MR model is more limited than general distributed or parallel computation models, the existing algorithms cannot be used in their current form. They must be adjusted and carefully designed for the MR model to be efficient.

Our contributions in this paper are:

• A novel algorithm for mining closed frequent itemsets in big, distributed data settings, using the Map-Reduce paradigm. Using Map-Reduce makes our algorithm very pragmatic and relatively easy to implement, maintain and execute. In addition, our algorithm does not require a duplication elimination step, which is common to most known algorithms (it makes both the mapper and reducer more complicated, but it gives better performance).
• A general algorithm for mining incremental frequent itemsets for general distributed environments with additional optimizations of the algorithm. Some of the optimizations are unique for the Map-Reduce environment but can be applied to other similar architectures.
• We conducted extensive experimental evaluation of our new algorithms and show their behavior under various conditions and their advantages over existing algorithms.

The rest of the paper is structured as follows. Section 2 presents the closed frequent itemset mining algorithm. Section 3 discusses the incremental frequent itemset algorithm. Section 5 is the conclusions section. A preliminary short presentation of the algorithms has appeared in [18,19].

2. Background and Related Work

In this section, we present the necessary background and describe the existing MR based algorithms. Some of them will be used for comparison in the evaluation sections.

2.1. Association Rules and Frequent Itemsets

Association rule mining was introduced in [5,6] as a market basket analysis for finding items that were bought together—if a customer bought item(s) X, then with high probability item(s) Y will be also purchased ($\mathrm{X}⟹\mathrm{Y}$) (e.g., 98% of customers who purchase tires and auto accessories also get an automotive service done). A pre-requisite to finding association rules is the mining of frequent itemsets (FIM) (itemsets that appear in at least some percentage of the transactions).

One of the most well-known algorithms for association rules is the Apriori algorithm described in [5,6]. This algorithm uses a pruning rule called Apriori, which states that an itemset may be frequent if all its subsets are also frequent. The algorithm is based on iteratively generating candidates for frequent itemsets and then pruning them. The algorithm starts with candidates of size one, which includes all possible items, and every iteration increases the length of the candidates by one. At the end of each iteration, the candidates are pruned by their count in the DB and those who survive (their count is larger than the minimal threshold) are added to the final set of frequent itemsets. Candidates for the next iteration are being generated based on the survivors. The algorithm stops when it cannot generate longer candidates, and then it generates all association rules from the frequent itemsets.

There are several versions of implementing Apriori in the distributed environment [20,21]. The most important idea is that if an itemset is frequent in a union of distributed databases, it must be frequent in at least one of them. A simple proof by contradiction goes like this:

Assume that itemset $x$ is frequent in union DB ($\mathcal{D}={{\displaystyle \cup }}^{\text{}}{\mathcal{D}}_{\mathrm{i}}$), then $su{p}_{\mathcal{D}}\left(x\right)$ (count of $x$ in the $\mathcal{D}$) is at least $minSup*\left|\mathcal{D}\right|$ times. Assume also that $x$ is not frequent in any partial ${\mathcal{D}}_{\mathrm{i}}$, then:

$$su{p}_{{\mathcal{D}}_i}\left(x\right)<\mathit{minSup}*\left|{\mathcal{D}}_i\right|.$$

Then:

$$su{p}_{\mathcal{D}}\left(x\right)={{\displaystyle \sum }}^{\text{}}su{p}_{{\mathcal{D}}_i}\left(x\right)<{{\displaystyle \sum }}^{\text{}}\mathit{minSup}*\left|{\mathcal{D}}_i\right|=\mathit{minSup}*{{\displaystyle \sum }}^{\text{}}\left|{\mathcal{D}}_i\right|=\mathit{minSup}*\left|\mathcal{D}\right|$$

and we get a contradiction of $x$ being frequent in the $\mathcal{D}$.

A similar idea will be used by us in the incremental case.

2.2. Mining Closed Frequent Itemsets Algorithms

An itemset is closed if there is no super itemset that has the same support count as the original itemset. Closed itemsets are more useful since they convey meaningful information, and their number is much smaller than standard itemsets.

The first algorithm for mining closed frequent itemsets, A-Close, was introduced in [14]. It presents the concept of a generator—a set of items that generates a single closed frequent itemset. A-Close implements an iterative generation-and-test method for finding closed frequent itemsets. On each iteration, generators are tested for frequency, and non-frequent generators are removed. An important step is duplication elimination: generators that create an already existing itemset are also removed. The surviving generators are used to generate the next candidate generators. A-Close was not designed to work in a distributed setting.

MT-Closed [22] is a parallel algorithm for mining closed frequent itemsets. It uses a divide-and-conquer approach on the input data to reduce the amount of data to be processed during each iteration. However, its parallelism feature is limited. MT-Closed is a multi-threaded algorithm designed for multi-core architecture. Though superior to single-core architecture, multi-core architecture is still limited in its number of cores and its memory is limited in size and must be shared among the threads. In addition, the input data is not distributed, and an index-building phase is required.

D-Closed [23] is a shared-nothing environment distributed algorithm for mining closed frequent itemsets. It is similar to MT-Closed in the sense that it recursively explores a sub-tree of the search space: in every iteration, a candidate is generated by adding items to a previously found closure, and the dataset is projected by all the candidates. It differs from MT-Closed in providing a clever method to detect duplicate generators: it introduces the concepts of pro-order and anti-order, and proves that among all candidates that produce the same closed itemset, only one will have no common items with its anti-order set. However, there are a few drawbacks to D-Closed: (1) it requires a pre-processing phase that scans the data and builds an index that needs to be shared among all the nodes; (2) the set of all possible items also needs to be shared among all the nodes; and (3) the input data to each recursion call is different, meaning that iteration-wise optimizations, like caching, cannot be used.

Sequence-Growth by Liang and Wu [24] is an algorithm for mining frequent itemsets based on Map-Reduce. The algorithm cleverly applies the idea of lexicographical order to construct the candidate sequence subsets to avoid expensive scanning. It does so by building a lexicographical sequence tree that finds all frequent itemsets without an exhaustive search over the transaction database. However, this algorithm does not directly mine closed itemsets, which is our goal. Closed itemsets can be derived from the output, however this requires further processing that makes it less efficient.

Wang et al. [25] have proposed a parallelized AFOPT-close algorithm [26] and have implemented it using Map-Reduce. AFOPT-close is a frequent itemset mining algorithm that uses a pattern growth approach. It uses dynamic ascending frequency order and three different structures to represent conditional databases, depending on the sparsity of the database. To prune non-closed itemsets, it uses a patterns tree data structure.

Like the previous algorithms, it also works in a divide-and-conquer way: first, a global list of frequent items is built, then a parallel mining of local closed frequent itemsets is performed, and finally, non-global closed frequent itemsets are filtered out, leaving only the global closed frequent itemsets. However, they still require that the final step (checking the globally closed frequent itemsets, which might be very heavy depending on the number of local results).

2.3. Incremental Frequent Itemsets Mining

The idea of maintenance of association rules and frequent itemsets during database update has been discussed shortly after the first algorithms for FIM appeared. The reason for it is that the updated part is usually much smaller than the full DB, and this fact could be used for faster algorithms. A well-known efficient algorithm for it is “Fast Update” (FUP) [15]. It is based on the fact that for an item to be frequent in the updated database (${\mathcal{D}}^{+}$), it must be frequent in the old DB (or simply $\mathcal{D}$), and/or the new added transactions ($\Delta$). Table 1 describes the options for an itemset to become frequent or not frequent in ${\mathcal{D}}^{+}$ (it is based on the same observation discussed in the previous chapter).

Table 1. Cases for item to be frequent and the outcome.

	$\mathbf{Frequent}\mathbf{in}\mathcal{D}$	$\mathbf{Not}\mathbf{Frequent}\mathbf{in}\mathcal{D}$
Frequent in $\Delta$	Frequent in ${\mathcal{D}}^{+}$	Unknown
Not frequent in $\Delta$	Unknown	Not frequent in ${\mathcal{D}}^{+}$

FUP is working iteratively by mining only new $\Delta$ by a method similar to Apriori. At the end of each iteration, for each FI, the algorithm decides if it is frequent, not frequent or needs to be counted in the old $\mathcal{D}$. The transactions being recounted in the old $\mathcal{D}$ are pruned away as necessary. The survivors are used to create candidates for the next iteration. By performing most of the work only on $\Delta$, the algorithm achieves better time compared to re-running the full mining algorithm on the whole ${\mathcal{D}}^{+}$.

ARMIDB [7] is based on FUP but tries to minimize scans over the original $\mathcal{D}$ while still calculating the incremented FI. It tries to use data from the original FI, update them and then uses a technique called “Look Ahead for Promising Items” (LAPI). It then scans for candidates in $\Delta$ only for those items that may be frequent in ${\mathcal{D}}^{+}$ (early pruning of candidates that cannot be frequent in ${\mathcal{D}}^{+}$ during the scan of $\Delta$). However, it is not a distributed algorithm like ours.

2.4. Map-Reduce Model

Map-Reduce is a parallel model and framework introduced in [1]. The abstract model requires defining two functions (algorithms):

$$map\left(k1,v1\right)\to list\left(k2,v2\right)$$

$$reduce\left(k2,list\left(v2\right)\right)\to list\left(v2\right)$$

Map is applied to all input elements and transforms them to a key/value pair. Reduce is applied to all elements with the same key (after transformation by “map”) and generates the final output. Reduce has access to all the values that are associated with some key, so it can output one, many or no values at all.

The framework takes care of everything else—reading the physical input, splitting it into distributed nodes, executing the worker processes on the remote machines for handling logical tasks, running the map function tasks on all the records from the input, sending the results to reduce function tasks, output of the final results from reducers, fault tolerance, and recovery if required, etc. The flow is shown in Figure 1. Each map and reduce combination that is executed on some input is called a job. Some algorithms may require multiple consecutive jobs of the same or different Map-Reduce functions to accomplish the algorithm goal (e.g., iterative algorithms like Apriori may require K iterations before finishing—one Map-Reduce for a candidate of length K—that would generate K Map-Reduce jobs). Data for Map-Reduce is saved in a distributed file system. In Hadoop [2], it is called Hadoop Distributed File System (HDFS) [27]. Data is kept in blocks of constant size. The most common values for block sizes that are being used are 32 megabytes (MB), 64 MB and 128 MB.

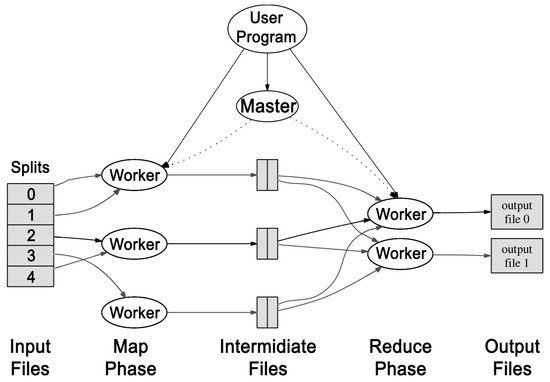
Figure 1. Map-Reduce Framework [1].

In Map-Reduce, each chunk of split input is called simply a “Split”. The standard way for Map-Reduce to split the input is by using a constant size. MR does this by using the HDFS file system blocks, so the sizes are mostly similar to HDFS or its multiplier. The MR framework makes sure not to split the logical input in the middle of an information unit. By default, information from a Split is being provided to a Mapper line-by-line. There is a strong correlation between a Split and a Mapper: each Split is related to a single Mapper and vice versa. The data from the Split is processed exactly once. The exceptions to it are in fault/recovery scenarios and speed optimization (if we have more than one idle machine, we can do the same computation twice and use the results of the fastest machine).

The Map-Reduce framework may have more stages in a job that supports executing map and reduce functions, e.g., Combiner can perform local “reduce” just after the Mapper on the same machine and the Partitioner is responsible for sending data from the Mapper/Combiner output to the Reducer input. Most of the steps could be customized to support more advanced scenarios via configuration, code or changing the source code of Hadoop itself, i.e., Input Reading: instead of reading input line-by-line, the whole file could be read and provided to the map stage as one large input. Another example is providing a custom partitioning function that would send input to the reducer by some algorithm logic instead of doing it by simple hash of the key.

2.5. Incremental Computation in Map-Reduce

Most of the time, when data is changed or added, the result of the algorithm also changes. Map-Reduce doesn’t provide built-in tools in the model or framework to support result updates. There are some attempts by researchers to enhance the Map-Reduce model to support it.

One of the attempts is the Incoop system [28]. This paper proposes a way (that is almost transparent to the user of Map-Reduce) to keep the results of the algorithm updated as new data is added. The system treats the computations as a Directed Acyclic Graph (DAG) of data that flows from input to output, and on the way, it is transformed by user functions. When data is updated, the system re-runs only the part of the graph that has some new input. This system uses a Memoization technique to keep the data–algorithm–result dependencies. This works well for the Mapper (map job), as only a few data records affect a small number of Mappers. In the case where a new key–value pair is generated for the Reducer (reduce job), then it will need to re-run its function on the whole previous input (new value and all old values). To treat this problem, Incoop also has a new stage called Contraction, which allows the user to supply additional functions that can combine several reducer input/outputs. It allows for dividing larger inputs into smaller parts and re-running the algorithm only on the updated part.

A similar approach can be found in DryadInc [29]. The idea was developed for a system called Dryad, which is a more general version of Map-Reduce. The main difference is that Dryad allows any DAG of computations, not only Map and Reduce. In the incremental version, there’s also a Cache server that keeps input/output relations and a new Merge function which can merge outputs of any function (and not only of Map as in Incoop).

Since Memoization and incremental caching of Incoop are not part of the standard Map-Reduce, and since their source code is not publicly available, we decided to do our experimental evaluation using the standard Map-Reduce framework only. Yet, we can assume that these enhancements may not work well for FIM (especially Apriori) algorithms. The basis for this claim is that new input records for Apriori may generate new frequent itemsets of any length, and in the following iterations the new input records generate even more frequent itemsets based on them. So, a small change in the input may propagate to a very large part of the output. Another reason is that each step requires a recount of frequent itemsets over the whole ${\mathcal{D}}^{+}$ (with new records), so none of the above systems would be able to use their Memoization/Caching data and will have to run all calculations from the beginning.

2.6. Map-Reduce Communication–Cost Model

In general, there may be several performance measures for evaluating the performance of an algorithm in the Map-Reduce model (see below). In this study, we follow the communication–cost model as described in [30]: a task is a single map or reduce process, executed by a single computer in the network. The communication cost of a task is the size of the input to this task. Note that the initial input to a map task (the input that resides in a file) is also counted as an input. Also note that we do not distinguish between map tasks and reduce tasks for this matter. The total communication cost is the sum of the communications costs of all the tasks in the Map-Reduce job.

Other proposed cost models, which we will not focus on, are total response time and the Amazon total cost. Total response time refers to the elapsed time from the start of the Map-Reduce job to the end of it, without considering the number of nodes that have participated in the job, the nodes’ specifications or the number of messages passed from node to node during the computation process. This model is practical because the most significant drive for the development of the Map-Reduce framework is the need to finish big tasks fast. However, it is difficult under these uncertain conditions to compare performance between different algorithms.

The Amazon total cost is the cost in dollars of the execution of this job over the Amazon Elastic Map-Reduce [31,32] service. This model considers all factors participating in the job: combined running time of all nodes that participated in the job weighted by the specifications of each node (a single time unit of a node with a fast CPU costs more than a single time unit of a node with a slow CPU), size of data communicated and the use of storage during the execution. This may be the most effective cost model, but it is bound to Amazon.

2.7. Apriori Map-Reduce Algorithms

There are several known Map-Reduce Apriori algorithms. The PApriori algorithm [11] is a porting of the classical algorithm to Map-Reduce. Everything is done inside the main program in a sequential way, except for the frequency count which is done in parallel with the Map-Reduce algorithm. This algorithm is depicted in Figure 2. Apriori-Map/Reduce [12] is similar to PApriori but also performs the candidate generation in parallel by using another Map-Reduce job. Both of these algorithms require K steps to find the frequent itemsets of length K, with one or two MR jobs per candidate length/step.

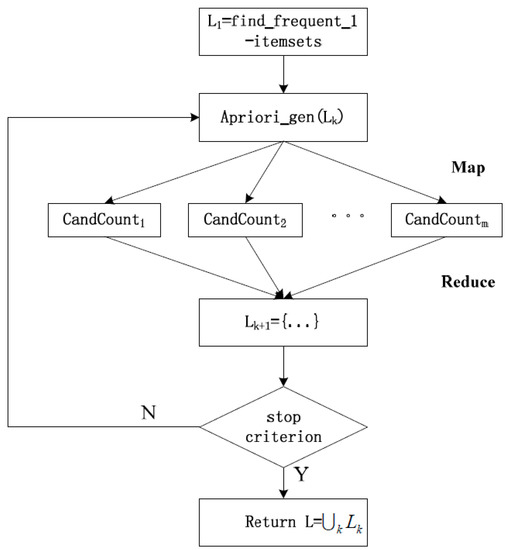
Figure 2. Map-Reduce Apriori Algorithm [11].

MRApriori [13] is different and presents a two-step algorithm. The first step is to divide $\mathcal{D}$ into Splits (done by the MR framework) and run the classical Apriori on each Split inside the Mapper (it reads the whole input into the memory of the Mapper as one chunk) to find “locally” frequent itemsets. After that, the Reducer joins the results of all Mappers and they become candidates for final frequent itemsets (if the itemset is frequent in $\mathcal{D}$, then it must be frequent in at least one of its Splits). The second job/step is just counting of all candidates’ appearance in each Split and filtering only the frequent itemsets that pass the minimum support level. Figure 3 demonstrates the algorithm’s block diagram for clarification.

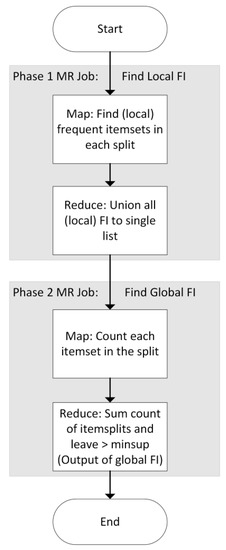
Figure 3. MRApriori and IMRApriori Block Diagram.

IMRApriori [10] works similarly to MRApriori with one add-on/observation that an itemset may become a candidate itemset only if it appeared locally frequent in “enough” Splits. More precisely, let ${\mathrm{S}}_1{,\text{…},\mathrm{S}}_{\mathrm{m}}$ be Splits of $\mathcal{D}$ in step 1. Denote their sizes to be ${|\mathrm{S}}_{\mathrm{i}}|$ if itemset $x$ is locally frequent in k ($\mathrm{k}\le \mathrm{m}$) Splits without loss of generality, called ${\mathrm{S}}_1{,\text{…},\mathrm{S}}_{\mathrm{k}}$. Let ${\mathrm{C}}_{\mathrm{i}}$ be the count of occurrence of X in Split Si. Let minSup be the minimum support. Then:

$$sup\left(x\right)\le {\displaystyle \sum }_1^k{C}_i+{\displaystyle \sum }_{k+1}^m\left(\left|S_i\right|*minSup-1\right)$$

If this number is less than $minSup*\left|\mathcal{D}\right|$, then there is no need to calculate the occurrence of $x$ in $\mathcal{D}$ in step 2 as it does not have a chance to be frequent any more (early pruning). This observation is applied in the first Reducer (“Union of all local FI”) of IMRApriori and can be seen in the block diagram in Figure 3. This algorithm is shown to outperform all previous ones and a variation of it will be used by us.

2.8. Join Operation and Map-Reduce

The “join” operation on two or more datasets is one of the standard operations in relational DBs and it is part of the SQL standard. The operation combines records from input datasets by some rule (predicate), so the output may contain information in a single record from any or all datasets. It is used in some steps of our algorithm and therefore it is relevant here.

Standard Map-Reduce does not provide built-in functions to join datasets, so several algorithms were proposed [30,33,34]. One of the strategies for join is called repartition join. The idea is that data from all datasets are being distributed across all Mappers. Each Mapper identifies which dataset is responsible for its Split and outputs the input line together with a dataset “tag”. The key of the map output is the predicate value (in case of equi-join, it would be the value by which the join is being done). Then the Reducer collects records and groups them by the input key. For each input key, it extracts the dataset tag that is associated with each record from all the records of the different datasets and generates all possible join combinations. It is used in our algorithm and is therefore relevant here.

3. Mining Closed Frequent Itemsets with Map-Reduce

3.1. Problem Definition

Let $I=\left\{i_1,i_2,\dots ,i_m\right\}$ be a set of items with lexicographic order. An itemset $x$ is a set of items such that $x\subseteq I$. A transactional database $\mathcal{D}=\left\{t_1,t_2,\dots ,t_n\right\}$ is a set of itemsets, each called a transaction. Each transaction in $\mathcal{D}$ is uniquely identified with a transaction identifier (TID) and assumed to be sorted lexicographically. The difference between a transaction and an itemset is that an itemset is an arbitrary subset of $I$, while a transaction is a subset of $I$ that exists in $\mathcal{D}$ and identified by its TID, $tid$. The support of an itemset $x$ in $\mathcal{D}$, denoted $su{p}_{\mathcal{D}}\left(x\right)$, or simply $sup\left(x\right)$ when $\mathcal{D}$ is clear from the context, is the number of transactions in $\mathcal{D}$ that contain $x$ (sometimes it is the percentage of transactions).

Given a user-defined minimum support denoted minSup, an itemset $x$ is called frequent if $sup\left(x\right)\ge minSup\times \left|\mathcal{D}\right|$.

Let $T\subseteq \mathcal{D}$ be a subset of transactions from $\mathcal{D}$ and let $x$ be an itemset. We define the following two functions $f$ and $g$:

$$f\left(T\right)=\{i\in I|\forall t\in T,i\in t\}$$

$$g\left(x\right)=\{t\in \mathcal{D}|\forall i\in x,i\in t\}$$

Function $f$ returns the intersection of all the transactions in $T$, and function $g$ returns the set of all the transactions in $\mathcal{D}$ that contain $x$. Notice that $g$ is antitone, meaning that for two itemsets $x_1$ and $x_2$: $x_1\subseteq x_2\to g\left(x_2\right)\subseteq g\left(x_1\right)$. It is trivial to see that $sup\left(x\right)=\left|g\left(x\right)\right|$. The function $h=f\circ g$ is called the Galois operator or closure operator.

An itemset $x$ is closed in $\mathcal{D}$ if $h\left(x\right)=x$. It is equivalent to say that an itemset $x$ is closed in $\mathcal{D}$ if no itemset, that is a proper superset of $x$ has the same support in $\mathcal{D}$, exists.

Given a database $\mathcal{D}$ and a minimum support minSup, the mining closed frequent itemsets problem is finding all frequent and closed itemsets in $\mathcal{D}$.

Let $I=\left\{a,b,c,d,e,f\right\}$, let $minSup$ = 3 ($minSup=60\%$) and let $\mathcal{D}$ be the transaction database presented in Table 2. Consider itemset $\left\{c\right\}$. It is a subset of transactions $t_1$, $t_3$, $t_4$ and $t_5$, meaning that $sup\left(\left\{c\right\}\right)=4$, which is greater than minSup$\times \left|\mathcal{D}\right|$. However, $\left\{c,f\right\}$, which is a proper superset of $\left\{c\right\}$, is also a subset of the same transactions. {c} is not a closed itemset since $sup\left(\left\{c,f\right\}\right)=sup\left(\left\{c\right\}\right)$. The list of all closed frequent itemsets is: $\left\{a\right\}$, $\left\{c,f\right\}$, $\left\{e\right\}$ and $\left\{c,e,f\right\}$.

Table 2. $\mathcal{D}$ Example. TID = transaction identifier.

TID	Transaction
$t_1$	$\left\{a,c,d,e,f\right\}$
$t_2$	$\left\{a,b,e\right\}$
$t_3$	$\left\{c,e,f\right\}$
$t_4$	$\left\{a,c,d,f\right\}$
$t_5$	$\left\{c,e,f\right\}$

We now present an algorithm for mining frequent closed itemsets in a distributed setting, using the Map-Reduce paradigm. It uses the generator idea mentioned in Section 2.2.

3.2. The Algorithm

3.2.1. Overview

Our algorithm is iterative, where each iteration is a Map-Reduce job. The inputs for iteration $i$ are:

• $\mathcal{D}$, the transaction database
• $C_{i-1}$, the set of the closed frequent itemsets found in the previous iteration ($C_o$, the input for the first iteration, is the empty set).

The output of iteration $i$ is $C_i$, a set of closed frequent itemsets that have a generator of length $i$. If $C_i\ne \varphi$, then another iteration, $i+1$, is performed. Otherwise, the algorithm stops. As mentioned earlier, each iteration is a Map-Reduce job (line 7 in Algorithm 1, see details in algorithms 2, 3 and 4), comprised of a map phase and a reduce phase. The map phase, which is equivalent to the $g$ function, emits sets of items called closure generators (or simply generators). The reduce phase, which is equivalent to the $f$ function, finds the closure that each generator produces, and decides whether or not it should be added to $C_i$. Each set added to $C_i$ is paired with its generator. The generator is needed for the next iteration.

The output of the algorithm, which is the set of all closed frequent itemsets, is the union of all $C_i$s.

Before the iteration begins, we have discovered that a pre-process phase which finds only the frequent items greatly improves performance, even though another Map-Reduce job is executed, and this data must be shared among all mapper tasks. This Map-Reduce job simply counts the support of all items and keeps only the frequent ones.

The pseudo-code of the algorithm is presented below (Algorithm 1). We provide explanations of the important steps in the algorithm.

3.2.2. Definitions

To better understand the algorithm, we need some definitions:

Definition 1.

Let$p$be an itemset, and let$c$be a closed itemset, such that$h\left(p\right)=c$, then$p$is called a generator of$c$.

Note, that a closed itemset might have more than one generator: in the example above, both $\left\{c\right\}$ and $\left\{f\right\}$ are the generators of $\left\{c,f\right\}$.

Definition 2.

An execution of a map function on a single transaction is called a map task.

Definition 3.

An execution of a reduce function on a specific key is called a reduce task.

3.2.3. Algorithm Steps

Map Step

A map task in iteration $i$ gets three parameters as an input: (1) a set of all the closed frequent itemsets (with their generators) found in the previous iteration, denoted $C_{i-1}$ (which is shared among all the mappers in the same iteration); (2) a single transaction denoted $t$; and (3) the set of all frequent items in $D$ (again, this set is also shared among all the mappers in the same iteration and in all iterations). Note that in the Hadoop implementation, the mapper gets a set of transactions called Split and the mapper object calls the map function for each transaction in its own Split only.

For each $c\in C_{i-1}$, if $c\subseteq t$, then $t$ holds the potential of finding new closed frequent itemsets by looking at the complement of $c$ in $t$ (line 3). For each $item\in \left(t\backslash c\right)$, we check if $item$ is frequent (line 5). If so, we concatenate $item$ to the generator of c (denoted c.generator), thus creating g (we denote that added item as g.item), a potential new generator for other closed frequent itemsets (line 6). The function emits a message where g is the key and the tuple $\left(t,1\right)$ is the value (line 7). The “1” is later summed up and used to count the support of the itemset.

Notice that g is not only a generator, but it is always a minimal generator. Concatenating an item not in its closure guarantees to reach another minimal generator. More precisely, it generates all minimal generators that are supersets of g with one additional item, and such, that t supports it. Since all transactions are taken, every minimal generator with a support of at least one is emitted at some point (this is proven later). The pseudo-code of the map function is presented in Algorithm 2.

Combine Step

A combiner is not a part of the Map-Reduce programming paradigm, but a Hadoop implementation detail that minimizes the data transferred between map and reduce tasks. Hadoop gives the user the option of providing a combiner function that is to run on the map output on the same machine running the mapper, and the output of the combiner function is the input for the reduce function.

In our implementation, we have used a combiner, which is quite similar to the reducer but much simpler. The input to the combiner is a key and a collection of values: the key is the generator g (which is an itemset), and the collection of values is a collection of tuples, composed of transactions T, all containing g and a number s indicating the support of the tuple. Since the combiner is “local” by nature, it has no use of the minimum support parameter, which must be applied in a global point of view. The combiner sums the support of the input tuples, stores it in the variable sum, and then performs an intersection on the tuples to get $t^{\prime }$.

The combiner emits a message where g is the key and the tuple $\left(t^{\prime },sum\right)$ is the value. The pseudo-code of the combiner function is presented in Algorithm 3.

Reduce Step

The reduce task gets a key as input, a collection of values and the minimum support. The key is the generator g (which is an itemset), a collection $\left(t_1,s_1\right),\dots ,\left(t_n,s_n\right)$ of n tuples, composed of a set of items $t_i$ (an intersection of transactions from the combiner), all containing g and a number $s_i$ indicating the support of the tuple. In addition, it gets, as a parameter, the user-given minimum support, minSup. The reducer is depicted in Algorithm 4.

At first, the frequency property is checked: $sup\left(g\right)={\displaystyle \sum _{i=1}^n}{s}_i\ge minSup*\left|\mathcal{D}\right|$. If so, then an intersection of $t_1,\dots ,t_n$ is performed and a closure, denoted c, is produced. If the item that was added in the map step is lexicographically greater than the first item in $c\backslash g$, then c is a duplication and can be discarded. Otherwise, a new closed frequent itemset is discovered and is added to $C_i$.

In other words, if the test in line 7 passes, then it is guaranteed that the same closure c is found (and kept) in another reduce task—the one that will get c from its first minimal generator in the lexicographical order (as is proven later).

The pseudo-code of the reduce function is presented below.

In line 5 in the algorithm, we apply the f function, which is actually an intersection of all the transactions in T. Notice that we do not need to read all of T and store in the RAM. T can be treated as a stream, reading transactions one at a time and performing the intersection.

3.2.4. Run Example

Consider the example database $\mathcal{D}$ in Table 2 with a minimum support of two transactions (minSup = 40%). To simulate a distributed setting, we assume that each transaction $t_i$ resides on a different machine in the network (mapper node), denoted $m_i$.

1st Map Step. We track node $m_1$. Its input is the transaction $t_1$, and since this is the first iteration then $C_{i-1}=C_0=\varphi$. For each item in the input transaction, we emit a message containing the item as a key and the transaction as a value. So, the messages that $m_1$ emits are the following: $<\left\{a\right\},\left\{a,c,d,e,f\right\}>$, $<\left\{c\right\},\left\{a,c,d,e,f\right\}>$, $<\left\{d\right\},\left\{a,c,d,e,f\right\}>$, $<\left\{e\right\},\left\{a,c,d,e,f\right\}>$, and $<\left\{f\right\},\left\{a,c,d,e,f\right\}>$. A similar mapping process is done on other nodes.

1st Reduce Step. According to the Map-Reduce paradigm, a reducer task is assigned to every key. We follow the reducer tasks assigned to keys $\left\{a\right\}$, $\left\{c\right\}$ and $\left\{f\right\}$, denoted $R_a$, $R_c$, and $R_f$ respectively.

First, consider $R_a$. According to the Map-Reduce paradigm, this reduce task receives in addition to the key $\left\{a\right\}$, all the transactions in $\left\{D\right\}$ that contain that key: $t_1$, $t_2$ and $t_4$. First, we must test the frequency: there are three transactions containing the key. Since minSup$*\left|\mathcal{D}\right|$ = 2, we pass the frequency test and go on. Next, we intersect all the transactions, producing the closure $\left\{a\right\}$. The final check is whether the closure is lexicographically larger than the generator. In our case it is not (because the generator and closure are equal), so we add $\left\{a\right\}$ to $C_1$.

Next, consider $R_c$. This reduce task receives the key $\left\{c\right\}$, and transactions $t_1$, $t_3$, $t_4$ and $t_5$. Since the number of transactions is four, we pass the frequency test. The intersection of the transactions is the closure $\left\{c,f\right\}$. Finally, $\left\{c\right\}$ is lexicographically smaller than $\left\{c,f\right\}$, so we add $\left\{c,f\right\}$ to $C_1$.

Finally, consider $R_f$. The transactions that contain the set $\left\{f\right\}$ are $t_1$, $t_3$, $t_4$ and $t_5$. We pass the frequency test, but the intersection is $\left\{c,f\right\}$, just like in reduce task $R_c$, so we have a duplicate result. However, $\left\{f\right\}$ is lexicographically greater than $\left\{c,f\right\}$, so this closure is discarded.

The final set of all closed frequent itemsets found on the first iteration is: $C_1=\left\{\left\{a:a\right\},\left\{c,f:c\right\},\left\{e:e\right\}\right\}$ (the itemset after the semicolon is the generator of this closure).

2nd Map Step. As before, we follow node $m_1$. This time the set of closed frequent itemsets is not empty, so according to the algorithm, we iterate over all $c\in C_1$. If the input transaction $t$ contains $c$, we add to $c$ all the items in $t\backslash c$, each at a time, and emit it. So, the messages that $m_1$ emits are the following:

$$\begin{array}{c}<\left\{a,c\right\},\left\{a,c,d,e,f\right\}>,\\ <\left\{a,d\right\},\left\{a,c,d,e,f\right\}>,\\ <\left\{a,e\right\},\left\{a,c,d,e,f\right\}>,\\ <\left\{a,f\right\},\left\{a,c,d,e,f\right\}>,\\ <\left\{c,d\right\},\left\{a,c,d,e,f\right\}>,\\ <\left\{c,e\right\},\left\{a,c,d,e,f\right\}>,\\ <\left\{c,f\right\},\left\{a,c,d,e,f\right\}>,\\ <\left\{e,f\right\},\left\{a,c,d,e,f\right\}>.\end{array}$$

2nd Reduce Step. Consider reduce task $R_{ac}$. According to the Map-Reduce paradigm, this reduce task receives all the messages containing the key $\left\{a,c\right\}$, which are transactions $t_1$ and $t_4$. Since minSup = 2, we pass the frequency test. Next, we consider the key $\left\{a,c\right\}$ as a generator and intersect all the transactions getting the closure $\left\{a,c,d,f\right\}$. The final check is whether the added item c is lexicographically larger than the closure minus the generator. In our case it is not, so we add $\left\{a,c,d,f\right\}$ to the set of closed frequent itemsets.

The full set of closed frequent itemsets is shown in Table 3. Next, we prove the soundness and completeness of the algorithm.

Table 3. Closed Frequent Itemsets of D.

Closed Item Set	Generator	Support
$\left\{a\right\}$	$\left\{a\right\}$	3
$\left\{c,f\right\}$	$\left\{c\right\}$	4
$\left\{e\right\}$	$\left\{e\right\}$	4
$\left\{a,c,d,f\right\}$	$\left\{a,c\right\}$	2
$\left\{a,e\right\}$	$\left\{a,e\right\}$	2
$\left\{c,e,f\right\}$	$\left\{c,e\right\}$	3

3.2.5. Soundness

The mapper phase makes sure that the input to the reducer is a key which is a subset of items p, and a set of all transactions that contain p, denoted by definition $T=g\left(p\right)$. The reducer first checks that $sup\left(p\right)\ge minSup*\left|\mathcal{D}\right|$ by checking $\left|T\right|\ge minSup*\left|\mathcal{D}\right|$ and then performs an intersection of all the transactions in $T$, which by definition is the result of the function $f\left(T\right)$, and outputs the result. So, by definition, all outputs are the result of $f\circ g$, which is a closed frequent itemset.

3.2.6. Completeness

We need to show that the algorithm outputs all the frequent closed itemsets. Assume negatively, considering that $c=i_1,\dots , i_n$ is a closed frequent itemset (that we assume was not produced). Suppose, that $c$ has no proper subset that is a closed frequent itemset. Therefore, for all items $i_j\in c$, $sup\left(i_j\right)=sup\left(c\right)$ and $g\left(i_j\right)=g\left(c\right)$. Therefore $h\left(i_j\right)=h\left(c\right)=c$. Since $h\left(i_j\right)=c$, then $i_j$ is a generator of $c$, and the algorithm will output $c$ at the first iteration.

Suppose that $c$ has one or more proper subsets and each is a closed frequent itemset. We examine the largest one and denote it $l$. $l$ is generated by the algorithm because its generator is shorter than the generator of $c$. We also denote its generator $g_l$, meaning that $g\left(l\right)=g\left(g_l\right)$. Since $g$ is antitone and since $g_l\subset c$, then $g\left(c\right)\subset g\left(g_l\right)$. What we show next is that if we add one of the items not in $l$ to $g_l$, we will generate c. Consider an item $i$, such that $i\in c\backslash l$. Let $g_l^{\prime }=g_l{{\displaystyle \cup }}^{\text{}}\left\{i\right\}$. Therefore, $g\left(g_l^{\prime }\right)=g\left(g_l\right){{\displaystyle \cap }}^{\text{}}g\left(i\right)=g\left(l\right){{\displaystyle \cap }}^{\text{}}g\left(i\right)$. Assume that $g\left(g_l^{\prime }\right)\supset g\left(c\right)$. It implies that $l\prime$ is a generator of a closed itemset $h\left(g_l^{\prime }\right)$ that is a proper subset of $c$ in contradiction to $l$ being the largest closed subset of $c$, therefore $g\left(g_l^{\prime }\right)=g\left(c\right)$, meaning that $c$ will be found by the mapper by adding an item to $g_l$ (see lines 3–4 in Algorithm 2. Mapper).

3.2.7. Duplication Elimination

As we saw in the run example in Section 3.2.4, a closed itemset can have more than one generator, meaning that two different reduce tasks can produce the same closed itemset. Furthermore, these two reduce tasks can be in two different iterations. We have to identify duplicate closed itemsets and eliminate them. The naive way to eliminate duplications is by submitting another Map-Reduce job that sends all identical closed itemsets to the same reducer. However, this means that we need another Map-Reduce job for that, which greatly damages performance. Line 7 in Algorithm 4 takes care of that without the need for another Map-Reduce round. In the run example, we have already seen how it works when the duplication happens on the same round.

What we would like to show is that the duplication elimination step does not “lose” any closed itemsets. We now explain the method.

Consider that itemset $c=\left\{i_1,i_2,\dots ,i_n\right\}$ is a closed, frequent itemset, and its generator $g=\left\{i_{g_1},i_{g_2},\dots ,i_{g_m}\right\}$, $m<n$, such that $h\left(g\right)=c$. According to our algorithm, $g$ was created by adding an item to a previously found closed itemset. We denote that itemset $f$, and the added item $i_{g_j}$ such that $g=f{{\displaystyle \cup }}^{\text{}}\{i_{g_j}\}$. Suppose that $i_{g_j}>c\backslash g$. Our algorithm will eliminate $c$. We should show that $c$ can be produced by a different generator. Consider $i_k$ to be the smallest item in $c\backslash g$. Since $i_k\in c$ is frequent, and since $i_k\notin g$, then surely $i_k\notin f$, meaning that the algorithm will add it to $f$, creating $g\prime =f{{\displaystyle \cup }}^{\text{}}\left\{i_k\right\}$. It is possible that $h\left(g^{\prime }\right)\subset c$, however if we keep growing $g^{\prime }$ with the smallest items, we will eventually get $c$.

3.3. Experiments

We have performed several experiments in order to verify the efficiency of our algorithm and to compare it with other renowned algorithms.

3.3.1. Data

We tested our algorithm on both real and synthetic datasets. The real dataset was downloaded from the FIMI repository [35,36], and is called “webdocs”. It contains close to 1.7 million transactions (each transaction is a web document) with 5.3 million distinct items (each item is a word). The maximal length of a transaction is about 71,000 items. The size of the dataset is 1.4 gigabytes (GB). A detailed description of the “webdocs” dataset, that also includes various statistics, can be found in [36].

The synthetic dataset was generated using the IBM data generator [37]. We have generated six million transactions with an average of ten items per transaction—a total of 100,000 items. The total size of the input data is 600 MB.

3.3.2. Setup

We ran all the experiments on the Amazon Elastic Map-Reduce [31] infrastructure. Each run was executed on sixteen machines; each is an SSD-based instance storage for fast I/O performance with a quad core CPU and 15 GB of memory. All machines run Hadoop version 2.6.0 with Java 8.

3.3.3. Measurement

We used communication–cost (see Section 2.6) as the main measurement for comparing the performance of the different algorithms. The input records to each map task and reduce task were simply counted and summed up at the end of the execution. This count is performed on each machine in a distributive manner. The implementation of Hadoop provides an internal input records counter that makes the counting and summing task extremely easy. Communication–cost is an infrastructure-free measurement, meaning that it is not affected by weaker/stronger hardware or temporary network overloads, making it our measurement of choice. However, we also measured the time of execution. We ran each experiment three times and gave the average time.

3.3.4. Experiments Internals

We have implemented the following algorithms: (1) an adaptation of Closet to Map-Reduce; (2) the AFOPT-close adaptation to Map-Reduce; and (3) our proposed algorithm. All algorithms were implemented in Java 8, taking advantage of its new lambda expressions support.

We ran the algorithms on the two datasets with different minimum supports, and measured the communication cost and execution time for each run.

3.3.5. Results

The first batch of runs was conducted on the synthetic dataset. The results can be seen in Figure 4 and Figure 5. In Figure 4, the lines represent the communication cost of each of the three algorithms for different minimum supports. The bars present the number of closed frequent itemsets found for each minimum support. The number of closed frequent itemsets depends only on the minimum support and gets higher when the minimum support gets higher. As can be seen, our algorithm outperforms the others in terms of communication cost in all the minimum supports. In addition, the communication raise gradient is lower than the others, meaning that further increases in the minimum support will make the difference even greater. Figure 5 shows the running time of the three algorithms for the same minimum supports. Again, as can be seen, our algorithm outperforms the others.

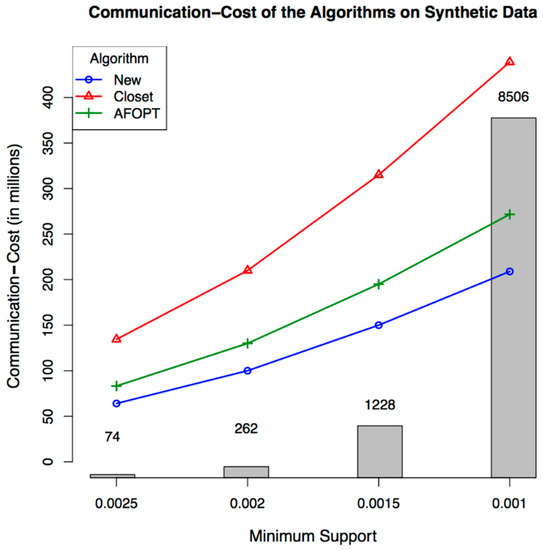
Figure 4. Communication–cost of the algorithms on synthetic data.

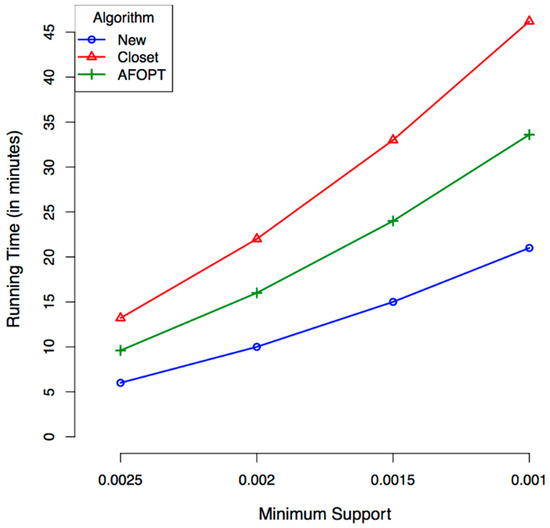
Figure 5. Running time of the algorithms on the synthetic data.

In the second batch of runs, we run the implemented algorithms on the real dataset with four different minimum supports, and measured the communication cost and execution time for each run. The results can be seen in the figures below (Figure 6 and Figure 7). The figures are similar to the two previous figures, and as can be seen, our algorithm outperforms the existing algorithms.

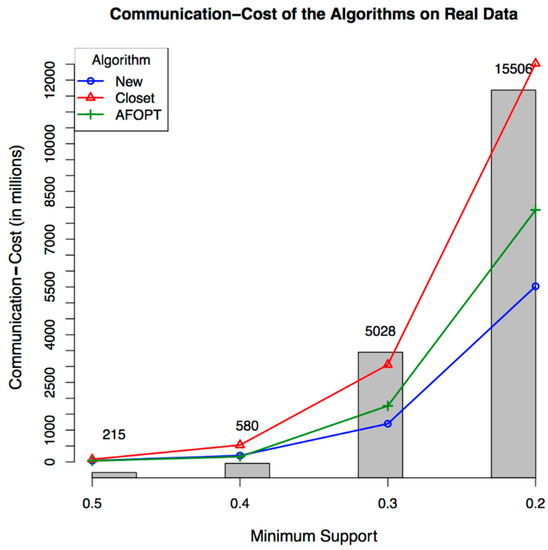
Figure 6. Communication–cost of the algorithms on real data.

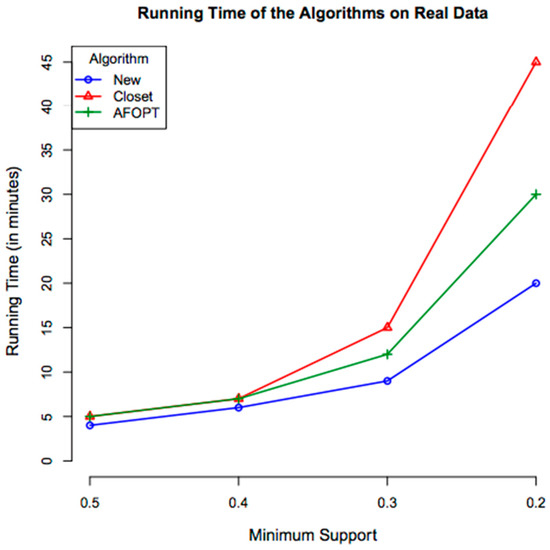
Figure 7. Comparing execution time of the algorithms on real data.

4. Incremental Frequent Itemset Mining with Map-Reduce

4.1. Problem Definition

Let $\mathcal{D}$ be a database of transactions, I a set of items and minSup the minimum support level as described in Section 3.1. Define FI to be a set of all frequent items in $\mathcal{D}$:$FI(\mathcal{D},minSup)=\left\{x|su{p}_{\mathcal{D}}\left(x\right)\ge minSup*\mathcal{D}\right\}$. Let PK be some previous knowledge that we produced during the FIM process of the $\mathcal{D}$. Let $\Delta$ be the set of additional transactions. Let ${\mathcal{D}}^{+}$ be a new database defined as ${\mathcal{D}}^{+}=\mathcal{D}\cup \Delta$. The problem is to find $FI({\mathcal{D}}^{+},minSup),$ the set of all frequent itemsets in the updated database. We denote $FI(\Delta )$ deltaFI. We may omit minSup from functions if the support level is clear from the context. We call any $x$ s.t. $x\in FI$ a frequent itemset or just “frequent”.

4.2. The Algorithms

4.2.1. General Scheme

We first propose a general algorithm (Algorithm 5) for incremental frequent itemset mining. It can be used for any distributed or parallel framework, but it also suits the model of Map-Reduce. The algorithm is loosely based on the FUP [15] algorithm and shares similarities with ARMIDB [7] (see Section 2.3). The idea is to first find all frequent itemsets in the new database (only deltaFI) and then unite (join) the new frequent itemsets with the old frequent itemsets, and finally revalidate itemsets which are in the “unknown” state in each of the databases. This algorithm is general because it doesn’t set any constraints on the FIM algorithm that is used (any Map-Reduce algorithm for finding frequent itemsets will suit). We show some optimizations of it later.

Brief description of the algorithm (Algorithm 5): Step 1 is the execution of the MR main program (“driver”). Step 2 is getting all parameters and filling the MR job configuration. Steps 3 and 4 are the execution of any standard MR FIM algorithm on the incremental DB ($\Delta$), and saving its output back to HDFS (Step 4). For example, the use of IMRApriori as a MR FIM will include running first an MR job with a mapper that finds FI for each data Split and then its reducer will merge all “local” FI to a single candidate list. A second MR job will use its mapper to count all candidate occurrences in each data Split, and the reducer will be used to summarize the candidate occurrences, and to output only “globally” frequent itemsets.

Steps 5 and 6 check if it is incremental run or not; in the latter case, the algorithm just stops. If it is the incremental run, then we need to find “globally” frequent itemsets (GFI) from $\mathrm{FI}(\Delta )$, and previous $\mathrm{FI}\left(\mathcal{D}\right)$, i.e., $\mathrm{FI}\left({\mathcal{D}}^{+},\mathit{minSup}\right)$. As mentioned in Section 2.3, when adding new transactions, locally frequent itemsets have three options. To determine to which option each itemset applies, we propose using a MR job for joining itemsets (Steps 7–8). Any join MR algorithm may be used here (during result evaluation, we have used repartition join for this task). The key of the Join reducer would be the itemset itself, and the list of values would be occurrences of the itemset in the different DB parts, together with its count. During our evaluation, Step 7 (Join’s mapper) read itemsets from the databases, and outputted them together with their database mark. Step 8 (Join’s reducer) read an itemset and all its database marks, and determined the further processing required for each itemset. It is composed of three cases:

• In case that it is locally frequent in $\Delta$ and old $\mathcal{D}$, then it is globally frequent so it may be outputted immediately (step 9).
• If it is locally frequent only in $\Delta$, then we need to count it in old $\mathcal{D}$ (steps 10–11 by using the additional count MR job).
• If it is locally frequent in old $\mathcal{D}$, we need to count it in $\Delta$ (steps 12–13 by using the same MR job as in steps 10–11 with other input).

All three outputs (9, 11 and 13) are collected in step 14, and represent together $\mathrm{FI}\left({\mathcal{D}}^{+},\mathit{minSup}\right)$.

The proposed scheme contains at least three different kinds of MR jobs:

• Find deltaFI by using any suitable MR algorithm (may have more than one job inside).
• Join MR job. Any Join algorithm may be in use. The Mapper output is just a copy of the input (Identity function); the Reducer should have three output files/directories (instead of just one) for each case.
• Count itemsets inside the database. The same MR count algorithm may be used for both old $\mathcal{D}$ and $\Delta$. Counts in both DBs could be executed in parallel on the same MR cluster.

There is (at most) one pass over the old $\mathcal{D}$ for counting—Steps 10–13 use the same algorithm for counting. The mapper reads a list of itemsets for counting and counts them in its data split. The reducer summarizes each itemset, and leaves only “globally” frequent itemsets. There is no requirement for any additional input for general FIM (e.g., previous knowledge, PK), but any advanced algorithm may use any additional acquired knowledge from mining old $\mathcal{D}$ as an input to the incremental algorithm.

4.2.2. Early Pruning Optimizations

In the scheme described above, only one step requires accessing the old $\mathcal{D}$, whose size may be huge compared to $\Delta$. This is the step of recounting local frequent itemsets from $\Delta$, which did not appear to be in FI($\mathcal{D}$). To minimize access to the old $\mathcal{D}$, we suggest using early pruning techniques which consider the relation between the old $\mathcal{D}$ size and the $\Delta$ size. These techniques are additions to the early pruning of the IMRApriori technique but are not unique for Map-Reduce algorithms, and could be used in every incremental FIM algorithm. All of the following lemmas are trying to numerically determine the potential of a candidate itemset to be frequent as soon as possible.

Let inc be the size of $\Delta$ relative to the size of $\mathcal{D}$. Let n be the size of $\mathcal{D}$ ($\mathrm{n}=\left|\mathcal{D}\right|$); then, the size of $\Delta$ is $inc*n$ or $inc*\left|\mathcal{D}\right|$.

Observation 1:

$$xϵFI\left({\mathcal{D}}^{+},minSup\right)\to su{p}_{{\mathcal{D}}^{+}}\left(x\right)\ge minSup*\left(\left|\mathcal{D}\right|+inc*\left|\mathcal{D}\right|\right)$$

Proof. 

$$\begin{array}{c}su{p}_{\mathcal{D}}\left(x\right)+su{p}_{\Delta }\left(x\right)=su{p}_{{\mathcal{D}}^{+}}\left(x\right)\ge minSup*\left|{\mathcal{D}}^{+}\right|=minSup*\left(\left|\mathcal{D}\right|+|\Delta |\right)\\ =minSup*\left(\left|\mathcal{D}\right|+inc*\left|\mathcal{D}\right|\right);\end{array}$$

□

Lemma 1.

(Absolute Count):

$$\mathit{x}\mathit{ϵ}\mathit{F}\mathit{I}\left(\mathcal{D},\mathit{m}\mathit{i}\mathit{n}\mathit{S}\mathit{u}\mathit{p}*\left(\mathbf{1}+\mathit{i}\mathit{n}\mathit{c}\right)\right)\to \mathit{x}\mathit{ϵ}\mathit{F}\mathit{I}\left({\mathcal{D}}^{+},\mathit{m}\mathit{i}\mathit{n}\mathit{S}\mathit{u}\mathit{p}\right);$$

Proof of Lemma 1.

$$\begin{array}{l}x\in FI\left(\mathcal{D},minSup*\left(1+inc\right)\right)\to \\ \begin{array}{ll}su{p}_{{\mathcal{D}}^{+}}\left(x\right)=& su{p}_{\mathcal{D}}\left(x\right)+su{p}_{\Delta }\left(x\right)\ge su{p}_{\mathcal{D}}\left(x\right)\ge minSup*\left(1+inc\right)*\left|\mathcal{D}\right|\\ & =minSup*\left(\left|\mathcal{D}\right|+inc*\left|\mathcal{D}\right|\right)=minSup*\left(\left|\mathcal{D}\right|+|\Delta |\right)\\ & =minSup*\left|{\mathcal{D}}^{+}\right|;\end{array}\end{array}$$

i.e., $su{p}_{\mathcal{D}}\left(x\right)\ge minSup\left(1+inc\right)n\to IϵFI\left({\mathcal{D}}^{+},minSup\right);$

Lemma 1 ensures that if $\mathit{x}$ is “very” frequent in the old $\mathcal{D}$ (support of at least $\mathit{minSup}*\left(1+\mathit{inc}\right)$), then it will be frequent in ${\mathcal{D}}^{+}$ even if it does not appear in $\mathbf{\Delta }$ at all. □

Lemma 2.

(Minimum Count):

$$\mathit{x}\mathit{ϵ}\mathit{F}\mathit{I}\left({\mathcal{D}}^{+},\mathit{m}\mathit{i}\mathit{n}\mathit{S}\mathit{u}\mathit{p}\right)\to \mathit{s}\mathit{u}{\mathit{p}}_{\mathcal{D}}\left(\mathit{x}\right)\ge \mathit{n}*\left(\mathit{m}\mathit{i}\mathit{n}\mathit{s}\mathit{u}\mathit{p}+\mathit{m}\mathit{i}\mathit{n}\mathit{s}\mathit{u}\mathit{p}*\mathit{i}\mathit{n}\mathit{c}-\mathit{i}\mathit{n}\mathit{c}\right);$$

Proof. 

$$su{p}_{\Delta }\left(x\right)\le |\Delta |=inc*n;$$

$$|\Delta |+su{p}_{\mathcal{D}}\left(x\right)\ge su{p}_{\Delta }\left(x\right)+su{p}_{\mathcal{D}}\left(x\right)$$

$$\ge minSup*\left|{\mathcal{D}}^{+}\right|=minSup*\left(1+inc\right)*n;$$

$$su{p}_{\mathcal{D}}\left(x\right)\ge minSup*\left(1+inc\right)*n-|\Delta |$$

$$=minSup*\left(1+inc\right)*n-inc*n$$

$$=n*\left(minSup+minSup*inc-inc\right);$$

For answering if $x$ can be in $FI\left({\mathcal{D}}^{+},minSup\right)$ without even looking at $\Delta$, we need to know if $xϵ\mathrm{FI}\left(\mathcal{D},\mathit{minSup}+\mathit{minSup}*\mathit{inc}-\mathit{inc}\right)$. Of course, $\mathit{minSup}+\mathit{minSup}*\mathit{inc}-\mathit{inc}$ may be less than zero (or $\mathit{minSup}\ge \mathit{inc}(\mathit{inc}+1)$), there is no minimum level.

Lemma 2 puts a lower bound of occurrences of itemset $\mathit{x}$ in old $\mathcal{D}$ for it to have a possibility to appear in FI of ${\mathcal{D}}^{+}$ (even if $\mathit{x}$ appears in 100% of transactions in $\mathbf{\Delta }$, it must obey this criterion and therefore it is a pruning condition). See below for its use for non-frequent itemsets. □

Lemma 3.

$$\mathit{s}\mathit{u}{\mathit{p}}_{\mathbf{\Delta }}\left(\mathit{x}\right)\ge \mathit{m}\mathit{i}\mathit{n}\mathit{S}\mathit{u}\mathit{p}*\left(\mathbf{1}+\mathit{i}\mathit{n}\mathit{c}\right)*\mathit{n}\to \mathit{x}\in \mathit{F}\mathit{I}\left({\mathcal{D}}^{+},\mathit{m}\mathit{i}\mathit{n}\mathit{s}\mathit{u}\mathit{p}\right);$$

Proof. 

Similar to Lemma 1 conclusion:

$$su{p}_{{\mathcal{D}}^{+}}\left(x\right)=su{p}_{\Delta }\left(x\right)+su{p}_{\mathcal{D}}\left(x\right)\ge su{p}_{\Delta }\left(x\right)\ge minSup*\left(1+inc\right)*n=minSup*\left|{\mathcal{D}}^{+}\right|;$$

Lemma 3 tells us that if $\mathit{x}$ is “very” frequent in $\mathbf{\Delta }$ and $\mathbf{\Delta }$ is large enough or minSup is small enough, then x will appear in FI of ${\mathcal{D}}^{+}$ (even if it never appeared in old $\mathcal{D}$). This lemma is also a pruning condition. If itemset $\mathit{x}$ satisfies it, then there is no need to count it in the old $\mathcal{D}$.

Observation 2 (Absolute Count Delta):

$$xϵFI\left(\Delta ,minsup*\left(1+1/inc\right)\right)\to IϵFI\left({\mathcal{D}}^{+},minSup\right);$$

□

Proof. 

$$\begin{array}{l}xϵFI\left(\Delta ,minsup*\left(1+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$inc$}\right.\right)\right)\to su{p}_{\Delta }\left(x\right)\ge minSup*\left(1+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$inc$}\right.\right)*|\Delta |\\ =minSup*\left(1+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$inc$}\right.\right)*inc*n=minSup*\left(1+inc\right)*n;\end{array}$$

To use Lemma 3, $\mathit{minSup}*\left(1+\mathit{inc}\right)$ must be less than one. □

To use the above lemmas in our algorithm, we modify the FIM algorithm to keep the itemset together with its potential “minimum count” and “maximal count” (for each Split of $\Delta$ and $\mathcal{D}$). Each Split that has information about the exact count of itemsets adds the count to the total of “minimum count” and “maximal count” (potential count is between these values). When there is no information from the Split about some itemset I, we use observations from IMRApriori, and we update the “maximal count” to be $\mathrm{Ceil}\left(\left|\mathrm{Split}\mathrm{Size}\right|*\mathit{minSup}\right)-1$ (otherwise it would appear as locally frequent and we would have exact information about it), and “minimum count” is set to 0 (total “minimum count’’ is not updated). This is done in the Reducer of Stage 1 of IMRApriori. Let ${\mathsf{\chi }}_{\mathrm{i}}\left(\mathrm{x}\right)$ be an indicator function that is 1 if $x$ was locally frequent in split ${\mathrm{S}}_{\mathrm{i}}$ and 0 otherwise. The reducer would output a triple <x,mincount,maxcount>, where

$$mincount={{\displaystyle \sum }}_{i=1}^{\left|Splits\right|}{\chi }_i\left(x\right)*su{p}_{S_i}\left(x\right)$$

$$maxcount={{\displaystyle \sum }}_{i=1}^{\left|Splits\right|}{\chi }_i\left(x\right)*su{p}_{S_i}\left(x\right)+\left(1-{\chi }_i\left(x\right)\right)*\left(\left|S_i\right|*minSup-1\right)$$

Note, that when the exact count is known, then mincount equals to maxcount. If $\mathrm{maxcount}<\mathit{minSup}*\left|{\mathcal{D}}^{+}\right|,$ then $x$ is pruned (by the original IMRApriori algorithm). If $\mathrm{mincount}\ge \mathit{minSup}*\left|{\mathcal{D}}^{+}\right|$, then $x$ is globally frequent, and should not need to be recounted in the missed Splits. Previously defined lemmas are applied in the algorithm during the Join in Step 8. In this step, we already know the sizes of $\mathcal{D}$ and $\Delta$, and therefore we know n and inc. So, we compare potential counts of itemsets directly to sizes of databases. The map phase of Join extracts the potential counts for some DB part (old $\mathcal{D}$ or $\Delta$) from the input and outputs it immediately together with the DB “marker” (variable that determines if it is $\mathcal{D}$ or $\Delta$). Algorithm 6 determines the total potential counts and makes the decision about itemset future processing.

Split size information and total $\mathcal{D}$ size is being passed as “previous knowledge” (PK) input into the FIM incremental algorithm in “General Scheme” at Step 3, and in our implementation of IMRApriori in phase 1.

4.2.3. Early Pruning Example

The following is an example of “minimal count” (mincount) and “maximal count” (maxcount) for a small DB with 1001 transactions ($\left|\mathcal{D}\right|=1001)$. In case we have two Mappers, the MR framework would split the DB to two Splits of roughly equal sizes. Table 4 is a table showing the calculation per two Splits with the support ratio of 20%. For example, for an itemset to be frequent in $\mathcal{D}$, it needs to be contained in at least $⎾1001*0.2⏋=201$ transactions. This example will examine itemsets $\mathrm{A}=\left\{\mathrm{a}\right\}$, and $\mathrm{B}=\left\{\mathrm{b}\right\}$, and their possible appearance in $\mathcal{D}$.

Table 4. Early pruning example values for $\mathcal{D}$.

	$\mathbf{S}\mathbf{p}\mathbf{l}\mathbf{i}{\mathbf{t}}_1$	$\mathbf{S}\mathbf{p}\mathbf{l}\mathbf{i}{\mathbf{t}}_2$
Transaction count	$\left|Spli{t}_1\right|=501$	$\left|Spli{t}_1\right|=500$
Min support level	$501*0.2=101$	$500*0.2=100$
A Count in the Split as found by the relevant mapper	101	Unknown (not locally frequent)
mincount of A	101	0 (may not appear at all)
maxcount of A	101	$100-1=99$
Total mincount of A	101
Total maxcount of A	200	Less than $\mathcal{D}$ min support level (201). Pruned away.
B Count in the Split as found by the relevant mapper	101	100
mincount of B	101	100
maxcount of B	101	100
Total mincount of B	201	Frequent in $\mathcal{D}$
Total maxcount of B	201

Table 4 shows how A is being preemptively pruned in $\mathcal{D}$. Table 5 shows an example of incremental computation with $\Delta$. If $\Delta$ consists of only five similar transactions $\left\{\mathrm{a}\right\}$ ($|\Delta |=5$, minimum support level is 1), then $\mathrm{FI}\left(\Delta ,\mathit{minSup}\right)=\left\{\mathrm{a}\right\}$. Also $\left|{\mathcal{D}}^{+}\right|=1006$, and the new minimum threshold is 202. The following table shows how decisions for A and B are being made:

Table 5. Early pruning example values for incremental D and $\Delta$.

	$\mathbf{\Delta }$	$\mathcal{D}$
A Count	5	Unknown (was pruned)
mincount A	5	0
maxcount A	5	$201-1=200$
Total mincount of A	5
Total maxcount of A	205	Could be frequent in ${\mathcal{D}}^{+}$
B Count	0	201 (was frequent in $\mathcal{D}$)
mincount B	0	201
maxcount B	0	201
Total mincount of B	201
Total maxcount of B	201	Less than minimum support level of ${\mathcal{D}}^{+}$. Pruned away.

This example shows that B cannot be frequent in ${\mathcal{D}}^{+}$, so it will not even be resent to $\Delta$ for recounting (if we would omit this optimization, then we would have to go over $\Delta$ again to count B).

By using early pruning optimization, we are able to reduce the number of candidates which reduces the output of MR, and saves CPU resources in future jobs that otherwise would require counting of the non-potential “candidates”. The above optimization is valid for any distributed framework.

Next, we show an optimization which is tailored specifically to Map-Reduce.

4.2.4. Map-Reduce Optimized Algorithm

There are few known drawbacks of the Map-Reduce framework [4,38] that can harm the performance of any algorithm. We will concentrate on the overhead of establishing a new computational job, creation of a physical process for the Mapper and the Reducer, on each of the distributed machines, and I/O consumption when it needs to read or write data from/to a remote location, e.g., read input from HDFS.

Our performance evaluation (see Section 4.3) of the General Scheme, even with the early pruning optimization, showed that the CPU time of the algorithms is lower compared to the full process of ${\mathcal{D}}^{+}$ from scratch, but parallel run time could be the same. It happens for databases that are small, and that their delta is also small. The first reason for this is that the Incremental Scheme has many more MR jobs compared to non-incremental FIM. The overhead of job creation time for each of the jobs is summed, and if it is of the same degree as the total algorithm time (happens for small databases/deltas), there could be no benefit for the incremental algorithm run time (although each machine in the cluster runs faster and consumes less energy). Another reason is that the general scheme needs to read the $\Delta$ several times from a remote location as it is required as the input for different jobs. In the non-incremental FIM algorithm, the number of I/O reads of whole ${\mathcal{D}}^{+}$ ($\mathcal{D}$ and $\Delta$) is dependent on the underlying FIM algorithm, and the later output of $\mathrm{FI}({\mathcal{D}}^{+})$. In the General Scheme, the same FIM is executed only on $\Delta$ with an output of FI(Δ), but there is also the requirement to read all FI(Δ) back from the network disk to join it with $\mathrm{FI}\left(\mathcal{D}\right)$. Moreover, it is required to read the whole $\Delta$ again for the recounting step.

To work around these limitations of the Incremental Scheme, we suggest reducing the number of jobs that are used in the General Scheme. It will allow us to reduce start times, and will imply less I/O communication. We will start with the observation that the Join job (Steps 7–8 of Algorithm 5) is required to read the output of the previous FIM job (Step 4) immediately. We suggest merging the FIM output of Step 4 with the Join job. It should receive an additional input ($\mathrm{FI}\left(\mathcal{D}\right)$), and instead of writing $\mathrm{FI}(\Delta ),$ it will “join” the results. It will still have three outputs like the original Join job. All optimizations discussed in Section 4.2.2 should be also applied in this combined step.

The next job that would be removed is the recounting step in $\Delta$ (Steps 12–13). The only itemsets that could be qualified for this output are itemsets that were not frequent in $\Delta$, and were frequent in $\mathcal{D}$. We suggest counting all itemsets from $\mathrm{FI}\left(\mathcal{D}\right)$ during Step 3 of FIM in $\Delta$, as there is already a pass over $\Delta$ anyway. IMRApriori phase 2 could be enhanced to do the counting not only for new candidates, but also for $\mathrm{FI}\left(\mathcal{D}\right)$. The updated algorithm is depicted in Figure 8.

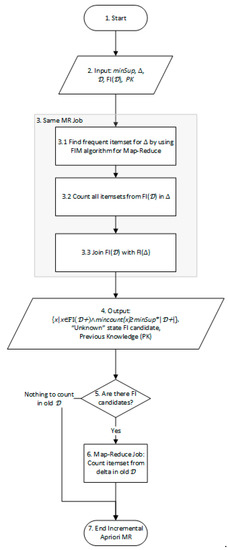
Figure 8. Optimized incremental algorithm with reduced overhead.

Our performance evaluation also revealed additional conditions when the incremental algorithm performs worse than the non-incremental one. It happens when the input for a Split is very small, and the minimum support level is also small. Under such conditions, the minimum required occurrences for an itemset to become candidate for frequent itemset is very low—it may be as low as a single transaction, and then almost all combinations of items would become candidates. Such a small job may run longer than mining the whole ${\mathcal{D}}^{+}$ with non-incremental FIM. To overcome this problem, we propose few simple but effective techniques:

• When the $\Delta$ is being split by the MR framework to Splits, it is being split to chunks of equal predefined sizes. Only the last chunk may be of different size. We need to make sure that the last chunk is larger than the previous chunk (rather than smaller). Fortunately, MR systems, like Hadoop, do append the last smaller input part to a previous chunk of predefined size. So, the last Split is actually larger than the others.
• If the total input divided by the minimum Split amounts is still too small, it is preferable to manually control the number of Splits. In most cases, it is better to sacrifice parallel computation for gaining speed with less workers or even using a single worker. Once again, it is possible to control the splitting process in Hadoop’s system via the configuration parameters.
• If $\Delta$ is still very small for a single worker to process it effectively, it is better to use a non-incremental algorithm for the calculation of ${\mathcal{D}}^{+}$.

The detection of Split sizes, configuration of Split number, and deciding which algorithm to use could be implemented in the main driver of the MR algorithm.

Merging MR jobs into one, allowed us to achieve an algorithm that has only two steps. The first step is the Map-Reduce FIM step for $\Delta$ only. For comparison, the non-incremental algorithm would have a Map-Reduce FIM calculation for the much bigger ${\mathcal{D}}^{+}$. The second step is the optional step of counting candidates in the old $\mathcal{D}$ (at most one pass over old $\mathcal{D}$), and it is triggered only when there is an itemset that must be recounted in the old $\mathcal{D}$. The price for our algorithm is a slightly more complicated FIM input and output step.

4.2.5. Reuse of Discarded Information

During the MR algorithm, we generate many itemset candidates which were “locally” frequent in some Splits, but discarded in the end as they were not globally frequent. We propose to keep the previously discarded itemsets. For this, we keep the non-frequent itemsets ($NFI\left(\mathcal{D}\right)$) in another file that will be created during the process of FIM on $\mathcal{D}$. In our algorithm from Section 4.2.1, we require this file as an additional input (Previous Knowledge). The algorithm will “join” $\mathrm{FI}(\Delta )$ with $FI\left(\mathcal{D}\right)\cup NFI\left(\mathcal{D}\right)$. With this additional information available, there is a higher chance of an itemset to have an exact count so it will not need to be recounted. As we join itemsets from $\mathrm{FI}(\Delta )$ with $NFI\left(\mathcal{D}\right)$, we are reducing the counts over $\mathcal{D}$. As the old $\mathcal{D}$ tend to be much larger than $\Delta$, reducing (and possibly eliminating completely) the count improves the run time of the algorithm. It is important to mention that NFI tends to be much smaller than all possible itemset combinations of $\mathcal{D}$, and we can keep them as they were already calculated and saved by at least one mapper anyway.

4.3. Experimental Evaluation

4.3.1. Data

The first tested dataset is synthetically generated T20I10D100000K (will be referenced as T20) [37]. It contains almost 100,000,000 (D100000K) transactions of an average length of 20 (T20), and an average length of maximal potential itemset of 10 (I10). It is 13.7 GB in size. The second dataset is “WebDocs” [35,36] (similar to Section 3.3.1).

The datasets were each cut into two equal halves. The first half of each dataset was used as the baseline of 100% size ($\mathcal{D}$). The other part was used to generate the different $\Delta$. For example, WebDocs was cut to a file size of 740 MB. Its delta of 5% was cut from the part that was left out, and its size was then 37 MB. The running time of the incremental algorithms on the 5% delta was compared to the full process of the 777 MB file (merged the 740 MB base file and the 5% delta of 37 MB as a single file for the test). Similarly, the T20 baseline of 100% has a size of 6.7 GB with 10% increments of 700 MB. We used different minSup values for each dataset. For T20, we tested minSup 0.1% and 0.2%. WebDocs was tested with 15%, 20%, 25%, 30% (although we show graphs only of 15% and 20%).

4.3.2. Setup

We ran all the experiments on the Google Compute Engine Cloud (GCE) by directly spanning VMs with Hadoop version 1 (old numbering 0.20.XX). We used different cluster sizes with 4 cores, 5 cores, 10 cores and 20 cores, and GCE instance types of n1-standard-1 or n1-standard-2.

4.3.3. Measurement

We measured various times: “run time” is measured by the “Driver” program from the start of the algorithm until all outputs are ready (“Driver” is responsible for communicating with the MR API). The “CPU time” is the time that all cluster machines consumed as measured by the MR framework.

During the experiments, we changed the size of $\Delta$, minimal support (the lower the support, the larger the candidate set size and therefore the algorithm run time should go up), and cluster sizes.

4.3.4. Experiment Internals

We compare the performance of three algorithms described in Section 4.2. We denote the algorithm from Section 4.2.2, incremental algorithm with IMRApriori and early pruning optimization—as “Delta”. The algorithm from Section 4.2.4 with minimum steps/jobs is called “DeltaMin”. The algorithm from Section 4.2.5, that also keeps count of non-frequent itemsets, is called “DeltaMinKeep”. The baseline for the comparison of the algorithms is the previously published non-incremental FIM algorithm IMRApriori [10] on ${\mathcal{D}}^{+}$. It is called “Full”.

4.3.5. Results

Figure 9a,b demonstrate the run and CPU times of each algorithm for dataset T20 on GCE cluster of size 5 and minSup 0.1%. It shows that incremental algorithms behave better than full in both parameters. The increase in delta size increases the computation time.

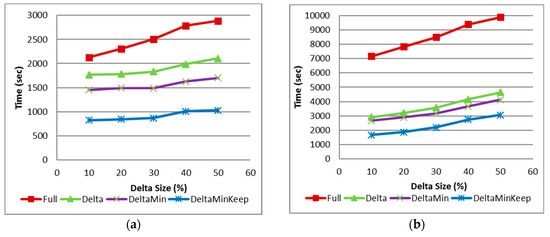
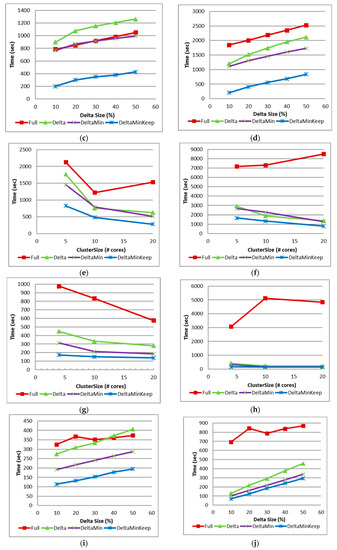
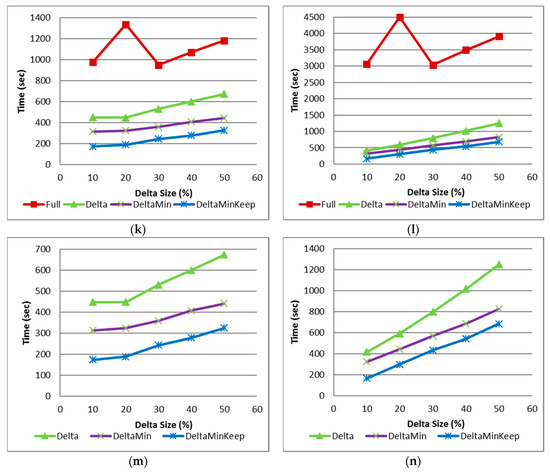
Figure 9. (a) T20 Run Time minSup 0.1% Cluster 5; (b) T20 CPU Time minSup 0.1% Cluster 5; (c) T20 Run Time minSup 0.2% Cluster 5; (d) T20 CPU Time minSup 0.2% Cluster 5; (e) T20 Run Time minSup 0.1%, inc 10%; (f) T20 CPU Time minSup 0.1%, inc 10%; (g) WebDocs Run time minSup 15% inc 10%; (h) WebDocs CPU time minSup 15% inc 10%; (i) WebDocs minSup 20% Run Time; (j) WebDocs minSup 20% CPU Time; (k) WebDocs minSup 15% Run Time; (l) WebDocs minSup 15% CPU Time; (m) WebDocs minSup 15% Run Time Close Up; (n) WebDocs minSup 15% CPU Time Close Up.

Figure 9c,d are similar to Figure 9a,b, but they depict the algorithm’s behavior for minSup 0.2%. In this case, the run time of “Delta” is higher than “Full” and “DeltaMin” behaves almost the same as “Full”. The CPU time of “Delta” and “DeltaMin” is still lower than that of “Full”. “DeltaMinKeep” is better by all parameters than “Full”. The large difference between “DeltaMinKeep” and “DeltaMin” is explained by eliminating the need to run the recount Job in old $\mathcal{D}$.

Figure 9e,f show the algorithm’s run, and CPU time behavior for T20, minSup 0.1%, and inc 10% as the GCE cluster size changes from 5 to 10, and to 20 nodes/cores. We can see that the incremental algorithms scale well with more cores added to the system, although it is not linear. “Full” recalculation scaled even worse when the cluster size changed. This is explained by the fact, that as long as the input data size divided by the number of workers is larger than the HDFS block size, each mapper gets exactly the same Split, and its work is the same. Once the cluster size scales above this point, the data split size gets lower than the HDFS block. In most algorithms, the smaller the input, the faster the algorithm runs. In our case, this is true for the counting jobs (second step of IMRApriori or recounting in case of old DB check) and the “Join” job. The first step of IMRApriori finds all FI of its data split by running Apriori on its data Split. This algorithm is not linear in its input size and may perform worse on a very small input size (see Section 4.2.4).

Figure 9g,h show the algorithm’s run and CPU time behavior for WebDocs, minSup 15% and inc 10% as GCE cluster size changes from 5 to 10 and to 20 nodes/cores. We can see that incremental algorithms scale well when more cores are added to the system. “Full” recalculation CPU time does not scale that well when cluster size changes, similar to the previous case.

Figure 9i,j show WebDocs with minSup 20% run, and CPU time as delta size varies. It shows that run time of “Delta” is no better than “Full”, but its CPU time is better.

Figure 9k,l show similar graphs to Figure 9i,j, but for minSup 15%. As frequent itemset mining for minSup of 15% is more computationally extensive than 20%, the resulted times are higher. We can see that in this case, all incremental algorithms behave much better than the full algorithm. In some cases, a full run takes 2–3 times longer than incremental algorithms.

Figure 9m,n are similar to Figure 9k,l, but show a close up of the incremental algorithms only, and their run/CPU times. It shows that “Delta” behaves worse than “DeltaMin”, and “DeltaMin” behaves worse than “DeltaMinKeep”.

Our evaluation shows that the incremental algorithms do similarly or better than full recalculation on smaller sized datasets with larger support in terms of CPU time, while the Run time was not always better for less optimized “Delta” and “DeltaMin” algorithms

As the support threshold decreased, all incremental algorithms had better Run and CPU times than “Full” re-computation. They outperformed the “Full” algorithm several times (in some of the tests, even by a factor of 10). The explanation for this is that more time is required to mine FI than just doing candidate counting.

The Run and CPU times of “DeltaMin” is always superior to “Delta”. “DeltaMinKeep” showed results superior to “DeltaMin” according to Run time and CPU time. The large differences were observed in execution when the algorithm managed to completely eliminate the counting step of old $\mathcal{D}$.

Algorithm run time and CPU time showed almost linear growth with an increase in input size (increase in $\Delta$ size), as long as the Split size stayed constant.

Cluster size change showed that larger clusters improve the run time. It is not always linear, as there is a limit at which splitting the input into too many small chunks generates too many locally frequent itemsets, which requires longer recounting steps.

4.3.6. Comparison to Previous Works

The FUP algorithm [15] was the first to provide an Incremental Scheme which is based on mining the $\Delta$. The algorithm is not distributed or parallel. It mines $\Delta$ by iterative steps from candidates of size 1 to K, and stops when no more candidates are available. At each step, this algorithm scans the old $\mathcal{D}$ to check the validity of its candidates. Implementing this algorithm in MR would require K scans over the old $\mathcal{D}$, which would generate K-times more I/O than our algorithms and would be less effective.

ARM IDB [7] provides optimizations on incremental mining by using the TID–list intersection and its “LAPI” optimization. The algorithm does not deal with a distributed environment (i.e., MR), so it has no way to scale out.

Incoop and DryadInc do not support more than one input for DAG (and we need to be able to have DB and the candidate set as an input). As there is no known way to overcome this difference, it does not allow us a direct comparison. These systems cannot extract useful information from the knowledge of the algorithm goal or its specific implementation and therefore improve their run time.

4.3.7. The Algorithm Relation to the Spark Architecture

Spark [3] is a distributed parallel system that has recently gathered popularity. The main difference from Map-Reduce is that it tries to make all computations in memory. Spark uses notation of Resilient Distributed Datasets (RDDs), which can be recomputed in case of failure. On the contrary, Map-Reduce saves all intermediate and final results on a local or a distributed file system (DFS). The fact that Spark uses in-memory computation, and in-memory distributed cache allows Spark to achieve better performance. It has much less I/O operations as data is being cached in memory. This provides a significant boost to many algorithms.

Our general algorithm is not going to change due to the switch of the computation framework to Spark. We still need to assume that there is a way to compute frequent itemsets in Spark (and indeed Spark’s mllib library contains the FIM algorithm, which is currently based on a FP-Growth–FPGrowth class). Joining two lists/tables is also easily done in Spark. Spark has many kinds of joins implemented (“join” function). The last parts are recounting transactions in different datasets, which could be once again easily done via a set of calls to “map” and “reduceByKey” Spark functions. Broadcasting and caching datasets of all new potential frequent itemsets on each node will improve the overall run time (SparkContext.broadcast). This is possible as the amount of potential frequent itemsets tends to be much lower than all datasets and could be cached in the memory of each partition. As the calculation of frequent itemsets is a computationally intensive operation, the Spark incremental scheme for FIM would have better performance than full re-computation in most cases, similar to Map-Reduce.

The early pruning optimization that was introduced in Section 4.2.2 would have a positive effect in Spark too, as there will be less itemsets to cache in memory, and less itemsets to check against the different datasets.

Job reduction optimizations from Section 4.2.4 are less effective in Spark because of the following: Spark does not spawn a new process/VM for each task, but utilizes multi-threading, so it achieves a better job start time. Spark also encourages writing programs in declarative ways so some “job merging” is achieved naturally by allowing the SparkContext executors to decide for themselves how to solve the problem more effectively. If the size of a dataset tends to be much larger than the total RAM of the cluster, then the cache would be frequently flushed, and data would be re-read from the disk. In such cases, manually forcing a data read only once would be still beneficial, so joining a few computations into a single pass on data will be preferable.

The reuse of discarded data from Section 4.2.5 tends to reduce the number of itemsets that need to be checked in the old dataset. The issue is that the default FIM algorithm in Spark does not produce any intermediate results as it is based on FP-Growth. If some other algorithm for FIM could be used that would produce additional itemsets, we suggest using them and this optimization.

Spark streaming is based on re-running the algorithm on “micro batches” of newly arrived data. Our algorithm could be used to achieve this task. However, the sizes of batches that are suitable for efficient streaming computation should be further studied.

5. Conclusions

This work presented methods for mining frequent itemsets. For closed frequent itemset mining, we have presented a new, distributed, and parallel algorithm using the popular Map-Reduce programming paradigm. Besides its novelty, using Map-Reduce makes this algorithm easy to implement, relieving the programmer from the work of handling concurrency, synchronization and node management which are part of a distributed environment, and focus on the algorithm itself.

Incremental frequent itemset mining algorithms, that were presented in this work, range from a General Scheme that could be used with any distributed environment, to a Map-Reduce heavily optimized version which mostly works much better than other algorithms in experiments. The lower the support rate, the harder the computations are, and the more benefit that can be achieved by the incremental algorithms.

A general direction for future research for both presented schemes involves implementing and testing them on other distributed environments like Spark. We assume that most of the proposed algorithms will work effectively, although some methods may become redundant once the distributed engine becomes more effective with less overhead.