Weak Fault Detection of Tapered Rolling Bearing Based on Penalty Regularization Approach
Abstract
:1. Introduction
2. Augmented Huber Non-Convex Penalty Regularization
2.1. Sparse Representation
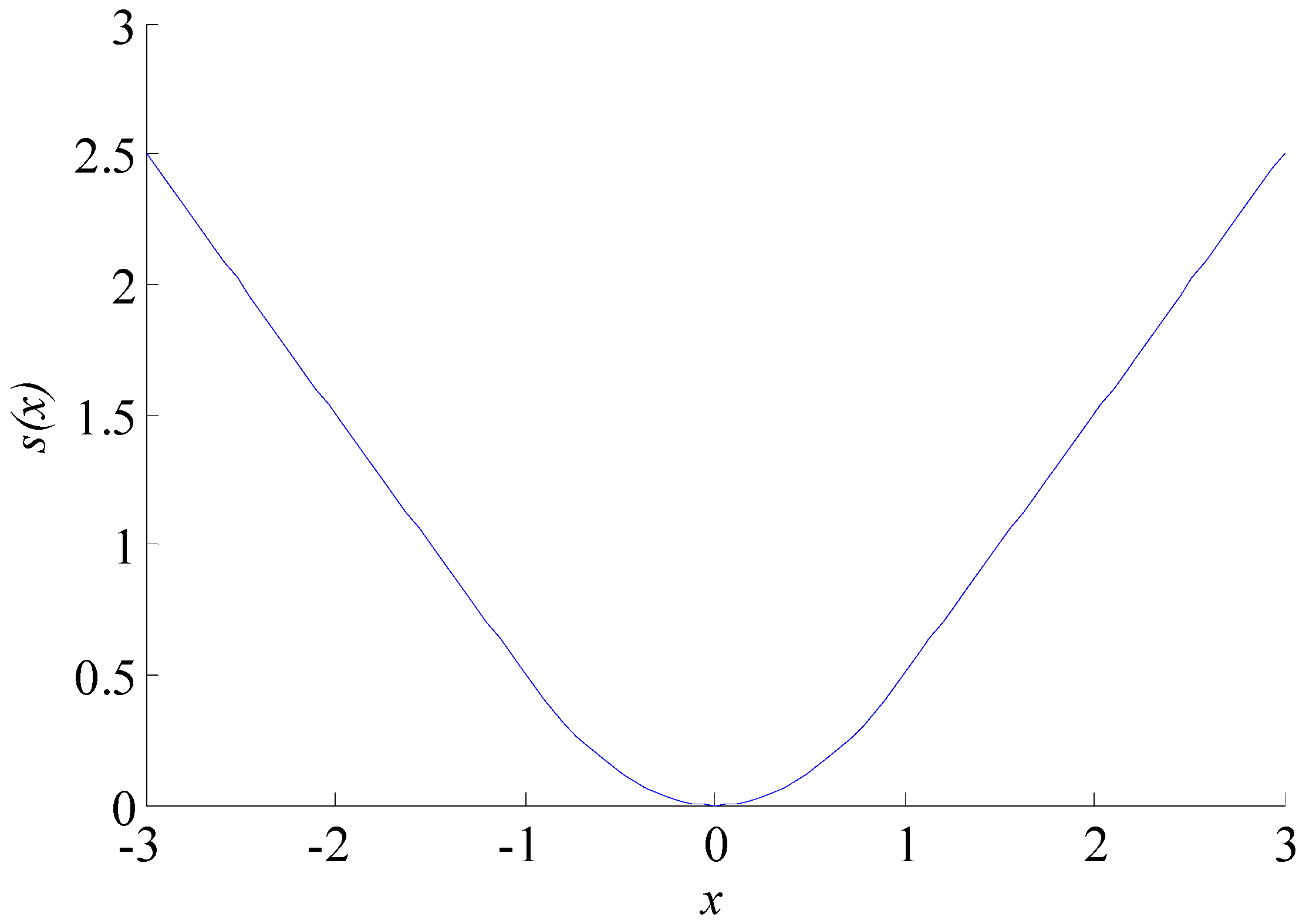
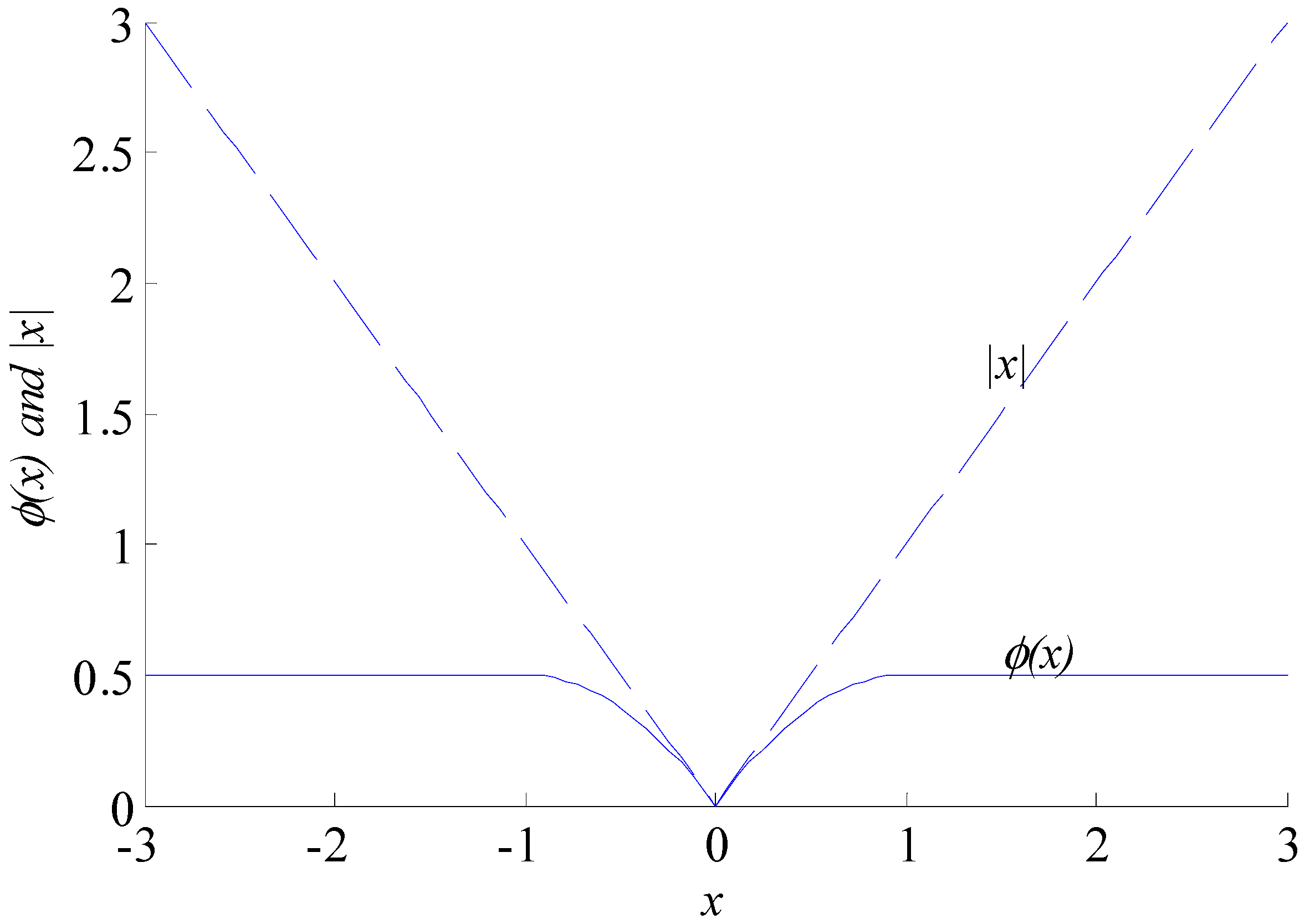
2.2. The Augmented Huber Non-Convex Penalty Regularization
2.3. Convexity Condition
| Algorithm 1 Iterative algorithm for the proposed AHNPR method |
| Initialization: ,, ; |
| For ; |
| end return: |
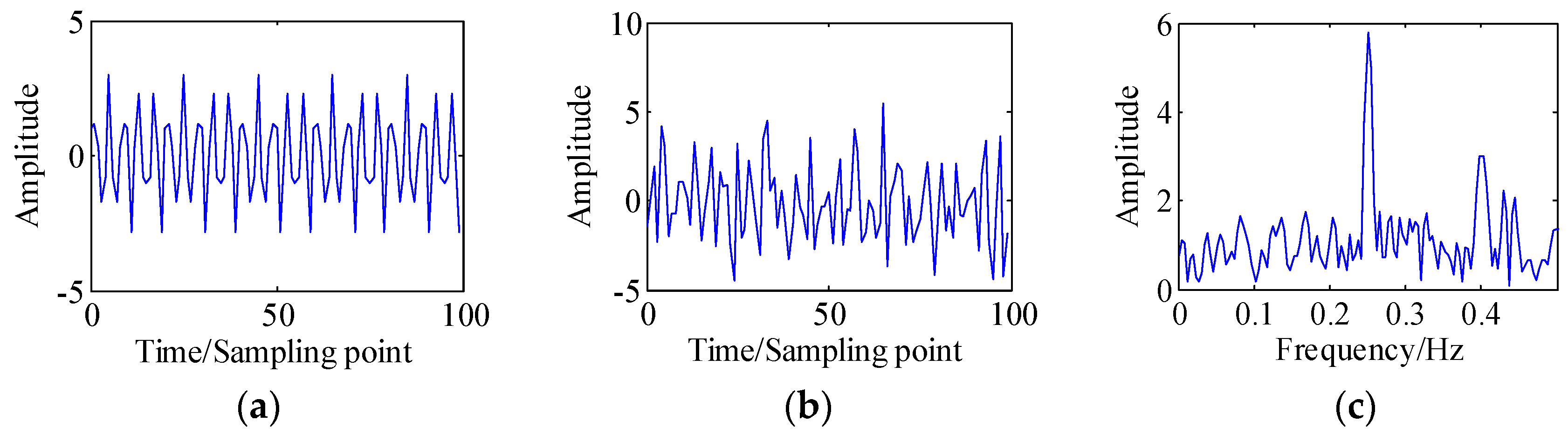
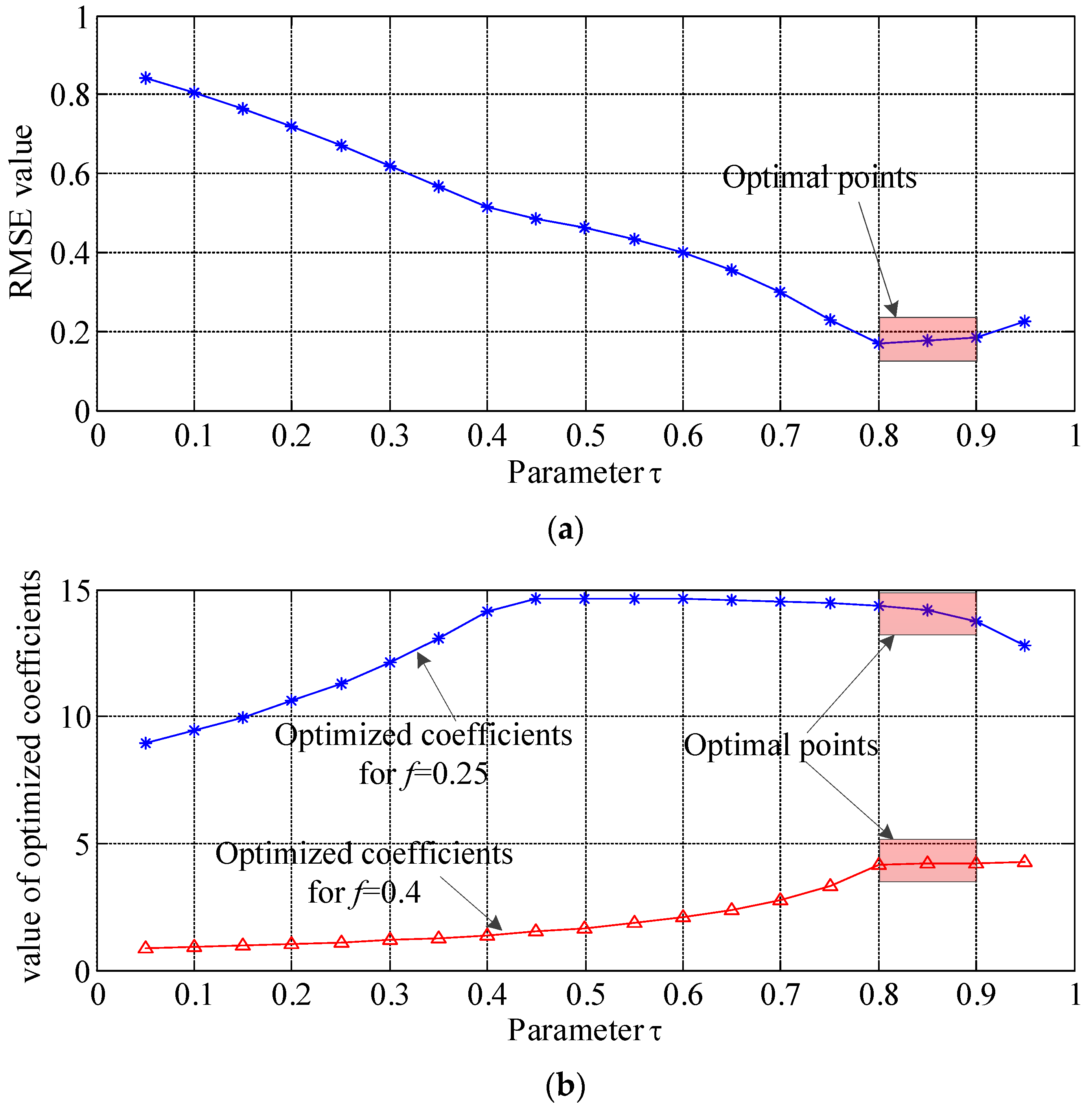
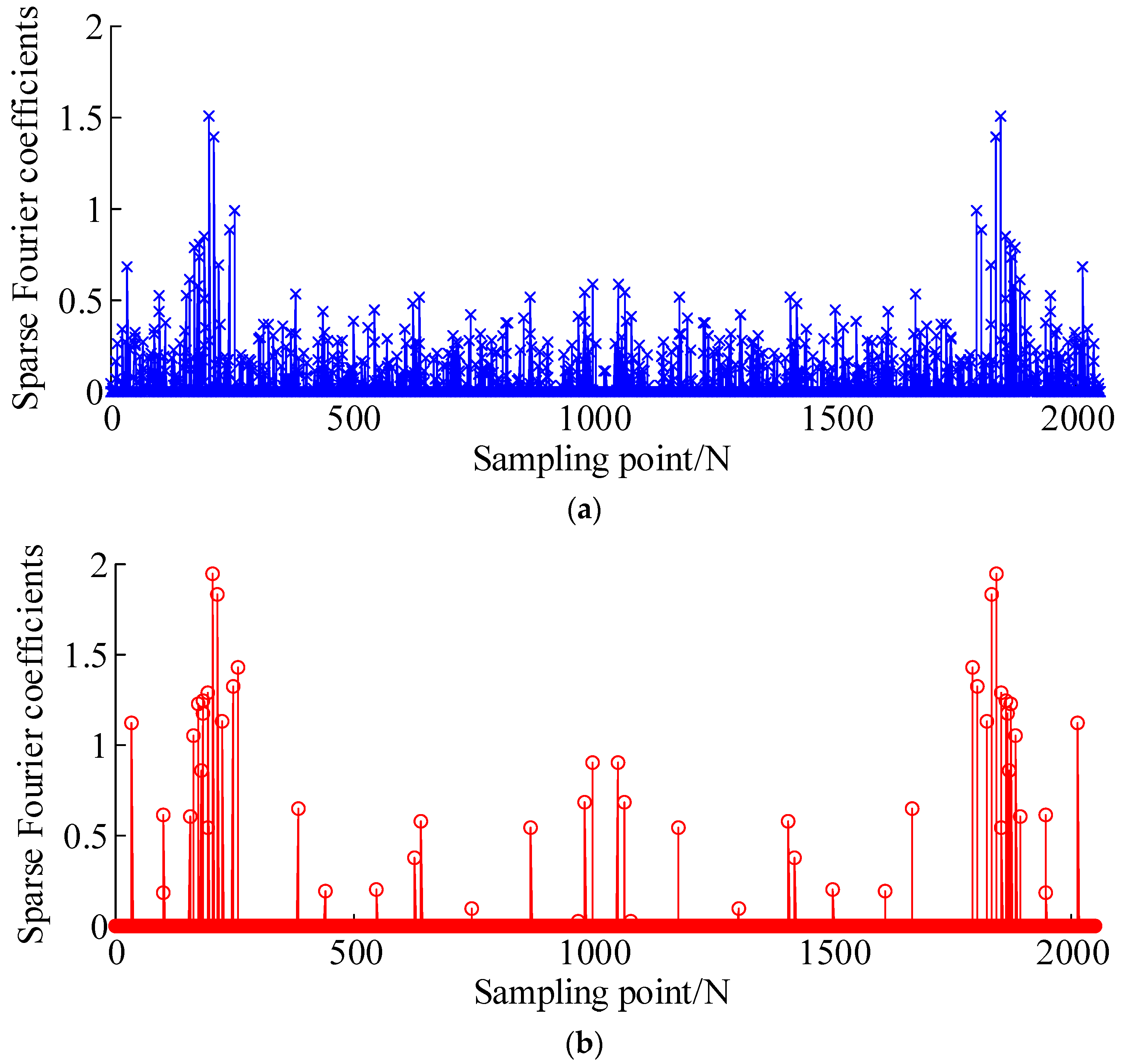
3. Numerical Simulation
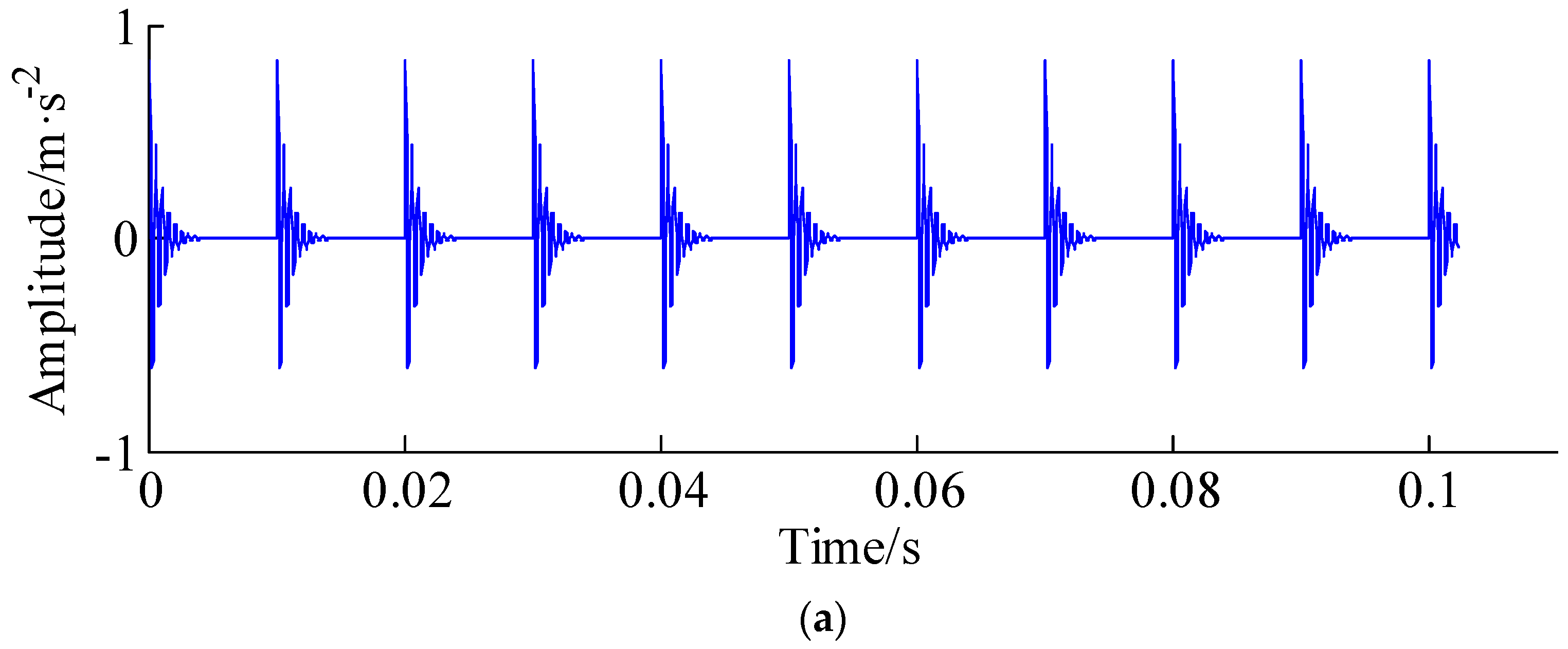
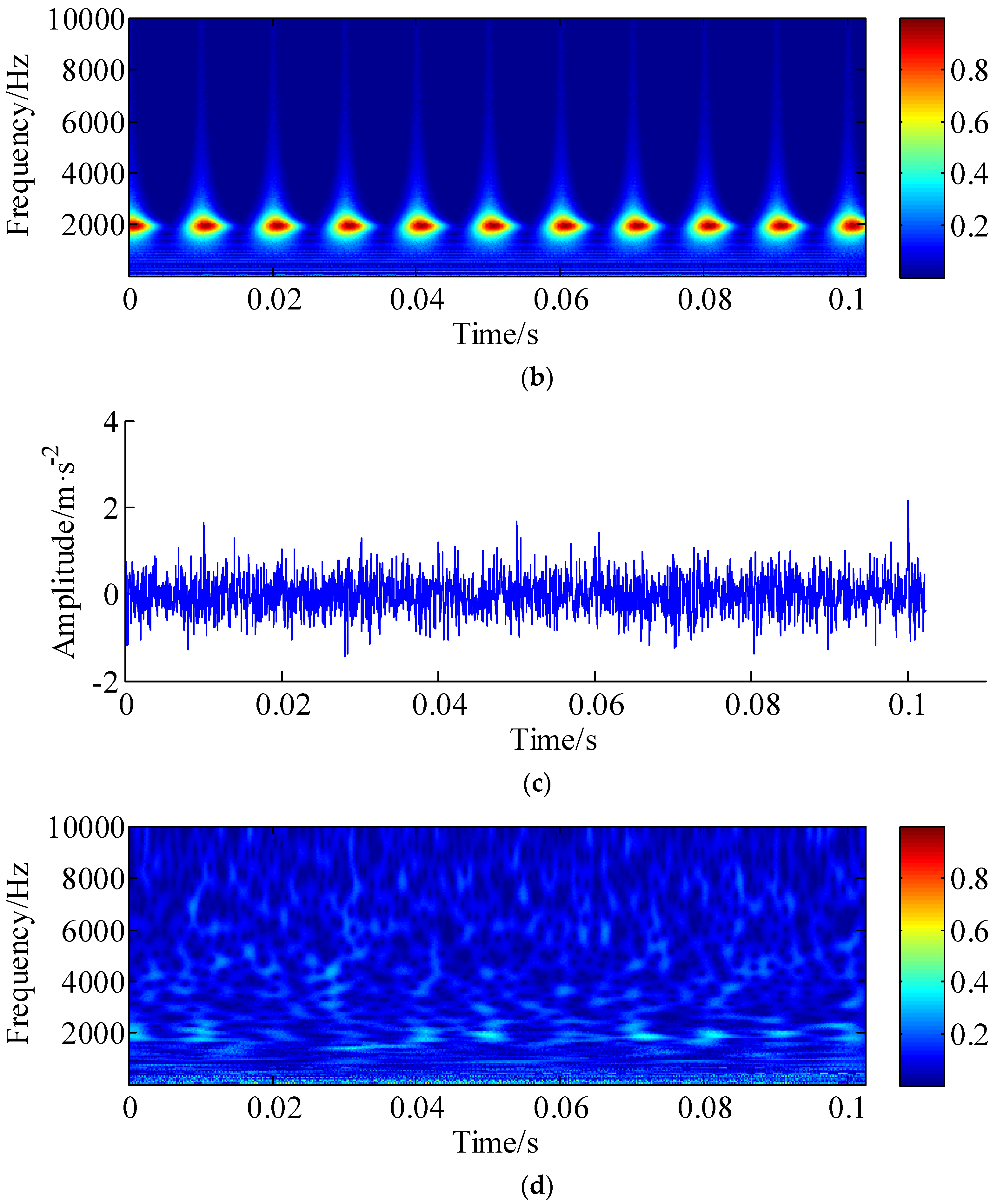
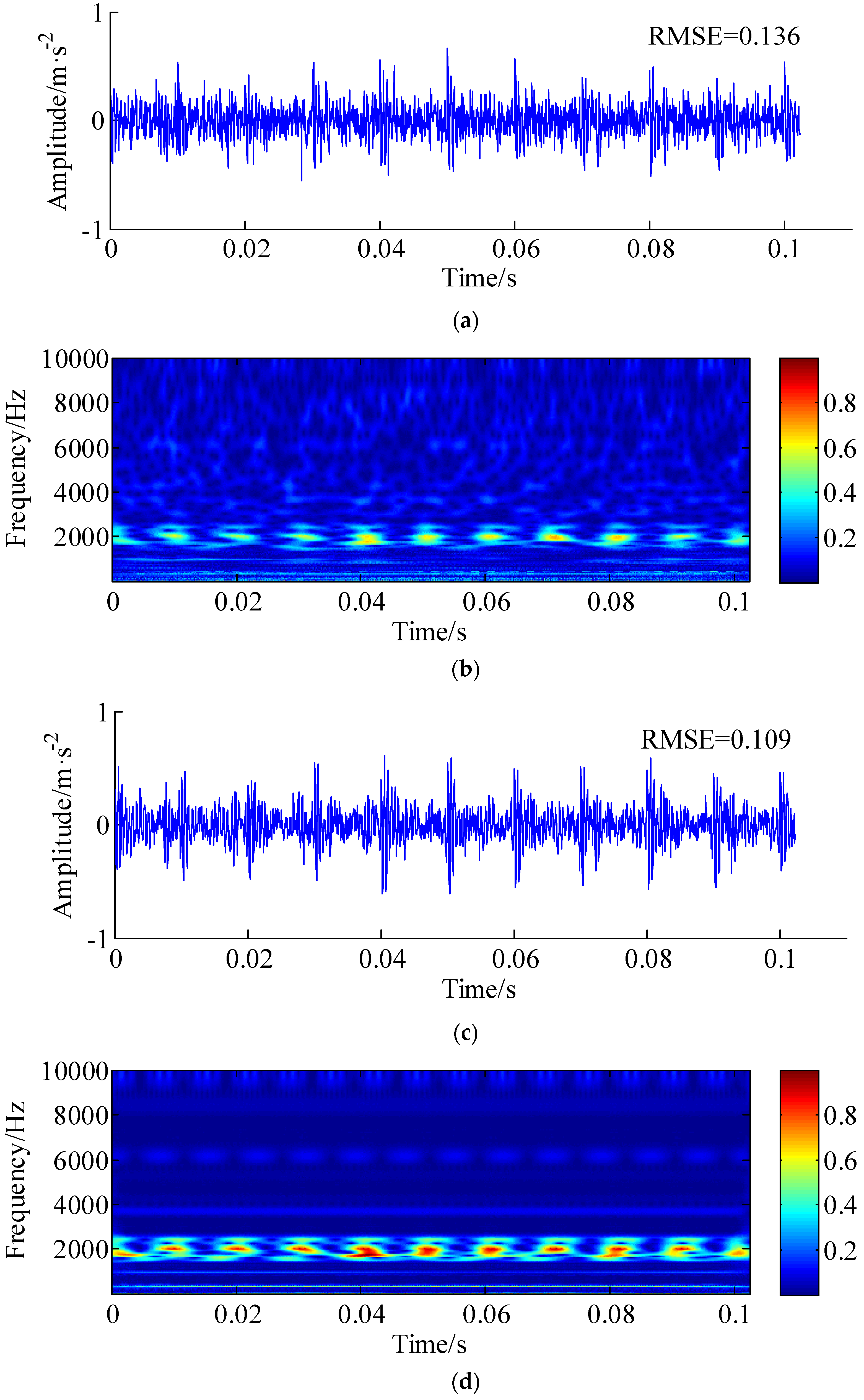
4. Experimental Verification
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lin, J.S.; Dou, C.H. A novel method for condition monitoring of rotating machinery based on statistical linguistic analysis and weighted similarity measures. J. Sound Vib. 2017, 390, 272–288. [Google Scholar] [CrossRef]
- Li, Q.; Liang, S.Y. Degradation trend prognostics for rolling bearing using improved R/S statistic model and fractional Brownian motion approach. IEEE Access 2018, 6, 21103–21114. [Google Scholar] [CrossRef]
- Li, Q.; Liang, S.Y. Intelligent Prognostics of Degradation Trajectories for Rotating Machinery Based on Asymmetric Penalty Sparse Decomposition Model. Symmetry 2018, 10, 214. [Google Scholar] [CrossRef]
- Chen, J.L.; Li, Z.P.; Pan, J.; Chen, G.G.; Zi, Y.Y.; Yuan, J.; Chen, B.Q.; He, Z.J. Wavelet transform based on inner product in fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2016, 70–71, 1–35. [Google Scholar] [CrossRef]
- Shen, C.Q.; Wang, D.; Kong, F.R.; Tse, P.W. Fault diagnosis of rotating machinery based on the statistical parameters of wavelet packet paving and a generic support vector regressive classifier. Measurement 2013, 46, 1551–1564. [Google Scholar] [CrossRef]
- Lei, Y.G.; He, Z.J.; Zi, Y.Y. Application of the EEMD method to rotor fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2009, 23, 1327–1338. [Google Scholar] [CrossRef]
- Li, Q.; Ji, X.; Liang, S.Y. Incipient fault feature extraction for rotating machinery based on improved AR-minimum entropy deconvolution combined with variational mode decomposition approach. Entropy 2017, 19, 317. [Google Scholar] [CrossRef]
- Li, Q.; Liang, S.Y.; Song, W.Q. Revision of bearing fault characteristic spectrum using LMD and interpolation correction algorithm. Procedia CIRP 2016, 56, 182–187. [Google Scholar] [CrossRef]
- Ming, Y.; Chen, J.; Dong, G.M. Weak fault feature extraction of rolling bearing based on cyclic Wiener filter and envelope spectrum. Mech. Syst. Signal Process. 2011, 25, 1773–1785. [Google Scholar] [CrossRef]
- Saidi, L.; Ali, J.B.; Fnaiech, F. Application of higher order spectral features and support vector machines for bearing faults classification. ISA. Trans. 2015, 54, 193–206. [Google Scholar] [CrossRef] [PubMed]
- Du, Z.H.; Chen, X.F.; Zhang, H.; Yang, B.Y.; Zhai, Z.; Yan, R.Q. Weighted low-rank sparse model via nuclear norm minimization for bearing fault detection. J. Sound Vib. 2017, 400, 270–287. [Google Scholar] [CrossRef]
- He, Q.B.; Ding, X.X. Sparse representation based on local time-frequency template matching for bearing transient fault feature extraction. J. Sound Vib. 2016, 370, 424–443. [Google Scholar] [CrossRef]
- He, G.L.; Ding, K.; Lin, H.B. Fault feature extraction of rolling element bearings using sparse representation. J. Sound Vib. 2016, 366, 514–527. [Google Scholar] [CrossRef]
- Li, Q.; Liang, S.Y. Incipient Fault Diagnosis of rolling bearings based on impulse-step impact dictionary and re-weighted minimizing nonconvex penalty Lq regular technique. Entropy 2017, 19, 421. [Google Scholar] [CrossRef]
- Cui, L.L.; Wu, N.; Ma, C.Q.; Wang, H.Q. Quantitative fault analysis of roller bearings based on a novel matching pursuit method with a new step-impulse dictionary. Mech. Syst. Signal Process. 2016, 68–69, 34–43. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B.; Boyd, S.P. Enhancing sparsity by reweighted L1 minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Parekh, A.; Selesnick, I.W. Improved sparse low-rank matrix estimation. Signal Process. 2017, 139, 62–69. [Google Scholar] [CrossRef] [Green Version]
- Rakotomamonjy, A.; Flamary, R.; Gasso, G.; Canu, S. ℓp-ℓq penalty for sparse linear and sparse multiple kernel multitask learning. IEEE Trans. Neural Netw. 2011, 22, 1307–1320. [Google Scholar] [CrossRef] [PubMed]
- Wipf, D.; Nagarajan, S. Iterative reweighted L1 and L2 methods for finding sparse solutions. IEEE J. Sel. Top. Signal Process. 2010, 4, 317–329. [Google Scholar] [CrossRef]
- Lin, X.F.; Wei, G. Generalized non-convex non-smooth sparse and low rank minimization using proximal average. Neurocomputing 2016, 174, 1116–1124. [Google Scholar] [CrossRef]
- Pan, Z.; Zhang, C.S. Relaxed sparse eigenvalue conditions for sparse estimation via non-convex regularized regression. Pattern Recogn. 2015, 48, 231–243. [Google Scholar] [CrossRef] [Green Version]
- Majumdar, A.; Ward, R.K.; Aboulnasr, T. Non-convex algorithm for sparse and low-rank recovery: Application to dynamic MRI reconstruction. Magn. Reson. Imaging 2013, 31, 448–455. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Gu, Y. The convergence guarantees of a non-convex approach for sparse recovery. IEEE Trans. Signal Process. 2014, 62, 3754–3767. [Google Scholar] [CrossRef]
- Li, Q.; Liang, S.Y. An improved sparse regularization method for weak fault diagnosis of rotating machinery based upon acceleration signals. IEEE Sens. J. 2018, 18, 6693–6705. [Google Scholar] [CrossRef]
- Li, Q.; Liang, S.Y. Multiple faults detection for rotating machinery based on bicomponent sparse low-rank matrix separation approach. IEEE Access 2018, 6, 20242–20254. [Google Scholar] [CrossRef]
- Natarajan, B.K. Sparse approximate solutions to linear systems. SIAM J. Comput. 1995, 24, 227–234. [Google Scholar] [CrossRef]
- Donoho, D.L. De-noising by soft-thresholding. IEEE Trans. Inform. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef] [Green Version]
- Selesnick, I.W. Total variation denoising via the Moreau envelope. IEEE Signal Process. Lett. 2017, 24, 216–220. [Google Scholar] [CrossRef]
- Selesnick, I.W.; Graber, H.L.; Pfeil, D.S.; Barbour, R.L. Simultaneous low-pass filtering and total variation denoising. IEEE Trans. Signal Process. 2014, 62, 1109–1124. [Google Scholar] [CrossRef]
- Condat, L. A direct algorithm for 1-D total variation denoising. IEEE Signal Proc. Let. 2013, 20, 1054–1057. [Google Scholar] [CrossRef] [Green Version]
- Huber, P.J. Robust regression: Asymptotics, conjectures and Monte Carlo. Ann Stat. 1973, 1, 799–821. [Google Scholar] [CrossRef]
- Huber, P.J. Robust Statistics; Wiley: New York, NY, USA, 1981. [Google Scholar]
- Donoho, D.L.; Johnstone, I.M. Ideal spatial adaptation by wavelet shrinkage. Biometrika 1993, 81, 425–455. [Google Scholar] [CrossRef]
- Bauschke, H.H.; Combettes, P.L. Convex Analysis and Monotone Operator Theory in Hilbert Spaces; Springer: Berlin, Germany, 2011. [Google Scholar]
- Li, Q.; Liang, S.Y. Weak Fault Detection for Gearboxes Using Majorization–Minimization and Asymmetric Convex Penalty Regularization. Symmetry 2018, 10, 243. [Google Scholar] [CrossRef]


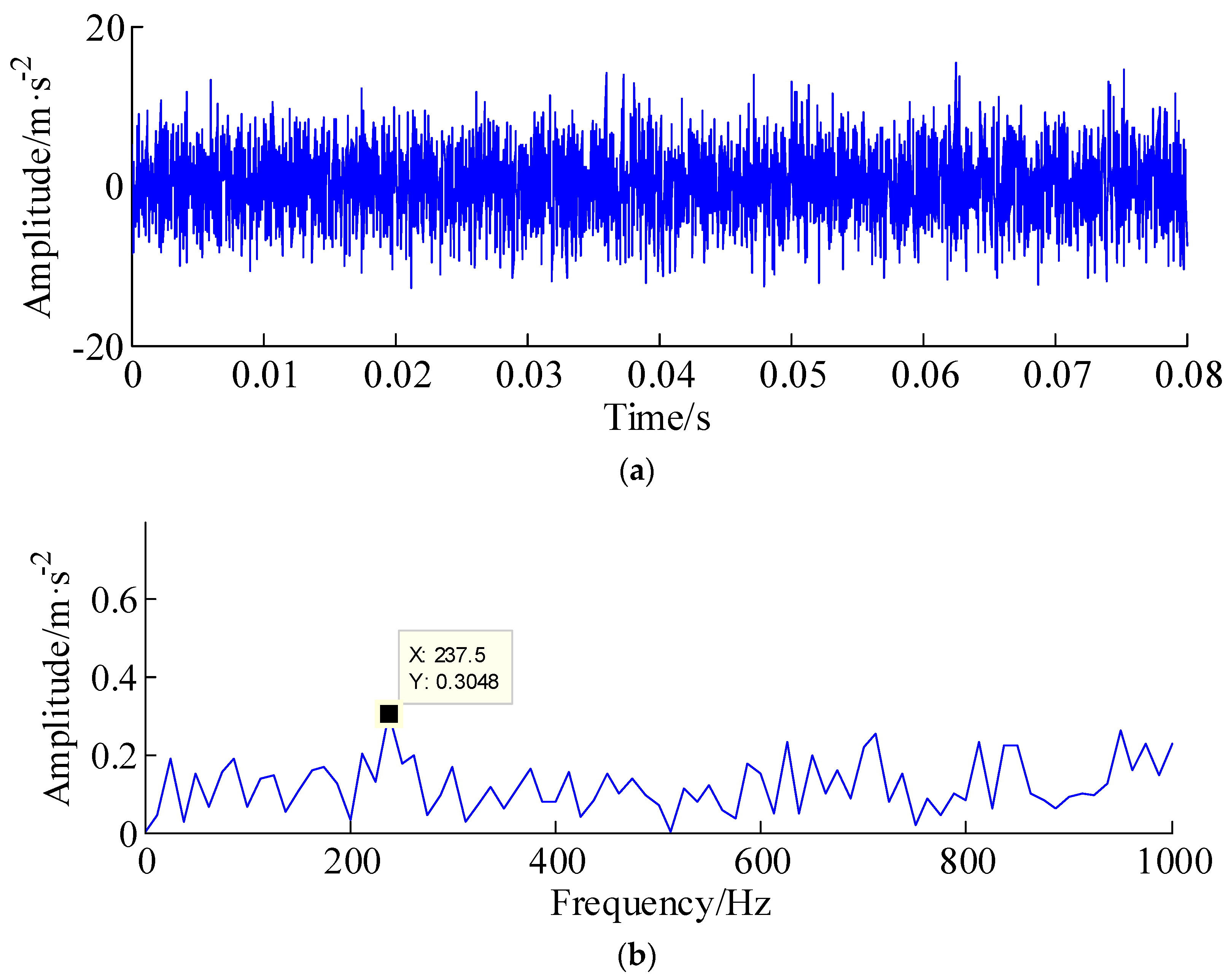
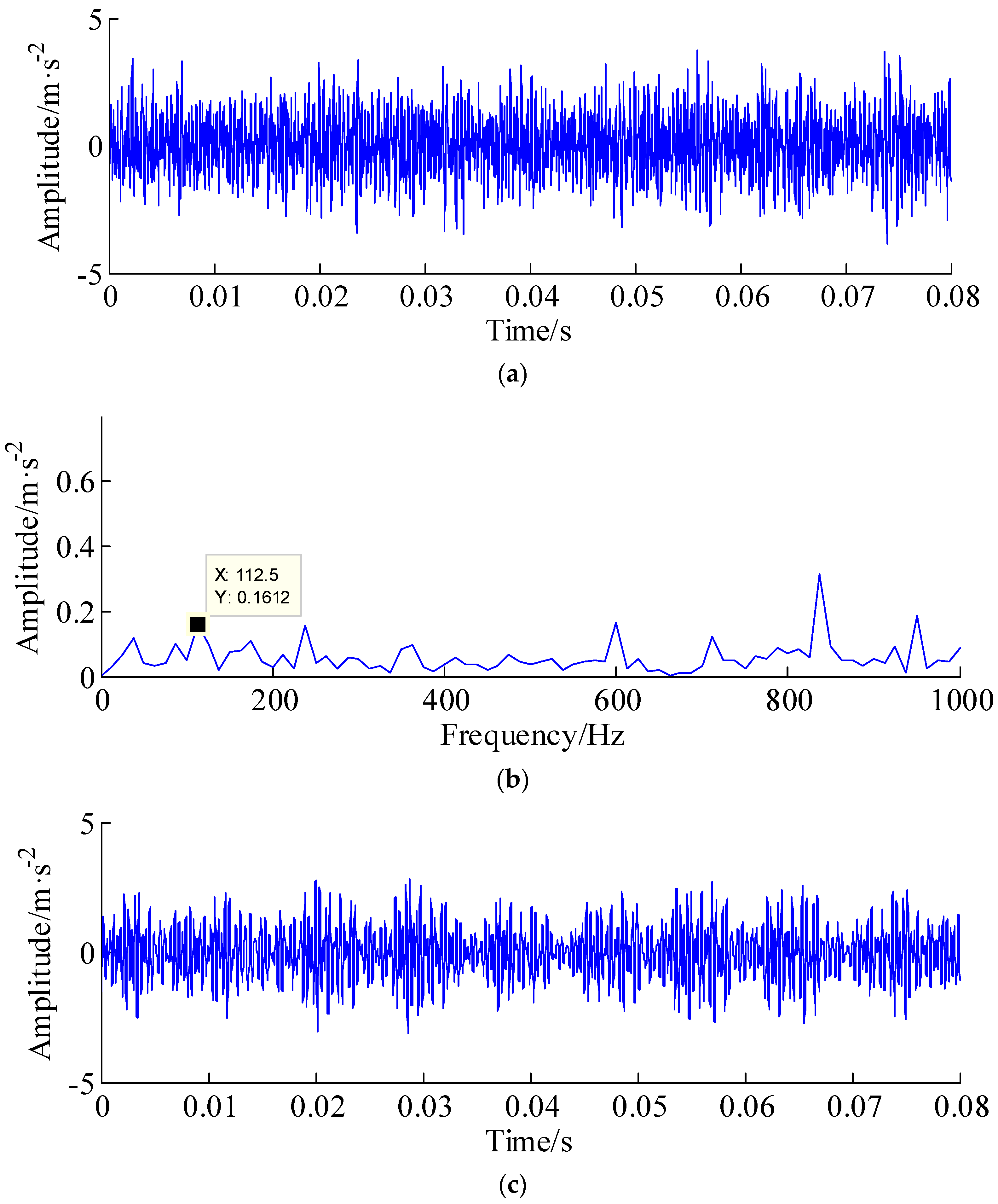
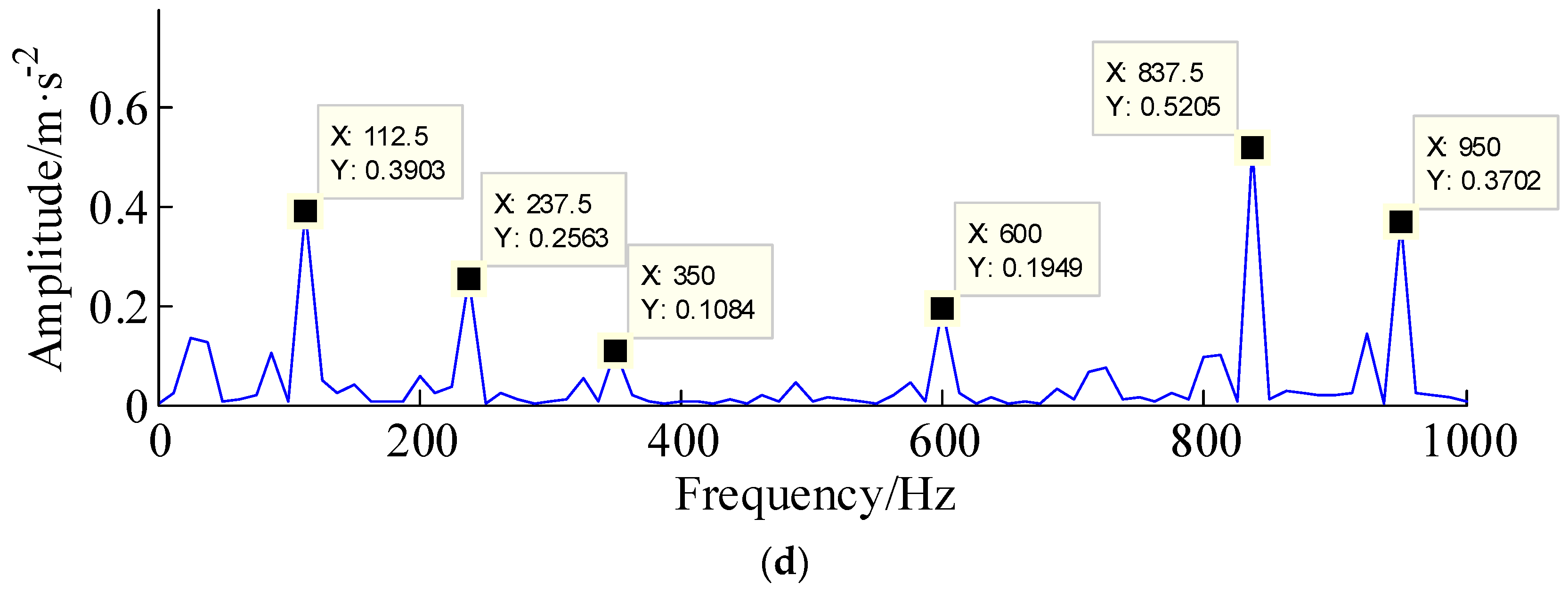
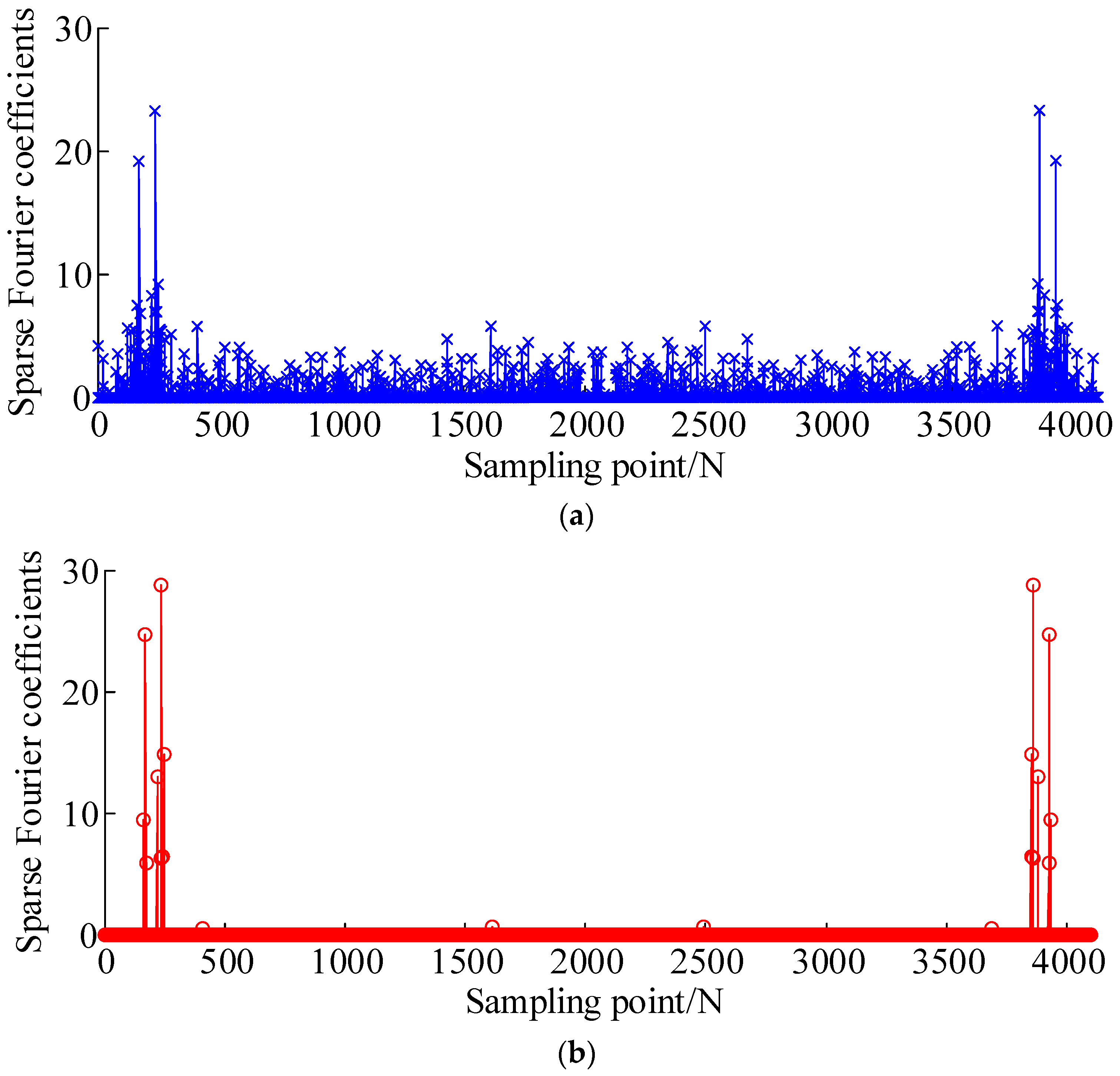
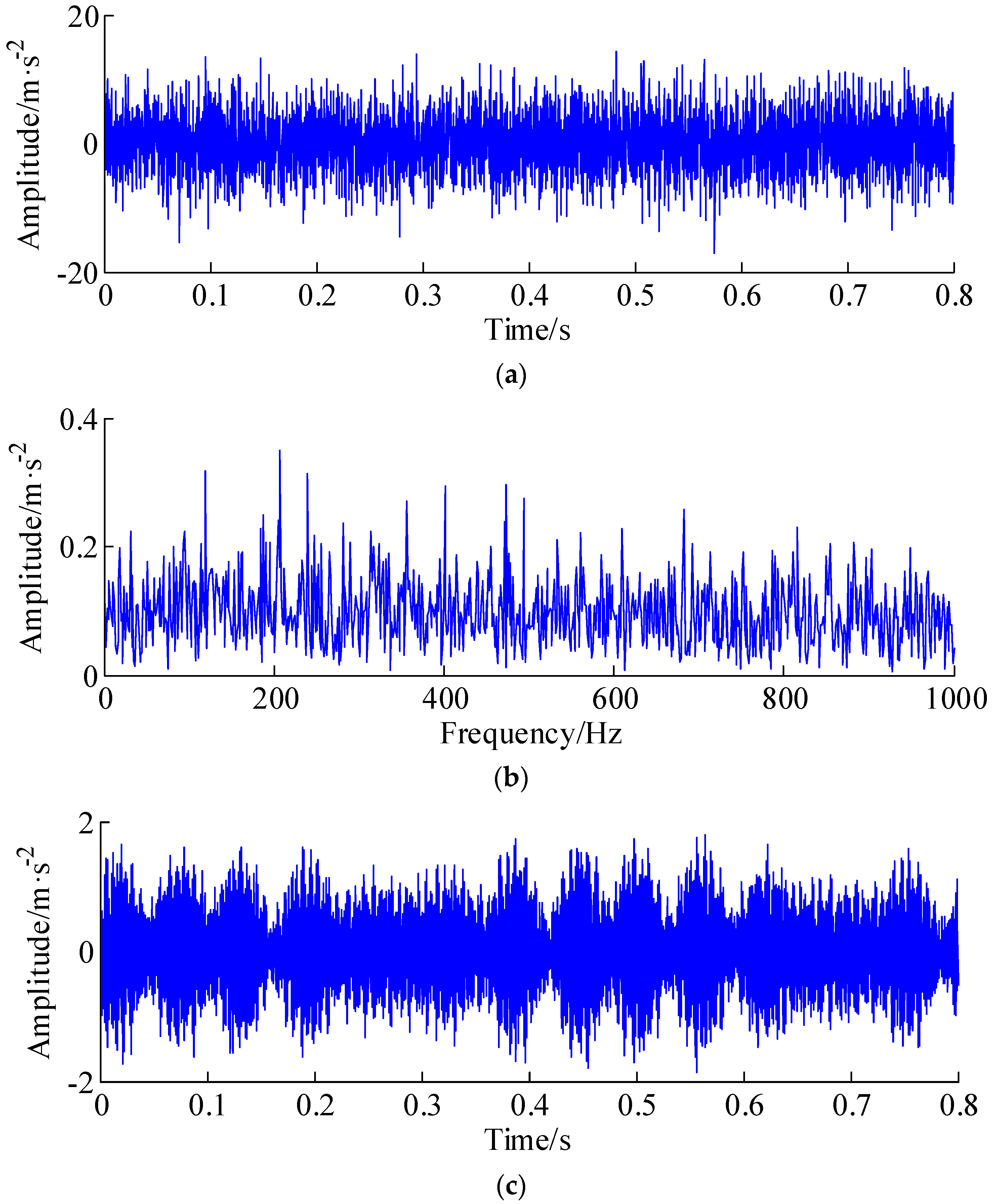
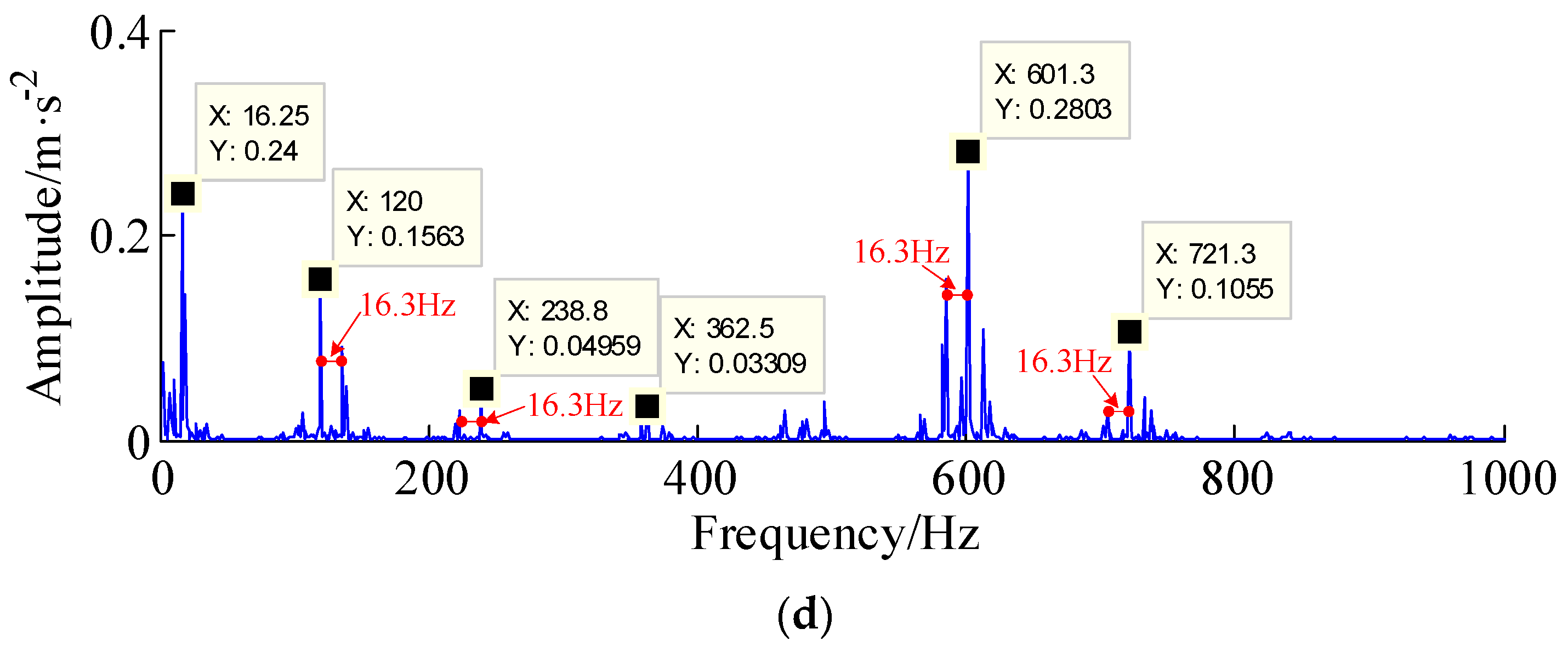
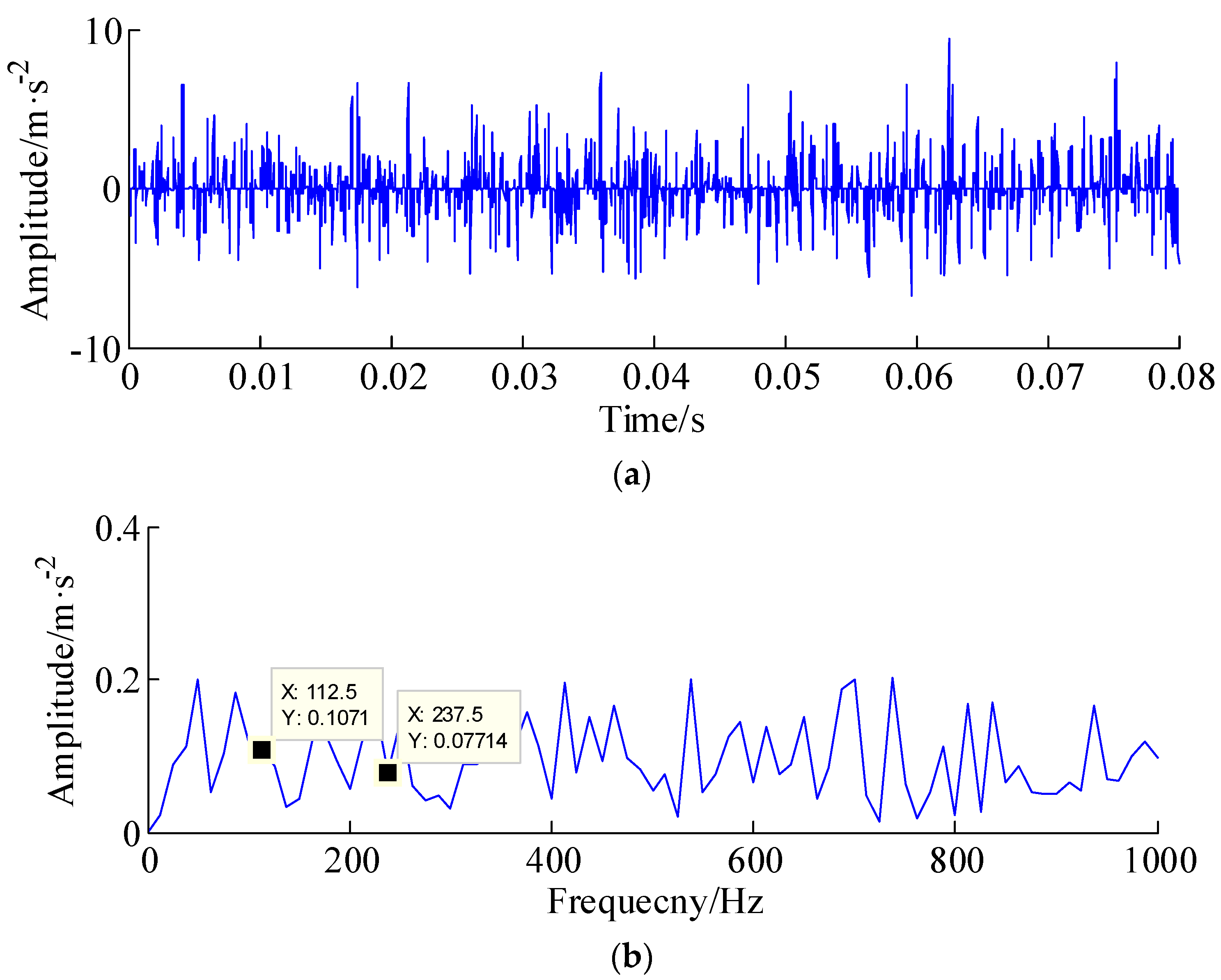
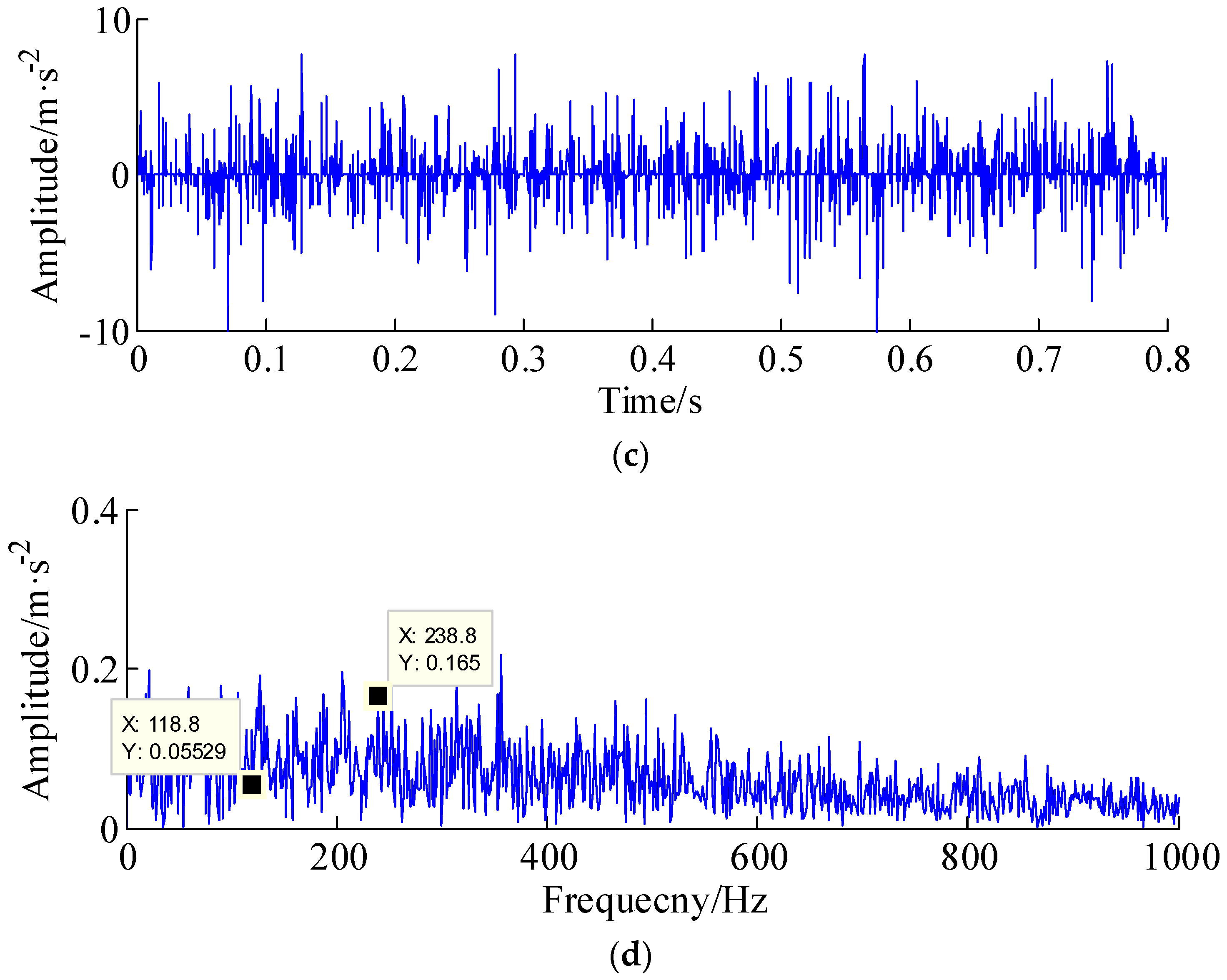
| Bearing Type | Fault Type | Number of Balls | Inner Diameter | Outer Diameter | Fault Frequency |
|---|---|---|---|---|---|
| FAG-32212-A | Outer race | 9 | 60 mm | 110 mm | 118.8 Hz |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Liang, S.Y. Weak Fault Detection of Tapered Rolling Bearing Based on Penalty Regularization Approach. Algorithms 2018, 11, 184. https://doi.org/10.3390/a11110184
Li Q, Liang SY. Weak Fault Detection of Tapered Rolling Bearing Based on Penalty Regularization Approach. Algorithms. 2018; 11(11):184. https://doi.org/10.3390/a11110184
Chicago/Turabian StyleLi, Qing, and Steven Y. Liang. 2018. "Weak Fault Detection of Tapered Rolling Bearing Based on Penalty Regularization Approach" Algorithms 11, no. 11: 184. https://doi.org/10.3390/a11110184
APA StyleLi, Q., & Liang, S. Y. (2018). Weak Fault Detection of Tapered Rolling Bearing Based on Penalty Regularization Approach. Algorithms, 11(11), 184. https://doi.org/10.3390/a11110184






