Iterative Identification for Multivariable Systems with Time-Delays Based on Basis Pursuit De-Noising and Auxiliary Model
Abstract
:1. Introduction
1.1. Background
1.2. Formulation of the Problem of Interest for this Investigation
1.3. Literature Survey
1.4. Scope and Contribution of this Study
1.5. Organization of the Paper
2. Problem Description
3. Identification Algorithm
- Collect the input–output data {, : ; } and set the parameter estimation accuracy .
- Construct the stacked output vector Y by Equation (9).
- Initialize the iteration: let and be random sequences.
- Call the function to obtain the optimum solution and compute by Equation (31).
- Set a threshold to obtain and recover the parameter vector estimate by (32).
- Compare with : if , update the auxiliary model outputs by Equations (15) and (16) and go to Step 4. Otherwise, stop the iteration and obtain the parameter vector estimate .
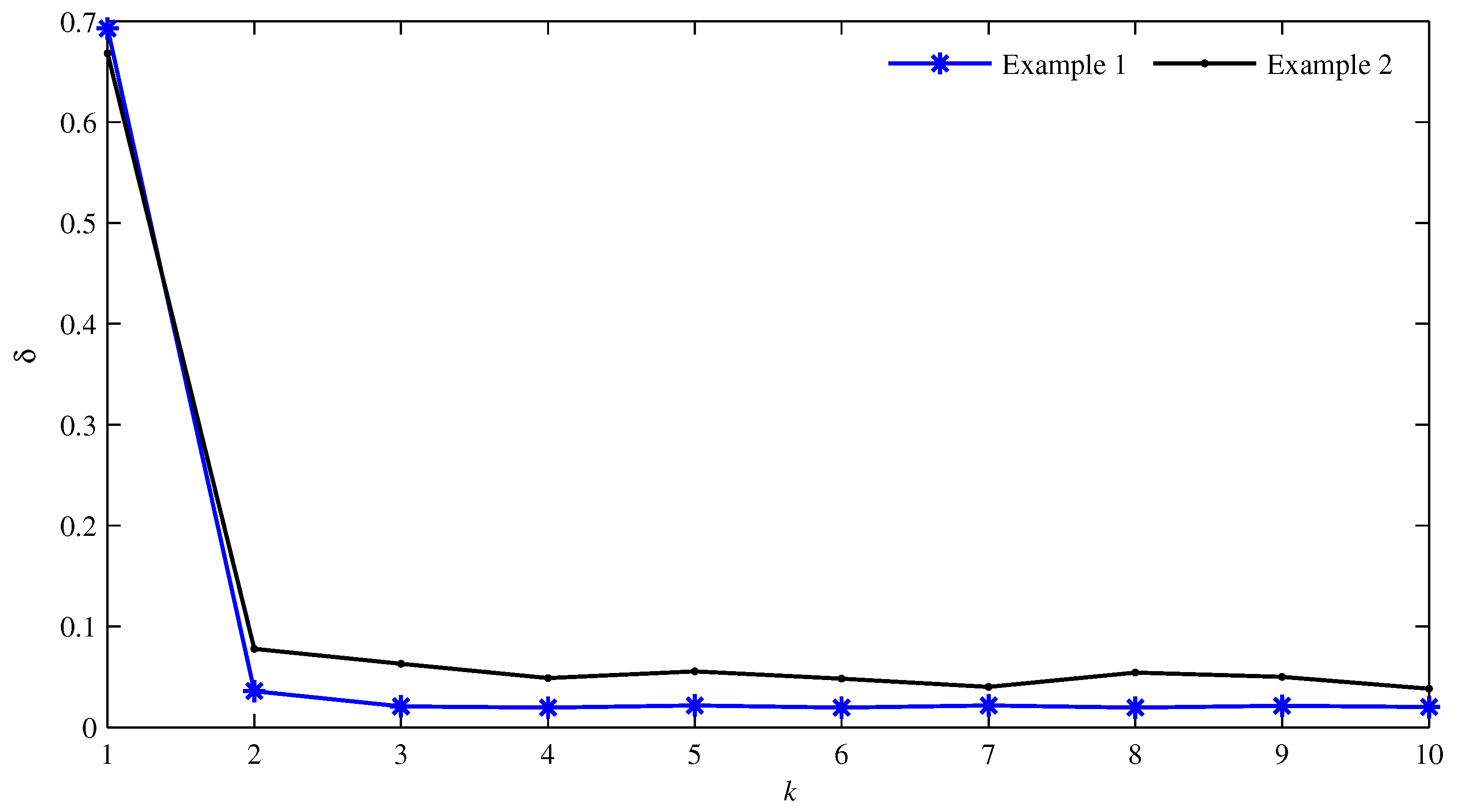
4. Simulation Example
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Prochazka, A.; Kingsbury, N.; Payner, P.J.W.; Uhlir, J. Signal Analysis and Prediction; Birkhäuser Basel: Boston, MA, USA, 1998. [Google Scholar]
- Pappalardo, C.M.; Guida, D. System identification algorithm for computing the modal parameters of linear mechanical systems. Machines 2018, 6, 12. [Google Scholar]
- Pappalardo, C.M.; Guida, D. System identification and experimental modal analysis of a frame structure. Eng. Lett. 2018, 2018 26, 56–68. [Google Scholar]
- Pappalardo, C.M.; Guida, D. A time-domain system identification numerical procedure for obtaining linear dynamical models of multibody mechanical systems. Arch. Appl. Mech. 2018, 88, 1325–1347. [Google Scholar] [CrossRef]
- Gibson, S.; Ninness, B. Robust maximum-likelihood estimation of multivariable dynamic systems. Automatica 2005, 41, 1667–1682. [Google Scholar] [CrossRef] [Green Version]
- Romano, R.A.; Pait, F. Matchable-observable linear models and direct filter tuning: an approach to multivariable identification. IEEE Trans. Autom. Control 2017, 62, 2180–2193. [Google Scholar] [CrossRef]
- Patwardhan, S.C.; Shah, S.L. From data to diagnosis and control using generalized orthonormal basis filters. Part I: Development of state observers. J. Process Control 2005, 15, 819–835. [Google Scholar] [CrossRef]
- Selvanathan, S.; Tangirala, A.K. Time-delay estimation in multivariate systems using Hilbert transform relation and partial coherence functions. Chem. Eng. Sci. 2010, 65, 660–674. [Google Scholar] [CrossRef]
- Tropp, J.A. Just relax: Convex programming methods for identifying sparse signals in noise. IEEE Trans. Inf. Theory 2006, 52, 1030–1051. [Google Scholar] [CrossRef]
- Elad, M. Sparse and Redundant Representations: From Theory to Applications in Signal and Image Processing; Springer: New York, NY, USA, 2010. [Google Scholar]
- Sanandaji, B.M.; Vincent, T.L.; Wakin, M.B.; Tóth, R.; Poolla, K. Compressive system identification of LTI and LTV ARX models. In Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 791–798. [Google Scholar]
- Tóth, R.; Sanandaji, B.M.; Poolla, K.; Vincent, T.L. Compressive system identification in the Linear Time-Invariant framework. In Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 783–790. [Google Scholar]
- Donoho, D.L. Compressed Sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C.; Strauss, M.J. Algorithms for simultaneous sparse approximation. Part I: Greedy pursuit. Signal Process. 2006, 86, 572–588. [Google Scholar] [CrossRef]
- Tropp, J.A. Algorithms for simultaneous sparse approximation. Part II: Convex relaxation. Signal Process. 2006, 86, 589–602. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.S.; Donoho, D.L.; Saunders, M.A. Atomic decomposition by basis pursuit. SIAM Rev. 2001, 43, 129–159. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Statist. Soc. Ser. B (Methodological) 1996, 58, 267–288. [Google Scholar]
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R. Least angel regression. Ann. Statist. 2004, 32, 407–451. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Liu, Y.J.; Tao, T.Y. A CS recovery algorithm for model and time delay identification of MISO-FIR systems. Algorithms 2015, 8, 743–753. [Google Scholar] [CrossRef]
- Liu, Y.J.; Tao, T.Y.; Ding, F. Parameter and time-delay identification for MISO systems based on orthogonal matching pursuit algorithm. Control Decis. 2015, 30, 2103–2107. [Google Scholar]
- Liu, Y.J.; H, X.; Ding, F. An instrumental variable based compressed sampling matching pursuit method for closed-loop identification. Control Decis. 2017, 32, 1837–1843. [Google Scholar]
- Sánchez-Peña, R.S.; Casín, J.Q.; Cayuela, V.P. Identification and Control: The Gap Between Theory and Practice; Springer: London, UK, 2007. [Google Scholar]
- Ding, F.; Chen, T. Combined parameter and output estimation of dual-rate systems using an auxiliary model. Automatica 2004, 40, 1739–1748. [Google Scholar] [CrossRef]
- Liu, Q.Y.; Ding, F. The data filtering based generalized stochastic gradient parameter estimation algorithms for multivariate output-error autoregressive systems using the auxiliary model. Multidimens. Syst. Signal Process. 2018, 29, 1781–1800. [Google Scholar] [CrossRef]
- Wang, Y.J.; Ding, F. Novel data filtering based parameter identification for multiple-input multiple-output systems using the auxiliary model. Automatica 2016, 71, 308–313. [Google Scholar] [CrossRef]
- Wang, Y.J.; Ding, F. The filtering based iterative identification for multivariable systems. IET Control Theory Appl. 2016, 10, 894–902. [Google Scholar] [CrossRef]
- Ma, J.X.; Ding, F.; Yang, E.F. Data filtering-based least squares iterative algorithm for Hammerstein nonlinear systems by using the model decomposition. Nonlinear Dyn. 2016, 83, 1895–1908. [Google Scholar] [CrossRef] [Green Version]
- Cand‘es, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.X.; Yang, R.; Lai, Y.C.; Kovanis, V.; Grebogi, C. Predicting catastrophes in nonlinear dynamical systems by cmpressive sensing. Phys. Rev. Lett. 2011, 106, 154101. [Google Scholar] [CrossRef] [PubMed]
- Naik, M.; Cochran, D. Nonlinear system identification using compressed sensing. In Proceedings of the 2012 Conference Record of the Forty Sixth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 4–7 November 2012; pp. 426–430. [Google Scholar]
- Figueiredo, M.A.T.; Nowak, R.D.; Wright, S.J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems. IEEE J. Sel. Top. Signal Process. 2007, 1, 586–597. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
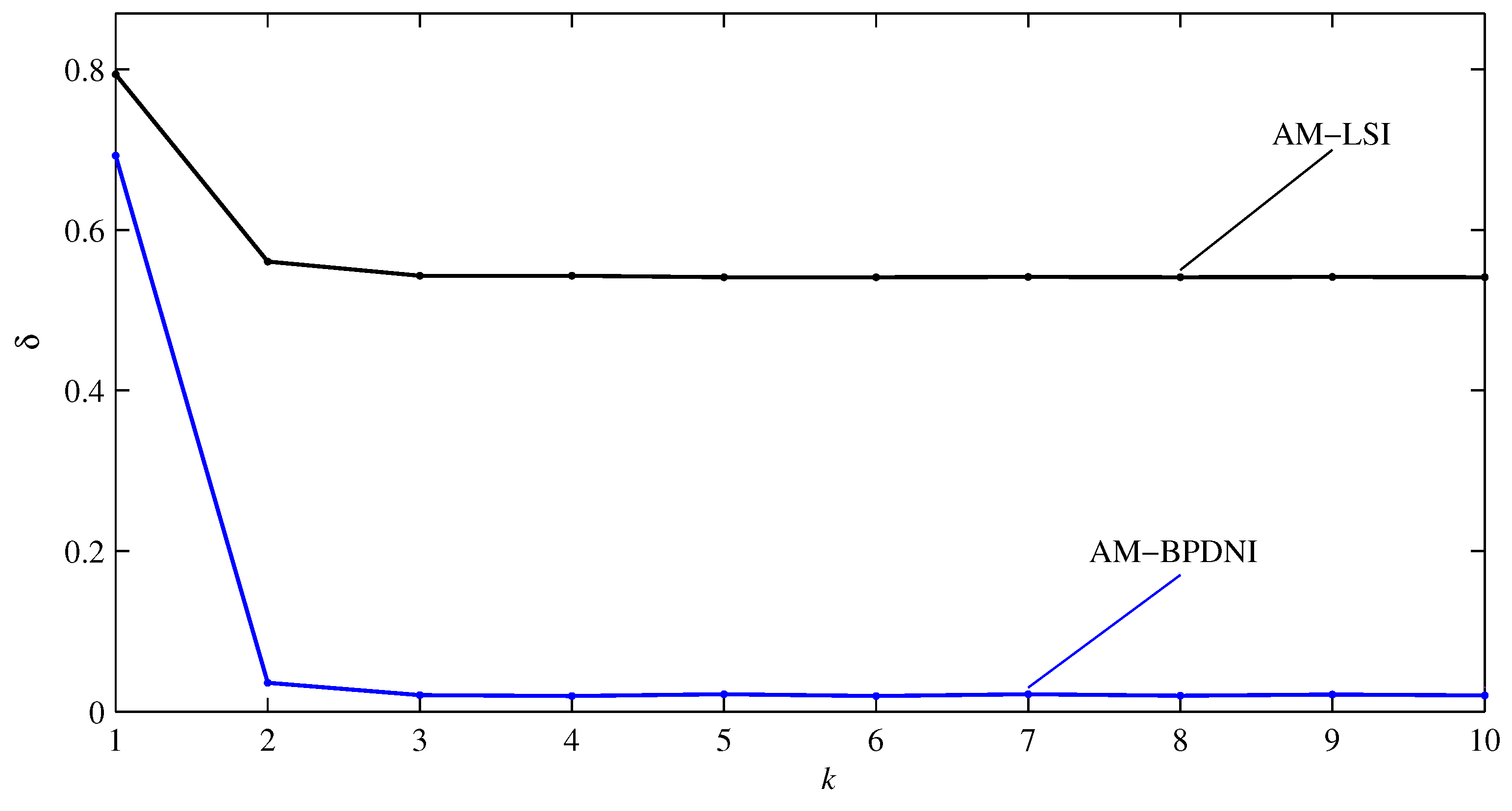



| 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.40 | |
|---|---|---|---|---|---|---|
| AM-LSI | 53.4284 | 53.7175 | 54.2753 | 55.3337 | 55.8435 | 57.2966 |
| AM-BPDNI | 1.9974 | 2.9825 | 4.7985 | 8.6665 | 8.9512 | 9.8808 |
| k | (%) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.000 | 0.000 | 1.483 | 1.058 | 0.000 | 0.000 | 0.148 | 1.742 | 0.000 | 0.000 | –0.076 | 1.963 | 69.2788 |
| 2 | –0.077 | 0.685 | 1.491 | 0.908 | 0.296 | 0.477 | 0.170 | 1.771 | –0.190 | –0.375 | –0.104 | 1.983 | 3.5707 |
| 5 | –0.095 | 0.684 | 1.470 | 0.893 | 0.289 | 0.484 | 0.168 | 1.778 | –0.190 | –0.396 | –0.078 | 1.960 | 2.1595 |
| 10 | –0.100 | 0.694 | 1.474 | 0.888 | 0.290 | 0.482 | 0.170 | 1.778 | –0.192 | –0.396 | –0.080 | 1.963 | 1.9974 |
| True value | –0.100 | 0.700 | 1.500 | 0.900 | 0.300 | 0.500 | 0.200 | 1.800 | –0.200 | –0.400 | –0.100 | 2.000 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, J.; Liu, Y. Iterative Identification for Multivariable Systems with Time-Delays Based on Basis Pursuit De-Noising and Auxiliary Model. Algorithms 2018, 11, 180. https://doi.org/10.3390/a11110180
You J, Liu Y. Iterative Identification for Multivariable Systems with Time-Delays Based on Basis Pursuit De-Noising and Auxiliary Model. Algorithms. 2018; 11(11):180. https://doi.org/10.3390/a11110180
Chicago/Turabian StyleYou, Junyao, and Yanjun Liu. 2018. "Iterative Identification for Multivariable Systems with Time-Delays Based on Basis Pursuit De-Noising and Auxiliary Model" Algorithms 11, no. 11: 180. https://doi.org/10.3390/a11110180
APA StyleYou, J., & Liu, Y. (2018). Iterative Identification for Multivariable Systems with Time-Delays Based on Basis Pursuit De-Noising and Auxiliary Model. Algorithms, 11(11), 180. https://doi.org/10.3390/a11110180





