The Bias Compensation Based Parameter and State Estimation for Observability Canonical State-Space Models with Colored Noise
Abstract
:1. Introduction
- By using the bias compensation, this paper derives the identification model and achieves the unbiased parameter estimation for observability canonical state-space models with colored noise.
- By employing the interactive identification, this paper explores the relationship between the noise parameters and variance and the bias correction term and realizes the simultaneous estimation of the system parameters, noise parameters and system states.
2. Problem Description and Identification Model
3. The Bias Compensation-Based Parameter and State Estimation Algorithm
3.1. The Parameter Estimation Algorithm
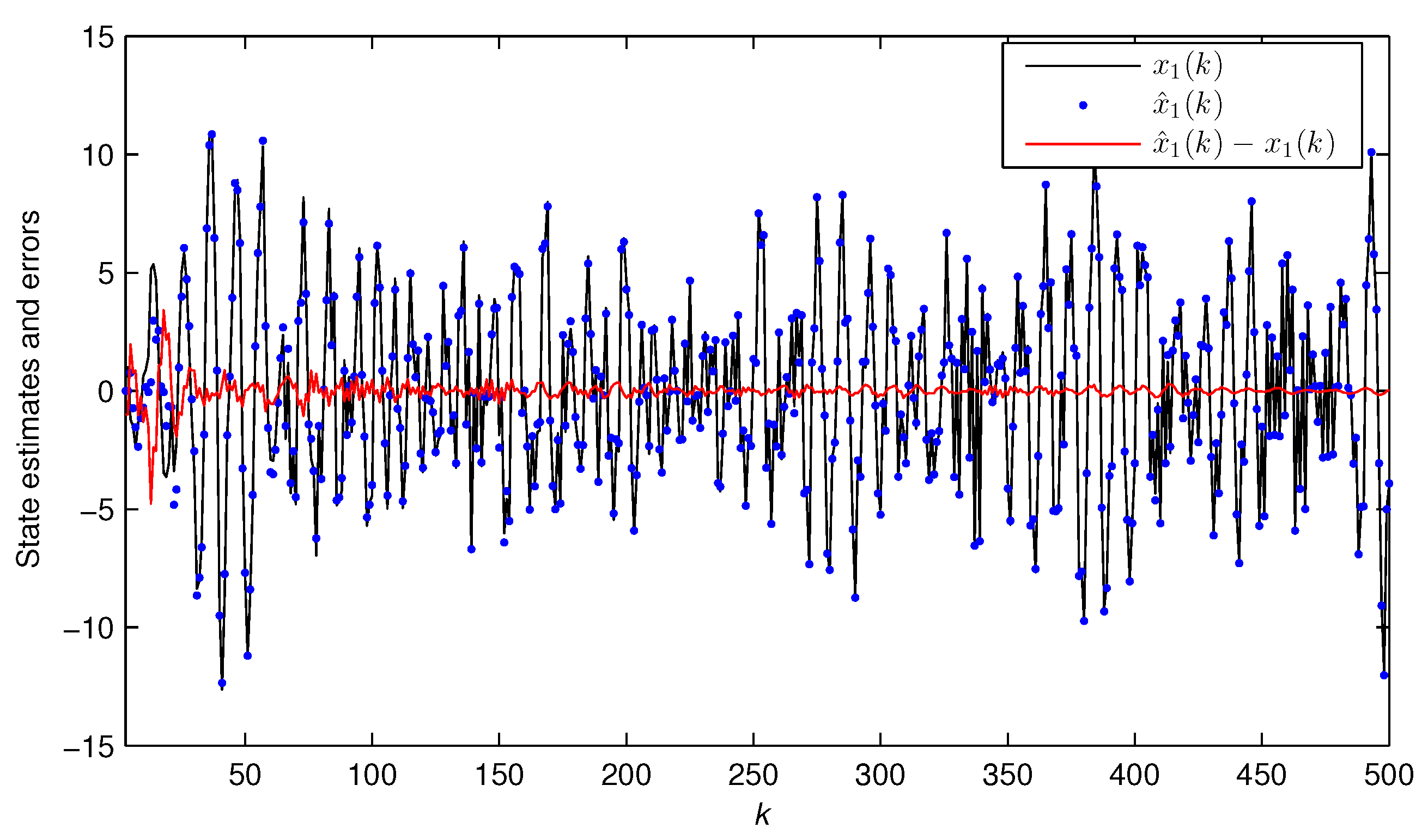
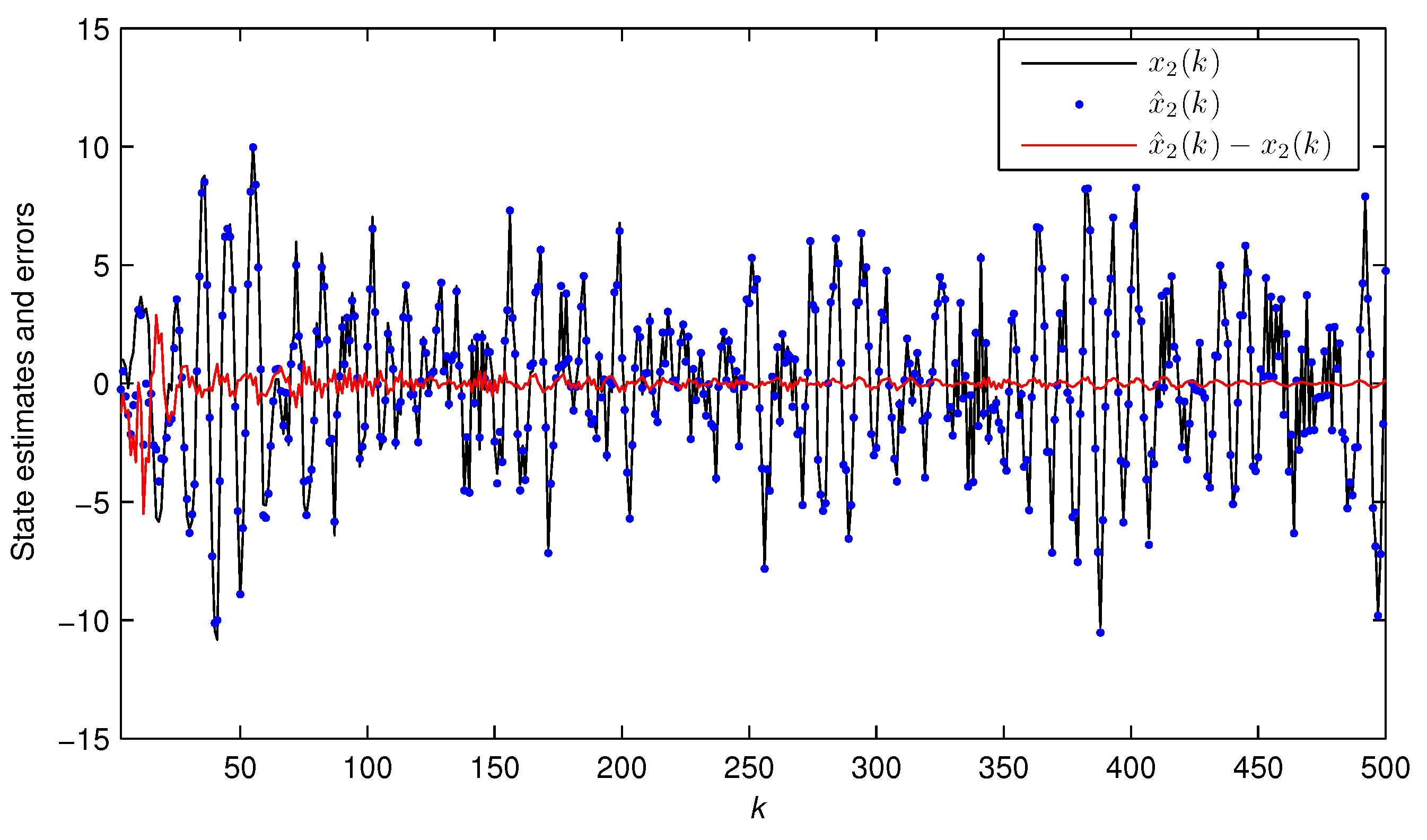
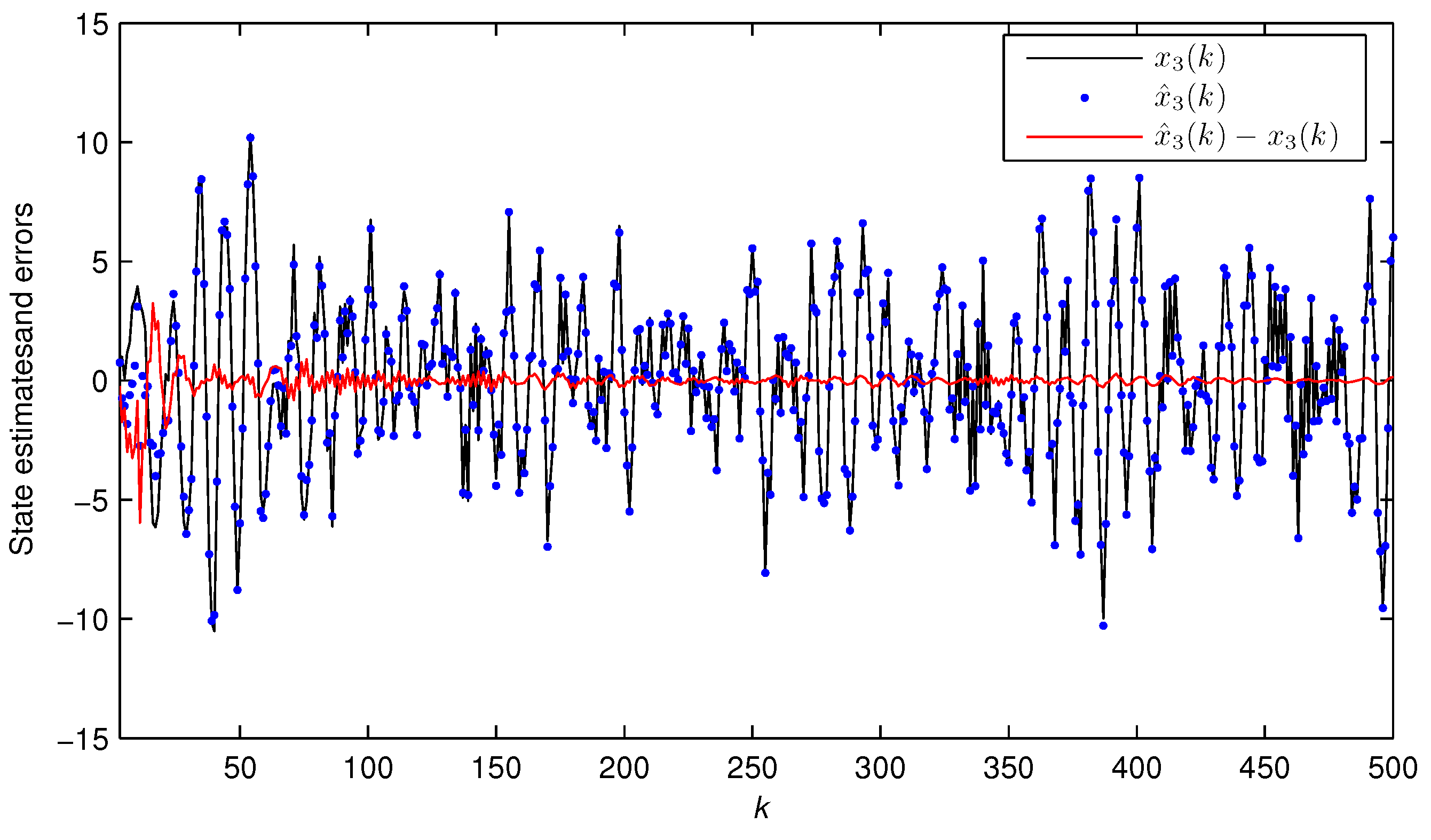
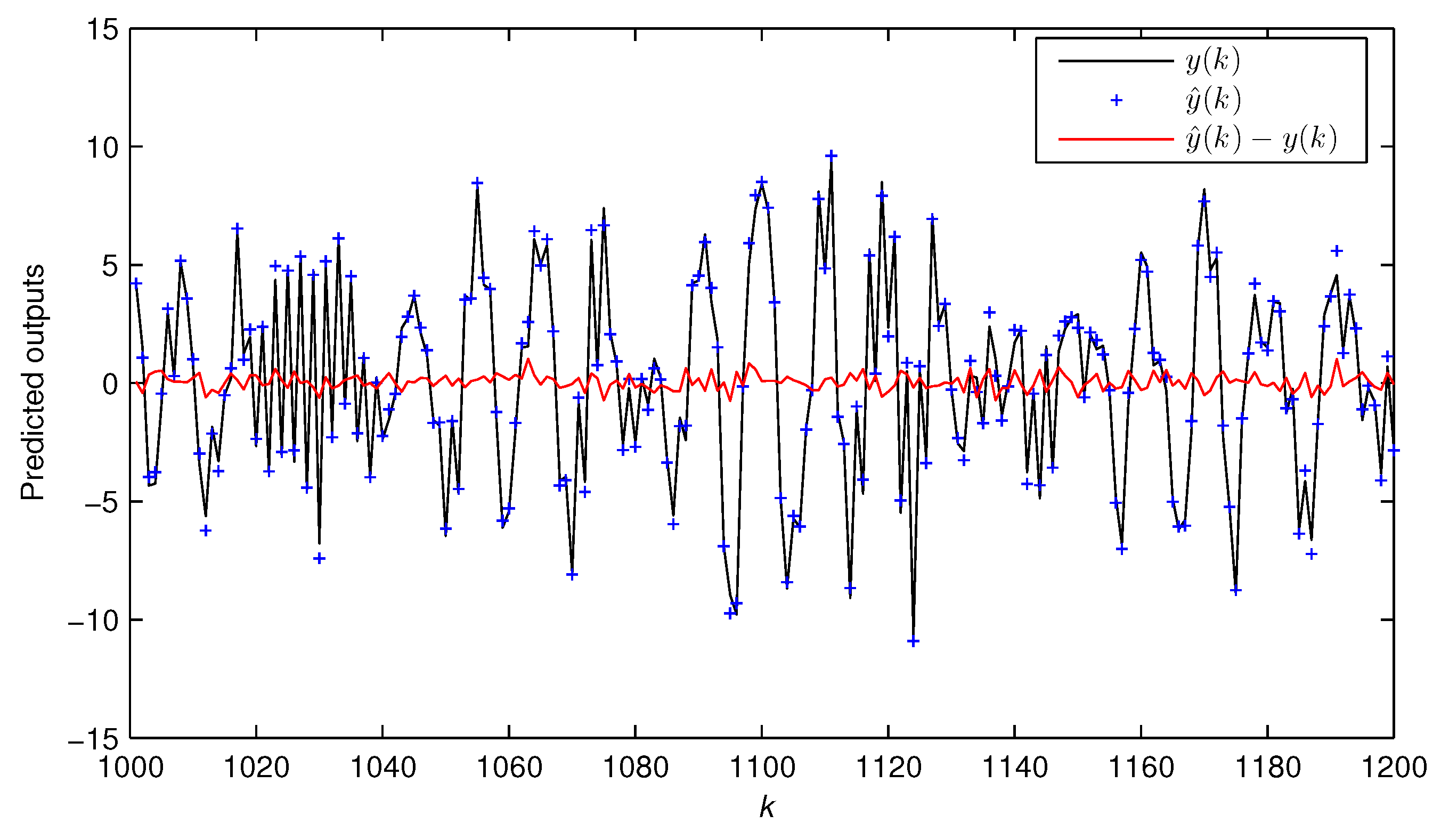
3.2. The State Estimation Algorithm
- Let , and set the initial values , , , , .
- Compute the state estimate using Equation (43).
- Let . If , increase k by one, and go to Step 2; otherwise, stop, and obtain the parameter estimation vector .
4. Examples
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Na, J.; Yang, J.; Wu, X.; Guo, Y. Robust adaptive parameter estimation of sinusoidal signals. Automatica 2015, 53, 376–384. [Google Scholar] [CrossRef]
- Kalafatis, A.D.; Wang, L.; Cluett, W.R. Identification of time-varying pH processes using sinusoidal signals. Automatica 2005, 41, 685–691. [Google Scholar] [CrossRef]
- Na, J.; Yang, J.; Ren, X.M.; Guo, Y. Robust adaptive estimation of nonlinear system with time-varying parameters. Int. J. Adapt. Control Process. 2015, 29, 1055–1072. [Google Scholar] [CrossRef]
- Liu, S.Y.; Xu, L.; Ding, F. Iterative parameter estimation algorithms for dual-frequency signal models. Algorithms 2017, 10, 118. [Google Scholar] [CrossRef]
- Na, J.; Mahyuddin, M.N.; Herrmann, G.; Ren, X.; Barber, P. Robust adaptive finite-time parameter estimation and control for robotic systems. Int. J. Robust Nonlinear Control 2015, 25, 3045–3071. [Google Scholar] [CrossRef] [Green Version]
- Huang, W.; Ding, F. Coupled least squares identification algorithms for multivariate output-error systems. Algorithms 2017, 10, 12. [Google Scholar] [CrossRef]
- Goos, J.; Pintelon, R. Continuous-time identification of periodically parameter-varying state space models. Automatica 2016, 71, 254–263. [Google Scholar] [CrossRef]
- AlMutawa, J. Identification of errors-in-variables state space models with observation outliers based on minimum covariance determinant. J. Process Control 2009, 19, 879–887. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, H.; Wu, Y.; Zhu, T.; Ding, H. Bayesian learning-based model predictive vibration control for thin-walled workpiece machining processes. IEEE/ASME Trans. Mechatron. 2017, 22, 509–520. [Google Scholar] [CrossRef]
- Ding, F. Combined state and least squares parameter estimation algorithms for dynamic systems. Appl. Math. Model. 2014, 38, 403–412. [Google Scholar] [CrossRef]
- Ma, J.X.; Xiong, W.L.; Chen, J.; Ding, F. Hierarchical identification for multivariate Hammerstein systems by using the modified Kalman filter. IET Control Theory Appl. 2017, 11, 857–869. [Google Scholar] [CrossRef]
- Fatehi, A.; Huang, B. Kalman filtering approach to multi-rate information fusion in the presence of irregular sampling rate and variable measurement delay. J. Process Control 2017, 53, 15–25. [Google Scholar] [CrossRef]
- Zhao, S.; Shmaliy, Y.S.; Liu, F. Fast Kalman-like optimal unbiased FIR filtering with applications. IEEE Trans. Signal Process. 2016, 64, 2284–2297. [Google Scholar] [CrossRef]
- Zhou, Z.P.; Liu, X.F. State and fault estimation of sandwich systems with hysteresis. Int. J. Robust Nonlinear Control 2018, 28, 3974–3986. [Google Scholar] [CrossRef]
- Zhao, S.; Huang, B.; Liu, F. Linear optimal unbiased filter for time-variant systems without apriori information on initial condition. IEEE Trans. Autom. Control 2017, 62, 882–887. [Google Scholar] [CrossRef]
- Zhao, S.; Shmaliy, Y.S.; Liu, F. On the iterative computation of error matrix in unbiased FIR filtering. IEEE Signal Process. Lett. 2017, 24, 555–558. [Google Scholar] [CrossRef]
- Erazo, K.; Nagarajaiah, S. An offline approach for output-only Bayesian identification of stochastic nonlinear systems using unscented Kalman filtering. J. Sound Vib. 2017, 397, 222–240. [Google Scholar] [CrossRef]
- Verhaegen, M.; Verdult, V. Filtering and System Identification: A Least Squares Approach; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Ljung, L. System Identification: Theory for the User, 2nd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 1999. [Google Scholar]
- Yu, C.P.; Ljung, L.; Verhaegen, M. Identification of structured state-space models. Automatica 2018, 90, 54–61. [Google Scholar] [CrossRef]
- Naitali, A.; Giri, F. Persistent excitation by deterministic signals for subspace parametric identification of MISO Hammerstein systems. IEEE Trans. Autom. Control 2016, 61, 258–263. [Google Scholar] [CrossRef]
- Ase, H.; Katayama, T. A subspace-based identification of Wiener-Hammerstein benchmark model. Control Eng. Pract. 2015, 44, 126–137. [Google Scholar] [CrossRef]
- Xu, L.; Ding, F.; Gu, Y.; Alsaedi, A.; Hayat, T. A multi-innovation state and parameter estimation algorithm for a state space system with d-step state-delay. Signal Process. 2017, 140, 97–103. [Google Scholar] [CrossRef]
- Zhang, X.; Ding, F.; Xu, L.; Yang, E.F. State filtering-based least squares parameter estimation for bilinear systems using the hierarchical identification principle. IET Control Theory Appl. 2018, 12, 1704–1713. [Google Scholar] [CrossRef]
- Pavelkova, L.; Karny, M. State and parameter estimation of state-space model with entry-wise correlated uniform noise. Int. J. Adapt. Control Signal Process. 2014, 28, 1189–1205. [Google Scholar] [CrossRef]
- Ma, J.X.; Wu, O.Y.; Huang, B.; Ding, F. Expectation maximization estimation for a class of input nonlinear state space systems by using the Kalman smoother. Signal Process. 2018, 145, 295–303. [Google Scholar] [CrossRef]
- Li, J.H.; Zheng, W.X.; Gu, J.P.; Hua, L. A recursive identification algorithm for Wiener nonlinear systems with linear state-space subsystem. Circuits Syst. Signal Process. 2018, 37, 2374–2393. [Google Scholar] [CrossRef]
- Wang, H.W.; Liu, T. Recursive state-space model identification of non-uniformly sampled systems using singular value decomposition. Chin. J. Chem. Eng. 2014, 22, 1268–1273. [Google Scholar] [CrossRef]
- Ding, J.L. Data filtering based recursive and iterative least squares algorithms for parameter estimation of multi-input output systems. Algorithms 2016, 9, 49. [Google Scholar] [CrossRef]
- Yu, C.P.; You, K.Y.; Xie, L.H. Quantized identification of ARMA systems with colored measurement noise. Automatica 2016, 66, 101–108. [Google Scholar] [CrossRef]
- Jafari, M.; Salimifard, M.; Dehghani, M. Identification of multivariable nonlinear systems in the presence of colored noises using iterative hierarchical least squares algorithm. ISA Trans. 2014, 53, 1243–1252. [Google Scholar] [CrossRef] [PubMed]
- Sagara, S.; Wada, K. On-line modified least-squares parameter estimation of linear discrete dynamic systems. Int. J. Control 1977, 25, 329–343. [Google Scholar] [CrossRef]
- Mejari, M.; Piga, D.; Bemporad, A. A bias-correction method for closed-loop identification of linear parameter-varying systems. Automatica 2018, 87, 128–141. [Google Scholar] [CrossRef]
- Ding, J.; Ding, F. Bias compensation based parameter estimation for output error moving average systems. Int. J. Adapt. Control Signal Process. 2011, 25, 1100–1111. [Google Scholar] [CrossRef]
- Diversi, R. Bias-eliminating least-squares identification of errors-in-variables models with mutually correlated noises. Int. J. Adapt. Control Signal Process. 2013, 27, 915–924. [Google Scholar] [CrossRef]
- Zhang, Y. Unbiased identification of a class of multi-input single-output systems with correlated disturbances using bias compensation methods. Math. Comput. Model. 2011, 53, 1810–1819. [Google Scholar] [CrossRef]
- Zheng, W.X. A bias correction method for identification of linear dynamic errors-in-variables models. IEEE Trans. Autom. Control 2002, 47, 1142–1147. [Google Scholar] [CrossRef]
- Wang, X.H.; Ding, F.; Alsaedi, A.; Hayat, T. Filtering based parameter estimation for observer canonical state space systems with colored noise. J. Frankl. Inst. 2017, 354, 593–609. [Google Scholar] [CrossRef]
- Pan, W.; Yuan, Y.; Goncalves, J.; Stan, G.B. A sparse Bayesian approach to the identification of nonlinear state-space systems. IEEE Trans. Autom. Control 2016, 61, 182–187. [Google Scholar] [CrossRef]
- Yang, X.Q.; Yang, X.B. Local identification of LPV dual-rate system with random measurement delays. IEEE Trans. Ind. Electron. 2018, 65, 1499–1507. [Google Scholar] [CrossRef]
- Xu, L.; Xiong, W.L.; Alsaedi, A.; Hayat, T. Hierarchical parameter estimation for the frequency response based on the dynamical window data. Int. J. Control Autom. Syst. 2018, 16, 1756–1764. [Google Scholar] [CrossRef]
- Gan, M.; Chen, C.L.P.; Chen, G.Y.; Chen, L. On some separated algorithms for separable nonlinear squares problems. IEEE Trans. Cybern. 2018, 48, 2866–2874. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.Y.; Gan, M.; Chen, G.L. Generalized exponential autoregressive models for nonlinear time series: Stationarity, estimation and applications. Inf. Sci. 2018, 438, 46–57. [Google Scholar] [CrossRef]
| Nomenclature | |||
|---|---|---|---|
| matrix/vector transpose | inverse of the matrix A | ||
| expectation operator | z | unit forward shift operator | |
| 2-norm of a matrix X | identity matrix | ||
| n-dimensional column vector whose elements are 1 | |||
| estimate of the parameter vector at instant k | |||
| a vector consisting of the first entry to the m-th entry of | |||
| k | ||||||||
|---|---|---|---|---|---|---|---|---|
| 20 | −0.90672 | 0.58805 | 2.47895 | −2.33308 | 0.12542 | −1.41696 | 74.94801 | |
| 50 | −0.91146 | 0.77864 | 1.56458 | −1.45439 | 0.06347 | −0.68669 | 21.66474 | |
| 100 | −0.89769 | 0.78062 | 1.45065 | −1.56252 | 0.11477 | −0.61555 | 15.33989 | |
| 200 | −0.89947 | 0.79122 | 1.18977 | −1.58852 | 0.18174 | −0.62250 | 4.02568 | |
| 500 | −0.90289 | 0.79326 | 1.19050 | −1.56703 | 0.17911 | −0.62993 | 4.35605 | |
| 1000 | −0.89502 | 0.79742 | 1.14729 | −1.63721 | 0.18966 | −0.61945 | 2.71347 | |
| 20 | −0.89902 | 0.68391 | 1.87036 | −1.86695 | 0.37006 | −0.70475 | 35.74537 | |
| 50 | −0.90830 | 0.79067 | 1.34730 | −1.49092 | 0.18690 | −0.51892 | 11.92791 | |
| 100 | −0.90003 | 0.79044 | 1.28652 | −1.56142 | 0.20501 | −0.50891 | 8.91773 | |
| 200 | −0.90083 | 0.79596 | 1.15147 | −1.58293 | 0.22360 | −0.53086 | 3.84174 | |
| 500 | −0.90199 | 0.79695 | 1.14809 | −1.57856 | 0.20617 | −0.56528 | 2.67739 | |
| 1000 | −0.89776 | 0.79869 | 1.12493 | −1.61634 | 0.20773 | −0.57641 | 1.63983 | |
| True values | −0.90000 | 0.80000 | 1.10000 | −1.60000 | 0.20000 | −0.60000 | 0.00000 | |
| k | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 20 | −0.62874 | 0.23404 | 0.69918 | 2.71399 | −0.51430 | 0.03521 | 0.55758 | 0.54550 | 40.52480 | |
| 50 | −0.63162 | 0.17455 | 0.82387 | 2.36896 | −0.10338 | 0.17046 | 0.57261 | 0.36257 | 24.04086 | |
| 100 | −0.72920 | 0.37705 | 0.69853 | 2.10786 | 0.00205 | 0.03490 | 0.53153 | 0.47341 | 15.57075 | |
| 200 | −0.77990 | 0.43541 | 0.64826 | 2.07686 | 0.11157 | 0.16642 | 0.52363 | 0.43391 | 9.54558 | |
| 500 | −0.80210 | 0.49447 | 0.60384 | 2.19878 | 0.24877 | 0.16126 | 0.56242 | 0.43637 | 3.76452 | |
| 1000 | −0.80600 | 0.50437 | 0.59777 | 2.23514 | 0.29924 | 0.19105 | 0.52608 | 0.42701 | 2.04986 | |
| 20 | −0.70399 | 0.32858 | 0.67496 | 2.51439 | −0.09217 | 0.18308 | 0.56489 | 0.42596 | 21.34339 | |
| 50 | −0.69558 | 0.29717 | 0.73981 | 2.28977 | 0.11809 | 0.20666 | 0.54171 | 0.38144 | 13.16282 | |
| 100 | −0.77049 | 0.44740 | 0.64636 | 2.15712 | 0.16039 | 0.13532 | 0.48821 | 0.46680 | 7.35863 | |
| 200 | −0.79424 | 0.47428 | 0.62275 | 2.14390 | 0.21064 | 0.19565 | 0.49299 | 0.43757 | 4.56623 | |
| 500 | −0.80223 | 0.49921 | 0.60237 | 2.20136 | 0.27695 | 0.18522 | 0.53537 | 0.42783 | 2.05074 | |
| 1000 | −0.80385 | 0.50317 | 0.59907 | 2.21845 | 0.30107 | 0.19783 | 0.51498 | 0.41939 | 1.21121 | |
| True values | −0.80000 | 0.50000 | 0.60000 | 2.20000 | 0.30000 | 0.20000 | 0.50000 | 0.40000 | 0.00000 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Ding, F.; Liu, Q.; Jiang, C. The Bias Compensation Based Parameter and State Estimation for Observability Canonical State-Space Models with Colored Noise. Algorithms 2018, 11, 175. https://doi.org/10.3390/a11110175
Wang X, Ding F, Liu Q, Jiang C. The Bias Compensation Based Parameter and State Estimation for Observability Canonical State-Space Models with Colored Noise. Algorithms. 2018; 11(11):175. https://doi.org/10.3390/a11110175
Chicago/Turabian StyleWang, Xuehai, Feng Ding, Qingsheng Liu, and Chuntao Jiang. 2018. "The Bias Compensation Based Parameter and State Estimation for Observability Canonical State-Space Models with Colored Noise" Algorithms 11, no. 11: 175. https://doi.org/10.3390/a11110175
APA StyleWang, X., Ding, F., Liu, Q., & Jiang, C. (2018). The Bias Compensation Based Parameter and State Estimation for Observability Canonical State-Space Models with Colored Noise. Algorithms, 11(11), 175. https://doi.org/10.3390/a11110175





