Fractional Order Sliding Mode Control of a Class of Second Order Perturbed Nonlinear Systems: Application to the Trajectory Tracking of a Quadrotor

Abstract

A Fractional Order Sliding Mode Control (FOSMC) is proposed in this paper for an integer second order nonlinear system with an unknown additive perturbation term. A sufficient condition is given to assure the attractiveness to a given sliding surface where trajectory tracking is assured, despite the presence of the perturbation term. The control scheme is applied to the model of a quadrotor vehicle in order to have trajectory tracking in the space. 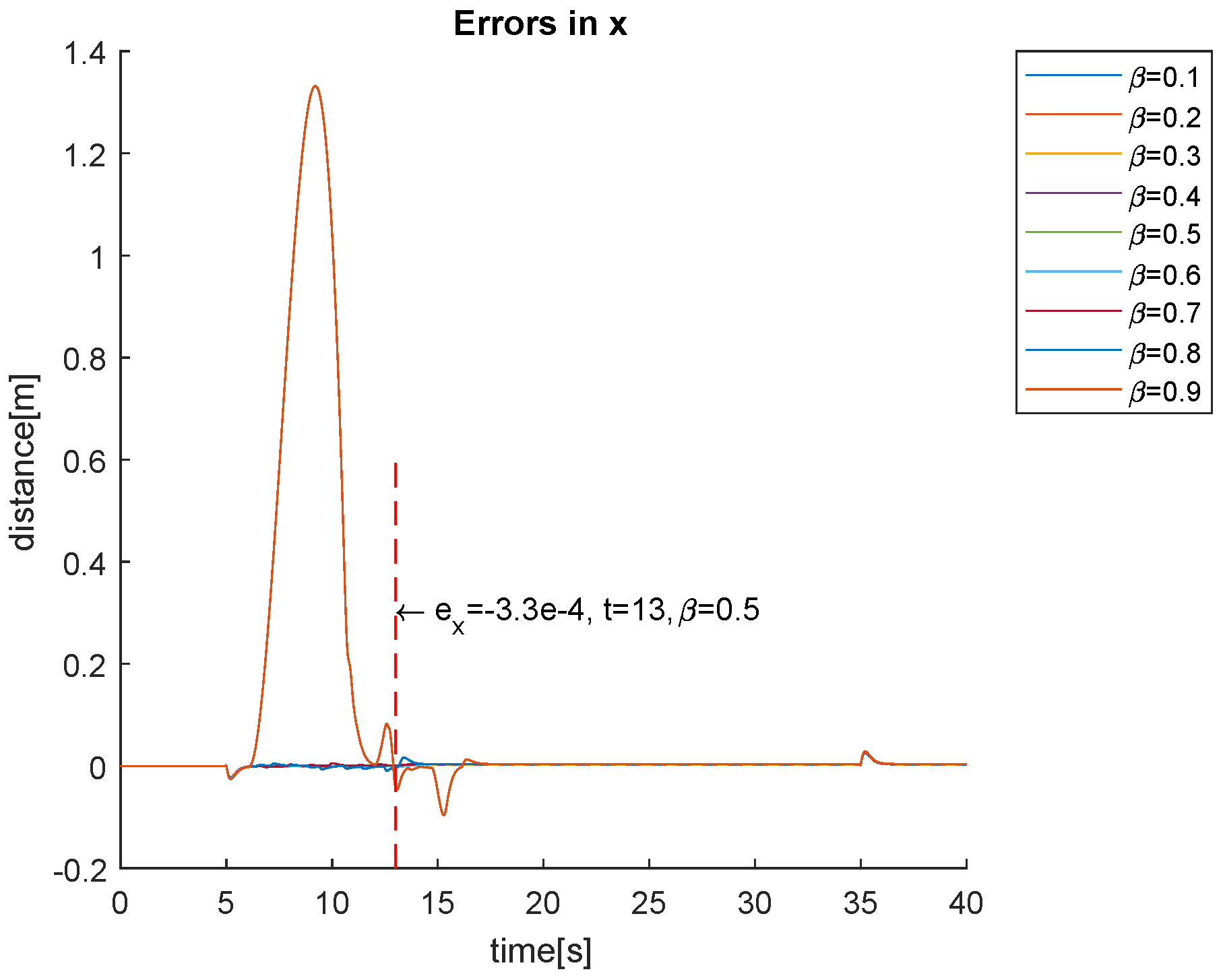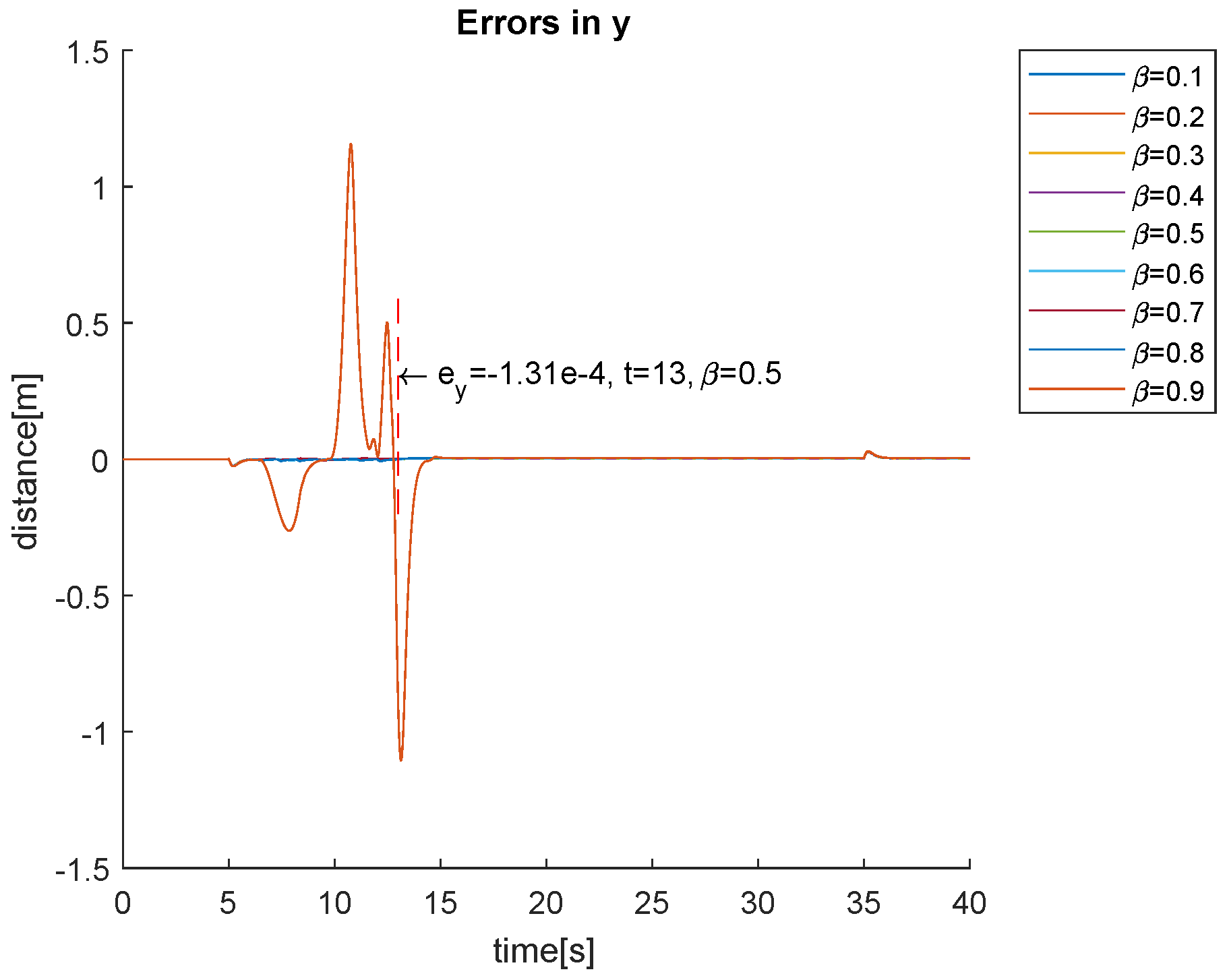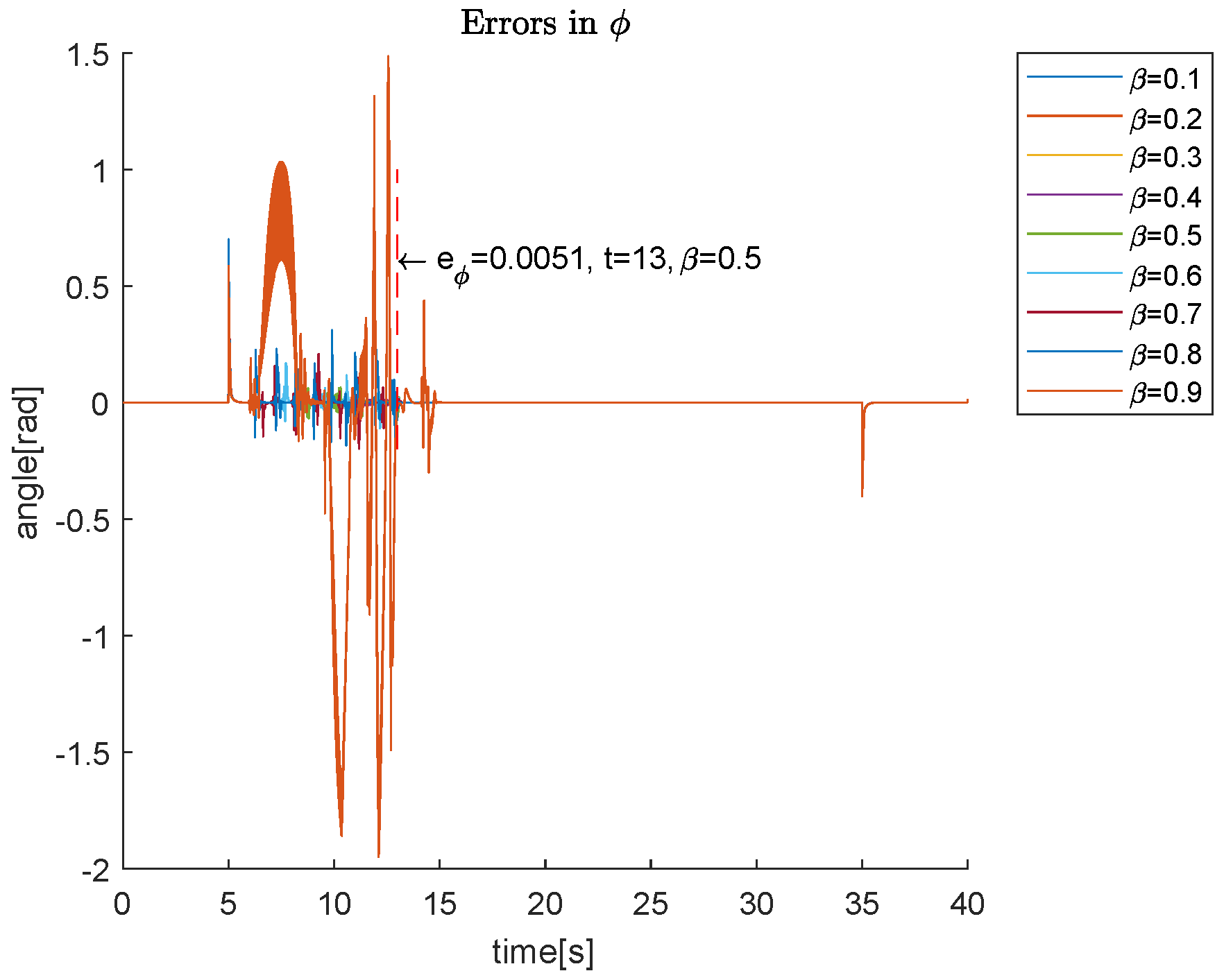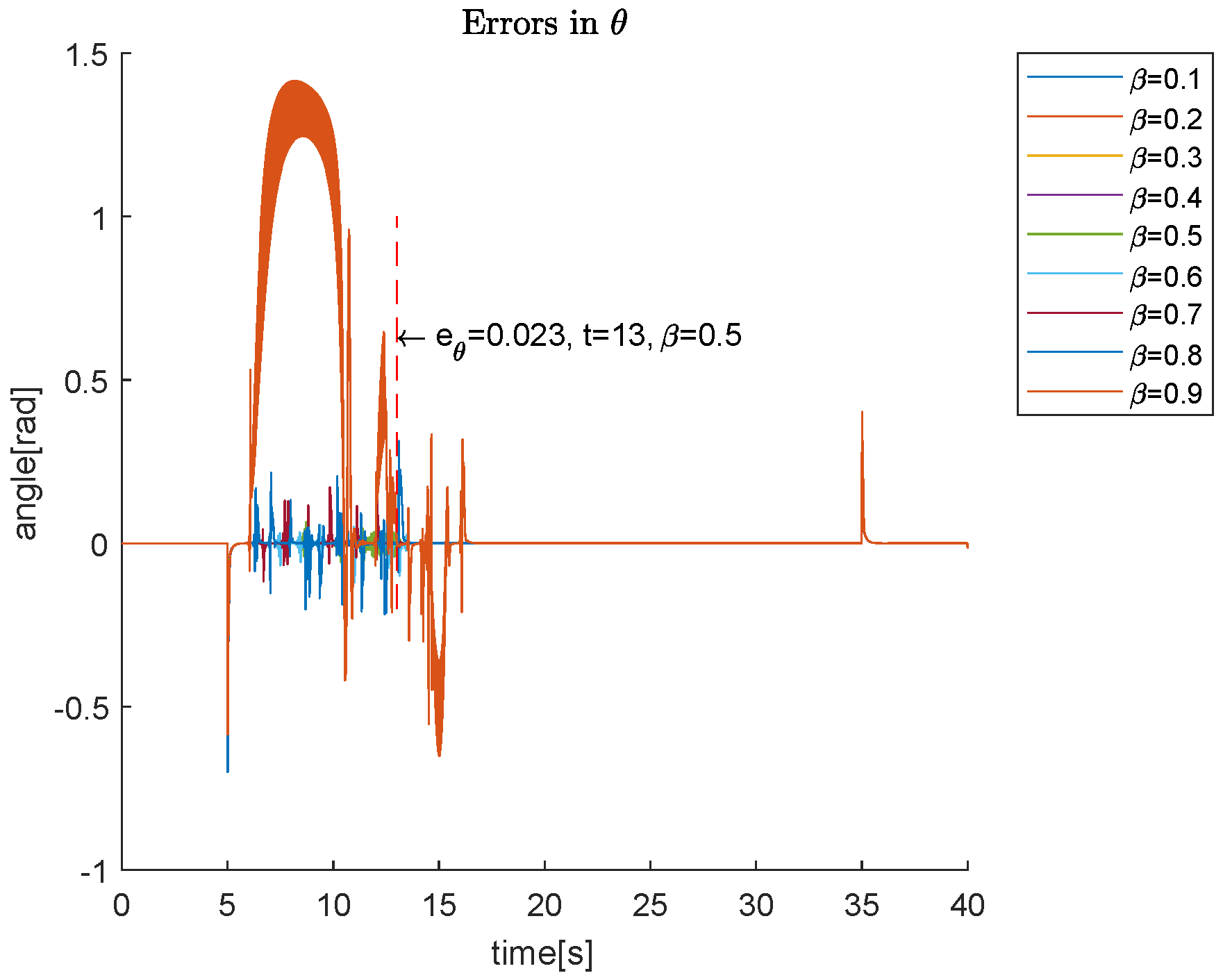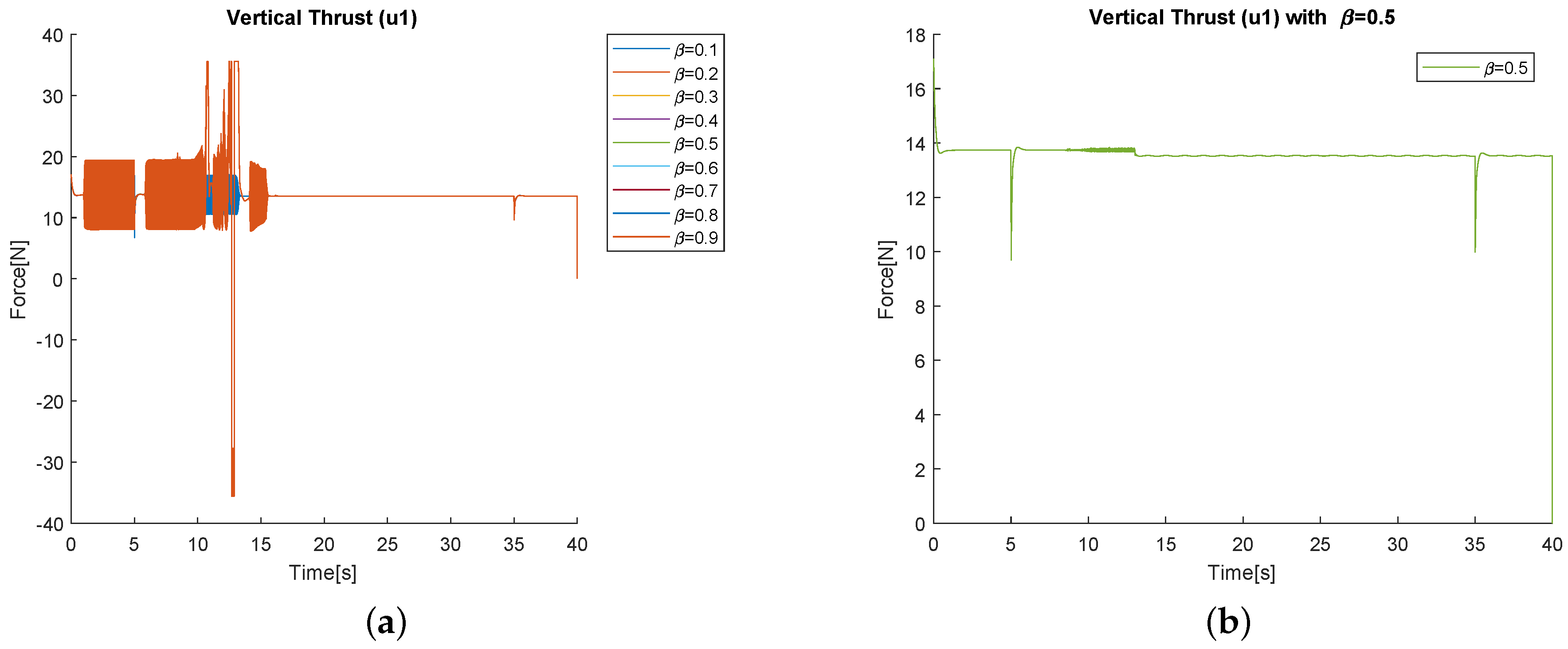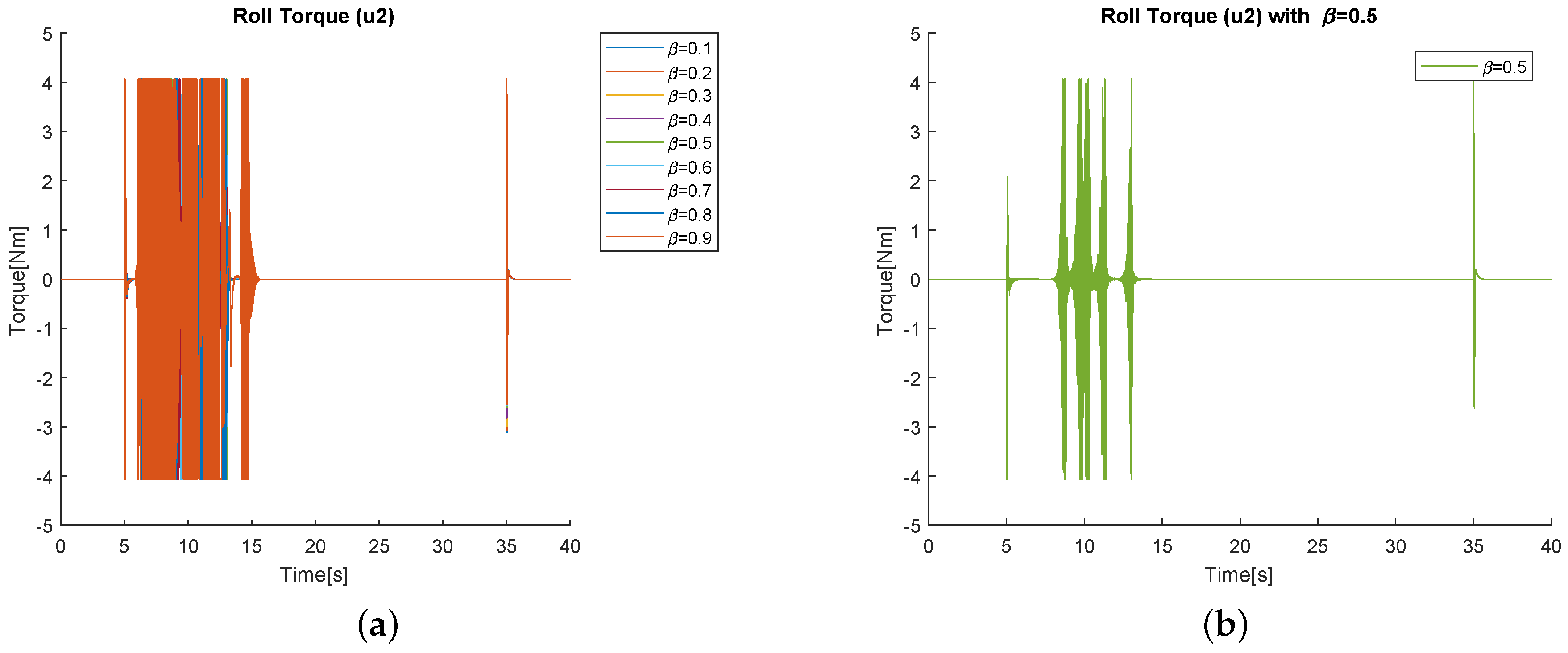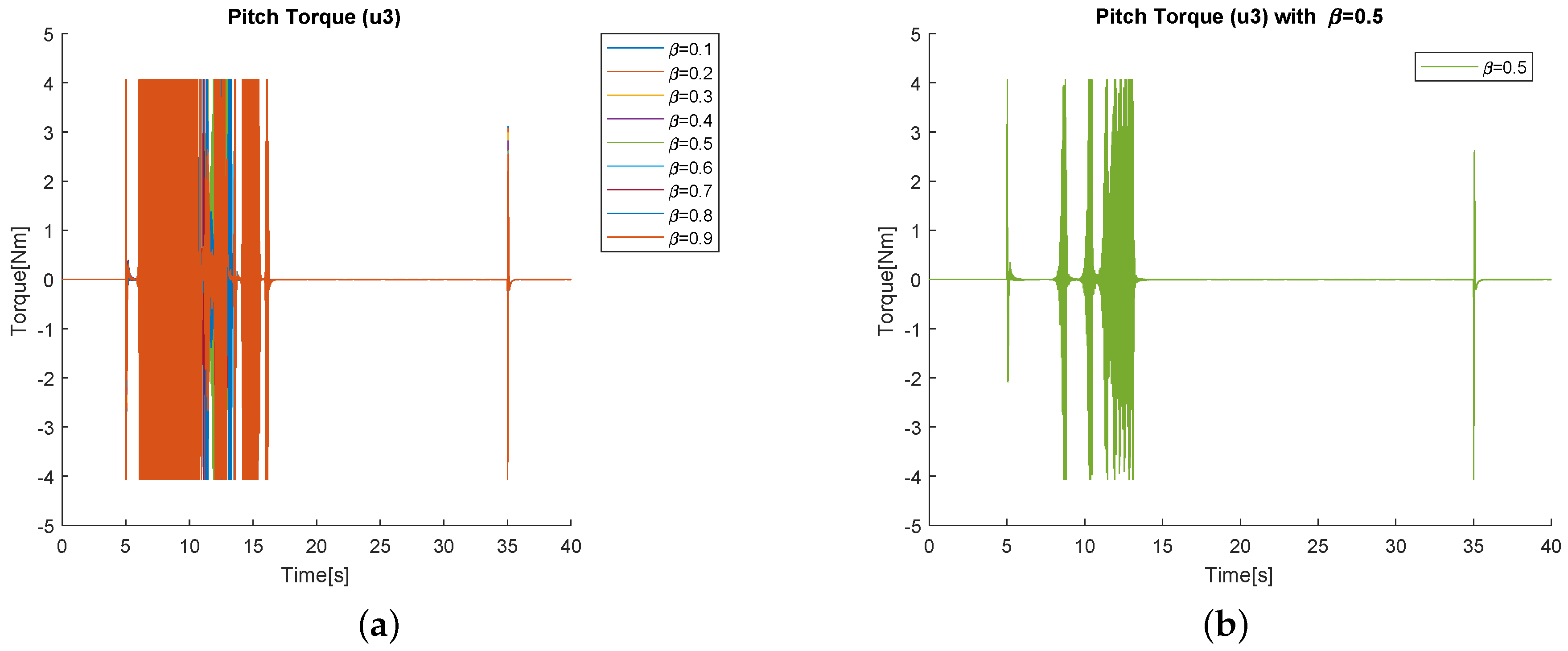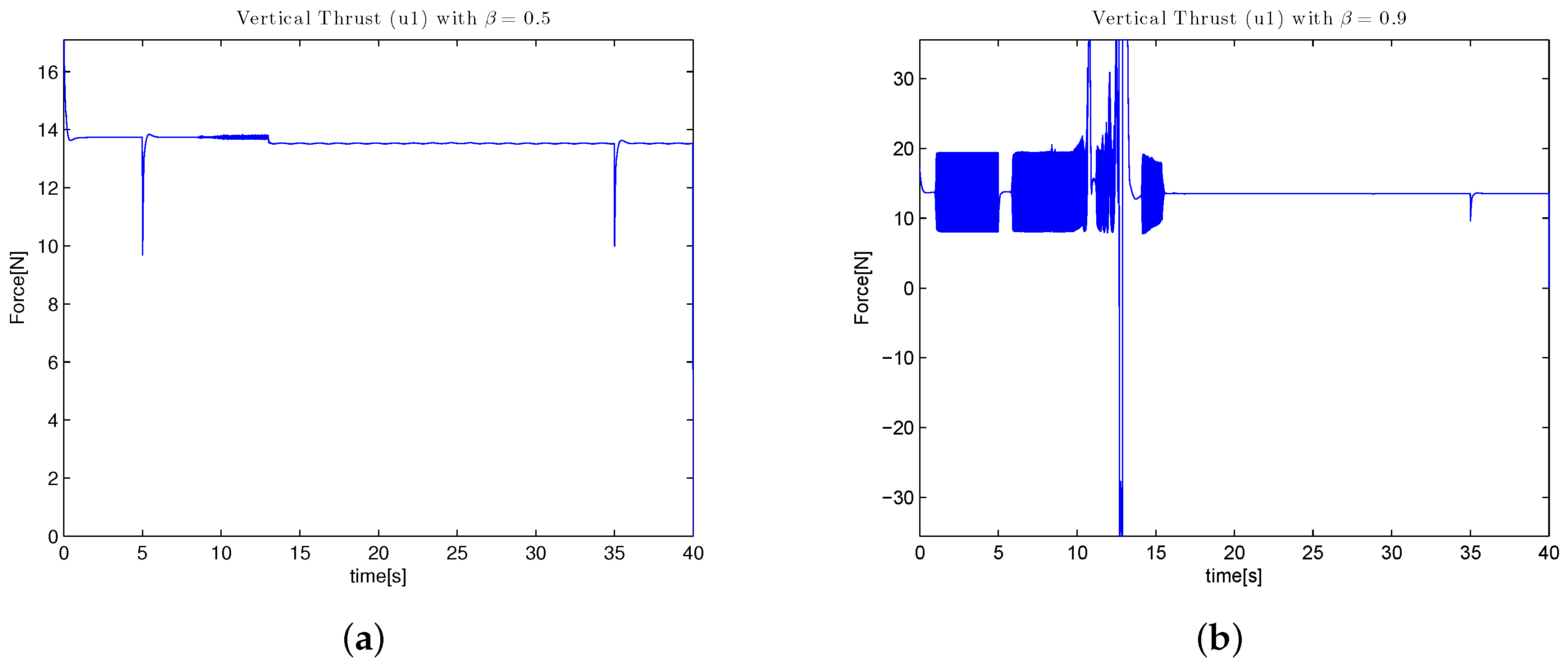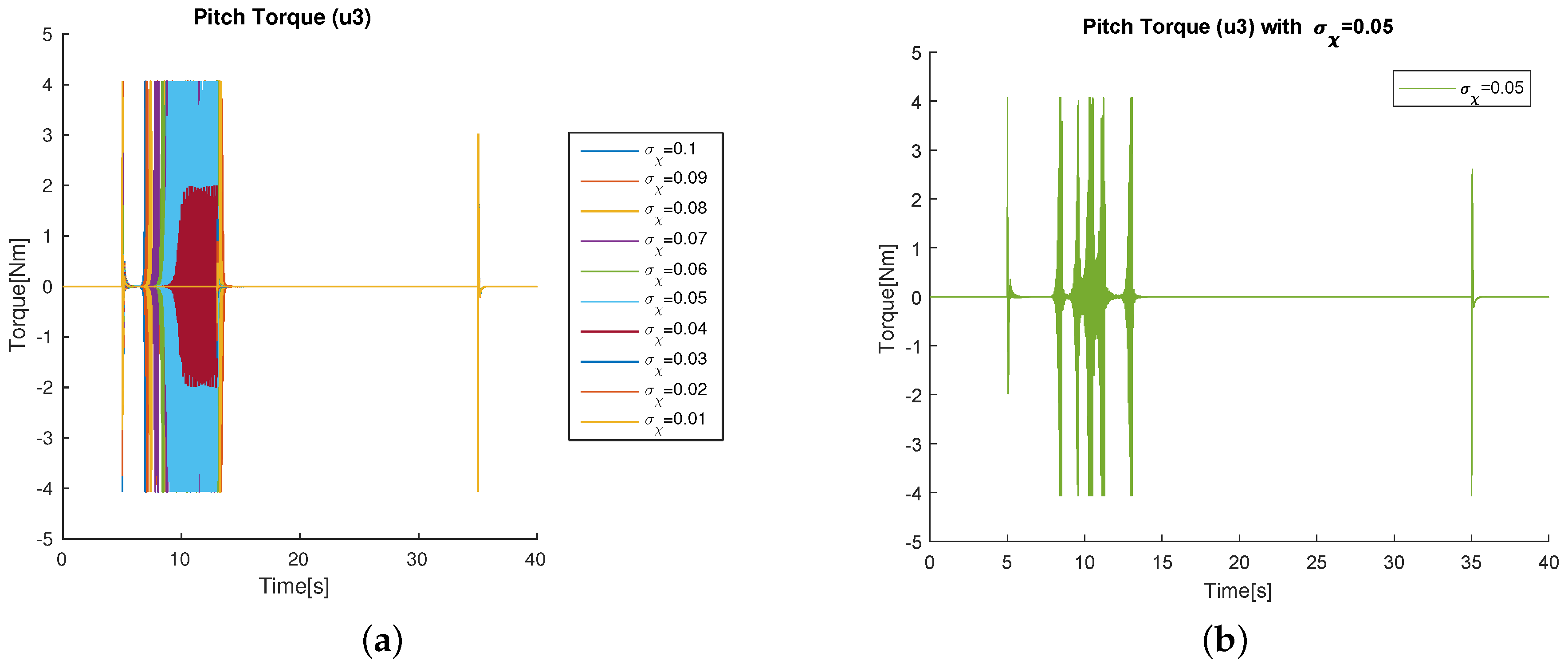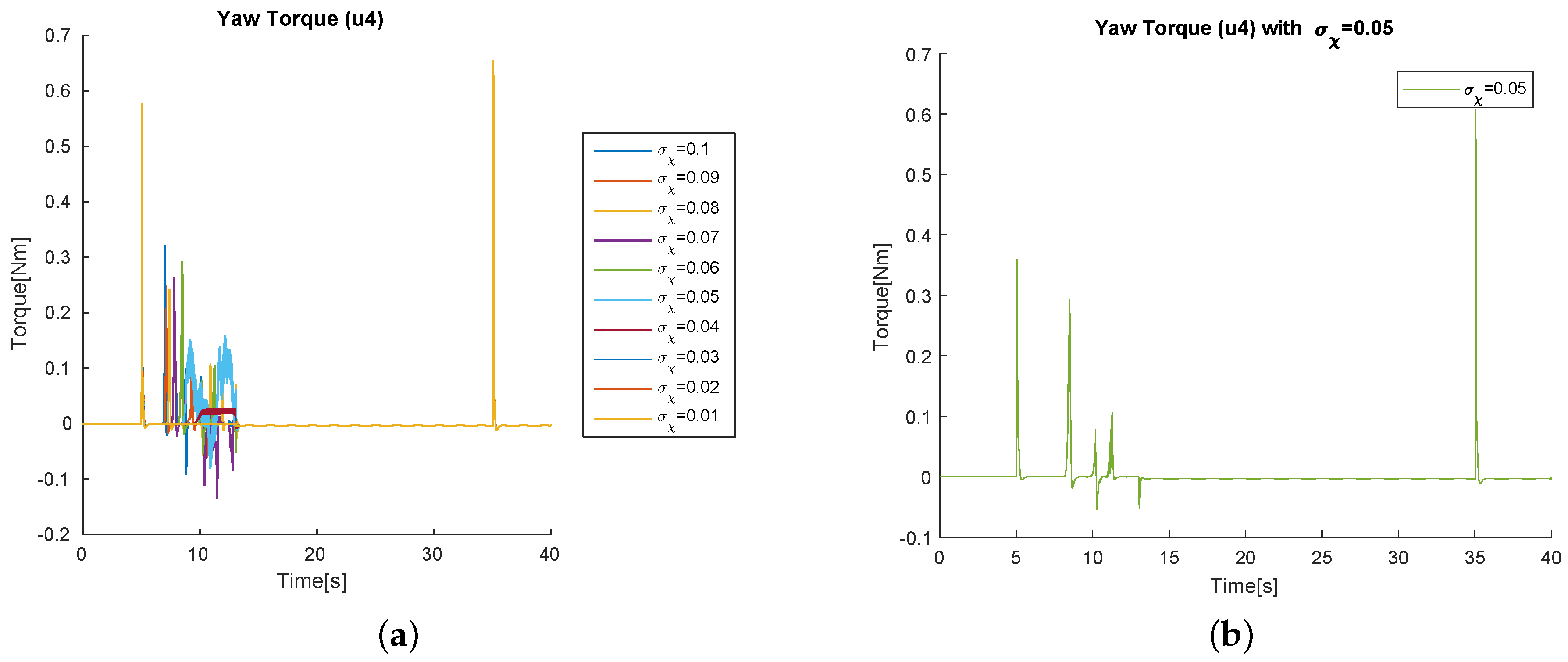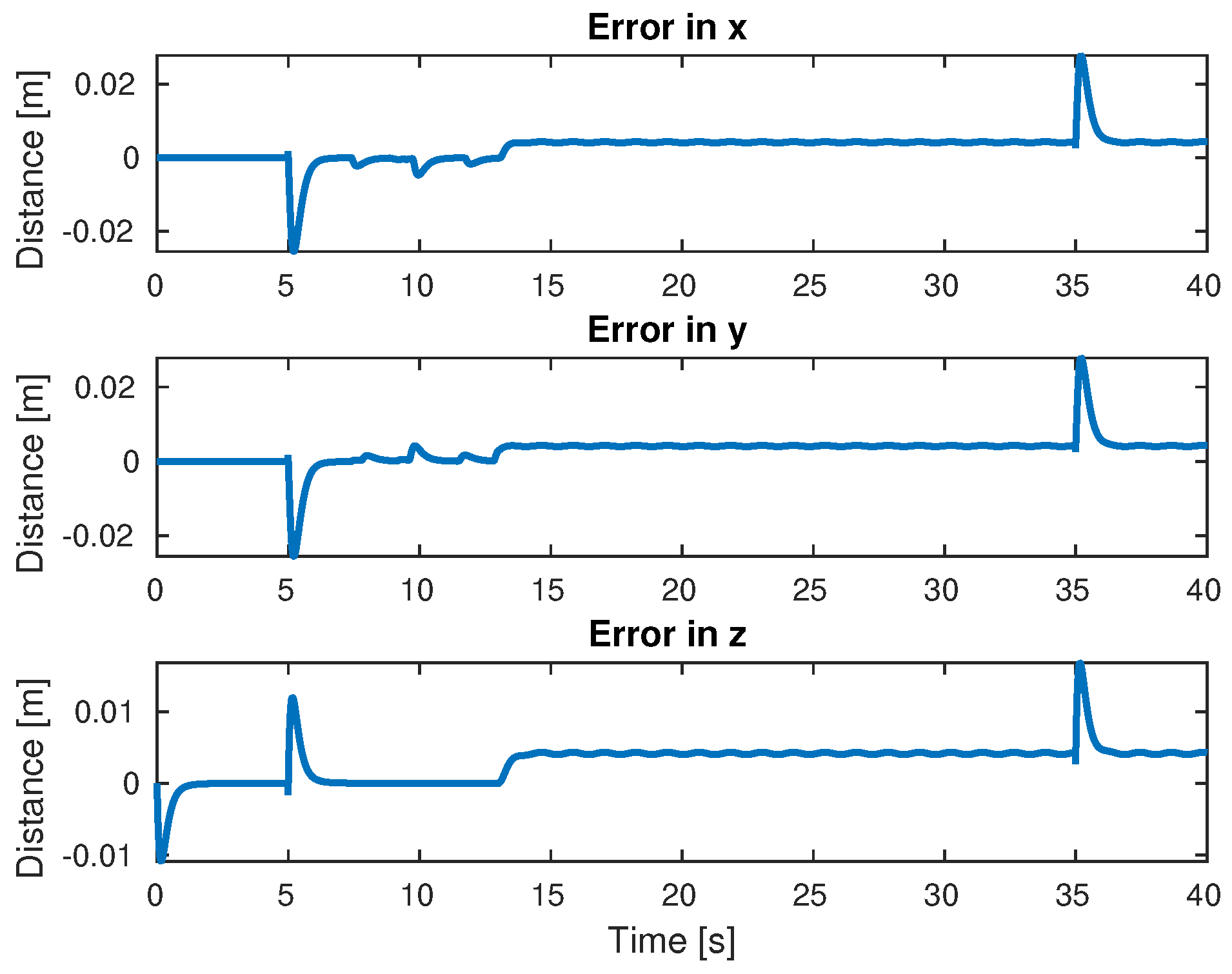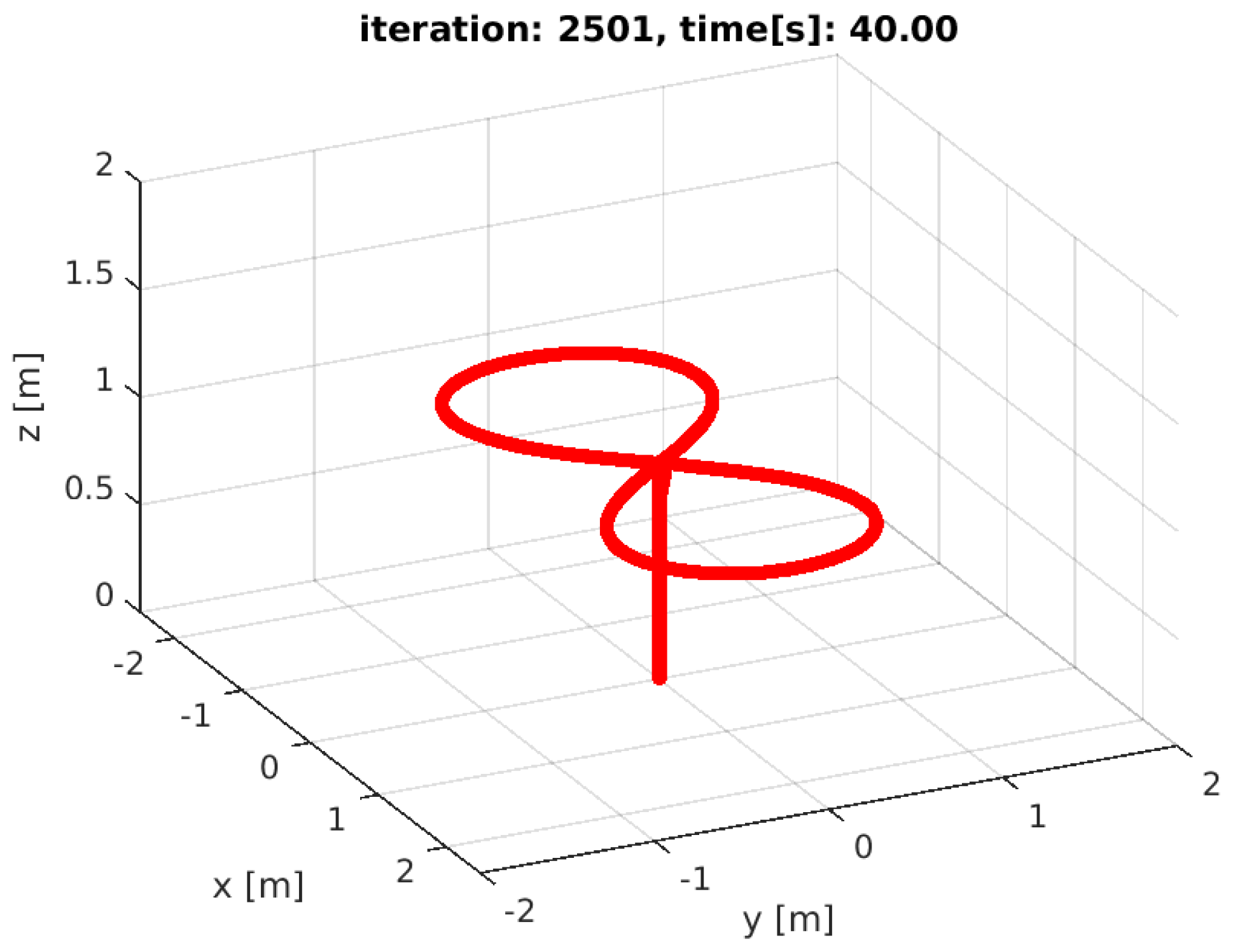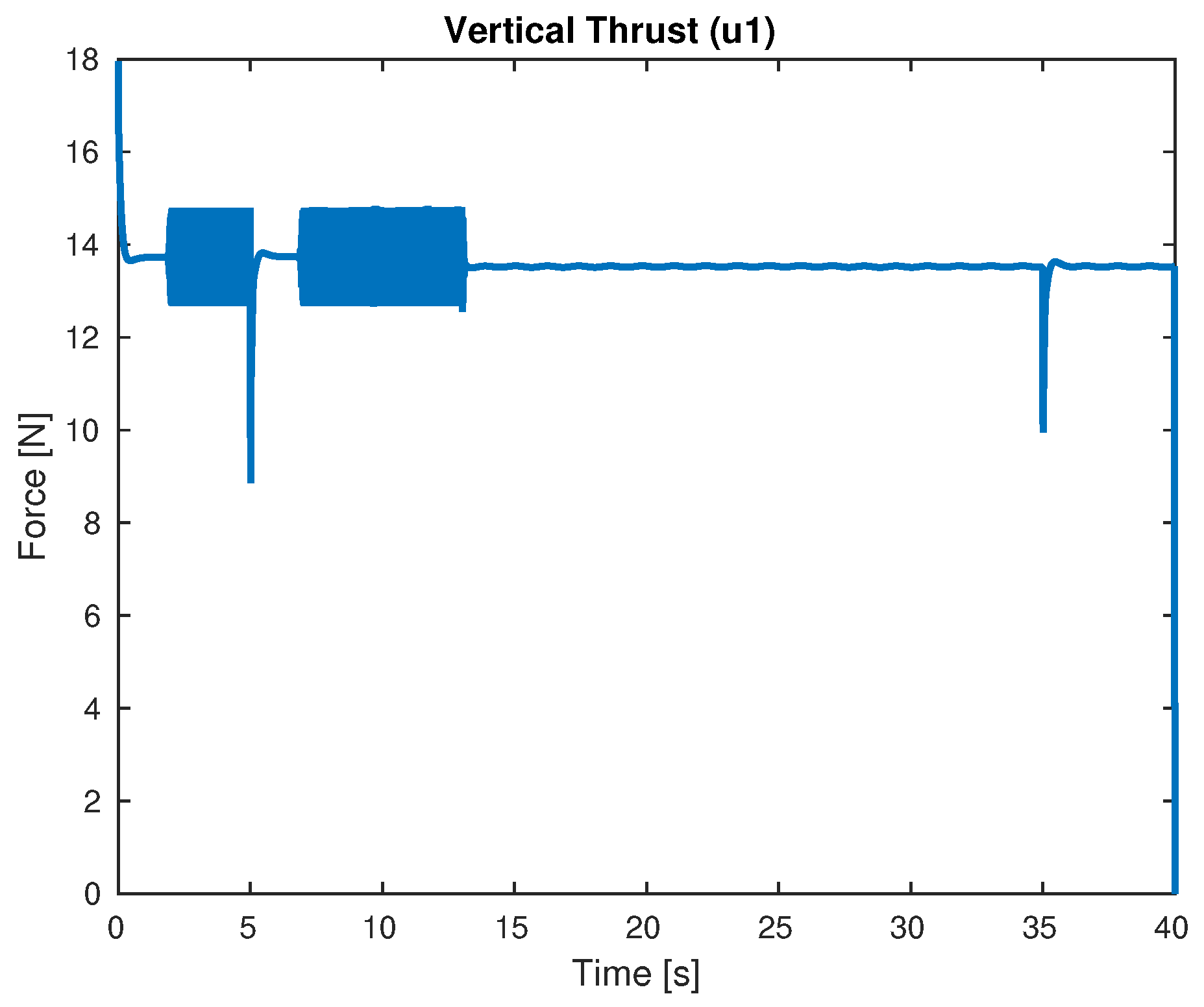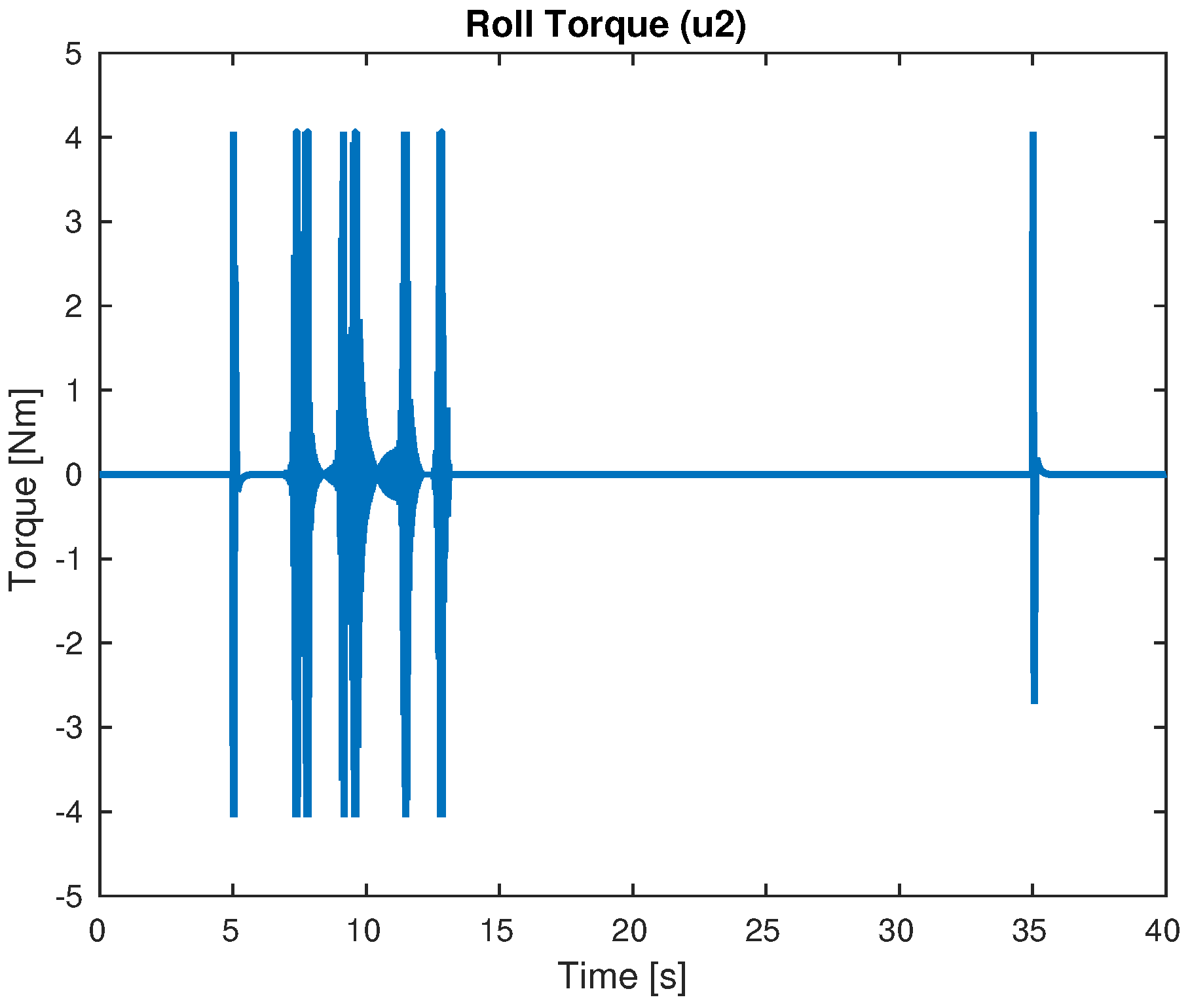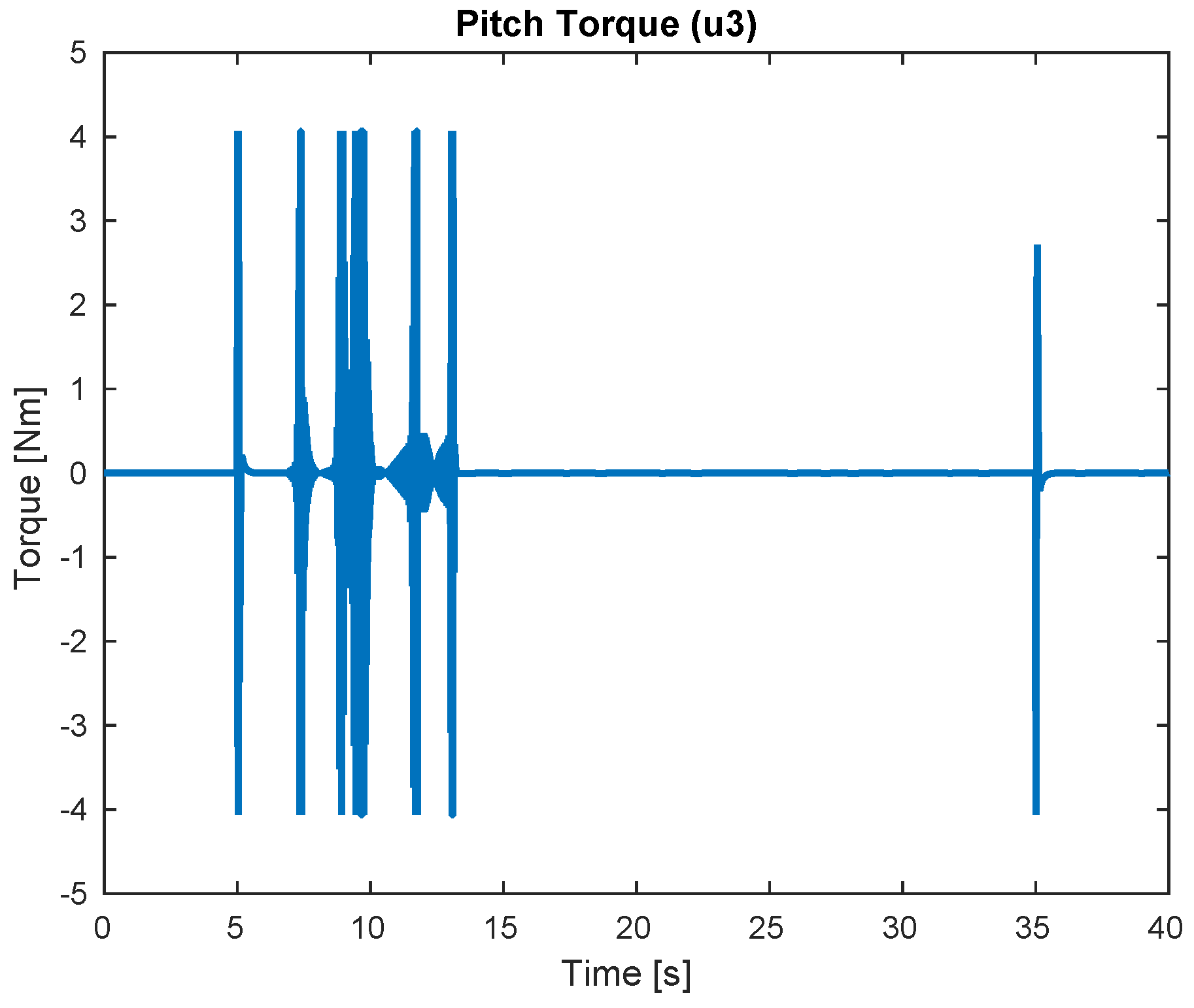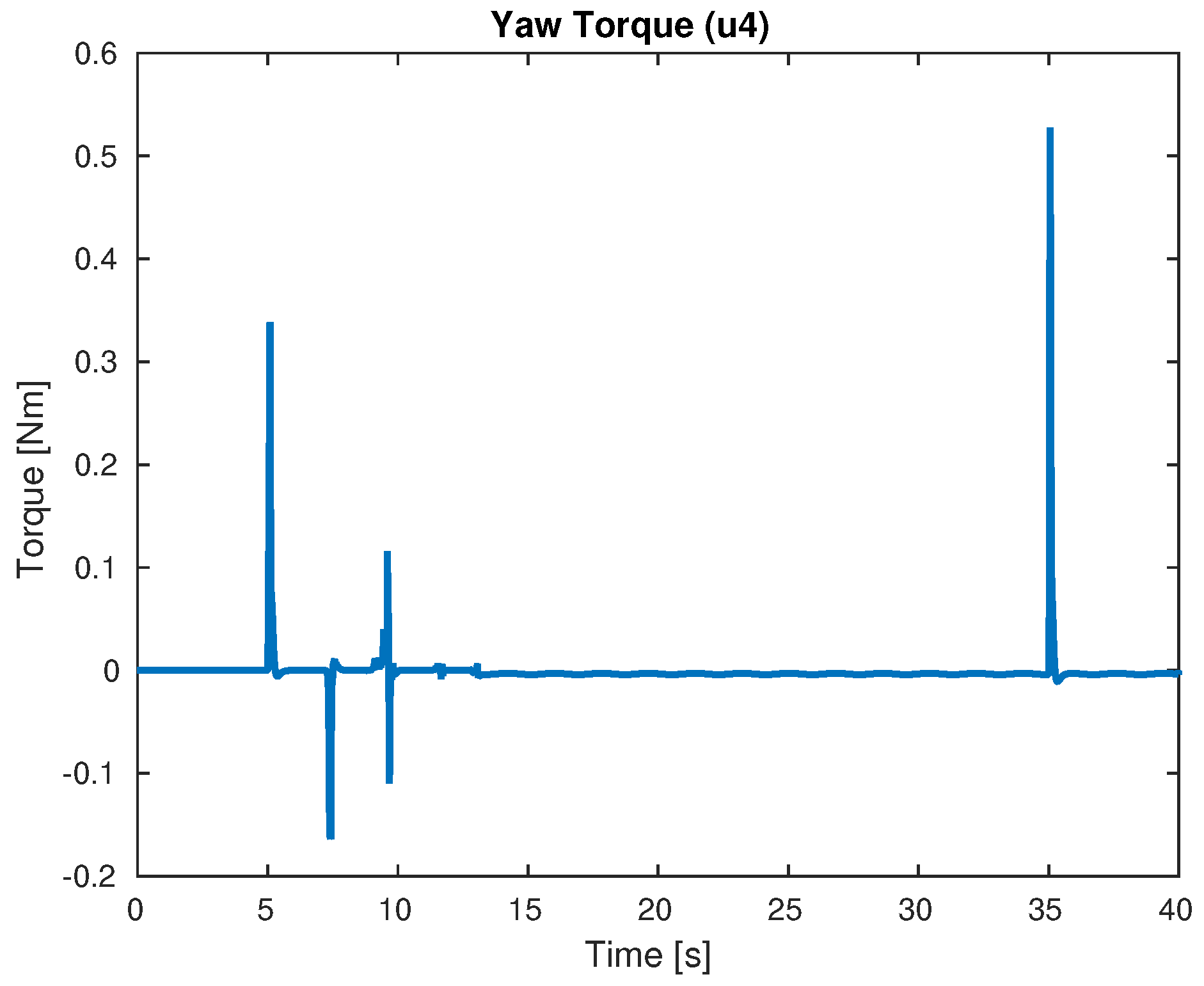Simulation results are presented to evaluate the performance of the control scheme.

1. Introduction

Recently, the design of fractional order controllers has become one of the most exciting topics in control theory leading to interesting applications in the control of physical systems such as suspension systems, permanent magnet synchronous motors, power electronic systems and unmanned aerial vehicles, among others. The idea of fractional order control was first proposed by [1] introducing a robust fractional order control scheme. Also Podlubny [2,3] introduced the well known fractional order proportional-integral-derivative controller. Then, many fractional order controllers have been proposed in the literature, including tilt integral derivative (TID) controllers [4], fractional order lead-lag compensators [5,6], fractional order optimal controllers [7,8], and fractional order adaptive controllers [9,10].

On the other hand sliding mode control (SMC) is a well known control technique that is applied to both linear and nonlinear systems allowing to deal with uncertainties [11]. However, the monotonous switching feedback produced by these controllers causes high frequency chattering in the control signals, which leads to undesirable loads on control actuators [12,13]. In recent years, fractional order sliding mode control (FOSMC) has been employed to overcome these drawbacks. For example, in [14], a control strategy called fractional order terminal sliding mode control (FOTSMC) is designed for a class of uncertain dynamical systems; a fractional order switching surface is proposed to satisfy a sliding condition and numerical simulations are provided that show the finite time stability of the closed-loop system. Also, in [15] a FOSMC is proposed for the control of a single-link flexible manipulator constructing a switching surface based on fractional derivatives; such a controller achieves better performance with small control chattering and robustness with respect to external load disturbances and parameter variations. A FOSMC for antilock braking systems (ABS) is proposed in [16,17] to regulate the slip to a desired value; these controllers deal with the uncertainties in the ABS and track the desired slip faster than conventional integer order sliding mode control (IOSMC). Aditionally, FOSMC has been used for speed control of permanent magnet synchronous motors [18], for vibration suppression of uncertain structures [19], for control of fractional order chaotic systems [20,21] and so on leading to better control performance.

In [22], the stability of a FOSMC has been studied showing that a stable reaching law, in the fractional order case, corresponds to a stable reaching law, in the integer order case. Also, a sufficient condition is derived to guarantee global attraction to the sliding surface when a fractional order linear system with uncertainties is considered. Motivated by this result, in this paper FOSMC design is proposed to solve a trajectory tracking problem for an integer order nonlinear system where an unknown additive perturbation term is present. A sufficient condition is also given that assures the reaching of a suitable sliding surface; on this surface trajectory tracking is performed. The FOSMC proposed is applied to the trajectory tracking problem of a quadrotor. For vertical take-off, trajectory tracking and landing, an error sliding surface is considered. Numerical simulations show the robustness of the FOSMC with respect to additive uncertainties (the error tracking is bounded to a small region around zero) and the chattering in the control signals is reduced when compared to a integer order sliding mode controller.

The paper is organized as follows. In Section 2, fractional order differentiation is briefly presented together with the FOSMC proposed and the sufficient condition for the attractiveness of the sliding surface. Section 3 presents the FOSMC design for the trajectory control of a quadrotor model. Some simulations results are given in Section 4. Finally, in Section 5 some conclusions are presented.

2. FOSMC of an Integer Second Order Perturbed Nonlinear System

Fractional calculus is mainly the calculus of derivatives and integrals of fractional order that can be real or complex [23] and it has many applications in science and engineering. In this article a Sliding Mode Control of Fractional Order is proposed for the trajectory tracking of a quadrotor. Among the definitions of fractional derivative the most cited are the Riemman-Liouville and Caputo definitions. Here, the Caputo definition is used which is expressed as

$$D^{\alpha }\varphi ={\varphi }^{\alpha }:=\frac{1}{\mathsf{\Gamma }(n-\alpha )}{\int }_0^t\frac{{\varphi }^{\left(n\right)}\left(\xi \right)}{{(t-\xi )}^{\alpha +n-1}}d\xi ,$$

(1)

where $\mathsf{\Gamma }$ is the so called gamma function defined as $\mathsf{\Gamma }\left(n\right)={\int }_0^{\infty }{t}^{z-1}{e}^{-t}dt$ and $n-1\le \alpha \le n$ with n being an integer. From this definition, one can notice that when $\alpha <0$ one has integration and when $\alpha >0$ one has differentiation; when $\alpha =1.0$ one has the first order derivative of a function. The gamma function generalizes the notion of a number raised to an arbitrary real number (or complex number). Thus the gamma function somehow involves the computation of a fractional derivative. The definition of a fractional derivative, as stated above, can not be used in practice, thus numeric methods such as the one based on the Grünwald-Letnikov approach is commonly used.

Let us consider a perturbed nonlinear system described by a second order differential equation of the form

$$\ddot{\chi }=f_{\chi }(\chi ,t)+g_{\chi }(\chi ,t)u\left(t\right)+{\Delta }_{\chi }(\chi ,t),$$

(2)

where $\chi (·)\in \mathbb{R}$, $f_{\chi }(·)$ and $g_{\chi }(·)$ are bounded functions of their arguments and $u(·)\in \mathbb{R}$ is the system input. ${\Delta }_{\chi }(·,·)\in \mathbb{R}$ is a disturbance term which includes uncertainties associated to the modelling of a process and external perturbations. The following assumption is made on ${\Delta }_{\chi }(·,·)$.

Assumption A1.

The disturbance term ${\Delta }_{\chi }(·,·)$ is unknown but bounded, more precisely ${\Delta }_{\chi }(·,·)$ satisfies

$$|{\Delta }_{\chi }(\chi ,t)|\le {\kappa }_{\Delta },$$

(3)

for all $\chi (·)$ which are solutions of (2) and all $t\ge 0$ with ${\kappa }_{\Delta }$ being a real positive constant different from 0.

It is desired that the signal $\chi$ tracks a given reference signal ${\chi }_d$, despite the presence of the disturbance term ${\Delta }_{\chi }$. Thus a tracking error e is defined as follows:

$$e=\chi -{\chi }_d.$$

(4)

In accordance to the sliding mode control methodology [24] a so called switching function $s_{\chi }$ is chosen as

$$s_{\chi }=\dot{e}+{\lambda }_{\chi }e,$$

(5)

where ${\lambda }_{\chi }$ is a real constant parameter. The switching function (5) defines the sliding surface

$$s_x=0=\dot{e}+{\lambda }_{\chi }e.$$

(6)

Thus, ${\lambda }_{\chi }$ is selected in such a way that the first order differential Equation (6) has a solution that exponentially converges to zero; as a consequence $\chi$ also converges to ${\chi }_d$ exponentially.

Let us also consider the nominal nonlinear system associated to the perturbed system (2), this is with ${\Delta }_{\chi }(\chi ,t)=0$, for all $\chi \in \mathbb{R}$ and all $t>0$, given by

$$\ddot{\chi }=f_{\chi }(\chi ,t)+g_{\chi }(\chi ,t)u\left(t\right).$$

(7)

In order to attract the dynamics of system (2) to the sliding surface (6) and based on the strategy proposed in [25], the $(1+\beta )$ fractional order derivative of $s_{\chi }$ is set to be

$$s_{\chi }^{1+\beta }=-{\sigma }_{\chi }sgn\left(s_{\chi }\right)-{\mu }_{\chi }{s}_{\chi }^{\beta },$$

(8)

where ${\sigma }_{\chi }$ and ${\mu }_{\chi }$ are positive real constants and $sgn(·)$ is the signum function. The derivative of (8) to the order $(-\beta )$ is now taken (this is equivalent to integrate (8) to the order $\beta$), leading to

$$\dot{s_{\chi }}=-{\sigma }_{\chi }(D^{-\beta }sgn(s_{\chi }))-{\mu }_{\chi }{s}_{\chi }.$$

(9)

On the other hand, from (5) and the nominal nonlinear system (7), one has that

$$\dot{s_{\chi }}=\ddot{\chi }-\ddot{x_d}+{\lambda }_{\chi }\dot{e}=f_x+g_{x}u-\ddot{x_d}+{\lambda }_{\lambda }\dot{e}.$$

(10)

Thus by combining Equations (9) and (10), the following FOSMC is obtained:

$$u=\frac{1}{g_{\chi }(\chi ,t)}[-f_{\chi }(\chi ,t)+P_{\chi }(\chi ,\dot{\chi },t)],$$

(11)

where

$$P_{\chi }(\chi ,\dot{\chi },t)=\ddot{{\chi }_d}-{\lambda }_{\chi }\dot{e}-{\sigma }_{\chi }(D^{-\beta }sgn(s_{\chi }))-{\mu }_{\chi }{s}_{\chi }.$$

(12)

In fact, the FOSMC Equations (11) and (12) can achieve the attraction of the perturbed dynamics (2) to the sliding surface (6) under a sufficient condition on the size of the perturbation term ${\Delta }_{\chi }$, the parameters ${\sigma }_{\chi }$, ${\mu }_{\chi }$ and the discontinuous term $D^{-\beta }sgn\left(s_{\chi }\right)$, as stated in the following result.

Theorem 1.

Consider the perturbed nonlinear system (2) together with Assumption A1. If the parameters ${\sigma }_{\chi }$, ${\mu }_{\chi }$ and the bound ${\kappa }_{\Delta }$ satisfy

$${\sigma }_{\chi }|D^{-\beta }sgn(s_{\chi })|+{\mu }_{\chi }>{\kappa }_{\Delta },$$

(13)

then the FOSMC Equations (11) and (12) assures the attractiveness of the perturbed system to the switching surface $s_{\chi }=0$ defined by (6).

Proof. 

Let us consider the following Lyapunov function candidate:

$$V_{\chi }\left(s_{\chi }\right)=\frac{1}{2}{s}_{\chi }^2,$$

(14)

which is positive definite. The time derivative of $V_{\chi }$ has the form

$$\dot{V_{\chi }}=s_{\chi }\dot{s_{\chi }}=s_{\chi }(\ddot{\chi }-\ddot{{\chi }_d}+{\lambda }_{\chi }\dot{e}).$$

(15)

substituting the dynamics of the perturbed system (2) into (15) together with the FOSMC Equations (11) and (12) leads to

$$\dot{V_{\chi }}=-{\sigma }_{\chi }(D^{-\beta }sgn(s_{\chi }))s_{\chi }-{\mu }_{\chi }{s}_{\chi }^2+s_{\chi }{\Delta }_{\chi }.$$

(16)

Since $s_{\chi }=|s_{\chi }|sgn(s_{\chi })$, $\dot{V_{\chi }}$ can also be written as

$$\dot{V_{\chi }}=-{\sigma }_{\chi }(D^{-\beta }sgn(s_{\chi }))|s_{\chi }|sgn(s_{\chi })-{\mu }_{\chi }{s}_{\chi }^2+s_{\chi }{\Delta }_{\chi }.$$

(17)

Also $0<\beta <1$, thus $sgn(D^{-\beta }sgn(s_{\chi }))=sgn(s_{\chi })$ [25], then (17) takes the form

$$\begin{array}{cc}\hfill \dot{V_{\chi }}& =-{\sigma }_{\chi }\left|s_{\chi }\right|(D^{-\beta }sgn(s_{\chi }))sgn(D^{-\beta }sgn(s_{\chi }))-{\mu }_{\chi }{s}_{\chi }^2+s_{\chi }{\Delta }_{\chi }\hfill \\ & =-{\sigma }_{\chi }|s_{\chi }||D^{-\beta }sgn(s_{\chi })|-{\mu }_{\chi }{s}_{\chi }^2+s_{\chi }{\Delta }_{\chi }.\hfill \end{array}$$

(18)

Majoring this last expression and using the bound ${\kappa }_{\Delta }$ in (3), one gets

$$\dot{V_{\chi }}\le -|s_{\chi }|[({\sigma }_{\chi }|D^{-\beta }sgn(s_{\chi })|+{\mu }_{\chi })-{\kappa }_{\Delta }].$$

(19)

Thus if Condition (3) is satisfied, $\dot{V_{\chi }}<0$ and the convergence to the surface $s_{\chi }=0$ is accomplished. □

Remark 1.

The FOSMC (11)-(12) compensate the effect of additive perturbations in a second order nonlinear system described by (2). In fact, the main idea to define a sliding surface (6) together with its $(1+\beta )$ fractional order derivative is that as soon as the disturbance appears, $s_{\chi }$ becomes nonzero and, at that time, the discontinuous control term becomes active and rejects the disturbance. Also, and similar to the control scheme proposed in [26], expression (19) shows that a stronger attraction to $s_{\chi }=0$ is achieved and that the attraction is higher for any $s_{\chi }$ with ${\mu }_{\chi }\ne 0$ than with ${\mu }_{\chi }=0$. In particular, the parameter ${\mu }_{\chi }$ is not used in [26] where a fractional order linear system is controlled.

3. Application to the Trajectory Tracking of a Quadrotor

3.1. Quadrotor’s Dynamic Model

Let us consider an inertial reference frame and a body fixed reference frame to specify the position, velocity and acceleration of the quadrotor. The world frame W, is defined by axes X, Y and Z, with Z pointing upward. The body frame B, $xB, yB, zB$, is attached to the center of mass of the quadrotor. A picture of a quadrotor with the corresponding reference frames is shown in Figure 1.

The Newton-Euler approach was used to obtain the dynamical behaviour of the quadrotor [27], which considers a quadrotor as a rigid body. Let us consider the generalized coordinates of the quadrotor denoted as $q=(\xi ,\eta ),$ where $\xi =(x,y,z)$ is the position vector, which goes from the center of mass of the quadrotor relative to the fixed reference frame ($X,Y,Z$), and $\eta =(\varphi ,\theta ,\psi )$ are the Euler angles of the quadrotor. These angles have the following names and they represent a rotation around their corresponding axis: $\varphi$ is the pitch angle around xB axis, $\theta$ is the roll angle around yB axis, and $\psi$ is the yaw angle around zB axis.The angular velocity vector $\mathsf{\Omega }=(p,q,r)$ is related to $\dot{\eta }$ by the equivalent form $\mathsf{\Omega }=W_{\eta }\dot{\eta }$, where

$$W_{\eta }=\left[\begin{array}{ccc}1& 0& -sin\left(\theta \right)\\ 0& cos\left(\varphi \right)& cos\left(\theta \right)sin\left(\varphi \right)\\ 0& -sin\left(\varphi \right)& cos\left(\theta \right)cos\left(\varphi \right)\end{array}\right]$$

is a standard kinematic matrix. Also $R(\varphi ,\theta ,\psi )ϵSO(3)$, is the so called rotation matrix that represents the quadrotor’s orientation that is relative to the fixed reference frame. Using the compact notation $c\left(\alpha \right)=cos\left(\alpha \right)$ and $s\left(\alpha \right)=sin\left(\alpha \right)$, this matrix is given by

$$\begin{array}{c}\hfill R=\left[\begin{array}{ccc}c\left(\theta \right)c\left(\psi \right)& c\left(\psi \right)s\left(\theta \right)s\left(\varphi \right)-c\left(\varphi \right)s\left(\psi \right)& s\left(\varphi \right)s\left(\psi \right)+c\left(\varphi \right)c\left(\psi \right)s\left(\theta \right)\\ c\left(\theta \right)s\left(\psi \right)& c\left(\varphi \right)c\left(\psi \right)+s\left(\theta \right)s\left(\varphi \right)s\left(\psi \right)& c\left(\varphi \right)s\left(\theta \right)s\left(\psi \right)-c\left(\psi \right)s\left(\varphi \right)\\ -s\left(\theta \right)& c\left(\theta \right)s\left(\varphi \right)& c\left(\theta \right)c\left(\varphi \right)\end{array}\right].\end{array}$$

Additionally, the inertia matrix is given by

$$I=\left[\begin{array}{ccc}Ixx& 0& 0\\ 0& Iyy& 0\\ 0& 0& Izz\end{array}\right],$$

where $I_{xx}$, $I_{yy}$ and $I_{zz}$ are the moments of inertia of the quadrotor about its corresponding axis, m is the mass of the quadrotor and g = 9.81 [m/s${}^2$] is the gravitational constant. Finally, the dynamics of a rigid body under external forces take the form

$$\dot{\xi }=\left[\begin{array}{c}{v}_x\\ v_y\\ v_z\end{array}\right],$$

(20)

$$m\dot{v}=R\left[\begin{array}{c}0\\ 0\\ T_f\end{array}\right]-\left[\begin{array}{c}0\\ 0\\ mg\end{array}\right],$$

(21)

$$\dot{R}=R\widehat{\mathsf{\Omega }},$$

(22)

$$I\dot{\mathsf{\Omega }}=-\mathsf{\Omega }\times I\mathsf{\Omega }+\tau ,$$

(23)

where $\widehat{\mathsf{\Omega }}$ is the anti-symmetric matrix of $\mathsf{\Omega }$, also called the wedge operator defined as

$$\widehat{\mathsf{\Omega }}=\left[\begin{array}{ccc}0& -r& q\\ r& 0& -p\\ -q& p& 0\end{array}\right],$$

and × denotes the cross product. $T_f$ is the total thrust applied to the quadrotor, this is $T_f={\sum }_{i=1}^4{f}_i=k{\sum }_{i=1}^4{\omega }_i^2$ and represents the first control signal, furthermore $\tau =({\tau }_{\varphi },{\tau }_{\theta },{\tau }_{\psi })$ is the vector of control signals for roll, pitch and yaw angles, respectively.

From Equations (20)–(23), one can obtain the dynamics of the quadrotor that describe its motion. These equations are the following ones [27,28]:

$$\ddot{x}=\frac{cos\left(\varphi \right)sin\left(\theta \right)cos\left(\psi \right)+sin\left(\varphi \right)sin\left(\psi \right)}{m}{u}_1,$$

(24)

$$\ddot{y}=\frac{cos\left(\varphi \right)sin\left(\theta \right)sin\left(\psi \right)-sin\left(\varphi \right)cos\left(\psi \right)}{m}{u}_1,$$

(25)

$$\ddot{z}=-g+\frac{cos\left(\varphi \right)cos\left(\theta \right)}{m}{u}_1,$$

(26)

$$\ddot{\varphi }=\dot{\theta }\dot{\psi }\frac{(I_{xx}+I_{yy}-I_{zz})}{I_{xx}}+\frac{u_2}{I_{xx}},$$

(27)

$$\ddot{\theta }=\dot{\varphi }\dot{\psi }\frac{(I_{zz}-I_{xx}-I_{yy})}{I_{yy}}+\frac{u_3}{I_{yy}},$$

(28)

$$\ddot{\psi }=\dot{\varphi }\dot{\theta }\frac{(I_{zz}+I_{xx}-I_{yy})}{I_{zz}}+\frac{u_4}{I_{zz}},$$

(29)

where $u_1=T_f$, $u_2={\tau }_{\varphi }$, $u_3={\tau }_{\theta }$ and $u_4={\tau }_{\psi }$ are considered as control signals.

It is possible to stablish a mapping between the control signals $u_1$, $u_2$, $u_3$ and $u_4$ and the angular velocity of each quadrotor’s electric motor ${\omega }_1$, ${\omega }_2$, ${\omega }_3$ and ${\omega }_4$. In fact, each motor produces a vertical force $F_i$ and a moment $M_i$ that is related to the motor angular velocity ${\omega }_i$ in the form [29]

$$F_i=k_F{\omega }_i^2,M_i=k_M{\omega }_i^2,$$

(30)

where $k_F$ and $k_M$ are positive constants that can be experimentally determined. The relation between the motor angular velocities and the control signals is then given by [29]

$$\left[\begin{array}{c}{u}_1\\ u_2\\ u_3\\ u_4\end{array}\right]=K_{MF}\left[\begin{array}{c}{\omega }_1^2\\ {\omega }_2^2\\ {\omega }_3^2\\ {\omega }_4^2\end{array}\right],$$

(31)

with $K_{MF}$ being an invertible matrix of the form

$$K_{MF}=\left[\begin{array}{cccc}{k}_F& k_F& k_F& k_F\\ 0& k_{F}L& 0& -k_{F}L\\ -k_{F}L& 0& k_{F}L& 0\\ k_M& -k_M& k_M& -k_M\end{array}\right],$$

(32)

where L is the distance from the rotation axis of the motors to the center of the quadrotor.

3.2. Trajectory Tracking of a Quadrotor

Let us first consider the z position dynamics in the quadrotor model (24)–(29), more precisely Equation (26). These dynamics have the form (2) with $x=z$, $u=u_1$ and

$$f_{\chi }=f_z=-g,g_{\chi }=g_z=\frac{cos\left(\varphi \right)cos\left(\theta \right)}{m},{\Delta }_{\chi }={\Delta }_z.$$

(33)

The tracking error e also takes the form $e=e_z=z-z_d$ with ${\chi }_d=z_d$ being the reference signal. In accordance with the methodology described in the previous section, the FOSMC that assures to have convergence to z towards $z_d$ despite the presence of the perturbation term ${\Delta }_z$ is given by

$$u_1=\frac{m}{cos\left(\varphi \right)cos\left(\theta \right)}[g+P_z(z,\dot{z},t)],$$

(34)

where

$$P_z(z,\dot{z},t)=P_{\chi }(\chi ,\dot{\chi },t)=\ddot{z_d}-{\lambda }_z\dot{e_z}-{\sigma }_z(D^{-\beta }sgn(s_z))-{\mu }_z{s}_z,$$

(35)

with $s_z=s_{\chi }=\dot{e}+{\lambda }_{\chi }e=\dot{e_z}+{\lambda }_z{e}_z$ as switching function (${\lambda }_{\chi }={\lambda }_z$) and ${\sigma }_z={\sigma }_{\chi }$, ${\mu }_z={\mu }_{\chi }$ in (35). ${\Delta }_z={\Delta }_{\chi }$ is assumed to satisfy (13), with a bound ${\kappa }_{\Delta }={\kappa }_{\Delta z}$.

In order to design the control signals $u_2$ and $u_3$, a desired reference signal is first defined for the angles $\varphi$ and $\theta$, this is ${\varphi }_d$ and ${\theta }_d$, respectively. For doing this, we adopt the small angle approximation widely used in the literature of unmanned aerial vehicles (see for example [28,30]). Under this assumption, the dynamics (24), (25), (27)–(29) take the form

$$\ddot{x}\approx tan\left(\theta \right)(g+P_z)+{\Delta }_x,$$

(36)

$$\ddot{y}\approx -tan\left(\varphi \right)(g+P_z)+{\Delta }_y,$$

(37)

$$\ddot{\varphi }=\frac{u_2}{I_{xx}},\ddot{\theta }=\frac{u_3}{I_{yy}},\ddot{\psi }=\frac{u_4}{I_{zz}},$$

(38)

where ${\Delta }_x$ and ${\Delta }_y$ are unknown perturbation terms bounded by the real positive constants ${\kappa }_{{\Delta }_x}$ and ${\kappa }_{{\Delta }_y}$ respectively affecting the dynamics of x and y.

It is now considered that $tan\left(\varphi \right)$ and $tan\left(\theta \right)$ are “virtual” input signals, this is $u_x=tan\left(\theta \right)$ and $u_y=tan\left(\varphi \right)$ in (36) and (37). Similar to the previous reasoning for the design of the control signal $u_1$, the tracking errors $e_x$ and $e_y$ are defined as

$$e_x=x-x_d,e_y=y-y_d,$$

(39)

where $x_d$ and $y_d$ are the reference signals for x and y, respectively. The following switching functions are then chosen:

$$s_x=\dot{e_x}+{\lambda }_x{e}_x,s_y=\dot{e_y}+{\lambda }_y{e}_y,$$

(40)

where, as before, ${\lambda }_x$ and ${\lambda }_y$ are real constant parameters selected in such a way that the first order linear differential equations defined by the sliding surfaces

$$s_x=0=\dot{e_x}+{\lambda }_x{e}_x,s_y=0=\dot{e_y}+{\lambda }_y{e}_y,$$

(41)

have solutions that exponentially converge to zero. In this same way, the $(1+\beta )$ fractional order derivative of $s_x$ and $s_y$ are set as

$$s_x^{1+\beta }=-{\sigma }_{x}sgn\left(s_x\right)-{\mu }_x{s}_x^{\left(\beta \right)},s_y^{1+\beta }=-{\sigma }_{y}sgn\left(s_y\right)-{\mu }_y{s}_y^{\left(\beta \right)},$$

(42)

where ${\sigma }_x$, ${\sigma }_y$, ${\mu }_x$ and ${\mu }_y$ are positive real constants. The ($-\beta$) order derivative of Equations (42) have the form (43), this is

$$\dot{s_x}=-{\sigma }_x{D}^{-\beta }sgn\left(s_x\right)-{\mu }_x{s}_x,\dot{s_y}=-{\sigma }_y{D}^{-\beta }sgn\left(s_y\right)-{\mu }_y{s}_y.$$

(43)

Also from the dynamics (36) and (37), with ${\Delta }_x={\Delta }_y=0$, one has that Equation (10) is given by

$$\dot{s_x}=\ddot{e_x}+{\lambda }_x\dot{e_x}=tan\left(\theta \right)(g+P_z)-\ddot{x_d}+{\lambda }_x\dot{e_x},$$

(44)

$$\dot{s_y}=\ddot{e_y}+{\lambda }_y\dot{e_y}=-tan\left(\varphi \right)(g+P_z)-\ddot{y_d}+{\lambda }_y\dot{e_y}.$$

(45)

The desired signals ${\theta }_d$ and ${\varphi }_d$ can then be computed from (44) and (45) when the signals $tan\left(\theta \right)$ and $tan\left(\varphi \right)$ are considered to be virtual input signals, as mentioned before. This consideration allows to have the following expressions for ${\theta }_d$ and ${\varphi }_d$:

$${\theta }_d=arctan\left(\frac{P_x}{P_z+g}\right),{\varphi }_d=-arctan\left(\frac{P_y}{P_z+g}\right),$$

(46)

where

$$P_x=\ddot{x_d}-{\lambda }_x\dot{e_x}-{\sigma }_x{D}^{-\beta }sgn\left(s_x\right)-{\mu }_x{s}_x,$$

(47)

$$P_y=\ddot{y_d}-{\lambda }_y\dot{e_y}-{\sigma }_y{D}^{-\beta }sgn\left(s_y\right)-{\mu }_y{s}_y.$$

(48)

Notice now that, when $\theta$ and $\varphi$ are managed to approach ${\theta }_d$ and ${\varphi }_d$ as soon as possible, the FOSMC strategy discussed above allows to reach the sliding surface $s_x=0$ and $s_y=0$ where the tracking errors $e_x$ and $e_y$ tend to zero exponentially. In this paper, a simple proportional and derivation action is implemented to allow that $\theta \to {\theta }_d$, $\varphi \to {\varphi }_d$ and $\psi \to {\psi }_d$, this is

$$u_2=I_{xx}[\ddot{{\varphi }_d}-K{d}_{\varphi }\dot{e_{\varphi }}-K{p}_{\varphi }{e}_{\varphi }],$$

(49)

$$u_3=I_{yy}[\ddot{{\theta }_d}-K{d}_{\theta }\dot{e_{\theta }}-K{p}_{\theta }{e}_{\theta }],$$

(50)

$$u_4=I_{zz}[-K{d}_{\psi }\dot{\psi }-K{p}_{\psi }\psi ],$$

(51)

where $e_{\varphi }=\varphi -{\varphi }_d$, $e_{\theta }=\theta -{\theta }_d$ and $e_{\psi }=\psi -{\psi }_d$ are the tracking errors in the angles $\varphi$, $\theta$ and $\psi$ respectively. Notice in particular, that ${\varphi }_d$ is set to 0 in (51).

4. Simulation Results

Some simulations were carried out to evaluate the performance of the control scheme proposed. The simulations were made in MATLAB by integrating the dynamic equations of the quadrotor (24)–(29) using a script that implements a Runge-Kutta method of fourth order. In order to calculate the fractional derivative used in Equations (35), (47) and (48) of the control scheme, the Grünwald-Letnikov numeric method is used, implementing the adaptive time step memory algorithm described in [31]. Different values of the fractional order $\beta$ were tested, in order to show the performance of the control scheme.Also the signum function was implemented using the expression

$$sgn\left(s_z\right)=\frac{s_z}{|s_z|+ϵ},$$

where the small quantity $ϵ>0$ is a real positive constant.

A piecewise trajectory was used as a tracking reference in the space as follows: the first 5 s are used for the take-off of the quadrotor until it reaches hover at 1 m, then a 2 m long lemniscata trajectory is followed once, with a period of 30 s per return, finally landing from 1 m to the floor is performed within the last 5 s.

A perturbation term was introduced at the right hand side of the quadrotor dynamic model (24)–(29) at $t=13$ s in order to simulate the effect of weather conditions, such as wind variations. This perturbation term used was given by

$${\Delta }_z={\Delta }_x={\Delta }_y=K_a+K_{b}sin(\frac{2\pi t}{T_1}),$$

$${\Delta }_{\varphi }={\Delta }_{\theta }={\Delta }_{\psi }=K_{\alpha }+K_{\beta }sin(\frac{2\pi t}{T_2}),$$

with $K_a=0.15$ [m/s${}^2$], $K_b=0.01$ [m/s${}^2$], $T_1=1.2$ [s], $K_{\alpha }$ = 0.087 [rad/s${}^2$], $K_{\beta }$ = 0.015 [rad/s${}^2$] and $T_2$ = 1.8 [s]. The model parameters used in the simulation are shown in

Table 1. Model Parameters.

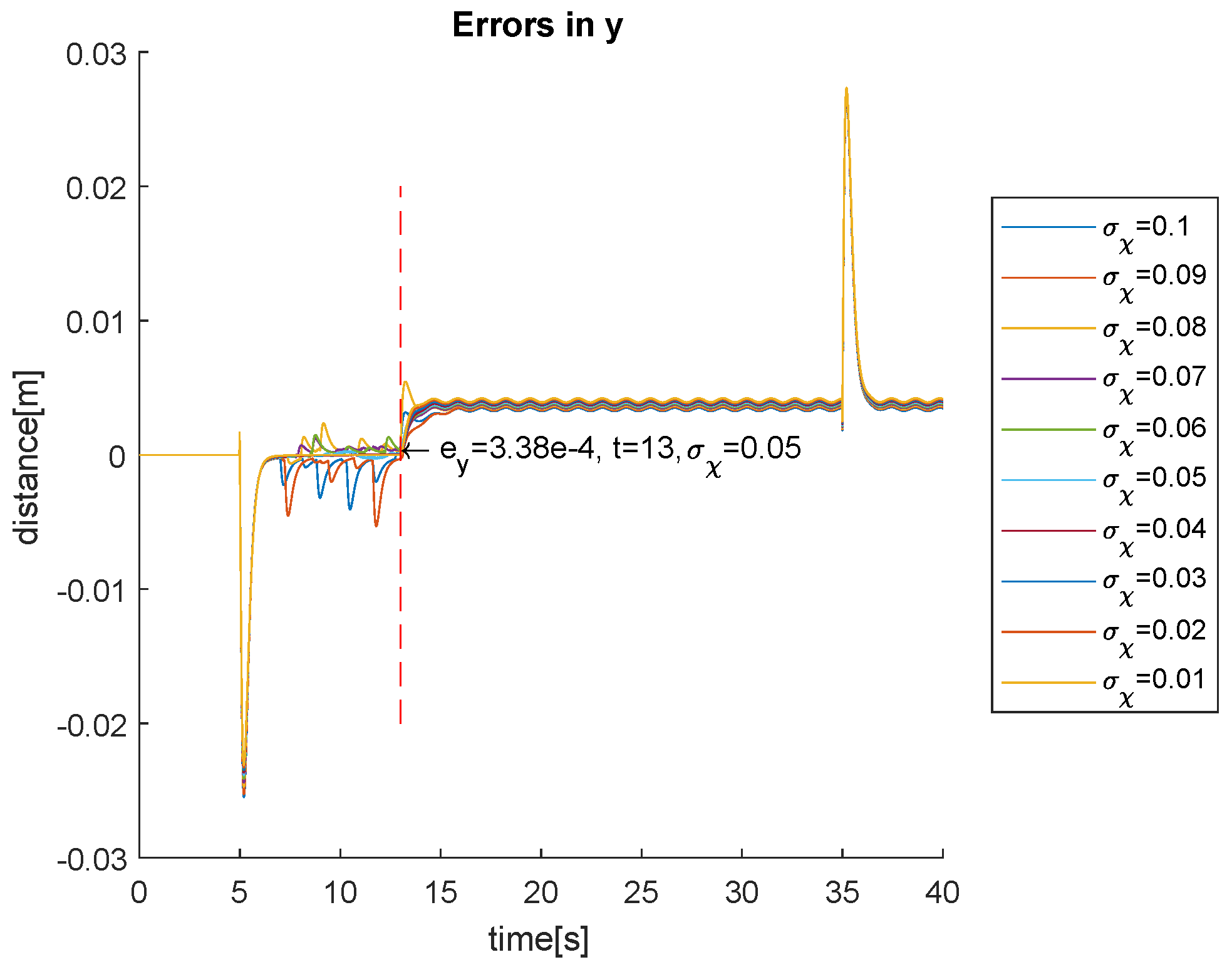
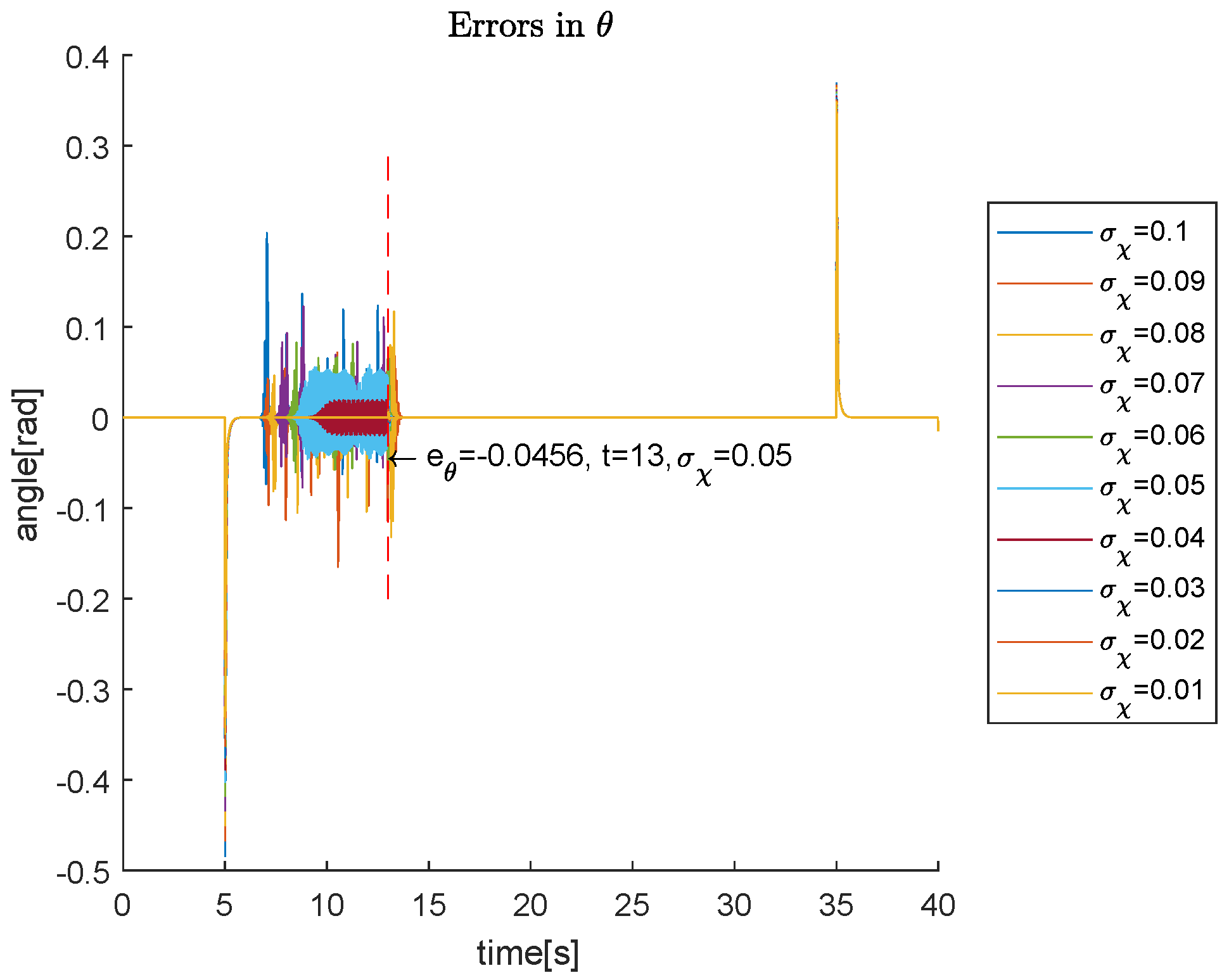
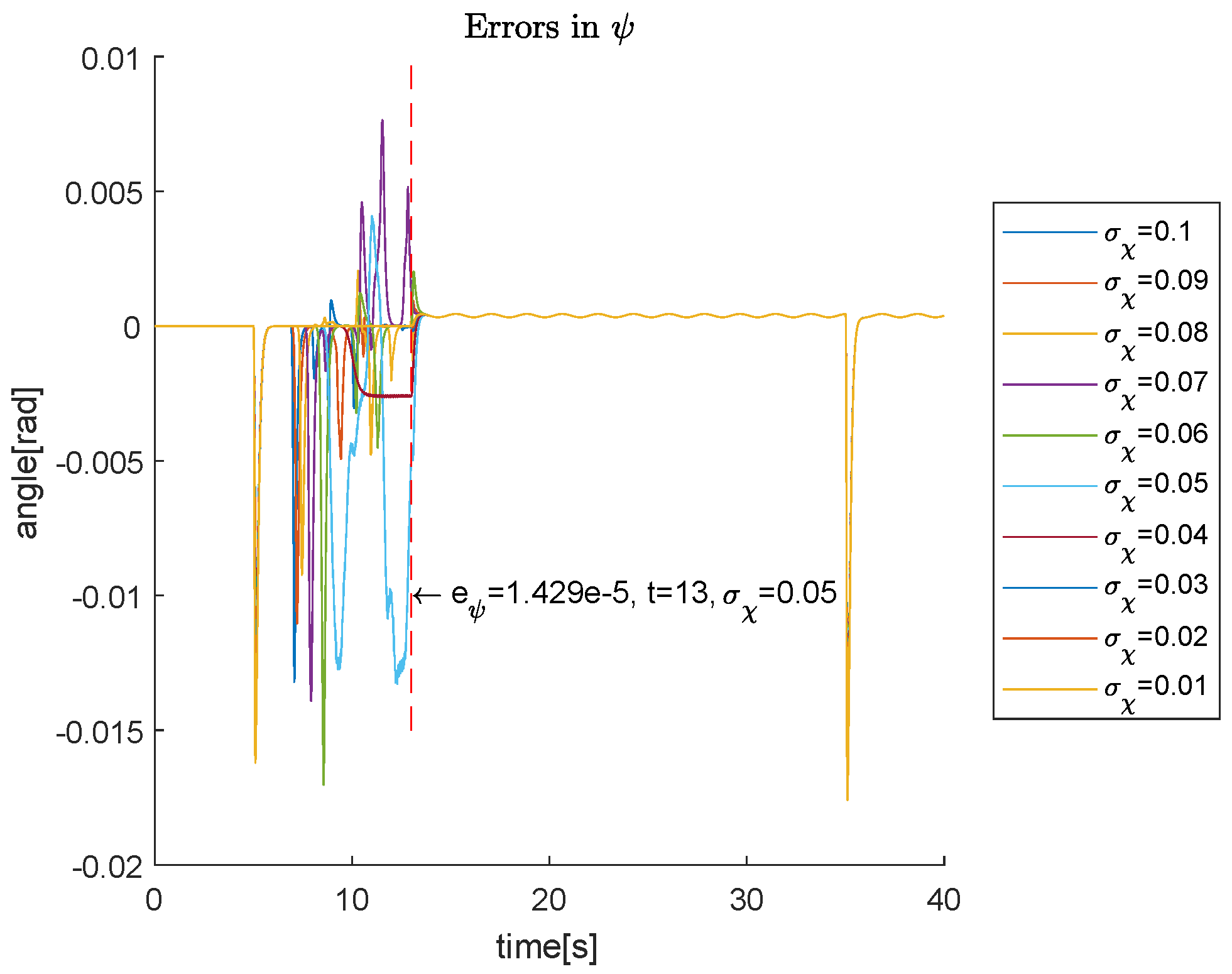
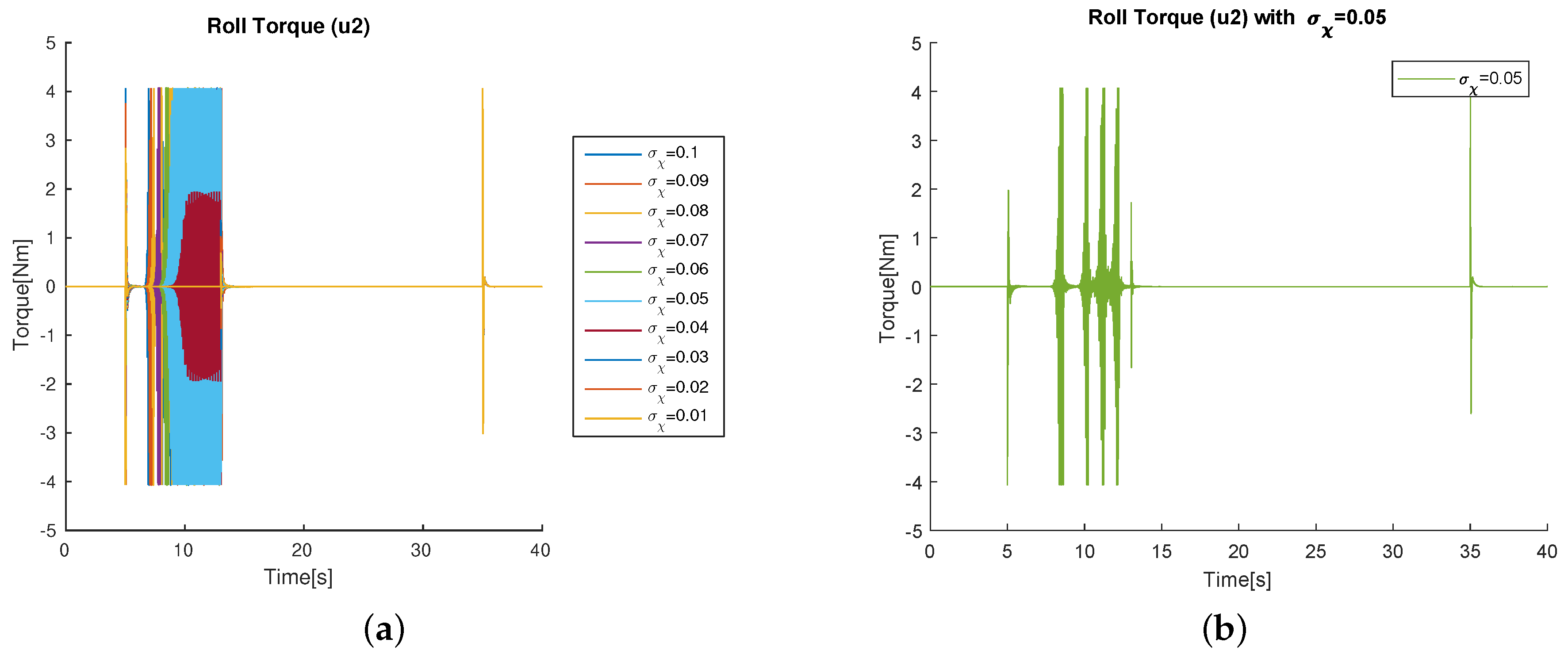
Parameter	Value	Units
Mass m	1.4	kg
Gravity g	9.81	$\frac{m}{s^2}$
Ixx	0.02	kg·m${}^2$
Iyy	0.02	kg·m${}^2$
Izz	0.04	kg·m${}^2$

while the control parameters are given in

Table 2. FOSMC Parameters.

Name	Value
$ϵ$	0.005
${\sigma }_z$	0.055
${\lambda }_z$	6.0
${\mu }_z$	6.0
${\sigma }_y$	0.055
${\lambda }_y$	6.0
${\mu }_y$	6.0
${\sigma }_x$	0.055
${\lambda }_x$	6.0
${\mu }_x$	6.0
$K{d}_{\varphi }$	1.5
$K{p}_{\varphi }$	25
$K{d}_{\theta }$	1.5
$K{p}_{\theta }$	25
$K{d}_{\psi }$	1.3
$K{p}_{\psi }$	9

. The model parameters correspond to a real quadrotor that will be used in real experimentation. The quadrotor has 23 cm of arm longitud; this is the length from the center of the quadrotor to the place where each motor is mounted. The motors used are the Emax MT2213-935KV; each motor can thrust up to 670 grams. An IMU um7 from RedShiftLabs is used and an Optitrack System will be used to locate the quadrotor in the space.

The trajectory of the quadrotor in the space is shown in Figure 2. Nine fractional orders are being plotted (from $\beta$ = 0.1 to 0.9); the colors used in the figures for each value of $\beta$ are listed in

Table 3. Distinct fractional orders $\mathit{\beta }$.

Fractional Order $\mathit{\beta }$	Color
0.1	Blue
0.2	Green
0.3	Red
0.4	Cyan
0.5	Purple
0.6	Yellow
0.7	Brown
0.8	Dark Blue
0.9	Light Green

. Notice that the evolution of the variables with some values of $\beta$ are indistinguishable, and the light green color, corresponding to the fractional order $\beta =0.9$, is predominant.

A projection of the trajectory in the x-y plane is depicted in Figure 3. The desired trajectory is not perfectly tracked, due to the presence of the disturbance, however the deviation error is small (see also Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9), having a better performance with $\beta =0.5$. Besides, by making a zoom into the projection, for a time interval from t = 0 s to t = 40 s, as it is shown in Figure 10, one can notice that the distinct trajectories for the distinct values of fractional order are very close one from another.

The position tracking error in the x, y and z directions, this is $e_x=x-x_d$, $e_y=y-y_d$ and $e_z=z-z_d$ are shown in Figure 4, Figure 5 and Figure 6. In fact, the error raises to almost 2 cm after the introduction of the disturbance at second 13, in the coordinates x and y, and 5 mm in the z direction when $\beta =0.5$. Notice that a significant overshoot and a much greater tracking error is obtained with $\beta =0.9$.

The Euler angle errors are depicted in Figure 7, Figure 8 and Figure 9. One can notice that they are within a 0.6 radians absolute error bound for values of $\beta$ between 0.1 and 0.8; the corresponding Euler angles evolve within a bound of 0.3 radians for $\beta =0.5$, as it is shown in Figure 11. Thus, the small angle approximation is assured through a great part the trajectory, except for take off and landing.

The four control signals are depicted in Figure 12, Figure 13, Figure 14 and Figure 15. It is important to mention that these control signals were limited to the values shown in

Table 4. Limitation of the control signals.

Signal	Maximal Value	Units
Thrust	35	N
Roll Torque	4	Nm
Pitch Torque	4	Nm
Yaw Torque	2	Nm

[32].This values are similar to the ones that correspond to the quadrotor that will be used in the real experiments. Since in a real application the absolute value of those signals are limited due to the actuators (motors).

Besides, the nine control signals, corresponding to the nine fractional orders, are indistinguishable one from the other, but when $\beta =0.1$ there is not chattering at all; higher fractional orders lead to a chattering to be present. This is even more noticeable when the fractional order tends to 1 ($\beta \to 1$). A comparison between the vertical thrust for a fractional order of $\beta =0.5$ and for a fractional order of $\beta =0.9$ is depicted in Figure 16.

4.1. Simulations Varying the Parameters ${\sigma }_{\chi }$

Some simulations were carried out varying the parameters ${\sigma }_z$, ${\sigma }_y$ and ${\sigma }_x$ in the range $[0.1, 0.01]$, and fixing the fractional order to $\beta =0.5$, in order to analyze the behaviour of the quadrotor system when the control parameters are given different values; the parameter ${\sigma }_{\chi }$ was selected since the closed-loop behaviour is more sensitive to changes in ${\sigma }_{\chi }$. From the results obtained (Figure 17, Figure 18 and Figure 19) one can observe that with lower values of ${\sigma }_z$, ${\sigma }_y$ and ${\sigma }_x$, the chattering in the position error signals is reduced.

With respect to Euler Angles, the simulations show some chattering with higher values of ${\sigma }_{\chi }$ while the disturbance does not significantly affect the Euler Angles; the disturbance appears at second 13 and it is kept for the rest of the simulation, the errors in Euler Angles are shown in Figure 20, Figure 21 and Figure 22. It can also be noticed that the control acts in the vicinity of the second 13 where the correction needs to be made.

The control signals are shown in Figure 23, Figure 24, Figure 25 and Figure 26. One can observe that these signals contain chattering for higher values of the ${\sigma }_{\chi }$ values. Thus, low values of ${\sigma }_{\chi }$ have to be used in order to reduce chattering in the control signals.

4.2. Comparison with the IOSMC

In order to compare the performance of the FOSMC design presented here, an IOSMC was implemented for the quadrotor’s simplified model. Using the small angle approximation discussed above this controller is given by Equations (26), (27)–(29) with

$$P_z=\ddot{z_d}-{\lambda }_z\dot{e_z}-{\sigma }_z\frac{d}{dt}sgn\left(s_z\right)-{\mu }_z{s}_z,$$

(52)

$$P_y=\ddot{y_d}-{\lambda }_y\dot{e_y}-{\sigma }_y\frac{d}{dt}sgn\left(s_y\right)-{\mu }_y{s}_y,$$

(53)

$$P_x=\ddot{x_d}-{\lambda }_x\dot{e_x}-{\sigma }_x\frac{d}{dt}sgn\left(s_x\right)-{\mu }_x{s}_x.$$

(54)

where, as before, ${\lambda }_z$, ${\lambda }_y$, ${\lambda }_x$, ${\sigma }_z$, ${\sigma }_y$, ${\sigma }_x$, ${\mu }_z$, ${\mu }_y$ and ${\mu }_x$, are real coefficients chosen in such a way that the corresponding solutions of the first order linear differential equations defined by the sliding surfaces

$$s_z=0=\dot{e_z}+{\lambda }_z{e}_z,$$

(55)

$$s_y=0=\dot{e_y}+{\lambda }_y{e}_y,$$

(56)

$$s_x=0=\dot{e_x}+{\lambda }_x{e}_x.$$

(57)

asymptotically converge to zero. The simulation carried out with this controller corresponds to the one using the FOSMC with the control parameters given in

Table 5. IOSMC Parameters.

Name	Value
$ϵ$	0.005
${\sigma }_z$	0.01
${\lambda }_z$	6.0
${\mu }_z$	6.0
${\sigma }_y$	0.01
${\lambda }_y$	6.0
${\mu }_y$	6.0
${\sigma }_x$	0.01
${\lambda }_x$	6.0
${\mu }_x$	6.0
$K{d}_{\varphi }$	1.5
$K{p}_{\varphi }$	25
$K{d}_{\theta }$	1.5
$K{p}_{\theta }$	25
$K{d}_{\psi }$	1.3
$K{p}_{\psi }$	9

. The tracking position errors and the Euler angles tracking errors are shown in Figure 27 and Figure 28, respectively, while the 3dPlot is depicted in Figure 29. One can notice that the tracking errors have a good performance when the disturbance appears. However, undesirable chattering appears in the control signals in particular with the vertical thrust $u_1$, as it can be seen in Figure 30, Figure 31, Figure 32 and Figure 33.

The errors in Euler Angles seems to have a good performance, again when the disturbance is presented, some deviations appears, see Figure 28.

The MATLAB code generated for the simulations shown in this section are available at the link: https://drive.google.com/drive/folders/1pszDBTfKHeGENOETDpS5Kutq1zGPX1qc?usp=sharing. It should be pointed out that the initial tests which have been carried out with a real quadrotor (the model parameters used in the simulations correspond to this quadrotor) give indications of a behaviour similar to the one shown here. It is expected to have complete experiments in the near future.

5. Conclusions

A fractional order sliding mode control (FOSMC) was proposed for the trajectory tracking control for an integer second order nonlinear system with an unknown perturbation term. A sufficient condition was given to assure the attraction of the sliding surface where trajectory tracking is achieved. The sufficient condition found allows to adjust two parameters (${\sigma }_{\chi }$ and ${\mu }_{\chi }$) of the FOSMC in order to assure the attraction to the sliding surface proposed. Besides, an application of the methodology to the trajectory tracking of a quadrotor dynamical model is given. Simulation results were obtained for a given trajectory, including take-off and landing. These results were also compared with an IOSMC showing that chattering can be diminished in some of the control signals, when using FOSMC, and in the presence of additive perturbations. The results obtained are promising and further research is being carried out together with experimentation with a real quadrotor.