Local Community Detection Based on Small Cliques
Abstract
:1. Introduction
1.1. Related Work
1.2. Preliminaries
2. Density-Based Local Community Detection Algorithms
2.1. GCE M/L
Implementation Details
2.2. Two-Phase L
- and
- and
- and
Implementation Details
2.3. LFM
Implementation Details
2.4. PageRank-Nibble
3. Local Community Detection Algorithms Based on Small Cliques
3.1. LTE
Implementation Details
3.2. Local T
Implementation Details
3.3. Clique Based Community Expansion
Implementation Details
3.4. Triangle Based Community Expansion
| Algorithm 1: Triangle Based Community Expansion (TCE) detects a community around a given node. Uses a node scoring function based on triangles to add nodes to the community. |
 |
Implementation Details
4. Experiments
4.1. Experimental Setup
4.2. Scoring
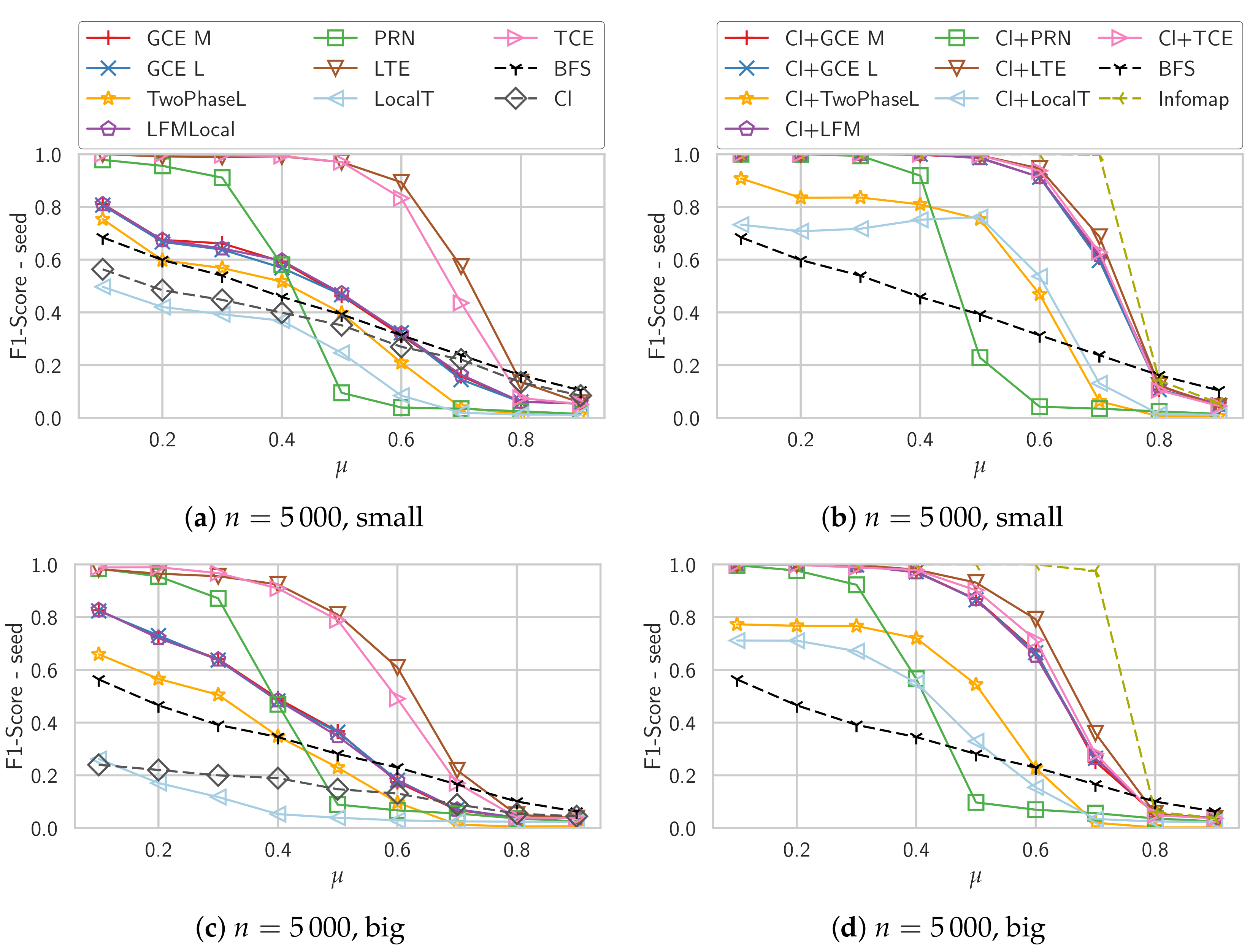
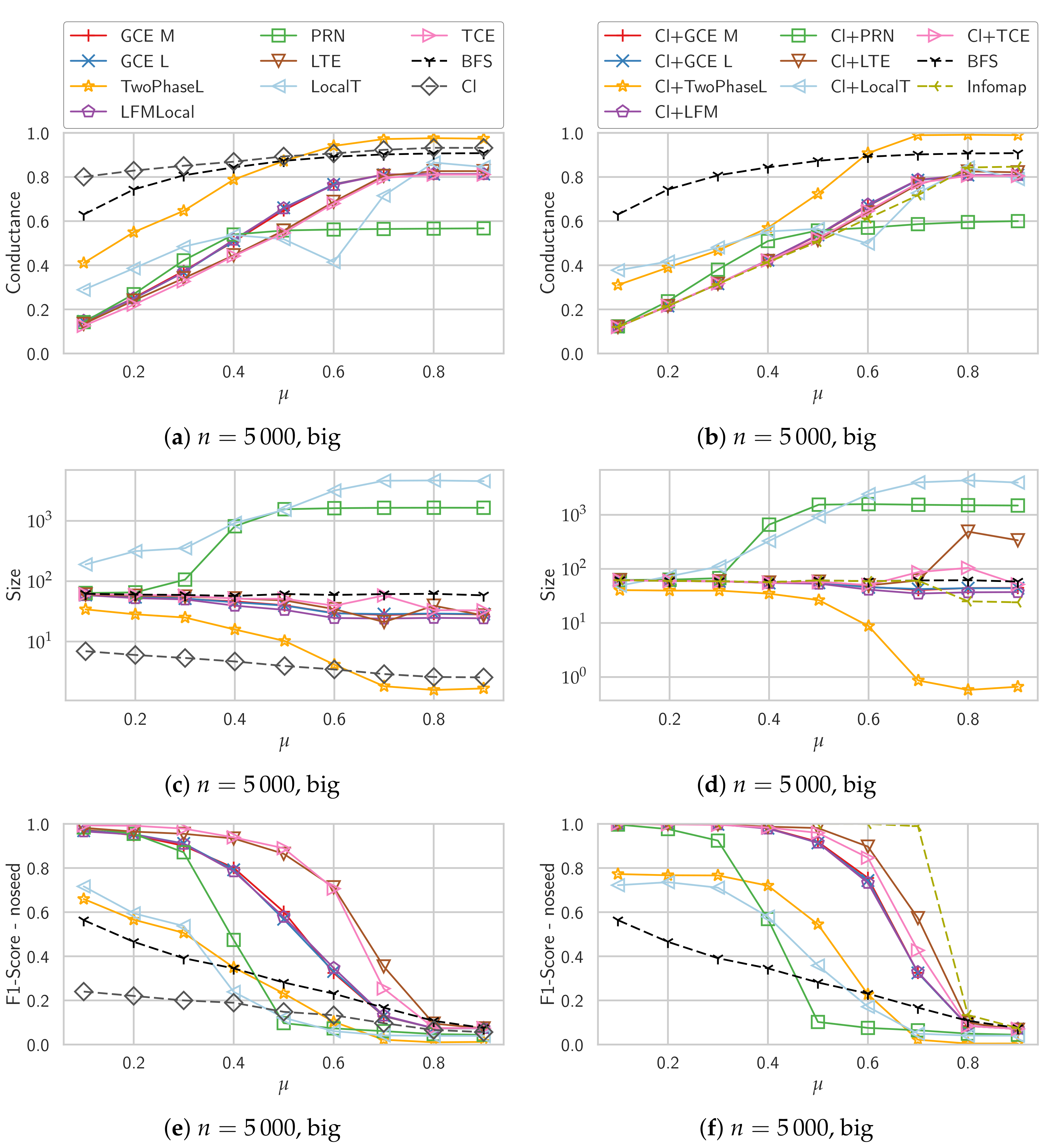
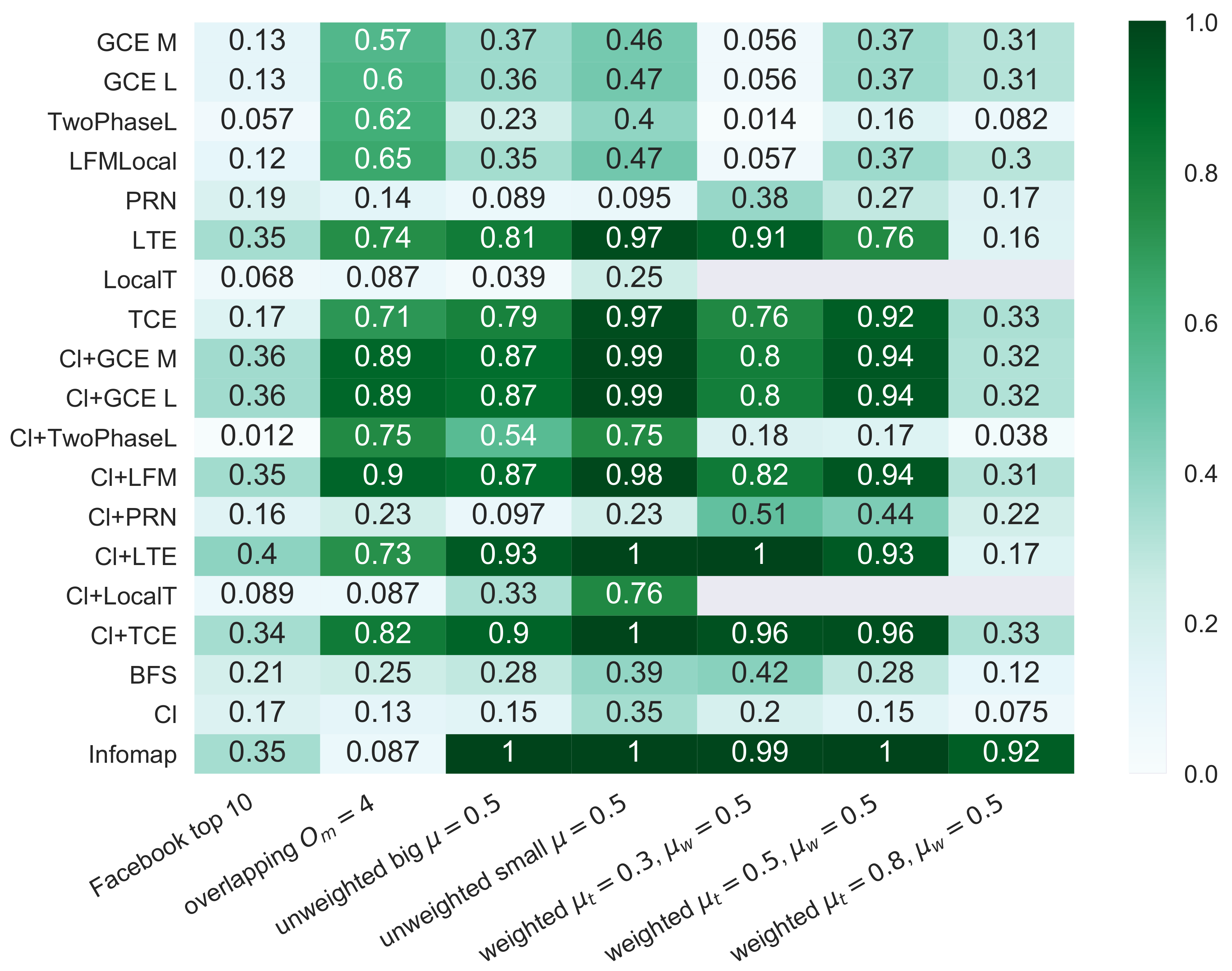
4.3. Synthetic Graphs
Unweighted Graphs
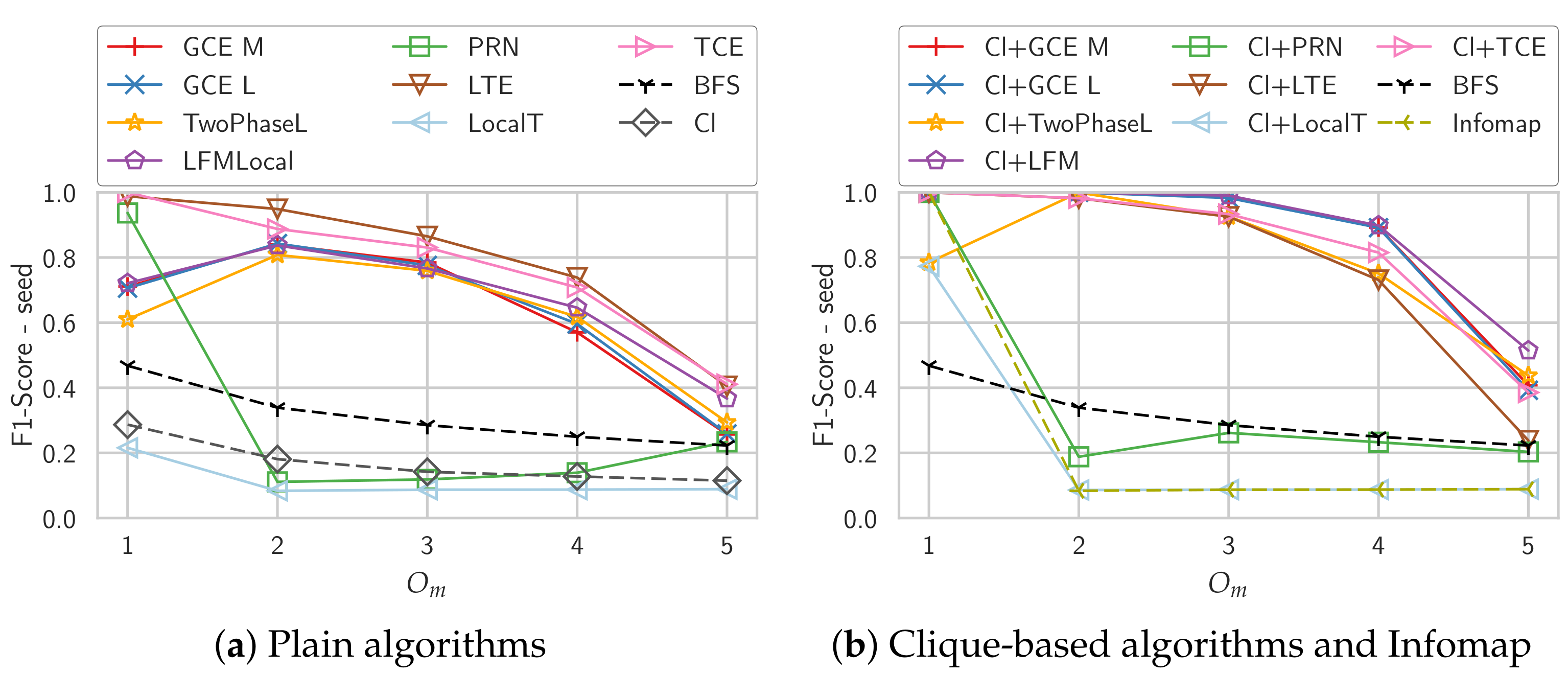
4.4. Overlapping Communities
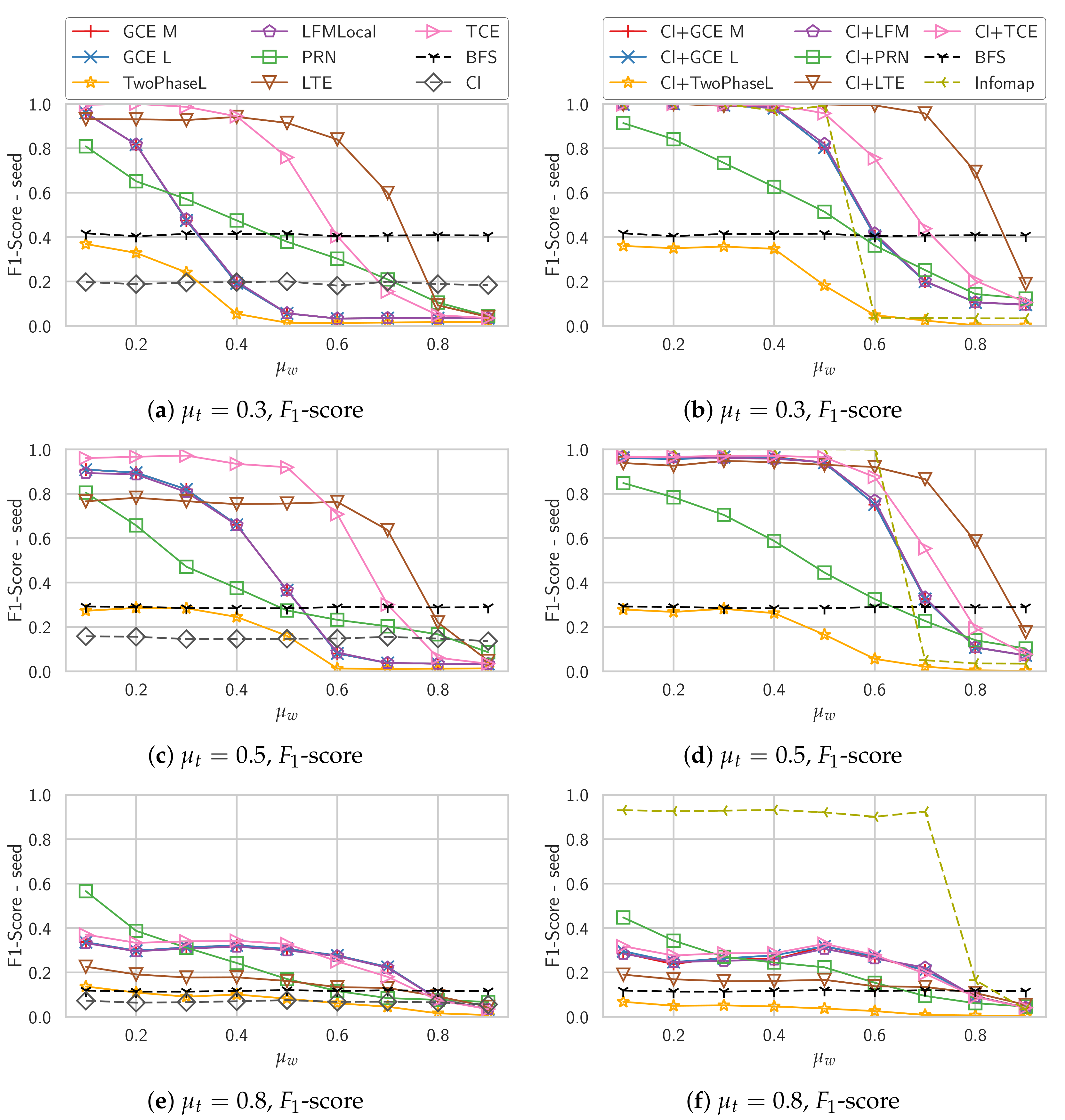
Weighted Graphs
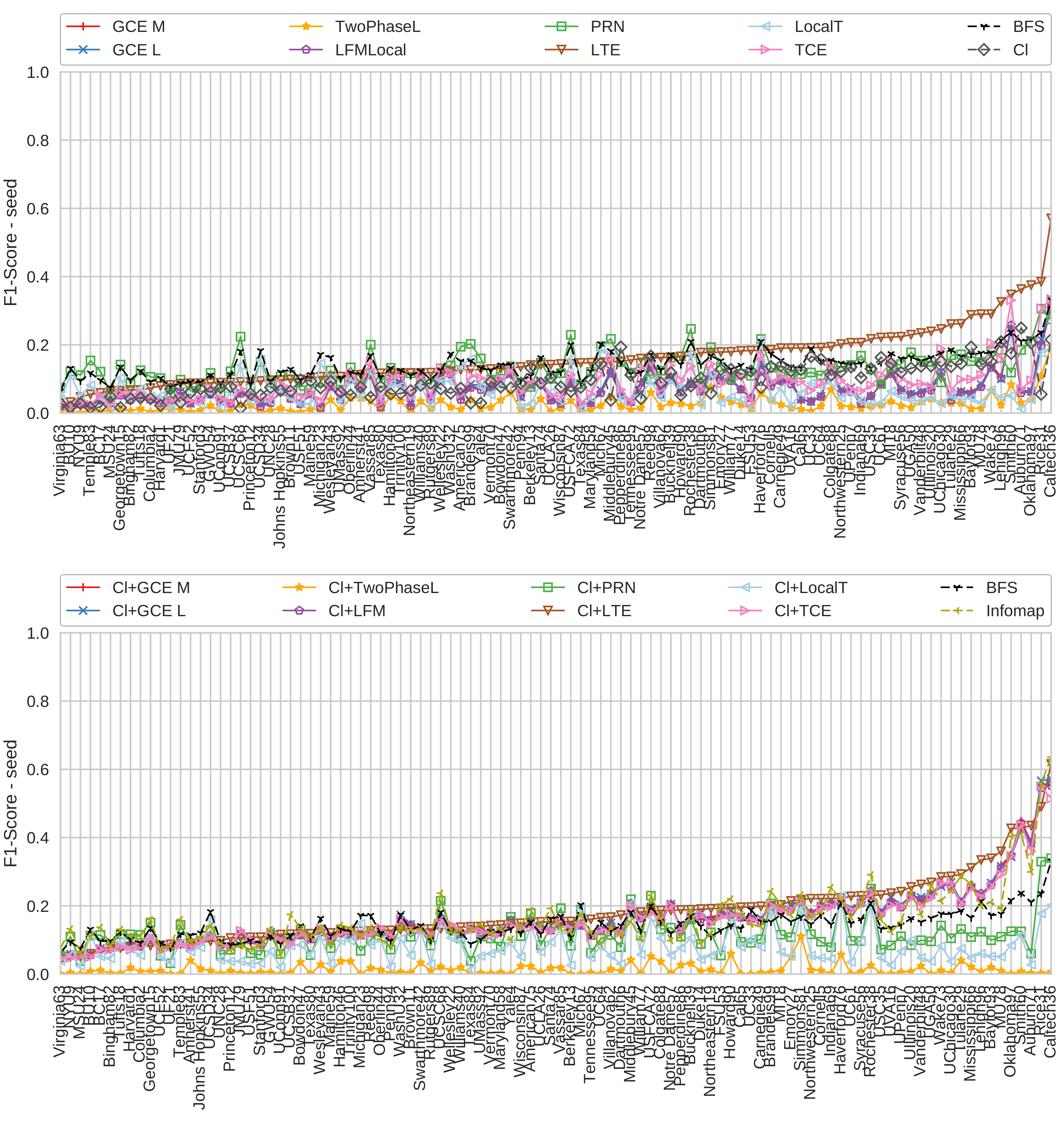
4.5. Facebook Graphs
4.6. Running Times
4.7. Summary
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fortunato, S. Community detection in graphs. Phys. Rep. 2010, 486, 75–174. [Google Scholar] [CrossRef]
- Fortunato, S.; Hric, D. Community detection in networks: A user guide. Phys. Rep. 2016, 659, 1–44. [Google Scholar] [CrossRef]
- Schaeffer, S.E. Graph clustering. Comput. Sci. Rev. 2007, 1, 27–64. [Google Scholar] [CrossRef]
- Staudt, C.; Marrakchi, Y.; Meyerhenke, H. Detecting communities around seed nodes in complex networks. In Proceedings of the IEEE International Conference on Big Data, Washington, DC, USA, 27–30 October 2014; pp. 62–69. [Google Scholar]
- Lancichinetti, A.; Fortunato, S.; Kertész, J. Detecting the overlapping and hierarchical community structure of complex networks. New J. Phys. 2009, 11. [Google Scholar] [CrossRef]
- Lancichinetti, A.; Radicchi, F.; Ramasco, J.J.; Fortunato, S. Finding Statistically Significant Communities in Networks. PLoS ONE 2011, 6, 1–18. [Google Scholar] [CrossRef] [PubMed]
- McDaid, A.; Hurley, N. Using Model-based Overlapping Seed Expansion to detect highly overlapping community structure. arXiv 2010, arXiv:1011.1970. [Google Scholar]
- Lee, C.; Reid, F.; McDaid, A.; Hurley, N. Detecting highly overlapping community structure by greedy clique expansion. arXiv 2010, arXiv:1002.1827. [Google Scholar]
- Fanrong, M.; Mu, Z.; Yong, Z.; Ranran, Z. Local Community Detection in Complex Networks Based on Maximum Cliques Extension. Mathe. Probl. Eng. 2014, 2014, 653670. [Google Scholar] [CrossRef]
- Radicchi, F.; Castellano, C.; Cecconi, F.; Loreto, V.; Parisi, D. Defining and identifying communities in networks. Proc. Natl. Acad. Sci. USA 2004, 101, 2658–2663. [Google Scholar] [CrossRef] [PubMed]
- Lancichinetti, A.; Fortunato, S. Community detection algorithms: A comparative analysis. Phys. Rev. E 2009, 80, 056117. [Google Scholar] [CrossRef] [PubMed]
- Lancichinetti, A.; Fortunato, S. Benchmarks for testing community detection algorithms on directed and weighted graphs with overlapping communities. Phys. Rev. E 2009, 80, 016118. [Google Scholar] [CrossRef] [PubMed]
- Staudt, C.; Sazonovs, A.; Meyerhenke, H. NetworKit: A tool suite for large-scale complex network analysis. Netw. Sci. 2016, 4, 508–530. [Google Scholar] [CrossRef]
- Hamann, M.; Röhrs, E.; Wagner, D. Local Community Detection Based on Small Cliques: Implementation and Evaluation Scripts. GitHub 2017. Available online: https://github.com/kit-algo/LCD-cliques-experiments (accessed on 10 August 2017).
- Huang, J.; Sun, H.; Liu, Y.; Song, Q.; Weninger, T. Towards Online Multiresolution Community Detection in Large-Scale Networks. PLoS ONE 2011, 6, e23829. [Google Scholar] [CrossRef] [PubMed]
- Clauset, A. Finding local community structure in networks. Phys. Rev. E 2005, 72, 026132. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Zaïane, O.R.; Goebel, R. Local Community Identification in Social Networks. In Proceedings of the 2009 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining, Athens, Greece, 20–22 July 2009; pp. 237–242. [Google Scholar]
- Bagrow, J.P. Evaluating local community methods in networks. J. Stat. Mech. Theory Exp. 2008, 2008, P05001. [Google Scholar] [CrossRef]
- Fagnan, J.; Zaiane, O.; Barbosa, D. Using triads to identify local community structure in social networks. In Proceedings of the 2014 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM), Beijing, China, 17–20 August 2014; pp. 108–112. [Google Scholar]
- Ngonmang, B.; Tchuente, M.; Viennet, E. Local Community Identification in Social Networks. Parallel Process. Lett. 2012, 22, 1240004. [Google Scholar] [CrossRef]
- Ma, L.; Huang, H.; He, Q.; Chiew, K.; Liu, Z. Toward seed-insensitive solutions to local community detection. J. Intell. Inf. Syst. 2014, 43, 183–203. [Google Scholar] [CrossRef]
- Andersen, R.; Chung, F.; Lang, K. Local Graph Partitioning using PageRank Vectors. In Proceedings of the 47th Annual IEEE Symposium on Foundations of Computer Science (FOCS’06), Berkeley, CA, USA, 21–24 October 2006; pp. 475–486. [Google Scholar]
- Panagiotakis, C.; Papadakis, H.; Fragopoulou, P. Local Community Detection via Flow Propagation. In Proceedings of the 2015 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining, Paris, France, 25–28 August 2015; pp. 81–88. [Google Scholar]
- Li, Y.; He, K.; Bindel, D.; Hopcroft, J.E. Uncovering the small community structure in large networks: A local spectral approach. In Proceedings of the 24th International Conference on World Wide Web, Florence, Italy, 18–22 May 2015; pp. 658–668. [Google Scholar]
- Danisch, M.; Guillaume, J.L.; Grand, B.L. Towards multi-ego-centred communities: A node similarity approach. Int. J. Web Based Communities 2013, 9, 299–322. [Google Scholar] [CrossRef]
- Jia, S.; Gao, L.; Gao, Y.; Wang, H. Anti-triangle centrality-based community detection in complex networks. Syst. Biol. IET 2014, 8, 116–125. [Google Scholar] [CrossRef] [PubMed]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Easley, D.; Kleinberg, J. Networks, Crowds, and Markets: Reasoning about a Highly Connected World; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Luo, F.; Wang, J.Z.; Promislow, E. Exploring local community structures in large networks. Web Intell. Agent Syst. An Int. J. 2008, 6, 387–400. [Google Scholar]
- Yang, J.; Leskovec, J. Defining and evaluating network communities based on ground-truth. Knowl. Inf. Syst. 2015, 42, 181–213. [Google Scholar] [CrossRef]
- Lin, M.C.; Soulignac, F.J.; Szwarcfiter, J.L. Arboricity, h-index, and dynamic algorithms. Theor. Comput. Sci. 2012, 426, 75–90. [Google Scholar] [CrossRef]
- Eppstein, D.; Löffler, M.; Strash, D. Listing All Maximal Cliques in Large Sparse Real-World Graphs. ACM J. Exp. Algorithm. 2013, 18. [Google Scholar] [CrossRef]
- Eppstein, D.; Löffler, M.; Strash, D. Listing All Maximal Cliques in Sparse Graphs in Near-Optimal Time. In International Symposium on Algorithms and Computation; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; pp. 403–414. [Google Scholar]
- Traud, A.L.; Mucha, P.J.; Porter, M.A. Social Structure of Facebook Networks. arXiv 2011, arXiv:1102.2166. [Google Scholar]
- Rosvall, M.; Axelsson, D.; Bergstrom, C.T. The map equation. Eur. Phys. J. Spec. Top. 2009, 178, 13–23. [Google Scholar] [CrossRef]
- Yang, J.; Leskovec, J. Structure and overlaps of ground-truth communities in networks. ACM Trans. Intell. Syst. Technol. 2014, 5, 26. [Google Scholar] [CrossRef]
- Lee, C.; Cunningham, P. Benchmarking community detection methods on social media data. arXiv 1302. [Google Scholar]
- Zakrzewska, A.; Bader, D.A. A Dynamic Algorithm for Local Community Detection in Graphs. In Proceedings of the 2015 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining, Paris, France, 25–28 August 2015; pp. 559–564. [Google Scholar]
- Eppstein, D.; Spiro, E.S. The h-Index of a Graph and Its Application to Dynamic Subgraph Statistics. In Proceedings of the WADS’09 11th International Symposium on Algorithms and Data Structures, Banff, AB, Canada, 21–23 August 2009; Lecture Notes in Computer Science. Dehne, F., Gavrilova, M., Sack, J.R., Tóth, C.D., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5664, pp. 278–289. [Google Scholar]
| Name | Description | Unweighted | Overlapping | Weighted |
|---|---|---|---|---|
| n | number of nodes | 5000 | 2000 | 5000 |
| k | average degree | 20 | 39.5, 61.5, 78.1, 91.8, 103.5 | 20 |
| maximum degree | 50 | 120 | 50 | |
| degree exponent | ||||
| minimum community size | 10, 20 | 60 | 20 | |
| maximum community size | 50, 100 | 120 | 100 | |
| community size exponent | ||||
| topological mixing | 0.1, …, 0.9 | 0.2 | 0.3, 0.5, 0.8 | |
| weight exponent | ||||
| weight mixing | 0.1, …, 0.9 | |||
| communities per node | 1 | 1, ..., 5 | 1 |
| (a) On the Overlapping LFR Benchmark. | (b) On the 100 Facebook Networks. | ||||
|---|---|---|---|---|---|
| Size | Time (ms) | Size | Time (ms) | ||
| Cl | 7 | 0.4 | TwoPhaseL | 38 | 1.7 |
| Cl+PRN | 419 | 2.1 | PRN | 975 | 4.2 |
| PRN | 605 | 2.9 | GCE M | 282 | 5.9 |
| Cl+GCE M | 321 | 3.5 | GCE L | 270 | 6.7 |
| GCE M | 405 | 3.7 | LFMLocal | 221 | 9.8 |
| Cl+GCE L | 333 | 4.0 | TCE | 321 | 11.4 |
| GCE L | 411 | 4.4 | Cl | 14 | 13.0 |
| LFMLocal | 249 | 4.8 | Cl+TwoPhaseL | 52 | 17.5 |
| Cl+LFM | 242 | 5.1 | Cl+PRN | 1086 | 18.5 |
| Cl+TwoPhaseL | 243 | 5.3 | Cl+GCE M | 1009 | 45.1 |
| TwoPhaseL | 329 | 6.8 | Cl+TCE | 930 | 46.5 |
| TCE | 320 | 10.2 | Cl+GCE L | 919 | 48.0 |
| Cl+TCE | 320 | 10.5 | Cl+LFM | 907 | 77.4 |
| LTE | 294 | 26.4 | LTE | 257 | 107.5 |
| Cl+LTE | 436 | 28.8 | Cl+LTE | 407 | 150.5 |
| LocalT | 1618 | 49.7 | LocalT | 8066 | 1028.1 |
| Cl+LocalT | 1589 | 49.7 | Cl+LocalT | 8207 | 1054.7 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamann, M.; Röhrs, E.; Wagner, D. Local Community Detection Based on Small Cliques. Algorithms 2017, 10, 90. https://doi.org/10.3390/a10030090
Hamann M, Röhrs E, Wagner D. Local Community Detection Based on Small Cliques. Algorithms. 2017; 10(3):90. https://doi.org/10.3390/a10030090
Chicago/Turabian StyleHamann, Michael, Eike Röhrs, and Dorothea Wagner. 2017. "Local Community Detection Based on Small Cliques" Algorithms 10, no. 3: 90. https://doi.org/10.3390/a10030090
APA StyleHamann, M., Röhrs, E., & Wagner, D. (2017). Local Community Detection Based on Small Cliques. Algorithms, 10(3), 90. https://doi.org/10.3390/a10030090




