Transformation-Based Fuzzy Rule Interpolation Using Interval Type-2 Fuzzy Sets
Abstract
1. Introduction
2. Background
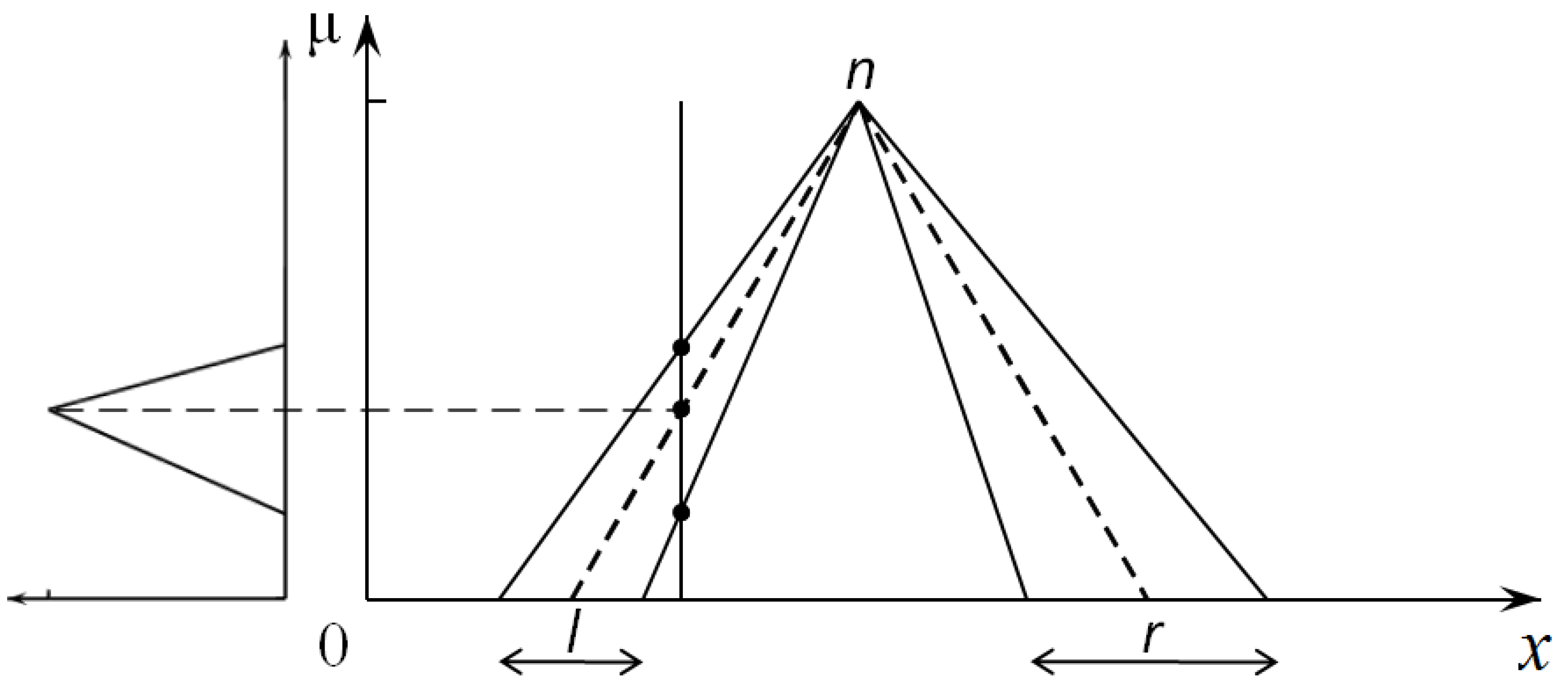
2.1. Scale and Move Transformation-Based Interpolation
2.1.1. N Closest Rules Selection
2.1.2. Intermediate Rule Construction
2.1.3. Scale Transformation
2.1.4. Move Transformation
2.2. Type-2 Fuzzy Sets
3. Proposed Interval Type-2 Transformation-Based Interpolation
- Calculate representative values:The lower and upper representative values and of a given interval type-2 fuzzy set are calculated first using Equation (19). The shape diversity factors and weight factors are computed according to Equations (20) and (21), respectively. The overall Rep is then obtained by Equation (22), . The calculations for all of the antecedent variables of all rules and their counterparts in the observation follow the same procedure.
- Choose closest N rules:
- Construct intermediate ruleThe normalised weight of the j-th antecedent of the i-th chosen rule, which is calculated by Equation (4), together with the parameter , which is calculated by Equation (6), are used in Equation (5) to obtain the value of each antecedent variable within the intermediate rule , , . From this, two parameters and are computed using Equation (8) and are then used to construct from Equation (7), resulting in the intermediate rule .
- Perform scale, move and height transformations:In conjunction with the given for each antecedent variable , the rates , and , , can then be calculated using Equations (9), (11) and (23). Due to the extra uncertainty encountered in the membership functions, a further transformation on the height of the LMF is needed (because the LMFs of different interval type-2 fuzzy sets may have different heights), while the height of the UMF remains the same owing to its normality. This additional transformation is introduced to transform the heights of to those of , with the height rate h being calculated by:where and , as defined previously. This constraint applies to the interpolated conclusion, as well. That is, if the height of is greater than the height of after the height transformation, then .
- Derive interpolated conclusion:The second intermediate term and the interpolated result can then be estimated by the combined , and , . Here, and are computed following Equations (9)–(13), respectively, and is computed according to Equation (23) such that:
- Implement modified procedure:To obtain intuitive interpolated conclusions for interval type-2 fuzzy sets, the relative location between the LA and UA of an interval type-2 fuzzy set should be considered [39]. For this purpose, is modified into to maintain the relative location both before and after the scale transformation. Here, a relative location factor is defined by:where and denote the “new” terms, which are modified from the given and , respectively, using the same . The combined and of are then computed as the mean of the corresponding two terms, such that:Similarly, the final interpolated conclusion can also be modified from to using the same to maintain the relative location both before and after the move transformation.
4. Experimentation and Discussion
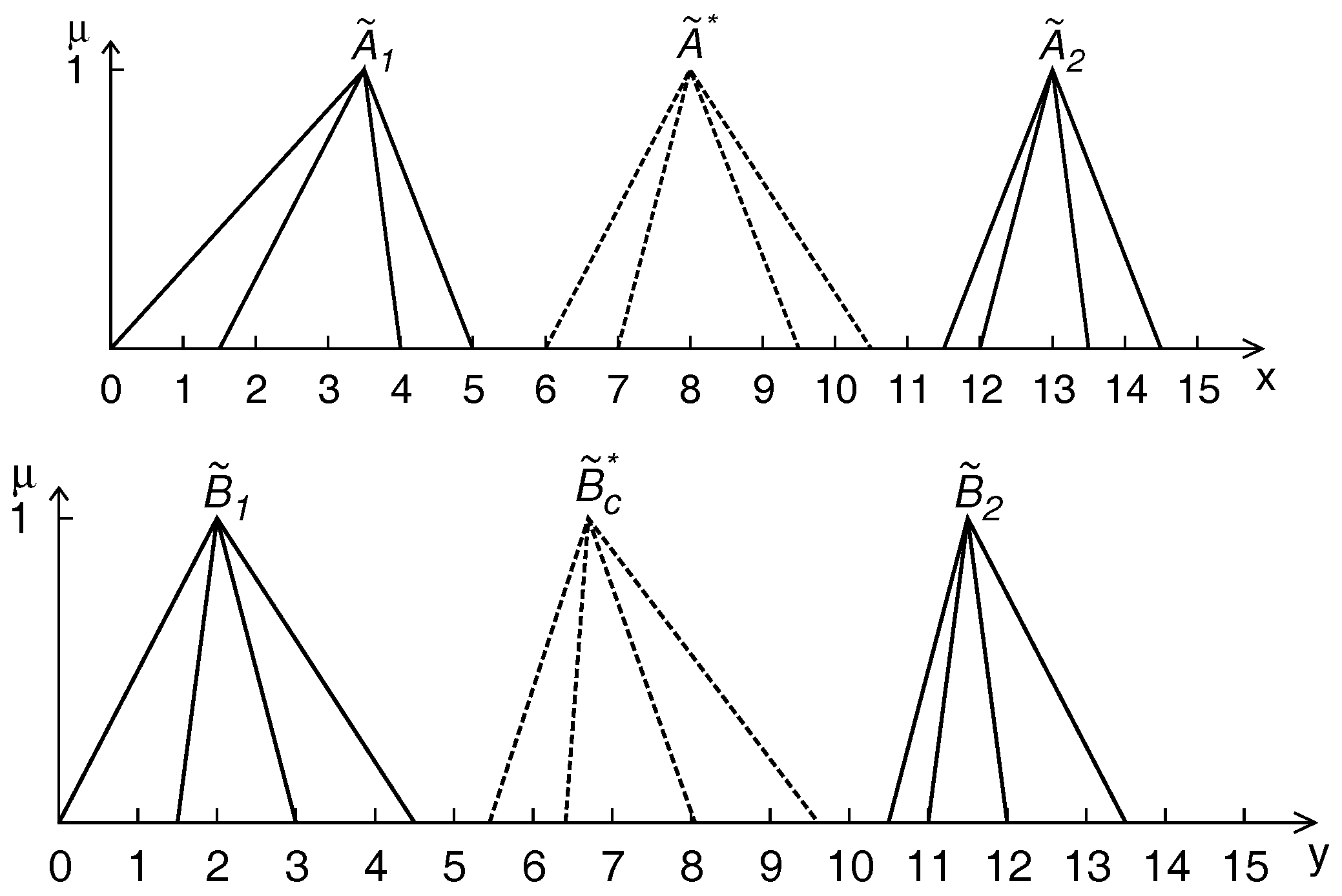
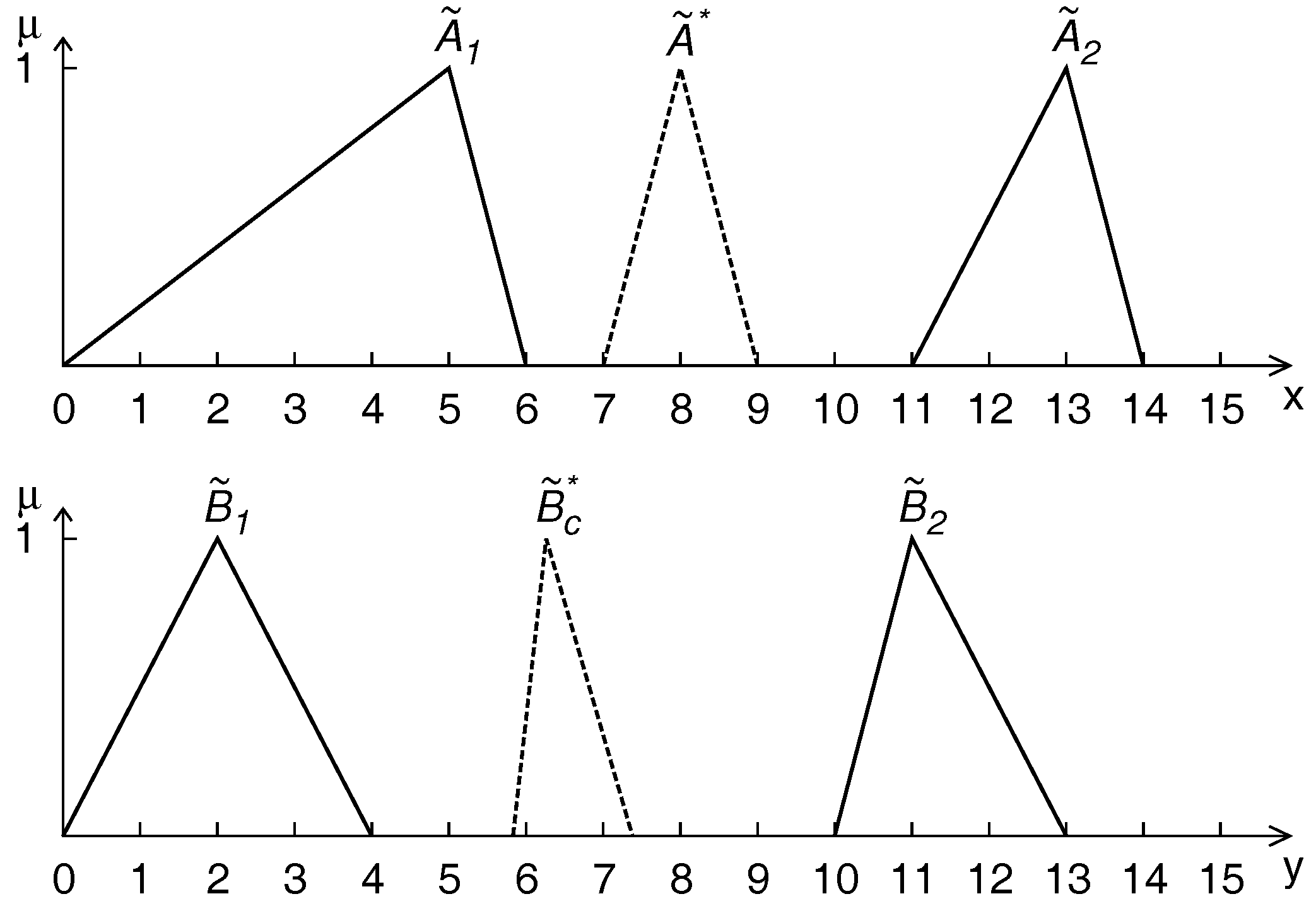
4.1. Case 1
4.2. Case 2
4.3. Case 3
4.4. Case 4
5. Type-2 Fuzzy Sets vs. Rough-Fuzzy Sets for T-FRI
5.1. Conceptual Comparison
5.2. Practical Application and Comparison
5.2.1. Application Problem
5.2.2. Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| FOU | Footprint of uncertainty |
| FRI | Fuzzy rule interpolation |
| LA | Lower approximation |
| LMF | Lower membership function |
| T-FRI | Scale and move transformation-based fuzzy rule interpolation approach |
| UA | Upper approximation |
| UMF | Upper membership function |
References
- Zadeh, L.A. Outline of a new approach to the analysis of complex systems and decision processes. IEEE Trans. Syst. Man Cybern. 1973, 3, 28–44. [Google Scholar] [CrossRef]
- Wong, K.; Tikk, D.; Gedeon, T.; Kóczy, L. Fuzzy rule interpolation for multidimensional input spaces with applications: A case study. IEEE Trans. Fuzzy Syst. 2005, 13, 809–819. [Google Scholar] [CrossRef]
- Kóczy, L.; Hirota, K. Approximate reasoning by linear rule interpolation and general approximation. Int. J. Approx. Reason. 1993, 9, 197–225. [Google Scholar] [CrossRef]
- Kóczy, L.; Hirota, K. Interpolative reasoning with insufficient evidence in sparse fuzzy rule bases. Inf. Sci. 1993, 71, 169–201. [Google Scholar] [CrossRef]
- Yan, S.; Mizumoto, M.; Qiao, W. Reasoning conditions on Kóczy’s interpolative reasoning method in sparse fuzzy rule bases. Fuzzy Sets Syst. 1995, 75, 63–71. [Google Scholar] [CrossRef]
- Baranyi, P.; Kóczy, L.; Gedeon, T. A generalized concept for fuzzy rule interpolation. IEEE Trans. Fuzzy Syst. 2004, 12, 820–837. [Google Scholar] [CrossRef]
- Chang, Y.; Chen, S.; Liau, C. Fuzzy interpolative reasoning for sparse fuzzy-rule-based systems based on the areas of fuzzy sets. IEEE Trans. Fuzzy Syst. 2008, 16, 1285–1301. [Google Scholar] [CrossRef]
- Chen, S.; Ko, Y. Fuzzy interpolative reasoning for sparse fuzzy rule-based systems based on α-cuts and transformations techniques. IEEE Trans. Fuzzy Syst. 2008, 16, 1626–1648. [Google Scholar] [CrossRef]
- Tikk, D.; Baranyi, P. Comprehensive analysis of a new fuzzy rule interpolation method. IEEE Trans. Fuzzy Syst. 2000, 8, 281–296. [Google Scholar] [CrossRef]
- Huang, Z.; Shen, Q. Fuzzy interpolative reasoning via scale and move transformations. IEEE Trans. Fuzzy Syst. 2006, 14, 340–359. [Google Scholar] [CrossRef]
- Huang, Z.; Shen, Q. Fuzzy interpolation and extrapolation: A practical approach. IEEE Trans. Fuzzy Syst. 2008, 16, 13–28. [Google Scholar] [CrossRef]
- Shen, Q.; Yang, L. Generalisation of scale and move transformation-based fuzzy interpolation. Adv. Comput. Intell. Intell. Inform. 2011, 15, 288–298. [Google Scholar] [CrossRef]
- Jin, S.; Diao, R.; Quek, C.; Shen, Q. Backward fuzzy rule interpolation. IEEE Trans. Fuzzy Syst. 2014, 22, 1682–1698. [Google Scholar] [CrossRef]
- Naik, N.; Diao, R.; Shen, Q. Dynamic fuzzy rule interpolation and its application to intrusion detection. In Proceedings of the 2016 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Vancouver, BC, Canada, 24–29 July 2017. [Google Scholar]
- Yang, L.; Shen, Q. Adaptive fuzzy interpolation. IEEE Trans. Fuzzy Syst. 2011, 19, 1107–1126. [Google Scholar] [CrossRef]
- Yang, L.; Chao, F.; Shen, Q. Generalised adaptive fuzzy rule interpolation. IEEE Trans. Fuzzy Syst. 2017, 25, 4. [Google Scholar] [CrossRef]
- Cheng, S.H.; Chen, S.M.; Chen, C.L. Adaptive fuzzy interpolation based on ranking values of polygonal fuzzy sets and similarity measures between polygonal fuzzy sets. Inf. Sci. 2016, 342, 176–190. [Google Scholar] [CrossRef]
- Chen, S.M.; Adam, S.I. Adaptive fuzzy interpolation based on general representative values of polygonal fuzzy sets and the shift and modification techniques. Inf. Sci. 2017, 414, 147–157. [Google Scholar] [CrossRef]
- Perfilieva, I. Closeness in similarity-based reasoning with an interpolation condition. Fuzzy Sets Syst. 2016, 292, 333–346. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Fu, X.; Shen, Q. Fuzzy compositional modeling. IEEE Trans. Fuzzy Syst. 2010, 18, 823–840. [Google Scholar]
- Mendel, J. Type-2 fuzzy sets: Some questions and answers. IEEE Connect. Newsl. IEEE Neural Netw. Soc. 2003, 1, 10–13. [Google Scholar]
- Chen, C.; Parthaláin, N.M.; Li, Y.; Price, C.; Quek, C.; Shen, Q. Rough-fuzzy rule interpolation. Inf. Sci. 2016, 351, 1–17. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning–I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Liang, Q.; Mendel, J. Interval type-2 fuzzy logic systems: Theory and design. IEEE Trans. Fuzzy Syst. 2000, 8, 535–550. [Google Scholar] [CrossRef]
- Wu, D. On the Fundamental Differences Between Interval Type-2 and Type-1 Fuzzy Logic Controllers. IEEE Trans. Fuzzy Syst. 2012, 20, 832–848. [Google Scholar] [CrossRef]
- Karnik, N.; Mendel, J.; Liang, Q. Type-2 fuzzy logic systems. IEEE Trans. Fuzzy Syst. 1999, 7, 643–658. [Google Scholar] [CrossRef]
- Bustince, H. Indicator of inclusion grade for interval-valued fuzzy sets. Application to approximate reasoning based on interval-valued fuzzy sets. Int. J. Approx. Reason. 2000, 23, 137–209. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Interval-valued fuzzy sets, possibility theory and imprecise probability. In Proceedings of the International Conference in Fuzzy Logic and Technology, Barcelona, Spain, 7–9 September 2005. [Google Scholar]
- Yang, Y.; Hinde, C. A new extension of fuzzy sets using rough sets: R-fuzzy sets. Inf. Sci. 2010, 180, 354–365. [Google Scholar] [CrossRef]
- Fu, X.; Shen, Q. Fuzzy complex numbers and their application for classifiers performance evaluation. Pat. Recognit. 2011, 44, 1403–1417. [Google Scholar] [CrossRef]
- Mendel, J.; John, R.; Liu, F. Interval type-2 fuzzy logic systems made simple. IEEE Trans. Fuzzy Syst. 2006, 14, 808–821. [Google Scholar] [CrossRef]
- Wu, D. Approaches for Reducing the Computational Cost of Interval Type-2 Fuzzy Logic Systems: Overview and Comparisons. IEEE Trans. Fuzzy Syst. 2013, 21, 80–99. [Google Scholar] [CrossRef]
- Mendel, J.M.; Liu, X. Simplified Interval Type-2 Fuzzy Logic Systems. IEEE Trans. Fuzzy Syst. 2013, 21, 1056–1069. [Google Scholar] [CrossRef]
- Mendel, J. Type-2 fuzzy sets and systems: An overview. Comput. Intell. Mag. 2007, 2, 20–29. [Google Scholar] [CrossRef]
- Chen, S.M.; Chang, Y.C.; Pan, J.S. Fuzzy Rules Interpolation for Sparse Fuzzy Rule-Based Systems Based on Interval Type-2 Gaussian Fuzzy Sets and Genetic Algorithms. IEEE Trans. Fuzzy Syst. 2013, 21, 412–425. [Google Scholar] [CrossRef]
- Chen, S.M.; Chen, Z.J. Weighted fuzzy interpolative reasoning for sparse fuzzy rule-based systems based on piecewise fuzzy entropies of fuzzy sets. Inf. Sci. 2016, 329, 503–523. [Google Scholar] [CrossRef]
- Chen, S.M.; Lee, L.W.; Shen, V.R. Weighted fuzzy interpolative reasoning systems based on interval type-2 fuzzy sets. Inf. Sci. 2013, 248, 15–30. [Google Scholar] [CrossRef]
- Chen, C.; Quek, C.; Shen, Q. Scale and move transformation-based fuzzy rule interpolation with interval type-2 fuzzy sets. In Proceedings of the IEEE International Conference on Fuzzy Systems, Hyderabad, India, 7–10 July 2013; pp. 1–8. [Google Scholar]
- Mendel, J.; John, R. Type-2 fuzzy sets made simple. IEEE Trans. Fuzzy Syst. 2002, 10, 117–127. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough sets. Int. J. Comput. Inf. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Pawlak, Z.; Grzymala-Busse, J.; Slowinski, R.; Ziarko, W. Rough sets. Commun. ACM 1995, 38, 88–95. [Google Scholar] [CrossRef]
- Colwell, R.R.; Epstein, P.R.; Gubler, D.; Maynard, N.; McMichael, A.J.; Patz, J.A.; Sack, R.B.; Shope, R. Climate and Human Health. Science 1998, 279, 968–969. [Google Scholar] [CrossRef] [PubMed]
- Morse, S.S. Factors in the emergence of infectious diseases. Emerg. Infect. Dis. 1995, 1, 7–15. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Shen, Q. Closed form fuzzy interpolation. Fuzzy Sets Syst. 2013, 225, 1–22. [Google Scholar] [CrossRef]
- Eisenberg, J.N.; Cevallos, W.; Ponce, K.; Levy, K.; Bates, S.J.; Scott, J.C.; Hubbard, A.; Vieira, N.; Endara, P.; Espinel, M.; et al. Environmental change and infectious disease: How new roads affect the transmission of diarrheal pathogens in rural Ecuador. Proc. Natl. Acad. Sci. USA 2006, 103, 19460–19465. [Google Scholar] [CrossRef] [PubMed]



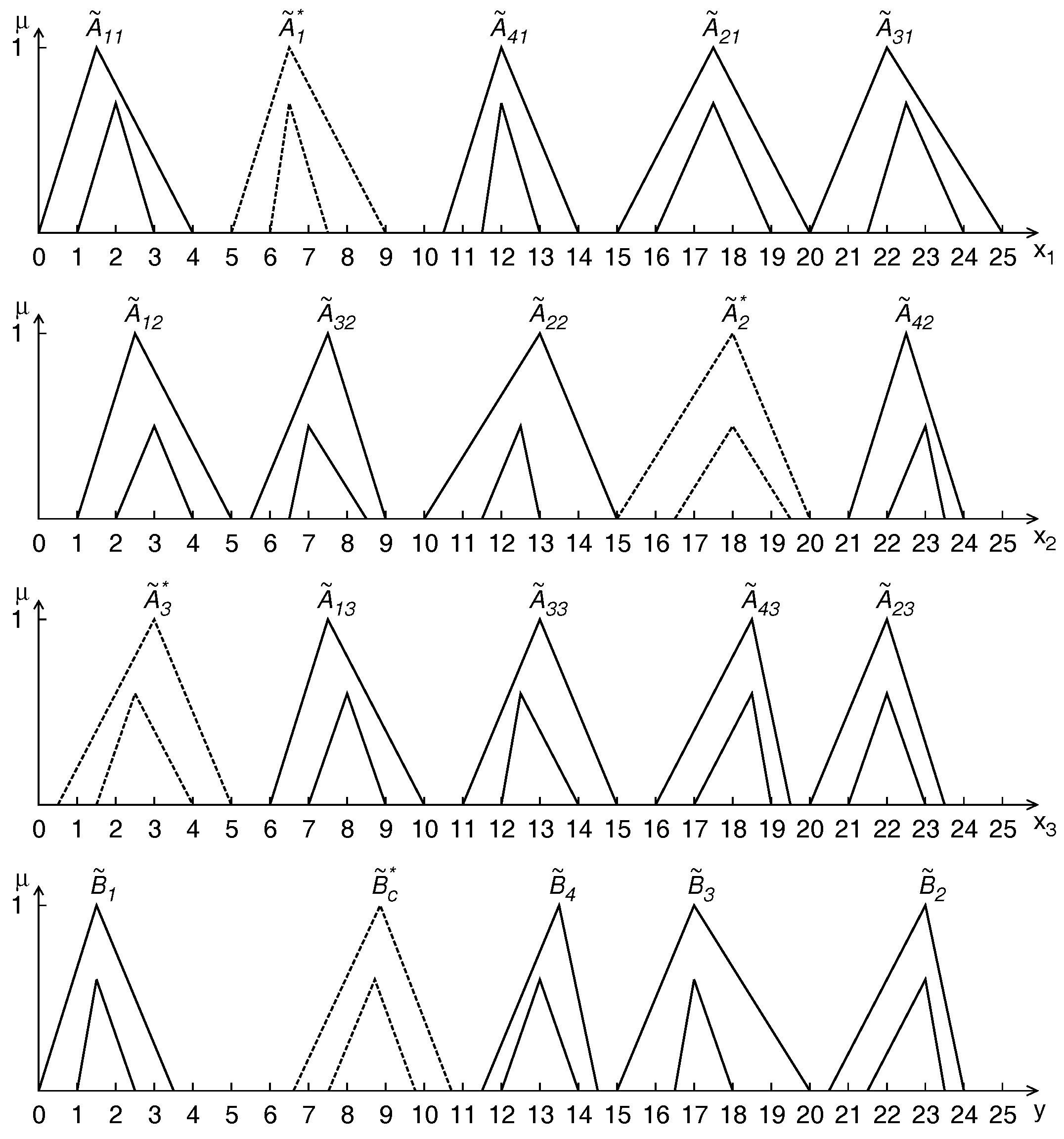

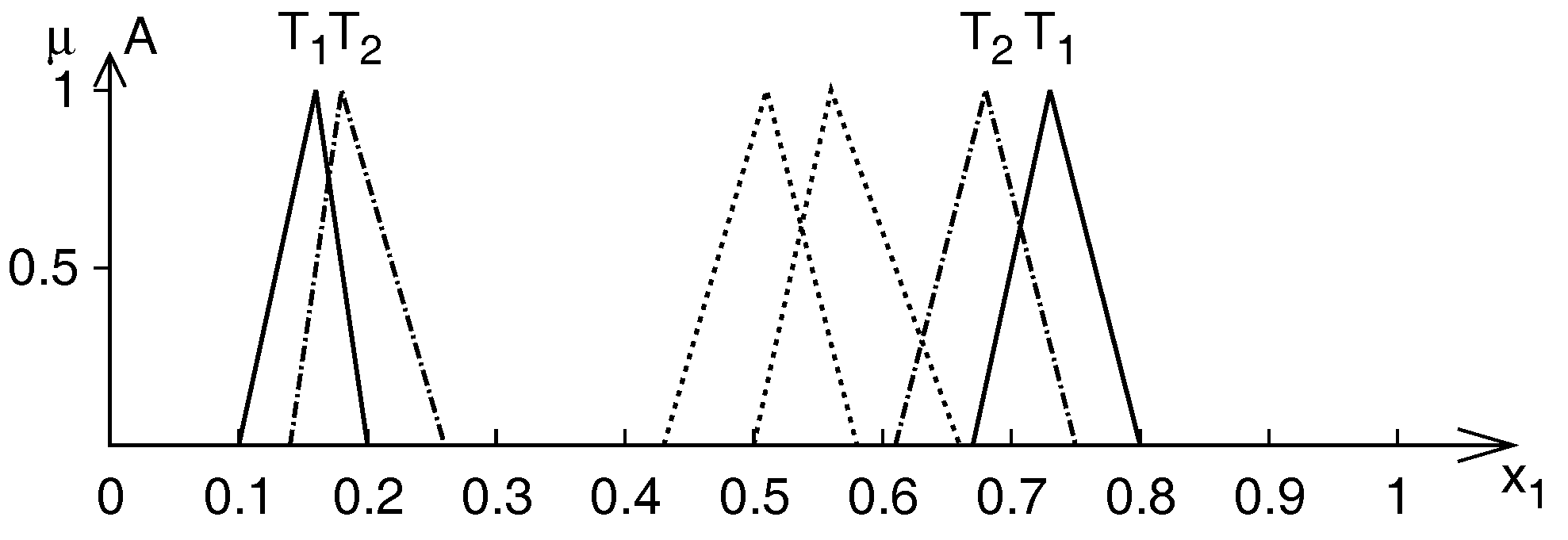

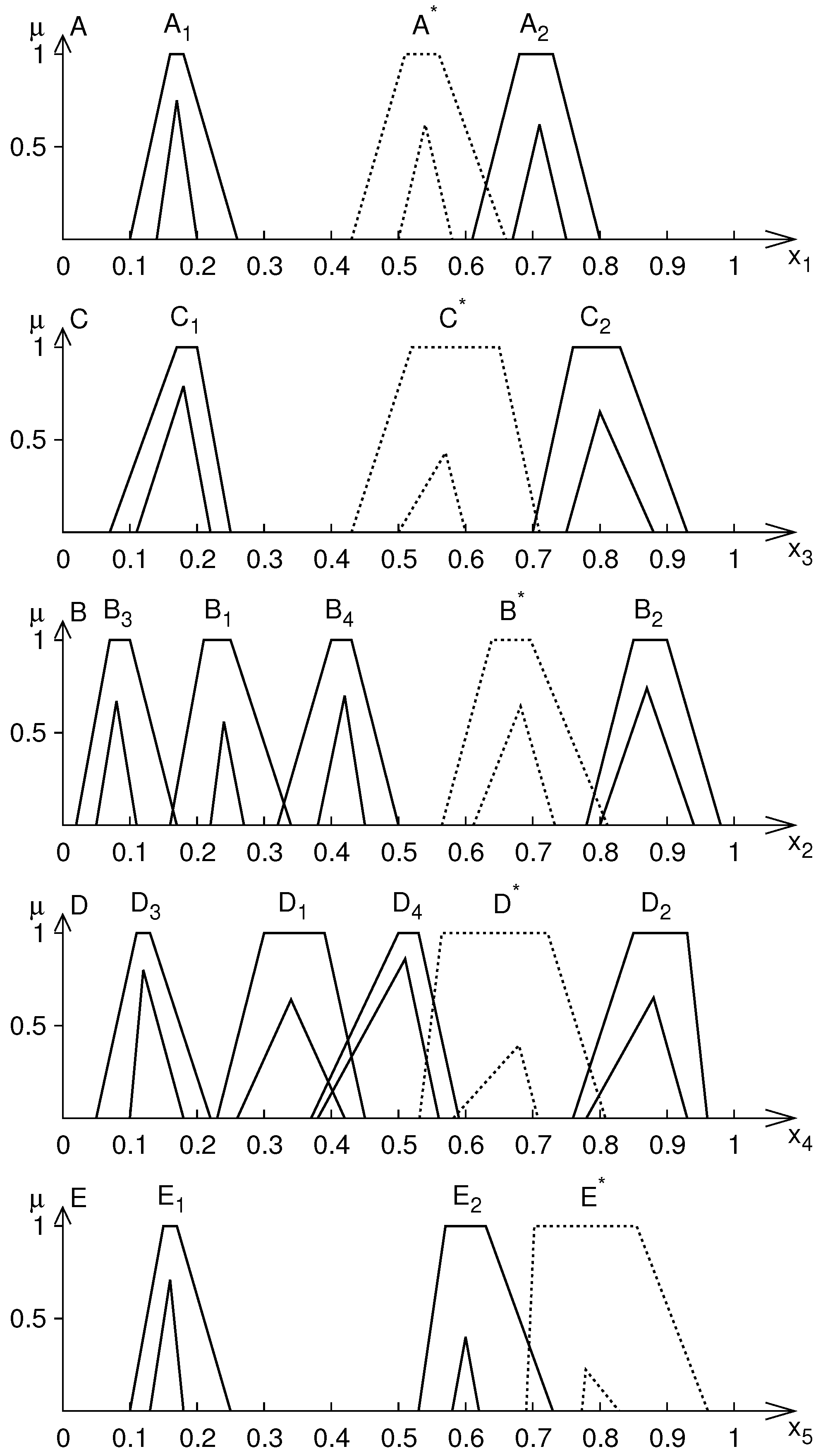
| Rule 1 | |
| Rule 2 | |
| Observation |
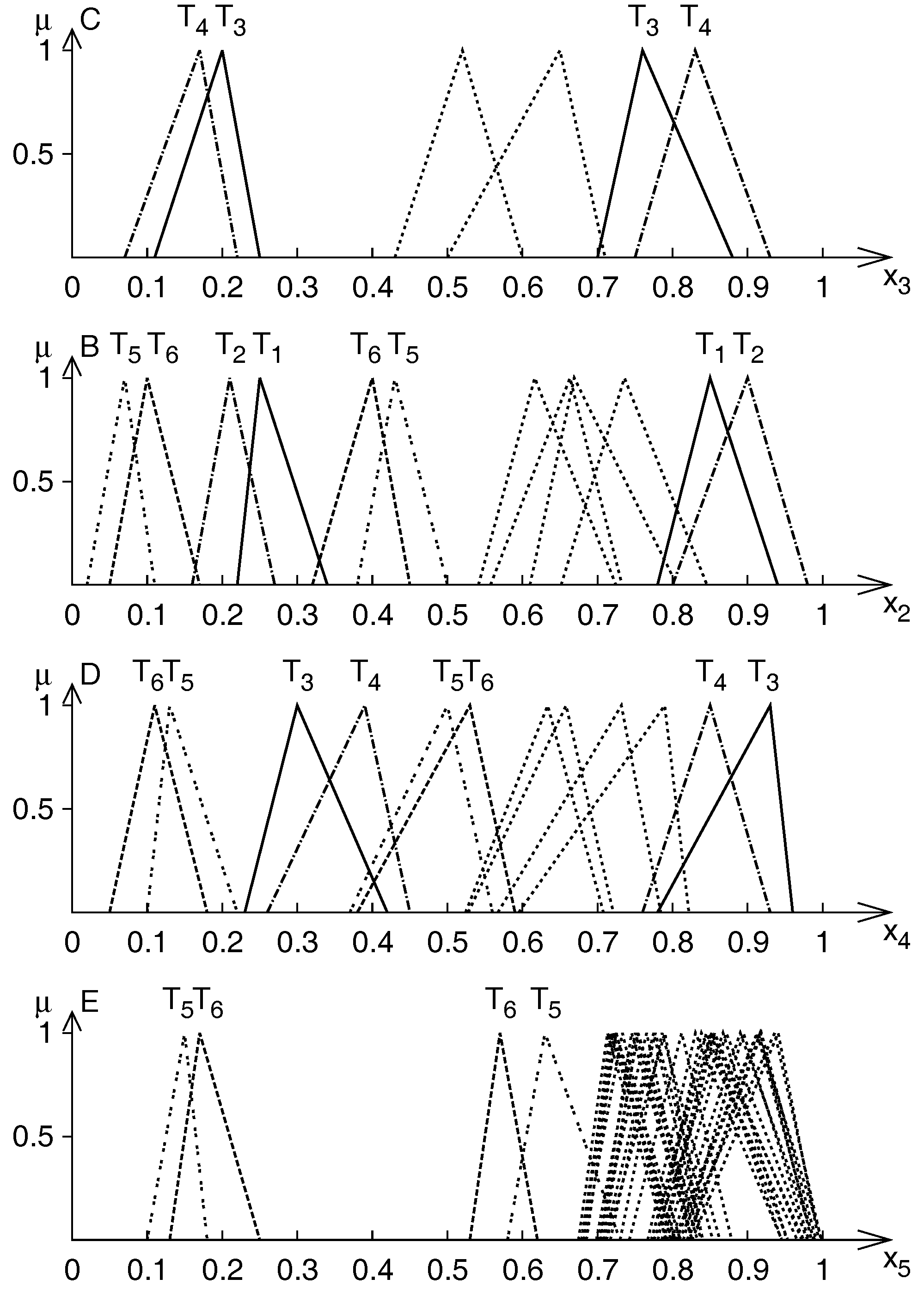
| Rule 1 | |
| Rule 2 | |
| Observation | |
| Rule 1 | |
| Rule 2 | |
| Rule 3 | |
| Rule 4 | |
| Observation | |
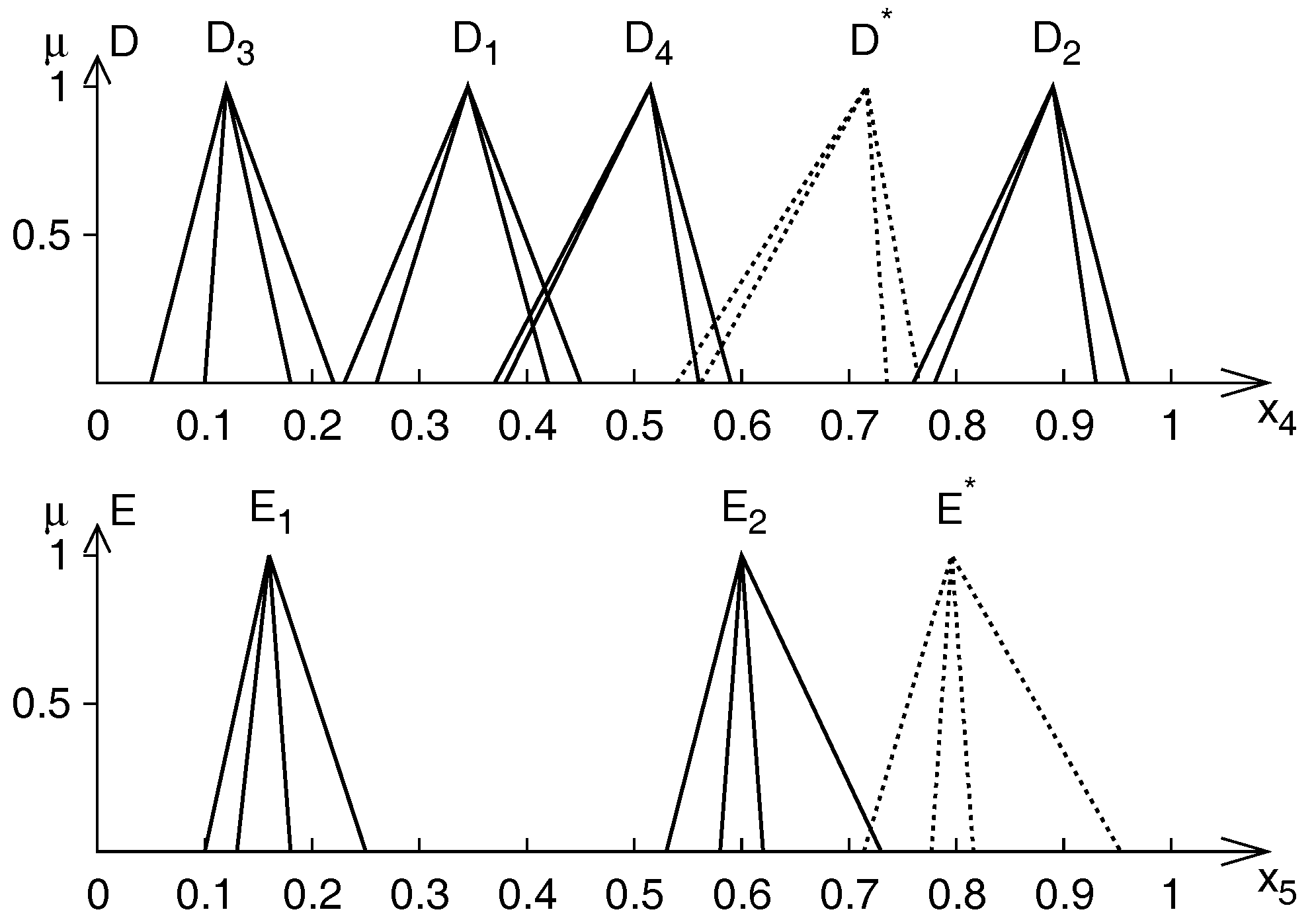
| Rule 1 | |
| Rule 2 | |
| Observation |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Shen, Q. Transformation-Based Fuzzy Rule Interpolation Using Interval Type-2 Fuzzy Sets. Algorithms 2017, 10, 91. https://doi.org/10.3390/a10030091
Chen C, Shen Q. Transformation-Based Fuzzy Rule Interpolation Using Interval Type-2 Fuzzy Sets. Algorithms. 2017; 10(3):91. https://doi.org/10.3390/a10030091
Chicago/Turabian StyleChen, Chengyuan, and Qiang Shen. 2017. "Transformation-Based Fuzzy Rule Interpolation Using Interval Type-2 Fuzzy Sets" Algorithms 10, no. 3: 91. https://doi.org/10.3390/a10030091
APA StyleChen, C., & Shen, Q. (2017). Transformation-Based Fuzzy Rule Interpolation Using Interval Type-2 Fuzzy Sets. Algorithms, 10(3), 91. https://doi.org/10.3390/a10030091




