Local Community Detection in Dynamic Graphs Using Personalized Centrality †
Abstract
:1. Introduction
1.1. Contributions
2. Background
2.1. Definitions
2.2. Measures of Community Quality
2.3. Centrality Measures
| Algorithm 1 Solve to tolerance using Jacobi algorithm. | |||||||||
| 1: | procedure Jacobi() | ||||||||
| 2: | k = 0 | ||||||||
| 3: | |||||||||
| 4: | |||||||||
| 5: | |||||||||
| 6: | |||||||||
| 7: | while do | ||||||||
| 8: | |||||||||
| 9: | ▹ Next residual | ||||||||
| 10: | |||||||||
| 11: | end while | ||||||||
| 12: | return | ||||||||
| 13: | end procedure | ||||||||
3. Related Work
3.1. Community Detection
| Algorithm 2 Static, Greedy Seed Set Expansion | |
| 1: | procedure GreedySeedset(graph G, seed set ) |
| 2: | |
| 3: | |
| 4: | while do |
| 5: | |
| 6: | |
| 7: | for do |
| 8: | |
| 9: | if then |
| 10: | |
| 11: | |
| 12: | end if |
| 13: | end for |
| 14: | if maxscore > 0 then |
| 15: | |
| 16: | else |
| 17: | |
| 18: | end if |
| 19: | end while |
| 20: | return C |
| 21: | end procedure |
3.2. Dynamic Algorithms for Centrality Measures
4. Communities from Personalized Centrality
4.1. Local Communities from Personalized Centrality
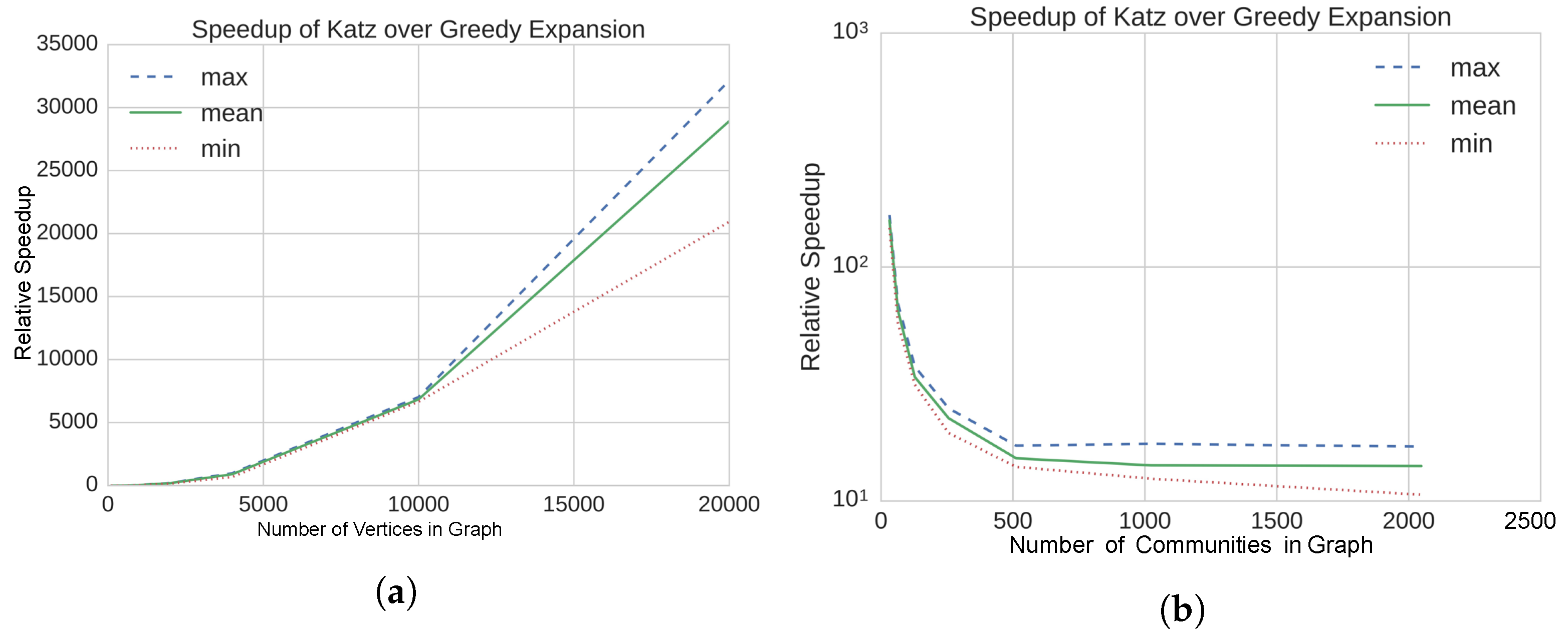
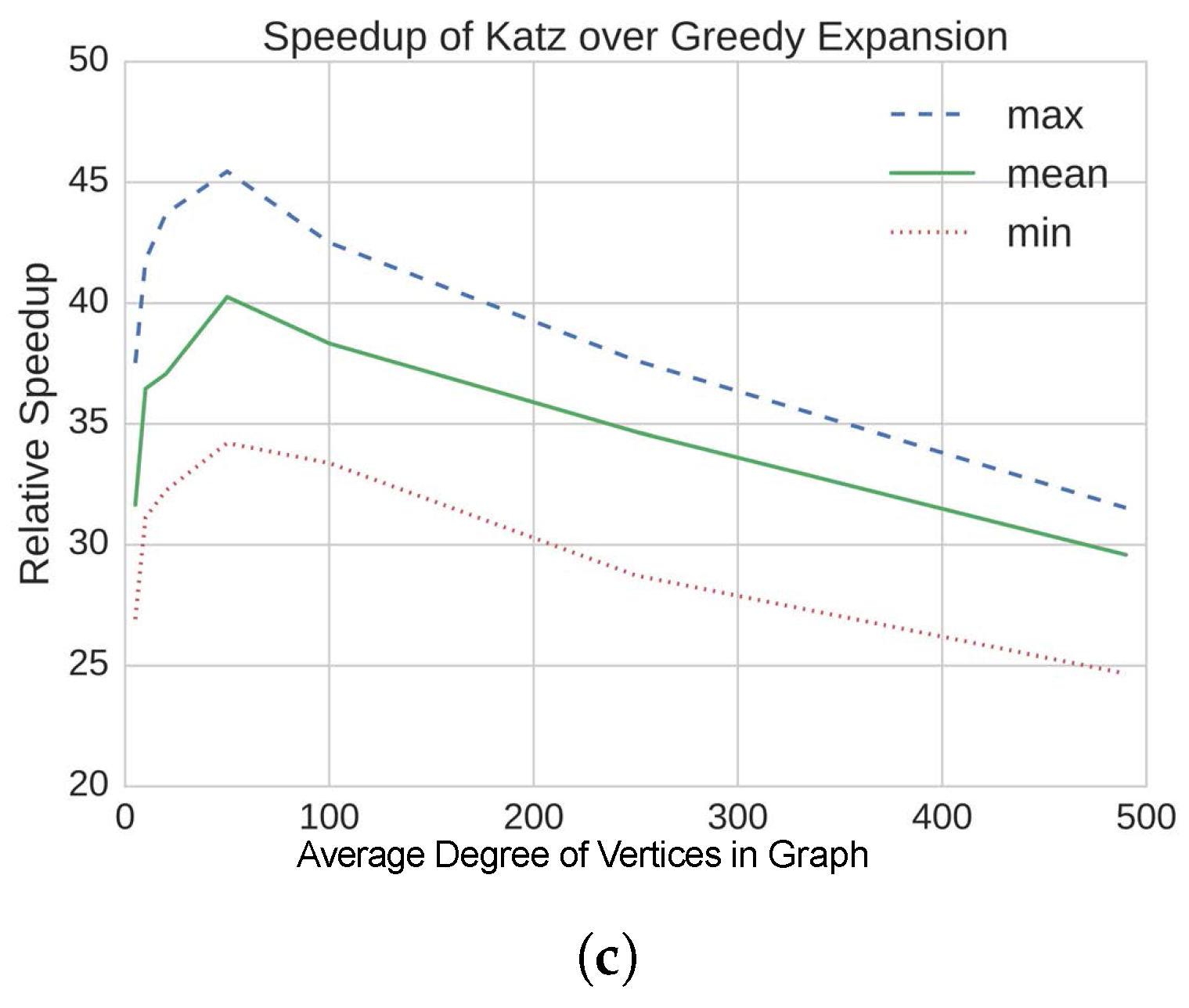
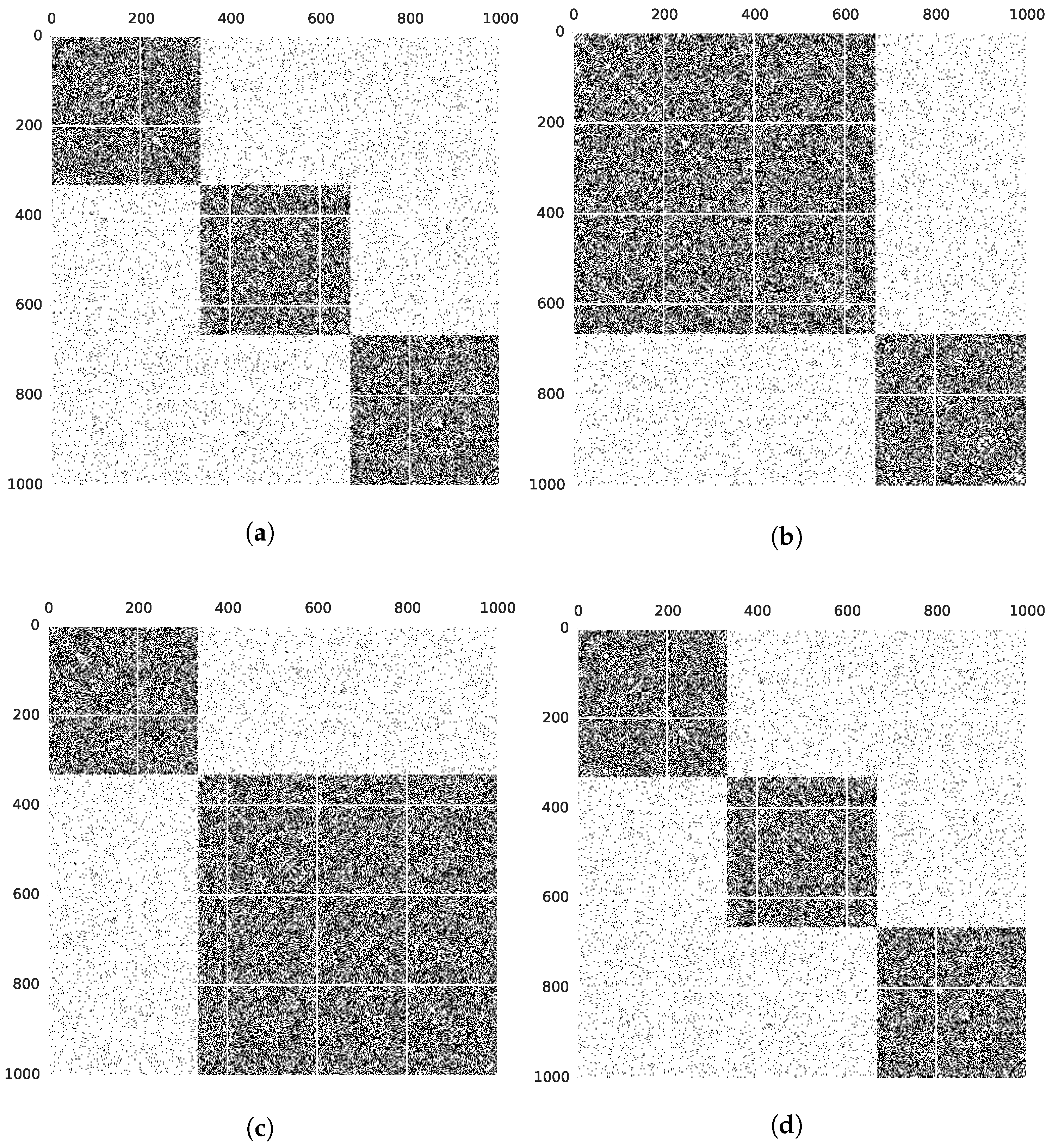
4.2. Results on Static, Synthetic Graphs
5. Dynamic Communities from Personalized Centrality
5.1. Methods
5.2. Synthetic Dynamic Graphs
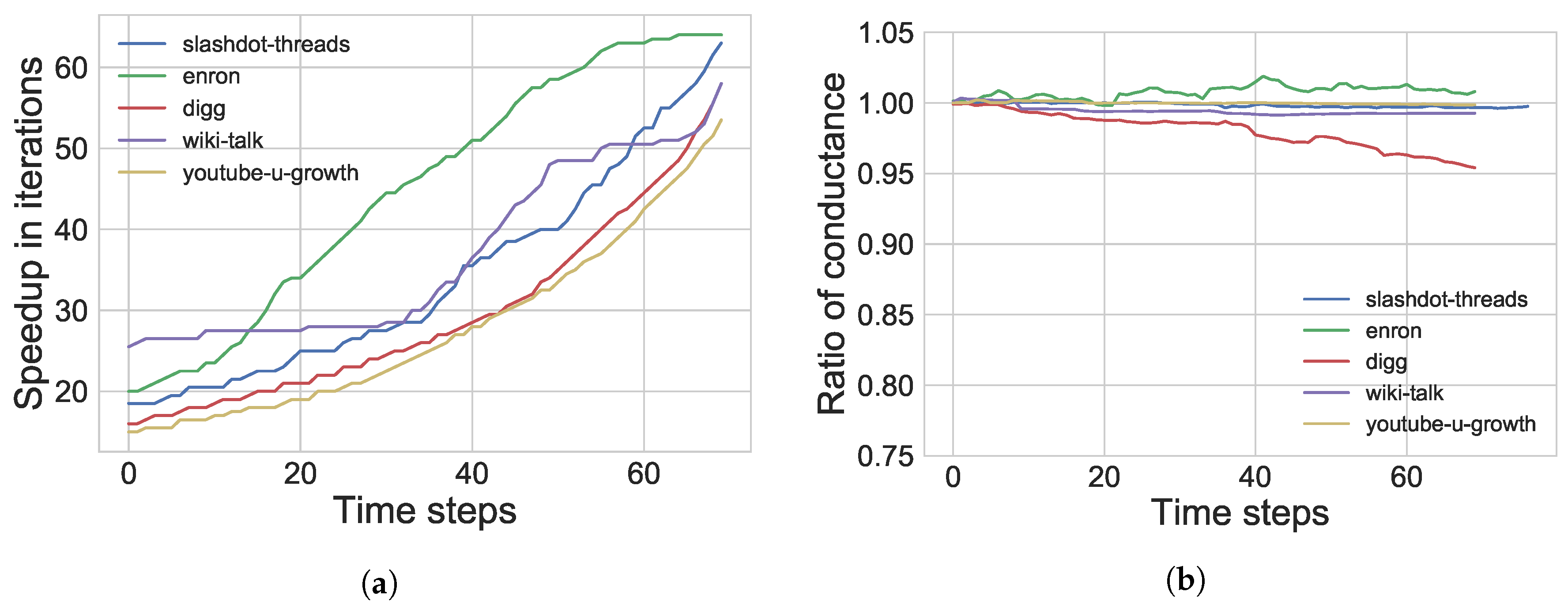
5.3. Real Graphs
5.3.1. Different Seeding Methods
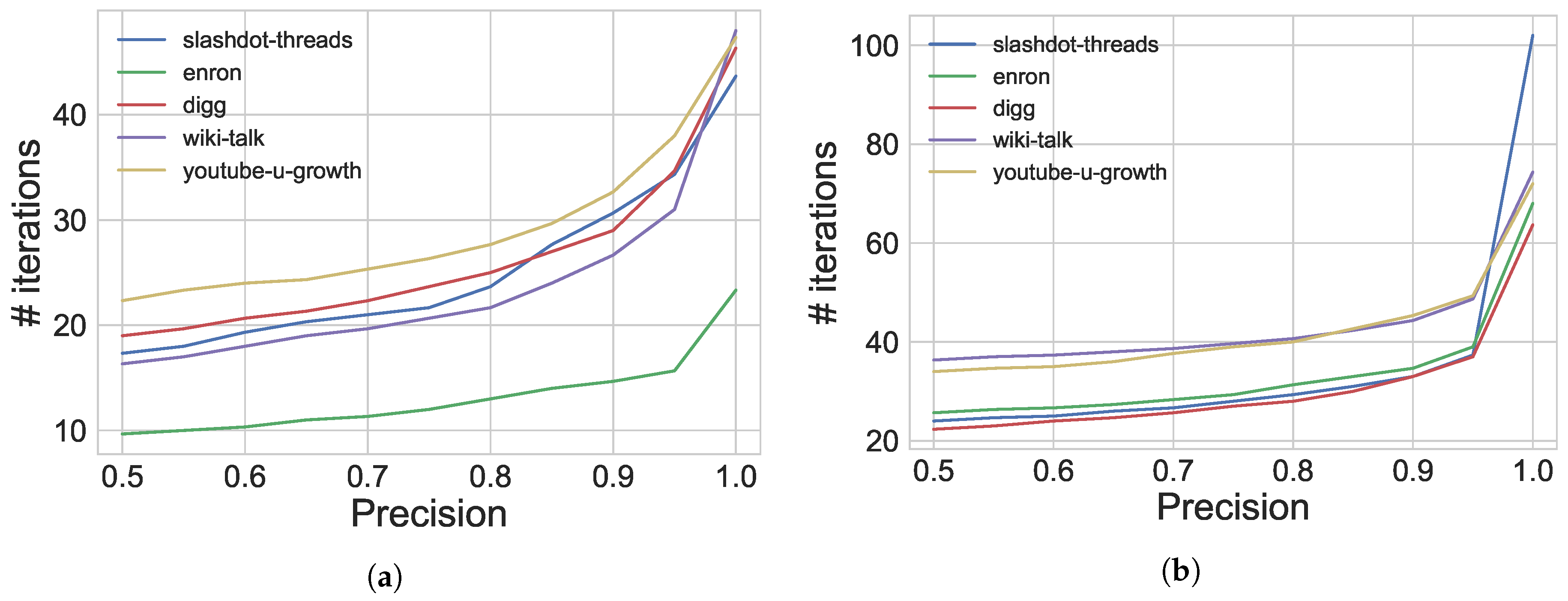
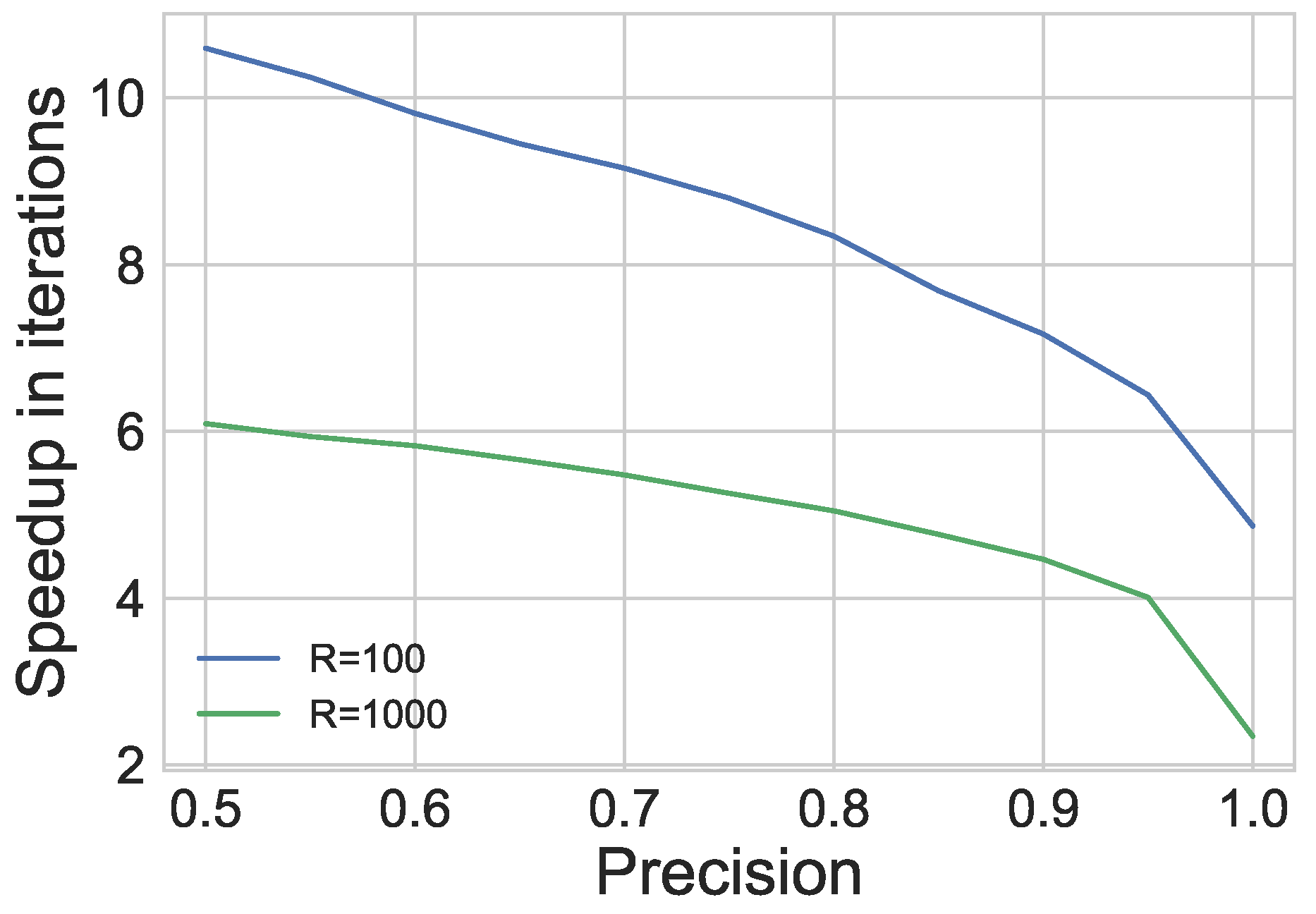
6. Guaranteed Ranking
6.1. Methods
6.1.1. New Stopping Criterion
6.2. Results
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Nathan, E.; Sanders, G.; Fairbanks, J.; Bader, D.A.; Henson, V.E. Graph Ranking Guarantees for Numerical Approximations to Katz Centrality. Procedia Comput. Sci. 2017, 108, 68–78. [Google Scholar] [CrossRef]
- Nathan, E.; Bader, D.A. A Dynamic Algorithm for Updating Katz Centrality in Graphs. In Proceedings of the 2017 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining, Sydney, Australia, 31 July–3 August 2017. [Google Scholar]
- Riedy, J. Updating PageRank for Streaming Graphs. In Proceedings of the 2016 IEEE International Parallel and Distributed Processing Symposium Workshops, Chicago, IL, USA, 23–27 May 2016; pp. 877–884. [Google Scholar]
- Chung, F.R. Spectral Graph Theory; American Mathematical Society: Providence, RI, USA, 1997; Volume 92. [Google Scholar]
- Havemann, F.; Heinz, M.; Struck, A.; Gläser, J. Identification of overlapping communities and their hierarchy by locally calculating community-changing resolution levels. J. Stat. Mech. Theory Exp. 2011. [Google Scholar] [CrossRef]
- Newman, M.E.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 026113. [Google Scholar] [CrossRef] [PubMed]
- Bader, D.A.; Meyerhenke, H.; Sanders, P.; Wagner, D. Graph partitioning and graph clustering. In Contemporary Mathematics, Proceedings of the 10th DIMACS Implementation Challenge Workshop, Atlanta, GA, USA, 13–14 February 2012; American Mathematical Society: Providence, RI, USA, 2013; Volume 588. [Google Scholar]
- Katz, L. A new status index derived from sociometric analysis. Psychometrika 1953, 18, 39–43. [Google Scholar] [CrossRef]
- Benzi, M.; Klymko, C. A matrix analysis of different centrality measures. arXiv 2014, arXiv:1312.6722. [Google Scholar]
- Page, L.; Brin, S.; Motwani, R.; Winograd, T. The PageRank Citation Ranking: Bringing Order to the Web; Technical Report 1999-66; Stanford InfoLab: Stanford, CA, USA, 1999. [Google Scholar]
- Brandes, U.; Pich, C. Centrality estimation in large networks. Int. J. Bifurc. Chaos 2007, 17, 2303–2318. [Google Scholar] [CrossRef]
- Saad, Y. Iterative Methods for Sparse Linear Systems; SIAM: Philadelphia, PA, USA, 2003. [Google Scholar]
- Clauset, A.; Newman, M.E.; Moore, C. Finding community structure in very large networks. Phys. Rev. E 2004, 70, 066111. [Google Scholar] [CrossRef] [PubMed]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008. [Google Scholar] [CrossRef]
- Pothen, A.; Simon, H.D.; Liou, K.P. Partitioning sparse matrices with eigenvectors of graphs. SIAM J. Matrix Anal. Appl. 1990, 11, 430–452. [Google Scholar] [CrossRef]
- Derényi, I.; Palla, G.; Vicsek, T. Clique percolation in random networks. Phys. Rev. Lett. 2005, 94, 160202. [Google Scholar] [CrossRef] [PubMed]
- Xie, J.; Szymanski, B.K.; Liu, X. SLPA: Uncovering overlapping communities in social networks via a speaker-listener interaction dynamic process. In Proceedings of the 2011 IEEE 11th International Conference on Data Mining Workshops (ICDMW), Vancouver, BC, Canada, 11 December 2011; pp. 344–349. [Google Scholar]
- Xie, J.; Szymanski, B.K. Towards linear time overlapping community detection in social networks. In Advances in Knowledge Discovery and Data Mining; Springer: Berlin, Germany, 2012; pp. 25–36. [Google Scholar]
- Evans, T.; Lambiotte, R. Line graphs of weighted networks for overlapping communities. Eur. Phys. J. B 2010, 77, 265–272. [Google Scholar] [CrossRef]
- Lancichinetti, A.; Radicchi, F.; Ramasco, J.J.; Fortunato, S. Finding statistically significant communities in networks. PLoS ONE 2011, 6, e18961. [Google Scholar] [CrossRef] [PubMed]
- Lancichinetti, A.; Fortunato, S.; Kertész, J. Detecting the overlapping and hierarchical community structure in complex networks. New J. Phys. 2009, 11, 033015. [Google Scholar] [CrossRef]
- Lee, C.; Reid, F.; McDaid, A.; Hurley, N. Detecting highly overlapping community structure by greedy clique expansion. In Proceedings of the 4th SNA-KDD Workshop, Washington, DC, USA, 25–28 July 2010; pp. 33–42. [Google Scholar]
- Staudt, C.L.; Meyerhenke, H. Engineering Parallel Algorithms for Community Detection in Massive Networks. IEEE Trans. Parallel Distrib. Syst. 2016, 27, 171–184. [Google Scholar] [CrossRef]
- Tantipathananandh, C.; Berger-Wolf, T.; Kempe, D. A framework for community identification in dynamic social networks. In Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Jose, CA, USA, 12–15 August 2007; pp. 717–726. [Google Scholar]
- Mucha, P.J.; Richardson, T.; Macon, K.; Porter, M.A.; Onnela, J.P. Community structure in time-dependent, multiscale, and multiplex networks. Science 2010, 328, 876–878. [Google Scholar] [CrossRef] [PubMed]
- Jdidia, M.B.; Robardet, C.; Fleury, E. Communities detection and analysis of their dynamics in collaborative networks. In Proceedings of the 2nd International Conference on Digital Information Management, Lyon, France, 28–31 October 2007; pp. 744–749. [Google Scholar]
- Chakrabarti, D.; Kumar, R.; Tomkins, A. Evolutionary clustering. In Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Philadelphia, PA, USA, 20–23 August 2006; pp. 554–560. [Google Scholar]
- Lin, Y.R.; Chi, Y.; Zhu, S.; Sundaram, H.; Tseng, B.L. Analyzing communities and their evolutions in dynamic social networks. ACM Trans. Knowl. Discov. Data 2009, 3, 8. [Google Scholar] [CrossRef]
- Aynaud, T.; Guillaume, J.L. Static community detection algorithms for evolving networks. In Proceedings of the WiOpt’10: Modeling and Optimization in Mobile, Ad Hoc, and Wireless Networks, Avignon, France, 31 May–4 June 2010; pp. 508–514. [Google Scholar]
- Shang, J.; Liu, L.; Xie, F.; Chen, Z.; Miao, J.; Fang, X.; Wu, C. A real-time detecting algorithm for tracking community structure of dynamic networks. arXiv 2014, arXiv:1407.2683. [Google Scholar]
- Dinh, T.N.; Xuan, Y.; Thai, M.T. Towards social-aware routing in dynamic communication networks. In Proceedings of the 2009 IEEE 28th International Performance Computing and Communications Conference (IPCCC), Scottsdale, AZ, USA, 14–16 December 2009; pp. 161–168. [Google Scholar]
- Riedy, J.; Bader, D.A. Multithreaded community monitoring for massive streaming graph data. In Proceedings of the 2013 IEEE 27th International Symposium on Parallel and Distributed Processing Workshops and PhD Forum IEEE, Boston, MA, USA, 20–24 May 2013; pp. 1646–1655. [Google Scholar]
- Görke, R.; Maillard, P.; Schumm, A.; Staudt, C.; Wagner, D. Dynamic graph clustering combining modularity and smoothness. ACM J. Exp. Algorithmics 2013, 18, 1–5. [Google Scholar] [CrossRef]
- Clauset, A. Finding local community structure in networks. Phys. Rev. E 2005, 72, 026132. [Google Scholar] [CrossRef] [PubMed]
- Freeman, L.C. A set of measures of centrality based on betweenness. Sociometry 1977, 40, 35–41. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [PubMed]
- Bagrow, J.P.; Bollt, E.M. Local method for detecting communities. Phys. Rev. E 2005, 72, 046108. [Google Scholar] [CrossRef] [PubMed]
- Andersen, R.; Chung, F.; Lang, K. Local graph partitioning using PageRank vectors. In Proceedings of the 47th Annual IEEE Symposium on Foundations of Computer Science, Berkeley, CA, USA, 21–24 October 2006; pp. 475–486. [Google Scholar]
- Chen, Y.Y.; Gan, Q.; Suel, T. Local methods for estimating PageRank values. In Proceedings of the thirteenth ACM International Conference on Information and Knowledge Management, Washington, DC, USA, 8–13 November 2004; pp. 381–389. [Google Scholar]
- Chien, S.; Dwork, C.; Kumar, R.; Sivakumar, D. Towards exploiting link evolution. In Proceedings of the Workshop on Algorithms and Models for the Web Graph; 2001. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.16.811 (accessed on 29 August 2017).
- Sarma, A.D.; Gollapudi, S.; Panigrahy, R. Estimating PageRank on graph streams. J. ACM 2011, 58, 13. [Google Scholar] [CrossRef]
- Gyöngyi, Z.; Garcia-Molina, H.; Pedersen, J. Combating web spam with trustrank. In Proceedings of the Thirtieth International Conference on Very Large Data Bases—Volume 30, Toronto, ON, Canada, 31 August–3 September 2004; pp. 576–587. [Google Scholar]
- Langville, A.N.; Meyer, C.D. Updating PageRank Using the Group Inverse and Stochastic Complementation; Technical Report CRSC-TR02-32; North Carolina State University: Raleigh, NC, USA, 2002. [Google Scholar]
- Langville, A.N.; Meyer, C.D. Updating the stationary vector of an irreducible Markov chain with an eye on Google’s PageRank. SIAM. J. Matrix Anal. Appl. 2004, 27, 968–987. [Google Scholar] [CrossRef]
- Langville, A.N.; Meyer, C.D. Updating PageRank with iterative aggregation. In Proceedings of the 13th International World Wide Web conference on Alternate Track Papers & Posters, New York, NY, USA, 17–22 May 2004; pp. 392–393. [Google Scholar]
- Bahmani, B.; Chowdhury, A.; Goel, A. Fast incremental and personalized PageRank. Proc. VLDB Endow. 2010, 4, 173–184. [Google Scholar] [CrossRef]
- Arrigo, F.; Grindrod, P.; Higham, D.J.; Noferini, V. Nonbacktracking Walk Centrality for Directed Networks; Technical Report MIMS Preprint 2017.9; University of Manchester: Manchester, UK, 2017. [Google Scholar]
- Leskovec, J.; Lang, K.J.; Dasgupta, A.; Mahoney, M.W. Statistical properties of community structure in large social and information networks. In Proceedings of the 17th International Conference on World Wide Web, Beijing, China, 21–25 April 2008; pp. 695–704. [Google Scholar]
- Kloumann, I.M.; Ugander, J.; Kleinberg, J.M. Block Models and Personalized PageRank. Proc. Natl. Acad. Sci. USA 2016, 114, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Moler, C.B. Iterative Refinement in Floating Point. J. ACM 1967, 14, 316–321. [Google Scholar] [CrossRef]
- Chakrabarti, D.; Zhan, Y.; Faloutsos, C. R-MAT: A Recursive Model for Graph Mining. In Proceedings of the Fourth SIAM International Conference on Data Mining, Lake Buena Vista, FL, USA, 22–24 April 2004; pp. 442–446. [Google Scholar]
- Kunegis, J. KONECT: the Koblenz network collection. In Proceedings of the 22nd International Conference on World Wide Web, Rio de Janeiro, Brazil, 13–17 May 2013; pp. 1343–1350. [Google Scholar]
- Riedy, J.; Bader, D.A.; Jiang, K.; Pande, P.; Sharma, R. Detecting Communities from Given Seeds in Social Networks; Technical Report; Georgia Institute of Technology: Atlanta, GA, USA, 2011. [Google Scholar]
| Contribution | Main Results | |
|---|---|---|
| New method of identifying local communities using personalized centrality metrics | • Comparisons to a modified version of greedy seed set expansion | 4 |
| • High recall values comparing our method to ground truth on stochastic block model graphs | ||
| • Several orders of magnitude of speedup obtained using our method | ||
| Dynamic algorithm to identify local communities in evolving networks | • Recalls of over 0.80 for synthetic networks showing community evolution | 5 |
| • Speedups of over 60× execution time improvement compared to static recomputation for real graphs | ||
| • Good quality of communities returned by our dynamic method w.r.t. ratios of conductance and normalized edge cut | ||
| • Quality of communities is preserved over time for real graphs | ||
| • Comparisons using multiple seeds for our algorithm show our method is robust to using many seeds | ||
| Numerical theory to guarantee the accuracy of an approximate solution to a centrality metric | • Development of a new stopping criterion for iterative solvers to terminate when we can guarantee rankings given desired precision | 6 |
| • Speedups obtained compared to running to preset tolerance versus using our new stopping criterion |
| (a) | ||||||||||
| Avg. Degree | Katz Recall | Greedy Recall | Forced Greedy Recall | |||||||
| Min | Mean | Max | Min | Mean | Max | Min | Mean | Max | ||
| 5 | 0.01 | 0.688 | 0.936 | 0.974 | 0.004 | 0.015 | 0.034 | 0.024 | 0.924 | 1.000 |
| 10 | 0.01 | 0.920 | 0.988 | 0.998 | 0.002 | 0.104 | 1.000 | 0.002 | 0.970 | 1.000 |
| 20 | 0.01 | 0.974 | 0.997 | 1.000 | 0.002 | 0.902 | 1.000 | 0.002 | 0.990 | 1.000 |
| 50 | 0.01 | 0.994 | 0.999 | 1.000 | 0.002 | 0.990 | 1.000 | 0.002 | 0.990 | 1.000 |
| 100 | 0.01 | 0.990 | 0.998 | 1.000 | 0.002 | 0.990 | 1.000 | 0.002 | 0.990 | 1.000 |
| 250 | 0.01 | 1.000 | 1.000 | 1.000 | 0.002 | 0.990 | 1.000 | 0.002 | 0.990 | 1.000 |
| 490 | 0.01 | 1.000 | 1.000 | 1.000 | 0.002 | 0.990 | 1.000 | 0.002 | 0.990 | 1.000 |
| (b) | ||||||||||
| Avg. Degree | Katz Recall | Greedy Recall | Forced Greedy Recall | |||||||
| Min | Mean | Max | Min | Mean | Max | Min | Mean | Max | ||
| 20 | 0.01 | 0.974 | 0.997 | 1.000 | 0.002 | 0.902 | 1.000 | 0.002 | 0.990 | 1.000 |
| 20 | 0.05 | 0.806 | 0.944 | 0.988 | 0.002 | 0.852 | 1.000 | 0.002 | 0.960 | 1.000 |
| 20 | 0.1 | 0.678 | 0.833 | 0.910 | 0.002 | 0.773 | 1.000 | 0.002 | 0.869 | 1.000 |
| 20 | 0.2 | 0.502 | 0.638 | 0.730 | 0.002 | 0.603 | 0.998 | 0.008 | 0.833 | 0.998 |
| 20 | 0.3 | 0.474 | 0.551 | 0.630 | 0.002 | 0.505 | 0.932 | 0.096 | 0.655 | 0.942 |
| 20 | 0.4 | 0.456 | 0.508 | 0.542 | 0.006 | 0.354 | 0.594 | 0.416 | 0.521 | 0.604 |
| (c) | ||||||||||
| Avg. Degree | Katz Recall | Greedy Recall | Forced Greedy Recall | |||||||
| Min | Mean | Max | Min | Mean | Max | Min | Mean | Max | ||
| 100 | 0.01 | 0.990 | 0.998 | 1.000 | 0.002 | 0.990 | 1.000 | 0.002 | 0.990 | 1.000 |
| 100 | 0.05 | 0.980 | 0.990 | 1.000 | 0.002 | 0.960 | 1.000 | 0.002 | 0.960 | 1.000 |
| 100 | 0.1 | 0.942 | 0.980 | 0.992 | 0.002 | 0.940 | 1.000 | 0.002 | 0.940 | 1.000 |
| 100 | 0.2 | 0.728 | 0.822 | 0.908 | 0.002 | 0.880 | 1.000 | 0.002 | 0.880 | 1.000 |
| 100 | 0.3 | 0.552 | 0.626 | 0.700 | 0.002 | 0.828 | 1.000 | 0.002 | 0.828 | 1.000 |
| 100 | 0.4 | 0.482 | 0.530 | 0.576 | 0.070 | 0.604 | 0.936 | 0.074 | 0.612 | 0.944 |
| Block Size = 100 | Block Size = 1000 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Parameters | Batch Size | t = | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| R = | 100 | 200 | 200 | 100 | 1000 | 2000 | 2000 | 1000 | ||
| = 0.2, = 0.01 | 10 | 0.86 | 0.94 | 0.93 | 0.85 | 0.93 | 0.97 | 0.98 | 9.98 | |
| 100 | 0.76 | 0.89 | 0.89 | 0.75 | 0.97 | 0.99 | 0.99 | 0.97 | ||
| 1000 | 0.76 | 0.84 | 0.84 | 0.66 | 0.93 | 0.97 | 0.97 | 0.93 | ||
| = 0.5, = 0.01 | 10 | 0.92 | 0.96 | 0.97 | 0.92 | 0.96 | 0.98 | 0.99 | 0.99 | |
| 100 | 0.79 | 0.89 | 0.90 | 0.78 | 0.95 | 0.98 | 0.98 | 0.95 | ||
| 1000 | 0.88 | 0.91 | 0.91 | 0.82 | 0.96 | 0.99 | 0.99 | 0.96 | ||
| Average | 0.83 | 0.91 | 0.91 | 0.80 | 0.95 | 0.98 | 0.98 | 0.96 | ||
| Graph | ||
|---|---|---|
| slashdot-threads | 51,083 | 140,778 |
| enron | 87,221 | 1,148,072 |
| digg | 279,630 | 1,731,653 |
| wiki-talk | 541,355 | 2,424,962 |
| youtube-u-growth | 3,223,589 | 9,375,374 |
| Graph | Batch Size | Performance | Quality | |||
|---|---|---|---|---|---|---|
| Recall | ||||||
| slashdot-threads | 10 | 52.94× | 34.02× | 0.93 | 0.99 | 1.03 |
| 100 | 26.88× | 21.46× | 0.96 | 1.00 | 1.01 | |
| 1000 | 39.65× | 31.09× | 0.96 | 1.00 | 1.00 | |
| enron | 10 | 75.42× | 45.04× | 0.97 | 1.00 | 1.00 |
| 100 | 63.61× | 41.28× | 0.98 | 1.01 | 0.98 | |
| 1000 | 46.20× | 29.57× | 0.96 | 1.01 | 0.98 | |
| digg | 10 | 54.29× | 29.41× | 0.86 | 0.97 | 1.18 |
| 100 | 47.64× | 25.69× | 0.90 | 0.98 | 1.07 | |
| 1000 | 50.64× | 26.87× | 0.97 | 0.99 | 1.02 | |
| wiki-talk | 10 | 56.02× | 36.68× | 0.95 | 1.00 | 1.02 |
| 100 | 48.87× | 31.46× | 0.91 | 0.99 | 1.19 | |
| 1000 | 56.22× | 36.95× | 0.96 | 1.00 | 1.02 | |
| youtube- u-growth | 10 | 56.47× | 27.66× | 0.96 | 1.00 | 0.94 |
| 100 | 50.00× | 26.58× | 0.96 | 1.00 | 1.00 | |
| 1000 | 40.17× | 20.44× | 0.91 | 1.00 | 0.92 | |
| Graph | Method | Number of Seeds | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| RW-1 | 46.9× | 54.4× | 49.3× | 41.7× | 39.4× | 30.3× | 32.4× | 47.3× | 41.5× | 29.3× | |
| RW-2 | 33.7× | 66.1× | 42.8× | 51.5× | 57.0× | 52.1× | 50.6× | 46.1× | 53.2× | 39.0× | |
| RW-3 | 44.5× | 53.4× | 54.0× | 44.3× | 53.6× | 44.5× | 53.0× | 63.2× | 68.5× | 47.8× | |
| RW-1 | 29.4× | 30.9× | 29.8× | 24.6× | 24.5× | 24.4× | 21.0× | 29.2× | 25.3× | 22.3× | |
| RW-2 | 20.4× | 37.3× | 24.4× | 30.9× | 31.8× | 29.2× | 29.0× | 28.4× | 30.1× | 24.1× | |
| RW-3 | 26.0× | 29.8× | 31.9× | 27.9× | 33.4× | 27.4× | 30.9× | 38.2× | 37.0× | 29.9× | |
| Recall | RW-1 | 0.99 | 0.98 | 1.00 | 0.98 | 1.00 | 1.00 | 0.99 | 0.98 | 1.00 | 1.00 |
| RW-2 | 0.96 | 0.98 | 0.95 | 0.99 | 0.96 | 0.99 | 1.00 | 0.99 | 0.99 | 0.99 | |
| RW-3 | 0.93 | 0.97 | 0.95 | 0.99 | 0.98 | 0.99 | 0.99 | 0.98 | 0.99 | 0.99 | |
| RW-1 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| RW-2 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| RW-3 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| RW-1 | 0.99 | 0.98 | 1.00 | 1.00 | 1.00 | 1.00 | 0.94 | 1.01 | 0.98 | 1.00 | |
| RW-2 | 1.00 | 0.97 | 0.99 | 1.01 | 1.03 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| RW-3 | 1.03 | 0.99 | 1.01 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.01 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nathan, E.; Zakrzewska, A.; Riedy, J.; Bader, D.A. Local Community Detection in Dynamic Graphs Using Personalized Centrality. Algorithms 2017, 10, 102. https://doi.org/10.3390/a10030102
Nathan E, Zakrzewska A, Riedy J, Bader DA. Local Community Detection in Dynamic Graphs Using Personalized Centrality. Algorithms. 2017; 10(3):102. https://doi.org/10.3390/a10030102
Chicago/Turabian StyleNathan, Eisha, Anita Zakrzewska, Jason Riedy, and David A. Bader. 2017. "Local Community Detection in Dynamic Graphs Using Personalized Centrality" Algorithms 10, no. 3: 102. https://doi.org/10.3390/a10030102
APA StyleNathan, E., Zakrzewska, A., Riedy, J., & Bader, D. A. (2017). Local Community Detection in Dynamic Graphs Using Personalized Centrality. Algorithms, 10(3), 102. https://doi.org/10.3390/a10030102





