A Pilot-Pattern Based Algorithm for MIMO-OFDM Channel Estimation
Abstract
:1. Introduction
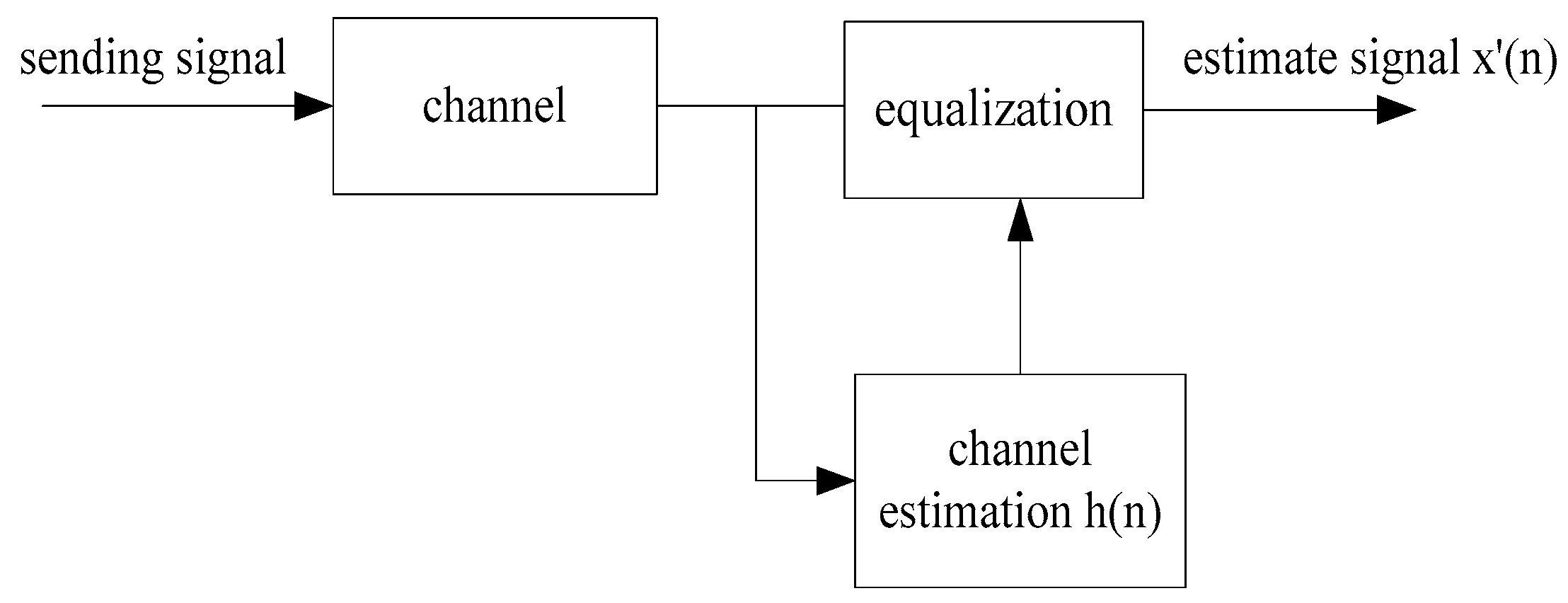
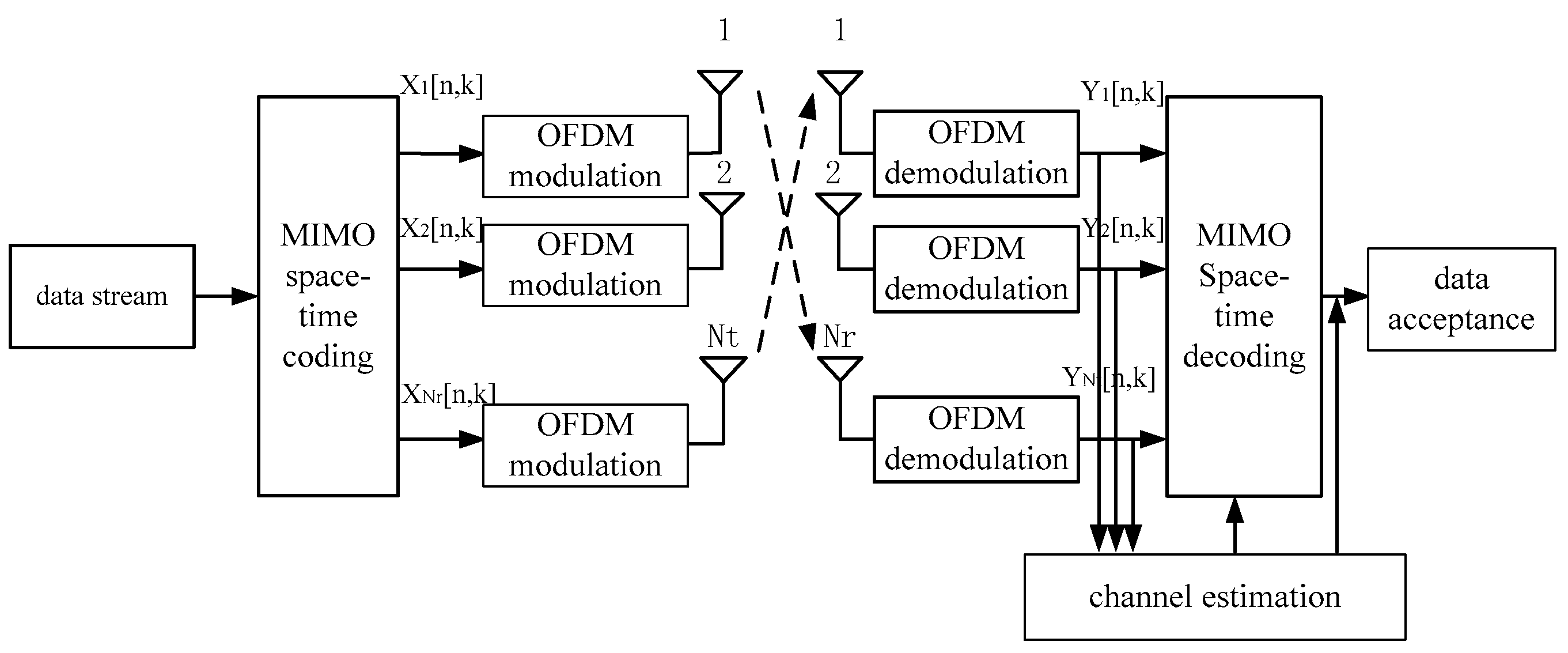
2. System Modeling on MIMO-OFDM
3. Channel Estimation Algorithm Based on Space-Time Block-Code
3.1. Analysis on the Algorithm for LS Channel Estimation
3.2. LS Channel Estimation Algorithm Based on STBC
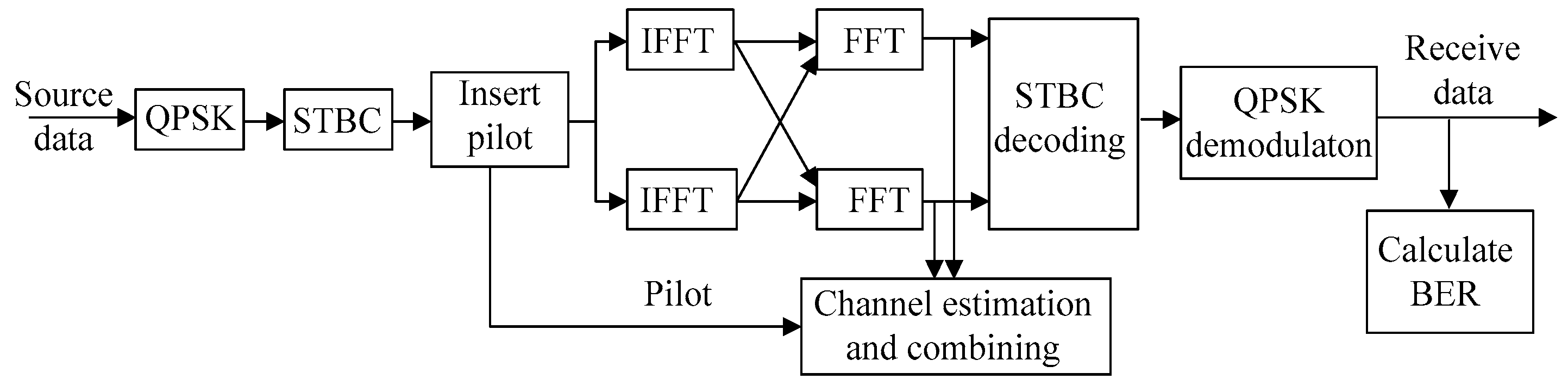
3.2.1. Channel Estimation Algorithm for the Single-Symbol Scheme
3.2.2. Channel Estimation Algorithm for a Double-Symbol scheme
4. Improved Channel Estimation Algorithm Based on STBC
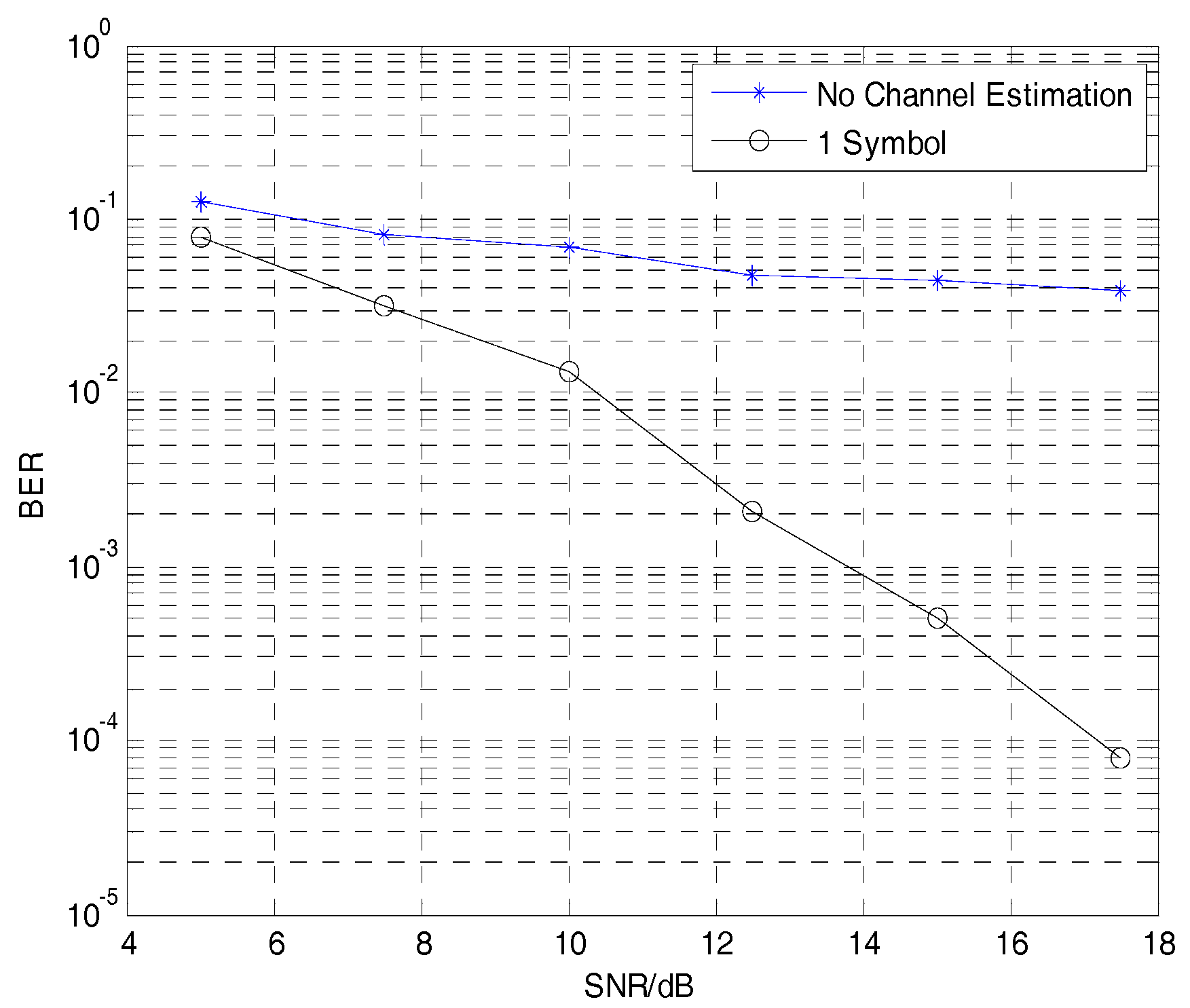
5. Simulations and Results
- (1)
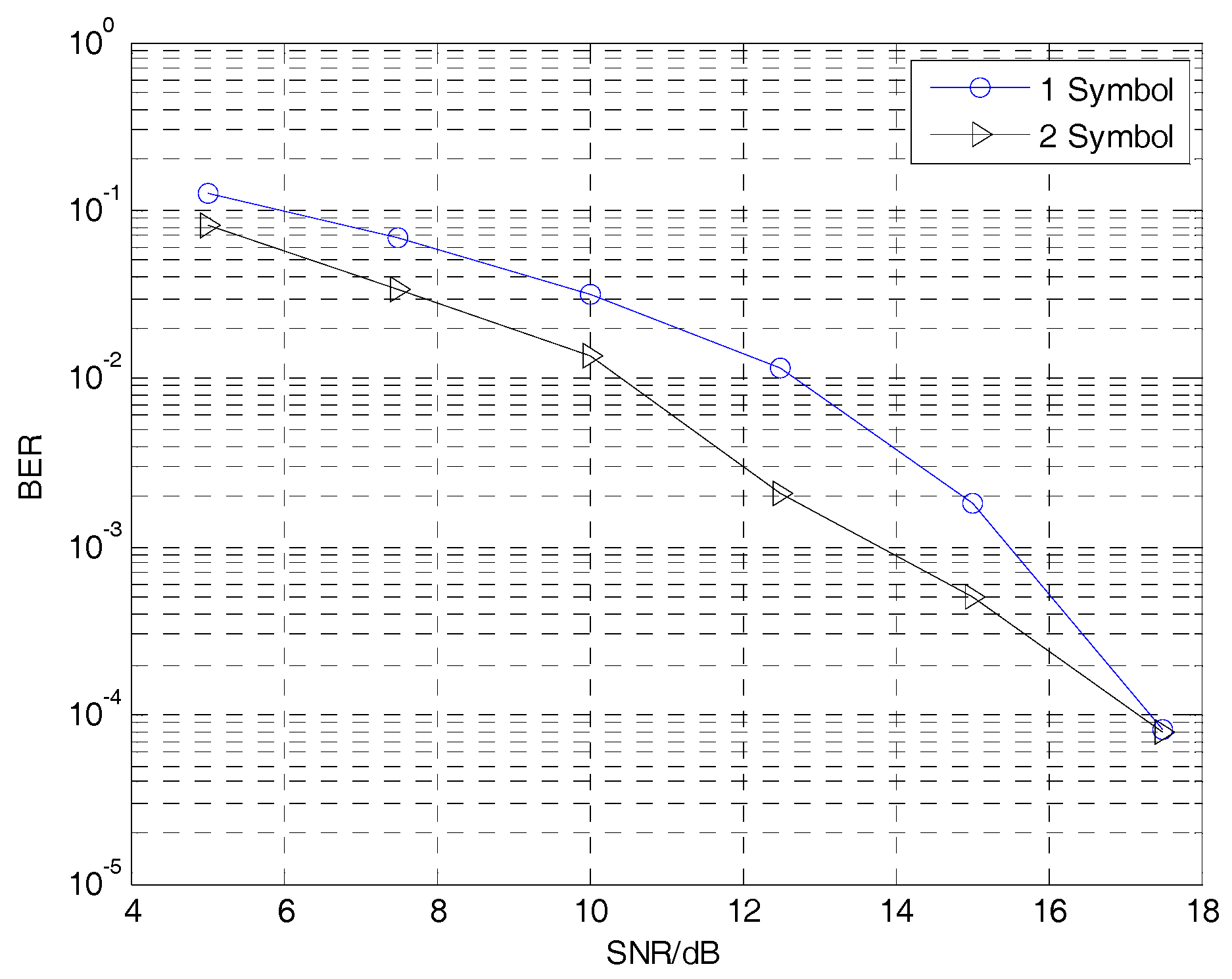
- Since the number of pilot signals of the double-symbol scheme is four times that of the single-symbol scheme, the interpolation is unnecessary. Thus, the interpolation error can be avoided. From this view, the double symbol-scheme is better than the single-symbol scheme, which has the advantage of more effective overhead.
- (2)
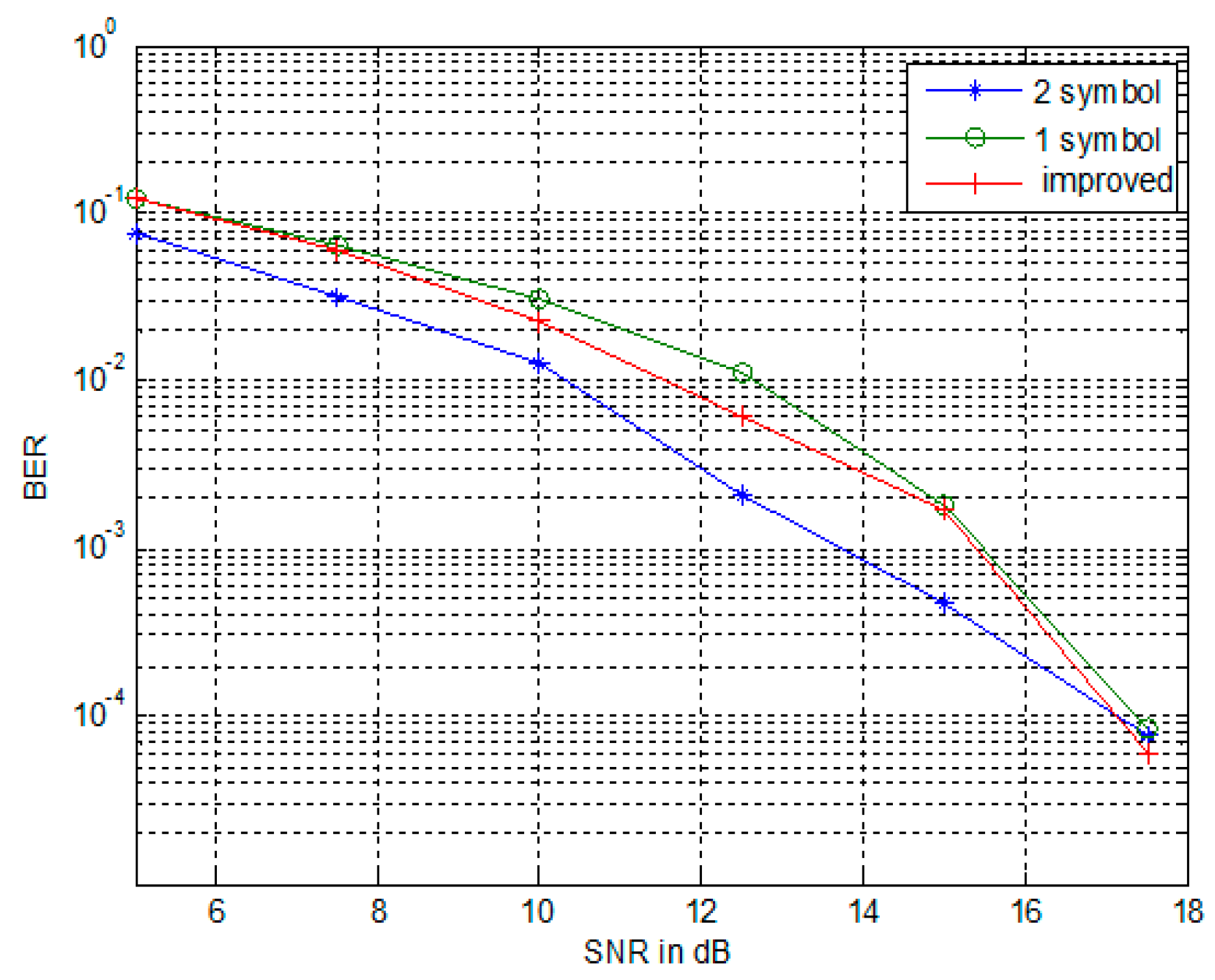
- The tradeoff scheme also does not need interpolation anymore; thus, it is better than the single-symbol scheme. Owing to the number of pilot signals being just half of that in the double-symbol scheme, the performance of tradeoff method is worse than the double-symbol scheme. However, the tradeoff method achieves an optimized balance between system performance and the overhead of the pilot pattern.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kang, S.H.; Ha, Y.M.; Joo, E.K. A comparative investigation on channel estimation algorithms for OFDM in mobile communications. IEEE Trans. Broadcast. 2003, 49, 142–149. [Google Scholar] [CrossRef]
- Gui, G.; Xu, L.; Matsushita, S. Improved adaptive sparse channel estimation using mixed square/fourth error criterion. J. Frankl. Inst. 2015, 352, 4579–4594. [Google Scholar] [CrossRef]
- El Ayach, O.; Peters, S.W.; Heath, R.W. The feasibility of interference alignment over measured MIMO-OFDM channels. IEEE Trans. Veh. Technol. 2010, 59, 4309–4321. [Google Scholar] [CrossRef]
- Zhou, P.; Zhao, C.M.; Sheng, B. Channel estimation based on pilot-assisted in the MIMO-OFDM system. J. Electron. Inf. Technol. 2007, 29, 133–137. [Google Scholar]
- Li, Y.G. Simplified channel estimation for OFDM systems with multiple transmit antennas. IEEE Trans. Commun. 2002, 1, 67–75. [Google Scholar]
- Gui, G.; Liu, N.; Xu, L.; Adachi, F. Low-complexity large-scale multiple-input multiple-output channel estimation using affine combination of sparse least mean square filters. IET Commun. 2015, 9, 2168–2175. [Google Scholar] [CrossRef]
- Guo, J.; Wang, D.; Ran, C. Simple channel estimator for STBC-based OFDM systems. IEEE Electron. Lett. 2003, 39, 445–447. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, J.; Tang, Y.; Li, S. Analysis of pilot-symbol aided channel estimation for MIMO-OFDM systems. In Proceedings of the 2004 International Conference on Communications, Circuits and Systems (IEEE Cat. No. 04EX914), Paris, France, 27–29 June 2004; pp. 299–303.
- Van Trees, H.L. Detection, Estimation, and Modulation Theory; John Wiley & Sons: New Jersey, NJ, USA, 2004. [Google Scholar]
- Van de Beek, J.J.; Edfors, O.S.; Sandell, M.; Wilson, S.K.; Börjesson, O.P. On channel estimation in OFDM systems. In Proceedings of the 45th IEEE Vehicular Technology Conference, Chicago, IL, USA, 25–28 July 1995; pp. 815–819.
- Negi, R.; Cioffi, J. Pilot tone selection for channel estimation in a mobile OFDM system. IEEE Trans. Consum. Electron. 1998, 44, 1122–1128. [Google Scholar] [CrossRef]
- Li, G.; Liu, X.; Kang, X.; Liao, G. Improved blind channel estimation for MIMO-OFDM system. J. Appl. Sci. Electron. Inf. Eng. 2016, 34, 286–292. [Google Scholar]
- Sampath, H.; Talwar, S.; Tellado, J.; Erceg, V. A fourth-generation MIMO-OFDM broadband wireless system: Design, performance, and field trial results. IEEE Commun. 2002, 40, 143–149. [Google Scholar] [CrossRef]
- Tong, J.; Gong, Y.H.; Sun, S.X. An adaptive channel tracking method for MIMO-OFDM systems. In Proceedings of the 2004 International Conference on Communications, Circuits and Systems (IEEE Cat. No. 04EX914), Okinawa, Japan, 27–29 June 2004; pp. 354–358.
- Tarokh, V.; Jafarkhani, H. A differential detection scheme for transmit diversity. IEEE Sel. Areas Commun. 2000, 18, 1169–1174. [Google Scholar] [CrossRef]
- Gui, G.; Adachi, F. Stable adaptive sparse filtering algorithms for estimating MIMO channels. IET Commun. 2014, 8, 1032–1040. [Google Scholar] [CrossRef]
- Liang, S.C.; Wu, W.L. Channel Estimation Based on Pilot Subcarrier in Space-Time Block Coded OFDM System. In Proceedings of the International Conference on Communication Technology, Beijing, China, 9–11 April 2003; Volume 2, pp. 1795–1798.
- Mim, H.; Kim, D.I.; Bharagava, V.K. A reduced complexity channel estimation for OFDM systems with transmit diversity in mobile wireless channels. IEEE Trans. Commun. 2002, 50, 799–807. [Google Scholar]
- Lu, X.; Liang, Y.S. STBC pilot channel estimation method based on LS. Commun. Technol. 2009, 41, 63–65. [Google Scholar]
- Wan, F.; Zhu, W.-P. Semiblind sparse channel estimation for MIMO-OFDM system. IEEE Trans. Veh. Technol. 2011, 60, 2569–2582. [Google Scholar] [CrossRef]
- Li, G.; Liao, G. A pilot pattern based algorithm for MIMO-OFDM channel estimation. In Proceedings of the 2016 IEEE International Symposium on Computer, Consumer and Control, Xi’an, China, 4–6 July 2016; pp. 985–989.
- Li, Y.; Zhang, L.; Jia, L. A robust timing synchronization method for OFDM system. In Proceedings of the 2011 Seventh International Conference on Natural Computation, Shanghai, China, 26–28 July 2011; pp. 52–55.
- Li, P.; Wang, P.; Song, Y.; Zhu, T.; Tan, H. Design of correlation-based real-time MIMO channel emulator. Chin. J. Radio Sci. 2015, 30, 929–935. [Google Scholar]
| Taps | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Relative time Delay | 0 | 100 | 200 | 300 | 500 | 700 |
| Average power (dB) | 0 | −3.60 | −7.20 | −10.8 | −18.0 | −25.0 |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Liao, G. A Pilot-Pattern Based Algorithm for MIMO-OFDM Channel Estimation. Algorithms 2017, 10, 3. https://doi.org/10.3390/a10010003
Li G, Liao G. A Pilot-Pattern Based Algorithm for MIMO-OFDM Channel Estimation. Algorithms. 2017; 10(1):3. https://doi.org/10.3390/a10010003
Chicago/Turabian StyleLi, Guomin, and Guisheng Liao. 2017. "A Pilot-Pattern Based Algorithm for MIMO-OFDM Channel Estimation" Algorithms 10, no. 1: 3. https://doi.org/10.3390/a10010003
APA StyleLi, G., & Liao, G. (2017). A Pilot-Pattern Based Algorithm for MIMO-OFDM Channel Estimation. Algorithms, 10(1), 3. https://doi.org/10.3390/a10010003






