Kernel Clustering with a Differential Harmony Search Algorithm for Scheme Classification
Abstract
:1. Introduction
2. Harmony Search and Kernel Fuzzy Clustering
2.1. Harmony Search Algorithm
- Step 1
- Initialize algorithm parameters
- Step 2
- Initializing the harmony memory
- Step 3
- Improvising a new harmony
| Algorithm 1 Improvisation of a New Harmony |
| For i = 1 to D do |
| If then |
| If then |
| end if |
| else |
| end if |
| end for |
- Step 4
- Update harmony memory
- Step 5
- Check the terminal criteria
2.2. Kernel Fuzzy Clustering
3. DHS-KFC
3.1. Differential Harmony Search Algorithm
3.1.1. A Self-Adaptive Solution Generation Strategy
3.1.2. A Differential Evolution-Based Population Update Strategy
3.1.3. Implementation of DHS
- Step 1
- Initialize the algorithm parameters
- Step 2
- Initialize the harmony memory
- Step 3
- Improvising a new harmony
| Algorithm 2 Improvisation of a New Harmony of DHS |
| for do |
| if () then |
| if () then |
| if () then |
| else |
| end if |
| end if |
| else |
| end if |
| end for |
- Step 4
- Update the harmony memory
| Algorithm 3 Update the Harmony Memory |
| if () then |
| Replace with |
| Set |
| end if |
| for do |
| if () then |
| for do |
| if () then |
| else |
| end if |
| end for |
| if () then |
| Replace with |
| end if |
| end if |
| end for |
- Step 5
- Check the stop criterion
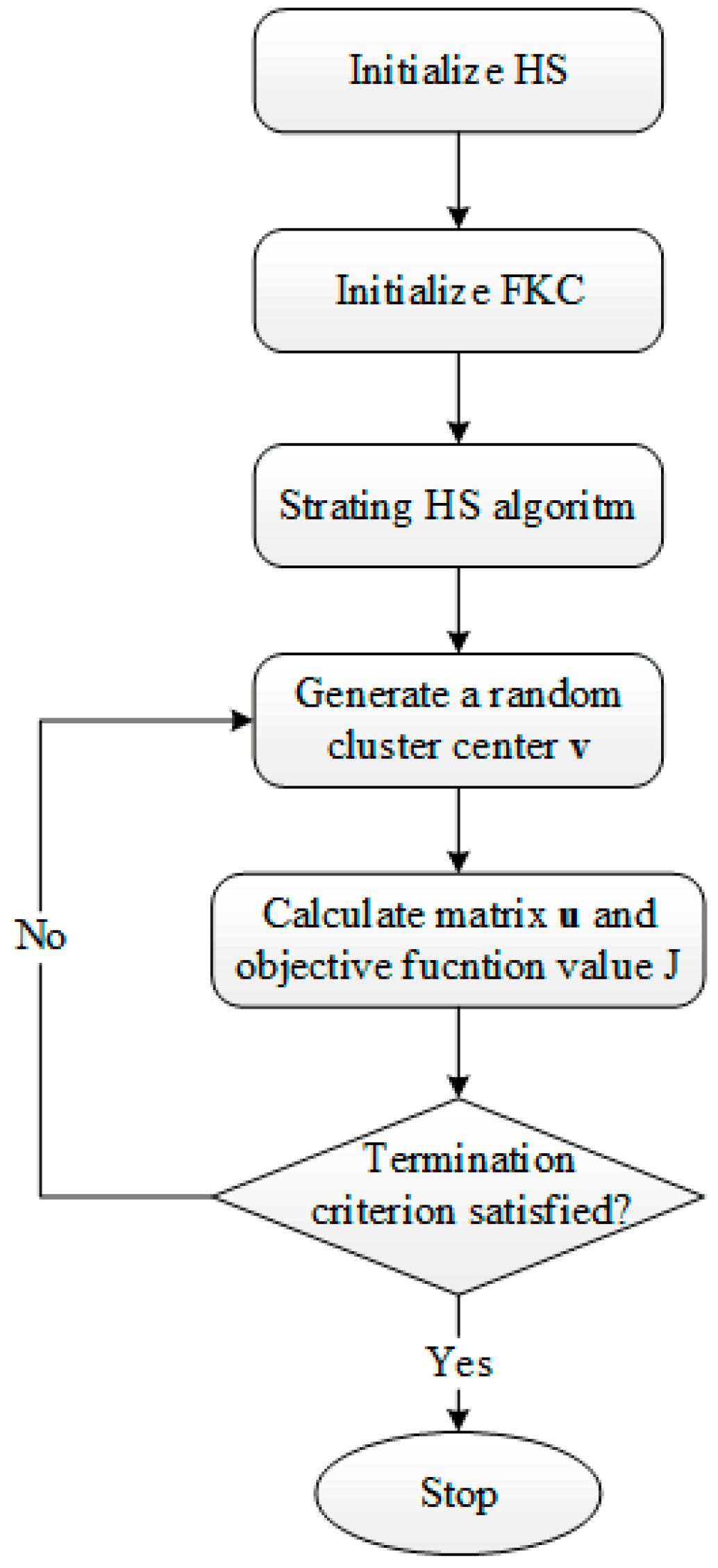
3.2. DHS-KFC
- Step 1
- initialize the parameters of the harmony search algorithm, initialize the harmony memory.
- Step 2
- initialize the parameters of the KFC, maximum generation N, and the weight matrix , set the initial value of the cluster center matrix to a randomly-generated matrix. Then the membership matrix can be obtained from Equation (10).
- Step 3
- generate a new solution vector based on the harmony search algorithm.
- Step 4
- obtain the cluster center matrix from the solution vector, calculate the membership matrix based on Equation (10), and then calculate based on Equation (16).
- Step 5
- compare with . If remains unchanged until 10 iterations, and go to Step 7.
- Step 6
- set the current iteration . If go to Step 7, otherwise go to Step 3.
- Step 7
- classify the samples based on their membership.
4. Experiments
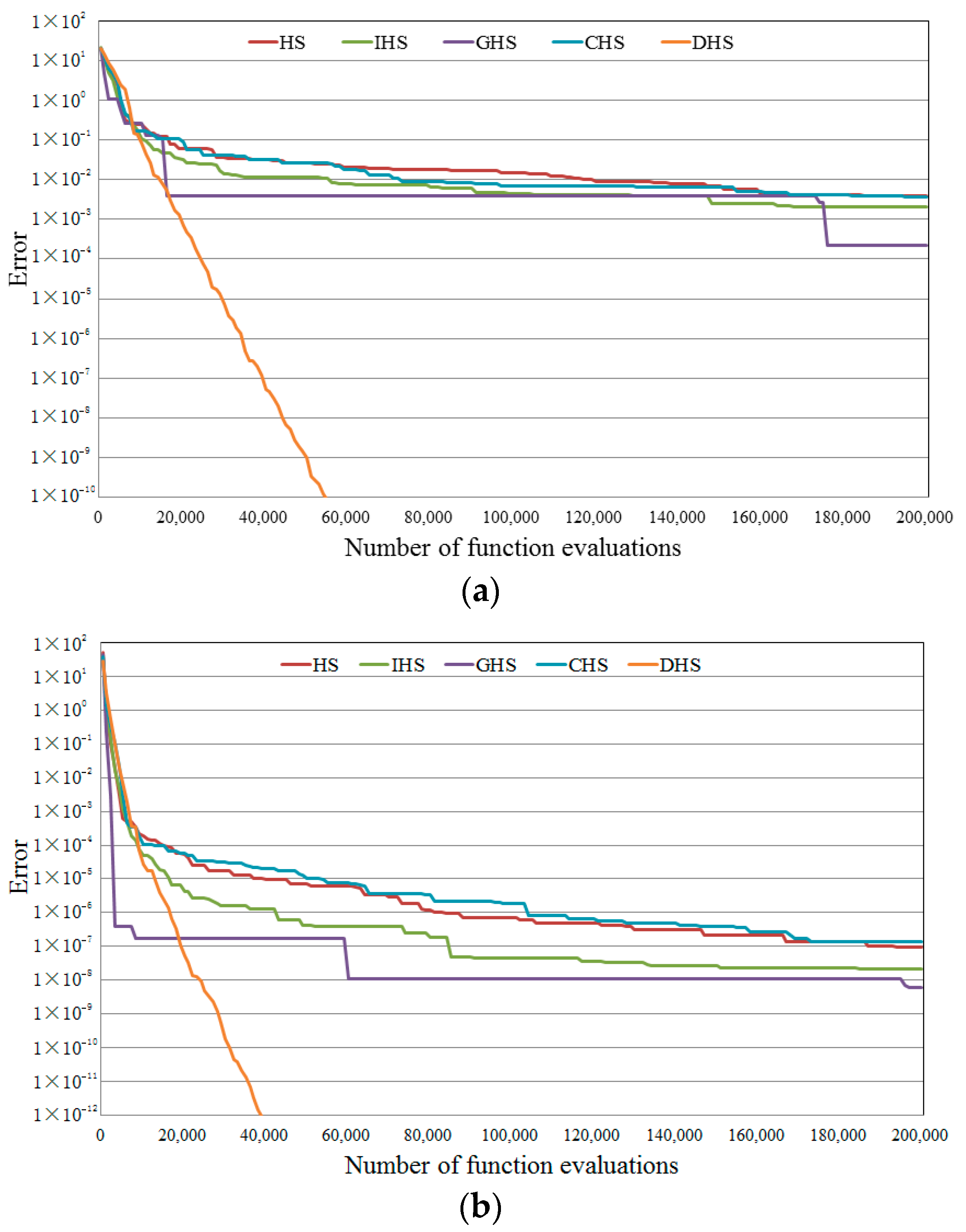
4.1. Numerical Experiments of DHS
4.1.1. Benchmark Function Tests
4.1.2. Sensitivity Analysis of Parameters
4.2. Numerical Experiments of DHS-KFC
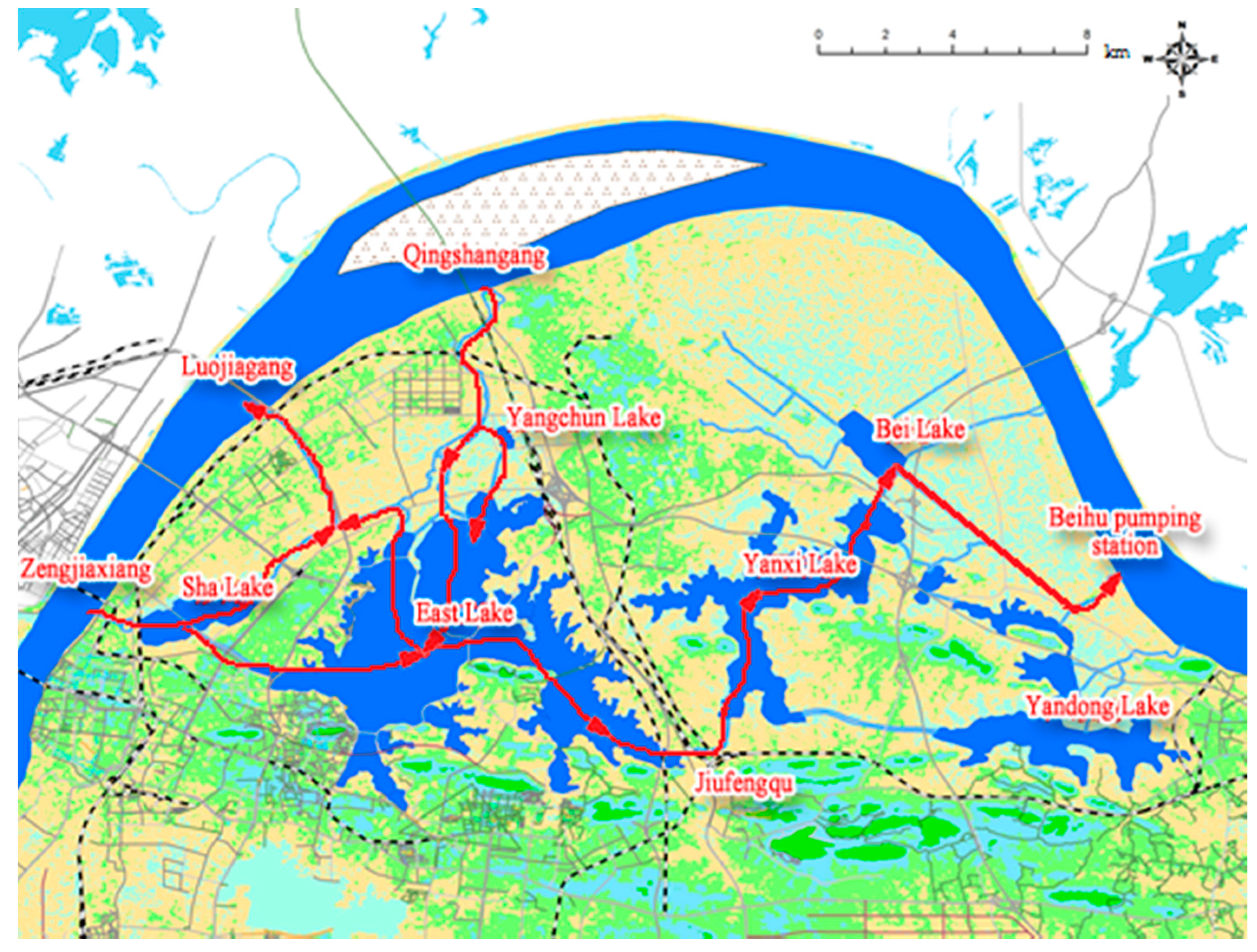
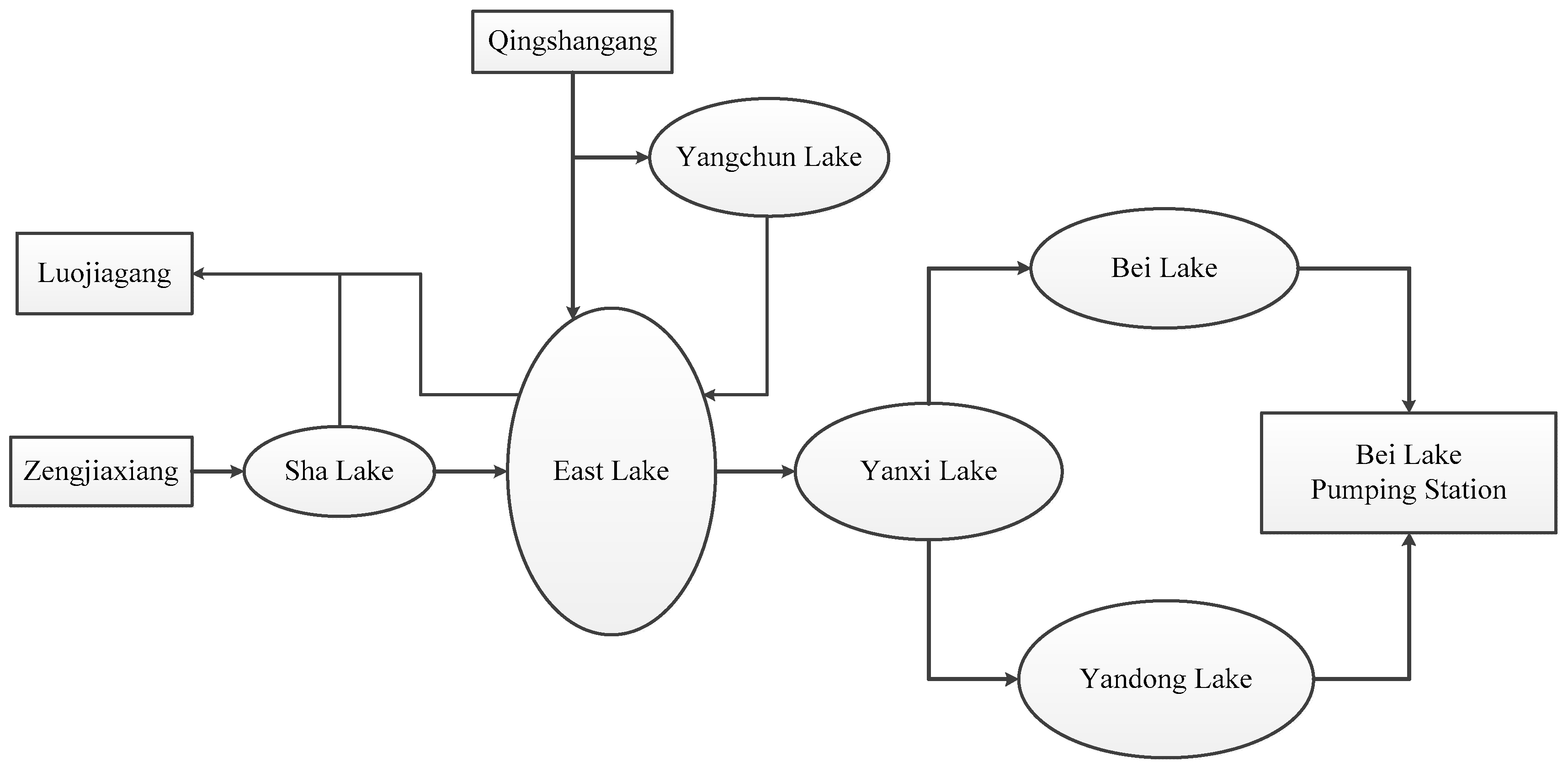
4.3. Case Study
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bianchi, L.; Dorigo, M.; Gambardella, L.M.; Gutjahr, W.J. A survey on metaheuristics for stochastic combinatorial optimization. Nat. Comput. 2009, 8, 239–287. [Google Scholar] [CrossRef]
- Blum, C.; Roli, A. Metaheuristics in combinatorial optimization: Overview and conceptual comparison. J. ACM Comput. Surv. 2001, 35, 268–308. [Google Scholar] [CrossRef]
- Almasi, M.H.; Sadollah, A.; Mounes, S.M.; Karim, M.R. Optimization of a transit services model with a feeder bus and rail system using metaheuristic algorithms. J. Comput. Civ. Eng. 2015, 29, 1–4. [Google Scholar] [CrossRef]
- Yazdi, J.; Sadollah, A.; Lee, E.H.; Yoo, D.; Kim, J.H. Application of multi-objective evolutionary algorithms for the rehabilitation of storm sewer pipe networks. J. Flood Risk Manag. 2015. [Google Scholar] [CrossRef]
- Yoo, D.G. Improved mine blast algorithm for optimal cost design of water distribution systems. Eng. Optim. 2014, 47, 1602–1618. [Google Scholar]
- Eskandar, H.; Sadollah, A.; Bahreininejad, A. Weight optimization of truss structures using water cycle algorithm. Int. J. Optim. Civ. Eng. 2013, 3, 115–129. [Google Scholar]
- Sadollah, A.; Eskandar, H.; Yoo, D.G.; Kim, J.H. Approximate solving of nonlinear ordinary differential equations using least square weight function and metaheuristic algorithms. Eng. Appl. Artif. Intell. 2015, 40, 117–132. [Google Scholar] [CrossRef]
- Glover, F.W.; Kochenberger, G.A. Handbook of Metaheuristics; Springer: New York, NY, USA, 2003; pp. 293–377. [Google Scholar]
- Geem, Z.W.; Kim, J.H.; Loganathan, G. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Feng, L.; Zhu, X. Novel feature selection method based on harmony search for email classification. Knowl. Based Syst. 2014, 73, 311–323. [Google Scholar] [CrossRef]
- Zammori, F.; Braglia, M.; Castellano, D. Harmony search algorithm for single-machine scheduling problem with planned maintenance. Comput. Ind. Eng. 2014, 76, 333–346. [Google Scholar] [CrossRef]
- Mahdavi, M.; Fesanghary, M.; Damangir, E. An improved harmony search algorithm for solving optimization problems. Appl. Math. Comput. 2007, 188, 1567–1579. [Google Scholar] [CrossRef]
- Omran, M.G.H.; Mahdavi, M. Global-best harmony search. Appl. Math. Comput. 2008, 198, 643–656. [Google Scholar] [CrossRef]
- Alatas, B. Chaotic harmony search algorithms. Appl. Math. Comput. 2010, 216, 2687–2699. [Google Scholar] [CrossRef]
- Jain, A.K.; Dubes, R.C. Algorithms for Clustering Data; Prentice hall Englewood Cliffs: Upper Saddle River, NJ, USA, 1988. [Google Scholar]
- Girolami, M. Mercer kernel-based clustering in feature space. IEEE Trans. Neural Netw. 2002, 13, 780–784. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.; Yang, J.; Wang, S.; Liu, X. Attribute weighted mercer kernel based fuzzy clustering algorithm for general non-spherical datasets. Soft Comput. 2006, 10, 1061–1073. [Google Scholar] [CrossRef]
- Yang, M.-S.; Tsai, H.-S. A gaussian kernel-based fuzzy c-means algorithm with a spatial bias correction. Pattern Recognit. Lett. 2008, 29, 1713–1725. [Google Scholar] [CrossRef]
- Ferreira, M.R.P.; de Carvalho, F.A.T. Kernel fuzzy c-means with automatic variable weighting. Fuzzy Sets Syst. 2014, 237, 1–46. [Google Scholar] [CrossRef]
- Graves, D.; Pedrycz, W. Kernel-based fuzzy clustering and fuzzy clustering: A comparative experimental study. Fuzzy Sets Syst. 2010, 161, 522–543. [Google Scholar] [CrossRef]
- Xing, H.-J.; Ha, M.-H. Further improvements in feature-weighted fuzzy c-means. Inf. Sci. 2014, 267, 1–15. [Google Scholar] [CrossRef]
- Chen, Z.P.; Yang, W. An magdm based on constrained fahp and ftopsis and its application to supplier selection. Math. Comput. Model. 2011, 54, 2802–2815. [Google Scholar] [CrossRef]
- Singh, R.K.; Benyoucef, L. A fuzzy topsis based approach for e-sourcing. Eng. Appl. Artif. Intell. 2011, 24, 437–448. [Google Scholar] [CrossRef]
| Function | Formula | Search Domain | Optimum |
|---|---|---|---|
| Ackley function | |||
| Griewank function | |||
| Rastrigin function | |||
| Rosenbrock function | |||
| Sphere function | |||
| Schwefel 2.22 function |
| Algorithm | hms | hmcr | par | fw | NI |
|---|---|---|---|---|---|
| HS | 50 | 0.9 | 0.3 | 0.005 | 100,000 |
| IHS | 50 | 0.9 | Max: 0.5 Min: 0.1 | Max: 0.01 Min: 0.001 | 100,000 |
| GHS | 50 | 0.9 | 0.3 | 0.005 | 100,000 |
| CHS | 50 | 0.9 | 0.3 | 0.005 | 100,000 |
| DHS | 50 | 0.9 | 0.3 | 0.005 | 100,000 |
| Function | HS | IHS | GHS | CHS | DHS | |
|---|---|---|---|---|---|---|
| Ackley function | Mean | 8.49 × 10−3 | 6.16 × 10−3 | 3.95 × 10−3 | 1.12 × 10−2 | 1.57 × 10−13 |
| Min | 3.29 × 10−3 | 2.44 × 10−3 | 1.35 × 10−5 | 3.56 × 10−3 | 4.57 × 10−14 | |
| Max | 1.62 × 10−2 | 1.16 × 10−2 | 2.10 × 10−2 | 2.54 × 10−2 | 4.69 × 10−13 | |
| Stdv | 2.43 × 10−3 | 1.67 × 10−3 | 3.48 × 10−3 | 3.79 × 10−3 | 6.78 × 10−14 | |
| Griewank function | Mean | 1.58 × 10−2 | 1.46 × 10−2 | 5.00 × 10−4 | 1.37 × 10−2 | 5.45 × 10−10 |
| Min | 8.62 × 10−5 | 1.92 × 10−5 | 1.59 × 10−7 | 9.62 × 10−5 | 0 | |
| Max | 8.13 × 10−2 | 7.38 × 10−2 | 1.13 × 10−2 | 9.15 × 10−2 | 1.69 × 10−8 | |
| Stdv | 1.81 × 10−2 | 1.76 × 10−2 | 1.24 × 10−3 | 1.54 × 10−2 | 2.06 × 10−9 | |
| Rastrigin function | Mean | 1.49 × 10−4 | 8.20 × 10−5 | 7.44 × 10−5 | 2.45 × 10−4 | 1.02 × 10−12 |
| Min | 2.66 × 10−5 | 1.35 × 10−5 | 1.82 × 10−8 | 4.33 × 10−5 | 0 | |
| Max | 3.30 × 10−4 | 2.01 × 10−4 | 1.17 × 10−3 | 9.92 × 10−4 | 6.20× 10−11 | |
| Stdv | 7.13 × 10−5 | 4.22 × 10−5 | 1.64 × 10−4 | 1.42 × 10−4 | 6.17× 10−12 | |
| Rosenbrock function | Mean | 2.10 | 1.98 | 1.77 | 2.32 | 7.16−1 |
| Min | 5.65 × 10−3 | 1.00 × 10−2 | 1.80 × 10−6 | 1.04 × 10−2 | 6.22 × 10−4 | |
| Max | 5.32 | 5.34 | 8.37 | 6.08 | 4.64 | |
| Stdv | 1.57 | 1.51 | 3.10 | 1.69 | 9.75 × 10−1 | |
| Sphere function | Mean | 7.33 × 10−7 | 4.30 × 10−7 | 3.35 × 10−7 | 1.01 × 10−6 | 1.85 × 10−28 |
| Min | 1.40 × 10−7 | 1.02 × 10−7 | 3.00 × 10−14 | 2.21 × 10−7 | 2.92 × 10−29 | |
| Max | 2.03 × 10−6 | 1.43 × 10−6 | 3.58 × 10−6 | 3.55 × 10−6 | 7.97 × 10−28 | |
| Stdv | 3.83 × 10−7 | 2.24 × 10−7 | 6.13 × 10−7 | 6.07 × 10−7 | 1.72 × 10−28 | |
| Schwefel 2.22 function | Mean | 3.07 × 10−3 | 2.41 × 10−3 | 3.23 × 10−3 | 3.68 × 10−3 | 3.12 × 10−12 |
| Min | 1.29 × 10−3 | 1.12 × 10−3 | 1.62 × 10−6 | 1.23 × 10−3 | 7.35 × 10−13 | |
| Max | 5.12 × 10−3 | 3.91 × 10−3 | 1.32 × 10−2 | 6.62 × 10−3 | 1.33 × 10−11 | |
| Stdv | 9.05 × 10−4 | 5.91 × 10−4 | 2.86 × 10−3 | 1.08 × 10−3 | 1.99 × 10−12 |
| Function | Precision | HS | IHS | GHS | CHS | DHS |
|---|---|---|---|---|---|---|
| Ackley function | <1 × 10−1 | 100% | 100% | 100% | 100% | 100% |
| <1 × 10−2 | 74% | 99% | 93% | 40% | 100% | |
| <1 × 10−3 | 0% | 0% | 23% | 0% | 100% | |
| <1 × 10−4 | 0% | 0% | 2% | 0% | 100% | |
| <1 × 10−5 | 0% | 0% | 0% | 0% | 100% | |
| <1 × 10−6 | 0% | 0% | 0% | 0% | 100% | |
| <1 × 10−7 | 0% | 0% | 0% | 0% | 100% | |
| Griewank function | <1 × 10−1 | 100% | 100% | 100% | 100% | 100% |
| <1 × 10−2 | 32% | 44% | 99% | 32% | 100% | |
| <1 × 10−3 | 30% | 44% | 84% | 27% | 100% | |
| <1 × 10−4 | 1% | 7% | 47% | 1% | 100% | |
| <1 × 10−5 | 0% | 0% | 17% | 0% | 100% | |
| <1 × 10−6 | 0% | 0% | 5% | 0% | 100% | |
| <1 × 10−7 | 0% | 0% | 0% | 0% | 100% | |
| Rastrigin function | <1 × 10−1 | 100% | 100% | 100% | 100% | 100% |
| <1 × 10−2 | 100% | 100% | 100% | 100% | 100% | |
| <1 × 10−3 | 100% | 100% | 99% | 100% | 100% | |
| <1 × 10−4 | 25% | 69% | 81% | 11% | 100% | |
| <1 × 10−5 | 0% | 0% | 43% | 0% | 100% | |
| <1 × 10−6 | 0% | 0% | 14% | 0% | 100% | |
| <1 × 10−7 | 0% | 0% | 4% | 0% | 100% | |
| Rosenbrock function | <1 × 10−1 | 6% | 9% | 49% | 4% | 34% |
| <1 × 10−2 | 2% | 0% | 29% | 0% | 10% | |
| <1 × 10−3 | 0% | 0% | 6% | 0% | 1% | |
| <1 × 10−4 | 0% | 0% | 3% | 0% | 0% | |
| <1 × 10−5 | 0% | 0% | 1% | 0% | 0% | |
| <1 × 10−6 | 0% | 0% | 0% | 0% | 0% | |
| <1 × 10−7 | 0% | 0% | 0% | 0% | 0% | |
| Sphere function | <1 × 10−1 | 100% | 100% | 100% | 100% | 100% |
| <1 × 10−2 | 100% | 100% | 100% | 100% | 100% | |
| <1 × 10−3 | 100% | 100% | 100% | 100% | 100% | |
| <1 × 10−4 | 100% | 100% | 100% | 100% | 100% | |
| <1 × 10−5 | 100% | 100% | 100% | 100% | 100% | |
| <1 × 10−6 | 77% | 98% | 89% | 59% | 100% | |
| <1 × 10−7 | 0% | 0% | 49% | 0% | 100% | |
| Schwefel 2.22 function | <1 × 10−1 | 100% | 100% | 100% | 100% | 100% |
| <1 × 10−2 | 100% | 100% | 98% | 100% | 100% | |
| <1 × 10−3 | 0% | 0% | 23% | 0% | 100% | |
| <1 × 10−4 | 0% | 0% | 4% | 0% | 100% | |
| <1 × 10−5 | 0% | 0% | 1% | 0% | 100% | |
| <1 × 10−6 | 0% | 0% | 0% | 0% | 100% | |
| <1 × 10−7 | 0% | 0% | 0% | 0% | 100% |
| Function | sc = 20 | sc = 40 | sc = 60 | sc = 80 | sc = 100 | |
|---|---|---|---|---|---|---|
| Ackley | Mean | 9.12 × 10−13 | 2.81 × 10−11 | 3.87 × 10−10 | 3.01 × 10−9 | 1.33 × 10−8 |
| Stdv | 3.38 × 10−13 | 1.15 × 10−11 | 1.48 × 10−10 | 1.18 × 10−9 | 4.91 × 10−9 | |
| Griewank | Mean | 4.65 × 10−6 | 2.63 × 10−5 | 7.38 × 10−4 | 3.13 × 10−3 | 3.80 × 10−3 |
| Stdv | 2.91 × 10−5 | 1.84 × 10−4 | 3.86 × 10−3 | 7.26 × 10−3 | 9.49 × 10−3 | |
| Rastrigin | Mean | 5.97 × 10−15 | 0 | 0 | 0 | 2.84 × 10−16 |
| Stdv | 4.22 × 10−14 | 0 | 0 | 0 | 2.01 × 10−15 | |
| Rosenbrock | Mean | 1.32 | 1.55 | 1.85 | 1.49 | 1.72 |
| Stdv | 1.36 | 1.40 | 1.64 | 1.29 | 1.57 | |
| Sphere | Mean | 7.18 × 10−27 | 9.36 × 10−24 | 1.56 × 10−21 | 9.81 × 10−20 | 1.92 × 10−18 |
| Stdv | 4.38 × 10−27 | 8.31 × 10−24 | 9.09 × 10−22 | 6.95 × 10−20 | 1.42 × 10−18 | |
| Schwefel 2.22 | Mean | 4.38 × 10−12 | 3.82 × 10−11 | 2.53 × 10−10 | 1.09 × 10−9 | 3.66 × 10−9 |
| Stdv | 1.99 × 10−12 | 1.76 × 10−11 | 9.65 × 10−11 | 4.93 × 10−10 | 1.64 × 10−9 |
| Function | hms = 10 | hms = 30 | hms = 50 | hms = 70 | hms = 90 | |
|---|---|---|---|---|---|---|
| Ackley | Mean | 1.71 × 10−11 | 3.11 × 10−15 | 3.76 × 10−13 | 1.58 × 10−9 | 1.68 × 10−7 |
| Stdv | 3.45 × 10−13 | 3.11 × 10−15 | 1.66 × 10−13 | 6.43 × 10−10 | 8.20 × 10−8 | |
| Griewank | Mean | 6.58 × 10−2 | 2.47 × 10−4 | 9.37 × 10−6 | 4.32 × 10−7 | 2.64 × 10−5 |
| Stdv | 7.93 × 10−2 | 1.74 × 10−3 | 6.62 × 10−5 | 7.10 × 10−7 | 1.92 × 10−5 | |
| Rastrigin | Mean | 0 | 0 | 0 | 2.72 × 10−6 | 2.46 × 10−6 |
| Stdv | 0 | 0 | 0 | 1.92 × 10−5 | 1.74 × 10−5 | |
| Rosenbrock | Mean | 1.94 | 1.38 | 8.70 × 10−1 | 7.11 × 10−1 | 1.09 |
| Stdv | 1.51 | 1.35 | 1.14 | 6.14 × 10−1 | 6.05 × 10−1 | |
| Sphere | Mean | 1.16 × 10−89 | 6.20 × 10−43 | 1.97 × 10−28 | 1.96 × 10−21 | 2.62 × 10−17 |
| Stdv | 2.96 × 10−89 | 8.53 × 10−43 | 1.93 × 10−28 | 1.36 × 10−21 | 1.20 × 10−17 | |
| Schwefel 2.22 | Mean | 1.57 × 10−41 | 9.47 × 10−19 | 2.92 × 10−12 | 3.76 × 10−9 | 2.27 × 10−7 |
| Stdv | 4.08 × 10−41 | 6.63 × 10−19 | 1.37 × 10−12 | 1.78 × 10−9 | 8.24 × 10−8 |
| Function | hmcr = 0.7 | hmcr = 0.8 | hmcr = 0.9 | hmcr = 0.99 | |
|---|---|---|---|---|---|
| Ackley | Mean | 3.95 × 10−10 | 5.27 × 10−12 | 1.73 × 10−13 | 6.09 × 10−15 |
| Stdv | 5.56 × 10−10 | 2.04 × 10−12 | 6.69 × 10−14 | 1.81 × 10−15 | |
| Griewank | Mean | 9.08 × 10−5 | 7.97 × 10−7 | 5.26 × 10−9 | 2.46 × 10−4 |
| Stdv | 1.34 × 10−4 | 1.13 × 10−6 | 3.17 × 10−8 | 1.74 × 10−3 | |
| Rastrigin | Mean | 7.39 × 10−14 | 5.23 × 10−14 | 2.58 × 10−8 | 4.18 × 10−1 |
| Stdv | 3.73 × 10−13 | 3.70 × 10−13 | 1.82 × 10−7 | 6.39 × 10−1 | |
| Rosenbrock | Mean | 7.88 × 10−1 | 5.49 × 10−1 | 1.26 | 1.72 |
| Stdv | 4.52 × 10−1 | 3.80 × 10−1 | 1.43 | 1.54 | |
| Sphere | Mean | 8.59 × 10−22 | 1.09 × 10−25 | 2.17 × 10−28 | 7.11 × 10−32 |
| Stdv | 5.18 × 10−21 | 8.31 × 10−26 | 1.65 × 10−28 | 6.02 × 10−32 | |
| Schwefel 2.22 | Mean | 3.53 × 10−8 | 5.96 × 10−10 | 3.10 × 10−12 | 1.43 × 10−14 |
| Stdv | 1.88 × 10−8 | 4.04 × 10−10 | 2.01 × 10−12 | 6.77 × 10−15 |
| Function | par = 0.1 | par = 0.3 | par = 0.5 | par = 0.7 | par = 0.9 | |
|---|---|---|---|---|---|---|
| Ackley | Mean | 3.04 × 10−15 | 1.54 × 10−13 | 5.74 × 10−10 | 5.64 × 10−9 | 3.02 × 10−8 |
| Stdv | 5.02 × 10−16 | 6.46 × 10−14 | 1.21 × 10−9 | 4.21 × 10−9 | 4.19 × 10−8 | |
| Griewank | Mean | 1.03 × 10−3 | 2.23 × 10−9 | 3.36 × 10−6 | 5.70 × 10−5 | 1.11 × 10−4 |
| Stdv | 3.37 × 10−3 | 1.35 × 10−8 | 1.06 × 10−5 | 1.83 × 10−4 | 2.98 × 10−4 | |
| Rastrigin | Mean | 0 | 1.64 × 10−7 | 1.88 × 10−5 | 8.43 × 10−2 | 4.59 × 10−1 |
| Stdv | 0 | 1.16 × 10−6 | 9.86 × 10−5 | 2.67 × 10−1 | 6.11 × 10−1 | |
| Rosenbrock | Mean | 3.36 × 10−1 | 1.05 | 1.14 | 1.89 | 2.18 |
| Stdv | 3.88 × 10−1 | 1.17 | 1.35 | 1.45 | 1.54 | |
| Sphere | Mean | 1.03 × 10−40 | 1.82 × 10−28 | 1.92 × 10−21 | 2.81 × 10−19 | 7.43 × 10−19 |
| Stdv | 1.08 × 10−40 | 1.59 × 10−28 | 4.61 × 10−21 | 3.63 × 10−19 | 2.10 × 10−18 | |
| Schwefel 2.22 | Mean | 7.58 × 10−21 | 2.85 × 10−12 | 2.21 × 10−8 | 6.46 × 10−8 | 7.54 × 10−8 |
| Stdv | 5.31 × 10−21 | 1.62 × 10−12 | 1.07 × 10−8 | 2.73 × 10−8 | 3.71 × 10−8 |
| Function | fw = 0.001 | fw = 0.004 | fw = 0.007 | fw = 0.01 | |
|---|---|---|---|---|---|
| Ackley | Mean | 3.11 × 10−15 | 2.97 × 10−15 | 3.04 × 10−15 | 2.82 × 10−15 |
| Stdv | 0 | 7.03 × 10−16 | 5.02 × 10−16 | 9.74 × 10−16 | |
| Griewank | Mean | 2.24 × 10−3 | 2.41 × 10−3 | 1.24 × 10−3 | 2.95 × 10−3 |
| Stdv | 4.77 × 10−3 | 5.48 × 10−3 | 3.73 × 10−3 | 5.86 × 10−3 | |
| Rastrigin | Mean | 1.90 × 10−5 | 0 | 0 | 0 |
| Stdv | 1.34 × 10−4 | 0 | 0 | 0 | |
| Rosenbrock | Mean | 4.10 × 10−1 | 3.37 × 10−1 | 4.42 × 10−1 | 3.03 × 10−1 |
| Stdv | 6.34 × 10−1 | 5.74 × 10−1 | 8.63 × 10−1 | 4.94 × 10−1 | |
| Sphere | Mean | 8.78 × 10−58 | 2.91 × 10−57 | 2.44 × 10−56 | 1.23 × 10−55 |
| Stdv | 1.73 × 10−57 | 4.10 × 10−57 | 3.88 × 10−56 | 2.55 × 10−55 | |
| Schwefel 2.22 | Mean | 7.58 × 10−33 | 2.49 × 10−32 | 7.39 × 10−32 | 2.05 × 10−31 |
| Stdv | 9.03 × 10−33 | 1.94 × 10−32 | 6.15 × 10−32 | 1.92 × 10−31 |
| Dataset | k-Means | Fuzzy Cluster | DHS-KFC | ||
|---|---|---|---|---|---|
| Wine data set | Class 1 | 59 | 61 | 63 | 59 |
| Class 2 | 71 | 63 | 63 | 70 | |
| Class 3 | 48 | 54 | 52 | 49 | |
| Error rates (%) | 4.49% | 4.49% | 0.56% | ||
| Iris data set | Class 1 | 50 | 50 | 50 | 50 |
| Class 2 | 50 | 61 | 60 | 58 | |
| Class 3 | 50 | 39 | 40 | 42 | |
| Error rates (%) | 11.33% | 12.00% | 10.67% |
| Lake | COD (mg/L) | TN (mg/L) | TP (mg/L) |
|---|---|---|---|
| East Lake | 24 | 2.32 | 0.196 |
| Sha Lake | 50 | 6.11 | 0.225 |
| Yangchun Lake | 26 | 1.14 | 0.085 |
| Yanxi Lake | 34 | 3.82 | 0.2 |
| Yandong Lake | 10 | 0.7 | 0.05 |
| Bei Lake | 32 | 3.81 | 0.122 |
| No. | 1–5 Days | 6–10 Days | 11–15 Days | 16–20 Days | 21–25 Days | 26–30 Days | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| qz | ql | qz | ql | qz | ql | qz | ql | qz | ql | qz | ql | |||||||
| 1 | 10 | 0 | 10 | 10 | 30 | 40 | 10 | 30 | 20 | 10 | 30 | 20 | 10 | 30 | 20 | 10 | 30 | 20 |
| 2 | 10 | 0 | 10 | 10 | 30 | 40 | 5 | 22.5 | 13.8 | 5 | 22.5 | 13.8 | 5 | 22.5 | 13.8 | |||
| 3 | 10 | 0 | 10 | 10 | 30 | 40 | 10 | 30 | 40 | 10 | 30 | 20 | 10 | 30 | 20 | 10 | 30 | 20 |
| 4 | 10 | 0 | 10 | 10 | 30 | 40 | 10 | 30 | 40 | 7.5 | 30 | 18.8 | 7.5 | 30 | 18.8 | 7.5 | 30 | 18.8 |
| 5 | 10 | 0 | 10 | 10 | 30 | 40 | 10 | 30 | 40 | 5 | 27.5 | 16.2 | 5 | 27.5 | 16.2 | 5 | 27.5 | 16.2 |
| 6 | 10 | 0 | 10 | 10 | 30 | 40 | 10 | 30 | 40 | 5 | 22.5 | 13.8 | 5 | 22.5 | 13.8 | 5 | 22.5 | 13.8 |
| 7 | 10 | 0 | 10 | 10 | 30 | 40 | 10 | 30 | 40 | 10 | 30 | 40 | 7.5 | 20 | 13.8 | |||
| 8 | 10 | 0 | 10 | 10 | 25 | 35 | 5 | 25 | 15 | 5 | 25 | 15 | 5 | 25 | 15 | 5 | 25 | 15 |
| 9 | 10 | 0 | 10 | 10 | 25 | 35 | 10 | 20 | 15 | 10 | 20 | 15 | 10 | 20 | 15 | 10 | 20 | 15 |
| 10 | 10 | 0 | 10 | 10 | 25 | 35 | 5 | 20 | 12.5 | 5 | 20 | 12.5 | 5 | 20 | 12.5 | |||
| 11 | 10 | 0 | 10 | 10 | 25 | 35 | 10 | 25 | 35 | 5 | 25 | 15 | 5 | 25 | 15 | |||
| 12 | 10 | 0 | 10 | 10 | 25 | 35 | 10 | 25 | 35 | 10 | 25 | 35 | 7.5 | 27.5 | 17.5 | 7.5 | 27.5 | 17.5 |
| 13 | 10 | 0 | 10 | 10 | 25 | 35 | 10 | 25 | 35 | 10 | 25 | 35 | 5 | 25 | 15 | 5 | 25 | 15 |
| 14 | 10 | 0 | 10 | 5 | 30 | 35 | 10 | 22.5 | 16.2 | 10 | 22.5 | 16.2 | 10 | 22.5 | 16.2 | |||
| 15 | 10 | 0 | 10 | 5 | 30 | 35 | 5 | 30 | 35 | 7.5 | 27.5 | 17.5 | 7.5 | 27.5 | 17.5 | |||
| 16 | 10 | 0 | 10 | 5 | 30 | 35 | 5 | 30 | 35 | 7.5 | 27.5 | 17.5 | 7.5 | 27.5 | 17.5 | 7.5 | 27.5 | 17.5 |
| 17 | 10 | 0 | 10 | 5 | 30 | 35 | 5 | 30 | 35 | 5 | 30 | 17.5 | 5 | 25 | 15 | |||
| 18 | 10 | 0 | 10 | 5 | 30 | 35 | 5 | 30 | 35 | 5 | 30 | 35 | 5 | 22.5 | 13.8 | 5 | 22.5 | 13.8 |
| No. | Sha Lake | Yangchun Lake | East Lake | Yandong Lake | Bei Lake | Water | Cost | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TP | TN | COD | TP | TN | COD | TP | TN | COD | TP | TN | COD | TP | TN | COD | |||
| 1 | 0.108 | 2.386 | 17.569 | 0.066 | 0.997 | 10.602 | 0.16 | 2.136 | 19.43 | 0.198 | 3.294 | 30.023 | 0.165 | 3.907 | 32.88 | 9072 | 226.8 |
| 2 | 0.126 | 2.942 | 22.051 | 0.066 | 0.998 | 10.773 | 0.172 | 2.23 | 20.895 | 0.2 | 3.366 | 30.644 | 0.161 | 3.912 | 32.93 | 5724 | 143.1 |
| 3 | 0.108 | 2.386 | 17.569 | 0.066 | 0.997 | 10.602 | 0.161 | 2.14 | 19.438 | 0.2 | 3.366 | 30.566 | 0.161 | 3.917 | 32.943 | 9072 | 226.8 |
| 4 | 0.115 | 2.593 | 19.413 | 0.066 | 0.997 | 10.602 | 0.162 | 2.161 | 19.668 | 0.2 | 3.365 | 30.566 | 0.161 | 3.917 | 32.943 | 8748 | 218.7 |
| 5 | 0.12 | 2.751 | 20.453 | 0.066 | 0.997 | 10.602 | 0.165 | 2.177 | 19.95 | 0.2 | 3.367 | 30.581 | 0.161 | 3.917 | 32.943 | 8100 | 202.5 |
| 6 | 0.12 | 2.751 | 20.453 | 0.066 | 0.997 | 10.602 | 0.168 | 2.209 | 20.321 | 0.2 | 3.369 | 30.607 | 0.161 | 3.917 | 32.943 | 7452 | 186.3 |
| 7 | 0.116 | 2.624 | 19.634 | 0.066 | 0.998 | 10.773 | 0.168 | 2.211 | 20.482 | 0.202 | 3.627 | 32.489 | 0.144 | 3.877 | 32.597 | 6804 | 170.1 |
| 8 | 0.123 | 2.865 | 21.321 | 0.066 | 0.997 | 10.602 | 0.17 | 2.222 | 20.575 | 0.199 | 3.301 | 30.12 | 0.165 | 3.907 | 32.881 | 7128 | 178.2 |
| 9 | 0.108 | 2.386 | 17.569 | 0.066 | 0.997 | 10.602 | 0.168 | 2.221 | 20.431 | 0.2 | 3.306 | 30.184 | 0.165 | 3.907 | 32.882 | 7128 | 178.2 |
| 10 | 0.126 | 2.942 | 22.051 | 0.066 | 0.998 | 10.773 | 0.175 | 2.26 | 21.26 | 0.2 | 3.369 | 30.684 | 0.161 | 3.912 | 32.93 | 5184 | 129.6 |
| 11 | 0.122 | 2.827 | 21.174 | 0.066 | 0.998 | 10.773 | 0.17 | 2.217 | 20.659 | 0.201 | 3.469 | 31.382 | 0.155 | 3.906 | 32.87 | 6048 | 151.2 |
| 12 | 0.113 | 2.536 | 18.893 | 0.066 | 0.997 | 10.602 | 0.165 | 2.185 | 19.988 | 0.201 | 3.473 | 31.379 | 0.156 | 3.91 | 32.882 | 7992 | 199.8 |
| 13 | 0.117 | 2.668 | 19.823 | 0.066 | 0.997 | 10.602 | 0.167 | 2.2 | 20.24 | 0.201 | 3.474 | 31.383 | 0.156 | 3.91 | 32.882 | 7560 | 189 |
| 14 | 0.115 | 2.62 | 19.627 | 0.066 | 0.998 | 10.773 | 0.169 | 2.23 | 20.719 | 0.2 | 3.366 | 30.648 | 0.161 | 3.912 | 32.93 | 6156 | 153.9 |
| 15 | 0.126 | 2.932 | 22.261 | 0.066 | 0.998 | 10.773 | 0.169 | 2.208 | 20.578 | 0.201 | 3.468 | 31.368 | 0.155 | 3.906 | 32.87 | 6480 | 162 |
| 16 | 0.122 | 2.818 | 21.328 | 0.066 | 0.997 | 10.602 | 0.167 | 2.203 | 20.236 | 0.2 | 3.367 | 30.583 | 0.161 | 3.917 | 32.943 | 7992 | 199.8 |
| 17 | 0.134 | 3.204 | 24.488 | 0.066 | 0.998 | 10.773 | 0.172 | 2.207 | 20.752 | 0.202 | 3.627 | 32.488 | 0.144 | 3.877 | 32.597 | 6264 | 156.6 |
| 18 | 0.133 | 3.137 | 23.92 | 0.066 | 0.997 | 10.602 | 0.171 | 2.22 | 20.632 | 0.201 | 3.473 | 31.375 | 0.156 | 3.91 | 32.882 | 7344 | 183.6 |
| No. | Classification | No. | Classification | No. | Classification |
|---|---|---|---|---|---|
| 1 | I | 7 | IV | 13 | II |
| 2 | III | 8 | V | 14 | III |
| 3 | I | 9 | V | 15 | III |
| 4 | I | 10 | III | 16 | II |
| 5 | II | 11 | III | 17 | IV |
| 6 | II | 12 | II | 18 | II |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Y.; Zhou, J.; Tayyab, M. Kernel Clustering with a Differential Harmony Search Algorithm for Scheme Classification. Algorithms 2017, 10, 14. https://doi.org/10.3390/a10010014
Feng Y, Zhou J, Tayyab M. Kernel Clustering with a Differential Harmony Search Algorithm for Scheme Classification. Algorithms. 2017; 10(1):14. https://doi.org/10.3390/a10010014
Chicago/Turabian StyleFeng, Yu, Jianzhong Zhou, and Muhammad Tayyab. 2017. "Kernel Clustering with a Differential Harmony Search Algorithm for Scheme Classification" Algorithms 10, no. 1: 14. https://doi.org/10.3390/a10010014
APA StyleFeng, Y., Zhou, J., & Tayyab, M. (2017). Kernel Clustering with a Differential Harmony Search Algorithm for Scheme Classification. Algorithms, 10(1), 14. https://doi.org/10.3390/a10010014





