A Fault Detection and Data Reconciliation Algorithm in Technical Processes with the Help of Haar Wavelets Packets †
Abstract
:1. Introduction
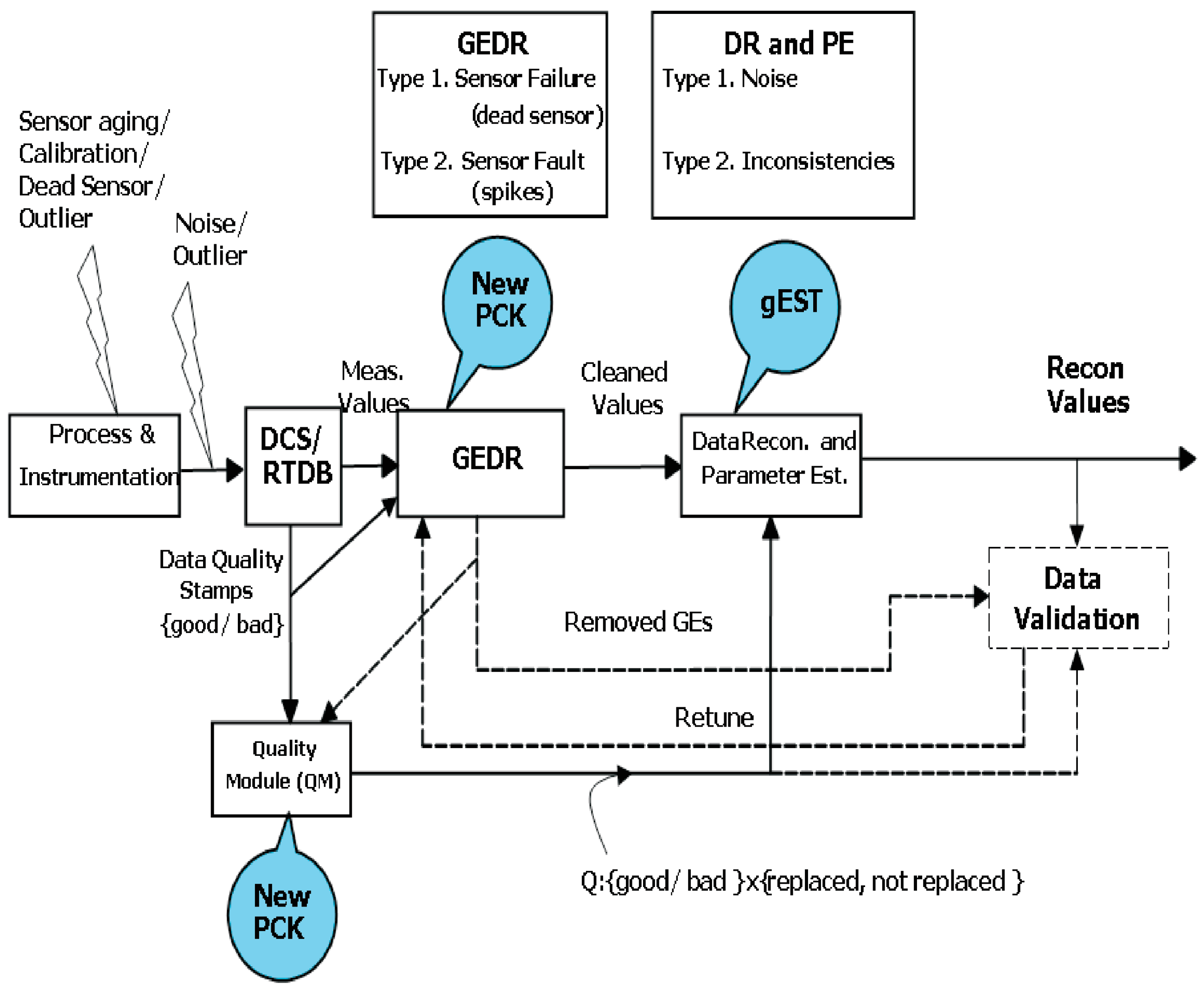
1.1. Modules
- Process and Instrumentation: The process values can be influenced by sensor aging or incorrect calibration. Biases model effects them, and they are supposed to be smaller in comparison with Gross Errors (GEs).
- DCS/RTDB (Distributed control system/Real-time database systems): The data logged by DCS/RTDB includes the values from the process and instrumentation block such as noise, outliers and the interference from the measurement; possible effects to the anti-aliasing, analogous digital (AD) conversion, and quantization noise; and possibly LP filtering.
- Quality Module (QM): DC includes some functions of the QM. In the case of measuring the same physical property by three independent sensors, the value with a “bad” stamp is automatically discarded, and the values of other two sensors will be applied. Other scenarios, including soft sensors, are possible and they depend on the DCS system and configurations. In our case, the QM can bring more performance by means of information from GEDR. Therefore, on input, QM incorporates two streams of information. One of the streams is derived from the DCS/RTDB and the other stream is derived from the GEDR. Properties being referred to the data points combined and gave additional information to other devices: DR, PE, and Data Verification. Series of properties developed by DCS/RTDB can be good/bad, while series of properties developed by GEDR can be replaced/not replaced.
- GEDR: The data based on the DCS/RTDB block must be elaborated by Gross Error Detection and replacement. The data will be cleared by means of GEDR before proceeding with data (DR) reconciliation (DR) and parameter estimation (PE). The GEs, after being found and deleted, are to be put under analysis made after the DR and PE. It should be done to estimate if they are really GEs and consecutively to configure the filter parameters newly. GE is substituted by GEDR, whose value corresponds to the local behavior of the discovered variable. For this purpose, the average of the last couple of valid data points can be applied. This module is an important part of our research.
1.2. Gross Error Types and Examples
- Type 1 GEs, which are produced by sensor failures and lead to a stable measurement error. Preparation for the detection of type 1 GEs is made. In this case, some user interaction is needed—for example, identifying the number of continuous measurements in type 1 GE. It can succeed for variables such as analyzers, for which clogging may cause such a reaction. In the future, both the number of regular measurements and the dead band must be treated by an expert in this process.
- Type 2 GEs are caused, for example, by sensor faults, which can have brief, spike-like errors in the measurements as a result.
2. Problem Formulation
2.1. Mathematical Preliminary
2.2. Outlier Detection Problem (ODP) and Algorithm (ODA)
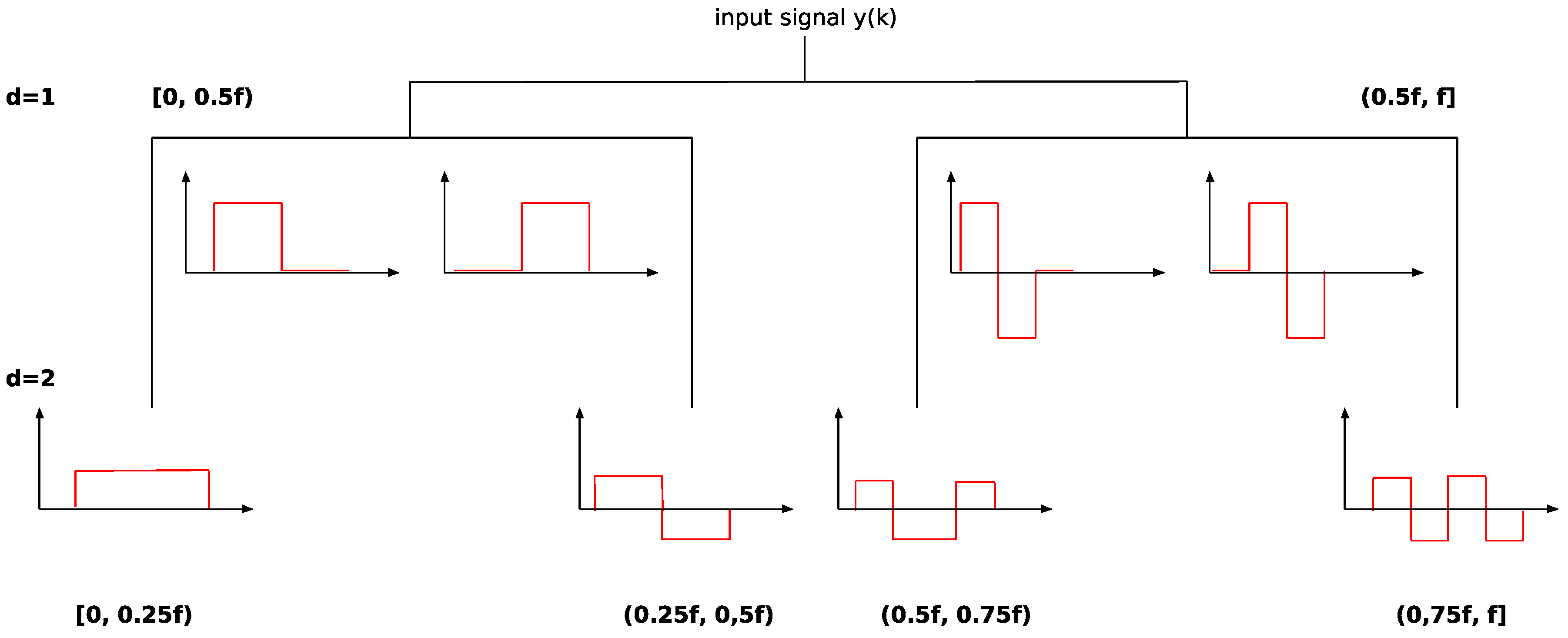
3. Short Remarks on Haar Wavelets
- the are orthonormal,
- any function can be approximated, up to arbitrarily low precision, by a finite linear combination of the .
4. The Proposed Algorithm and Its Verification
- Obtain the coefficients by applying the Haar wavelet transform to the signal affected by faults;
- Threshold those elements in the wavelet coefficients, which are considered to refer to faults;
- Replace the fault in the considered sequence.
Structure of the Algorithm
- Step 1 The signal is located in a register and the standard σ of the local Lipschitz (L) constant of its first seven samples is computed by means of the scalar product between two consecutive samples and Haar functions having two samples. Subsequently, one calculates the local Lipschitz constant considering the 7th and 8th sample correspondingly.
- Step 2a In case of the local Lipschitz constant being calculated considering the 7th and 8th sample of signal which is less than constant , the examined element of the sequence is not an outlier and the local Lipschitz constant is summed up with σ.
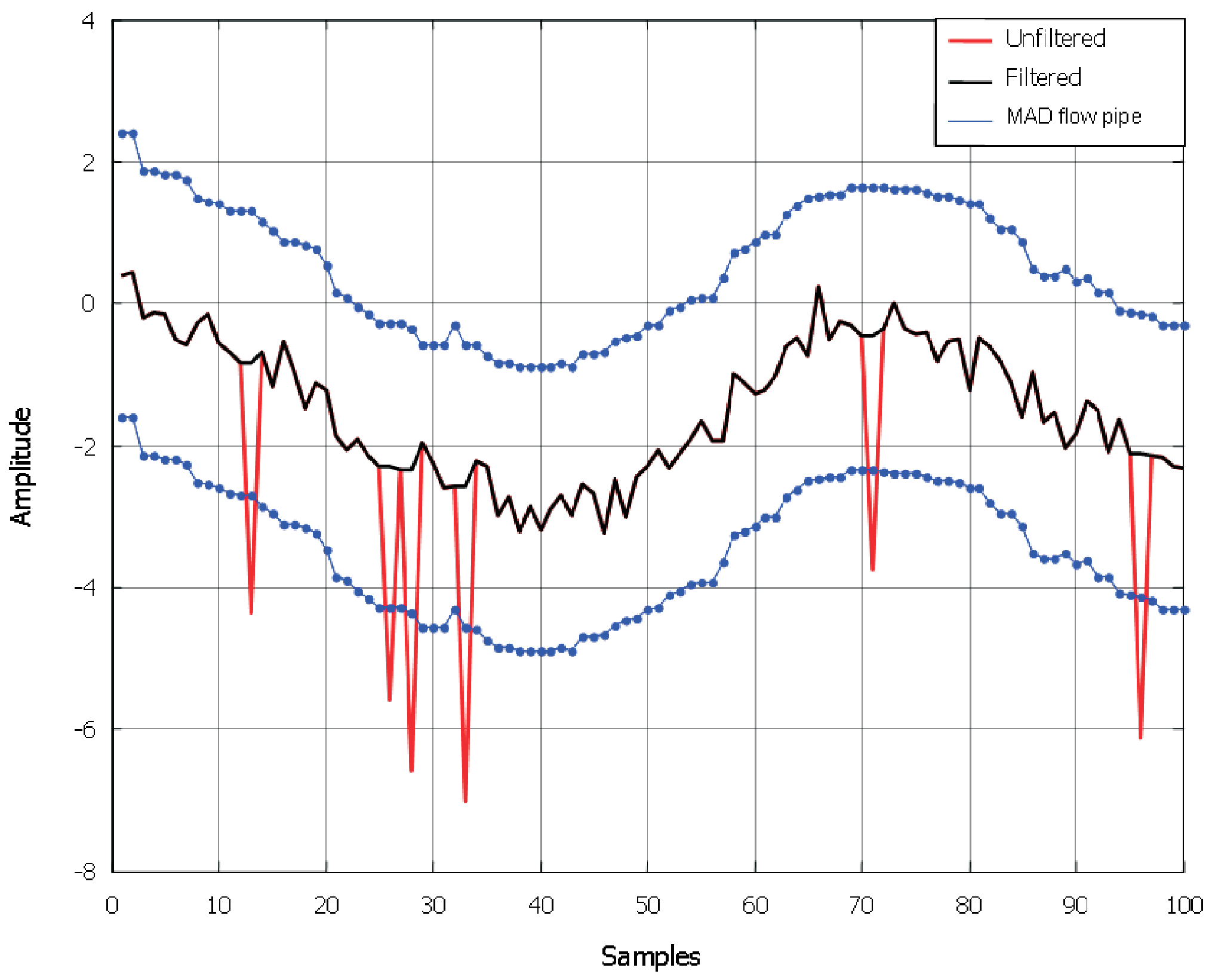
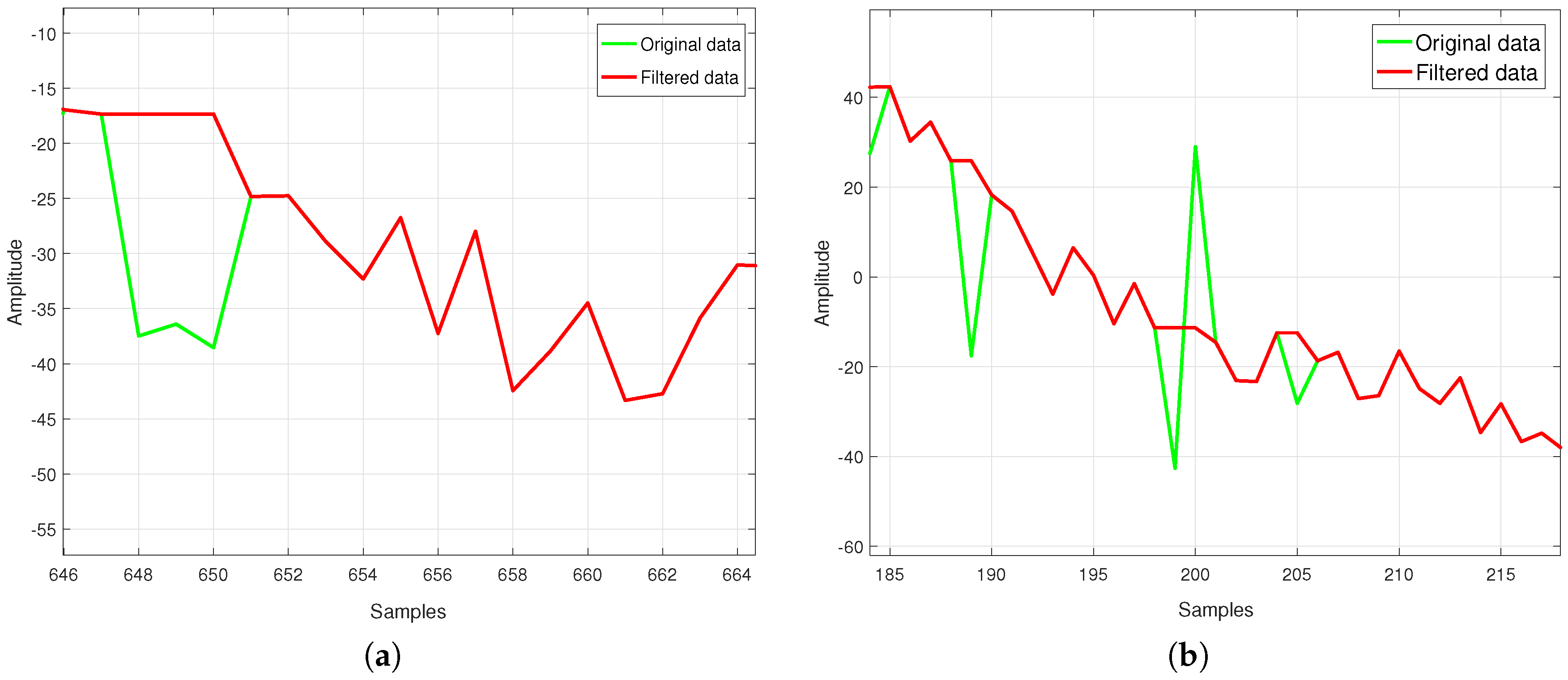
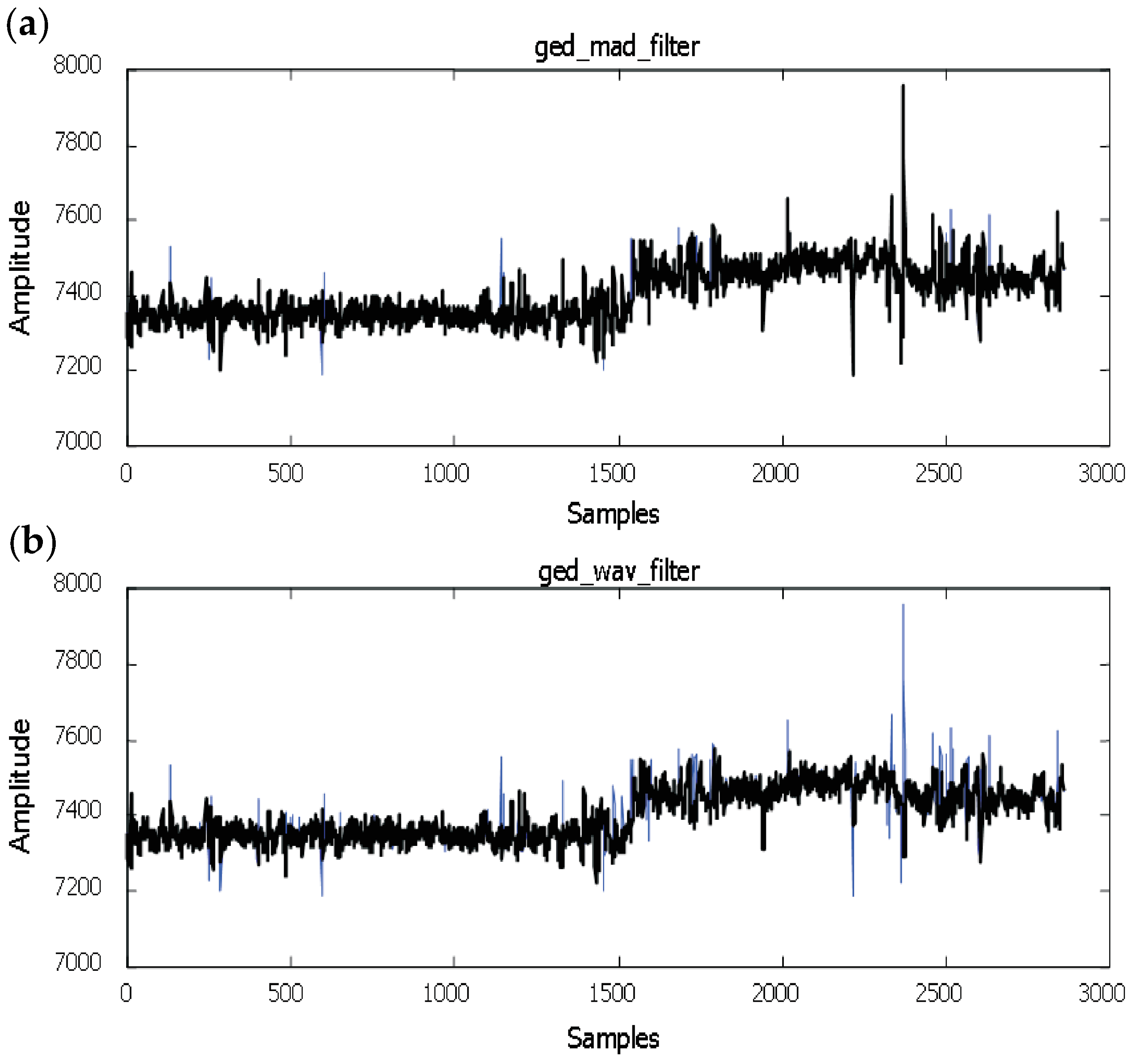
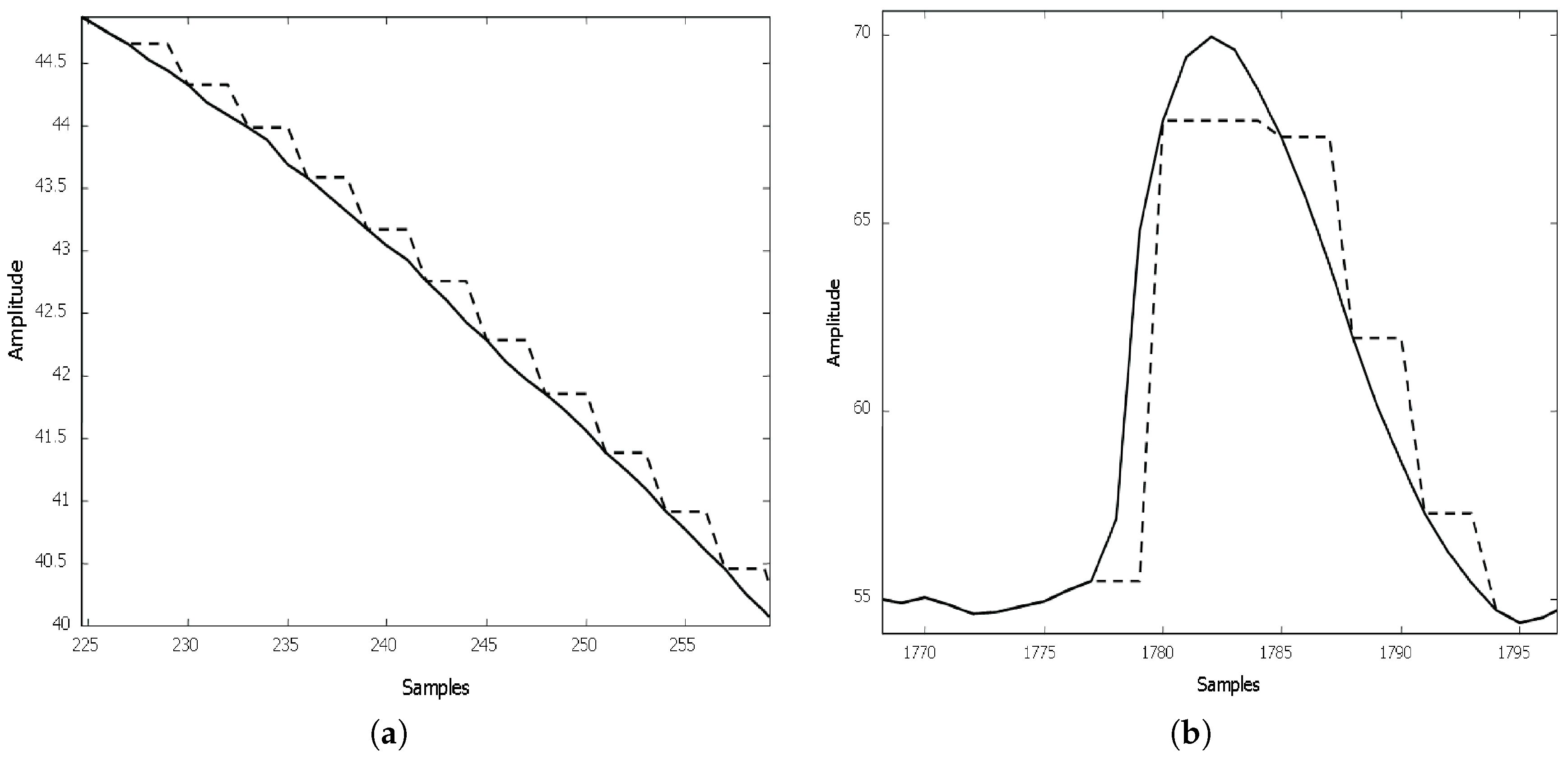
- Step 2b In case of the local Lipschitz constant computed considering the 7th and 8th sample being bigger than constant , then the examined element of the sequence is an outlier and its local Lipschitz constant is not saved. The case of single outliers is reported in Figure 3.
- Step 3 The local Lipschitz constant is saved and the next step of the sequence is taken under consideration.
- Step 4 If the saved local Lipschitz constant value is bigger than , then the sign of the last two computed local Lipschitz constants is analyzed. In case of their not being opposite signs, multi-outliers appear (see Figure 6a).
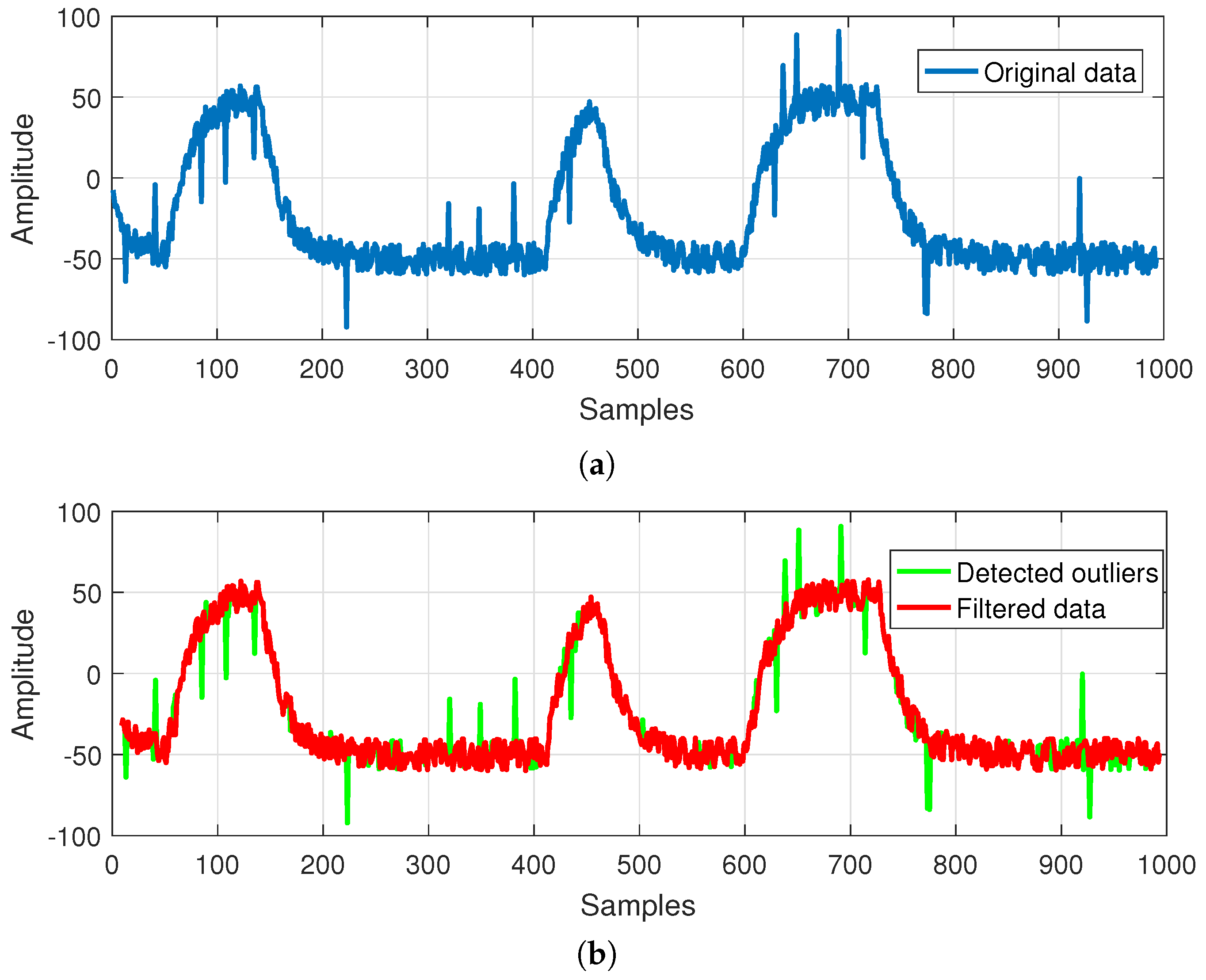
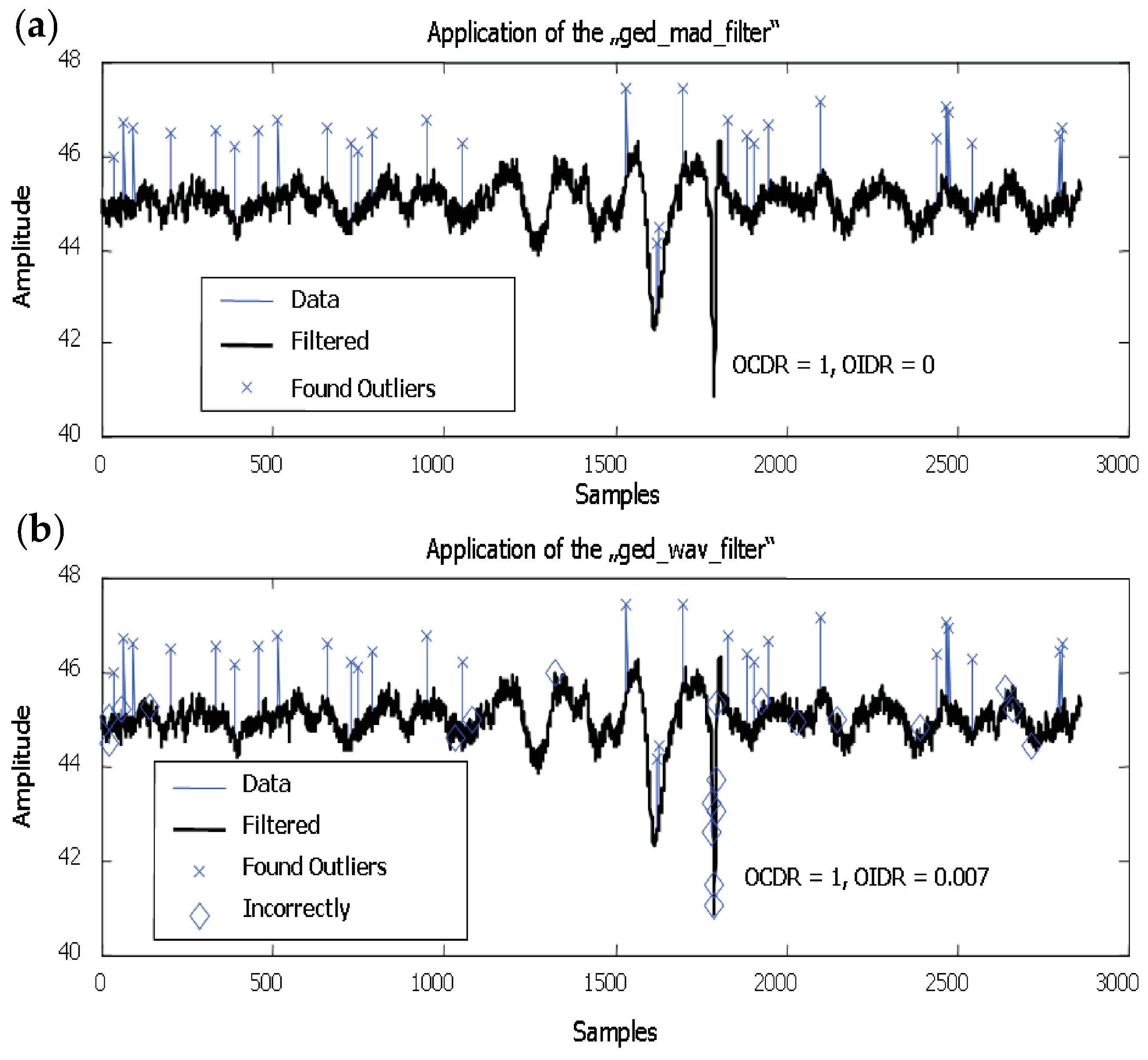
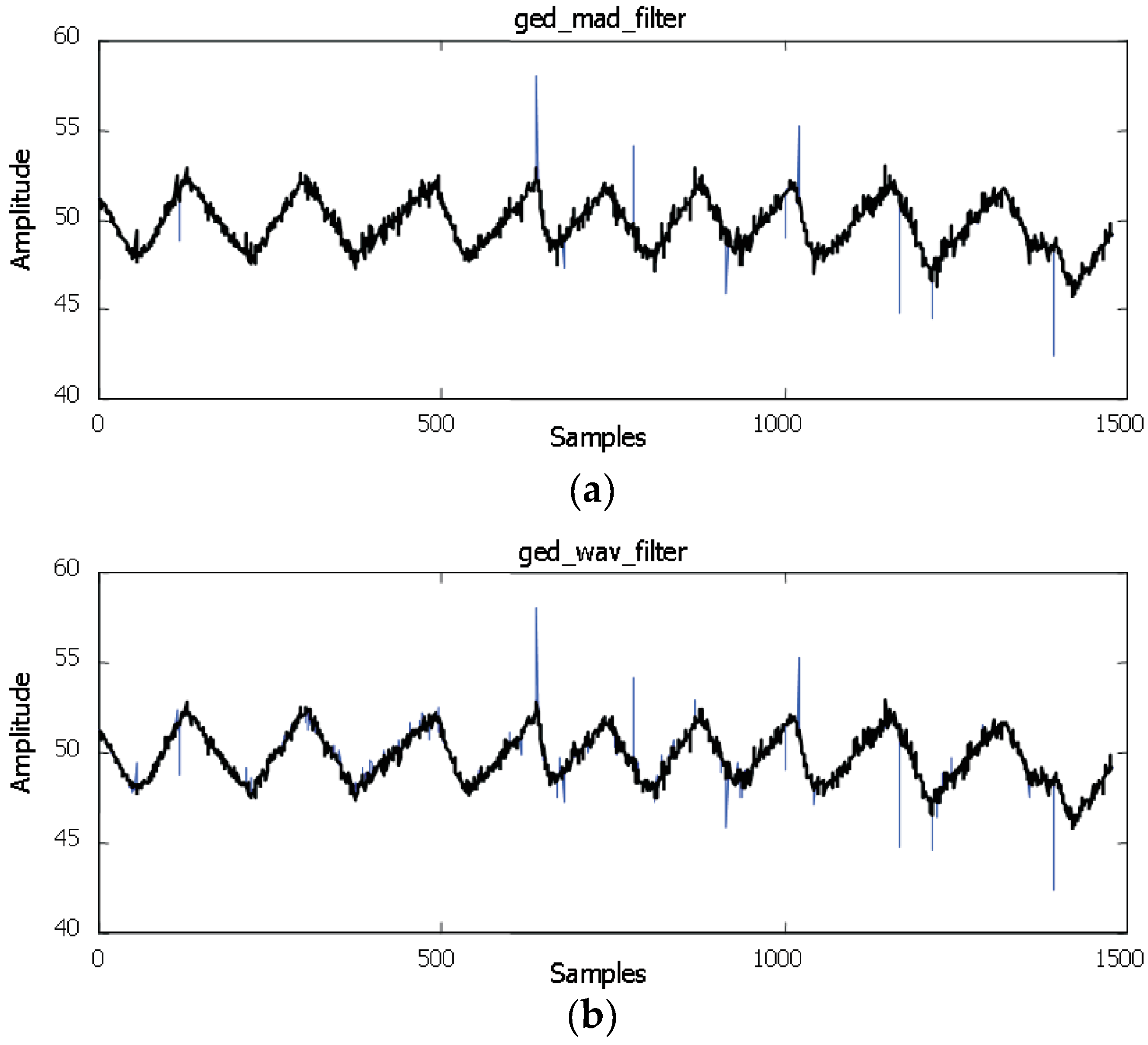
5. Results
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Albuquerque, J.; Biegler, L. Data reconciliation and gross-error detection for dynamic systems. AIChE J. 1996, 42, 2841–2856. [Google Scholar] [CrossRef]
- Coifman, R.; Wickerhauser, M. Entropy based algorithm for best basis selection. IEEE Trans. Inf. Theory 1992, 38, 712–718. [Google Scholar] [CrossRef]
- Shao, R.; Jia, F.; Martin, E.; Morris, A. Wavelets and non linear principal component analysis for process monitoring. Control Eng. Pract. 1999, 7, 865–879. [Google Scholar] [CrossRef]
- Beheshti, S.; Dahleh, M. On denoising and signal representation. In Proceedings of the 10th Mediterranean Conference on Control and Automation (MED2002), Lisbon, Portugal, 9–12 July 2002.
- Menold, P.; Pearson, R.; Allgöwer, F. Online outlier detection and removal. In Proceedings of the 7th Mediterranean Conference on Control and Automation (MED1999), Heifa, Israel, 28–30 June 1999.
- Pearson, R. Exploring process data. J. Process Control 2001, 11, 179–194. [Google Scholar] [CrossRef]
- Pearson, R. Outliers in process modelling and identification. IEEE Trans. Control Syst. Technol. 2002, 10, 55–63. [Google Scholar] [CrossRef]
- Beheshti, S.; Dahleh, M. Noise variance and signal denoising. In Proceedings of the 2003 IEEE International Conference on Acustic Speech, and Signal Processing (ICASSP), Hong Kong, China, 6–10 April 2003; pp. 185–188.
- Schimmack, M.; Mc Gaw, D.; Mercorelli, P. Wavelet based Fault Detection and RLS Parameter Estimation of Conductive Fibers with a Simultaneous Estimation of Time-Varying Disturbance. In Proceedings of the 15th IFAC Symposium on Information Control Problems in Manufacturing, INCOM 2015, Ottawa, ON, Canada, 11–13 May 2015; Volume 48, pp. 1773–1778.
- Mercorelli, P.; Frick, A. Industrial applications using wavelet packets for gross error detection (Chapter 4). In Computational Intelligence in Information Assurance and Security; Nadjah, A.A.N., Mourelle, L., Eds.; Springer-Verlag: Berlin/Heidelberg, Germany; New York, NY, USA, 2007; pp. 89–127. [Google Scholar]
- Mercorelli, P. Using Haar Wavelets for Fault Detection in Technical Processes. In Proceedings of the 13th IFAC and IEEE Conference on Programmable Devices and Embedded Systems, Cracow, Poland, 3–15 May 2015; Volume 48, pp. 37–42.
- Donoho, D.L. Denoising by soft thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef]
- Rakowski, W. Prefiltering in Wavelet Analysis Applying Cubic B-Splines. Int. J. Electron. Telecommun. 2014, 60, 331–340. [Google Scholar]
- Frick, A.; Mercorelli, P. Spurious Measurement Value Detection Method Uses Wavelet Functions in Defining a Reporting Window for Rejecting Spurious Values in a Continuous Digital Sequence of Measurement Values. DE Patent 10225343 (A1), 18 December 2003. (In German)[Google Scholar]
- Donoho, D.L. Denoising and soft Thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef]
- Donoho, D.L.; Johnstone, I.M.; Kerkyacharian, G.; Picard, D. Density estimation by wavelet thesholding. Ann. Stat. 1996, 24, 508–539. [Google Scholar]
- Mercorelli, P. A Wavelet Based Algorithm without a Priori Knowledge of Noise Level for Gross Errors Detection. In Advances in Intelligent Systems Research; Atlantis Press: Amsterdam The Netherlands, 2015; ISBN 978-94-6252-000-4. ISSN: 1951–6851. [Google Scholar]

© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mercorelli, P. A Fault Detection and Data Reconciliation Algorithm in Technical Processes with the Help of Haar Wavelets Packets. Algorithms 2017, 10, 13. https://doi.org/10.3390/a10010013
Mercorelli P. A Fault Detection and Data Reconciliation Algorithm in Technical Processes with the Help of Haar Wavelets Packets. Algorithms. 2017; 10(1):13. https://doi.org/10.3390/a10010013
Chicago/Turabian StyleMercorelli, Paolo. 2017. "A Fault Detection and Data Reconciliation Algorithm in Technical Processes with the Help of Haar Wavelets Packets" Algorithms 10, no. 1: 13. https://doi.org/10.3390/a10010013
APA StyleMercorelli, P. (2017). A Fault Detection and Data Reconciliation Algorithm in Technical Processes with the Help of Haar Wavelets Packets. Algorithms, 10(1), 13. https://doi.org/10.3390/a10010013





