Numerical Study of Laminar Flow and Convective Heat Transfer Utilizing Nanofluids in Equilateral Triangular Ducts with Constant Heat Flux
Abstract
:1. Introduction
2. Mathematical Modeling
2.1. Assumptions and Governing Equations
2.2. Physical Properties of the Nanofluid
2.2.1. Density and Heat Capacity
2.2.2. Viscosity
2.2.3. Thermal Conductivity
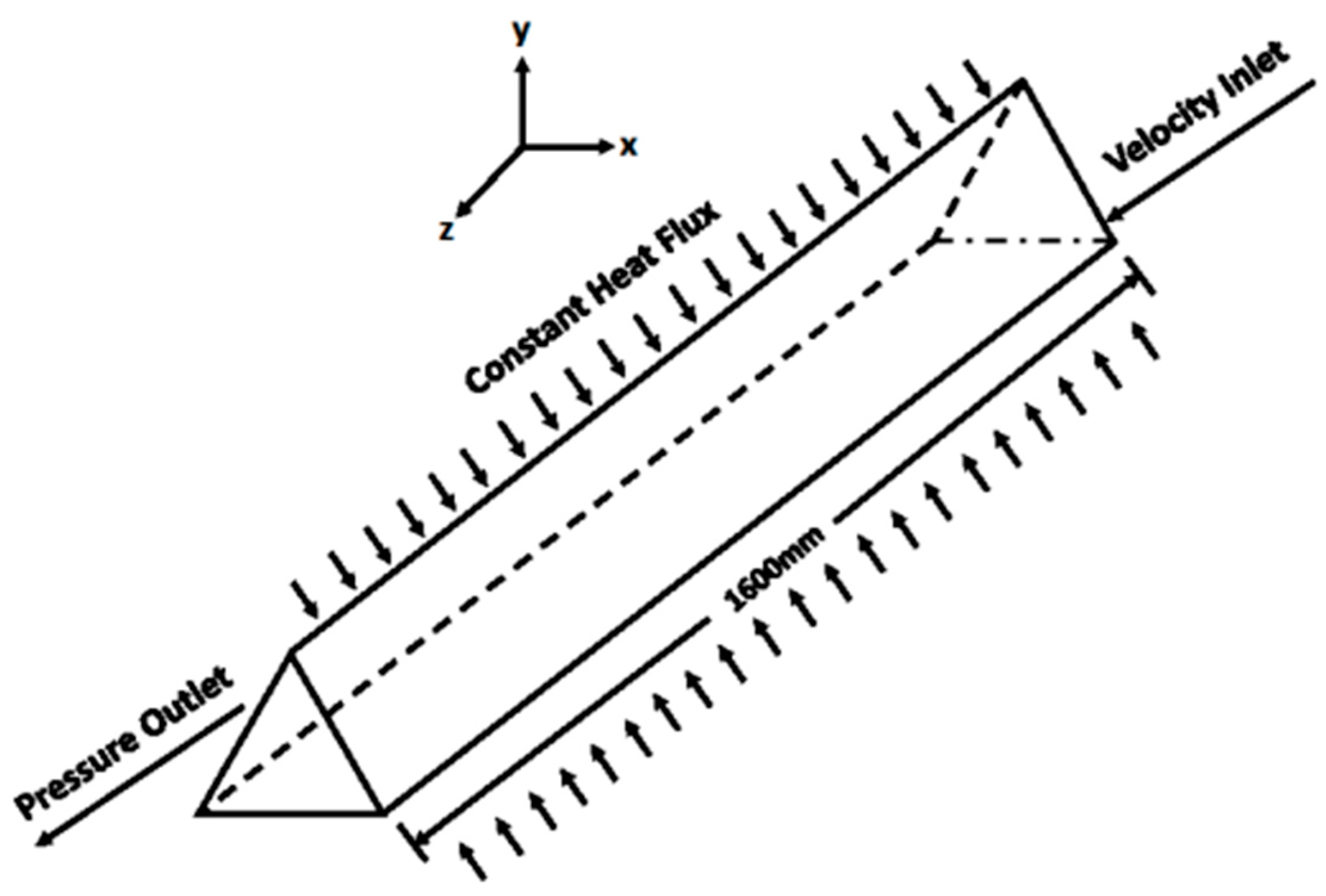
2.3. Boundary Conditions
2.4. Solver
- Guess the pressure p*.
- Solve the momentum equations to obtain u*, v*, w*. Notice that unless the correct pressure field is employed, the resulting velocity field will not satisfy the continuity equation. Such an imperfect field based on a guessed pressure field p* will be denoted by u*, v*, w*.
- Solve p′ equation. p′ is the pressure correction.
- Calculate corrected pressure p (p = p* + p′).
- Calculate corrected velocity components u, v, w (u= u* + u′, v = v* + v′, w = w* + w′). u′, v′, and w′ are the velocity corrections for u, v, and w, respectively.
- Solve other variables (such as T).
- Treat the corrected pressure p as a new guessed pressure p*.
3. Results and Discussion
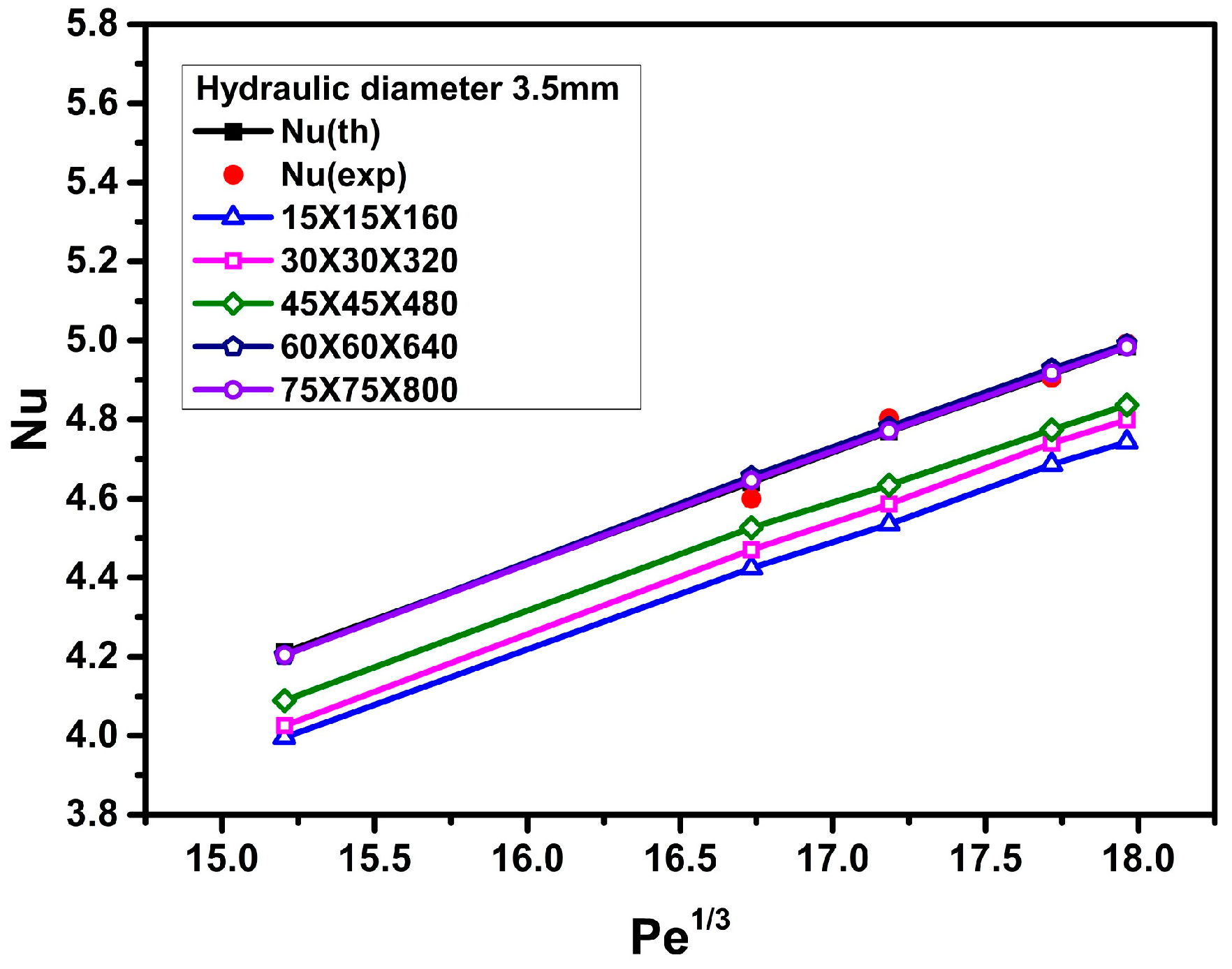
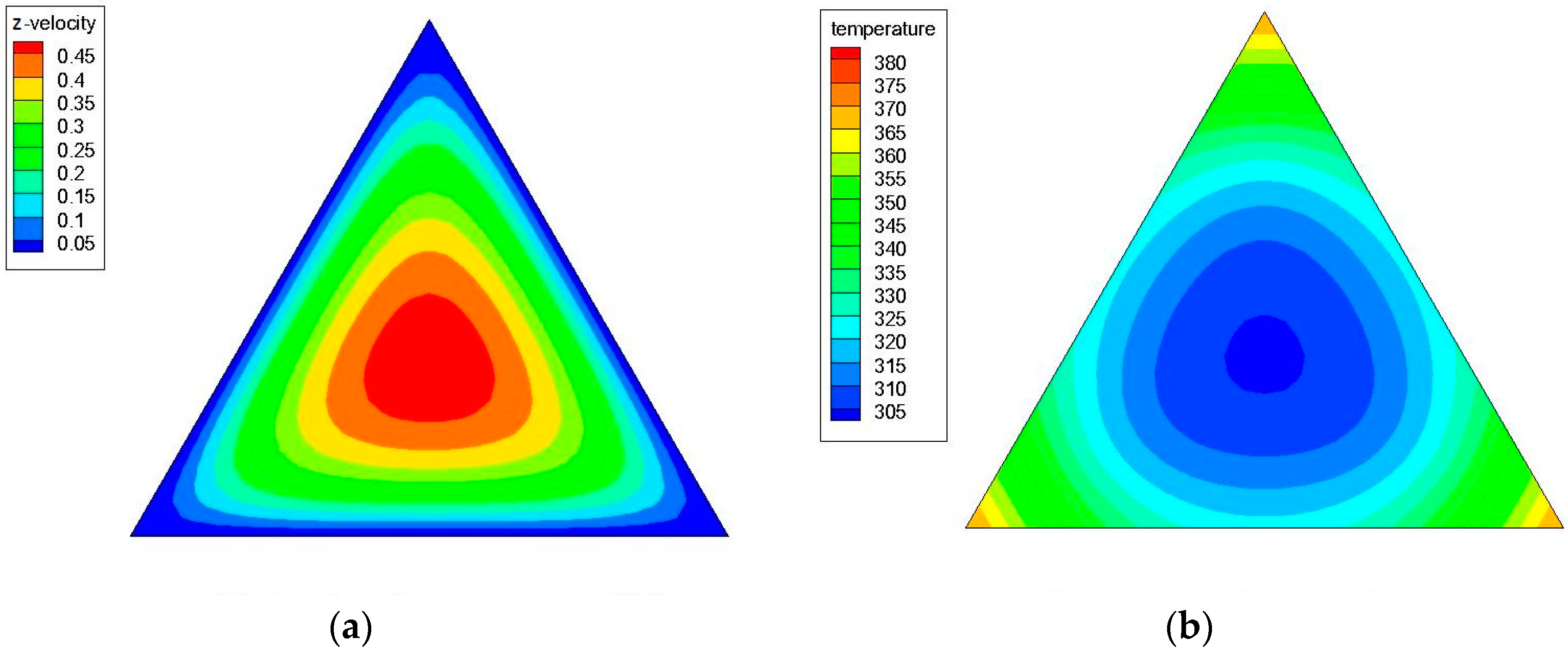
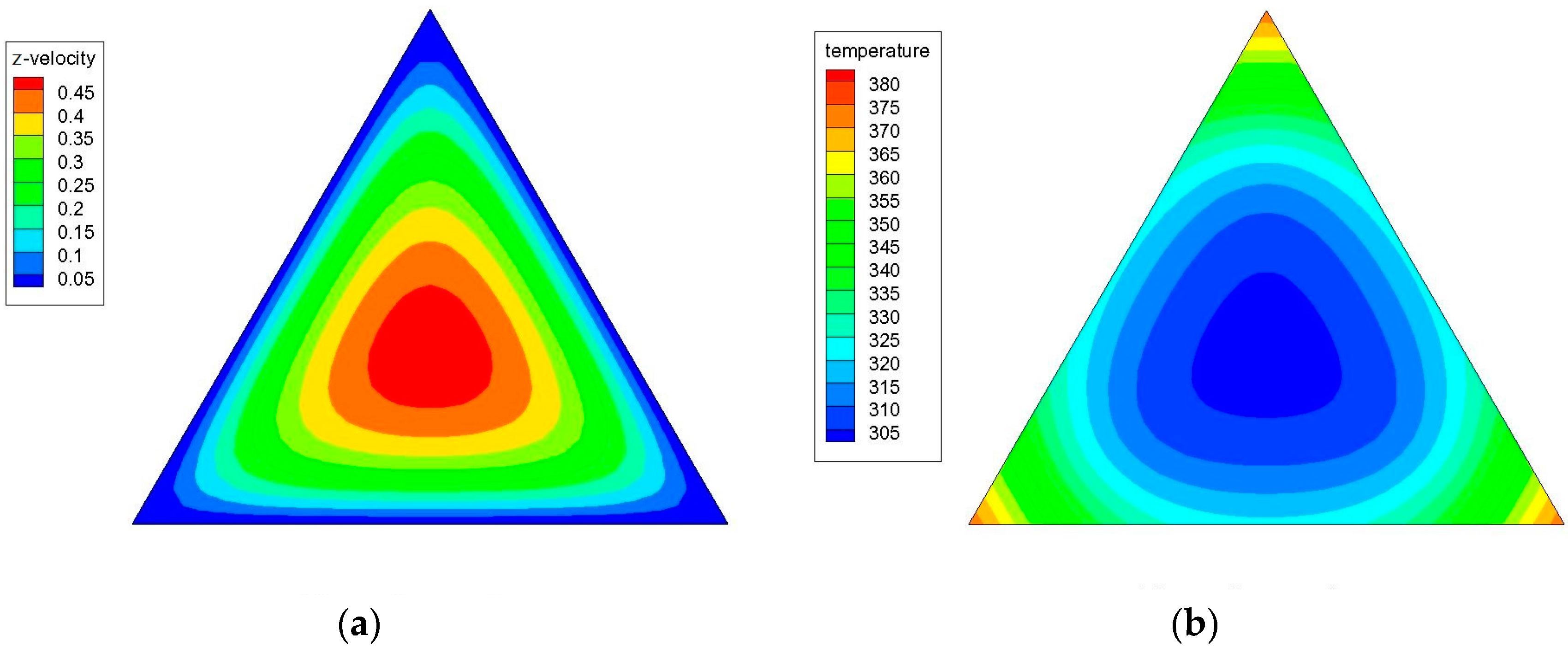
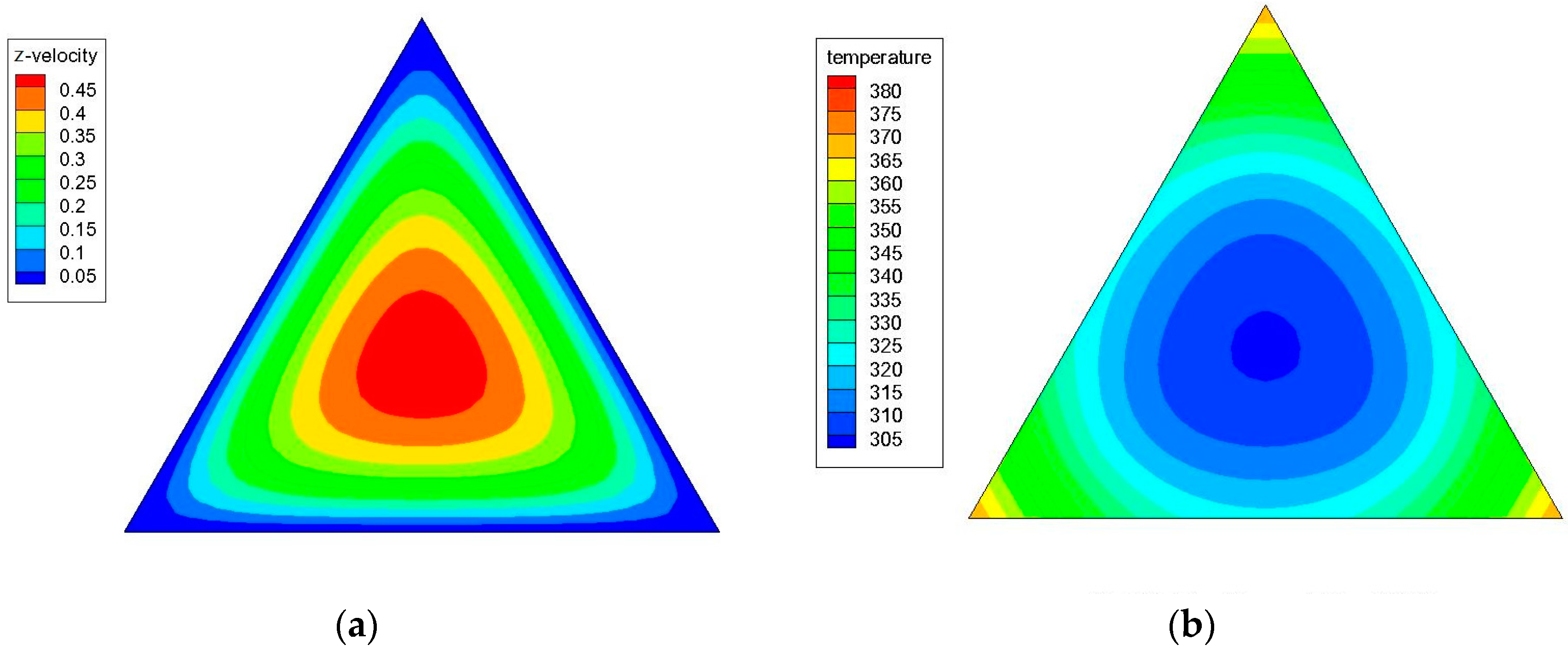
3.1. Grid-Independence Analysis
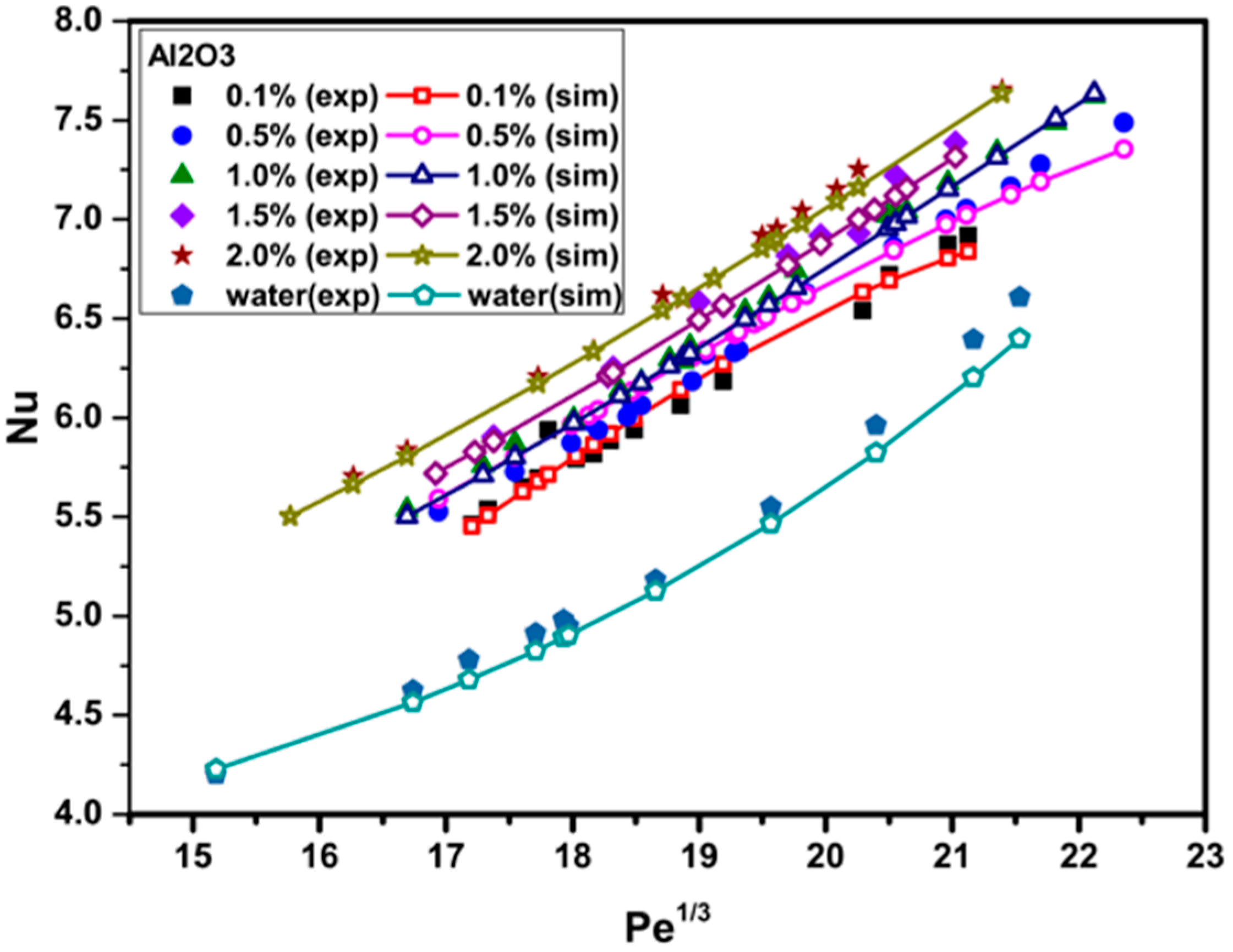
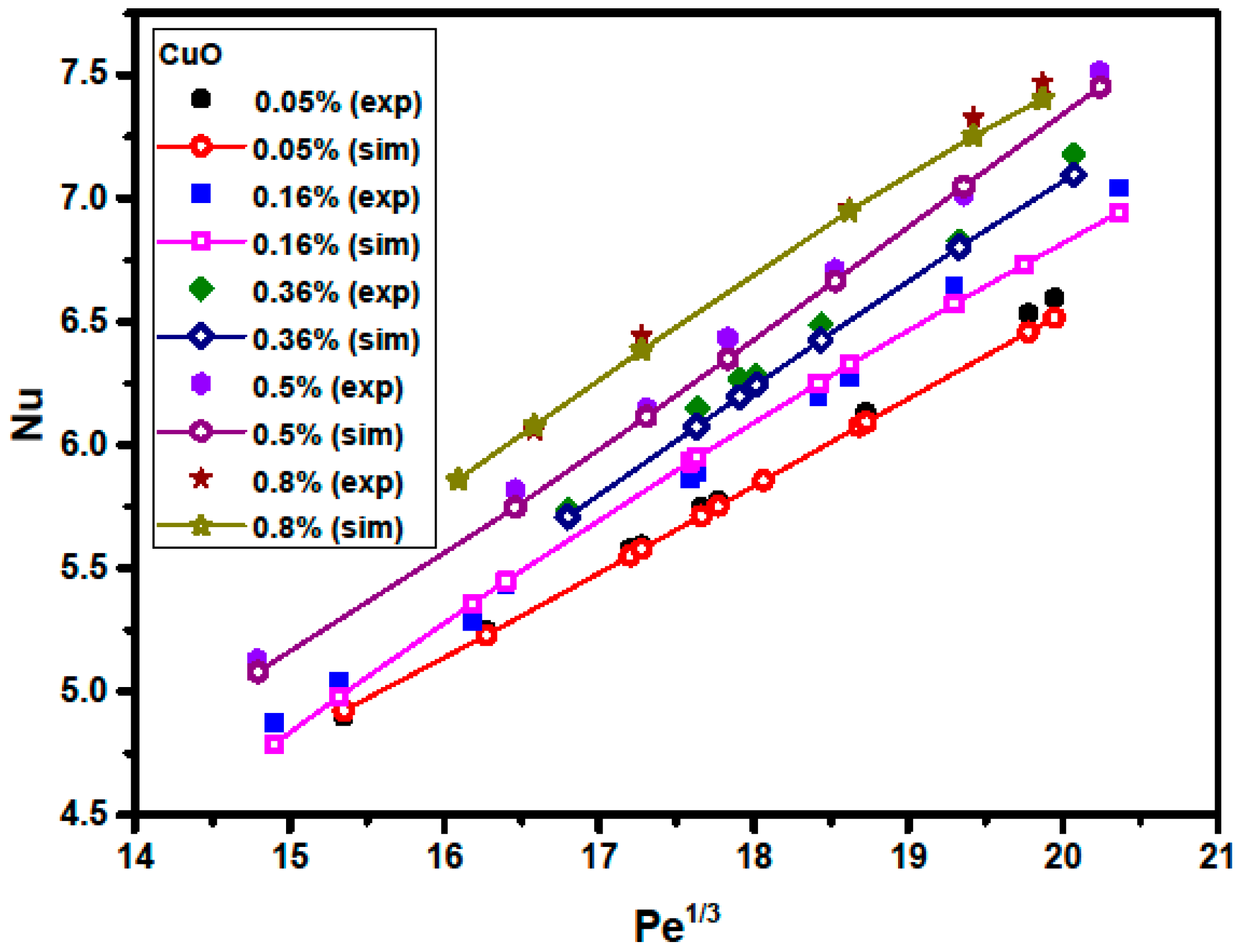
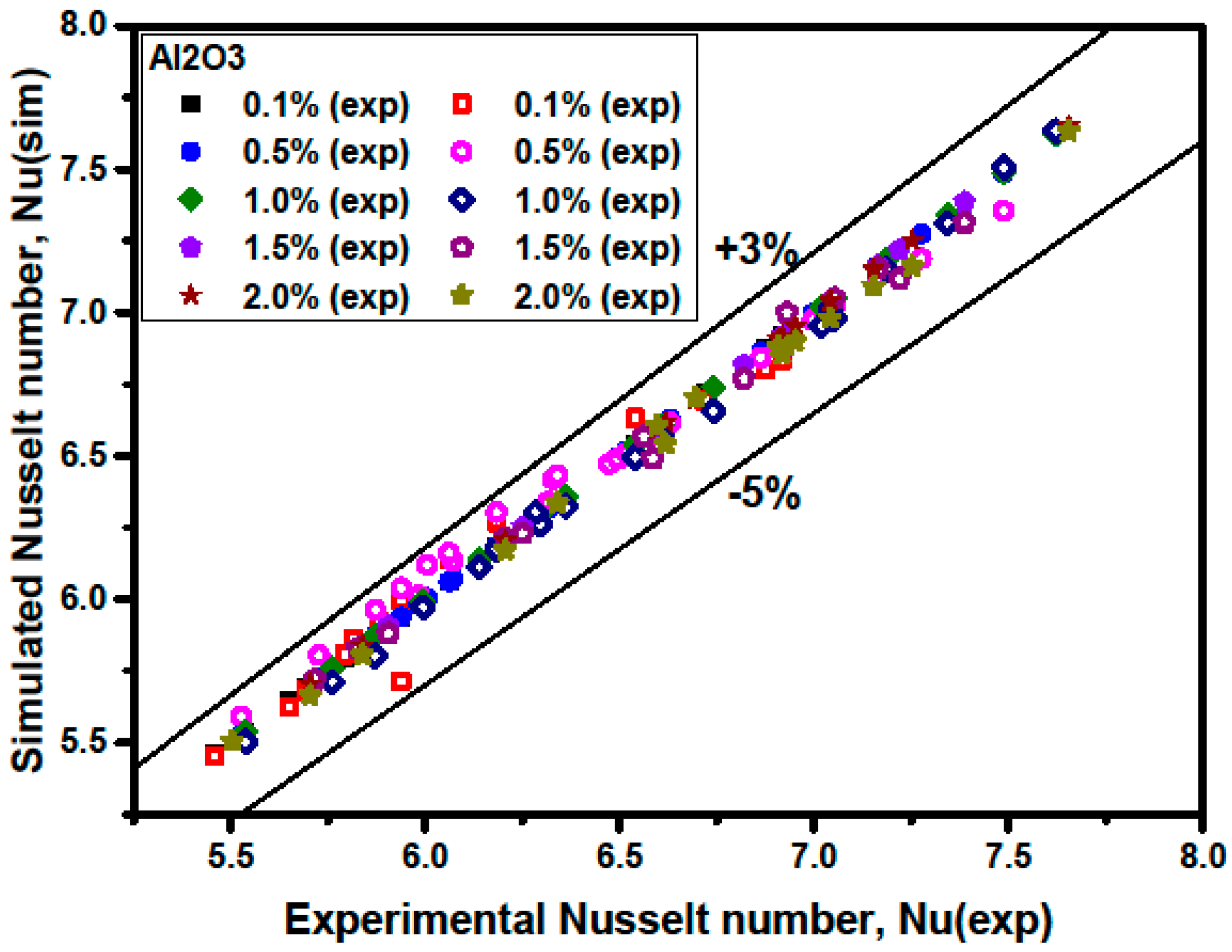
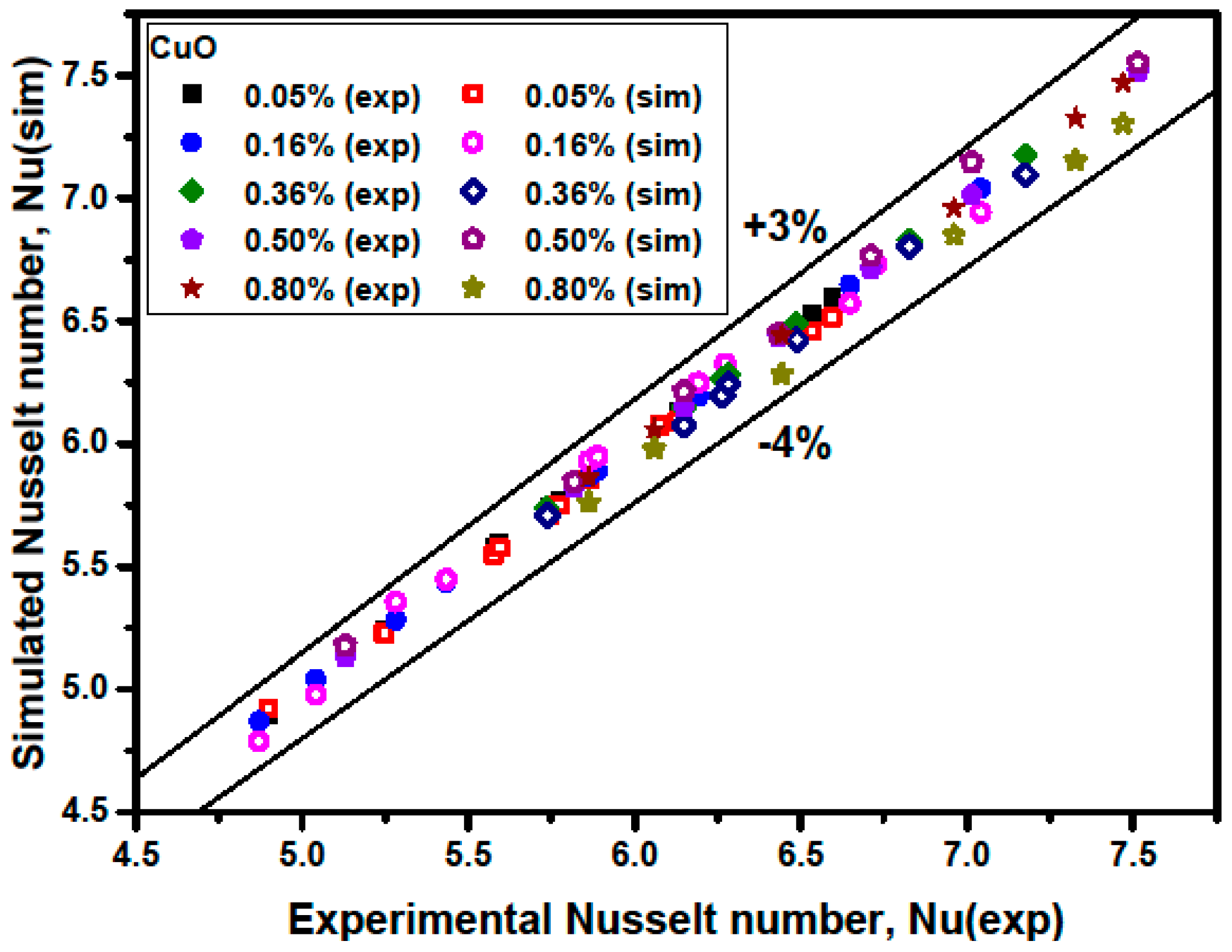
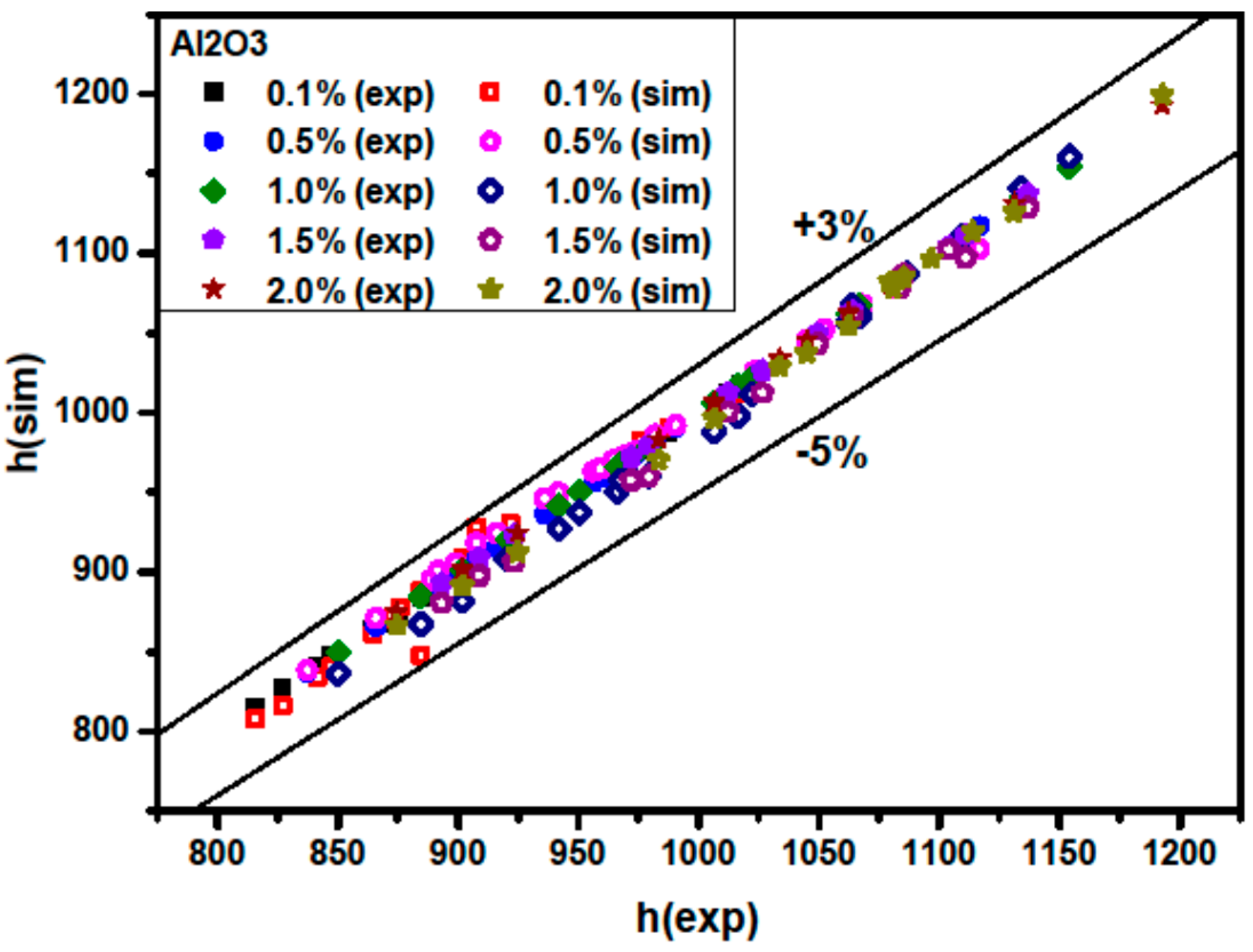
3.2. Validation
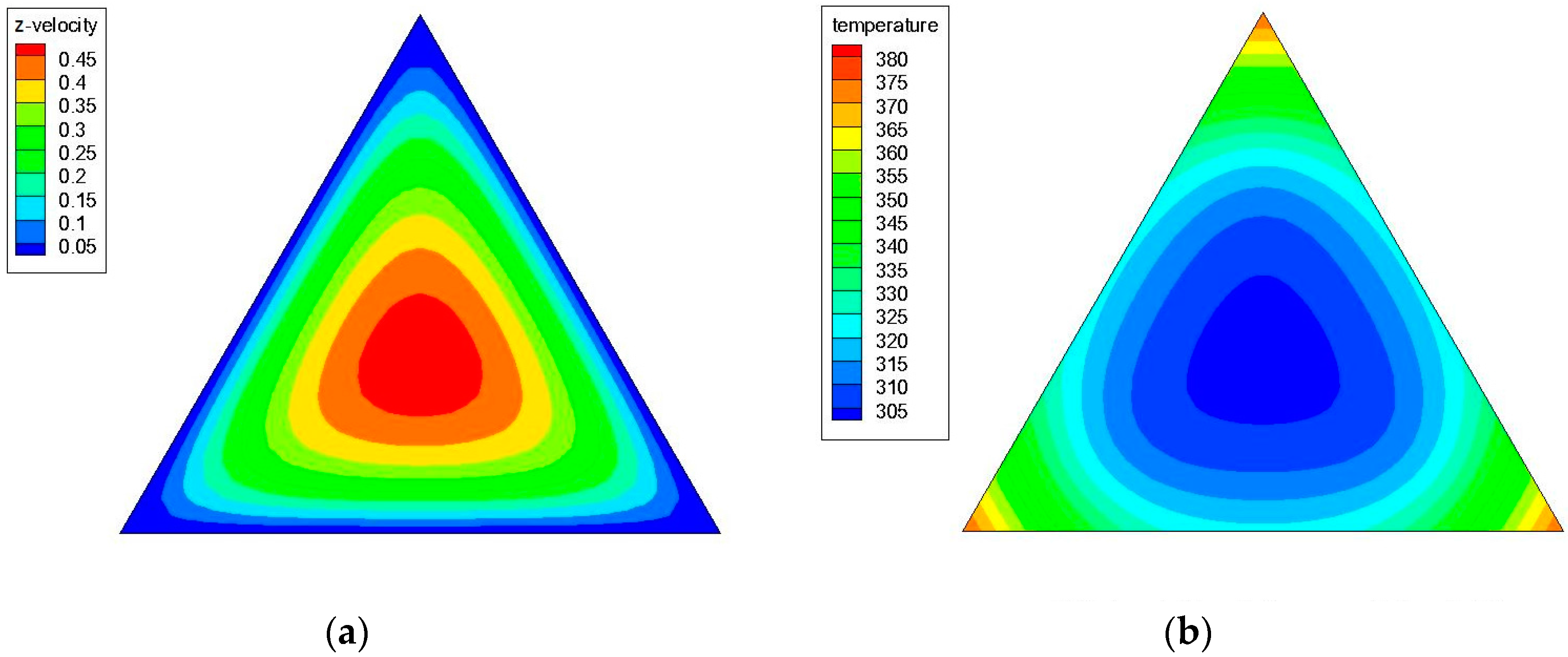
3.3. Effects of Peclet Number and Particle Volume Concentrations
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Surface area of square cross-section duct (m2) | |
| C | Specific heat (kJ·kg−1·K−1) |
| Dh | Hydraulic diameter (m) |
| Experimental average nanofluid heat transfer coefficient (W·m−2·K−1) | |
| Simulated average nanofluid heat transfer coefficient (W·m−2·K−1) | |
| k | Thermal conductivity (W·m−1·K−1) |
| L | Duct length (m) |
| Average nanofluid Nusselt number obtained from experiments | |
| Average nanofluid Nusselt number calculated from CFD analysis | |
| Pe | Peclet number |
| Pr | Prandtl number |
| q | Heat flux (W/m2) |
| Re | Reynolds number |
| Tb | Bulk temperature (K) |
| Tw | Duct wall temperature (K) |
| Average fluid velocity (m·s−1) | |
| u | The x-component of the velocity (m−1·s−1) |
| v | The y-component of the velocity (m−1·s−1) |
| w | The z-component of the velocity (m−1·s−1) |
| Greek Symbols | |
| γ | Ratio of the nano-layer thickness to original particle radius |
| μ | Viscosity (Pa s) |
| μwnf | Nanofluid viscosity at duct wall temperature (Pa s) |
| Nanoparticle volume fraction (%) | |
| Density (kg·m−3) | |
| Subscripts | |
| bf | Base fluid |
| i | Inlet |
| nf | Nanofluid |
| o | Outlet |
| p | Solid nanoparticles |
| w | Wall |
References
- Nasiri, M.; Etemad, S.G.; Bagheri, R. Experimental heat transfer of nanofluid through an annular duct. Int. Commun. Heat Mass Transf. 2011, 38, 958–963. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, A. Thermal and fluid dynamic characteristics of flow through triangular cross-sectional duct: A review. Renew. Sust. Energ. Rev. 2016, 61, 123–140. [Google Scholar] [CrossRef]
- Heris, S.Z.; Ahmadi, F.; Mahian, O. Pressure drop and performance characteristics of water-based Al2O3 and CuO nanofluids in a triangular duct. J. Disper. Sci. Technol. 2013, 34, 1368–1375. [Google Scholar] [CrossRef]
- Heris, S.Z.; Edalati, Z.; Noie, S.H.; Mahian, O. Experimental investigation of Al2O3/water nanofluid through equilateral triangular duct with constant wall heat flux in laminar flow. Heat Transf. Eng. 2014, 35, 1173–1182. [Google Scholar] [CrossRef]
- Edalati, Z.; Heris, S.Z.; Noie, S.H. The study of laminar convective heat transfer of CuO/water nanofluid through an equilateral triangular duct at constant wall heat flux. Heat Transf. Asian Res. 2012, 41, 418–429. [Google Scholar] [CrossRef]
- Heris, S.Z.; Noie, S.H.; Talaii, E.; Sargolzaei, J. Numerical investigation of Al2O3/water nanofluid laminar convective heat transfer through triangular ducts. Nanoscale Res. Lett. 2011, 6. [Google Scholar] [CrossRef]
- Akbarzadeh, M.; Rashidi, S.; Bovand, M.; Ellahi, R. A sensitivity analysis on thermal and pumping power for the flow of nanofluid inside a wavy channel. J. Mol. Liq. 2016, 220, 1–13. [Google Scholar] [CrossRef]
- Ellahi, R.; Raza, M.; Vafai, K. Series solutions of non-Newtonian nanofluids with Reynolds’ model and Vogel’s model by means of the homotopy analysis method. Math. Comput. Model. 2012, 55, 1876–1891. [Google Scholar] [CrossRef]
- Ellahi, R. The effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe: Analytical solutions. Appl. Math. Model. 2013, 37, 1451–1457. [Google Scholar] [CrossRef]
- Ellahi, R.; Aziz, S.; Zeeshan, A. Non-Newtonian nanofluids flow through a porous medium between two coaxial cylinders with heat transfer and variable viscosity. J. Porous Media 2013, 16, 205–216. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ellahi, R. Electrohydrodynamic nanofluid hydrothermal treatment in an enclosure with sinusoidal upper wall. Appl. Sci. 2015, 5, 294–306. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Chamkha, A.J. Electrohydrodynamic free convection heat transfer of a nanofluid in a semi-annulus enclosure with a sinusoidal wall. Numer. Heat Transf. Part A Appl. 2016, 69, 781–793. [Google Scholar] [CrossRef]
- Zeeshan, A.; Majeed, A.; Ellahi, R. Effect of magnetic dipole on viscous ferro-fluid past a stretching surface with thermal radiation. J. Mol. Liq. 2016, 215, 549–554. [Google Scholar] [CrossRef]
- Rashidi, S.; Dehghan, M.; Ellahi, R.; Riaz, M.; Jamal-Abad, M.T. Study of stream wise transverse magnetic fluid flow with heat transfer around an obstacle embedded in a porous medium. J. Magn. Magn. Mater. 2015, 378, 128–137. [Google Scholar] [CrossRef]
- Rahman, S.U.; Ellahi, R.; Nadeem, S.; Zia, Q.Z. Simultaneous effects of nanoparticles and slip on Jeffrey fluid through tapered artery with mild stenosis. J. Mol. Liq. 2016, 218, 484–493. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ellahi, R. Three dimensional mesoscopic simulation of magnetic field effect on natural convection of nanofluid. Int. J. Heat Mass Transf. 2015, 89, 799–808. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Study of natural convection MHD nanofluid by means of single and multi-walled carbon nanotubes suspended in a salt-water solution. IEEE Trans. Nanotechnol. 2015, 14, 726–734. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Shape effects of nanosize particles in Cu–H2O nanofluid on entropy generation. Int. J. Heat Mass Transf. 2015, 81, 449–456. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D.; Javed, M.Y.; Ellahi, R. Effect of thermal radiation on magnetohydrodynamics nanofluid flow and heat transfer by means of two phase model. J. Magn. Magn. Mater. 2015, 374, 36–43. [Google Scholar] [CrossRef]
- Kandelousi, M.S.; Ellahi, R. Simulation of ferrofluid flow for magnetic drug targeting using the lattice boltzmann method. Z. Naturforsch. A 2015, 70, 115–124. [Google Scholar] [CrossRef]
- Akbar, N.S.; Raza, M.; Ellahi, R. Influence of induced magnetic field and heat flux with the suspension of carbon nanotubes for the peristaltic flow in a permeable channel. J. Magn. Magn. Mater. 2015, 381, 405–415. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hassan, M. A study of Fe3O4 nanoparticles aggregation in engine oil base nanofluid over the vertical stretching of a permeable sheet in a mixed convection. J. Zhejiang Univ. Sci. A 2016, in press. [Google Scholar]
- Ting, H.H.; Hou, S.S. Investigation of laminar convective heat transfer for Al2O3-water nanofluids flowing through a square cross-section duct with a constant heat flux. Materials 2015, 8, 5321–5335. [Google Scholar] [CrossRef]
- Koo, J.; Kleinstreuer, C. Laminar nanofluid flow in microheat-sinks. Int. J. Heat Mass Transf. 2005, 48, 2652–2661. [Google Scholar] [CrossRef]
- Santra, A.K.; Sen, S.; Chakraborty, N. Study of heat transfer due to laminar flow of copper-water nanofluid through two isothermally heated parallel plates. Int. J. Therm. Sci. 2009, 48, 391–400. [Google Scholar] [CrossRef]
- Pak, B.C.; Cho, Y.I. Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particles. Exp. Heat Transf. 1998, 11, 151–170. [Google Scholar] [CrossRef]
- Masoumi, N.; Sohrabi, N.; Behzadnehr, A. A new model for calculating the effective viscosity of nanofluids. J. Phys. D Appl. Phys. 2009, 42. [Google Scholar] [CrossRef]
- Koo, J.; Kleinstreuer, C. A new thermal conductivity model for nanofluids. J. Nanoparticle Res. 2004, 6, 577–588. [Google Scholar] [CrossRef]
- Koo, J.; Kleinstreuer, C. Impact analysis of nanoparticle motion mechanisms on the thermal conductivity of nanofluids. Int. Commun. Heat Mass Transf. 2005, 32, 1111–1118. [Google Scholar] [CrossRef]
- Li, J. Computational Analysis of Nanofluid Flow in Microchannels with Applications to Micro-Heat Sinks and Bio-MEMS. Ph.D Thesis, NC State University, Raleigh, NC, USA, 5 December 2008. [Google Scholar]
- Kleinstreuer, C.; Feng, Y. Experimental and theoretical studies of nanofluid thermal conductivity enhancement: A review. Nanoscale Res. Lett. 2011, 6, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Maxwell, J. A Treatise on Electricity and Magnetism, 2nd ed.; Oxford University Press: Cambridge, UK, 1904. [Google Scholar]
- ANSYS FLUENT Workbench User’s Guide; Release 12.1; ANSYS, Inc.: Cecil Township, PA, USA, 2009.
- Sieder, E.N.; Tate, G.E. Heat transfer and pressure drop of liquid in tubes. Ind. Eng. Chem. 1936, 28, 1429–1435. [Google Scholar] [CrossRef]
- Xuan, Y.; Li, Q. Heat transfer enhancement of nanofluids. Int. J. Heat Fluid Flow 2000, 21, 58–64. [Google Scholar] [CrossRef]
- Heris, S.Z.; Nassan, T.H.; Noie, S.H.; Sardarabadi, H.; Sardarabadi, M. Laminar convective heat transfer of Al2O3/water nanofluid through square cross-sectional duct. Int. J. Heat Fluid Flow 2003, 44, 375–382. [Google Scholar] [CrossRef]
- Mehrjou, B.; Heris, S.Z.; Mohamadifard, K. Experimental study of CuO/Water nanofluid turbulent convective heat transfer in square cross-section duct. Exp. Heat Transf. 2015, 28, 282–297. [Google Scholar] [CrossRef]
- Mikkola, V.; Puupponen, S.; Granbohm, H.; Saari, K.; Ala-Nissilä, T.; Seppälä, A. Convective Heat Transfer Performance of Polystyrene, SiO2, Al2O3 and Micelle Nanofluids. In Proceedings of the 12th International Conference on Heat Transfer, Fluid Mechanics and Thermodynamics, Costa del Sol, Málaga, Spain, 11–13 July 2016.
- Utomo, A.T.; Haghighi, E.B.; Zavareh, A.I.; Ghanbarpourgeravi, M.; Poth, H.; Khodabandeh, R.; Palm, B.; Pacek, A.W. The effect of nanoparticles on laminar heat transfer in a horizontal tube. Int. J. Heat Mass Transf. 2014, 69, 77–91. [Google Scholar] [CrossRef]
- Martínez-Cuenca, R.; Mondragón, R.; Hernández, L.; Segarra, C.; Jarque, J.C.; Hibiki, T.; Julia, J.E. Forced-convective heat-transfer coefficient and pressure drop of water-based nanofluids in a horizontal pipe. Appl. Therm. Eng. 2016, 98, 841–849. [Google Scholar] [CrossRef]
- Buschmann, M.H. Nanofluid heat transfer in laminar pipe flow with twisted tape. Heat Transf. Eng. 2016. [Google Scholar] [CrossRef]
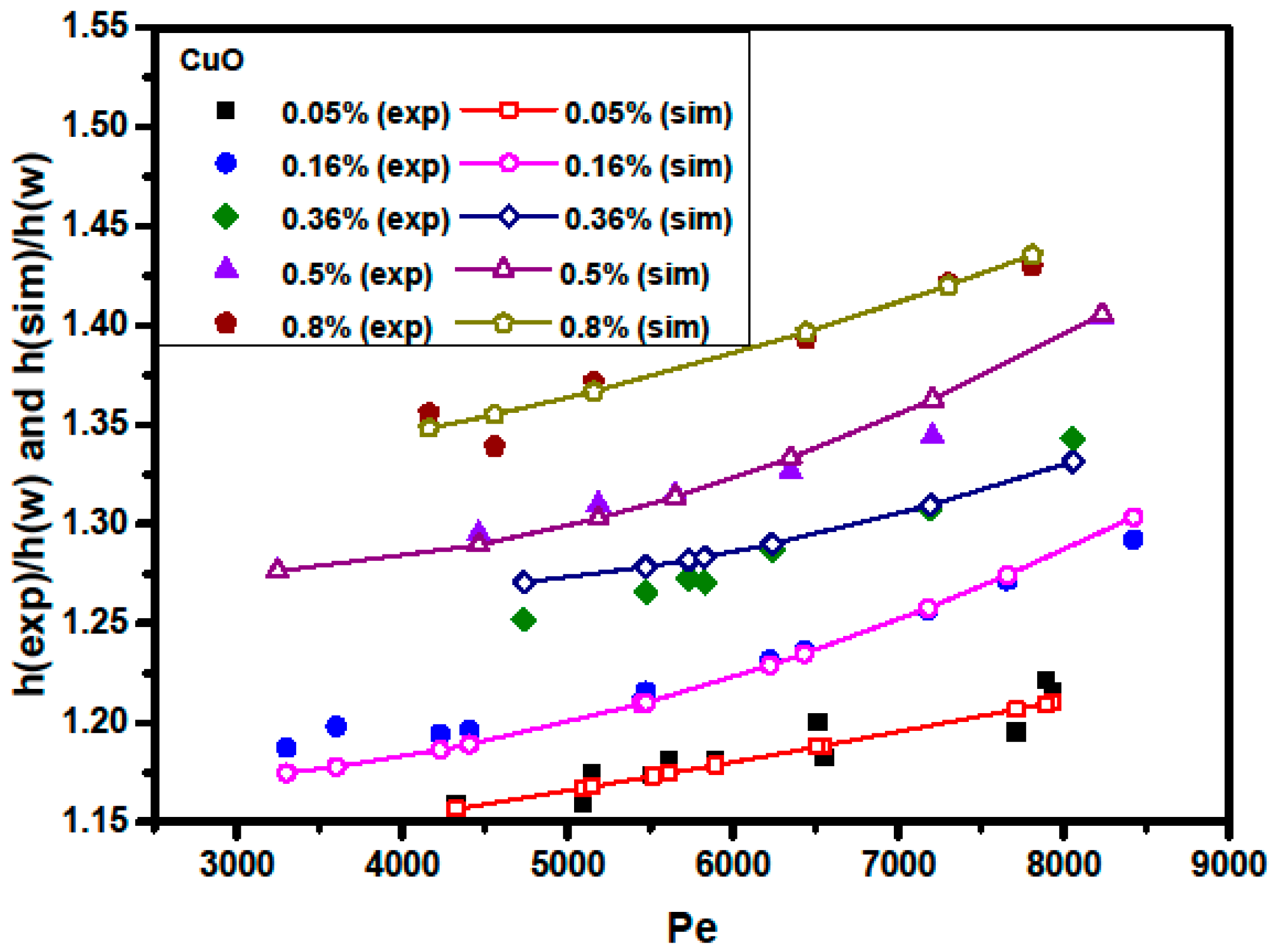
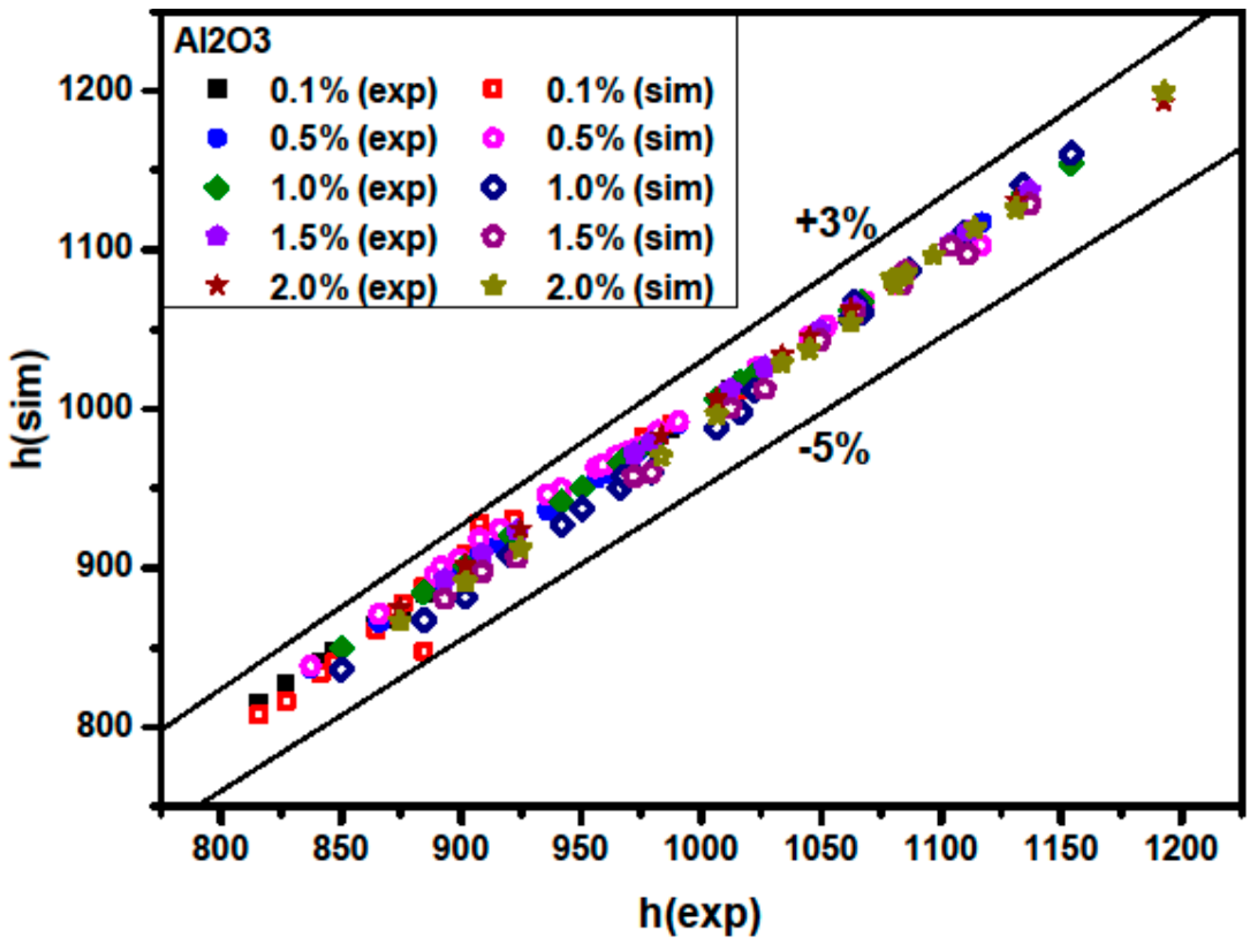
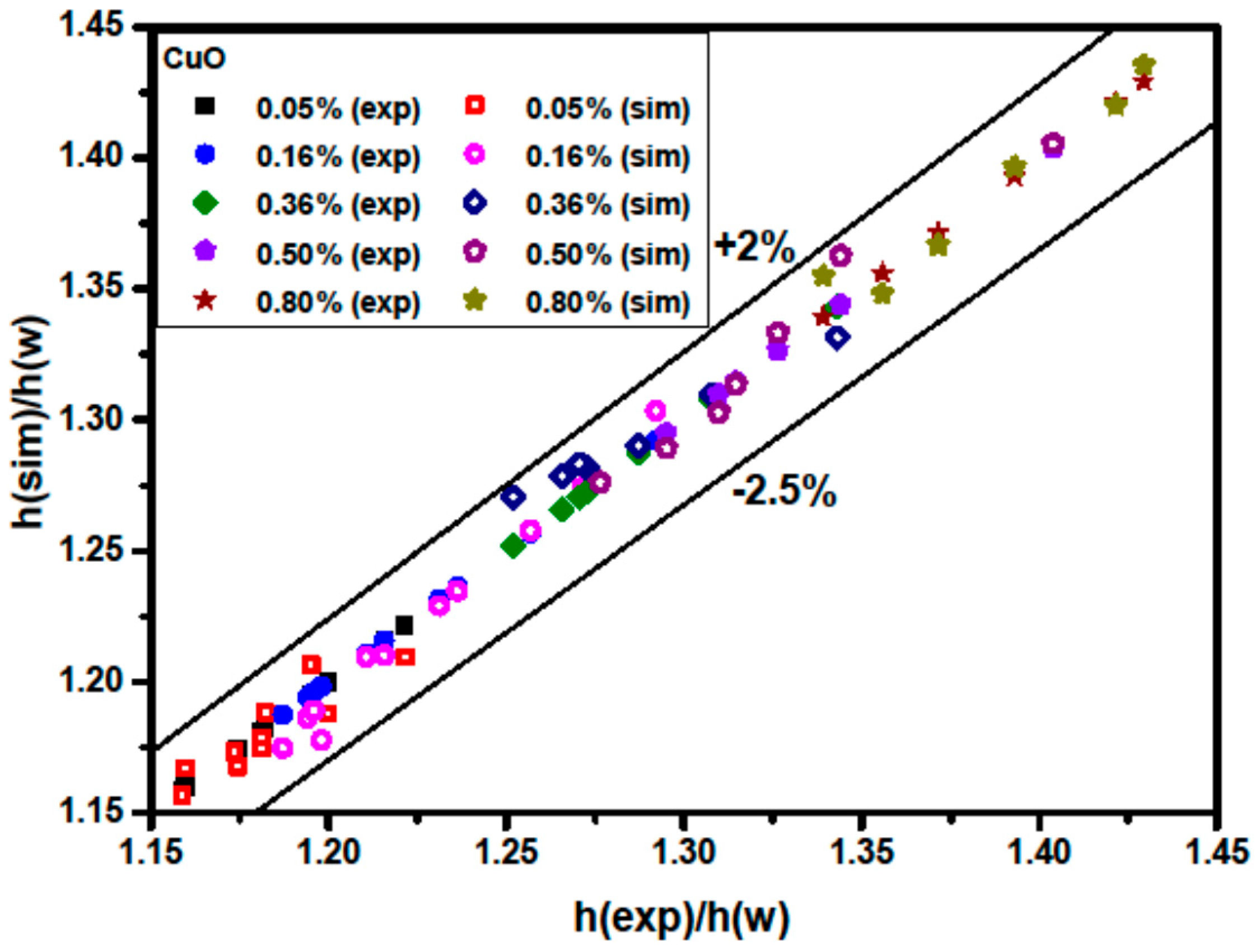
| Property | Basic Fluid (Water) | γ-Al2O3 | CuO |
|---|---|---|---|
| Specific heat (J/kg K) | 4182 | 880 | 535.6 |
| Density (kg/m3) | 998.2 | 3890 | 6350 |
| Thermal conductivity (W/m K) | 0.597 | 46 | 69 |
| Viscosity (kg/ms) | 9.93 × 10−4 | - | - |
| Nanoparticle | (%) | ||||
|---|---|---|---|---|---|
| Al2O3 | 0.1 | 1.0029 | 0.9968 | 1.0843 | 1.0031 |
| 0.5 | 1.0145 | 0.9844 | 1.1557 | 1.0157 | |
| 1.0 | 1.0289 | 0.9692 | 1.2178 | 1.0315 | |
| 1.5 | 1.0434 | 0.9544 | 1.2802 | 1.0475 | |
| 2.0 | 1.0579 | 0.9400 | 1.3521 | 1.0637 | |
| CuO | 0.05 | 1.0027 | 0.9972 | 1.0184 | 1.0045 |
| 0.16 | 1.0086 | 0.9912 | 1.0275 | 1.0143 | |
| 0.36 | 1.0193 | 0.9804 | 1.0371 | 1.0322 | |
| 0.50 | 1.0269 | 0.9729 | 1.0423 | 1.0447 | |
| 0.80 | 1.0430 | 0.9574 | 1.0519 | 1.0715 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ting, H.-H.; Hou, S.-S. Numerical Study of Laminar Flow and Convective Heat Transfer Utilizing Nanofluids in Equilateral Triangular Ducts with Constant Heat Flux. Materials 2016, 9, 576. https://doi.org/10.3390/ma9070576
Ting H-H, Hou S-S. Numerical Study of Laminar Flow and Convective Heat Transfer Utilizing Nanofluids in Equilateral Triangular Ducts with Constant Heat Flux. Materials. 2016; 9(7):576. https://doi.org/10.3390/ma9070576
Chicago/Turabian StyleTing, Hsien-Hung, and Shuhn-Shyurng Hou. 2016. "Numerical Study of Laminar Flow and Convective Heat Transfer Utilizing Nanofluids in Equilateral Triangular Ducts with Constant Heat Flux" Materials 9, no. 7: 576. https://doi.org/10.3390/ma9070576
APA StyleTing, H.-H., & Hou, S.-S. (2016). Numerical Study of Laminar Flow and Convective Heat Transfer Utilizing Nanofluids in Equilateral Triangular Ducts with Constant Heat Flux. Materials, 9(7), 576. https://doi.org/10.3390/ma9070576






