Antireflective Coatings: Conventional Stacking Layers and Ultrathin Plasmonic Metasurfaces, A Mini-Review
Abstract
:1. Introduction
2. Conventional Antireflective Coatings (ARCs)
2.1. Single-Layer ARC
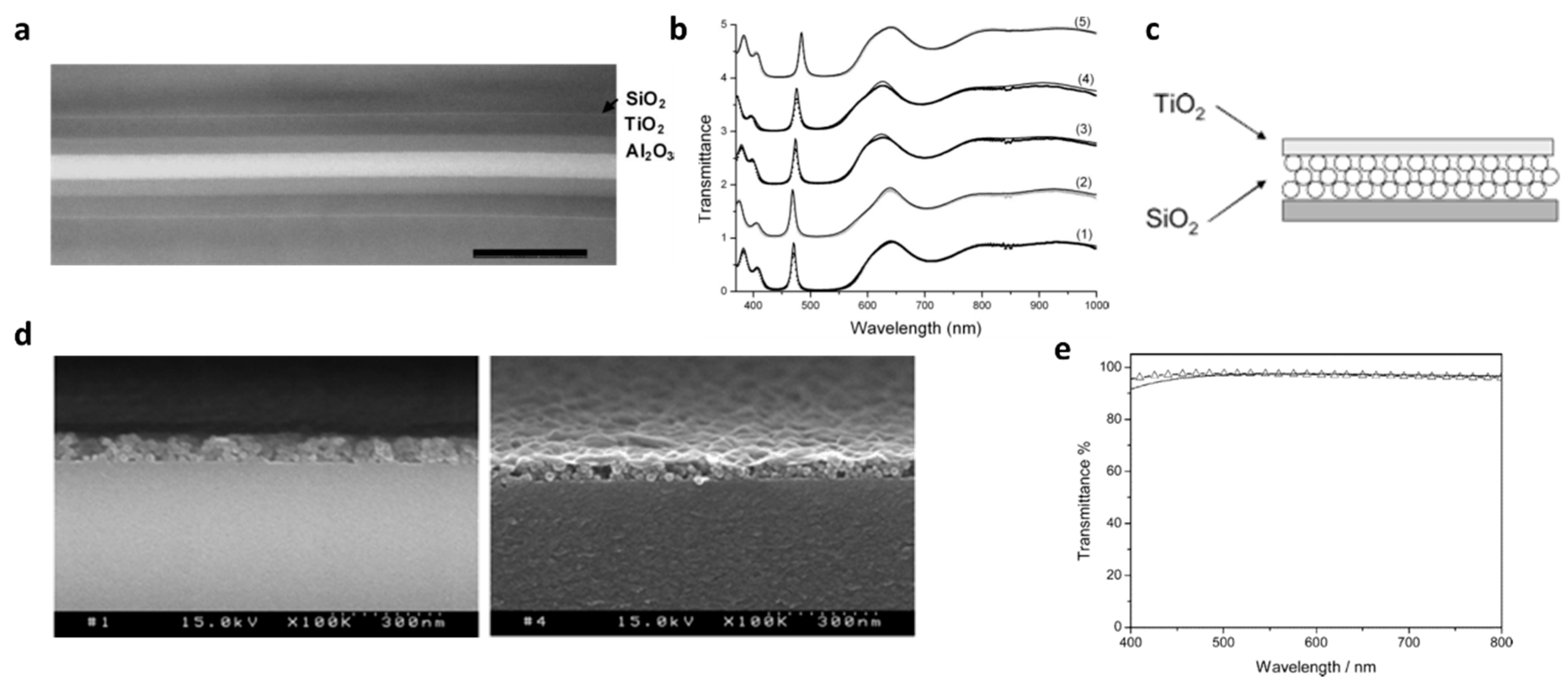
2.2. Double-Layer ARC
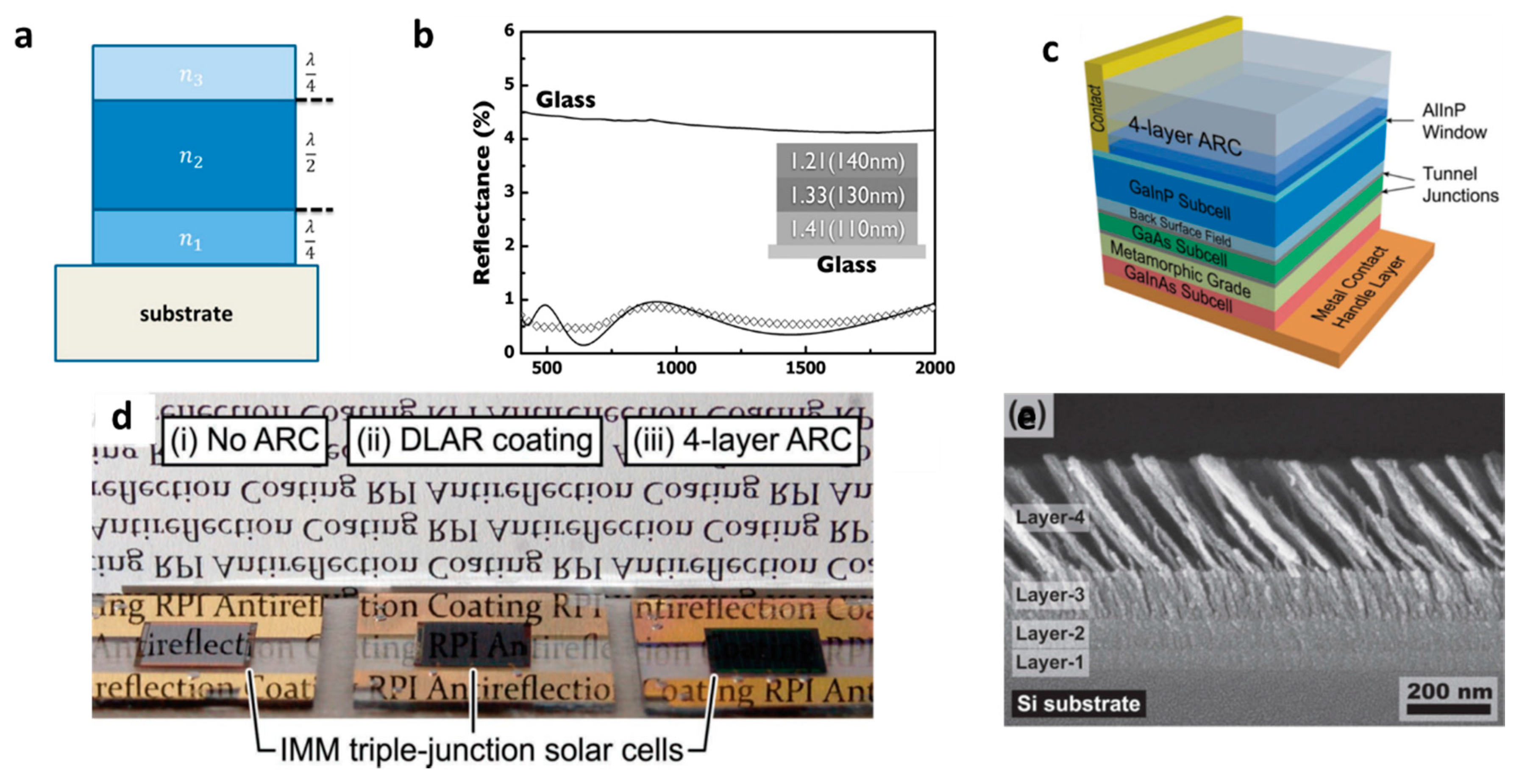
2.3. Multilayer Gradient Film as ARC
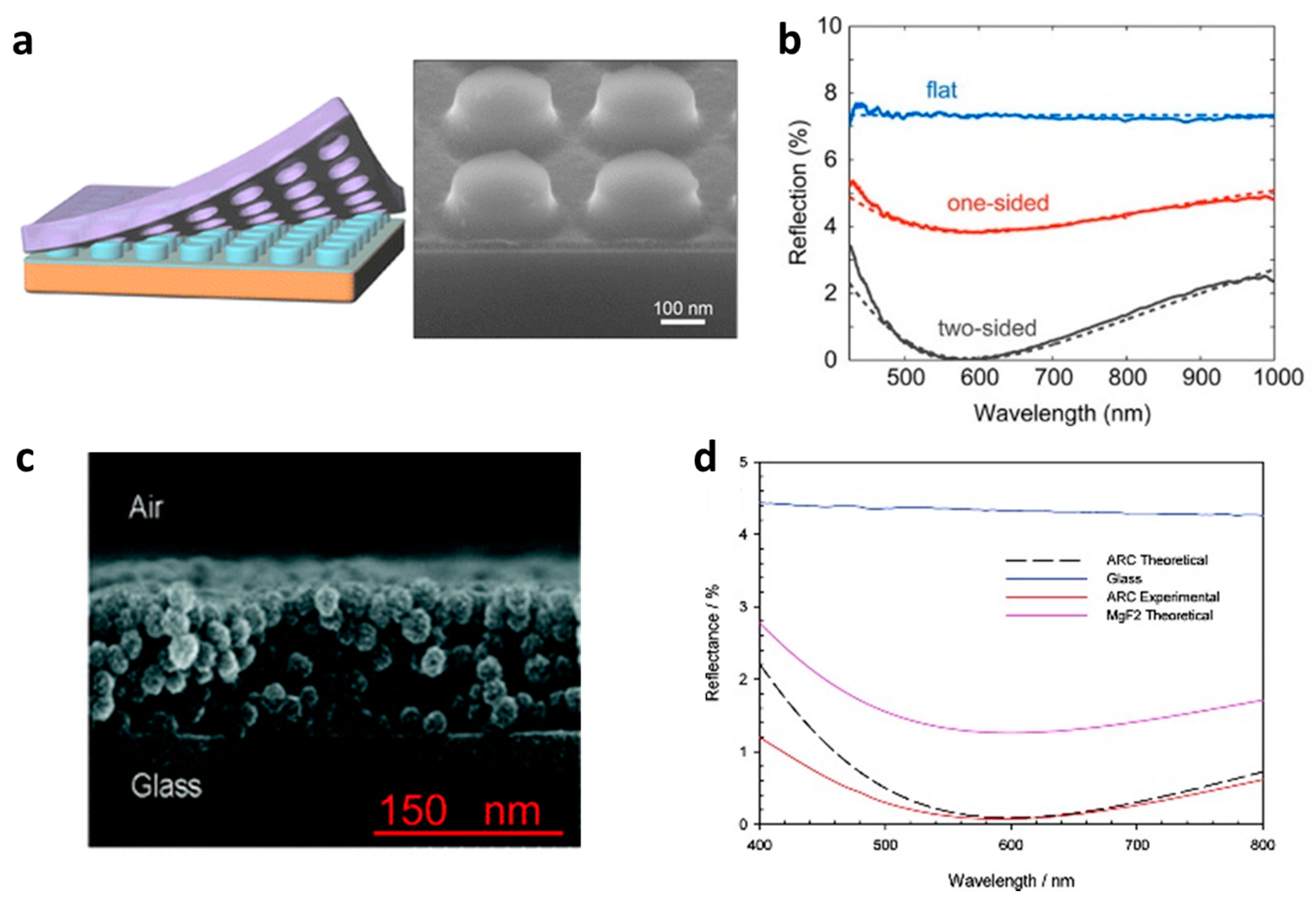
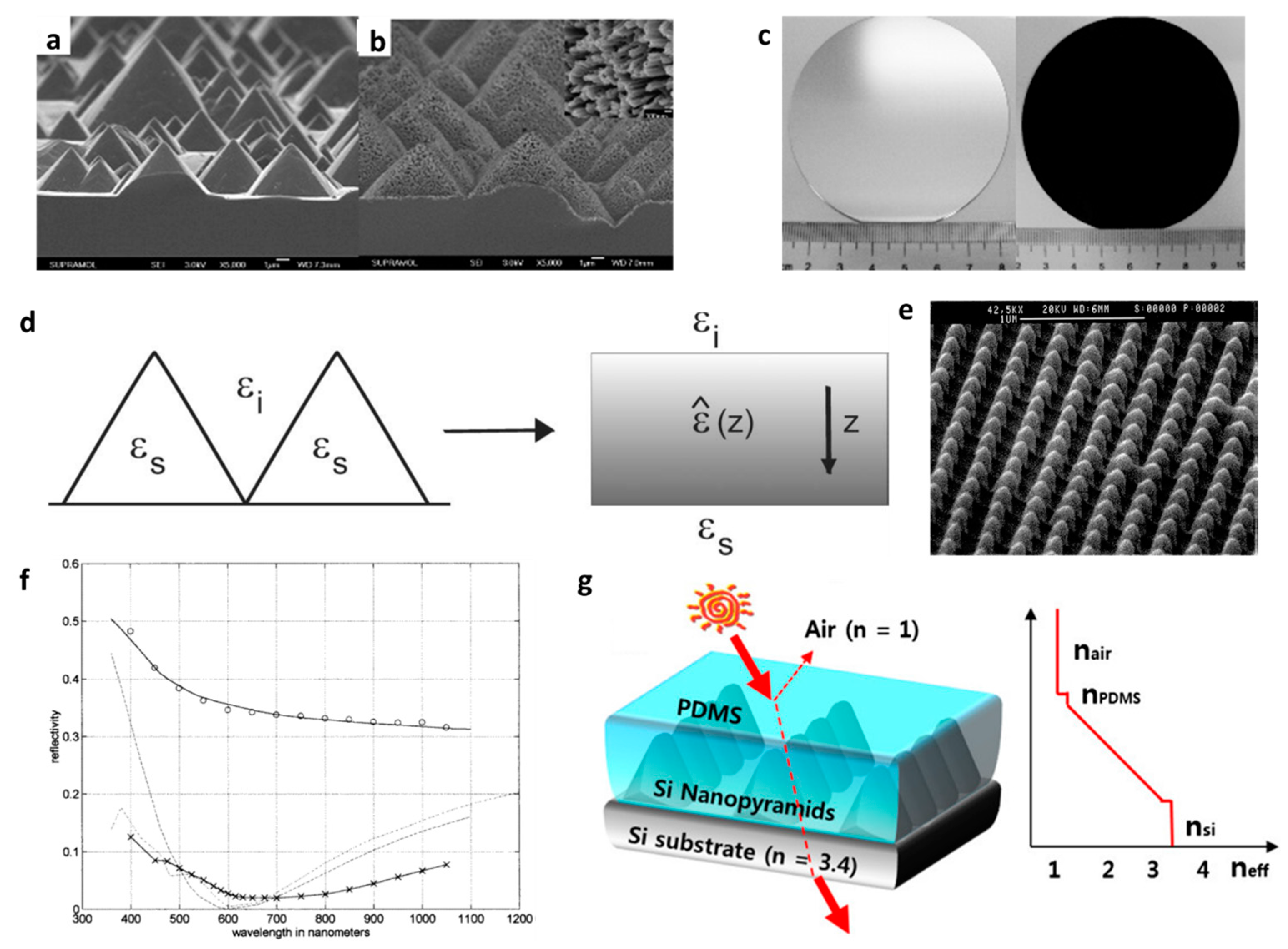
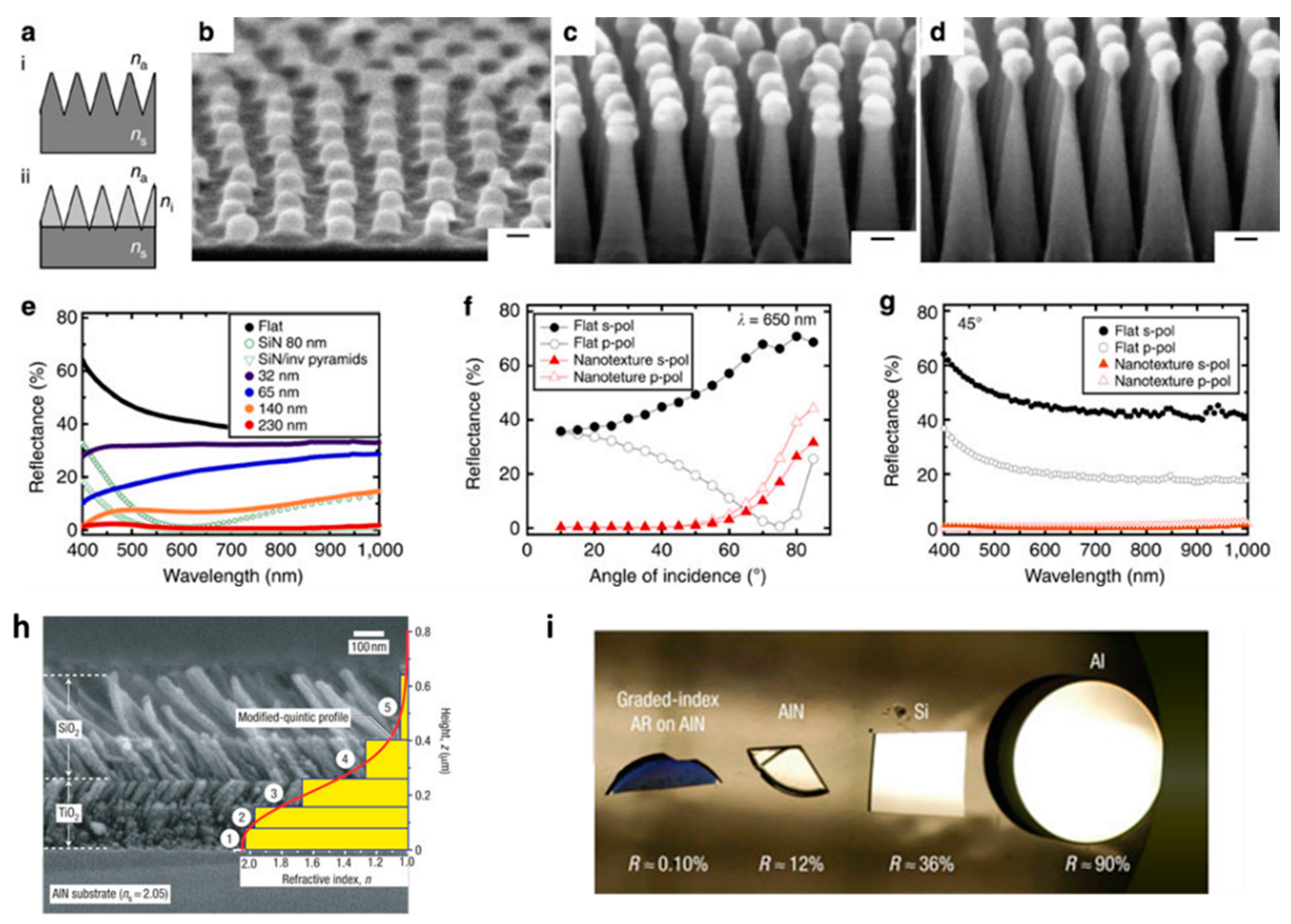
2.4. Structured Surface as ARC
3. Unconventional ARCs
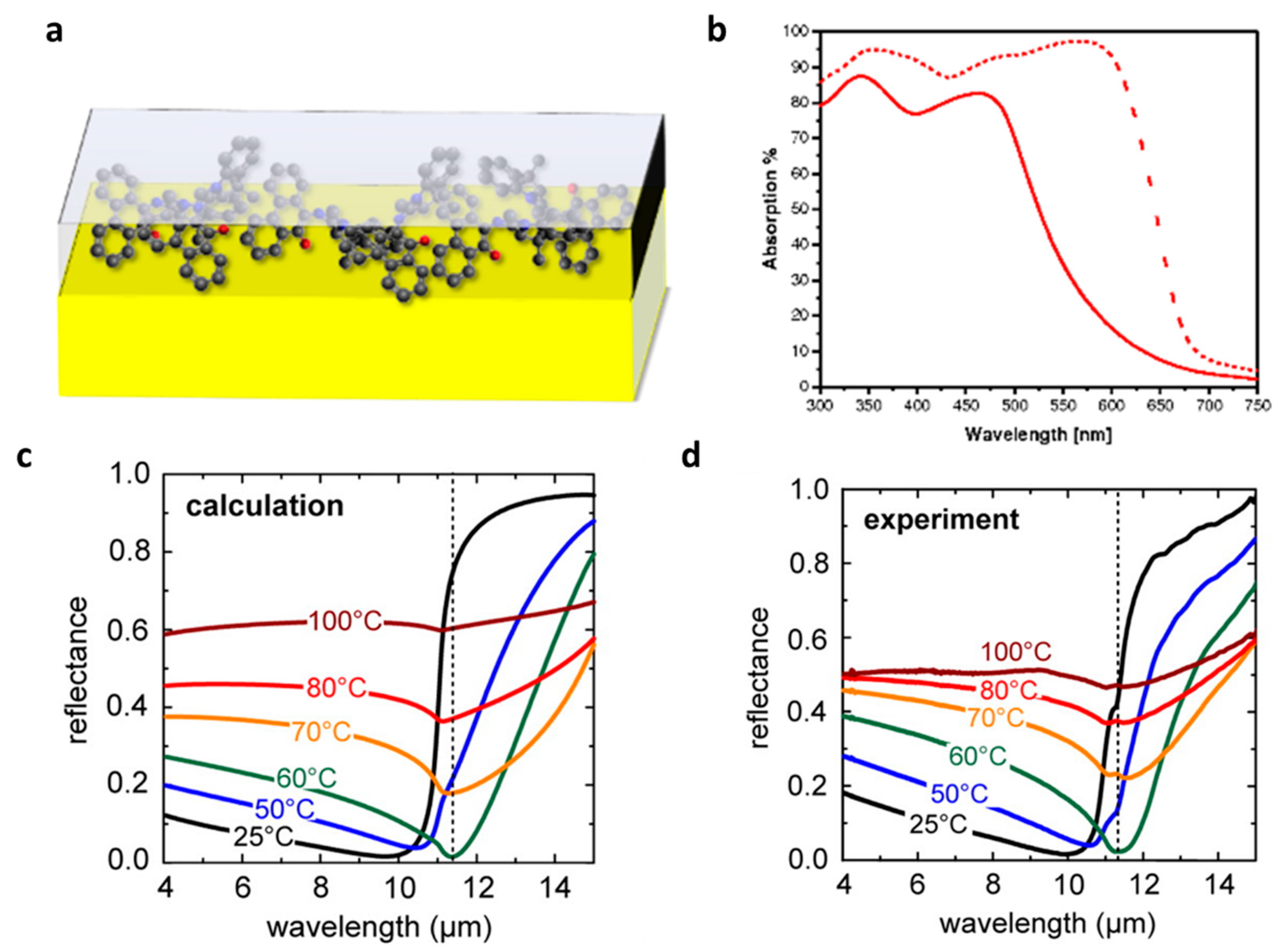
3.1. Absorbing ARCs
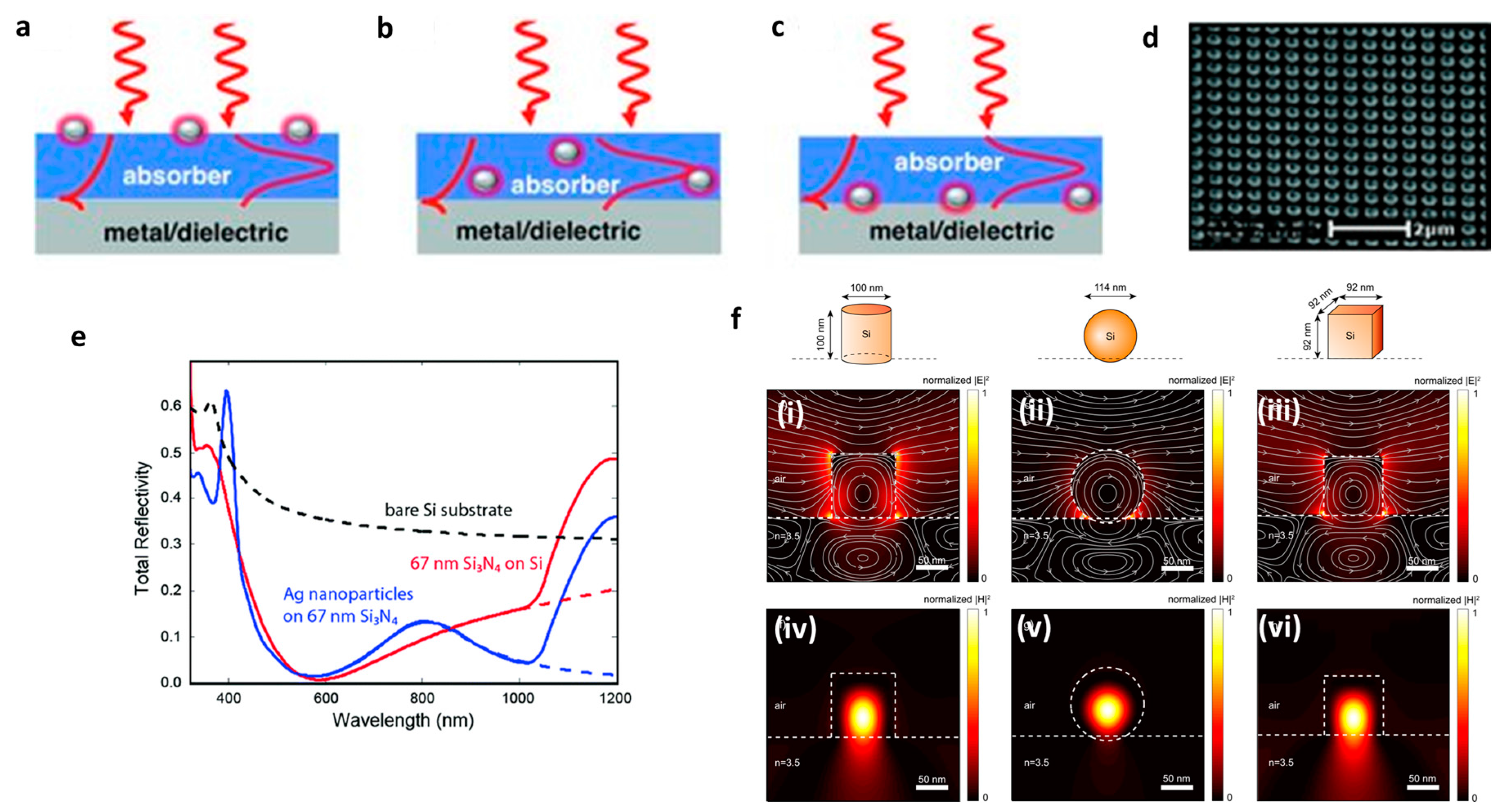
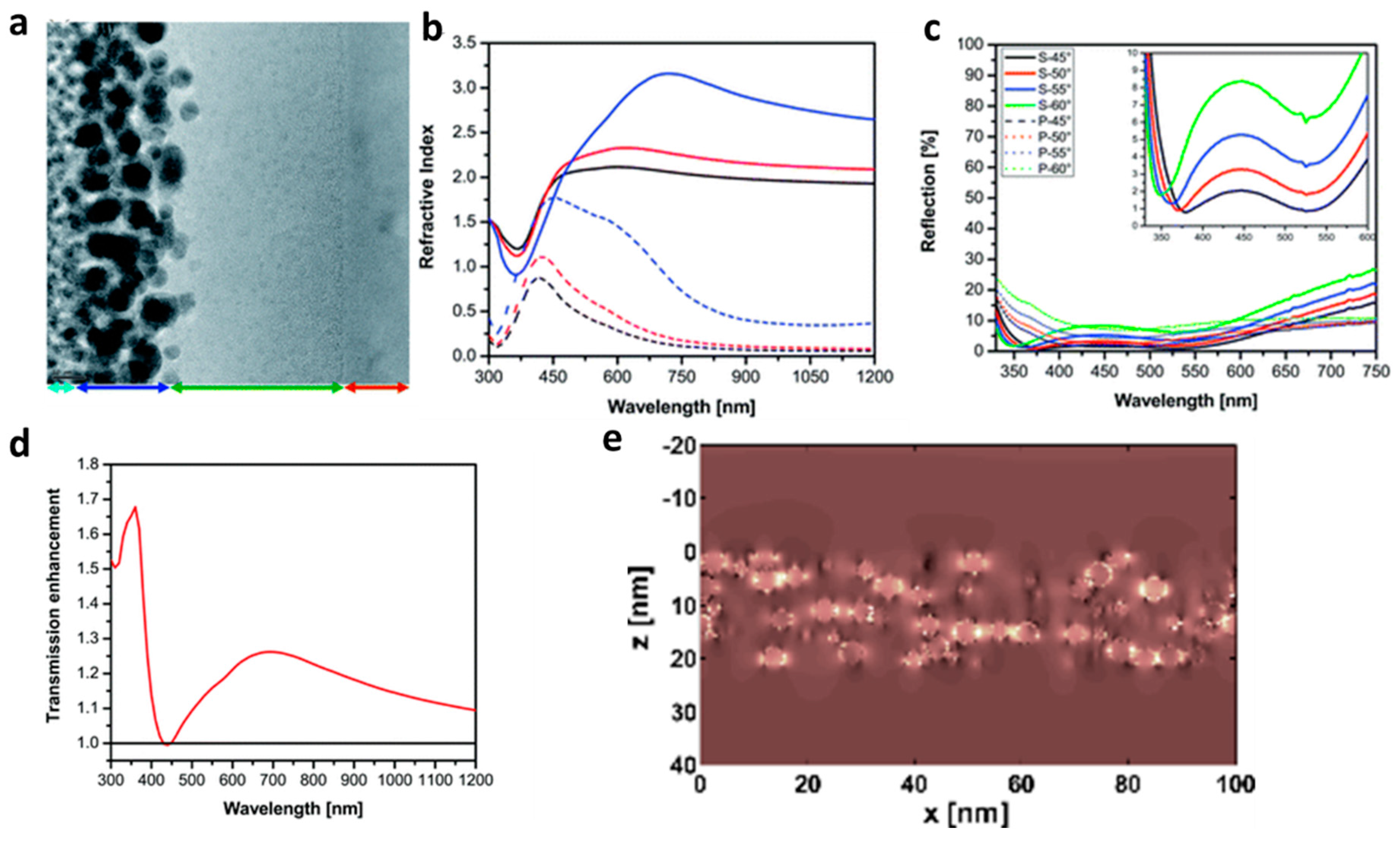
3.2. Plasmonic and Metamaterial (Metasurface) ARCs
4. Applications
5. Summary
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ruhl, J.; Ade, P.; Carlstrom, J.; Cho, H.; Crawford, T.; Dobbs, M.; Greer, C.; Holzapfel, W.; Lanting, T.; Lee, A.; et al. The south pole telescope. Proc. SPIE 2004, 5498. [Google Scholar] [CrossRef]
- Bureau, B.; Zhang, X.; Smektala, F.; Adam, J.; Troles, J.; Ma, H.; Boussard-Plèdel, C.; Lucas, J.; Lucas, P.; le Coq, D.; et al. Recent advances in chalcogenide glasses. J. Non-Cryst. Solids 2004, 345, 276–283. [Google Scholar] [CrossRef]
- Rayleigh, L. On reflection of vibrations at the confines of two media between which the transition is gradual. Proc. Lond. Math. Soc. 1879, 1, 51–56. [Google Scholar] [CrossRef]
- Moulton, H. Optical characteristics. Ind. Eng. Chem. 1940, 32, 1428–1432. [Google Scholar] [CrossRef]
- Strong, J. On a Method of Decreasing the Reflection from Nonmetallic Substances. J. Opt. Soc. Am. A 1936, 26, 73–74. [Google Scholar] [CrossRef]
- Fresnel, A. Mémoire sur la loi des Modifcations que la Réflexion Imprime a la Lumiere Polarisée. IBID 1823, 11, 393–433. [Google Scholar]
- Philipp, H. Optical properties of silicon nitride. J. Electrochem. Soc. 1973, 120, 295–300. [Google Scholar] [CrossRef]
- Garnett, J.M. Colours in Metal Glasses and in Metallic Films. Philos. Trans. R. Soc. A 1904, 203, 385–420. [Google Scholar] [CrossRef]
- Choy, T. Effective Medium Theory: Principles and Applications; Oxford University Press: New York, NY, USA, 2015. [Google Scholar]
- Van de Groep, J.; Spinelli, P.; Polman, A. Single-Step Soft-Imprinted Large-Area Nanopatterned Antireflection Coating. Nano Lett. 2015, 15, 4223–4228. [Google Scholar] [CrossRef] [PubMed]
- Hattori, H. Anti-Reflection Surface with Particle Coating Deposited by Electrostatic Attraction. Adv. Mater. 2001, 13, 51–54. [Google Scholar] [CrossRef]
- Moghal, J.; Kobler, J.; Sauer, J.; Best, J.; Gardener, M.; Watt, A.; Wakefield, G. High-performance, single-layer antireflective optical coatings comprising mesoporous silica nanoparticles. ACS Appl. Mater. Interfaces 2012, 4, 854–859. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Zhang, B.; Fan, W.; Wu, D.; Sun, Y. Sol–gel broadband anti-reflective single-layer silica films with high laser damage threshold. Thin Solid Films 2003, 440, 180–183. [Google Scholar] [CrossRef]
- Liu, B.; Yeh, W. Antireflective surface fabricated from colloidal silica nanoparticles. Colloids Surf. A Physicochem. Eng. Asp. 2010, 356, 145–149. [Google Scholar] [CrossRef]
- Gao, L.; He, J. A facile dip-coating approach based on three silica sols to fabrication of broadband antireflective superhydrophobic coatings. J. Colloid Interface Sci. 2013, 400, 24–30. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Wang, Z.; Yang, X.; Xu, X.; Zhang, L.; Zhao, N.; Xu, J. Antifogging and antireflective silica film and its application on solar modules. Surf. Coat. Technol. 2011, 206, 1490–1494. [Google Scholar] [CrossRef]
- Philipavičius, J.; Kazadojev, I.; Beganskienė, A.; Melninkaitis, A.; Sirutkaitis, V.; Kareiva, A. Hydrophobic antireflective silica coatings via sol–gel process. Mater. Sci. 2008, 14, 283–287. [Google Scholar]
- Li, X.; He, J. In situ assembly of raspberry-and mulberry-like silica nanospheres toward antireflective and antifogging coatings. ACS Appl. Mater. Interfaces 2012, 4, 2204–2211. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Gao, L.; He, J. Fabrication of visible/near-IR antireflective and superhydrophobic coatings from hydrophobically modified hollow silica nanoparticles and poly (methyl methacrylate). RSC Adv. 2012, 2, 12764–12769. [Google Scholar] [CrossRef]
- Zheng, L.; Geng, C.; Yan, Q. Hierarchically ordered arrays based on solvent vapor annealed colloidal monolayers for antireflective coating. Thin Solid Films 2013, 544, 403–406. [Google Scholar] [CrossRef]
- Koo, H.; Yi, D.; Yoo, S.; Kim, D. A Snowman-like Array of Colloidal Dimers for Antireflecting Surfaces. Adv. Mater. 2004, 16, 274–277. [Google Scholar] [CrossRef]
- Floch, H.; Belleville, P. A scratch-resistant single-layer antireflective coating by a low temperature sol-gel route. J. Sol-Gel Sci. Technol. 1994, 1, 293–304. [Google Scholar] [CrossRef]
- Jamali, M.; Hedayati, M.; Mozooni, B.; Javaherirahim, M.; Abdelaziz, R.; Zillohu, A.; Elbahri, M. Photoresponsive transparent conductive metal with a photobleaching nose. Adv. Mater. 2011, 23, 4243–4247. [Google Scholar] [CrossRef] [PubMed]
- Hedayati, M.K.; Javaheri, M.; Zillohu, A.U.; El-Khozondar, H.J.; Bawa’aneh, M.S.L.A.; Faupel, F.; Elbahri, M. Photo-driven Super Absorber as an Active Metamaterial. Adv. Opt. Mater. 2014, 2, 705–710. [Google Scholar] [CrossRef]
- Wydeven, T. Plasma polymerized coating for polycarbonate: Single layer, abrasion resistant, and antireflection. Appl. Opt. 1977, 16, 717–721. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Sato, O.; Taguchi, M.; Einaga, Y.; Murakami, T.; Fujishima, A. Self-cleaning particle coating with antireflection properties. Chem. Mater. 2005, 17, 696–700. [Google Scholar] [CrossRef]
- Helsch, G.; Deubener, J. Compatibility of antireflective coatings on glass for solar applications with photocatalytic properties. Sol. Energy 2012, 86, 831–836. [Google Scholar] [CrossRef]
- Kern, K.; Tracy, E. Titanium dioxide antireflection coating for silicon solar cells by spray deposition. RCA Rev 1980, 41. [Google Scholar]
- Kaminski, P.; Bass, K.; Claudio, G. High bandgap dielectrics for antireflective coating in silicon solar cells by reactive ion sputtering. Phys. Status Solidi (C) 2011, 8, 1311–1314. [Google Scholar] [CrossRef]
- Bouhafs, D.; Moussi, A.; Chikouche, A.; Ruiz, J. Design and simulation of antireflection coating systems for optoelectronic devices: Application to silicon solar cells. Sol. Energy Mater. Sol. Cells 1998, 52, 79–93. [Google Scholar] [CrossRef]
- Glaubitt, W.; Löbmann, P. Antireflective coatings prepared by sol–gel processing: Principles and applications. J. Eur. Ceram. Soc. 2012, 32, 2995–2999. [Google Scholar] [CrossRef]
- Chen, D.; Yan, Y.; Westenberg, E.; Niebauer, D.; Sakaitani, N.; Chaudhuri, S.; Sato, Y.; Takamatsu, M. Development of anti-reflection (AR) coating on plastic panels for display applications. J. Sol-Gel Sci. Technol. 2000, 19, 77–82. [Google Scholar] [CrossRef]
- Raut, H.; Ganesh, V.; Nair, A.; Ramakrishna, S. Anti-reflective coatings: A critical, in-depth review. Energy Environ. Sci. 2011, 4, 3779–3804. [Google Scholar] [CrossRef]
- Lee, S.; Choi, S.; Yi, J. Double-layer anti-reflection coating using MgF2 and CeO2 films on a crystalline silicon substrate. Thin Solid Films 2000, 376, 208–213. [Google Scholar] [CrossRef]
- Szeghalmi, A.; Helgert, M.; Brunner, R.; Heyroth, F.; Gösele, U.; Knez, M. Atomic layer deposition of Al2O3 and TiO2 multilayers for applications as bandpass filters and antireflection coatings. Appl. Opt. 2009, 48, 1727–1732. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Fujishima, A.; Jin, M.; Emeline, A.; Murakami, T. Double-layered TiO2-SiO2 nanostructured films with self-cleaning and antireflective properties. J. Phys. Chem. B 2006, 110, 25142–25148. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Cui, X.; Zhang, C.; Zhang, C.; Ding, R.; Xu, Y. A broadband antireflective coating based on a double-layer system containing mesoporous silica and nanoporous silica. J. Mater. Chem. C 2015, 3, 7187–7194. [Google Scholar] [CrossRef]
- Wiktorczyk, T.; Oleś, M. Design, fabrication and optical characterization of cerium oxide-magnesium fluoride double layer antireflection coatings on monocrystalline silicon substrates. Opt. Mater. 2007, 29, 1768–1773. [Google Scholar] [CrossRef]
- Kavakli, İ.; Kantarli, K. Single and double-layer antireflection coatings on silicon. Turk. J. Phys. 2002, 26, 349–354. [Google Scholar]
- Martinet, C.; Paillard, V.; Gagnaire, A.; Joseph, J. Deposition of SiO2 and TiO2 thin films by plasma enhanced chemical vapor deposition for antireflection coating. J. Non-Cryst. Solids 1997, 216, 77–82. [Google Scholar] [CrossRef]
- Pettit, R.; Brinker, C.; Ashley, C. Sol-gel double-layer antireflection coatings for silicon solar cells. Sol. Cells 1985, 15, 267–278. [Google Scholar] [CrossRef]
- Wright, D.; Marstein, E.; Holt, A. Double layer anti-reflective coatings for silicon solar cells. In Proceedings of the Conference Record of the Thirty-First IEEE Photovoltaic Specialists Conference, Lake Buena Vista, FL, USA, 3–7 January 2005.
- Zheo, J.; Wang, A.; Atermatt, P.; Green, M. Twenty-Four Percent Efficient Silicon Solar Cells with Double Layer Antireflection Coatings and Reduced Resistance Loss. Appl. Phys. Lett. 1995, 66, 3636. [Google Scholar] [CrossRef]
- Chen, Z.; Sana, P.; Salami, J.; Rohatgi, A. A novel and effective PECVD SiO2/SiN antireflection coating for Si solar cells. IEEE Trans. Electron Devices 1993, 40, 1161–1165. [Google Scholar] [CrossRef]
- Dhungel, S.; Yoo, J.; Kim, K.; Jung, S.; Ghosh, S.; Yi, J. Double-layer antireflection coating of MgF2/SiN x for crystalline silicon solar cells. J. Korean Phys. Soc. 2006, 49, 885–889. [Google Scholar]
- Lien, S.; Wuu, D.; Yeh, W.; Liu, J. Tri-layer antireflection coatings (SiO2/SiO2–TiO2/TiO2) for silicon solar cells using a sol–gel technique. Sol. Energy Mater. Sol. Cells 2006, 90, 2710–2719. [Google Scholar] [CrossRef]
- Chen, C.; Lin, D.; Don, T.; Huang, F.; Cheng, L. Preparation of organic–inorganic nano-composites for antireflection coatings. J. Non-Cryst. Solids 2008, 354, 3828–3835. [Google Scholar] [CrossRef]
- Wang, X.; Shen, J. Sol–gel derived durable antireflective coating for solar glass. J. Sol-Gel Sci. Technol. 2010, 53, 322–327. [Google Scholar] [CrossRef]
- Li, J.; Lu, Y.; Lan, P.; Zhang, X.; Xu, W.; Tan, R.; Song, W.; Choy, K. Design, preparation, and durability of TiO2/SiO2 and ZrO2/SiO2 double-layer antireflective coatings in crystalline silicon solar modules. Sol. Energy 2013, 89, 134–142. [Google Scholar] [CrossRef]
- Ye, L.; Zhang, Y.; Zhang, X.; Hu, T.; Ji, R.; Ding, B.; Jiang, B. Sol–gel preparation of SiO2/TiO2/SiO2–TiO2 broadband antireflective coating for solar cell cover glass. Sol. Energy Mater. Sol. Cells 2013, 111, 160–164. [Google Scholar] [CrossRef]
- Kesmez, Ö.; Çamurlu, H.; Burunkaya, E.; Arpaç, E. Sol–gel preparation and characterization of anti-reflective and self-cleaning SiO2–TiO2 double-layer nanometric films. Sol. Energy Mater. Sol. Cells 2009, 93, 1833–1839. [Google Scholar] [CrossRef]
- Richards, B. Single-material TiO2 double-layer antireflection coatings. Sol. Energy Mater. Sol. Cells 2003, 79, 369–390. [Google Scholar] [CrossRef]
- Winderbaum, S.; Yun, F.; Reinhold, O. Application of plasma enhanced chemical vapor deposition silicon nitride as a double layer antireflection coating and passivation layer for polysilicon solar cells. J. Vac. Sci. Technol. A 1997, 15, 1020–1025. [Google Scholar] [CrossRef]
- Jiao, K.; Anderson, W. SiO2/TiO2 double-layer antireflective coating deposited at room temperature for metal/insulator/n-Si/p-Si solar cells. Sol. Cells 1987, 22, 229–236. [Google Scholar] [CrossRef]
- Lee, J.; Tanaka, T.; Uchiyama, S.; Tsuchiya, M.; Kamiya, T. Broadband double-layer antireflection coatings for semiconductor laser amplifiers. Jpn. J. Appl. Phys. 1997, 36, L52. [Google Scholar] [CrossRef]
- Chiou, B.; Tsai, J. Antireflective coating for ITO films deposited on glass substrate. J. Mater. Sci. Mater. Electron. 1999, 10, 491–495. [Google Scholar] [CrossRef]
- Aroutiounian, V.; Martirosyan, K.; Soukiassian, P. Almost zero reflectance of a silicon oxynitride/porous Silicon Double layer Antireflection Coating for Silicon Photovoltaic Cells. J. Phys. D Appl. Phys. 2006, 39, 1623. [Google Scholar] [CrossRef]
- Aroutiounian, V.; Martirosyan, K.; Soukiassian, P. Low reflectance of diamond-like carbon/porous silicon double layer antireflection coating for silicon solar cells. J. Phys. D Appl. Phys. 2004, 37, L25. [Google Scholar] [CrossRef]
- Kats, M.; Blanchard, R.; Genevet, P.; Capasso, F. Nanometre optical coatings based on strong interference effects in highly absorbing. Nat. Mater. 2012, 12, 20–24. [Google Scholar] [CrossRef] [PubMed]
- Orfanidis, S.J. Electromagnetic Waves and Antenna. Available online: http://eceweb1.rutgers.edu/~orfanidi/ewa/ (accessed on 15 April 2016).
- Greiner, H. Robust optical coating design with evolutionary strategies. Appl. Opt. 1996, 35, 5477–5483. [Google Scholar] [CrossRef] [PubMed]
- Wiesmann, D.; Hammel, U.; Bäck, T. Robust design of multilayer optical coatings by means of evolutionary algorithms. IEEE Trans. Evol. Comput. 1998, 2, 162–167. [Google Scholar] [CrossRef]
- Schubert, M.; Mont, F.; Chhajed, S.; Poxson, D.; Kim, J.; Schubert, E. Design of multilayer antireflection coatings made from co-sputtered and low-refractive-index materials by genetic algorithm. Opt. Express 2008, 16, 5290–5298. [Google Scholar] [CrossRef] [PubMed]
- Braun, D.; Jungerman, R. Broadband multilayer antireflection coating for semiconductor laser facets. Opt. Lett. 1995, 20, 1154–1156. [Google Scholar] [CrossRef] [PubMed]
- Marszałek, K.; Winkowski, P.; Jaglarz, J. Optical properties of the Al2O3/SiO2 and Al2O3/HfO2/SiO2 antireflective coatings. Mater. Sci. Pol. 2014, 32, 80–87. [Google Scholar] [CrossRef]
- Chhajed, S.; Schubert, M.; Kim, J.; Schubert, E. Nanostructured multilayer graded-index antireflection coating for Si solar cells with broadband and omnidirectional characteristics. Appl. Phys. Lett. 2008, 93, 251108. [Google Scholar] [CrossRef]
- Zhang, H.; Hu, X.; Sun, Y.; Zheng, Y.; Yan, L.; Jiang, B.; Chen, H.; Zhang, X. Design and sol-gel preparation of six-layer tri-wavelength ORMOSIL antireflective coating for high power laser system. RSC Adv. 2016, 6, 31769–31774. [Google Scholar]
- Jeong, O.; Lee, A.; Raum, C.; Suzuki, A. Broadband Plasma-Sprayed Anti-reflection Coating for Millimeter-Wave Astrophysics Experiments. J. Low Temp. Phys. 2016, 183, 1–6. [Google Scholar] [CrossRef]
- Loh, J.; Puzzo, D.; O’Brien, P.; Ozin, G.; Kherani, N. Enhancing photovoltaics with broadband high-transparency glass using porosity-tuned multilayer silica nanoparticle anti-reflective coatings. RSC Adv. 2014, 4, 31188–31195. [Google Scholar] [CrossRef]
- Mazur, M.; Wojcieszak, D.; Domaradzki, J.; Kaczmarek, D.; Song, S.; Placido, F. TiO2/SiO2 multilayer as an antireflective and protective coating deposited by microwave assisted magnetron sputtering. Opto-Electron. Rev. 2013, 21, 233–238. [Google Scholar] [CrossRef]
- Szczyrbowski, J.; Bräuer, G.; Teschner, G.; Zmelty, A. Antireflective coatings on large scale substrates produced by reactive twin-magnetron sputtering. J. Non-Cryst. Solids 1997, 218, 25–29. [Google Scholar] [CrossRef]
- Mazur, M.; Wojcieszak, D.; Kaczmarek, D.; Domaradzki, J.; Song, S.; Gibson, D.; Placido, F.; Mazur, P.; Kalisz, M.; Poniedzialek, A. Functional photocatalytically active and scratch resistant antireflective coating based on TiO2 and SiO2. Appl. Surf. Sci. 2016, 380, 165–171. [Google Scholar] [CrossRef]
- Glöß, D.; Frach, P.; Gottfried, C.; Klinkenberg, S.; Liebig, J.-S.; Hentsch, W.; Liepack, H.; Krug, M. Multifunctional high-reflective and antireflective layer systems with easy-to-clean properties. Thin Solid Films 2008, 516, 4487–4489. [Google Scholar] [CrossRef]
- Yan, X.; Poxson, D.; Cho, J.; Welser, R.; Sood, A.; Kim, J.; Schubert, E. Enhanced Omnidirectional Photovoltaic Performance of Solar Cells Using Multiple-Discrete-Layer Tailored-and Low-Refractive Index Anti-Reflection Coatings. Adv. Funct. Mater. 2013, 23, 583–590. [Google Scholar] [CrossRef]
- Buskens, P.; Burghoorn, M.; Mourad, M.; Vroon, Z. Antireflective Coatings for Glass and Transparent Polymers. Langmuir 2016. [Google Scholar] [CrossRef] [PubMed]
- Joo, W.; Kim, H.; Kim, J. Broadband antireflection coating covering from visible to near infrared wavelengths by using multilayered nanoporous block copolymer films. Langmuir 2009, 26, 5110–5114. [Google Scholar] [CrossRef] [PubMed]
- Craighead, H.; Howard, R.; Sweeney, J.; Tennant, D. Textured surfaces: Optical storage and other applications. J. Vac. Sci. Technol. 1982, 20, 316–319. [Google Scholar] [CrossRef]
- Chang, Y.; Mei, G.; Chang, T.; Wang, T.; Lin, D.; Lee, C. Design and fabrication of a nanostructured surface combining antireflective and enhanced-hydrophobic effects. Nanotechnology 2007, 18, 285303. [Google Scholar] [CrossRef]
- Bernhard, C. Structural and functional adaptation in a visual system. Endeavour 1967, 26, 79. [Google Scholar]
- Clapham, P.; Hutley, M. Reduction of lens reflexion by the “Moth Eye” principle. Nature 1973, 244, 281–282. [Google Scholar] [CrossRef]
- Morhard, C.; Pacholski, C.; Lehr, D.; Brunner, R.; Helgert, M.; Sundermann, M.; Spatz, J. Tailored antireflective biomimetic nanostructures for UV applications. Nanotechnology 2010, 21, 425301. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Chang, W.; Huang, C.; Sun, K. Biomimetic nanostructured antireflection coating and its application on crystalline silicon solar cells. Opt. Express 2011, 19, 14411–14419. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.; Jiang, P.; Jiang, B. Broadband moth-eye antireflection coatings on silicon. Appl. Phys. Lett. 2008, 92, 061112. [Google Scholar] [CrossRef]
- Min, W.; Jiang, B.; Jiang, P. Bioinspired Self-Cleaning Antireflection Coatings. Adv. Mater. 2008, 20, 3914–3918. [Google Scholar] [CrossRef]
- Chen, H.; Chuang, S.; Lin, C.; Lin, Y. Using colloidal lithography to fabricate and optimize sub-wavelength pyramidal and honeycomb structures in solar cells. Opt. Express 2007, 15, 14793–14803. [Google Scholar] [CrossRef] [PubMed]
- Campbell, P.; Green, M. Light trapping properties of pyramidally textured surfaces. J. Appl. Phys. 1987, 62, 243–249. [Google Scholar] [CrossRef]
- Bean, K. Anisotropic etching of silicon. IEEE Trans. Electron Devices 1978, 25, 1185–1193. [Google Scholar] [CrossRef]
- Deinega, A.; Valuev, I.; Potapkin, B.; Lozovik, Y. Minimizing light reflection from dielectric textured surfaces. J. Opt. Soc. Am. A 2011, 28, 770–777. [Google Scholar] [CrossRef] [PubMed]
- Munday, J.; Atwater, H. Large integrated absorption enhancement in plasmonic solar cells by combining metallic gratings and antireflection coatings. Nano Lett. 2010, 11, 2195–2201. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, A.; Motoyama, M.; Kosaku, A.; Miyamoto, K. Antireflective nanoprotuberance array in the transparent wing of a hawkmoth, Cephonodes hylas. Zool. Sci. 1997, 14, 737–741. [Google Scholar] [CrossRef]
- Qi, D.; Lu, N.; Xu, H.; Yang, B.; Huang, C.; Xu, M.; Gao, L.; Wang, Z.; Chi, L. Simple approach to wafer-scale self-cleaning antireflective silicon surfaces. Langmuir 2009, 25, 7769–7772. [Google Scholar] [CrossRef] [PubMed]
- Lalanne, P.; Morris, G. Antireflection behavior of silicon subwavelength periodic structures for visible light. Nanotechnology 1997, 8, 53–56. [Google Scholar] [CrossRef]
- Ha, J.; Yoo, S.; Cho, J.; Cho, Y.; Cho, S. Enhancement of antireflection property of silicon using nanostructured surface combined with a polymer deposition. Nanoscale Res. Lett. 2014, 9, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Walheim, S.; Schaffer, E.; Mlynek, J.; Steiner, U. Nanophase-separated polymer films as high-performance antireflection coatings. Science 1999, 283, 520–522. [Google Scholar] [CrossRef] [PubMed]
- Park, M.; Lee, Y.; Kim, J. One-step preparation of antireflection film by spin-coating of polymer/solvent/nonsolvent ternary system. Chem. Mater. 2005, 17, 3944–3950. [Google Scholar] [CrossRef]
- Huang, Y.; Chattopadhyay, S.; Jen, Y.; Peng, C.; Liu, T.; Hsu, Y.; Pan, C.; Lo, H.; Hsu, C.; Chang, Y.; et al. Improved broadband and quasi-omnidirectional anti-reflection properties with biomimetic silicon nanostructures. Nat. Nanotechnol. 2007, 2, 770–774. [Google Scholar] [CrossRef] [PubMed]
- Hsu, C.; Lo, H.; Chen, C.; Wu, C.; Hwang, J.; Das, D.; Tsai, J.; Chen, L.; Chen, K. Generally applicable self-masked dry etching technique for nanotip array fabrication. Nano Lett. 2004, 4, 471–475. [Google Scholar] [CrossRef]
- Prasad, A.; Balakrishnan, S.; Jain, S.; Jain, G. Porous Silicon Oxide Anti-Reflection Coating for Solar Cells. J. Electrochem. Soc. 1982, 129, 596–599. [Google Scholar] [CrossRef]
- Föll, H.; Christophersen, M.; Carstensen, J.; Hasse, G. Formation and application of porous silicon. Mater. Sci. Eng. R. Rep. 2002, 39, 93–141. [Google Scholar] [CrossRef]
- Srivastava, S.; Kumar, D.; Singh, P.; Kar, M.; Kumar, V.; Husain, M. Excellent antireflection properties of vertical silicon nanowire arrays. Sol. Energy Mater. Sol. Cells 2010, 94, 1506–1511. [Google Scholar] [CrossRef]
- Minot, M. Single-layer, gradient refractive index antireflection films effective from 0.35 to 2.5 μ. J. Opt. Soc. Am. 1976, 66, 515–519. [Google Scholar] [CrossRef]
- Jones, F.; Homer, H. Chemical methods for increasing the transparency of glass surfaces. JOSA 1941, 31, 34–38. [Google Scholar] [CrossRef]
- Nicoll, F.; Williams, F. Properties of low reflection films produced by the action of hydrofluoric acid vapor. JOSA 1943, 33, 434–435. [Google Scholar] [CrossRef]
- Hiller, J.; Mendelsohn, J.; Rubner, M. Reversibly erasable nanoporous anti-reflection coatings from polyelectrolyte multilayers. Nat. Mater. 2002, 1, 59–63. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Gao, J.; Xue, L.; Han, Y. Porous Polymer Films with Gradient-Refractive-Index Structure for Broadband and Omnidirectional Antireflection Coatings. Adv. Funct. Mater. 2010, 20, 259–265. [Google Scholar] [CrossRef]
- Li, X.; Xue, L.; Han, Y. Broadband antireflection of block copolymer/homopolymer blend films with gradient refractive index structures. J. Mater. Chem. 2011, 21, 5817–5826. [Google Scholar] [CrossRef]
- Li, X.; Yu, X.; Han, Y. Polymer thin films for antireflection coatings. J. Mater. Chem. C 2013, 1, 2266–2285. [Google Scholar] [CrossRef]
- Rahman, A.; Ashraf, A.; Xin, H.; Tong, X.; Sutter, P.; Eisaman, M.; Black, C. Sub-50-nm self-assembled nanotextures for enhanced broadband antireflection in silicon solar cells. Nat. Commun. 2015, 6, 5963. [Google Scholar] [CrossRef] [PubMed]
- Xi, J.; Schubert, M.; Kim, J.; Schubert, E.; Chen, M.; Lin, S.; Liu, W.; Smart, J. Optical thin-film materials with low refractive index for broadband elimination of Fresnel reflection. Nat. Photonics 2007, 1, 176–179. [Google Scholar]
- Kats, M.; Sharma, D.; Lin, J.; Genevet, P.; Blanchard, R.; Yang, Z.; Qazilbash, M.; Basov, D.; Ramanathan, S.; Capasso, F. Ultra-thin perfect absorber employing a tunable phase change material. Appl. Phys. Lett. 2012, 101, 221101. [Google Scholar] [CrossRef]
- Rensberg, J.; Zhang, S.; Zhou, Y.; McLeod, A.; Schwarz, C.; Goldflam, M.; Liu, M.; Kerbusch, J.; Nawrodt, R.; Ramanathan, S.; et al. Active optical metasurfaces based on defect-engineered phase-transition materials. Nano Lett. 2016, 16, 1050–1055. [Google Scholar] [CrossRef] [PubMed]
- Berreman, D. Infrared Absorption at Longitudinal Optic Frequency in Cubic Crystal Films. Phys. Rev. 1963, 130, 2193. [Google Scholar] [CrossRef]
- Oyama, T.; Ohsaki, H.; Tachibana, Y.; Hayashi, Y.; Ono, Y.; Horie, N. A new layer system of anti-reflective coating for cathode ray tubes. Thin Solid Films 1999, 351, 235–240. [Google Scholar] [CrossRef]
- Park, J.; Kang, J.; Vasudev, A.; Schoen, D.; Kim, H.; Hasman, E.; Brongersma, M. Omnidirectional near-unity absorption in an ultrathin planar semiconductor layer on a metal substrate. ACS Photonics 2014, 1, 812–821. [Google Scholar] [CrossRef]
- Taliercio, T.; Guilengui, V.; Cerutti, L.; Tournié, E.; Greffet, J. Brewster “mode” in highly doped semiconductor layers: An all-optical technique to monitor doping concentration. Opt. Express 2014, 22, 24294–24303. [Google Scholar] [CrossRef] [PubMed]
- Schlich, F.; Spolenak, R. Strong interference in ultrathin semiconducting layers on a wide variety of substrate materials. Appl. Phys. Lett. 2013, 103, 213112. [Google Scholar] [CrossRef]
- Tischler, J.; Bradley, M.; Bulović, V. Critically coupled resonators in vertical geometry using a planar mirror and a 5 nm thick absorbing film. Opt. Lett. 2006, 31, 2045–2047. [Google Scholar] [CrossRef] [PubMed]
- Ding, B.; Qiu, M.; Blaikie, R. Manipulating light absorption in dye-doped dielectric films on reflecting surfaces. Opt. Express 2014, 22, 25965–25975. [Google Scholar] [CrossRef] [PubMed]
- Kumari, M.; Ding, B.; Blaikie, R. Enhanced resonant absorption in dye-doped polymer thin-film cavities for water vapour sensing. Sens. Actuators B Chem. 2016, 231, 88–94. [Google Scholar] [CrossRef]
- Elbahri, M.; Zillohu, U.; Gothe, B.; Hedayati, M.; Abdelaziz, R.; El-Khozondar, H.; Bawa’aneh, M.; Abdelaziz, M.; Lavrinenko, A.; Zhukovsky, S.; et al. Photoswitchable molecular dipole antennas with tailored coherent coupling in glassy composite. Light Sci. Appl. 2015, 4, e316. [Google Scholar] [CrossRef]
- Mirshafieyan, S.; Guo, J. Silicon colors: Spectral selective perfect light absorption in single layer silicon films on aluminum surface and its thermal tunability. Opt. Express 2014, 22, 31545–31554. [Google Scholar] [CrossRef] [PubMed]
- Derkacs, D.; Lim, S.; Matheu, P.; Mar, W.; Yu, E. Improved performance of amorphous silicon solar cells via scattering from surface plasmon polaritons in nearby metallic nanoparticles. Appl. Phys. Lett. 2006, 89, 093103. [Google Scholar] [CrossRef]
- Nakayama, K.; Tanabe, K.; Atwater, H. Plasmonic nanoparticle enhanced light absorption in GaAs solar cells. Appl. Phys. Lett. 2008, 93, 121904. [Google Scholar] [CrossRef]
- Nishioka, K.; Sueto, T.; Saito, N. Formation of antireflection nanostructure for silicon solar cells using catalysis of single nano-sized silver particle. Appl. Surf. Sci. 2009, 255, 9504–9507. [Google Scholar] [CrossRef]
- Wang, K.; Yu, Z.; Sandhu, S.; Liu, V.; Fan, S. Condition for perfect antireflection by optical resonance at material interface. Optica 2014, 1, 388–395. [Google Scholar] [CrossRef]
- Pillai, S.; Catchpole, K.; Trupke, T.; Green, M. Surface plasmon enhanced silicon solar cells. J. Appl. Phys. 2007, 101, 093105. [Google Scholar] [CrossRef]
- Kim, S.; Na, S.; Jo, J.; Kim, D.; Nah, Y. Plasmon enhanced performance of organic solar cells using electrodeposited Ag nanoparticles. Appl. Phys. Lett. 2008, 93, 073307. [Google Scholar] [CrossRef]
- Pala, R.; White, J.; Barnard, E.; Liu, J.; Brongersma, M. Design of plasmonic thin-film solar cells with broadband absorption enhancements. Adv. Mater. 2009, 21, 3504–3509. [Google Scholar] [CrossRef]
- Spinelli, P.; Hebbink, M.; de Waele, R.; Black, L.; Lenzmann, F.; Polman, A. Optical impedance matching using coupled plasmonic nanoparticle arrays. Nano Lett. 2011, 11, 1760–1765. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Ouyang, Z.; Stokes, N.; Jia, B.; Shi, Z.; Gu, M. Low cost and high performance Al nanoparticles for broadband light trapping in Si wafer solar cells. Appl. Phys. Lett. 2012, 100, 151101. [Google Scholar] [CrossRef]
- Villesen, T.; Uhrenfeldt, C.; Johansen, B.; Hansen, J.; Ulriksen, H.; Larsen, A. Aluminum nanoparticles for plasmon-improved coupling of light into silicon. Nanotechnology 2012, 23, 085202. [Google Scholar] [CrossRef] [PubMed]
- Hylton, N.; Li, X.; Giannini, V.; Lee, K.; Ekins-Daukes, N.; Loo, J.; Vercruysse, D.; van Dorpe, P.; Sodabanlu, H.; Sugiyama, M.; et al. Loss mitigation in plasmonic solar cells: Aluminium nanoparticles for broadband photocurrent enhancements in GaAs photodiodes. Sci. Rep. 2013, 3, 2874. [Google Scholar] [CrossRef] [PubMed]
- Cai, J.; Qi, L. Recent advances in antireflective surfaces based on nanostructure arrays. Mater. Horiz. 2015, 2, 37–53. [Google Scholar] [CrossRef]
- Ferry, V.; Munday, J.; Atwater, H. Design considerations for plasmonic photovoltaics. Adv. Mater. 2010, 22, 4794–4808. [Google Scholar] [CrossRef] [PubMed]
- Van de Groep, J.; Polman, A. Designing dielectric resonators on substrates: Combining magnetic and electric resonances. Opt. Express 2013, 21, 26285–26302. [Google Scholar] [CrossRef] [PubMed]
- Spinelli, P.; Verschuuren, M.; Polman, A. Broadband omnidirectional antireflection coating based on subwavelength surface Mie resonators. Nat. Commun. 2012, 3, 692. [Google Scholar] [CrossRef] [PubMed]
- Spinelli, P.; Macco, B.; Verschuuren, M.; Kessels, W.; Polman, A. Al2O3/TiO2 nano-pattern antireflection coating with ultralow surface recombination. Appl. Phys. Lett. 2013, 102, 233902. [Google Scholar] [CrossRef]
- Evlyukhin, A.; Reinhardt, C.; Evlyukhin, E.; Chichkov, B. Multipole analysis of light scattering by arbitrary-shaped nanoparticles on a plane surface. JOSA B 2013, 30, 2589–2598. [Google Scholar] [CrossRef]
- Fahim, N.; Ouyang, Z.; Jia, B.; Zhang, Y.; Shi, Z.; Gu, M. Enhanced photocurrent in crystalline silicon solar cells by hybrid plasmonic antireflection coatings. Appl. Phys. Lett. 2012, 101, 261102. [Google Scholar] [CrossRef]
- Yang, H.; Chen, S.; Lin, I.; Li, J. Enhanced light trapping for the silver nanoparticles embedded in the silica layer atop the silicon substrate. Appl. Phys. A 2013, 112, 525–532. [Google Scholar] [CrossRef]
- Lee, Y.; Ho, W.; Chen, Y. Performance of plasmonic silicon solar cells using indium nanoparticles deposited on a patterned TiO2 matrix. Thin Solid Films 2014, 570, 194–199. [Google Scholar] [CrossRef]
- Hedayati, M.; Fahr, S.; Etrich, C.; Faupel, F.; Rockstuhl, C.; Elbahri, M. The hybrid concept for realization of an ultra-thin plasmonic metamaterial antireflection coating and plasmonic rainbow. Nanoscale 2014, 6, 6037–6045. [Google Scholar] [CrossRef] [PubMed]
- Etrich, C.; Fahr, S.; Hedayati, M.; Faupel, F.; Elbahri, M.; Rockstuhl, C. Effective optical properties of plasmonic nanocomposites. Materials 2014, 7, 727–741. [Google Scholar] [CrossRef]
- Temple, T.; Dligatch, S. Role of the spacer layer in plasmonic antireflection coatings comprised of gold or silver nanoparticles. J. Photonics Energy 2015, 5, 053095. [Google Scholar] [CrossRef]
- Wang, P.; Millard, M.; Brolo, A. Optimizing plasmonic silicon photovoltaics with Ag and Au nanoparticle mixtures. J. Phys. Chem. C 2014, 118, 5889–5895. [Google Scholar] [CrossRef]
- Töfflinger, J.; Pedrueza, E.; Chirvony, V.; Leendertz, C.; García-Calzada, R.; Abargues, R.; Gref, O.; Roczen, M.; Korte, L.; Martínez-Pastor, J.; et al. Photoconductivity and optical properties of silicon coated by thin TiO2 film in situ doped by Au nanoparticles. Phys. Status Solidi (A) 2013, 210, 687–694. [Google Scholar] [CrossRef]
- Bauer, C.; Giessen, H. Light harvesting enhancement in solar cells with quasicrystalline plasmonic structures. Opt. Express 2013, 21, A363–A371. [Google Scholar] [CrossRef] [PubMed]
- Singh, H.; Sharma, P.; Solanki, C. Broadband reflection minimization using silver ultra thin film sandwiched between silicon nitride layers for c-Si solar cell application. Plasmonics 2014, 9, 1409–1416. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, X.; Ouyang, Z.; Lu, H.; Jia, B.; Shi, Z.; Gu, M. Improved multicrystalline Si solar cells by light trapping from Al nanoparticle enhanced antireflection coating. Opt. Mater. Express 2013, 3, 489–495. [Google Scholar] [CrossRef]
- Uhrenfeldt, C.; Villesen, T.; Johansen, B.; Jung, J.; Pedersen, T.; Larsen, A. Diffractive coupling and plasmon-enhanced photocurrent generation in silicon. Opt. Express 2013, 21, A774–A785. [Google Scholar] [CrossRef] [PubMed]
- Dislich, H. Glassy and crystalline systems from gels: Chemical basis and technical application. J. Non-Cryst. Solids 1983, 57, 371–388. [Google Scholar] [CrossRef]
- Lau, J.; Fowler, J.; Marriage, T.; Page, L.; Leong, J.; Wishnow, E.; Henry, R.; Wollack, E.; Halpern, M.; Marsden, D.; et al. Millimeter-wave antireflection coating for cryogenic silicon lenses. Appl. Opt. 2006, 45, 3746–3751. [Google Scholar] [CrossRef] [PubMed]
- Jeram, S.; Ge, J.; Jiang, P.; Phillips, B. Characterization of Silicon Moth-Eye Antireflection Coatings for Astronomical Applications in the Infrared. In American Astronomical Society Meeting Abstracts; AAS: Kissimmee, FL, USA, 2016. [Google Scholar]
- Kim, J.; Chhajed, S.; Schubert, M.; Schubert, E.; Fischer, A.; Crawford, M.; Cho, J.; Kim, H.; Sone, C. Light-extraction enhancement of GaInN light-emitting diodes by graded-refractive-index indium tin oxide anti-reflection contact. Adv. Mater. 2008, 20, 801–804. [Google Scholar] [CrossRef]
- Brinker, C.; Harrington, M. Sol-gel Derived Antireflective Coatings for Silicon. Sol. Energy Mater. 1981, 5, 159–172. [Google Scholar] [CrossRef]
- Li, D.; Kunz, T.; Wolf, N.; Liebig, J.; Wittmann, S.; Ahmad, T.; Hessmann, M.; Auer, R.; Göken, M.; Brabec, C. Silicon nitride and intrinsic amorphous silicon double antireflection coatings for thin-film solar cells on foreign substrates. Thin Solid Films 2015, 583, 25–33. [Google Scholar] [CrossRef]
- Min, W.; Betancourt, A.; Jiang, P.; Jiang, B. Bioinspired broadband antireflection coatings on GaSb. Appl. Phys. Lett. 2008, 92, 141109. [Google Scholar] [CrossRef]
- Yoldas, B.; Partlow, D. Formation of broad band antireflective coatings on fused silica for high power laser applications. Thin Solid Films 1985, 129, 1–14. [Google Scholar] [CrossRef]
- Fimberger, M.; Behrendt, A.; Jakopic, G.; Stelzer, F.; Kumbaraci, V.; Wiesbrock, F. Modification Pathways for Copoly (2-oxazoline) s Enabling Their Application as Antireflective Coatings in Photolithography. Macromol. Rapid Commun. 2015, 37, 233–238. [Google Scholar] [CrossRef] [PubMed]
- Naik, G.; Schroeder, J.; Ni, X.; Kildishev, A.; Sands, T.; Boltasseva, A. Titanium nitride as a plasmonic material for visible and near-infrared wavelengths. Opt. Mater. Express 2012, 2, 478–489. [Google Scholar] [CrossRef]
- Guler, U.; Boltasseva, A.; Shalaev, V. Refractory plasmonics. Science 2014, 344, 263–264. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Keshavarz Hedayati, M.; Elbahri, M. Antireflective Coatings: Conventional Stacking Layers and Ultrathin Plasmonic Metasurfaces, A Mini-Review. Materials 2016, 9, 497. https://doi.org/10.3390/ma9060497
Keshavarz Hedayati M, Elbahri M. Antireflective Coatings: Conventional Stacking Layers and Ultrathin Plasmonic Metasurfaces, A Mini-Review. Materials. 2016; 9(6):497. https://doi.org/10.3390/ma9060497
Chicago/Turabian StyleKeshavarz Hedayati, Mehdi, and Mady Elbahri. 2016. "Antireflective Coatings: Conventional Stacking Layers and Ultrathin Plasmonic Metasurfaces, A Mini-Review" Materials 9, no. 6: 497. https://doi.org/10.3390/ma9060497
APA StyleKeshavarz Hedayati, M., & Elbahri, M. (2016). Antireflective Coatings: Conventional Stacking Layers and Ultrathin Plasmonic Metasurfaces, A Mini-Review. Materials, 9(6), 497. https://doi.org/10.3390/ma9060497





