A General Accelerated Degradation Model Based on the Wiener Process
Abstract
:1. Introduction
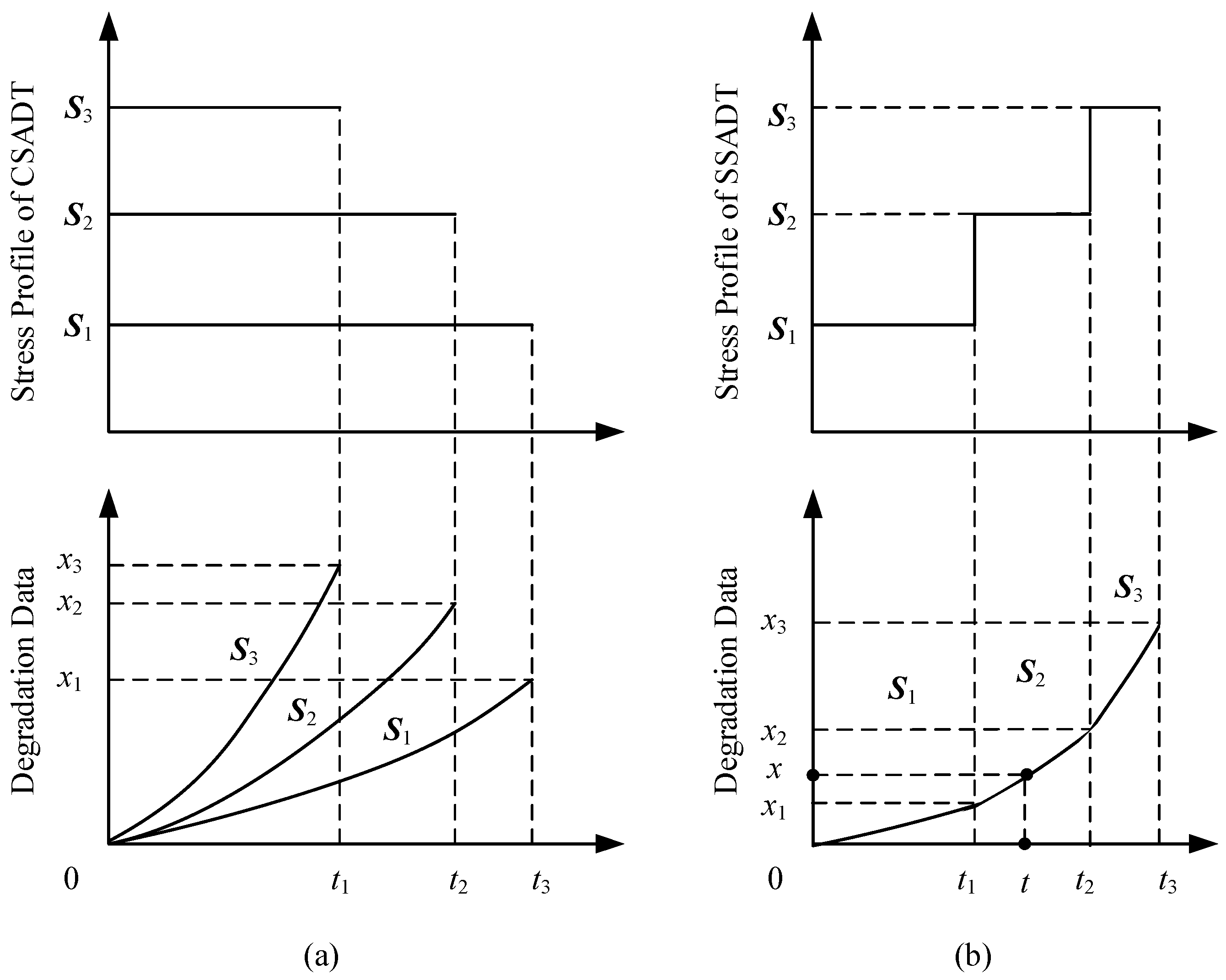
2. The General ADT Model
2.1. Models
2.2. Derivation of the Failure Time Distribution under the Given Stress Level
3. Statistical Inference
3.1. Estimation of Ω1 for CSADT
3.2. Estimation of Ω2 for CSADT
3.3. Estimation of Ω1 and Ω2 for SSADT
4. Case Study
4.1. Simulation Example
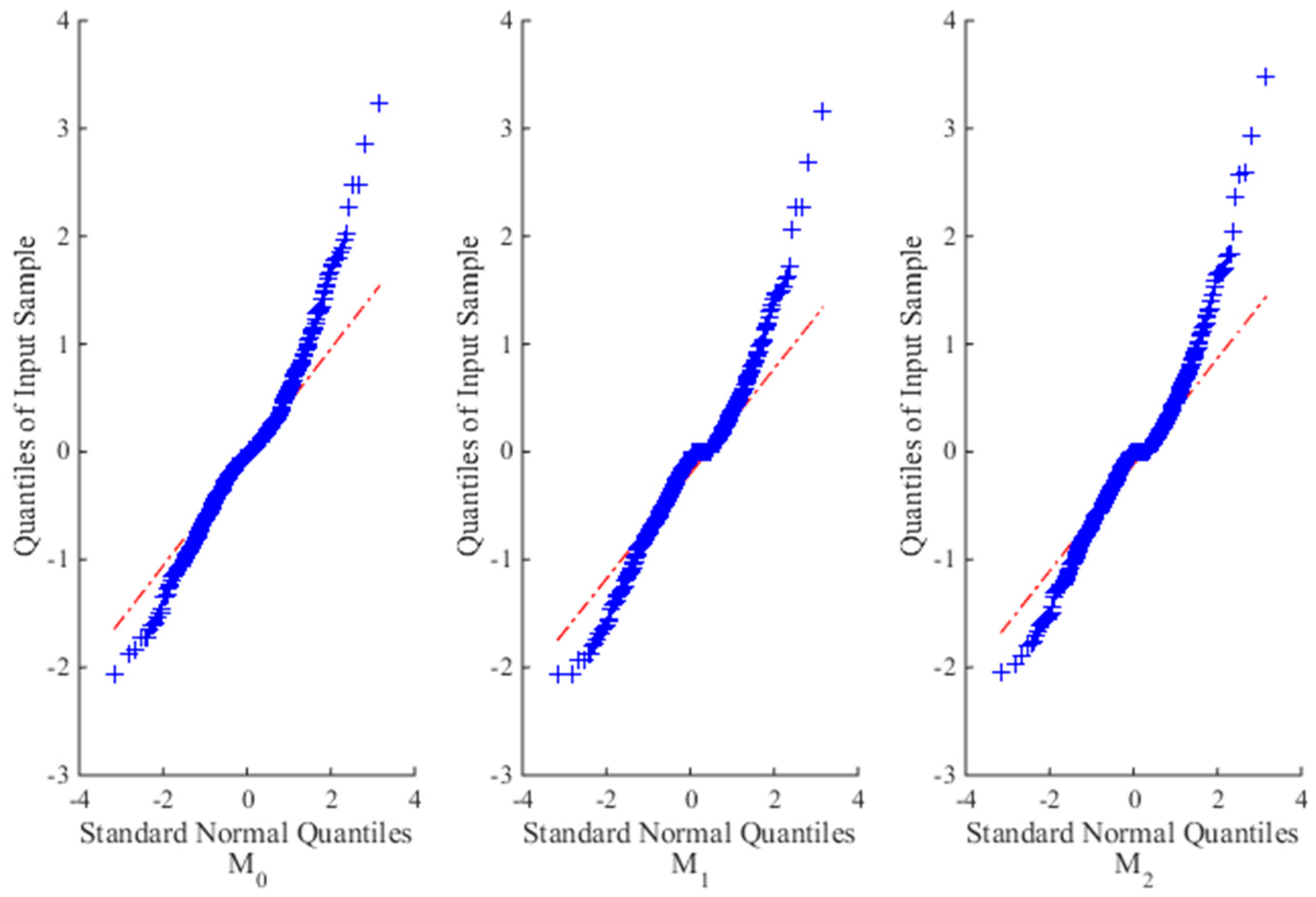
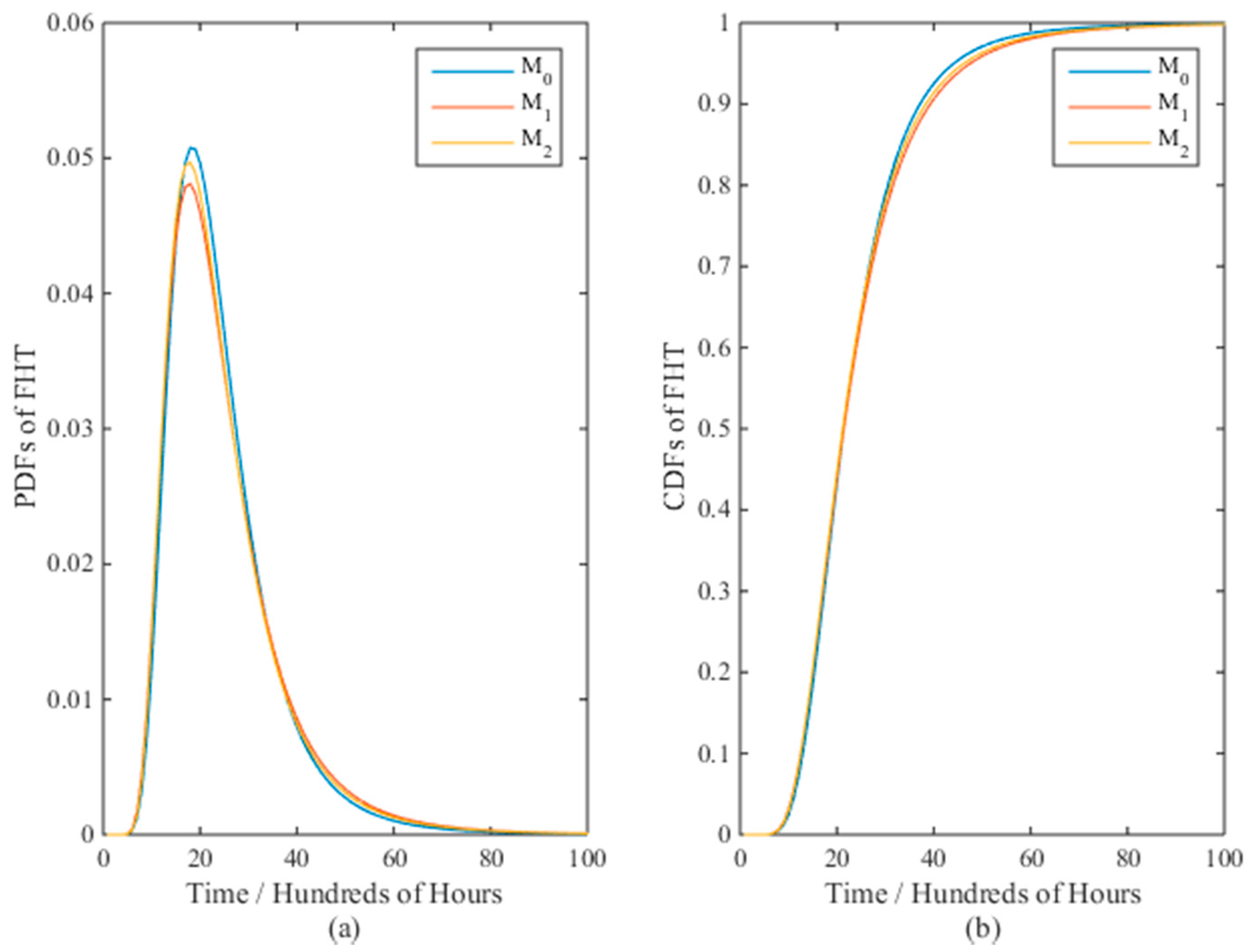
4.1.1. Model Comparison
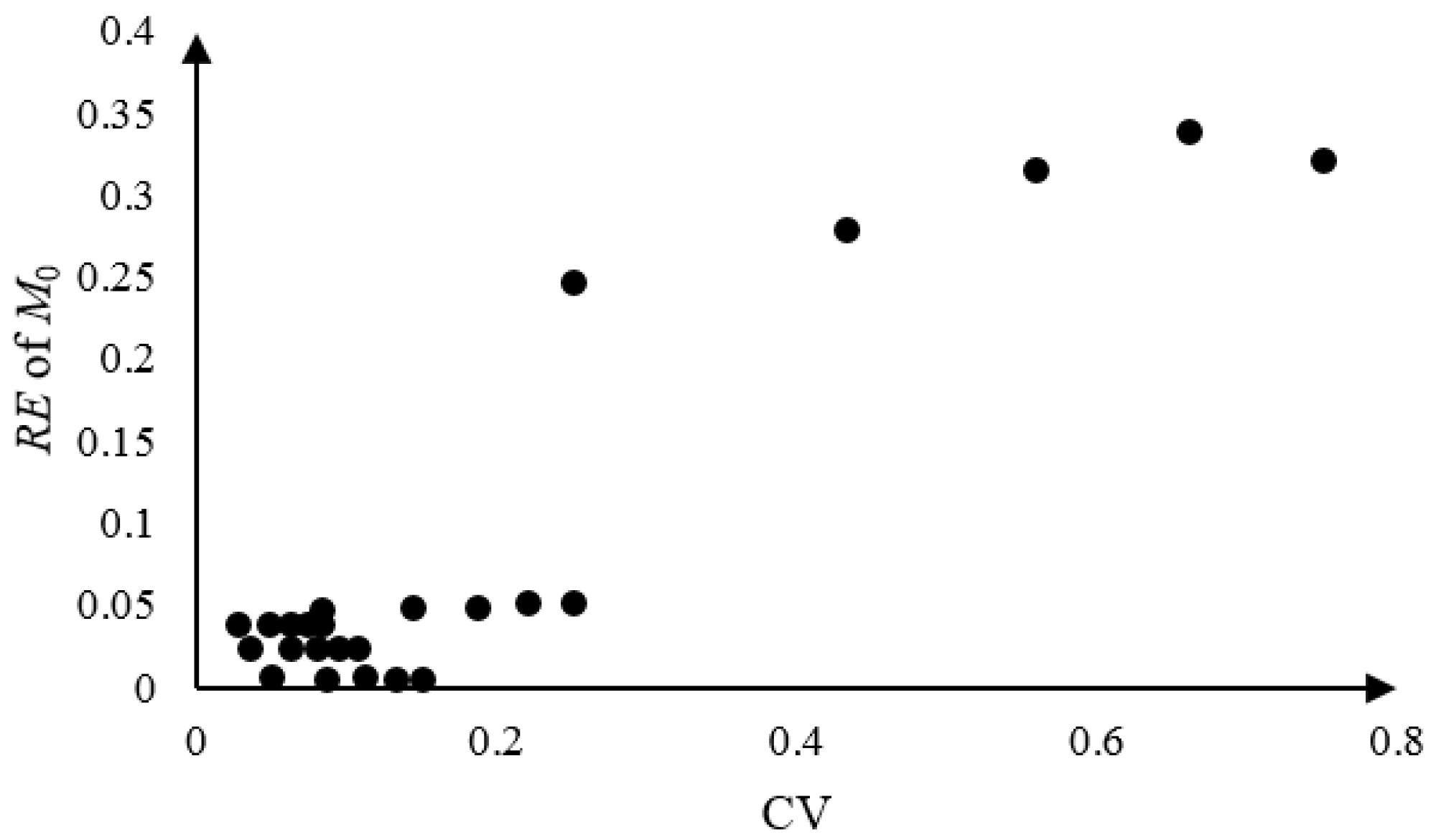
4.1.2. Sensitivity Analysis
4.2. Real Applications
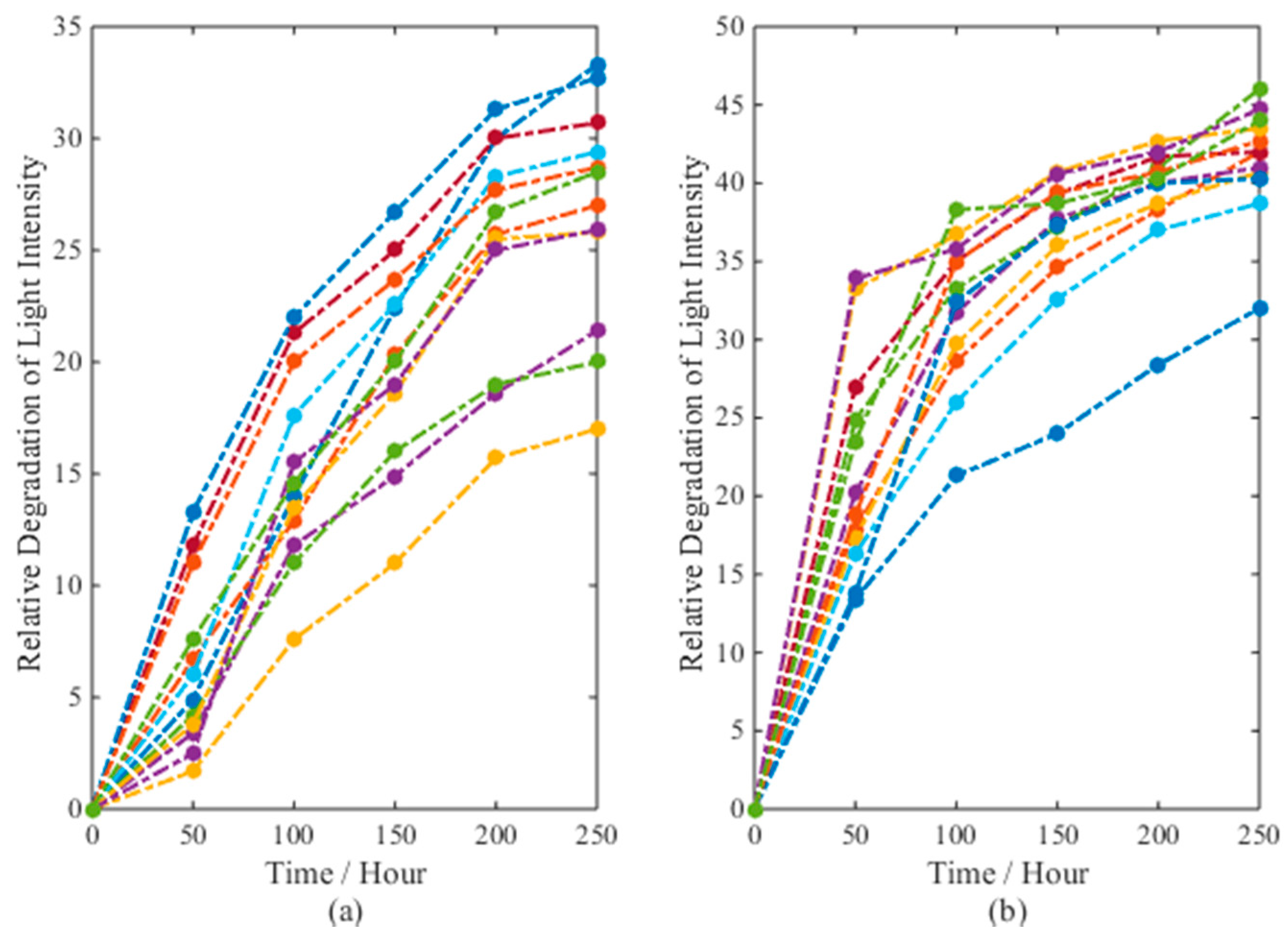
4.2.1. LED Application
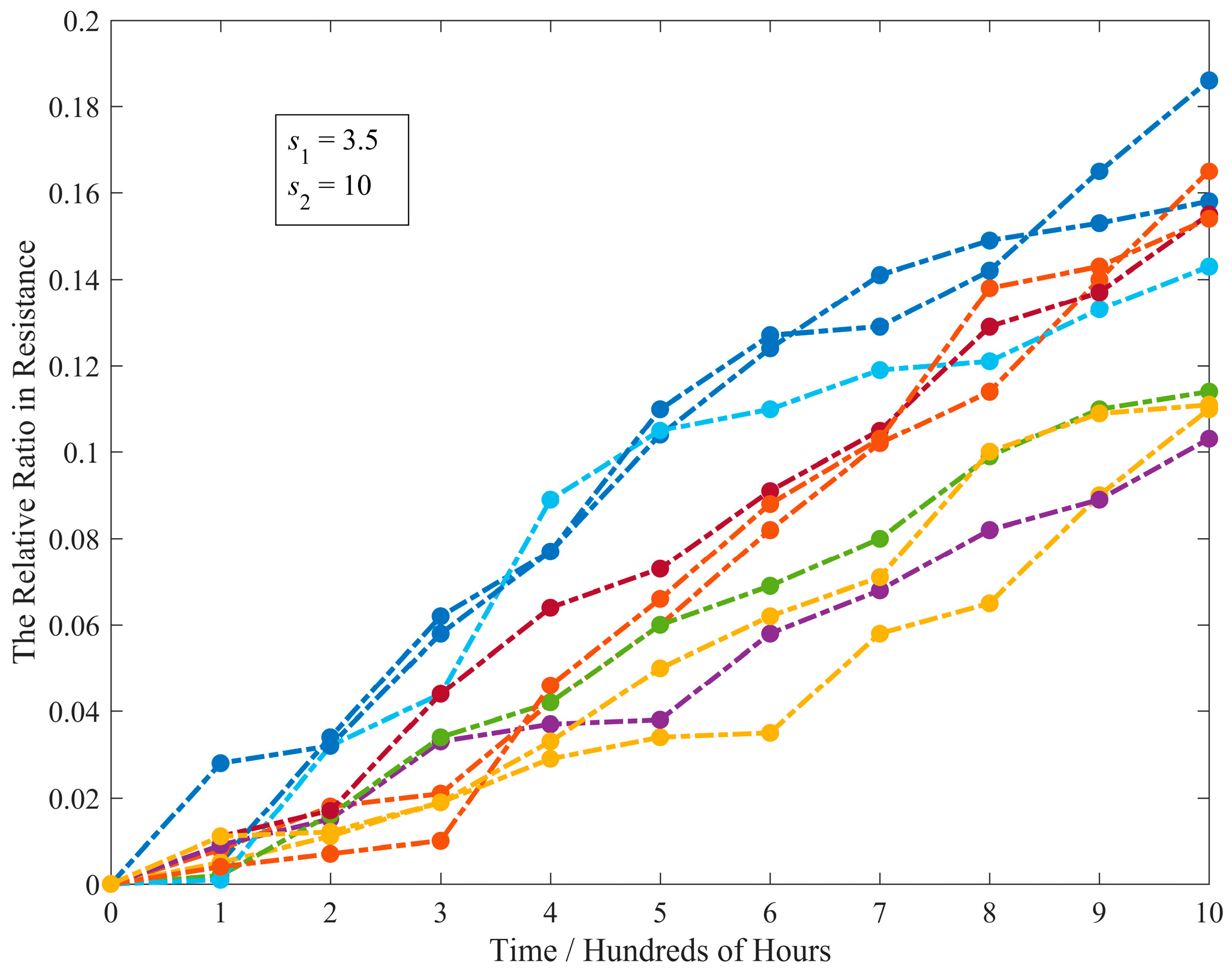
4.2.2. Resistor Application
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Elsayed, E.A.; Chen, A.C.K. Recent research and current issues in accelerated testing. In Proceedings of the 1998 IEEE International Conference on Systems, Man, and Cybernetics, San Diego, CA, USA, 11–14 October 1998; pp. 4704–4709.
- Meeker, W.Q.; Escobar, L.A. Statistical Methods for Reliability Data; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Nelson, W.B. Accelerated Testing: Statistical Models, Test Plans, and Data Analysis; John Wiley & Sons: New York, NY, USA, 1990. [Google Scholar]
- Thomas, E.V.; Bloom, I.; Christophersen, J.P.; Battaglia, V.S. Statistical methodology for predicting the life of lithium-ion cells via accelerated degradation testing. J. Power Sources 2008, 184, 312–317. [Google Scholar] [CrossRef]
- Bae, S.J.; Kim, S.-J.; Park, J.I.; Lee, J.-H.; Cho, H.; Park, J.-Y. Lifetime prediction through accelerated degradation testing of membrane electrode assemblies in direct methanol fuel cells. Int. J. Hydrogen Energy 2010, 35, 9166–9176. [Google Scholar] [CrossRef]
- Wang, F.-K.; Lu, Y.-C. Useful lifetime analysis for high-power white LEDs. Microelectron. Reliab. 2014, 54, 1307–1315. [Google Scholar] [CrossRef]
- Wang, F.-K.; Chu, T.-P. Lifetime predictions of LED-based light bars by accelerated degradation test. Microelectron. Reliab. 2012, 52, 1332–1336. [Google Scholar] [CrossRef]
- Meeker, W.Q.; Escobar, L.A.; Lu, C.J. Accelerated degradation tests: Modeling and analysis. Technometrics 1998, 40, 89–99. [Google Scholar] [CrossRef]
- Park, J.I.; Bae, S.J. Direct prediction methods on lifetime distribution of organic light-emitting diodes from accelerated degradation tests. IEEE Trans. Reliab. 2010, 59, 74–90. [Google Scholar] [CrossRef]
- Ling, M.H.; Tsui, K.L.; Balakrishnan, N. Accelerated degradation analysis for the quality of a system Based on the gamma process. IEEE Trans. Reliab. 2015, 64, 463–472. [Google Scholar] [CrossRef]
- Whitmore, G.A.; Schenkelberg, F. Modelling accelerated degradation data using wiener diffusion with A time scale transformation. Lifetime Data Anal. 1997, 3, 27–45. [Google Scholar] [CrossRef] [PubMed]
- Ye, Z.S.; Chen, L.P.; Tang, L.C.; Xie, M. Accelerated degradation test planning using the inverse gaussian process. IEEE Trans. Reliab. 2014, 63, 750–763. [Google Scholar] [CrossRef]
- Escobar, L.A.; Meeker, W.Q. A review of accelerated test models. Stat. Sci. 2006, 21, 552–577. [Google Scholar] [CrossRef]
- Park, C.; Padgett, W.J. Accelerated degradation models for failure based on geometric Brownian motion and gamma processes. Lifetime Data Anal. 2005, 11, 511–527. [Google Scholar] [CrossRef] [PubMed]
- Pan, Z.Q.; Balakrishnan, N. Multiple-steps step-stress accelerated degradation modeling based on wiener and gamma processes. Commun. Stat. Simul. Comput. 2010, 39, 1384–1402. [Google Scholar] [CrossRef]
- Wang, L.Z.; Pan, R.; Li, X.Y.; Jiang, T.M. A Bayesian reliability evaluation method with integrated accelerated degradation testing and field information. Reliab. Eng. Syst. Saf. 2013, 112, 38–47. [Google Scholar] [CrossRef]
- Liao, H.T.; Elsayed, E.A. Reliability inference for field conditions from accelerated degradation testing. Nav. Res. Logist. 2006, 53, 576–587. [Google Scholar] [CrossRef]
- Tang, S.J.; Guo, X.S.; Yu, C.Q.; Xue, H.J.; Zhou, Z.J. Accelerated degradation tests modeling based on the nonlinear wiener process with random effects. Math. Probl. Eng. 2014, 2014, 1–11. [Google Scholar] [CrossRef]
- Wang, X.L.; Jiang, P.; Guo, B.; Cheng, Z.J. Real-time reliability evaluation with a general wiener process-based degradation model. Qual. Reliab. Eng. Int. 2014, 30, 205–220. [Google Scholar] [CrossRef]
- Wang, X.L.; Balakrishnan, N.; Guo, B. Residual life estimation based on a generalized Wiener degradation process. Reliab. Eng. Syst. Saf. 2014, 124, 13–23. [Google Scholar] [CrossRef]
- Liu, L.; Li, X.-Y.; Jiang, T.-M. Nonlinear accelerated degradation analysis based on the general wiener process. In Proceedings of the 25th European Safety and Reliability Conference (ESREL 2015), Zurich, Switzerland, 7–10 September 2015; pp. 2083–2088.
- Peng, C.Y.; Tseng, S.T. Mis-specification analysis of linear degradation models. IEEE Trans. Reliab. 2009, 58, 444–455. [Google Scholar] [CrossRef]
- Wang, X. Wiener processes with random effects for degradation data. J. Multivar. Anal. 2010, 101, 340–351. [Google Scholar] [CrossRef]
- Si, X.S.; Wang, W.B.; Hu, C.H.; Zhou, D.H.; Pecht, M.G. Remaining useful life estimation based on a nonlinear diffusion degradation process. IEEE Trans. Reliab. 2012, 61, 50–67. [Google Scholar] [CrossRef]
- Park, C.; Padgett, W.J. Stochastic degradation models with several accelerating variables. IEEE Trans. Reliab. 2006, 55, 379–390. [Google Scholar] [CrossRef]
- Li, X.; Jiang, T.; Sun, F.; Ma, J. Constant stress ADT for superluminescent diode and parameter sensitivity analysis. In Proceedings of the 8th International Conference on Reliability, Maintainability and Safety, Chengdu, China, 20–24 July 2009.
- Lim, H.; Yum, B.-J. Optimal design of accelerated degradation tests based on Wiener process models. J. Appl. Stat. 2011, 38, 309–325. [Google Scholar] [CrossRef]
- Si, X.-S.; Wang, W.; Hu, C.-H.; Chen, M.-Y.; Zhou, D.-H. A Wiener-process-based degradation model with a recursive filter algorithm for remaining useful life estimation. Mech. Syst. Signal Process. 2013, 35, 219–237. [Google Scholar] [CrossRef]
- Chhikara, R.S.; Folks, J.L. The Inverse Gaussian Distribution: Theory, Methodology, and Applications; CRC Press: New York, NY, USA, 1988; Volume 95, p. 232. [Google Scholar]
- Ye, Z.-S.; Xie, M. Stochastic modelling and analysis of degradation for highly reliable products. Appl. Stoch. Model. Bus. 2015, 31, 16–32. [Google Scholar] [CrossRef]
- Tang, L.C.; Yang, G.; Xie, M. Planning of step-stress accelerated degradation test. In Proceedings of the 2004 Annual Reliability and Maintainability Symposium, Los Angeles, CA, USA, 26–29 January 2004; pp. 287–292.
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence properties of the Nelder-Mead simplex method in low dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Van Noortwijk, J.M. A survey of the application of gamma processes in maintenance. Reliab. Eng. Syst. Saf. 2009, 94, 2–21. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Multimodel inference understanding AIC and BIC in model selection. Sociol. Method Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
- Taguchi, G.; Yokoyama, Y. Taguchi Methods: Design of Experiments; American Supplier Institute: Nasr City Cairo, Egypt, 1993; Volume 4. [Google Scholar]
- Chaluvadi, V. Accelerated Life Testing of Electronic Revenue Meters. Master Thesis, Clemson University, Clemson, SC, USA, 2008. [Google Scholar]
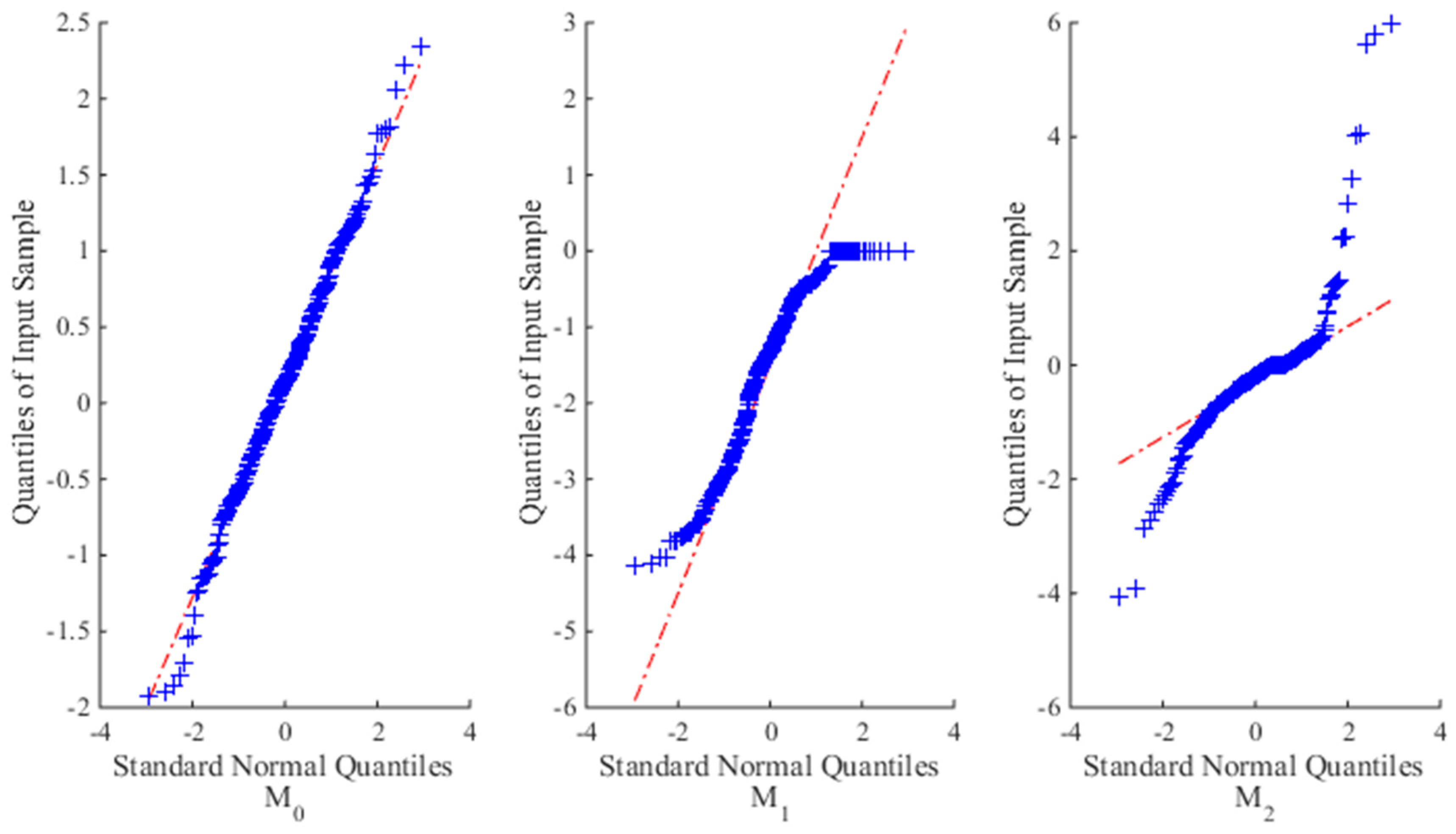
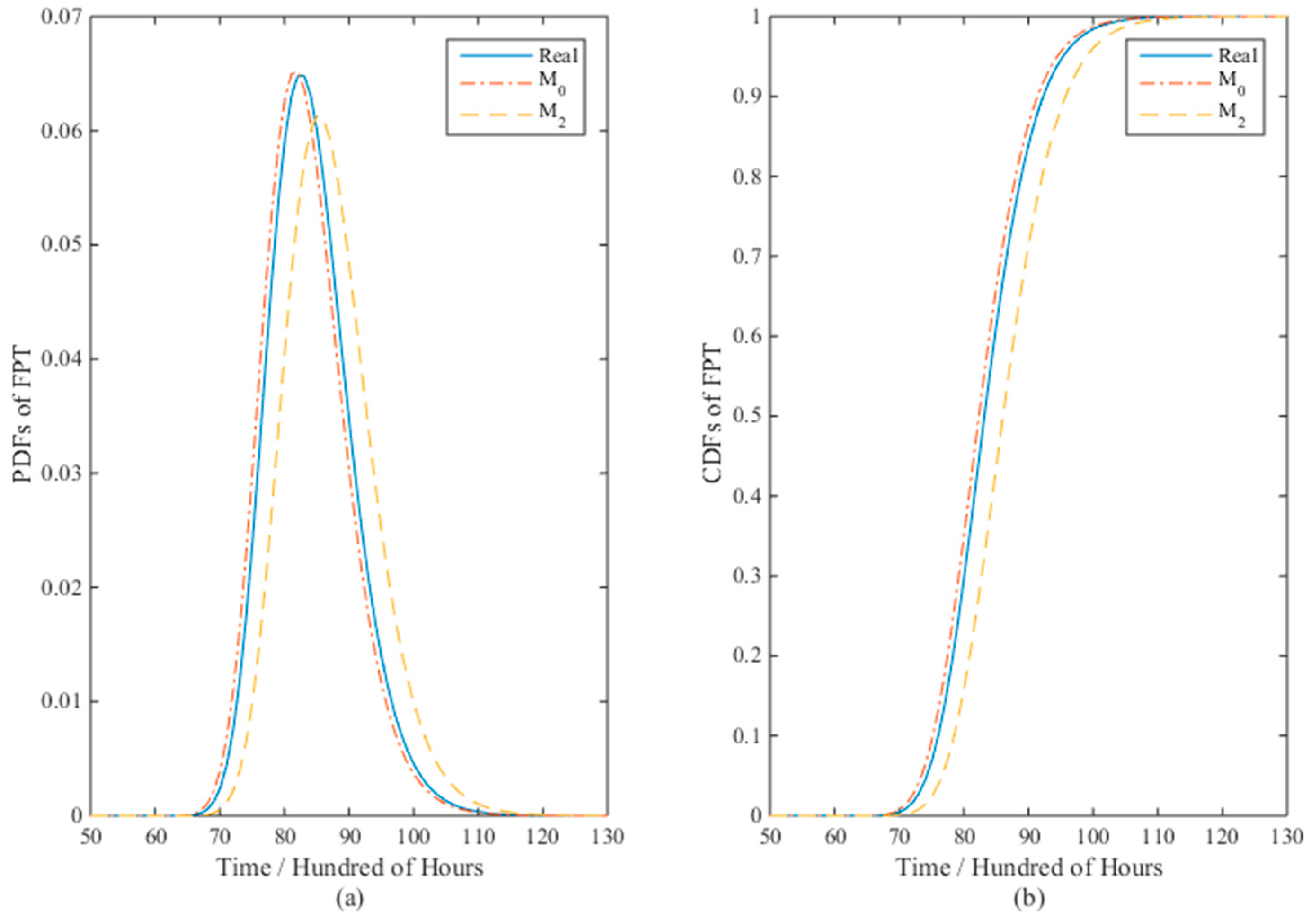
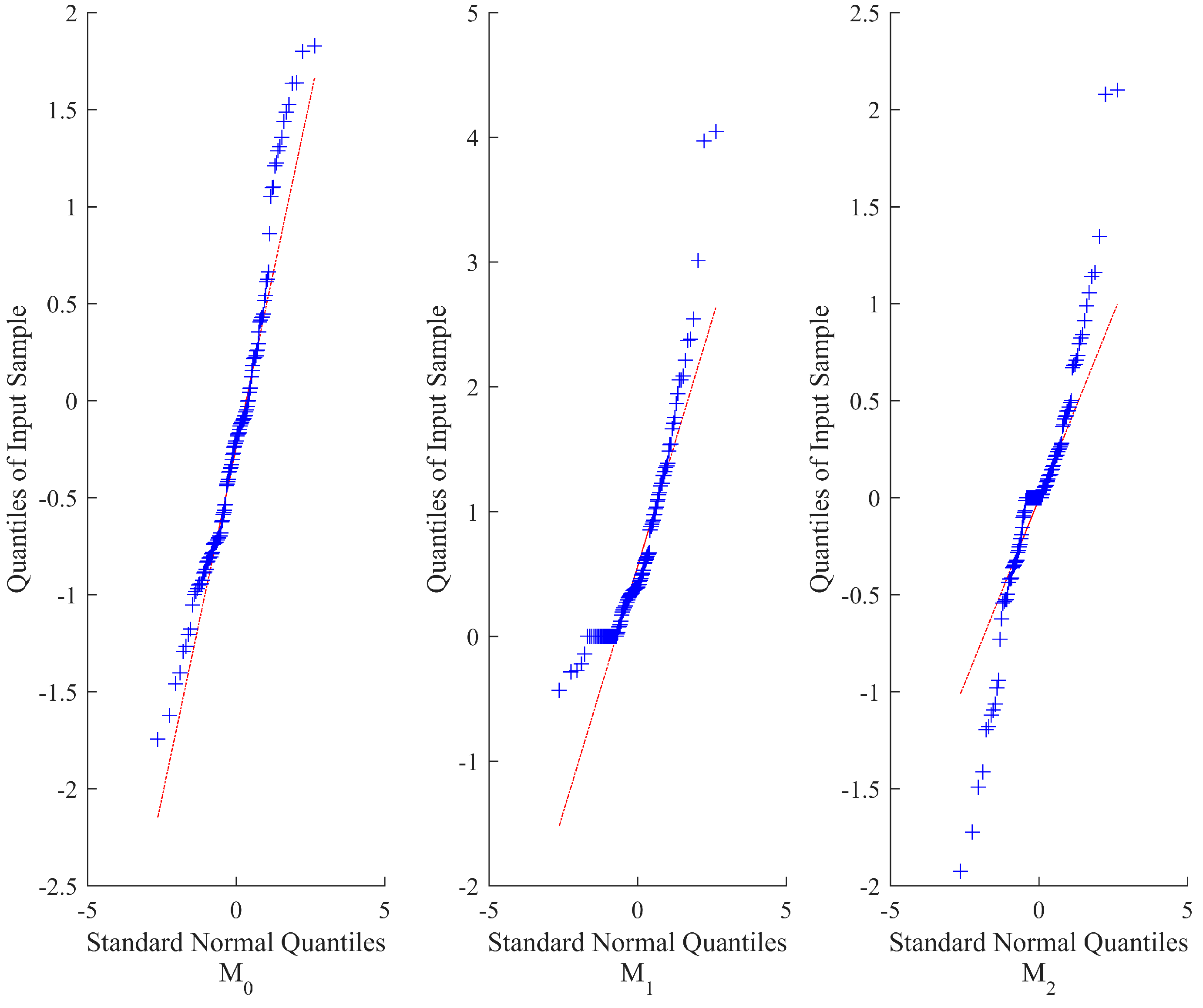
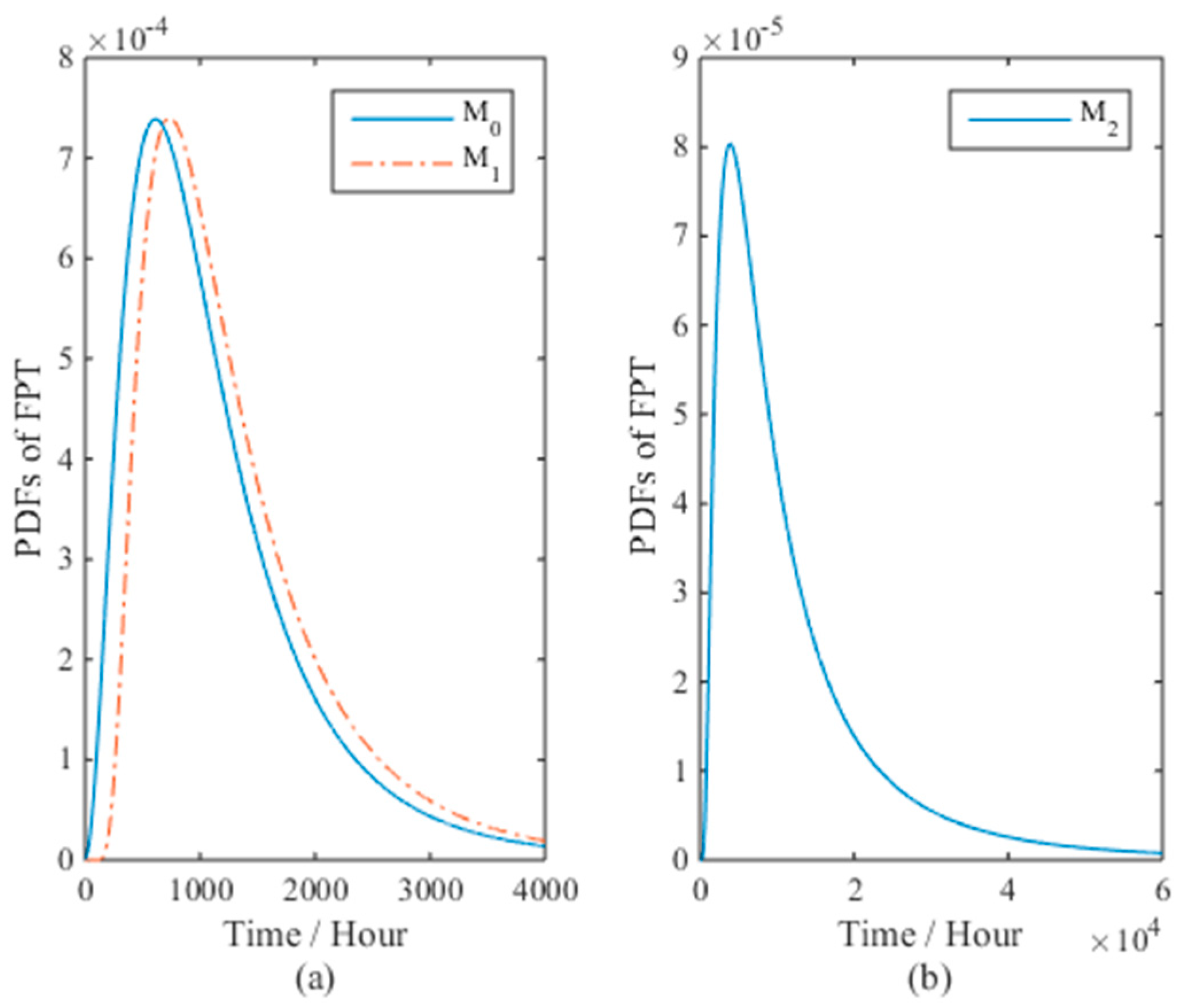
| Mi | n | θ | γ | σ2 | η0 | η1 | lmax | np | AIC | Δ | AE | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | |||||||||||
| M0 | 5 | 1.491 | 0.273 | 0.0177 | 21.62 | 4.33 | –1502 | 317 | 6 | –621 | 0 | –2.9×10−3 |
| (−0.57, 3.3 × 10−3) | (−32, 10) | (77, 59) | (8.1, 0.65) | (−13, 1.8) | (0.13, 1.7 × 10−4) | |||||||
| 10 | 1.502 | 0.381 | 0.0097 | 18.65 | 4.42 | –1477 | 635 | –1259 | 0 | –1.2 × 10−3 | ||
| (0.14, 2.0 × 10−4) | (−4.7, 0.22) | (−3.1, 0.096) | (−6.7, 0.45) | (−12, 1.3) | (−1.5, 0.023) | |||||||
| 30 | 1.501 | 0.352 | 0.0114 | 20.90 | 5.18 | –1515 | 1898 | –3784 | 0 | 2.7 × 10−4 | ||
| (0.055, 3.0 × 10−5) | (−12, 1.4) | (14, 2.1) | (4.5, 0.20) | (3.6, 0.13) | (1.0, 0.011) | |||||||
| M1 | 5 | 1 (fixed) | 1 (fixed) | 0.0607 | 8.5 × 103 | 7.9 × 105 | –3045 | −2.7 | 4 | 13.4 | 635 | 0.343 |
| (−33, 11) | (150, 225) | (507, 2.6 × 103) | (4.2 × 104, 1.8 × 107) | (1.6 × 107, 2.5 × 1012) | (103, 106) | |||||||
| 10 | 1 (fixed) | 1 (fixed) | 0.0579 | 8.2 × 103 | 8.3 × 105 | –3049 | 1.7 | 4.6 | 1263 | 0.365 | ||
| (−33, 11) | (150, 225) | (479, 2.3 × 103) | (4.1 × 104, 1.7 × 107) | (1.7 × 107, 2.8 × 1012) | (103, 107) | |||||||
| 30 | 1 (fixed) | 1(fixed) | 0.0578 | 9.2 × 103 | 1.1 × 106 | –3087 | 5.5 | –3.0 | 3781 | 0.374 | ||
| (−33, 11) | (150, 225) | (478, 2.3 × 103) | (4.6 × 104, 2.1 × 107) | (2.2 × 107, 4.6 × 1012) | (106, 112) | |||||||
| M2 | 5 | 1.461 | =θ | 7.29 × 10−4 | 29.55 | 8.27 | –1577 | 217 | 5 | –425 | 197 | 3.2 × 10−3 |
| (−2.6, 0.068) | (265, 704) | (−93, 86) | (48, 23) | (65, 43) | (5.1, 0.26) | |||||||
| 10 | 1.476 | =θ | 4.79 × 10−4 | 24.54 | 7.64 | –1544 | 490 | –971 | 288 | 4.2 × 10−3 | ||
| (−1.6, 0.026) | (269, 724) | (−95, 91) | (23, 5.2) | (53, 28) | (2.9, 0.087) | |||||||
| 30 | 1.477 | =θ | 5.87 × 10−4 | 26.96 | 8.58 | –1577 | 1380 | –2750 | 1034 | 5.3 × 10−3 | ||
| (−1.6, 0.025) | (269, 724) | (−94, 89) | (35, 12) | (72, 51) | (5.2, 0.27) | |||||||
| Test No. | θ | γ | σ2 | η0 | η1 | RE of M0 | |
|---|---|---|---|---|---|---|---|
| a | b | ||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.026812 |
| 2 | 1 | 2 | 2 | 2 | 2 | 2 | 0.049430 |
| 3 | 1 | 3 | 3 | 3 | 3 | 3 | 0.076352 |
| 4 | 1 | 4 | 4 | 4 | 4 | 4 | 0.107904 |
| 5 | 1 | 5 | 5 | 5 | 5 | 5 | 0.149784 |
| 6 | 2 | 1 | 2 | 3 | 4 | 5 | 0.101002 |
| 7 | 2 | 2 | 3 | 4 | 5 | 1 | 0.017453 |
| 8 | 2 | 3 | 4 | 5 | 1 | 2 | 0.005818 |
| 9 | 2 | 4 | 5 | 1 | 2 | 3 | 0.042759 |
| 10 | 2 | 5 | 1 | 2 | 3 | 4 | 0.068059 |
| 11 | 3 | 1 | 3 | 5 | 2 | 4 | 0.014726 |
| 12 | 3 | 2 | 4 | 1 | 3 | 5 | 0.060681 |
| 13 | 3 | 3 | 5 | 2 | 4 | 1 | 0.032238 |
| 14 | 3 | 4 | 1 | 3 | 5 | 2 | 0.018415 |
| 15 | 3 | 5 | 2 | 4 | 1 | 3 | 0.006743 |
| 16 | 4 | 1 | 4 | 2 | 5 | 3 | 0.019738 |
| 17 | 4 | 2 | 5 | 3 | 1 | 4 | 0.008050 |
| 18 | 4 | 3 | 1 | 4 | 2 | 5 | 0.010650 |
| 19 | 4 | 4 | 2 | 5 | 3 | 1 | 0.053845 |
| 20 | 4 | 5 | 3 | 1 | 4 | 2 | 0.031300 |
| 21 | 5 | 1 | 5 | 4 | 3 | 2 | 0.053440 |
| 22 | 5 | 2 | 1 | 5 | 4 | 3 | 0.044617 |
| 23 | 5 | 3 | 2 | 1 | 5 | 4 | 0.021416 |
| 24 | 5 | 4 | 3 | 2 | 1 | 5 | 0.009040 |
| 25 | 5 | 5 | 4 | 3 | 2 | 1 | 0.061280 |
| MR1 | 0.08206 | 0.04314 | 0.03371 | 0.03659 | 0.01129 | 0.03833 | T = 1.09155 |
| MR2 | 0.04702 | 0.03605 | 0.04649 | 0.03570 | 0.03577 | 0.06138 | |
| MR3 | 0.02656 | 0.02929 | 0.02977 | 0.05302 | 0.06248 | 0.03804 | |
| MR4 | 0.02472 | 0.04639 | 0.05108 | 0.03924 | 0.06341 | 0.04403 | |
| MR5 | 0.03796 | 0.06343 | 0.05725 | 0.05376 | 0.04536 | 0.06623 | |
| δ | 0.05734 | 0.03414 | 0.02748 | 0.01806 | 0.05212 | 0.03455 | |
| Rank | 1 | 4 | 5 | 6 | 2 | 3 | |
| Model | θ | γ | σ2 | η0 | η1 | lmax | np | AIC | Δ | |
|---|---|---|---|---|---|---|---|---|---|---|
| a | b | |||||||||
| M0 | 0.442 | 0.117 | 73.784 | 0.273 | 0.0018 | 0.677 | –310 | 6 | 633 | 0 |
| M1 | 1 (fixed) | 1 (fixed) | 0.761 | 1.69 × 10−6 | 5.62 × 10−14 | 3.112 | –389 | 4 | 785 | 152 |
| M2 | 0.450 | =θ | 5.840 | 3.52 × 10−5 | 2.43 × 10−11 | 3.112 | –317 | 5 | 644 | 11 |
| Model | θ | γ | σ2 | η0 = a | η1 | lmax | np | AIC | Δ |
|---|---|---|---|---|---|---|---|---|---|
| M0 | 0.448 | 0.171 | 45.429 | 0.012 | 1.179 | –314.6634 | 5 | 639 | 0 |
| M1 | 1 (fixed) | 1 (fixed) | 0.776 | 8.67 × 10−7 | 3.297 | –389.7358 | 3 | 785 | 146 |
| M2 | 0.4477 | =θ | 6.238 | 1.83 × 10−5 | 3.297 | –319.9119 | 4 | 648 | 9 |
| Model | θ | γ | σ2 | η0 | η1 | η2 | lmax | np | AIC | Δ | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | ||||||||||
| M0 | 1.076 | 0.918 | 3.02 × 10−4 | 8.96 × 10−4 | 4.19 × 10−8 | 0.462 | 0.108 | 1698 | 7 | –3383 | 0 |
| M1 | 1 (fixed) | 1 (fixed) | 2.59 × 10−4 | 0.0012 | 7.02 × 10−8 | 0.440 | 0.102 | 1694 | 5 | –3378 | 4.8 |
| M2 | 1.046 | =θ | 2.35 × 10−4 | 0.0010 | 5.12 × 10−8 | 0.451 | 0.106 | 1697 | 6 | –3381 | 1.6 |
| Model | θ | γ | σ2 | η0 = a | η1 | η2 | lmax | np | AIC | Δ |
|---|---|---|---|---|---|---|---|---|---|---|
| M0 | 1.020 | 0.9498 | 3.33 × 10−4 | 0.0011 | 0.445 | 0.104 | 1647 | 6 | –3282 | 2.7 |
| M1 | 1 (fixed) | 1 (fixed) | 3.02 × 10−4 | 0.0012 | 0.439 | 0.103 | 1646 | 4 | –3284 | 0 |
| M2 | 1.008 | =θ | 2.97 × 10−4 | 0.0011 | 0.442 | 0.103 | 1646 | 5 | –3283 | 1.8 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Li, X.; Sun, F.; Wang, N. A General Accelerated Degradation Model Based on the Wiener Process. Materials 2016, 9, 981. https://doi.org/10.3390/ma9120981
Liu L, Li X, Sun F, Wang N. A General Accelerated Degradation Model Based on the Wiener Process. Materials. 2016; 9(12):981. https://doi.org/10.3390/ma9120981
Chicago/Turabian StyleLiu, Le, Xiaoyang Li, Fuqiang Sun, and Ning Wang. 2016. "A General Accelerated Degradation Model Based on the Wiener Process" Materials 9, no. 12: 981. https://doi.org/10.3390/ma9120981
APA StyleLiu, L., Li, X., Sun, F., & Wang, N. (2016). A General Accelerated Degradation Model Based on the Wiener Process. Materials, 9(12), 981. https://doi.org/10.3390/ma9120981






