Prosthetic Meshes for Repair of Hernia and Pelvic Organ Prolapse: Comparison of Biomechanical Properties
Abstract
:1. Introduction
2. Experimental Section
| Image | Mesh | Application | Material, Weight |
|---|---|---|---|
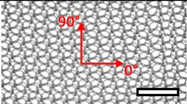 | Bard™ Mesh Marlex (BM) | Hernia | Polypropylene, standard |
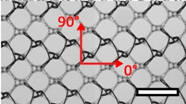 | DynaMesh® ENDOLAP (DM) | Hernia | PVDF (polyvinylidene fluoride), standard |
 | Ethicon Physiomesh® (PM) | Hernia | Polypropylene, ultralight |
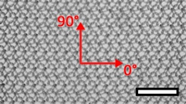 | Surgipro™ Polypropylene Monofilament Mesh (SPMM) | Hernia | Polypropylene, standard |
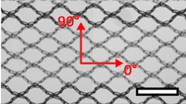 | Ethicon Ultrapro™ (UP) | Hernia | Polypropylene, light |
 | DynaMesh® PRS (DMPRS) | POP | PVDF, standard |
 | Gynecare PROLIFT™ (PE) | POP | Polypropylene, ultralight |
 | Coloplast Restorelle™ (Rest) | POP | Polypropylene, ultralight |
 | Parietex Ugytex® (UT) | POP | Polypropylene, light |
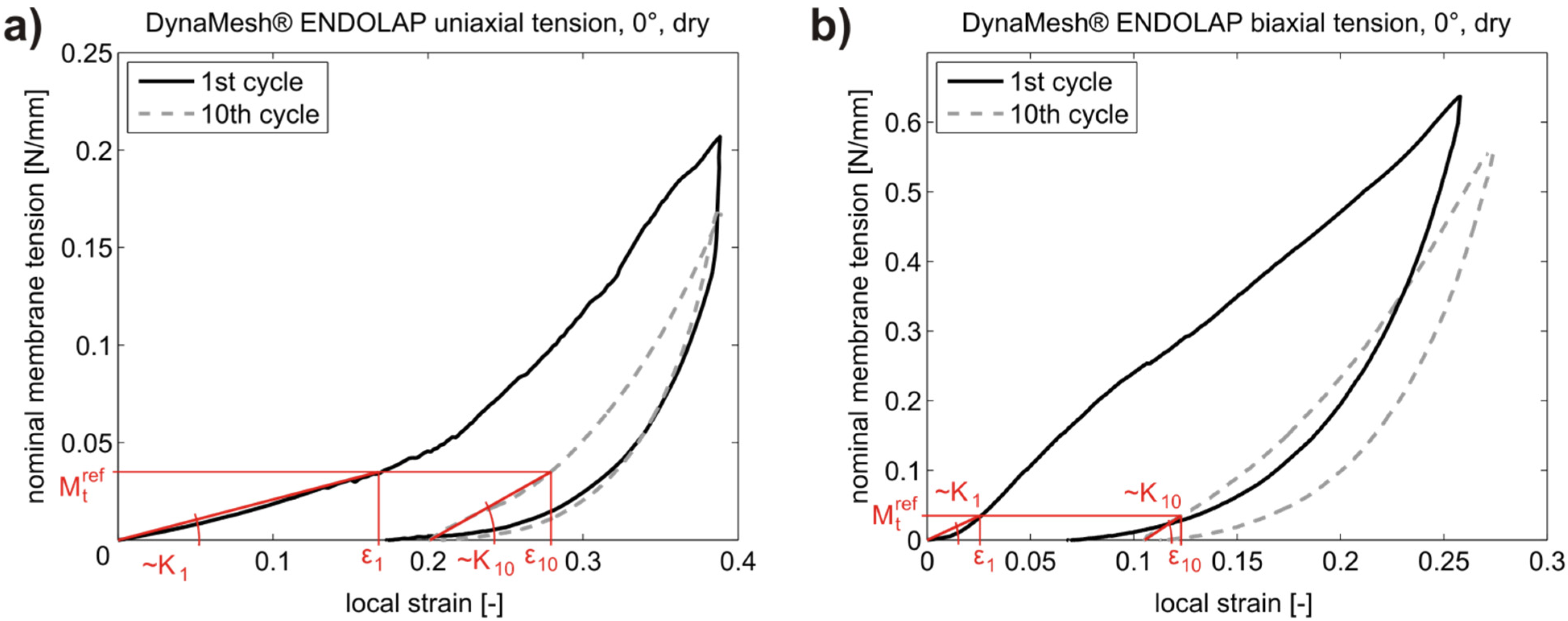
3. Results and Discussion
3.1. Results


| Testing configuration | K (N/mm) POP meshes | ||||
|---|---|---|---|---|---|
| DMPRS | PE | Restorelle | UT | mean | |
| uniaxial, dry, 1st cycle | 19.2 | 1.8 | 5.2 | 4.0 | 7.5 |
| uniaxial, dry, 10th cycle | 19.9 | 1.3 | 2.1 | 4.5 | 6.9 |
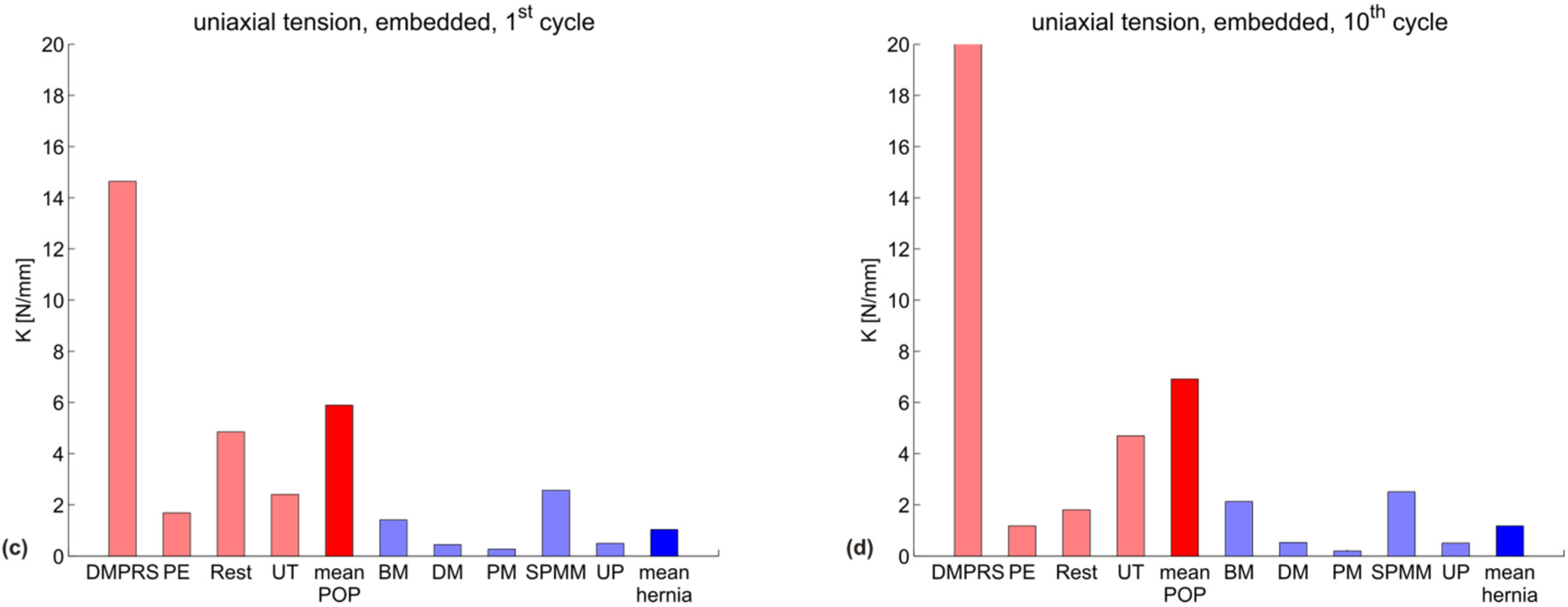
| uniaxial, embedded, 1st cycle | 14.6 | 1.7 | 4.8 | 2.4 | 5.9 |
| uniaxial, embedded, 10th cycle | 20.0 | 1.2 | 1.8 | 4.7 | 6.9 |
| biaxial, dry, 1st cycle | 6.2 | 2.0 | 4.0 | 2.1 | 3.6 |
| biaxial, dry, 10th cycle | 13.1 | 4.1 | 3.2 | 11.8 | 8.1 |
| biaxial, embedded, 1st cycle | 1.6 | 2.2 | 0.5 | 0.9 | 1.3 |
| biaxial, embedded, 10th cycle | 11.3 | 3.2 | 2.5 | 1.5 | 4.6 |
| Testing configuration | K (N/mm) hernia meshes | |||||
|---|---|---|---|---|---|---|
| BM | DM | PM | SPMM | UP | mean | |
| uniaxial, dry, 1st cycle | 2.5 | 0.3 | 0.2 | 2.0 | 0.3 | 1.1 |
| uniaxial, dry, 10th cycle | 3.5 | 0.4 | 1.1 | 1.1 | 1.3 | 1.5 |
| uniaxial, embedded, 1st cycle | 1.4 | 0.5 | 0.3 | 2.6 | 0.5 | 1.0 |
| uniaxial, embedded, 10th cycle | 2.1 | 0.5 | 0.2 | 2.5 | 0.5 | 1.2 |
| biaxial, dry, 1st cycle | 0.4 | 1.4 | 1.3 | 0.7 | 0.5 | 0.9 |
| biaxial, dry, 10th cycle | 0.9 | 2.0 | 1.4 | 2.1 | 1.4 | 1.6 |
| biaxial, embedded, 1st cycle | 0.6 | 0.5 | 0.5 | 0.5 | 1.3 | 0.7 |
| biaxial, embedded, 10th cycle | 1.6 | 0.7 | 0.5 | 1.2 | 1.6 | 1.1 |
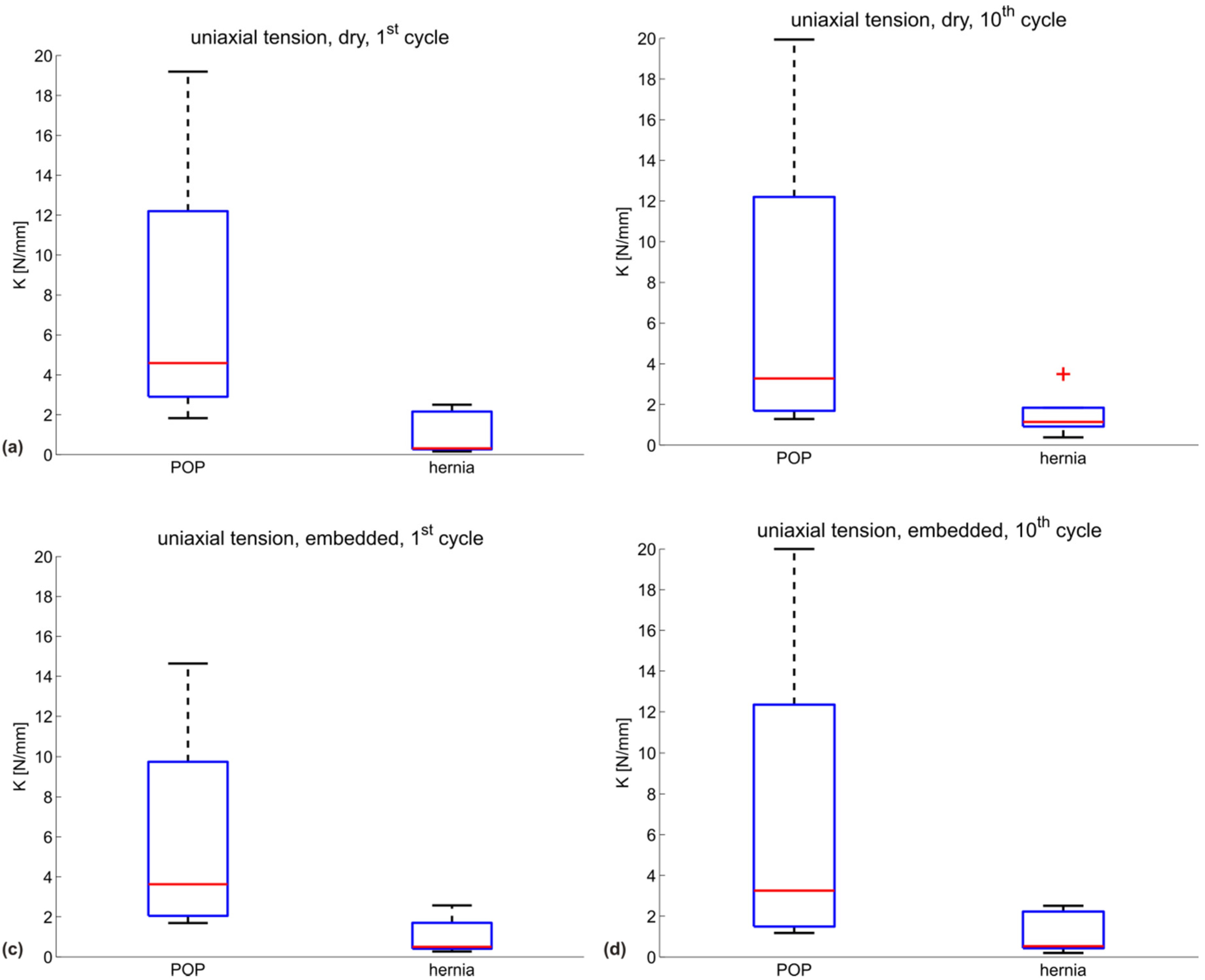
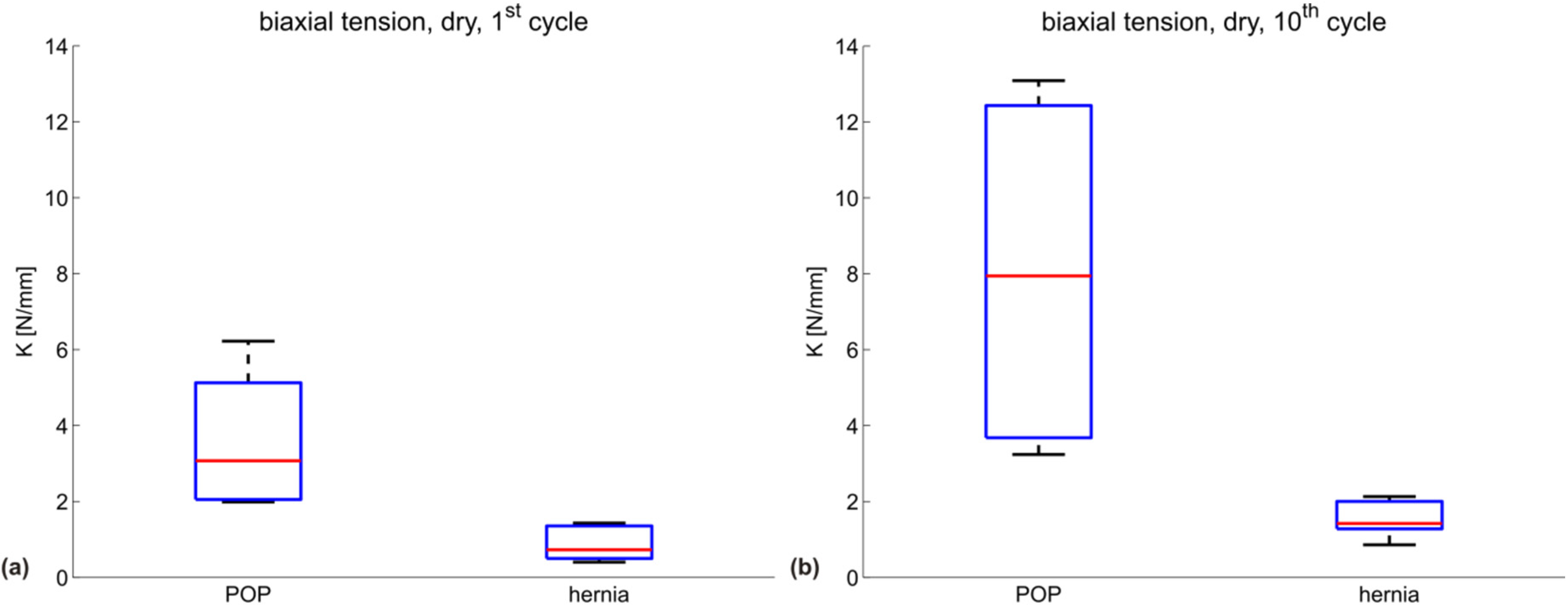
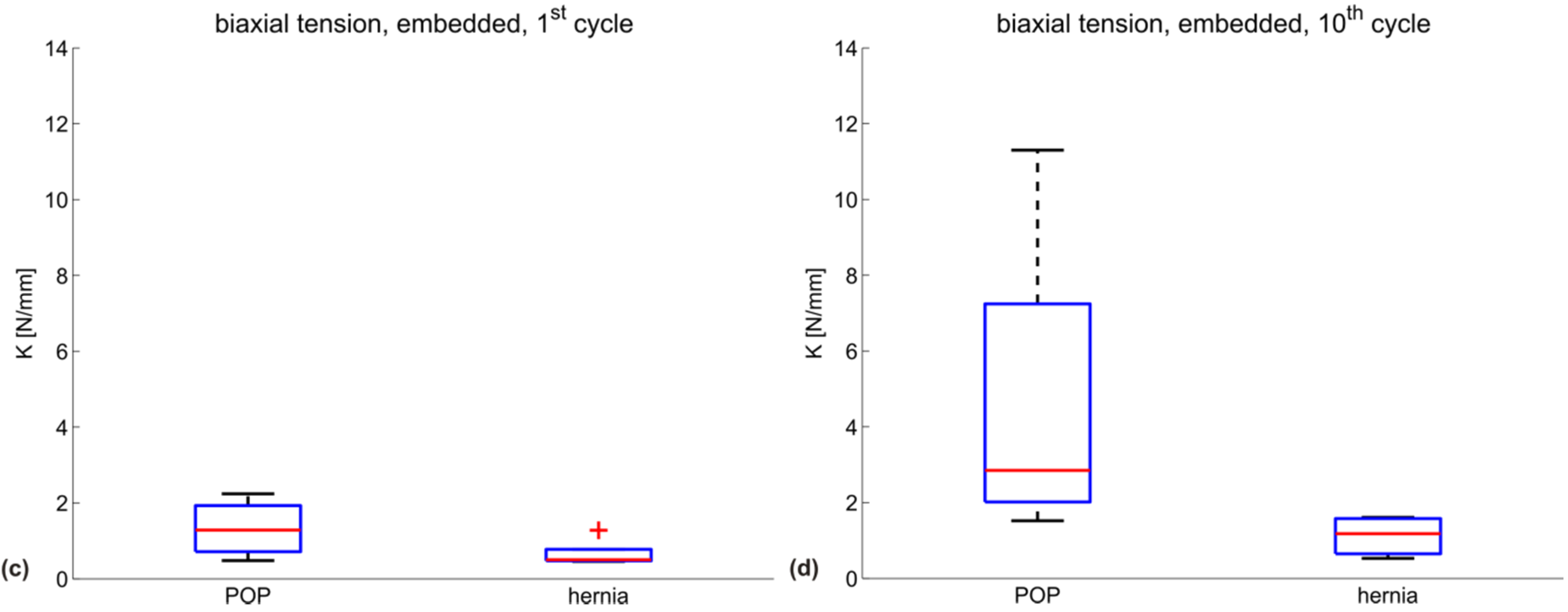
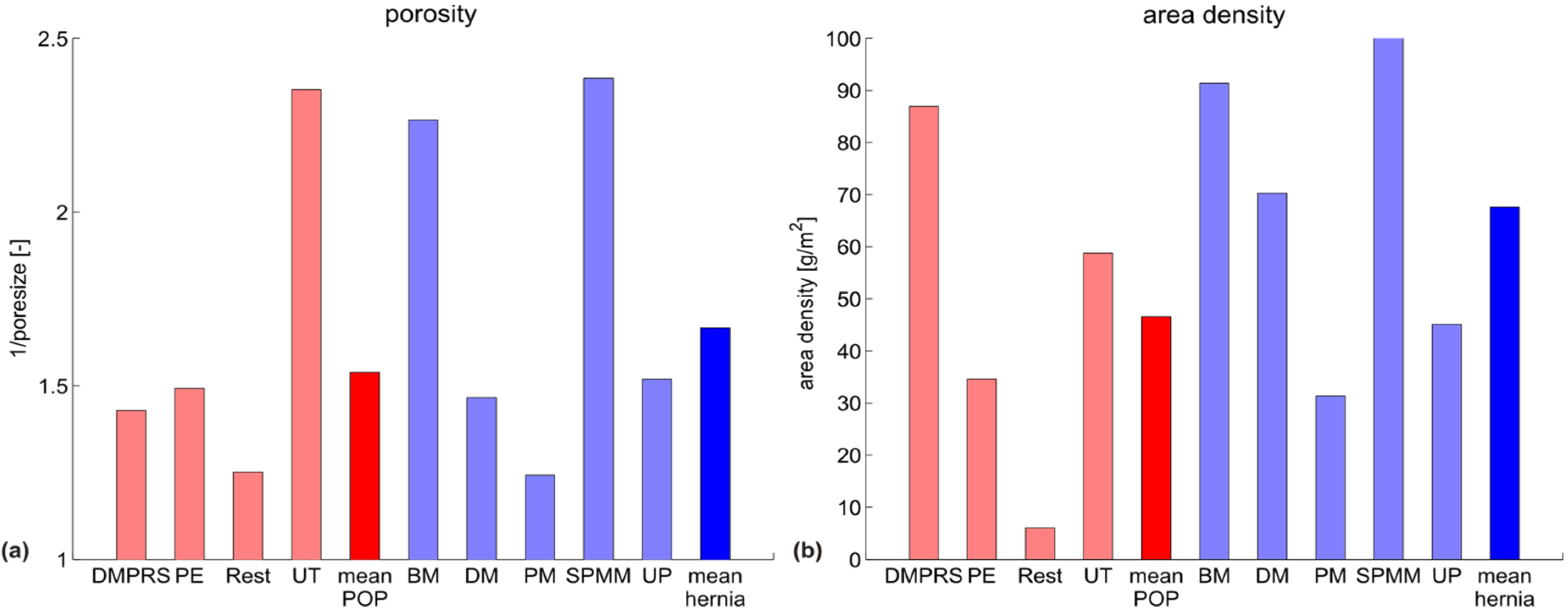
3.2. Discussion

4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Röhrnbauer, B. Mechanical Characterization and Modeling of Prosthetic Meshes; ETH Zurich: Zurich, Switzerland, 2013. [Google Scholar]
- Röhrnbauer, B.; Mazza, E. Uniaxial and biaxial mechanical characterization of a prosthetic mesh at different length scales. J. Mech. Behav. Biomed. Mater. 2014, 29, 7–19. [Google Scholar] [CrossRef] [PubMed]
- Mazza, E.; Ehret, A.E. Mechanical biocompatibility of highly deformable biomedical materials. J. Mech. Behav. Biomed. Mater. 2015, 48, 100–124. [Google Scholar] [CrossRef] [PubMed]
- Liang, R.; Abramowitch, S.; Knight, K.; Palcsey, S.; Nolfi, A.; Feola, A.; Stein, S.; Moalli, P.A. Vaginal degeneration following implantation of synthetic mesh with increased stiffness. BJOG Int. J. Obstet. Gynaecol. 2013, 120, 233–243. [Google Scholar] [CrossRef]
- Mangera, A.; Bullock, A.J.; Chapple, C.R.; Macneil, S. Are biomechanical properties predictive of the success of prostheses used in stress urinary incontinence and pelvic organ prolapse? A systematic review. Neurourol. Urodyn. 2012, 31, 13–21. [Google Scholar] [CrossRef]
- Konerding, M.A.; Chantereau, P.; Delventhal, V.; Holste, J.-L.; Ackermann, M. Biomechanical and histological evaluation of abdominal wall compliance with intraperitoneal onlay mesh implants in rabbits: A comparison of six different state-of-the-art meshes. Med. Eng. Phys. 2012, 34, 806–816. [Google Scholar] [CrossRef] [PubMed]
- Klinge, U.; Conze, J.; Limberg, W.; Brucker, C.; Ottinger, A.P.; Schumpelick, V. Pathophysiology of the abdominal wall. Der Chirurg 1996, 67, 229–233. [Google Scholar]
- Choe, J.M.; Kothandapani, R.; James, L.; Bowling, D. Autologous, cadaveric, and synthetic materials used in sling surgery: Comparative biomechanical analysis. Urology 2001, 58, 482–486. [Google Scholar] [CrossRef] [PubMed]
- Junge, K.; Klinge, U.; Prescher, A.; Giboni, P.; Niewiera, M.; Schumpelick, V. Elasticity of the anterior abdominal wall and impact for reparation of incisional hernias using mesh implants. Hernia 2001, 5, 113–118. [Google Scholar] [CrossRef] [PubMed]
- Cosson, M.; Debodinance, P.; Boukerrou, M.; Chauvet, M.P.; Lobry, P.; Crépin, G.; Ego, A. Mechanical properties of synthetic implants used in the repair of prolapse and urinary incontinence in women: Which is the ideal material? Int. Urogynecol. J. 2003, 14, 169–178. [Google Scholar] [CrossRef]
- Rubod, C.; Boukerrou, M.; Brieu, M.; Jean-Charles, C.; Dubois, P.; Cosson, M. Biomechanical properties of vaginal tissue: Preliminary results. Int. Urogynecol. J. 2008, 19, 811–816. [Google Scholar] [CrossRef]
- Claerhout, F.; Verbist, G.; Verbeken, E.; Konstantinovic, M.; de Ridder, D.; Deprest, J. Fate of collagen-based implants used in pelvic floor surgery: A 2-year follow-up study in a rabbit model. Am. J. Obst. Gyn. 2008, 198, 91–96. [Google Scholar] [CrossRef]
- Jones, K.A.; Feola, A.; Meyn, L.; Abramowitch, S.D.; Moalli, P.A. Tensile properties of commonly used prolapse meshes. Int. Urogynecol. J. 2009, 20, 847–853. [Google Scholar] [CrossRef]
- Ozog, Y.; Konstantinovic, M.L.; Werbrouck, E.; de Ridder, D.; Edoardo, M.; Deprest, J. Shrinkage and biomechanical evaluation of lightweight synthetics in a rabbit model for primary fascial repair. Int. Urogynecol. J. 2011, 22, 1099–1108. [Google Scholar] [CrossRef] [PubMed]
- Fenner, D.E. New surgical mesh. Clin. Obstet. Gynecol. 2000, 43, 650–658. [Google Scholar] [CrossRef] [PubMed]
- Dietz, H.P.; Vancaillie, P.; Svehla, M.; Walsh, W.; Steensma, A.B.; Vancaillie, T.G. Mechanical properties of urogynecologic implant materials. Int. Urogynecol. J. 2003, 14, 239–243. [Google Scholar] [CrossRef]
- Cobb, W.S.; Kercher, K.W.; Heniford, B.T. The argument for lightweight polypropylene mesh in hernia repair. Surg. Innov. 2005, 12, 63–69. [Google Scholar] [CrossRef] [PubMed]
- Feola, A.; Abramowitch, S.; Jallah, Z.; Stein, S.; Barone, W.; Palcsey, S.; Moalli, P. Deterioration in biomechanical properties of the vagina following implantation of a high-stiffness prolapse mesh. BJOG Int. J. Obstet. Gynaecol. 2013, 120, 224–232. [Google Scholar] [CrossRef]
- Lowman, J.K.; Jones, L.A.; Woodman, P.J.; Hale, D.S. Does the prolift system cause dyspareunia? Am. J. Obstet. Gynecol. 2008, 199, 701–706. [Google Scholar] [PubMed]
- Ozog, Y.; Konstantinovic, M.; Werbrouck, E.; de Ridder, D.; Mazza, E.; Deprest, J. Persistence of polypropylene mesh anisotropy after implantation: An experimental study. BJOG Int. J. Obstet. Gynaecol. 2011, 118, 1180–1185. [Google Scholar] [CrossRef]
- FDA Centre for Devices and Radiological Health. Fda safety communication: Update on serious complications associated with transvaginal placement of surgical mesh for pelvic organ prolapse. Avaiable online: http://www.fda.gov/medicaldevices/safety/alertsandnotices/ucm262435.htm (accessed on 23 March 2015).
- Maurer, M.M.; Roehrnbauer, B.; Feola, A.; Deprest, J.; Mazza, E. Mechanical biocompatibility of prosthetic meshes: A comprehensive protocol for mechanical characterization. J. Mech. Behav. Biomed. Mater. 2014, 40, 42–58. [Google Scholar] [CrossRef] [PubMed]
- Ozog, Y.; Deprest, J.; Haest, K.; Claus, F.; de Ridder, D.; Mazza, E. Calculation of membrane tension in selected sections of the pelvic floor. Int. Urogynecol. J. 2014, 25, 499–506. [Google Scholar] [CrossRef] [PubMed]
- Coda, A.; Lamberti, R.; Martorana, S. Classification of prosthetics used in hernia repair based on weight and biomaterial. Hernia J. Hernias Abdom. Wall Surg. 2012, 16, 9–20. [Google Scholar] [CrossRef]
- Farine, M. Instrumented Indentation of Soft Materials And Biological Tissues; ETH Zurich: Zurich, Switzerland, 2013. [Google Scholar]
- Hollenstein, M.; Ehret, A.E.; Itskov, M.; Mazza, E. A novel experimental procedure based on pure shear testing of dermatome-cut samples applied to porcine skin. Biomech. Modeling Mechanobiol. 2011, 10, 651–661. [Google Scholar] [CrossRef]
- Chu, C.C.; Welch, L. Characterization of morphologic and mechanical properties of surgical mesh fabrics. J. Biomed. Mater. Res. 1985, 19, 903–916. [Google Scholar] [CrossRef] [PubMed]
- Pourdeyhimi, B. Porosity of surgical mesh fabrics: New technology. J. Biomed. Mater. Res. 1989, 23, 145–152. [Google Scholar] [CrossRef] [PubMed]
- Peña, E.; Calvo, B.; Martínez, M.A.; Martins, P.; Mascarenhas, T.; Jorge, R.M.N.; Ferreira, A.; Doblaré, M. Experimental study and constitutive modeling of the viscoelastic mechanical properties of the human prolapsed vaginal tissue. Biomech. Modeling Mechanobiol. 2010, 9, 35–44. [Google Scholar] [CrossRef]
- Klinge, U.; Klosterhalfen, B.; Birkenhauer, V.; Junge, K.; Conze, J.; Schumpelick, V. Impact of polymer pore size on the interface scar formation in a rat model. J. Surg. Res. 2002, 103, 208–214. [Google Scholar] [CrossRef] [PubMed]
- Klosterhalfen, B.; Junge, K.; Klinge, U. The lightweight and large porous mesh concept for hernia repair. Expert Rev. Med. Devices 2005, 2, 103–117. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Alijani, A.; Frank, T.; Hanna, G.B.; Cuschieri, A. Mechanical properties of the human abdominal wall measured in vivo during insufflation for laparoscopic surgery. Surg. Endosc. 2006, 20, 987–990. [Google Scholar] [CrossRef] [PubMed]
- Gabriel, B.; Rubod, C.; Brieu, M.; Dedet, B.; de Landsheere, L.; Delmas, V.; Cosson, M. Vagina, abdominal skin, and aponeurosis: Do they have similar biomechanical properties? Int. Urogynecol. J. 2011, 22, 23–27. [Google Scholar] [CrossRef] [PubMed]
- Hernandez, B.; Pena, E.; Pascual, G.; Rodriguez, M.; Calvo, B.; Doblare, M.; Bellon, J.M. Mechanical and histological characterization of the abdominal muscle. A previous step to modelling hernia surgery. J. Mech. Behav. Biomed. Mater. 2011, 4, 392–404. [Google Scholar] [CrossRef]
- Rohrnbauer, B.; Ozog, Y.; Egger, J.; Werbrouck, E.; Deprest, J.; Mazza, E. Combined biaxial and uniaxial mechanical characterization of prosthetic meshes in a rabbit model. J. Biomech. 2013, 46, 1626–1632. [Google Scholar] [CrossRef] [PubMed]
- Feola, A.; Barone, W.; Moalli, P.; Abramowitch, S. Characterizing the ex vivo textile and structural properties of synthetic prolapse mesh products. Int. Urogynecol. J. 2013, 24, 559–564. [Google Scholar] [CrossRef] [PubMed]
- Shepherd, J.P.; Feola, A.J.; Abramowitch, S.D.; Moalli, P.A. Uniaxial biomechanical properties of seven different vaginally implanted meshes for pelvic organ prolapse. Int. Urogynecol. J. 2012, 23, 613–620. [Google Scholar] [CrossRef] [PubMed]
- Edwards, S.L.; Werkmeister, J.A.; Rosamilia, A.; Ramshaw, J.A.M.; White, J.F.; Gargett, C.E. Characterisation of clinical and newly fabricated meshes for pelvic organ prolapse repair. J. Mech. Behav. Biomed. Mater. 2013, 23, 53–61. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maurer, M.M.; Röhrnbauer, B.; Feola, A.; Deprest, J.; Mazza, E. Prosthetic Meshes for Repair of Hernia and Pelvic Organ Prolapse: Comparison of Biomechanical Properties. Materials 2015, 8, 2794-2808. https://doi.org/10.3390/ma8052794
Maurer MM, Röhrnbauer B, Feola A, Deprest J, Mazza E. Prosthetic Meshes for Repair of Hernia and Pelvic Organ Prolapse: Comparison of Biomechanical Properties. Materials. 2015; 8(5):2794-2808. https://doi.org/10.3390/ma8052794
Chicago/Turabian StyleMaurer, Manfred M., Barbara Röhrnbauer, Andrew Feola, Jan Deprest, and Edoardo Mazza. 2015. "Prosthetic Meshes for Repair of Hernia and Pelvic Organ Prolapse: Comparison of Biomechanical Properties" Materials 8, no. 5: 2794-2808. https://doi.org/10.3390/ma8052794
APA StyleMaurer, M. M., Röhrnbauer, B., Feola, A., Deprest, J., & Mazza, E. (2015). Prosthetic Meshes for Repair of Hernia and Pelvic Organ Prolapse: Comparison of Biomechanical Properties. Materials, 8(5), 2794-2808. https://doi.org/10.3390/ma8052794





