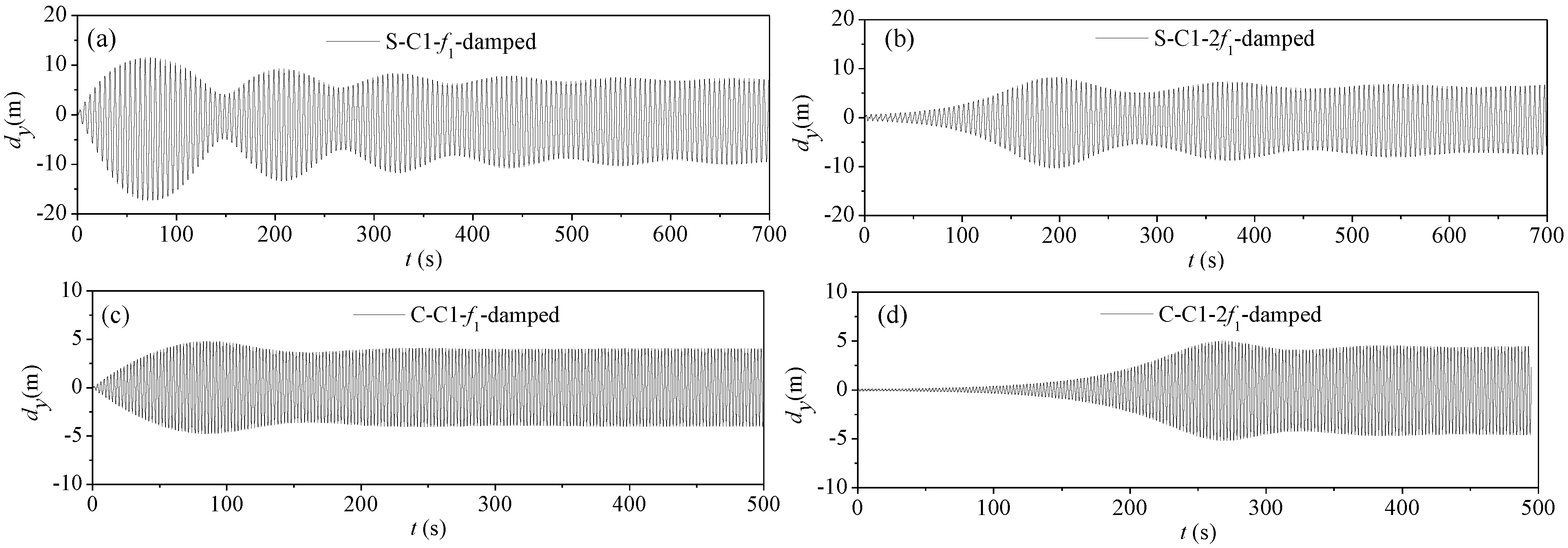
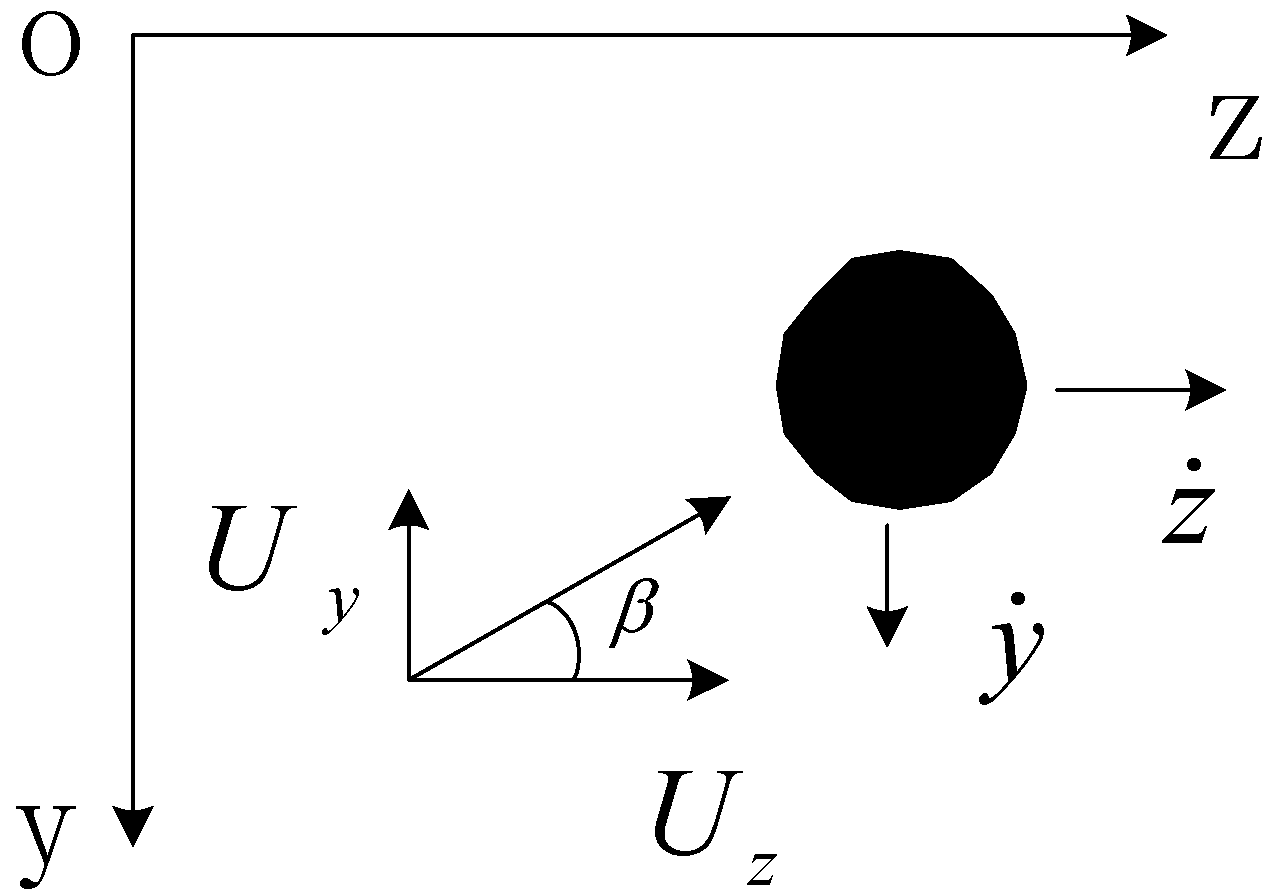
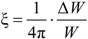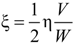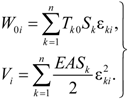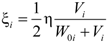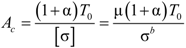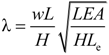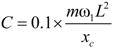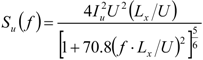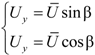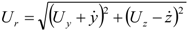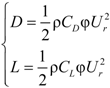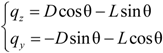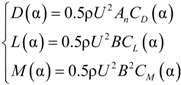2.1. Material Properties of CFRP Cables
At present, there is no uniform production standard for CFRP cables, so the material parameters of CFRP cables produced by different manufacturers differ considerably.
Table 1 shows the material properties of four types of CFRP cables, marked as A, B, C and D. In the table, γ,
E, σ
u, ε
u,
Re and ρ represent the unit weight, Young’s modulus, tensile strength, ultimate strain, relaxation ratio for 1000 h and linear expansion coefficient, respectively. It was here observed that the material characteristics of CFRP cables produced by different manufacturers are typically similar. The Young’s modulus is about 140 GPa, which is about 70% of steel cables. The tensile strength is 2.02–2.55 GPa, which is 1.3–1.6 times that of high-strength steel cables. The linear expansion coefficient is 0.6 × 10
−6/°C, and the temperature deformation is only 1/20 that of steel cables. The unit weight is 1/5 that of steel cables, and the relaxation rate is lower than that of steel cables. In addition, the ultimate strain of CFRP cable is so small that the stress-strain curve remains mostly linear before fissure, which indicates that CFRP cables are brittle.
Table 1.
Material properties of CFRP and steel cables.
Table 1.
Material properties of CFRP and steel cables.
| Cable types | γ (kN/mm3) | σu (MPa) | E (GPa) | σu /E | Re (%) | εu (%) | al (×10−6/°C) |
|---|
| A | 16 | 2,140 | 137 | 0.016 | 0.3 | 1.6 | 0.6 |
| B | 16 | 2,550 | 147 | 0.017 | 0.3 | 1.6 | 0.68 |
| C | 16 | 2,022 | 137 | 0.015 | 0.3 | 2 | 0.6 |
| D | 16 | 2,421 | 159 | 0.015 | 0.3 | 1.7 | 0.6 |
| steel | 77 | 1,570 | 196 | 0.008 | <2.5 | >4 | 12 |
2.2. Damping Properties of CFRP Cables
Cable damping is mainly associated with energy dissipation caused by material strain and air friction. There is so little air damping that it can usually be ignored during calculation. This paper focuses on the material damping characteristics of CFRP cables. According to the strain energy proportional damping theory of a single-degree-of-freedom vibration system, the damping ratio ξ can be calculated using the following expression:
Here, Δ
W is the energy absorbed due to the strain deformation during the vibration cycle, and
W is the modal potential energy. Assuming Δ
W is proportional to the strain energy Δ
W∝
V, replacing the proportionality sign with a constant [
20,
21,
22]:
Here, η is the energy loss factor, and
V is the strain energy. Substitution of the equation above into Equation (1) produces the following:
Because there is a large initial tension
T0 in the cable, therefore the modal potential energy
W of Formula (3) includes two parts, initial tension potential energy
W0 and strain energy
V, hence:
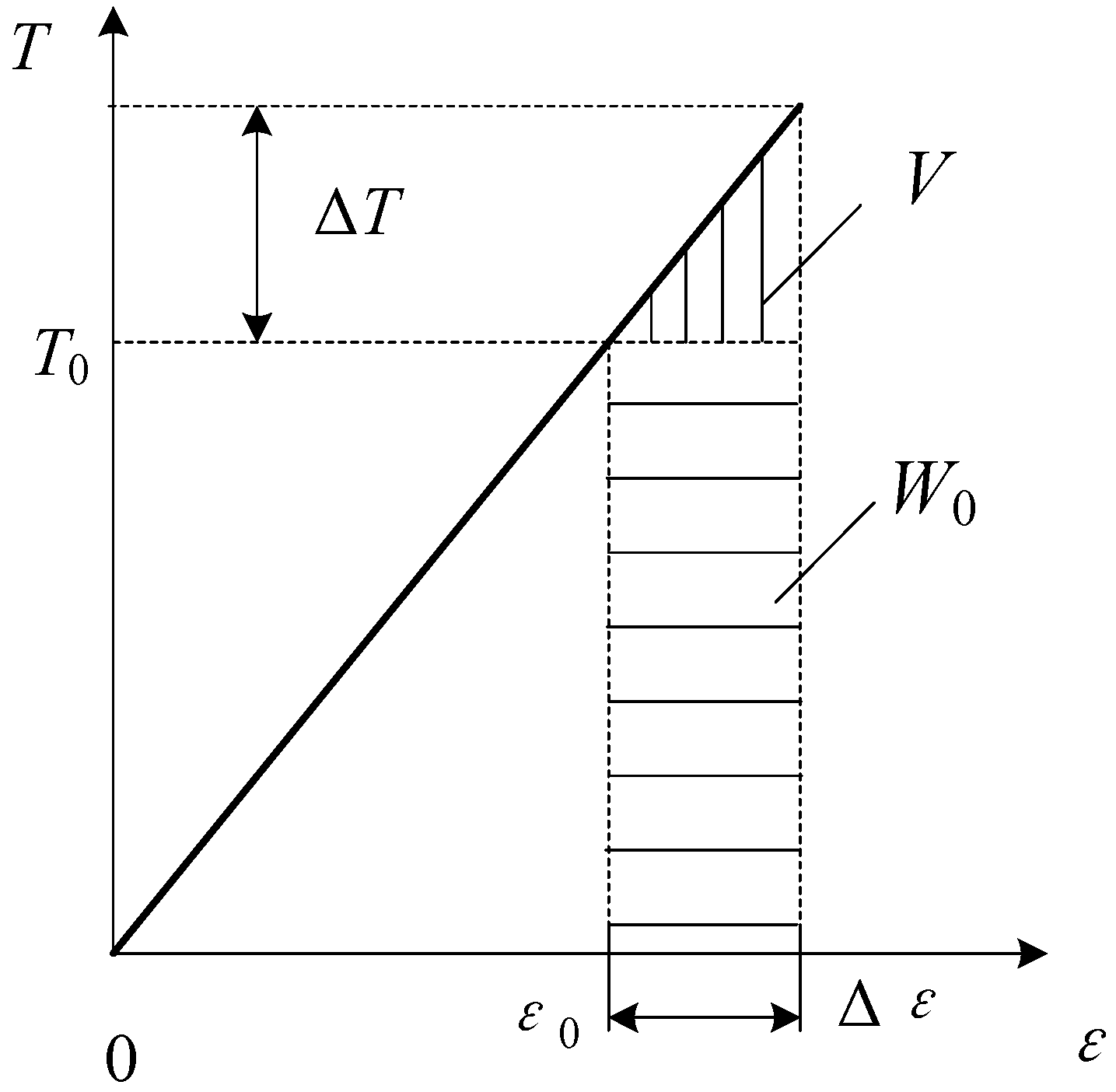
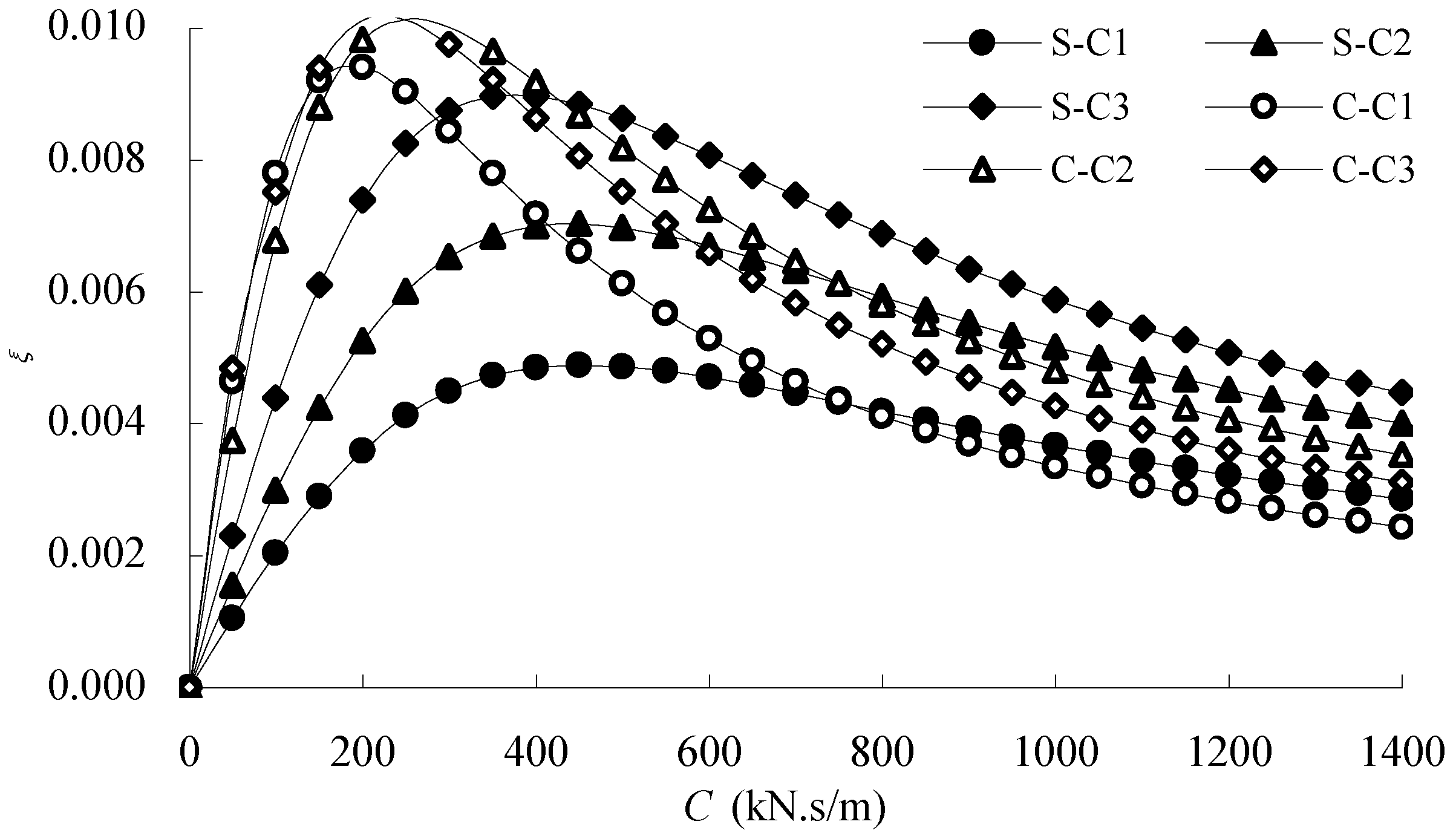
Because the flexible cable only bears axial tension, as indicated by the relationship of strain and tension shown in
Figure 1, the initial potential energy due to tension,
W0 and strain energy
V can be calculated as follows:
Figure 1.
Potential energy and strain energy in initial tension.
Figure 1.
Potential energy and strain energy in initial tension.
Here, ε
ki and
Sk are the strain and length of element
k generated by the
i-th vibration mode.
Tk0 is the initial tension in element
k, and
n is the total number of cable elements. Substitution of Equations (4) and (5) into (1) results in the following expression:
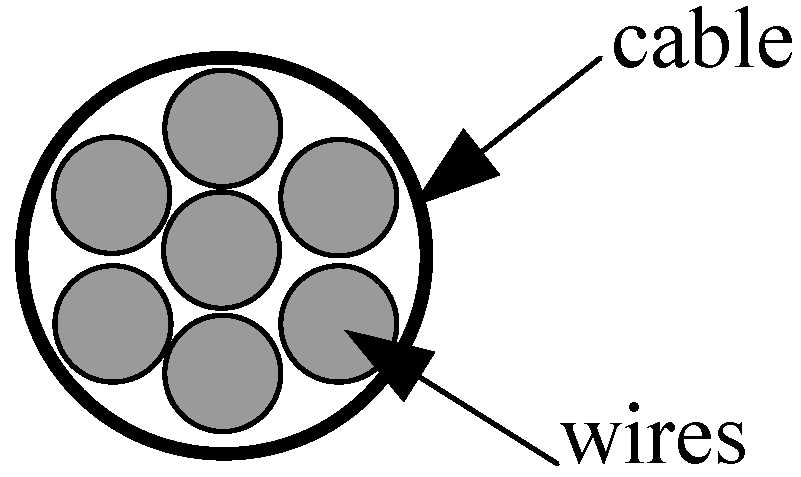
In order to compare the damping characteristics of steel and CFRP cables, a cable vibration test was carried out in Tokyo Metropolitan University [
22]. The test steel and CFRP cables were made at Rope Corporation Tokyo, Japan, wherein the steel cable, PCS
ϕ12.7 (
ϕ refers to diameter of the cable), was composed of seven 5.16-mm diameter steel wires, PCS
ϕ5.16, and the CFRP cable, CFCC
ϕ12.5, was composed of seven 5.0 mm-diameter CFRP wires, CFCC
ϕ5.0 (
Figure 2).
Table 2 lists the material parameters of cables and wires.
E,
w,
D,
A and σ
u represent Young’s modulus, the unit weight, the diameter, the cross-sectional area and the tensile strength of cables and wires, respectively.
Figure 2.
Cross-section of cable CFCCϕ12.5.
Figure 2.
Cross-section of cable CFCCϕ12.5.
Table 2.
Material properties of cables and wires.
Table 2.
Material properties of cables and wires.
| Cable and Wire Type | E (GPa) | w (g/m) | D (mm) | A (mm2) | σu (MPa) |
|---|
| CFCCϕ12.5 | 159 | 145 | 12.50 | 76.0 | 2,421 |
| PCSϕ12.7 | 197 | 774 | 12.70 | 98.7 | 1,854 |
| CFCCϕ5.0 | 152 | 29.9 | 5.00 | 15.2 | 2,980 |
| PCSϕ5.16 | 204 | 163.8 | 5.16 | 20.9 | 1,999 |
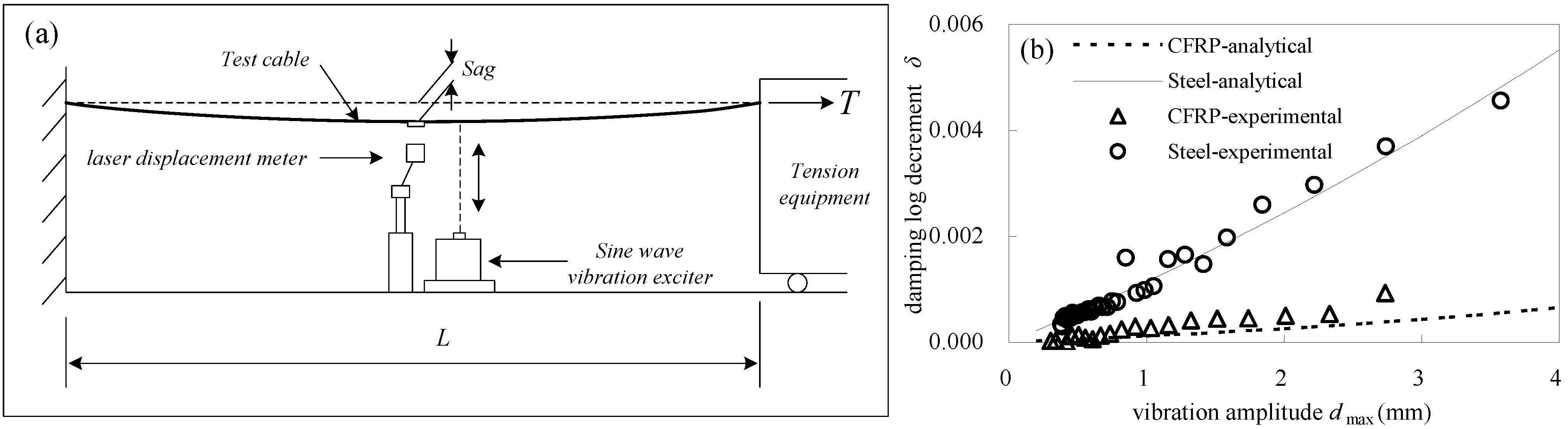
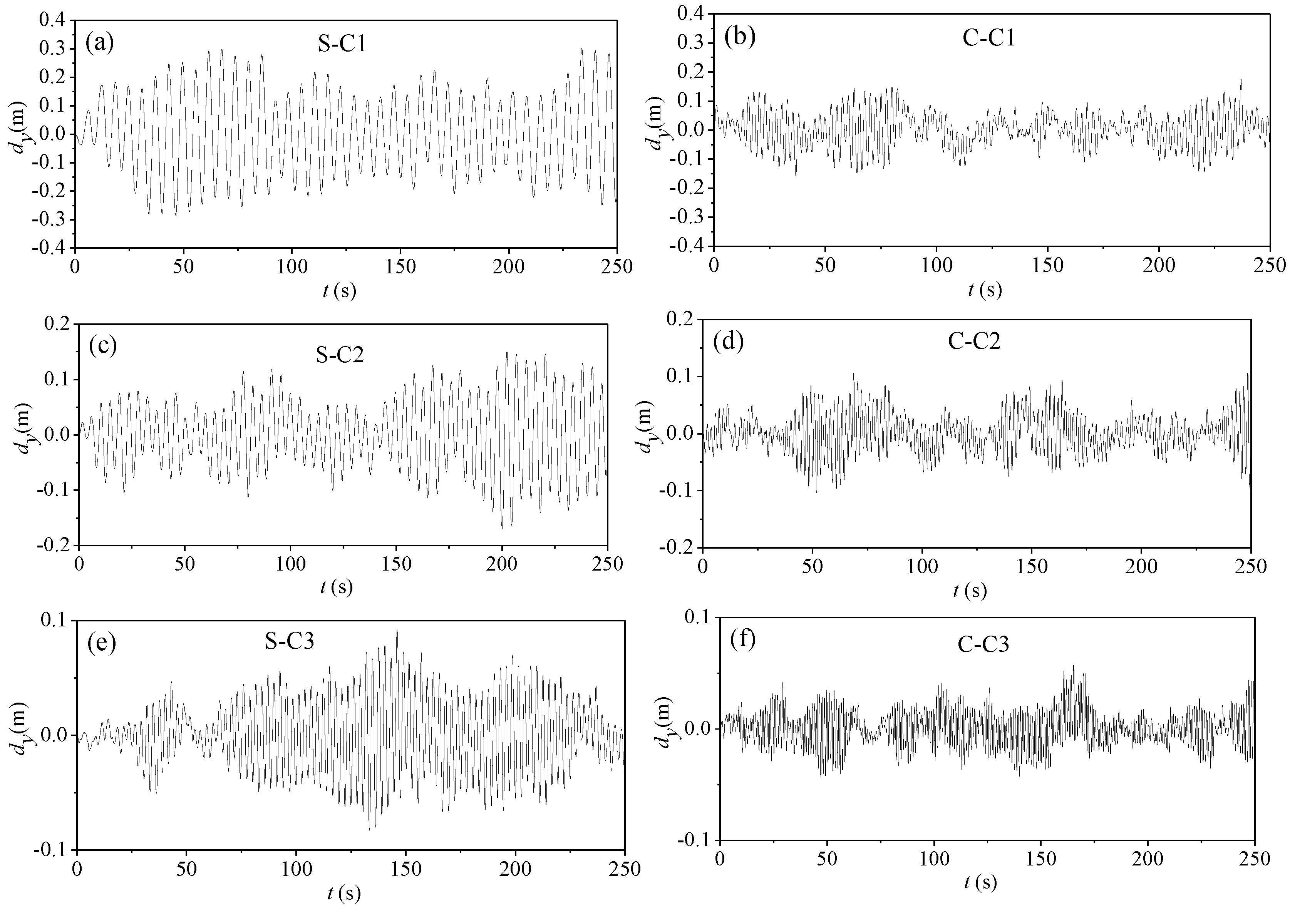
Figure 3a,b provides details of the cable damping test equipment. The test cable was 20 m-long with an initial tension of 30 kN. The resulting initial stresses in CFRP cables and steel cables were 395 and 304 MPa, respectively, which were equal to half of the service stresses. Here, the design safety factor of the test cable was 2.5. Continuous excitation force was applied at the midpoint of the cable to render the vibrations stable. Once the excitation force ceased, the cable entered free decay vibration, which was measured by a non-contact laser displacement meter at a sampling rate of 500 Hz.
Figure 3b shows the relationship between the cable damping and vibration amplitude. It can be found that, for steel and CFRP cables, damping increases with vibration amplitude, but the trend was more obvious for steel cables than CFRP cables. This indicted that the influence of vibration amplitude on cable damping is not as pronounced for CFRP cable as it is for the steel cable. In addition, the energy loss factor of cables shown in Equation (3) can be calculated from
Figure 3b. Here, the damping constant was 0.05 for both steel and CFRP cables, consistent with the test results reported by Kady
et al. [
23].
Figure 3.
(a) Cabledamping test; (b) cable damping log decrement vs. vibration amplitude.
Figure 3.
(a) Cabledamping test; (b) cable damping log decrement vs. vibration amplitude.
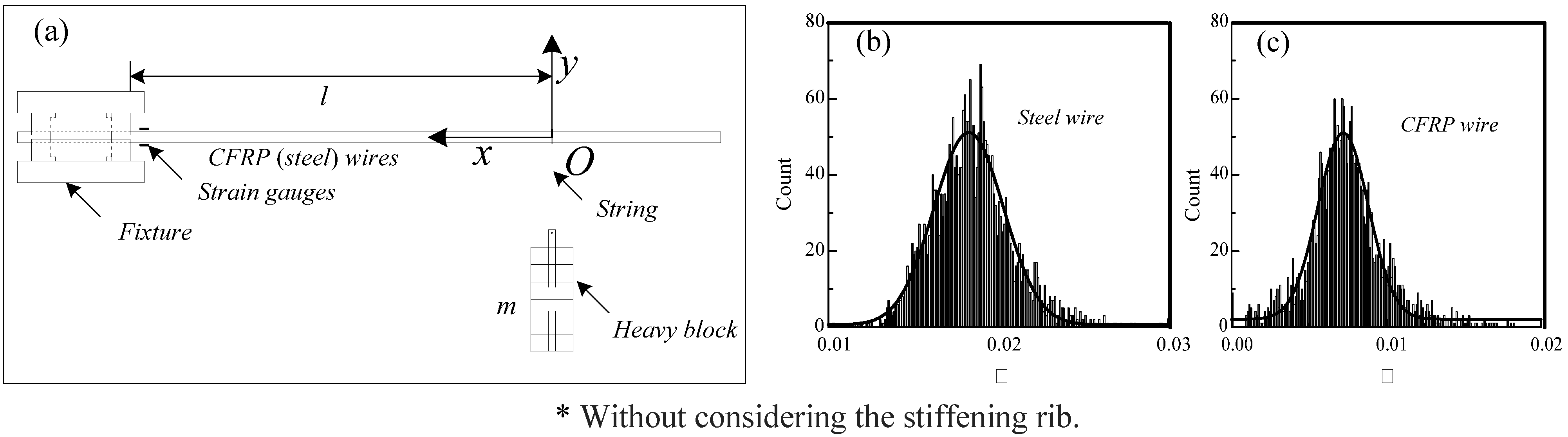
In order to determine the energy loss factors of wires comprising the cables, the bending deformation experiment of steel and CFRP wires under free vibration was conducted (
Figure 4a. A heavy block was hung on by a string on the fixed test wire at a distance of
l from the fixed end. An initial imposed displacement was used to place the wire in decay free vibration. The strain readings were recorded by the dynamic strain gauges fixed on the wire, at a sampling of 500 Hz. During the test, the distance
l and the mass of the heavy block were varied multiple times to obtain additional experimental data.
Figure 4.
(a) Bending deformation experiments of steel and CFRP wires; (b) distribution of energy loss coefficient for steel wires; (c) distribution of energy loss coefficient for CFRP wires.
Figure 4.
(a) Bending deformation experiments of steel and CFRP wires; (b) distribution of energy loss coefficient for steel wires; (c) distribution of energy loss coefficient for CFRP wires.
Figure 4b shows the distribution results of energy loss factors for steel and CFRP wires. As shown, the average energy loss factors for steel and CFRP wires are about 0.018 and 0.008, respectively, which is much smaller than the damping constant of steel and CFRP cables, 0.05. This indicates that the damping of the material strain ratio is only a part of the total cable damping, and other damping is relative to the friction among the wires of the cable.