Mechanical and Electrical Characterization of Entangled Networks of Carbon Nanofibers
Abstract
:1. Introduction
2. Experimental Section
2.1. Carbon Nanofiber Synthesis

2.2. Mechanical and Electrical Characterization Setups
3. Mechanical Properties
3.1. Tensile Tests
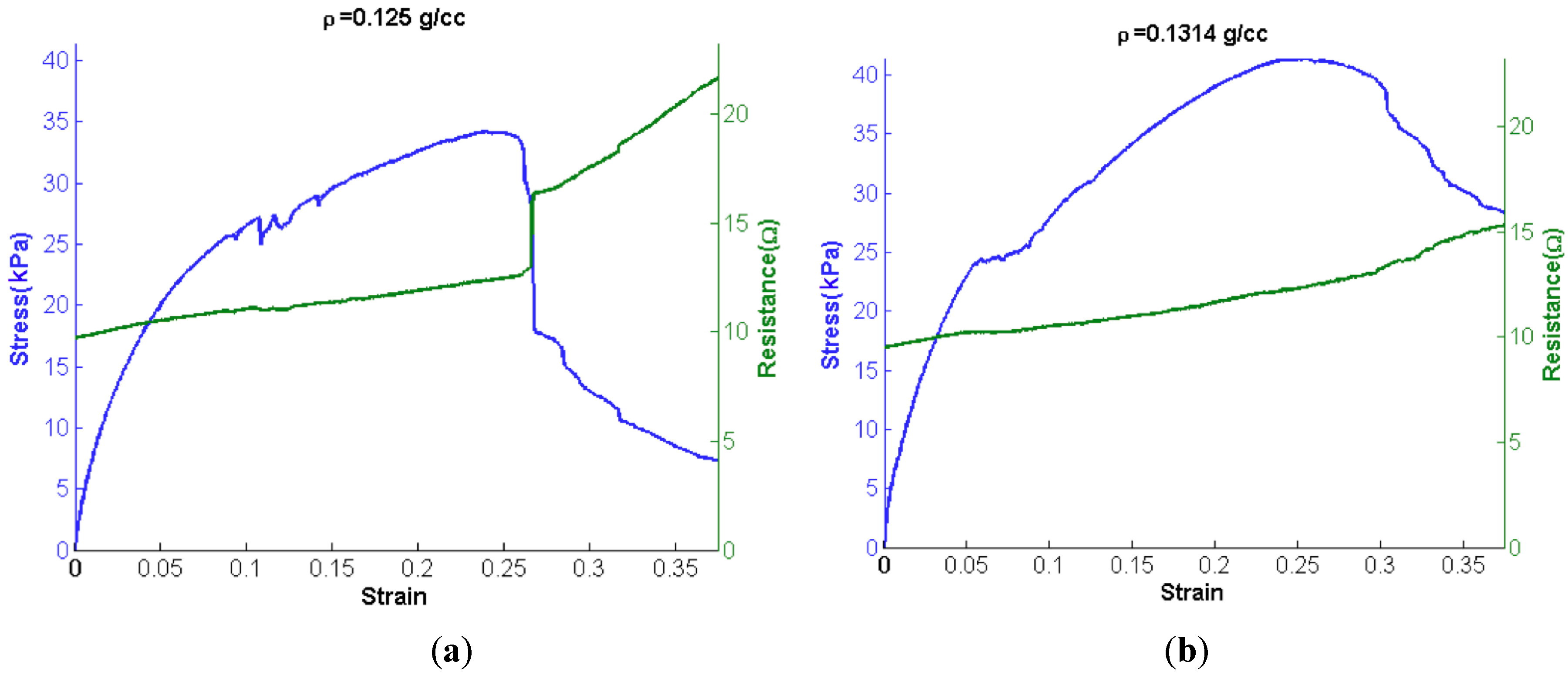
| ρ (g/cm3) | E(kPa) | σv (kPa) | σu (kPa) | Linear range Percentage (% of σu) |
|---|---|---|---|---|
| 0.125 | 600 | 13.4 | 34.2 | 39.2% |
| 0.131 | 627 | 16.9 | 41.3 | 40.8% |
3.2. Compression Tests
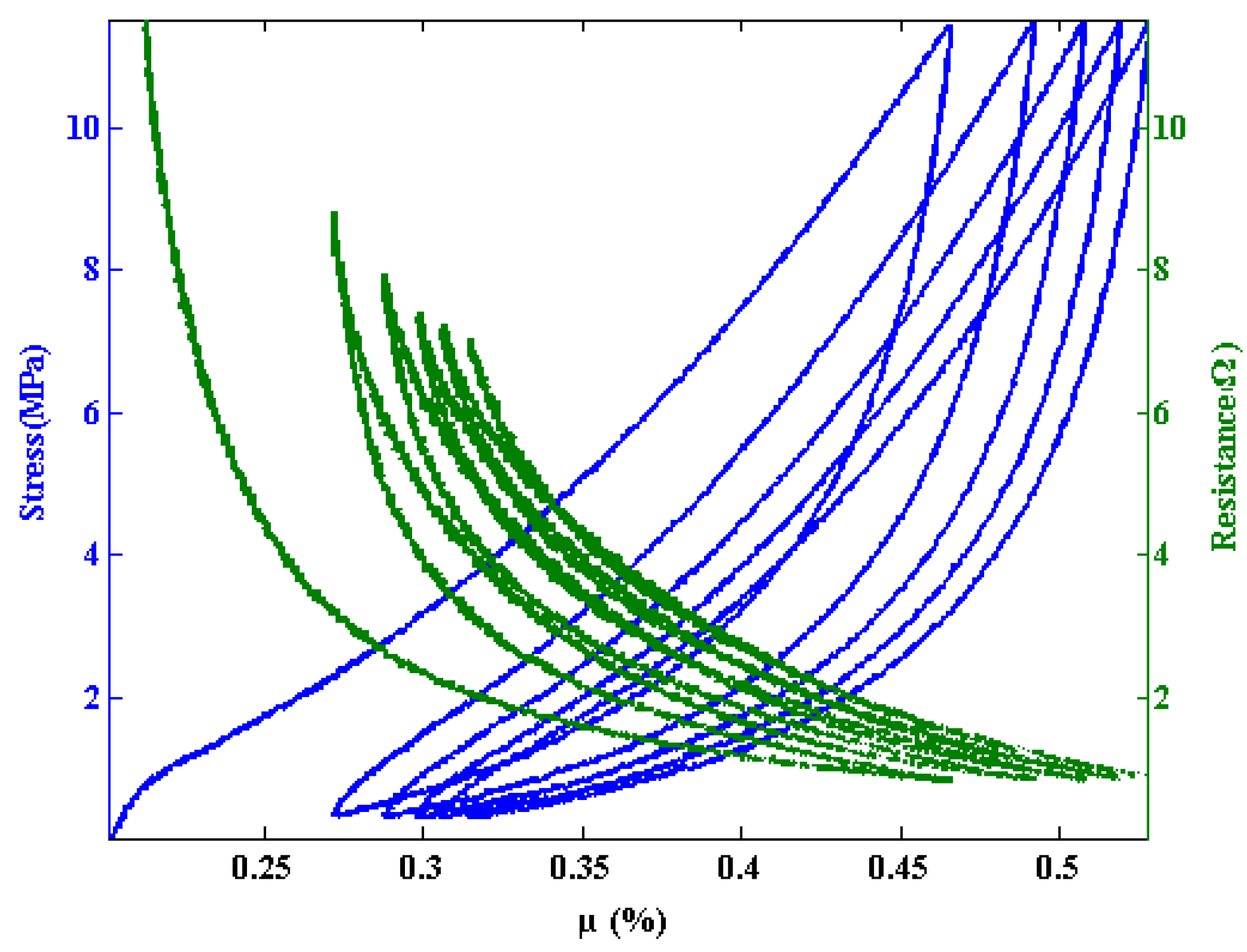
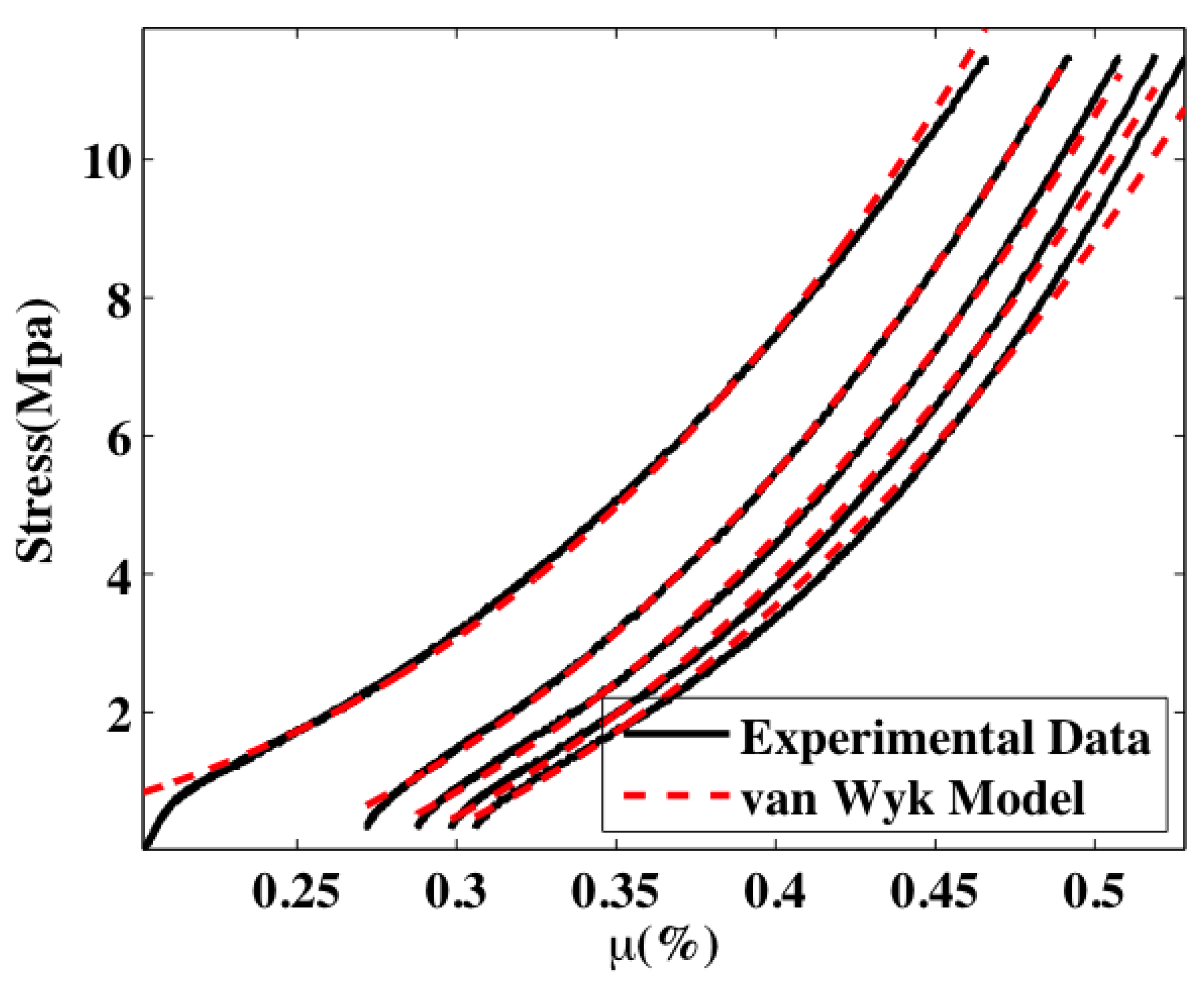
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Bachtold, A.; Hadley, P.; Nakanishi, T.; Dekker, C. Logic circuits with carbon nanotube transistors. Science 2001, 294, 1317–1320. [Google Scholar] [CrossRef]
- Baughman, R.H.; Zakhidov, A.A.; de Heer, W.A. Carbon nanotubes--The route toward applications. Science 2002, 297. [Google Scholar] [CrossRef]
- Allaoui, A.; Toll, S.; Evesque, P.; Bai, J. On the compressive response of carbon nanotube tangles. Phys. Lett. A 2009, 373, 3169–3173. [Google Scholar] [CrossRef]
- Thostenson, E.T.; Chou, T.-W. Carbon nanotube networks: Sensing of distributed strain and damage for life prediction and self healing. Adv. Mater. 2006, 18, 2837–2841. [Google Scholar] [CrossRef]
- Rahatekar, S.S.; Koziol, K.K.; Kline, S.R.; Hobbie, E.K.; Gilman, J.W.; Windle, A.H. Length-dependent mechanics of carbon-nanotube networks. Adv. Mater. 2009, 21, 874–878. [Google Scholar] [CrossRef]
- Skandani, A.A.; Masghouni, N.; Case, S.W.; Leo, D.J.; Al-Haik, M. Enhanced vibration damping of carbon fibers-ZnO nanorods hybrid composites. Appl. Phys. Lett. 2012, 101. [Google Scholar] [CrossRef]
- Bryning, M.B.; Islam, M.F.; Kikkawa, J.M.; Yodh, A.G. Very low conductivity threshold in bulk isotropic single-walled carbon nanotube-epoxy composites. Adv. Mater. 2005, 17, 1186–1191. [Google Scholar]
- Li, W.; Zhang, H.; Xiong, X. Properties of multi-walled carbon nanotube reinforced carbon foam composites. J. Mater. Sci. 2011, 46, 1143–1146. [Google Scholar]
- Tehrani, M.; Luhrs, C.C.; Al-Haik, M.S.; Trevino, J.; Zea, H. Synthesis of WS2 nanostructures from the reaction of WO3 with CS2 and mechanical characterization of WS2 nanotube composites. Nanotechnology 2011, 22. [Google Scholar] [CrossRef]
- Atwater, M.A.; Mousavi, A.K.; Leseman, Z.C.; Phillips, J. Direct synthesis and characterization of a nonwoven structure comprised of carbon nanofibers. Carbon N.Y. 2013, 57, 363–370. [Google Scholar] [CrossRef]
- Atwater, M.A.; Phillips, J.; Doorn, S.K.; Luhrs, C.C.; Fernández, Y.; Menéndez, J.A.; Leseman, Z.C. The production of carbon nanofibers and thin films on palladium catalysts from ethylene–oxygen mixtures. Carbon N.Y. 2009, 47, 2269–2280. [Google Scholar]
- Atwater, M.; Leseman, Z.C.; Phillips, J. Controlling carbon nanofibres morphology for improved composite reinforcement. Int. J. Mater. Struct. Integr. 2009, 3, 179–186. [Google Scholar] [CrossRef]
- Van Wyk, C.M. A study of the compressibility of wool, with special reference to South African merino wool. Onderstepoort J. Vet. Sci. Anim. Ind. 1946, 21, 99–226. [Google Scholar]
- Lundquist, L.; Willi, F.; Leterrier, Y.; Månson, J.E. Compression behavior of pulp fiber networks. 2004, 44, 45–55. [Google Scholar]
- Robitaille, F.; Gauvin, R. Compaction of textile reinforcements for composites manufacturing. III: Reorganization of the fiber network. Polym. Compos 1999, 20, 48–61. [Google Scholar] [CrossRef]
- Rodney, D.; Fivel, M.; Dendievel, R. Discrete modeling of the mechanics of entangled materials. Phys. Rev. Lett. 2005, 95. [Google Scholar] [CrossRef]
- Mousavi, A.K.; Kashamolla, M.R.; Leseman, Z.C. Improved model for the adhesion of μcantilevers: Theory and experiments. J. Micromech. Microeng. 2013, 23. [Google Scholar] [CrossRef]
- Leseman, Z.C.; Carlson, S.P.; Mackin, T.J. Experimental measurements of the strain energy release rate for stiction-failed microcantilevers using a single-cantilever beam peel test. J. Microelectromech. Syst. 2007, 16, 38–43. [Google Scholar] [CrossRef]
- De Boer, M.P.; Michalske, T.A. Accurate method for determining adhesion of cantilever beams. J. Appl. Phys. 1999, 86, 817–827. [Google Scholar] [CrossRef]
- Subramanian, G.; Picu, C.R. Mechanics of three-dimensional, nonbonded random fiber networks. Phys. Rev. E 2011, 83. [Google Scholar] [CrossRef]
- Serway, R.A.; Jewett, J.W. Principles of Physics, 2nd ed.; Saunders College Pub: Philadelphia, PA, USA, 1998. [Google Scholar]
- Pauleau, Y.; Barna, P.B.; Barna, P.B. Protective Coatings and Thin Films: Synthesis,Characterization,and Applications; Springer: Alvor, Portugal, 1997. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Mousavi, A.K.; Atwater, M.A.; Mousavi, B.K.; Jalalpour, M.; Taha, M.R.; Leseman, Z.C. Mechanical and Electrical Characterization of Entangled Networks of Carbon Nanofibers. Materials 2014, 7, 4845-4853. https://doi.org/10.3390/ma7064845
Mousavi AK, Atwater MA, Mousavi BK, Jalalpour M, Taha MR, Leseman ZC. Mechanical and Electrical Characterization of Entangled Networks of Carbon Nanofibers. Materials. 2014; 7(6):4845-4853. https://doi.org/10.3390/ma7064845
Chicago/Turabian StyleMousavi, Arash K., Mark A. Atwater, Behnam K. Mousavi, Mohammad Jalalpour, Mahmoud Reda Taha, and Zayd C. Leseman. 2014. "Mechanical and Electrical Characterization of Entangled Networks of Carbon Nanofibers" Materials 7, no. 6: 4845-4853. https://doi.org/10.3390/ma7064845
APA StyleMousavi, A. K., Atwater, M. A., Mousavi, B. K., Jalalpour, M., Taha, M. R., & Leseman, Z. C. (2014). Mechanical and Electrical Characterization of Entangled Networks of Carbon Nanofibers. Materials, 7(6), 4845-4853. https://doi.org/10.3390/ma7064845






